Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 Dec 1.
Published in final edited form as: Magn Reson Imaging. 2018 Sep 5;54:241–248. doi: 10.1016/j.mri.2018.09.002

Exploring the sensitivity of magnetic resonance fingerprinting to motion.

Zidan Yu 1,2,3, Tiejun Zhao 2,4, Jakob Assländer 1,2, Riccardo Lattanzi 1,2,3, Daniel K Sodickson 1,2,3, Martijn A Cloos 1,2,3
PMCID: PMC6215476  NIHMSID: NIHMS1506446  PMID: 30193953

Abstract

Purpose:

To explore the motion sensitivity of magnetic resonance fingerprinting (MRF), we performed experiments with different types of motion at various time intervals during multiple scans. Additionally, we investigated the possibility to correct the motion artifacts based on redundancy in MRF data.

Methods:

A radial version of the FISP-MRF sequence was used to acquire one transverse slice through the brain. Three subjects were instructed to move in different patterns (in-plane rotation, through-plane wiggle, complex movements, adjust head position, and pretend itch) during different time intervals. The potential to correct motion artifacts in MRF by removing motion-corrupted data points from the fingerprints and dictionary was evaluated.

Results:

Morphological structures were well preserved in multi-parametric maps despite subject motion. Although the bulk T1 values were not significantly affected by motion, fine structures were blurred when in-plane motion was present during the first part of the scan. On the other hand, T2 values showed a considerable deviation from the motion-free results, especially when through-plane motion was present in the middle of the scan (−44% on average). Explicitly removing the motion-corrupted data from the scan partially restored the T2 values (−10% on average).

Conclusion:

Our experimental results showed that different kinds of motion have distinct effects on the precision and effective resolution of the parametric maps measured with MRF. Although MRF-based acquisitions can be relatively robust to motion effects occurring at the beginning or end of the sequence, relying on redundancy in the data alone is not sufficient to assure the accuracy of the multi-parametric maps in all cases.

Keywords: Magnetic Resonance Fingerprinting, MRI, Motion, Quantitative Imaging

1. Introduction

Motion is one of the most common causes of artifacts in clinical magnetic resonance imaging (MRI). In conventional MRI, the k-space data are usually acquired line by line. When there is physiologic motion, or the subject moves between successive readouts, an inconsistency is introduced that can lead to ghosting artifacts [1]. Over the years many approaches have been proposed to make MRI more motion robust [2]. These techniques can roughly be divided into five categories: (1) fast imaging techniques that strive to “freeze” the motion [3,4]; (2) gating/triggering which monitors motion-related information (e.g. detecting the R-wave on an electrocardiogram) to identify the time window with minimal motion [5,6]; (3) sample averaging strategies which strive to overcome motion artifacts by repeatedly sampling the central k-space area [7, 8, 9]; (4) retrospective motion correction methods designed to mitigate motion artifacts using advanced reconstruction algorithms [9,10,11]; and (5) prospective motion methods which strive to update the gradients and radiofrequency waveforms in real time to compensate for subject motion [12,13,14].

It has been suggested that Magnetic resonance fingerprinting (MRF), a recently proposed quantitative imaging technique, may have some inherent motion robustness [15]. Compared to most traditional quantitative imaging techniques, MRF emphases a dense sampling of the spin dynamics at the expense of a reduced k-space sampling per measurement point. In other words, instead of striving to create a small series of artifact-free images, MRF attempts to capture the signal evolution with a large series of crudely sampled snap-shots. This measured signal evolution, called MR “fingerprint”, is then compared to a pre-computed dictionary of all possible signal evolutions to simultaneously extract the underlying longitudinal relaxation time (T1), transverse relaxation time (T2), and proton density (PD). It has been suggested that the MRF dictionary matching process can also provide some motion robustness. The idea is that the corrupted data will not be represented in the simulated dictionary, and therefore won’t influence the optimal match with the measured signal evolution. In other words, the proposition is that the dictionary matching process can leverage data redundancy to implicitly “reject” motion corrupted data, provided that the majority of the data is reliable.

In fact, the original work by Ma et al. [15] showed that the MRF framework can tolerate extreme subject motion towards the end of the scan. In their particular experiment, the subject rotated his head by a large angle during the last 3 seconds of a 15-second MRF scan. However, ordinary motion patterns are generally more subtle and unpredictable. More specifically, subjects can move in different directions and move at any time during the measurement.

The aim of this work was to explore the sensitivity of MRF to subject motion in more detail. First, we briefly looked at the spin physics to aid the design of our experiments. Based on the collected insights, we designed a series of experiments to disentangle the effects of in-plane and through-plane motion. After revealing the driving mechanisms behind motion artifacts in MRF, we shifted our focus towards more realistic motion patterns prone to appear during a clinical scan, such as the movements associated with an itch or a minor adjustment of the head position. Finally, we investigated if explicit rejection of the motion corrupted data, rather than relying on implicit data rejection during the dictionary matching process, can improve the motion robustness of MRF.

2. Material and methods

2.1. Theory

The motion sensitivity of a given MR sequence depends heavily on the details of its implementation. Sequences with balanced gradient moments, such as the balanced steady-state free precession (bSSFP) sequence [16], tend to be more motion robust than gradient spoiled designs, such as the steady state precession (FISP) sequence [17]. Consequently, the combination of balanced in-plane gradients and unbalanced slice gradients in the FISP-MRF sequence could lead to a difference in sensitivity to in-plane and through-plane motion.

2.1.1. In-plane motion in FISP-MRF

First, let’s consider what happens to a series of isochromats (spin-packets) distributed along the readout direction in a voxel. During the gradient, each isochromat experiences a slightly different magnetic field, which leads the spins to de-phase during the pre-phasor gradient and then re-phase during the first half of the readout, de-phase again during the second half, and finally re-phase after the rewind gradient (Fig. 1a, faded rainbow lines). Such a combination of gradients is flow compensated [16]. Thus, when the subject moves along the read-out direction, each isochromat will experience a progressively different net magnetic field, but still form an echo at the center of the readout, re-phase afterwards, and maintain the same net phase before and after the readout. In practice this means that, when there’s motion, the acquired k-space line will capture the object in its new position, but the spin-dynamics themselves remain relatively untouched.

Figure 1:

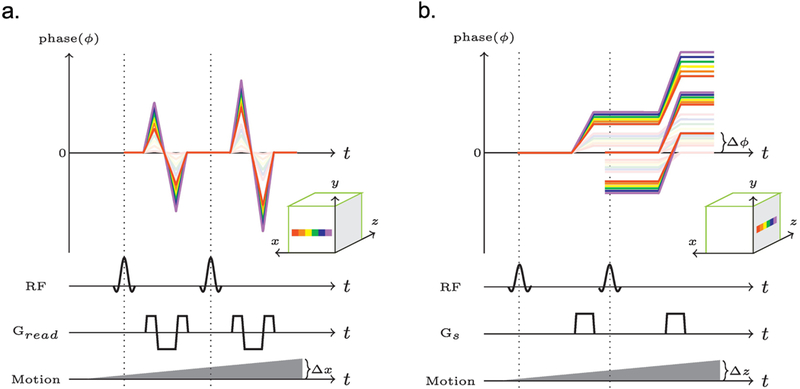
Figure 1:

Open in a new tab

The net phase change of a series of isochromats in a single voxel. a. The phase evolution during a balanced readout. b. The phase evolution produced by the spoiler gradient along the slice direction. The faded rainbows indicate phase evolutions without motion, while the bright rainbows show the motion corrupted phase evolutions. Delta ɸ indicates the phase difference between the first refocused coherence pathway and the magnetization that will be freshly excited by subsequent excitations.

2.1.2. Through-plane motion in FISP-MRF

Now let’s consider what happens to a series of isochromats placed some distance apart along the slice direction within the same voxel. Each spoiler gradient increases the phase differences between these isochromats. However, some of this magnetization may still be refocused by the refocusing component of the excitations. In the absence of motion, such coherence pathways refocus with zero phase difference relative to the freshly excited magnetization (Fig. 1b, faded rainbow lines).

Now, suppose the subject moved in the slice direction during scan. Isochromats at different locations will experience a stronger (or weaker) net magnetic field, but the amount of de-phasing per unit time relative to one another remains unchanged. Consequently, the different coherence pathways can still be refocused. However, they will accumulate a net phase (Δɸ, as we marked out in Figure 1b). Since the measured signal is the sum of all transverse components, a change in phase between different coherence pathways relative to one-another will lead to interferences that change the observed signal evolution. In addition, through-plane motion will also change which spins are excited or refocused, leading to a further decrease in refocused signal.

2.2. In vivo experiments

One axial slice was imaged through the brain of three asymptomatic volunteers. Experiments were performed on a 3 T scanner (MAGNETOM Skyra, Siemens Healthineers, Erlangen, Germany) using the commercial 20-element head coil array provided with the system. The study was approved by our institutional review board (IRB), and written informed consent was obtained prior to the examination. A radial version [18] of the FISP-MRF sequence [19] was used for each scan (RF time-bandwidth product = 2, pulse duration = 4 ms, one radial spoke per time frame, average TR = 13ms, total scan time ~ 13s). At the beginning of the scan, a 10 ms non-selective adiabatic inversion pulse was applied [20].

2.2.1. Motion patterns

The subjects were asked to perform different kinds of motion during a fraction of each scan. The different motion types were divided into two categories. The first category contained “oscillating movements” designed to isolate the influence of the balanced and unbalanced gradient moments. This category included in-plane motion, through-plane motion, and a combination of the first two movements (complex motion) (Fig2. a). In-plane motion was defined as a rotation of the head around the z-axis (head-foot), similar to the head gesture commonly used to indicate disapproval. In other words, in-plane motion only displaced the spins relative to the readout gradients. Through-plane motion resembled a nodding gesture as used to indicate agreement, which corresponds to a rotation of head around the x-axis (left-right). This motion displaced the spins relative to the spoiler gradient and moved spins in and out of the excited slice in this 2D experiment. For each type of motion, three datasets were acquired: one with the oscillation at the beginning of the scan, one in the middle of the scan, and another one at the end of the scan (Fig2. b). The duration of each motion segment lasted 200 TRs (~3s). Subjects performed one oscillation per segment. At the end of each interval, the subject was asked to try to return to the starting position by aligning the tip of their nose with a small piece of cardboard mounted to the coil. The second category, named “realistic movements”, contained motion patterns mimicking the typical small adjustments a subject could make to be a bit more comfortable during an MRI scan, or relieve an itch (Fig2. c). Unlike the first category, there was no periodic component to these movements, i.e., the subject was not asked to return the head to the starting position. Each subject performed all motion patterns in both categories, and all measurements were repeated five times. Note that, during the realistic movements’ patterns, the subject was free to move in any arbitrary direction. In addition, five motion-free reference scans per subject were acquired.

Figure 2:

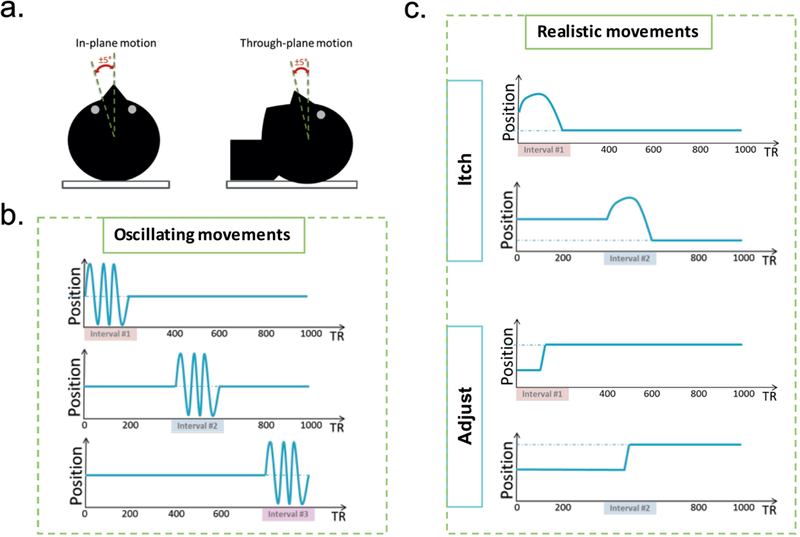
Figure 2:

Open in a new tab

a. Illustration of the oscillating motion directions relative to the acquired transversal slice. b. Oscillation movements were performed during three different time intervals, and returned to the approximate starting position. c. Realistic movements had no periodic component, and did not deliberately return to the starting position.

To recreate experimental conditions similar to an actual clinical exam, all movements were restricted to small angles (± 5°) by cushions placed around the subjects’ heads. All subjects were trained to perform the different motion patterns before entering the scanner. During the scan, the subject motion was monitored visually with a camera allowing us to qualitatively verify that the correct motion pattern was performed. The projector in the scanner room was used to instruct subjects when and how to move during each scan. The timing of the instructions was controlled by a trigger signal incorporated in the MR sequence.

2.2.2. Reconstruction

The radial FISP-MRF sequence used a train of 1000 RF pulses to sample the spin-dynamics. Each excitation is followed by a single radial readout [18], all of which were individually reconstructed using a non-uniform fast Fourier transform [21]. Collectively, these 1000 time frames contain the MR fingerprints for each voxel. The dictionary based matching process was performed as described in Refs. [15, 19], thus relying on the ability of dictionary matching process to implicitly reject the motion corrupted data, as suggested in [15]. The dictionary was created using the extended phase graph formalism [22, 23], and included the slice profile as detailed in Refs. [24, 25]. Each entry in the dictionary was normalized to have a unit L2 norm. In addition, we also reconstructed the same data after explicitly removing the motion-corrupted data points from the measured fingerprints based on the known starting and ending time of the motion interval #2. In this case, the corresponding data points were also removed from the dictionary, and the dictionary renormalized before matching.

2.2.3. Analysis

To quantify the effect of motion on the T1 and T2 maps, a region of interest (ROI) analysis was performed for each subject. The ROI contained 90 voxels in total, positioned bilaterally in the prefrontal white matter (45 voxels on each side, 10.5 mm diameter circular ROI). The ROI position was adjusted manually for each scan to make sure that it was properly centered in the prefrontal white matter.

3. Results

Figure 3 shows the T1 and T2 maps for all MRF scans from subject #1. The morphological structures were relatively well preserved in spite of motion. In agreement with the findings described in Ref. [15], motion at the end of the scan (interval#3) had only minor effects on the parameter maps. However, the measured T2 values change considerably when the motion occurred in the middle of the scan (interval#2). Although the T1 values appear to be more stable, blurring was observed when there was in-plane motion in the beginning of the scan (interval#1). This is most obvious when comparing the delineation of the gray/white matter boundaries (Fig. 4).

Figure 3:

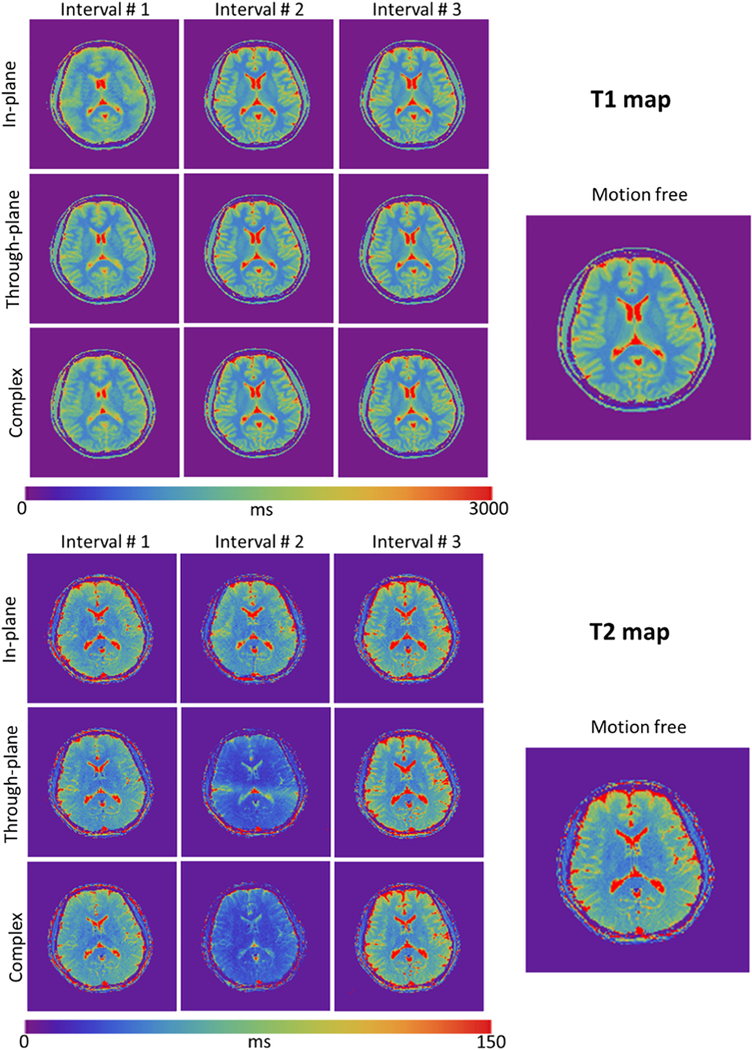
Figure 3:

Open in a new tab

T1 and T2 maps obtained with the radial FISP-MRF sequence (1.5×1.5×5mm3) in the presence of oscillating head movements. Columns correspond to different time intervals; rows correspond to different motion types. The morphological structures are well preserved in all T1 and T2 maps. Note that T2 values deviate from ground truth most notably in the middle column corresponding to the central time interval, especially for the cases of through-plane motion and complex motion.

Figure 4:

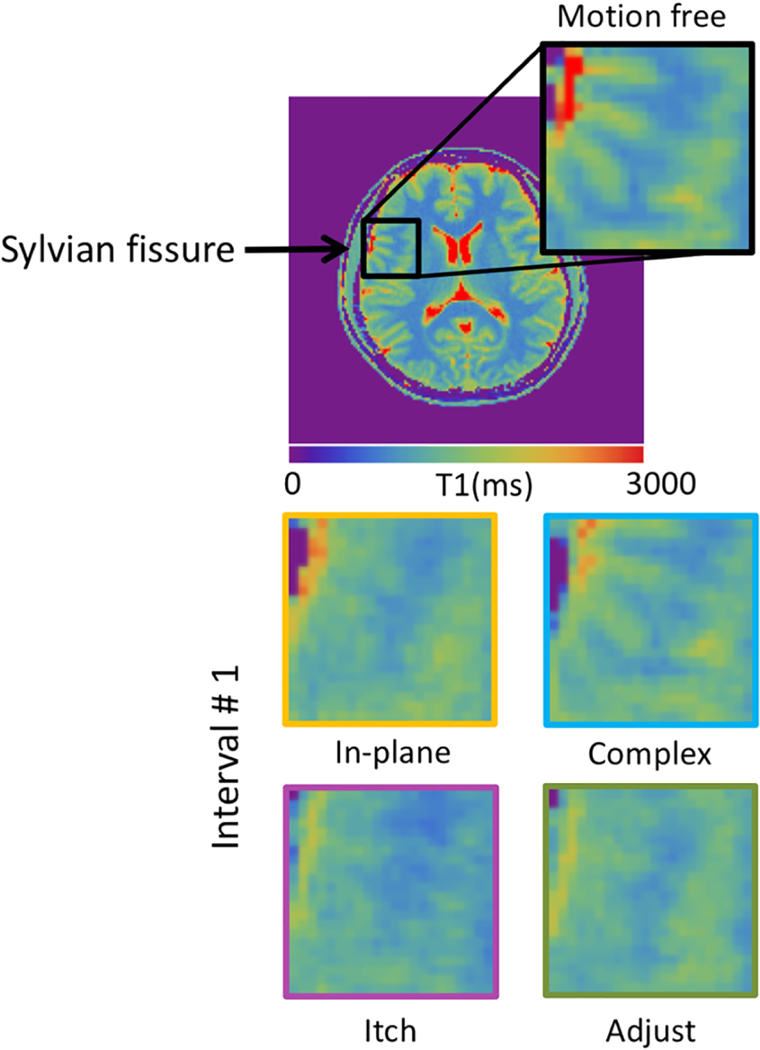
Figure 4:

Open in a new tab

Enlargements of T1 maps showing the sylvian fissure region. Note the blurred gray/white matter boundaries in the maps with motion.

Figure 5 shows the average T1 and T2 values of the prefrontal white matter ROI measured during each of the scans. The reference scans resulted in highly reproducible T1 {802±3.7, 815± 8.3, 792±15.2 ms} and T2 {49±0.4, 47±1.6 , 47±0.83 ms} measurements for subject one, two and three, respectively. As expected, measurements with motion during interval #3 remained tightly grouped around the reference. However, although the relative error was small (mean T1 0.2% ±1.1%, mean T2 −0.8% ±3.6%), several data points fell outside of the 95% confidence interval of the reference data, indicating a substantial increase in variability. Motion during the middle of the scan (interval #2) had a strong effect on the observed T2 (mean −36.7%±16.9%), and limited effect on T1 (mean −0.64%±1.6%). The observed T2 was found to be especially sensitive to through-plane motion, on average leading to a 44% reduction in T2. Although the multi-parametric maps derived from measurements with motion during interval #1 showed a smaller systematic error, the variability of both the T1 (mean 2.3% ± 4.6%) and T2 (mean −5.7% ± 9.9%) was much larger than the reference scan (far outside the 95% confidence interval indicated by a dashed ellipsoid in Fig. 5).

Figure 5:

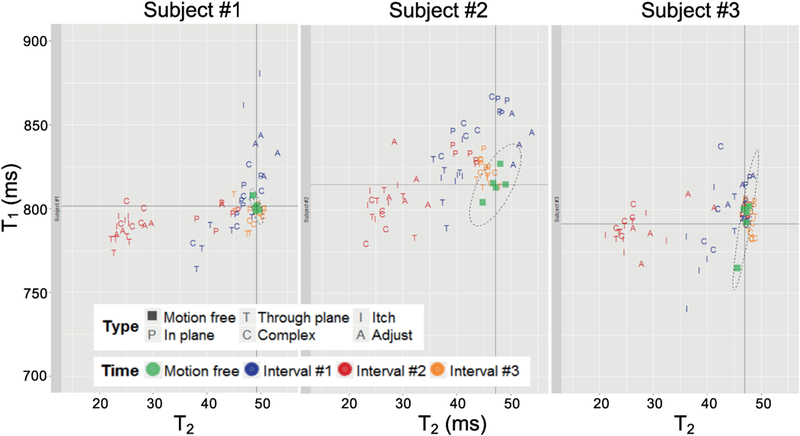
Figure 5:

Open in a new tab

Scatter plots of T1 and T2 values measured in the prefrontal white matter of three subjects. Values were averaged over an ROI (90 pixels) to get the corresponding T1 and T2 values. Each scan was repeated five times.

Explicitly removing the motion corrupted data points from interval #2 improved the T2 estimates (Fig. 6), thus revealing that the dictionary matching process cannot always implicitly reject all corrupted data points. However, even after explicitly removing the motion corrupted data points, a significant residual error remained (mean T1 0.8% ± 1.3%, mean T2 −10.7% ± 14.6%). Moreover, the more realistic motion patterns, such as the “itch” like motion in the middle of the scan, retained the largest deviation from the reference results after the explicit correction (mean T1 −1% ± 0.9%, mean T2 −16.5% ± 17.8%).

Figure 6:

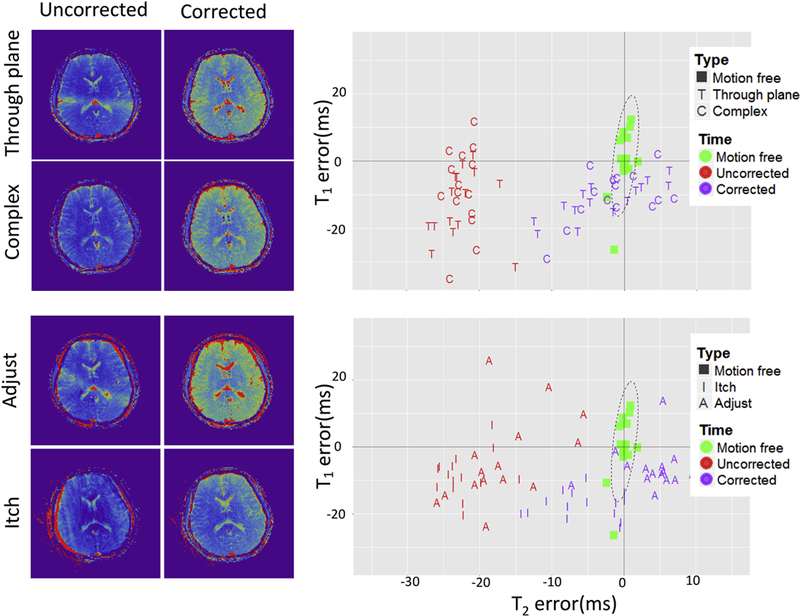
Figure 6:

Open in a new tab

The results obtained by leveraging data redundancy only to correct motion artifacts. On the left side is the T2 maps derived from uncorrected and corrected data are shown. On the right side the scatter plots of T1/T2 error are shown (Same ROI as in Fig. 5).

4. Discussion

We explored the motion sensitivity of MRF by instructing three subjects to nod, shake or “twist” their heads at different time intervals during the scan. Our data showed that the dictionary matching process is not always able to filter out the corrupted data. While, as was suggested by Ma et al. [15], in-plane motion at the end of the scan may have a relatively benign effect, we observed a substantial decrease in T2 values especially when through-plane motion occurred in the middle of the scan.

The difference in sensitivity to in-plane and through-plane motion can be explained by the spin-physics. The in-plane gradients (radial readout) are balanced, while the through-plane gradients are gradient spoiled. Therefore, when the subject moves in the through-plane direction, each of the coherence pathways will accumulate a different phase [22] and result in a net attenuation of the refocused signal component, which is interpreted by the matching algorithm as a shorter T2 time.

These effects could be avoided by switching to a steady-state free precession based sequence (bSSFP) such as used in the original MRF implementation. This may appear ideal from the perspective of motion robustness, but it incurs other technical challenges such as an enhanced B0 sensitivity [15]. Moreover, 2D bSSFP-based MRF sequences cannot solve all the problems associated with through-plane motion. When the subject moves in and out of the slice, slightly different batches of spins will be excited. Not only does this alter the observed spin-evolution, it may also imply that the desired slice is only imaged part of the time. These spin-evolution effects may be circumvented by moving to a 3D bSSFP-based MRF sequence and the miss registration problem may be solvable retrospectively. Alternatively, a prospective motion correction method could be used to simultaneously avoid the corruption of the spin-dynamics and the miss registration [26].

Compared to the strong effect of motion on the T2 values, T1 values were only modestly affected. However, this behavior could change when a selective inversion pulse is used. Nevertheless, even when using a non-selective inversion pulse, as for this work, fine details in the T1-maps can become blurred, especially when the motion occurs in the first part of the scan where T1 is strongly encoded. In general, the inversion at the beginning of the sequence creates an asymmetric weighting in the fingerprint. Consequently, data corruption at the start or end of the fingerprint will lead to different effects.

The observed robustness to motion at the end of the scan could perhaps be explained in terms of data redundancy. In fact, the data acquired during the first 12 s of the scan were already sufficient to identify the correct fingerprint in the dictionary and the motion corrupted data acquired during the last 3 s did not effectively contribute to the fit. However, when motion occurs in the middle of the scan, the quantitative maps are no longer accurate. This can be understood by looking at the flip-angle train in the sequence. Only the center part of the sequence contains large flip angles. As a result, T2 is most strongly encoded in the middle of the scan. When this vital information is destroyed, it is no longer possible to obtain accurate parametric maps. In fact, removing this interval from the motion free reference scans also reveals a strong T2 bias (supplemental Figure 1). This effect may be difficult to mitigate using different matching techniques or other forms of retrospective motion correction. Instead, it may be necessary to scatter large flip angle segments throughout the sequence such that there is more redundancy in the T2 encoding. Moreover, the dictionary matching process may not be able to effectively reject all motion corrupted data points. Although motion induced signal decay (due to improper refocusing of coherence pathways) is not represented in the dictionary, the best possible fit tends to correspond to a significantly lower T2. Explicitly removing the corrupted data points can therefore help reduce T2 bias produced by motion in the middle of the scan. Nevertheless, the obtained precision falls short compared to reference scans. Combined, these observations suggest that it may not suffice to rely on data redundancy alone to obtain motion robust MRF results.

MRF could also provide new opportunities to enhance motion robustness. For example, it is possible to incorporate the in-plane motion pattern into the dictionary, helping to de-blur the images and minimize the need for data rejection [27–30], but it is not clear if it can be extended to correct through plane motion.

As an alternative, prospective motion correction may be a good way to mitigate the corrupting effects of motion on the spin-dynamics. In particular, prospective techniques can adjust the gradient on the fly, which will assure that the coherence pathways properly refocus even in unbalanced sequences [26, 31, 32]. This way, the challenge of simultaneous B0 estimation associated with the bSSFP-based MRF sequences can be avoided. Moreover, the adaptive FOV and slice position can assure that the same group of spins is excited. In other words, prospective motion correction methods will maintain the proper spin-dynamics even in the presence of through-plane motion and circumvent the need to use 3D sequences. In general, prospective motion correction in MRF can eliminate the need to reject data due to motion corruption and simplify both the reconstruction and dictionary calculation at the expense of a more complex experimental setup.

In this work, we used radial trajectory for the k-space sampling instead of the spiral trajectory used in the original FISP-MRF sequence. Both spiral and radial sampling go through the k-space center during each readout and provide similar benefits with respect to motion robustness. In addition, both the spiral used in the original FISP-MRF implementation and our radial implementation are balanced. The only difference is that the spiral trajectory can provide a higher sampling density per time frame, which may allow more timepoints to be rejected from the fit. Nevertheless, the general mechanisms that can destroy the information content in the spin-dynamics remain the same. Therefore, we expect that our observations are largely independent of the trajectory used in the experiments.

5. Conclusions

Our experimental results showed that MRF-based T1 measurements based on a non-selective inversion pulse are relatively motion robust. Nevertheless, some blurring may appear if motion occurs early in the scan. The T2 measurements, on the other hand, are more sensitive to motion. In particular, through-plane motion during the large flip-angle segments in the middle of the scan leads to a systematic underestimation in T2. Interestingly, motion at the end of the sequence has a relatively small influence on the quantification of both T1 and T2, which suggest that the dictionary matching process effectively rejects these last data-points if they are corrupted. When there is motion in the middle of the scan, attempting to leverage the redundancy in the data alone, either through implicit or explicit rejection of corrupted data, is not sufficient to correct the multi-parametric maps.

Supplementary Material

1

Highlights:

  • Theory based experimental design to demonstrate motion sensitivity of MR fingerprinting.

  • Investigation of multiple combinations of movement directions and motion occurrences during a MRF scan.

  • Investigation of realistic in-vivo motion patterns during an MRF scan

  • Experimental evaluation of MRF derived T1 and T2 precision and accuracy in the presence of subject motion.

  • Investigation of the potential for data redundancy based motion correction in MRF.

Acknowledgements:

Research reported in this publication was supported by the National Institute of Arthritis and Musculoskeletal and Skin Diseases (Award Number R01 AR070297) and National Institute of Biomedical Imaging and Bioengineering (Award Number R21 EB020096) of the National Institutes of Health (NIH), and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH.

Footnotes

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Ehman RL, McNamara MT, Brasch RC, Felmlee JP, Gray JE, Higgins CB. Influence of physiologic motion on the appearance of tissue in MR images. Radiology, 1986; 159(3): 777–782. [DOI] [PubMed] [Google Scholar]
  • 2.Zaitsev M, Maclaren J, Herbst M. Motion artifacts in MRI: a complex problem with many partial solutions[J]. Journal of Magnetic Resonance Imaging, 2015; 42(4): 887–901. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Stehling MK, Turner R, Mansfield P. Echo-planar imaging: magnetic resonance imaging in a fraction of a second. Science, 1991; 254(5028): 43–50. [DOI] [PubMed] [Google Scholar]
  • 4.Rofsky NM, Lee VS, Laub G, Pollack MA, Krinsky GA, Thomasson D. Ambrosino MM, Weinreb JC. Abdominal MR imaging with a volumetric interpolated breath-hold examination 1. Radiology, 1999; 212(3): 876–884. [DOI] [PubMed] [Google Scholar]
  • 5.Fischer SE, Wickline SA, Lorenz CH. Novel real‐time R‐wave detection algorithm based on the vectorcardiogram for accurate gated magnetic resonance acquisitions. Magnetic Resonance in Medicine, 1999; 42(2): 361–370. [DOI] [PubMed] [Google Scholar]
  • 6.Chia JM, Fischer SE, Wickline SA, Lorenz CH. Performance of QRS detection for cardiac magnetic resonance imaging with a novel vectorcardiographic triggering method. Journal of Magnetic Resonance Imaging, 2000; 12(5): 678–688. [DOI] [PubMed] [Google Scholar]
  • 7.Meyer CH, Hu BS, Nishimura DG, Macovski A. Fast spiral coronary artery imaging. Magnetic Resonance in Medicine, 1992; 28(2): 202–213. [DOI] [PubMed] [Google Scholar]
  • 8.Chandarana H, Block TK, Rosenkrantz AB, Lim RP, Kim D, Mossa DJ, Babb JS, Kiefer B, Lee VS. Free-breathing radial 3D fat-suppressed T1-weighted gradient echo sequence: a viable alternative for contrast-enhanced liver imaging in patients unable to suspend respiration. Investigative radiology, 2011; 46(10): 648–653. [DOI] [PubMed] [Google Scholar]
  • 9.Pipe JG, Motion correction with PROPELLER MRI: application to head motion and free-breathing cardiac imaging. Magnetic Resonance in Medicine, 1999; 42(5): 963–969. [DOI] [PubMed] [Google Scholar]
  • 10.Hu X, Kim SG. Reduction of signal fluctuation in functional MRI using navigator echoes. Magnetic Resonance in Medicine, 1994; 31(5): 495–503. [DOI] [PubMed] [Google Scholar]
  • 11.Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD‐GRASP: Golden‐ angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing. Magnetic Resonance in Medicine, 2016; 75(2): 775–788 [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Tremblay M, Tam F, Graham S, Kucharczyk J, Marmurek J. Optical image-based position tracking for magnetic resonance imaging applications. US Patent 10,889,667 July 13, 2004.
  • 13.Qin L, van Gelderen P, Derbyshire JA, Jin F, Lee J, de Zwart JA, Tao Y, Duyn JH. Prospective head‐movement correction for high‐resolution MRI using an in‐bore optical tracking system. Magnetic Resonance in Medicine, 2009; 62(4): 924–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.White N, Roddey C, Shankaranarayanan A, et al. PROMO: real‐time prospective motion correction in MRI using image‐based tracking[J]. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 2010; 63(1): 91–105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Ma D, Gulani V, Seiberlich N, Liu K, Sunshine JL, Duerk JL, Griswold MA. Magnetic resonance fingerprinting. Nature, 2013; 495(7440): 187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Bieri O, Scheffler K. Fundamentals of balanced steady state free precession MRI. Journal of Magnetic Resonance Imaging, 2013; 38(1): 2–11. [DOI] [PubMed] [Google Scholar]
  • 17.Sekihara K Steady-state magnetizations in rapid NMR imaging using small flip angles and short repetition intervals. IEEE transactions on medical imaging, 1987; 6(2): 157–164. [DOI] [PubMed] [Google Scholar]
  • 18.Winkelmann S, Schaeffter T, Koehler T, Eggers H, Doessel O. An optimal radial profile order based on the Golden Ratio for time-resolved MRI. IEEE transactions on medical imaging, 2007; 26(1): 68–76. [DOI] [PubMed] [Google Scholar]
  • 19.Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold MA. MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout. Magnetic Resonance in Medicine, 2015; 74(6): 1621–1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Silver MS., Joseph RI, Hoult DI. Selective spin inversion in nuclear magnetic resonance and coherent optics through an exact solution of the Bloch-Riccati equation. Physical Review A, 1985; 31(4): 2753. [DOI] [PubMed] [Google Scholar]
  • 21.Fessler JA, Sutton BP. Nonuniform fast Fourier transforms using min-max interpolation. IEEE Trans. Signal Process 2003; 51: 560–574. [Google Scholar]
  • 22.Weigel M Extended phase graphs: Dephasing, RF pulses, and echoes‐pure and simple. Journal of Magnetic Resonance Imaging, 2015; 41(2): 266–295. [DOI] [PubMed] [Google Scholar]
  • 23.Hennig J Echoes—how to generate, recognize, use or avoid them in MR‐imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes. Concepts in Magnetic Resonance Part A, 1991; 3(3): 125–143. [Google Scholar]
  • 24.Cloos MA, Knoll F, Zhao T, Block KT, Bruno M, Wiggins GC, Sodickson DK. Multiparametric imaging with heterogeneous radiofrequency fields. Nature Communications, 2016, 7. [DOI] [PMC free article] [PubMed]
  • 25.Ma D, Coppo S, Chen Y, McGivney DF, Jiang Y, Pahwa S, Gulani V, Griswold MA. Slice profile and B1 corrections in 2D magnetic resonance fingerprinting. Magnetic Resonance in Medicine, 2017. 10.1002/mrm.26580. [DOI] [PMC free article] [PubMed]
  • 26.Maclaren J, Herbst M, Speck O, Zaitsev M. Prospective motion correction in brain imaging: a review. Magnetic resonance in medicine 2013; 69(3), 621–636. [DOI] [PubMed] [Google Scholar]
  • 27.Mehta B B, Ma D, Pierre E Y, et al. Image reconstruction algorithm for motion insensitive MR Fingerprinting (MRF): MORF. Magnetic Resonance in Medicine, 2018. [DOI] [PubMed]
  • 28.Xu Z, et al. “Motion correction for Magnetic Resonance Fingerprinting by using Sliding-Window Reconstruction and Image Registration.” ISMRM 2017 Annual Meeting & Exhibition Proceedings. International Society for Magnetic Resonance in Medicine, 2017. [Google Scholar]
  • 29.Costagli M, et al. ”Application of retrospective motion correction to magnetic resonance fingerprinting . “ ISMRM 2017 Annual Meeting & Exhibition Proceedings. International Society for Magnetic Resonance in Medicine, 2017. [Google Scholar]
  • 30.Cruz G, et al. “Motion corrected Magnetic Resonance Fingerprinting using Soft-weighted key-Hole (MRF- McSOHO)” ISMRM 2017 Annual Meeting & Exhibition Proceedings. International Society for Magnetic Resonance in Medicine, 2017. [Google Scholar]
  • 31.Lee CC, Jack CR, Grimm RC, Rossman PJ, Felmlee JP, Ehman RL, Riederer SJ. Real‐ time adaptive motion correction in functional MRI. Magnetic Resonance in Medicine, 1996; 36(3), 436–444. [DOI] [PubMed] [Google Scholar]
  • 32.Zaitsev M, Dold C, Sakas G, Hennig J, Speck O. Magnetic resonance imaging of freely moving objects: prospective real-time motion correction using an external optical motion tracking system. Neuroimage 2006; 31(3):1038–50. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
NIHMS1506446-supplement-1.pdf (262.4KB, pdf)

RESOURCES