Abstract
Under neutrality, linkage disequilibrium results from physically linked sites having nonindependent coalescent histories. In obligately sexual organisms, meiotic recombination is the dominant force separating linked variants from one another, and thus in determining the decay of linkage disequilibrium with physical distance. In facultatively sexual diploid organisms that principally reproduce clonally, mechanisms of mitotic exchange are expected to become relatively more important in shaping linkage disequilibrium. Here we outline mathematical and computational models of a facultative-sex coalescent process that includes meiotic and mitotic recombination, via both crossovers and gene conversion, to determine how linkage disequilibrium is affected with facultative sex. We demonstrate that the degree to which linkage disequilibrium is broken down by meiotic recombination simply scales with the probability of sex if it is sufficiently high (much greater than for population size N). However, with very rare sex (occurring with frequency on the order of ), mitotic gene conversion plays a particularly important and complicated role because it both breaks down associations between sites and removes within-individual diversity. Strong population structure under rare sex leads to lower average linkage disequilibrium values than in panmictic populations, due to the influence of low-frequency polymorphisms created by allelic sequence divergence acting in individual subpopulations. These analyses provide information on how to interpret observed linkage disequilibrium patterns in facultative sexuals and to determine what genomic forces are likely to shape them.
Keywords: facultative sex, coalescent theory, crossing over, recombination, gene conversion, linkage disequilibrium
COALESCENT theory is a powerful mathematical framework that is used to determine how natural selection and demographic history affect genetic diversity (Kingman 1982; Rosenberg and Nordborg 2002; Hein et al. 2005; Wakeley 2009). Traditional coalescent models assume that the population is obligately sexual, but there has been less attention on creating models that account for different reproductive modes. While the coalescent with self-fertilization has been extensively studied (Nordborg 1997, 2000; Nordborg and Donnelly 1997; Nordborg and Krone 2002), little theory exists on coalescent histories in organisms with other mixed reproductive systems.
Previous theory has investigated genetic diversity in facultatively sexual diploid organisms, which reproduce via a mixture of sexual and parthenogenetic reproduction (Brookfield 1992; Burt et al. 1996; Balloux et al. 2003; Bengtsson 2003; Ceplitis 2003). A general result arising from this work is that when an organism exhibits very rare population-level rates of sex [ for σ the probability of sex and population size N], they will exhibit “allelic sequence divergence” where both alleles within a diploid individual accumulate distinct polymorphisms from each other (Mark Welch and Meselson 2000; Butlin 2002). Hartfield et al. (2016) subsequently investigated a coalescent model of facultative sexuals and quantified how the presence of gene conversion can reduce within-individual diversity to less than that expected in sexual organisms, contrary to the effects of allelic sequence divergence. Hence these results provide a potential explanation as to why allelic divergence is not widely observed in empirical studies of facultatively sexual organisms (reviewed in Hartfield 2016).
However, this analysis only modeled the genetic history at a single, nonrecombining locus. Here, genealogies only greatly differed from those in obligately sexual organisms at very low frequencies of sex As a consequence, methods to estimate the frequency of sex can only do so based on the degree of allelic sequence divergence, and are expected to be ineffective if the frequency of sex is and/or gene conversion is prevalent (Ceplitis 2003; Hartfield et al. 2016). In contrast, many facultatively sexual organisms exhibit much higher occurrences of sex. Pea aphids reproduce sexually about once every 10–20 generations (Jaquiéry et al. 2012), while Daphnia undergo 1 sexual generation and 5–20 asexual generations a year (Haag et al. 2009). The wild yeast Saccharomyces paradoxus has an outcrossing frequency of 0.001; while low, this value is four orders of magnitude higher than (Tsai et al. 2008). If we wish to create a general coalescent model that can be used to estimate rates of sexual reproduction in species undergoing more frequent sex, then we need to increase the power of this coalescent analysis to consider how patterns of genetic diversity at multiple loci are affected with facultative sex.
This is achievable by considering how genealogies of multiple sites correlate along a chromosome. Two completely linked sites will reach a common ancestor in the past at the same time, so will share the same gene genealogy. However, if a recombination event (e.g., via meiotic crossing over) were to separate the sites, each subsegment may have different genetic histories (Hudson 1983). Breaking apart correlations between sites is reflected with lower linkage disequilibrium, which can be measured from genomic data (Griffiths 1981; Hudson and Kaplan 1985; Hudson 1990; Simonsen and Churchill 1997; McVean 2002). Gene conversion can also break apart correlations between sites through transferring genetic material across DNA strands (Wiuf and Hein 2000).
As meiotic crossing over occurs during sexual reproduction, one may expect that the extent to which linkage disequilibrium is broken down should scale with the probability of sex (see Nordborg 2000 for a related argument for the coalescent with self-fertilization). Tsai et al. (2008) used this logic to calculate the frequency of sex in the yeast S. paradoxus by comparing effective population sizes inferred from linkage disequilibrium decay (which should scale with the meiotic recombination rate and therefore the rate of sex) with those from nucleotide variation (which should be independent of sex if sufficiently high). Lynch et al. (2017) used similar arguments to conclude that even though the facultatively sexual water flea Daphnia pulex has a lower overall crossover recombination rate than Drosophila melanogaster, it has a higher crossover rate when sex does occur.
However, the logic used in these studies assumes that the frequency of sex only affects occurrences of meiotic crossing over. Low rates of sex also distort the underlying genealogies, leading to subsequent events (including allelic sequence divergence or removal of diversity via gene conversion) that also affect how polymorphisms are correlated along haplotypes. Hence these approaches may become problematic in species exhibiting low rates of sexual reproduction or if gene conversion is an important force in shaping genetic diversity, as observed in empirical studies of facultative sexuals (Crease and Lynch 1991; Schön et al. 1998; Normark 1999; Schön and Martens 2003; Flot et al. 2013).
We describe both mathematical theory and a routine for simulating multi-site genealogies with facultative sex, allowing for both meiotic and mitotic crossover recombination and gene conversion. We use these new models to investigate how linkage disequilibrium patterns are affected in facultatively sexual organisms, and how these results can be used to infer rates of sex from genome data. Specifically, we investigate when the breakdown of linkage disequilibrium scales with sex, as predicted by intuition, and when this logic does not hold.
Overview of the Facultative-Sex Coalescent and Recombination Events
Our primary goal is to examine how different frequencies of sex affect linkage disequilibrium. Heuristically speaking, the expected strength of disequilibrium depends on the probability that two sampled haplotypes (hereafter “samples”) coalesce before either haplotype is disrupted by recombination. Before presenting the formal model, we begin by discussing how facultative sex affects coalescence and then recombination.
In the standard coalescent, each member of a set of (nonrecombining) samples can be thought of as traveling independently backward in time through the generations. A coalescence event occurs if two samples independently “choose” the same parental allele as their ancestor. The waiting time until the next coalescence depends only on the number of remaining samples but, importantly, not on “where” the samples are currently found (i.e., in which individual organisms). However, for diploids with a low frequency of sex, the “where” information is crucial (Bengtsson 2003; Ceplitis 2003; Hartfield et al. 2016). For example, two samples can be the two haplotypes found in a single diploid individual (which we denote as “a paired sample”) or they can each come from different individuals (which we denote as “two unpaired samples”). The two haplotypes within a paired sample do not travel back in time independently, but rather they travel together for as long as reproduction is asexual. Coalescence between them is not possible for all the asexual generations they remain paired (ignoring gene conversion). A sexual event splits a paired sample into two unpaired samples that can then coalesce in a subsequent generation. For this reason, paired samples are expected to have longer average coalescence times than unpaired samples and low sex increases average coalescence time compared to high sex (Balloux et al. 2003; Bengtsson 2003; Ceplitis 2003). However, if the frequency of mitotic gene conversion is high relative to the frequency of sex, then these predictions are reversed (Hartfield et al. 2016). In this case, paired samples can coalesce faster than unpaired samples because each generation the samples are paired provides an opportunity for coalescence via mitotic gene conversion.
In sum, low sex in diploids requires a “structured” coalescent approach because paired and unpaired samples behave differently; this structure affects the distribution of coalescence times (including the mean and variance) and is sensitive to the amount of mitotic gene conversion. Technically, this structure occurs even in diploids that are obligately sexual; however, the coalescent can be safely modeled ignoring the structure because the time spent in paired states is infinitesimally brief on the coalescent timescale when sex is common. To affect coalescence times, sex must be sufficiently uncommon, i.e., where N is the population size and σ is the fraction of offspring sexually produced each generation via the random union of gametes (i.e., represents obligate sex and represents obligate asexuality; see Table 1 for a list of symbol definitions).
Table 1. Glossary of notation.
| Symbol | Usage |
|---|---|
| N | Diploid population size (with haplotypes), denoted if measured across a subdivided population |
| Frequency of derived allele at site A, B | |
| Frequency of haplotypes carrying derived allele at both sites | |
| Linkage disequilibrium between two sites, | |
| Standardized linkage disequilibrium, | |
| “Ratio of means” measure of linkage disequilibrium, | |
| Coalescent time at site A (if sampled from haplotypes i, j) | |
| σ | Fraction of offspring produced via sex |
| c, | Probability of meiotic (mitotic) crossing over between two sites |
| Probability of meiotic (mitotic) crossing over between two adjacent sites | |
| , | Probability of mitotic gene conversion covering one, two sites (analytical model) |
| Probability of meiotic gene conversion covering one, two sites (analytical model) | |
| g, | Probability of mitotic (meiotic) gene conversion initiating at a site |
| Population-level frequency of sex, | |
| ρ, | Population-level rate of meiotic (mitotic) crossing over, () |
| Population-level rate of mitotic crossing over between two adjacent sites, | |
| , | Population-level rate of mitotic (meiotic) gene conversion affecting a single site, () |
| G | Population-level rate of gene conversion initiation, |
| Average length of mitotic (meiotic) gene conversion event | |
| L | Number of sampled sites; is number of breakpoints |
| Q, | Number of breakpoints in units of average gene conversion length [e.g., for mitotic gene conversion] |
| R | Population-level meiotic crossing-over rate (simulation), |
| Population-level mitotic gene conversion rate (simulation), | |
| φ | Ratio of sex to mitotic gene conversion acting at a single site, |
| μ | Mutation rate over L sites |
| θ | Population-level mutation rate, |
| m | Probability of migration (island model) |
| M | Population-level rate of migration, |
| , | Probability of one, two gene conversion breakpoints within sample |
Different sites along a genetic segment can have different genealogical histories as long as there is some recombination. Low sex affects recombination in several ways. We consider both crossing over (the reciprocal exchange of genetic material between two haplotypes) and gene conversion (where genetic material is copied from one haplotype to its homolog). When sexual reproduction is rare, the frequency of meiotic recombination will necessarily be low. Mitotic crossovers and mitotic gene conversion can then become important for two reasons. First, in comparison to meiotic recombination, mitotic recombination becomes a relatively more important route of genetic exchange as meiosis becomes rare. Second, in paired samples (which are only an important consideration when sex is low), mitotic recombination can either lead to gene exchange (the splitting of a multi-site sample into separate pieces) or coalescence.
Figure 1 outlines the possible outcomes for recombination under facultative sex. Going back in time, sex involving a meiotic crossover will transform an unpaired sample into a paired sample (i.e., the unpaired sample descended from the two homologs in the parent; Figure 1A). For a paired sample, sex segregates the two samples into separate parents, creating two unpaired samples (Figure 1B). However, if a crossover also occurred on one of these samples, then the affected sample becomes a paired sample in the parent; the overall outcome is a new paired sample in one parent (each containing a section of ancestral material) and one unpaired sample in the other parent (Figure 1C). Mitotic crossovers can also act in paired samples unaffected by sex, swapping genetic material between homologs (Figure 1D).
Figure 1.
Schematic of different outcomes following gene exchange in the facultative-sex coalescent. Solid lines represent ancestral material, dotted lines represent nonancestral material. Outcomes are described for (A) meiotic crossing over acting on an unpaired sample, or gene conversion acting on an unpaired sample that only partially overlaps with the haplotype; (B) sex acting on a paired sample with no crossing over or gene conversion; (C) both sex and either crossing over, or gene conversion that only partially overlaps with the haplotype, acting on a paired sample; (D) mitotic crossing over acting on a paired sample; (E) gene conversion (meiotic or mitotic) acting on an unpaired sample, which fully lies within the sampled haplotype; (F) both sex and gene conversion (lying fully within a haplotype) acting on a paired sample; (G) mitotic gene conversion acting on a segment of a paired sample; and (H) mitotic gene conversion acting over the entire length of a paired sample (or over all remaining extant material).
Gene conversion can affect a sample in several ways, where (1) gene conversion initiates outside a tract of ancestral material but finishes within it, (2) gene conversion begins within a tract of ancestral material but extends beyond it, (3) both conversion breakpoints lie within ancestral material, or (4) gene conversion acts over all ancestral material in a paired sample (see Wiuf and Hein 2000 for a detailed discussion of the coalescent with gene conversion applicable to obligately sexual diploids). If gene conversion acts on an unpaired sample, then it becomes a paired sample with each haplotype carrying a segment of ancestral material, which is a similar outcome to that following a crossover (Figure 1E). There are either one or two breakpoints, depending on whether gene conversion lies partly or fully within ancestral material. If acting on paired samples, the outcome depends on whether sex has segregated the samples into different individuals. If so, then one of the two parents contains a paired sample with each part carrying ancestral material (Figure 1F). If not, then a segment of one sample coalesces into the other (Figure 1G). Finally, mitotic gene conversion acting completely over a paired sample reproducing asexually causes complete coalescence of one paired sample, converting it into an unpaired sample. This outcome is equivalent to “gene conversion” for the single-site coalescent model (Hartfield et al. 2016) (Figure 1H).
Overall, facultative sex will affect linkage disequilibrium for at least three reasons. First, the population-level rate of meiotic recombination will be proportional to the frequency of sexual reproduction. Second, when sex becomes very rare, the rate and patterns of coalescence change substantially, which is important because disequilibrium is affected by the rate of recombination relative to coalescence. Third, in the low-sex regime, mitotic gene conversion can become important as it becomes a key coalescence mechanism for a paired sample; alternatively, a single haplotype within an individual can be separated (with either one or two breakpoints) via gene conversion.
Two-Site Analytical Model
A commonly used metric of linkage disequilibrium is (Hill and Robertson 1968):
| (1) |
where is the frequency of the derived allele at site i ( or B), and with being the frequency of haplotypes carrying the derived allele at both sites. A related quantity
| (2) |
has been studied in analytical neutral models (Ohta and Kimura 1971; Weir and Hill 1986; McVean 2002) (we use to represent this quantity, rather than the traditional symbol , to avoid confusion with σ that is used to parameterize the frequency of sex in this analysis). overestimates the expected value of but the discrepancy is reduced if it is only applied to sites where the minor allele is not too rare (McVean 2002). In the classic analysis, which is applicable to obligately sexual diploids:
| (3) |
where with c being the per-generation probability of meiotic crossing over between two sites. McVean (2002) showed that a coalescence approach can be used to derive this result, demonstrating that is a function of the covariance in coalescence times between two sites. The goal here is to quantify how is altered by facultative sex. We use the coalescent approach of McVean (2002) for a two-site model in a diploid population of size N. Two samples at each of two sites in a diploid model can occur in 17 different states, as outlined in Figure 2. In the traditional haploid model, only 7 states are necessary, but here we must consider the full 17-state model to consider the pairing of haplotypes. The model is presented in detail in Section A of Supplemental Material, File S1, with an overview provided in Figure 2.
Figure 2.
The 17 possible states for two copies of each of two sites, for the analytical model. Each rounded rectangle represents a separate diploid individual. The two focal copies of the A site are represented by ○ and ●. The two focal copies of the B site are represented by □ and ▪. The shading of symbols, i.e., open vs. solid, has no meaning other than to distinguish focal copies. Haplotypes or parts of haplotypes that do not carry ancestral material (i.e., not carrying focal copies) are shaded. Coalesced sites are not shown.
The first key step in constructing the model is to derive the transition matrix giving the probabilities (going backward in time) of changing states. These probabilities depend on the biology of reproduction and inheritance. If meiosis occurs, there is a crossover between sites A and B with probability c. The probability of a mitotic crossover is per generation (which does not require meiosis). Regardless of reproductive mode, mitotic gene conversion can occur. With probability there is a mitotic gene conversion event whose tract length covers both sites. With probability a mitotic gene conversion event occurs where one end of the gene conversion tract lies at the breakpoint between the two sites, and the other end lies beyond them ( is the analogous probability for a meiotic gene conversion event, conditional on meiosis occurring). It is worth noting that enters the transition matrix for two separate reasons. It determines the probability that one site coalesces via mitotic gene conversion (e.g., transition from state S2 to S14; see Figure 2) and it determines the probability that samples at different sites on the same haplotype get split onto separate haplotypes by mitotic gene conversion (e.g., transition from state S3 to S9; see Figure 2). Note that gene conversion involving one site is functionally equivalent to a crossing over event. In contrast, only enters transitions involving coalescence affecting one or both sites. Using these parameters, the construction of the transition matrix is tedious but straightforward. Using first-step analysis (Wakeley 2009, Chap. 7) and following McVean (2002), we construct a system of equations for the expected value of the product of coalescent times at the two sites, given their current state z. These equations capture the expected time for the system to move out of the state z, before calculating the expected coalescent time of either one or both sites, given the new state k. These equations have the form:
| (4) |
where is the time to exit state z, is the probability that the system moves from state z to state k conditional on leaving state z, and is the expected time to coalescence of site x given it is currently in state k. As described in Section A of File S1, these components can be calculated from the transition matrix, either directly for discrete time or after appropriate transformation for the continuous time approximation (Möhle 1998; Wakeley 2009).
Following McVean (2002):
| (5) |
where is the expected product of the coalescent times at site A, where the two copies are sampled from haplotypes i and j; and at site B, where the two copies are sampled from haplotypes k and l (and different indexes denote other haplotype samples). Analogous to measuring from haploids where each haplotype represents an independent sample, we calculate assuming that each haplotype comes from a different individual (Figure 2) so that the three terms in the numerator represent coalescence times from states S1, S3, and S7.
We first consider the case of partial asexuality where sex may be rare at the individual level but is not too rare at the population level (i.e., but ). We find
| (6) |
where with scaled parameters and Simplifying the model by ignoring gene conversion and mitotic crossing over ( = 0), the result above is the same as the obligate sex result (Equation 3) but using an effective scaled crossover rate in place of ρ (Figure 3A).
Figure 3.
(A) Linkage disequilibrium, measured as when sex is high at the population level [i.e., ], measured as a function of the meiotic crossover rate ρ. Different frequencies of sex (σ) are shown. Other parameters: (B) when the frequency of sex is low [] and the only haplotype disrupting force is meiotic crossing over (). Different rates of sex () are shown. Other parameters: (C and D) when the frequency of sex is low [] as a function of the distance between two sites (measured in base pair distance), for different levels of mitotic gene conversion (). Results are shown without (C) and with (D) mitotic crossing over [i.e., with in (C) and in (D)]. Other parameters: (see Figure A in File S2 for similar plots using different values).
We next consider the case where sex is rare at the population level, as In the absence of mitotic gene conversion or mitotic crossing over () then:
| (7) |
where the rates of disruptive meiotic processes c, with ξ being a small term (). Equation 6 and Equation 7 differ in several important ways. First, their maximum values, and the conditions to achieve these maxima, differ. The maximum value of Equation 6 occurs as the haplotype disrupting forces (crossovers and gene conversion) become small, i.e., as In contrast, the maximum value of Equation 7 occurs as sex becomes increasingly rare, i.e., as Second, in Equation 6 has a strong dependence on physical distance because disruption via crossover or gene conversion is an increasing function of distance, i.e., is implicitly an increasing function of distance. In contrast, Equation 7 is very weakly dependent on physical distance through terms of (Figure 3B).
Equation 7 assumes no mitotic gene conversion or mitotic crossing over, but important changes to occur with either of these processes. An analytical approximation can be obtained but the expression is unwieldy (Section A of File S1). Both types of mitotic gene conversion events, represented via and as well as mitotic crossing over (), affect the leading-order term for and are functions of the distance between sites. Mitotic crossing over can be modeled as a linear function of distance d, Using a standard assumption of exponentially distributed gene conversion tract lengths (Wiuf and Hein 2000), the probabilities of mitotic gene conversion are given by and where λ is the average tract length and g is the probability of gene conversion initiation per base pair (more precisely, per breakpoint between adjacent base pairs). The derivation is provided in Section A of File S1.
Figure 3C shows that declines with physical distance when there is mitotic gene conversion but no mitotic crossing over. Note that does not decline down to zero with distance as it does in the classic model (Equation 3) of meiotic crossing over. Because gene conversion probabilities change slowly for there is little decline in beyond this point. Surprisingly, is not always a monotonically declining function of the probability of gene conversion initiation g (or the scaled parameter ), especially when [Figure B(a) in File S2]. Consequently, a species with a lower frequency of gene conversion events (i.e., smaller g) can have larger for small d but smaller for large d compared to an otherwise similar species with larger g (Figure 3C). This behavior of with respect to g is likely due to the dual (and conflicting) roles of gene conversion in increasing both the probability of coalescence and disruption of haplotypes. In contrast, mitotic crossing over, which only affects haplotype disruption, affects monotonically as expected [Figure B(b) in File S2]. The addition of mitotic crossing over reduces the minimum value of (Figure 3D). Even with mitotic crossing over, does not go to zero at large distances and can be considerably greater than zero when gene conversion is high (see Section A of File S1). The minimum value reached by is independent of the rate of mitotic crossing over (provided it is not zero), although the distance at which the minimum is reached is shorter with higher rates of mitotic crossing over.
Simulation Algorithm
We have previously developed an algorithm to build genealogies of facultative sexual organisms at a single nonrecombining locus (Hartfield et al. 2016). This algorithm simulates genealogies of n samples, of which are paired and the remaining samples are unpaired. The algorithm proceeds in a similar manner as other coalescent simulations, in that it tracks the genetic histories of samples into the past, sequentially enacting events that affect the genetic history (e.g., coalescence, sexual reproduction). The relative probability of each event occurring per generation is used to determine what the next event is, and at which time in the past it arises. To further investigate the effects of facultative sex on linkage disequilibrium, we extended this previous routine to consider coalescent histories of multiple sites and how various recombination phenomena affect how genetic histories are correlated along chromosomes. In the Appendix, we describe how the crossover routine of Hudson (1983) and the gene conversion routine of Wiuf and Hein (2000) are extended to consider the effects of facultative sex. As a consequence, the updated coalescent simulation now models the effects of meiotic and mitotic recombination on facultative sex, the outcomes of which are summarized in Figure 1.
Measuring linkage disequilibrium from simulations
We used the updated coalescent simulation to calculate expected linkage disequilibrium in facultatively sexual organisms. Following a single simulation of a coalescent process, a series of j genealogies are produced, one for each nonrecombined part of the genetic segment. Polymorphisms are added to each branch of the genealogy, drawn from a Poisson distribution with mean for the mutation rate of the segment covering of L total sites given μ is the mutation rate for a segment of L sites; and the length of branch i in segment j.
For each simulation, we measured linkage disequilibrium over each pairwise combination of polymorphisms; this measure was then normalized to Once was measured over all simulations, values were placed into 20 equally sized bins based on the distance between the two polymorphisms. However, the number of pairwise samples were different for each of the 20 bins. Samples in the last two bins produced noisy estimates of linkage disequilibrium, so we only reported linkage disequilibrium estimates from the first 18 bins. We randomly subsampled data in bins 1–18 so that they include the same number of pairwise comparisons as in the smallest bin that contained data, to standardize bin size per simulation. Mean values per bin were recorded for each simulation run. We then calculated the mean of means per bin over all 1000 simulations, omitting points where data were not present in a bin for a simulation. Confidence intervals (95%) were calculated as for s the SD for the bin; n, the number of points in the bin (maximum of one for each simulation run); and the 97.5% quantile for a t-distribution with degrees of freedom.
Measuring correlation in coalescence time between sites
For some cases with low sex and mitotic gene conversion, we measured the correlation in coalescence times between sites as a function of the distance between them, to investigate how these values relate to observed linkage disequilibrium patterns. For each simulation run, we obtained the number of nonrecombined regions and the times at which the ancestral segment of that region for each individual coalesced. If >100 segments existed, these were subsampled down to 100. We calculated the Pearson correlation in coalescent times for all segments; values were then placed into 1 of 20 bins based on the distance between blocks (the location of each segment was given by its midpoint). Values were only reported for the first 18 bins, with further subsampling performed on bins 1–18 so that they contained the same number of comparisons as the smallest bin that contained data for that simulation. The mean bin value for a simulation, the mean of means over all simulations, and 95% confidence intervals were calculated using the same method as for linkage disequilibrium measurements.
Data availability
The new simulation program, FacSexCoalescent, along with documentation is available at http://github.com/MattHartfield/FacSexCoalescent. We first rebuilt the single-locus simulation program in C to greatly increase execution speed, before adding the crossover and gene conversion routines. As with the previous version of the simulation, FacSexCoalescent uses a timescale of generations while ms uses generations. The documentation specifies other cases where FacSexCoalescent inputs and outputs differ from other coalescent simulations. We performed various tests of the simulation as described in Section B of File S2.
File S1 is a Mathematica notebook of analytical derivations. File S2 contains additional results and figures. File S3 is a copy of the simulation code and manual. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6949877.
Simulation Results
Linkage disequilibrium with crossing over
High frequencies of sex:
We looked at how patterns of linkage disequilibrium are affected by crossovers when sexual reproduction is frequent (that is, the scaled rate of sex ). Analytical results (Equation 6) suggest that the effect of meiotic crossovers on linkage disequilibrium is equal to that observed in an obligately sexual population with a rescaled probability (for the crossover probability over distance d). To further investigate this pattern, we simulated genealogies over sites with a fixed population-level meiotic crossover rate over the entire ancestral segment which acts during sexual reproduction. Results are reported over the first 900 sites.
Figure 4A plots how linkage disequilibrium decays over this region with different probabilities of sex, varying from (i.e., obligate sex) to . As expected, the decay in linkage disequilibrium is weakened with lower sex, since there exists fewer opportunities for crossovers to act (compare Figure 4A to analytical expectations in Figure 3A). We confirm that the observed decay is equivalent to an obligately sexual population with in three ways. First, we ran equivalent (but haploid and sexual) simulations in ms, using the rescaled crossover probability, and observed that the decay in linkage disequilibrium matches results from the facultative-sex simulation (Figure 4B). Second, we used the ‘pairwise’ routine in the LDhat software (McVean et al. 2002) to estimate crossover rates from facultative-sex simulation data and observed that they scaled linearly with σ (Figure 4C). Finally, Figure 4D plots linkage disequilibrium values for all facultative-sex coalescent simulations as a function of the effective recombination rate, alongside the analytical expectation for (Equation 6). is calculated after removing sites with minor allele frequency <10%, as is known to overestimate if all allele frequencies are considered. We see that the decay in linkage disequilibrium over all simulations is close to, but slightly overshoots, the theoretical expectation (Equation 6). Similar behavior was observed by McVean (2002) in their figure 3 (compare solid line to square points in that figure).
Figure 4.
Effects of facultative but not very low rates of sex (i.e., ) on estimates of meiotic crossing over. (A) Decay of linkage disequilibrium over 900 sites, as a function of distance between two sites. Different colors denote individual rates of sex, as shown in the legend. Solid line is the mean value over 1000 simulations; fainter curves represent 95% confidence intervals. A total of 50 paired samples were simulated (100 samples in total), scaled mutation rate scaled crossover rate during sex (B) As in (A) but instead shows results from obligate sex simulations ran using ms, using a crossover rate equal to as shown in the legend. Due to binning of samples, is shown for distances between 25 and 875 sites apart in (A and B). (C) Estimates of R using LDhat, as a function of the effective crossover rate used in the facultative-sex coalescent simulation. Points are mean estimates from 1000 simulations, bars are 95% confidence intervals. Black line denotes dashed red line is the linear regression fit. (D) Plot of all simulation results in (A) but instead as a function of the rescaled recombination rate (plotted on a natural log scale) and after omitting polymorphisms with minor allele frequency <10%. Dotted lines show analytical expectations (Equation 6). Note the different y-axis scale compared to (A).
Low frequencies of sex:
When the probability of sex is low [i.e., ], samples will diverge within individuals (Balloux et al. 2003; Bengtsson 2003; Ceplitis 2003; Hartfield et al. 2016). We examined how this allelic sequence divergence affects linkage disequilibrium by running simulations with (specifically we investigated 2, and 0.2), but with a fixed scaled crossover rate Although this scaled crossover rate is low, there is a high crossover rate when sex does occur, hence we expect to see some breakdown of linkage disequilibrium along the simulated genotype. We ran simulations over a larger number of sites () so there was enough distance to observe a decay in disequilibrium.
Figure 5A displays the linkage disequilibrium observed in low-sex cases, along with analytical expectations (Equation 7). After removing sites with minor allele frequency <10%, the simulation exhibits close to 0.45, which is as given by Equation 6 as the crossover rate goes to zero. However, lower rates of sex result in higher values of linkage disequilibrium, indicating that classic estimates of using the rescaled recombination rate (i.e. Equation 6) do not properly quantify disequilibrium when sex is low. Equation 7 captures the general behavior of under low frequencies of sex (i.e., elevated values and a weaker dependence on the meiotic crossover rate), but there are several reasons why the results do not quantitatively match. Specifically, the analytical result is based on rather than and finite sample sizes also introduce additional complications ignored in the calculation of expected Our analytical model is intended to allow comparisons of the main patterns with the comparable sexual model, rather than providing precise predictions of the quantity as estimated by empiricists (which can instead be estimated using the simulation).
Figure 5.
(A) Decay of linkage disequilibrium over 90,000 sites as a function of the rescaled recombination rate (on a natural log scale) and after omitting polymorphisms with minor allele frequency <10%. Different colors denote individual rates of sex, as shown in the legend. Solid line is the mean value over 1000 simulations; fainter curves represent 95% confidence intervals. A total of 50 paired samples were simulated (100 samples in total), scaled mutation rate scaled crossover rate over all 100,001 sites Colored dash-dotted lines are low-sex analytical expectations for (Equation 7). is shown for distances between 2500 and 87,500 sites apart. Results for short distances (125–4375 sites apart) are shown in Figure E in File S2. (B) Histogram of minor allele frequencies for the low-sex scenarios; the bin frequency is measured over all 1000 simulations. Bar colors correspond to the same rates of sex as used in (A).
Elevated occurs under low sex due to allelic sequence divergence creating highly differentiated haplotypes consisting of polymorphisms at intermediate frequencies (50%). These polymorphisms arise due to a lack of genetic segregation creating highly differentiated haplotypes (Balloux et al. 2003; Bengtsson 2003; Ceplitis 2003; Hartfield et al. 2016). Figure 5B shows the density of minor allele frequencies over all simulation data, demonstrating that the case has many sites with minor allele frequency between 45 and 50%. Consequently, is higher over the genomic sample than expected based on obligate sex results using the effective crossover probability We also observe that linkage disequilibrium decay is only weakly affected by the meiotic crossover frequency, in line with analytical expectations (Equation 7).
Linkage disequilibrium with mitotic gene conversion
High frequencies of sex:
We ran simulations with mitotic gene conversion to investigate its effect on linkage disequilibrium. We define gene conversion using the population-level rate per sample: We first ran simulations with no meiotic crossovers (i.e., some degree of sexual reproduction occurs, but not any meiosis-related processes); here, the decay of linkage disequilibrium is independent of the rate of sex (provided sex is not too low; Figure 6A). This decay is similar to that observed in obligate sexual populations experiencing the same gene conversion rate (Figure 6B). When meiotic crossovers are included with rate disequilibrium profiles separate out depending on the frequency of sex (Figure 6C) and are similar to those arising in obligate sexuals that experience the same gene conversion rate and an effective crossover probability (Figure 6D). The pattern of linkage disequilibrium decay is more dependent on the probability of sex when the frequency of mitotic gene conversion is low, relative to the crossover probability c (contrast Figure 6, which uses with Figure F in File S2, which uses ).
Figure 6.
Decay of linkage disequilibrium over 900 sites, as a function of distance between two sites as caused by mitotic gene conversion with high rates of sex (). A total of 50 paired samples are taken from a population of size scaled mutation rate and mitotic gene conversion occurs with rate (with average gene conversion tract length sites). Meiotic crossovers are either (A and B) absent or (C and D) present at rate (A and C) Results from the facultative-sex coalescent simulation with different probabilities of sex. Colors are as shown in the legend; shaded bands are 95% confidence intervals. (B and D) Results from ms with 100 samples and the same gene conversion rate, with crossover probability in (D). Note only one ms comparison is plotted in (B). Equivalent results with are shown in Figure F in File S2. is shown for distances between 25 and 875 sites apart.
Low frequencies of sex:
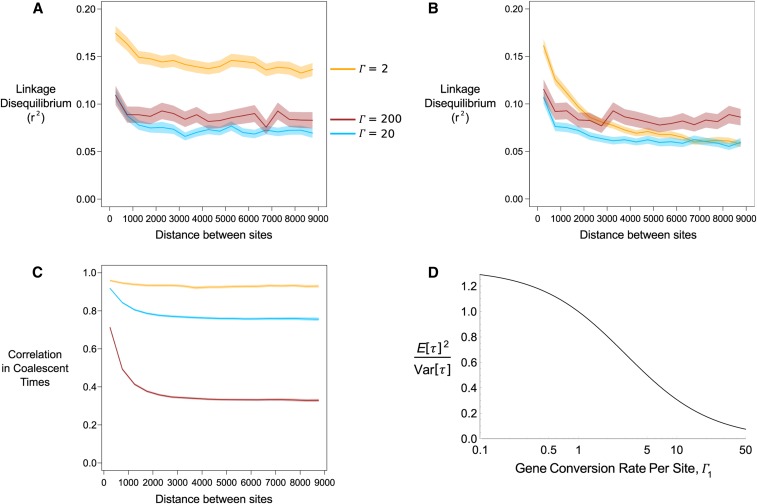
With low frequencies of sex [], within-individual diversity is affected by the ratio of sex to gene conversion at a site, denoted φ (Hartfield et al. (2016); φ is defined mathematically below). If sex occurs more frequently than gene conversion (), elevated within-individual diversity should be observed. However, if gene conversion arises at the same frequency or more often than sex (), then gene conversion will lead to reduced within-individual diversity compared to a sexual population (Hartfield et al. 2016, equation 11). Hence we next ran simulations with different φ values to explore the relative effects of both phenomena on linkage disequilibrium.
We considered a diploid population from which we simulated 50 paired samples, and a genetic segment that is sites long. To focus on the effects of gene conversion, we assumed no meiotic crossing over and only mitotic gene conversion was considered, with events having a mean tract length of sites, matching estimates of noncrossover events obtained from yeast (Judd and Petes 1988; Martini et al. 2011). We fixed and varied so that the ratio [for the number of breakpoints in units of mean gene conversion length], which determines neutral diversity at a single site, equals either 10, 1, or 0.1 (requiring 20, and 200, respectively). Note that we define the probability of gene conversion per haplotype rather than per diploid genotype, so the probability of gene conversion is scaled by as opposed to the scaling used in Hartfield et al. (2016) (i.e., there is an extra factor of two in the denominator of φ to account for two haplotypes per individual).
Figure 7A demonstrates the unusual behavior associated with high gene conversion with low rates of sex, with being a nonmonotonic function of the gene conversion frequency, in line with analytical findings (Figure 3C). Mitotic crossing over at rate breaks down linkage disequilibrium over a longer distance for and 20, but not for (Figure 7B). Both results are in line with analytical findings: is a nonmonotonic function of gene conversion when sex is rare (Figure 3C) and the presence of mitotic recombination can reduce long-distance , unless mitotic gene conversion acts at a much higher rate (Figure 3D).
Figure 7.
(A) Plot of linkage disequilibrium, measured using as a function of distance between two sites. For a fixed rate of sex gene conversion is set to (orange line), 20 (blue line), or 200 (red line) with Shading around lines indicate 95% confidence intervals. (B) As in (A) but also including mitotic recombination with rate Results over short distances for (A and B) (25–875 sites apart) are presented in Figure G in File S2. (C) Correlation in coalescent times ( in Equation 8) between sites for the three values, assuming no mitotic crossing over (i.e., ). Note that for and 200, confidence intervals are only slightly thicker than the mean line. (D) Ratio of for two samples taken from the same individual, as a function of the scaled gene conversion rate per site with (A–C) are shown for distances between 250 and 8750 sites apart.
Elevated linkage disequilibrium is likely related to the reduced mean coalescence times that arise under frequent gene conversion. To further understand this behavior, we can relate the observed values to Equation 11 of McVean (2002), which demonstrated how can be written as a function of both the correlation in coalescent times between sites and the ratio of the mean coalescent time to the variance:
| (8) |
in Equation 8 represents correlation in coalescent times between pairs of sites (e.g., is the correlation in coalescence times where site one is taken from haplotype i and j, and site two is taken from haplotype k and l). and are the mean and variance of coalescent times. Equation 8 shows that is not just reduced with lower covariances between pairs of loci, but it also decreases with higher This ratio equals one under the standard coalescent, but low sex alters the mean and variance of coalescent times (Hartfield et al. 2016), which will also affect this ratio and subsequently alter linkage disequilibrium values. Figure 7C plots the covariance in coalescent times over all simulations, for two sites sampled from a single individual. We see that they are consistently lower with higher rates of gene conversion, reflecting how genetic material is more frequently transferred between samples. We next looked at the ratio which can be calculated from equations 11 and 12 of Hartfield et al. (2016). We focused on the within-individual coalescence times, as these are directly affected by within-individual mitotic gene conversion. This ratio is shown in Figure 7D for as a function of the mitotic gene conversion rate for a single site, . As increases, the ratio decreases, leading to the observed increase in (Figure 7D). This result suggests that high rates of within-individual gene conversion distorts underlying genealogies, so that observed linkage disequilibrium is higher than that expected based on the rate of gene exchange alone. In contrast, meiotic crossing over has no direct effect on this ratio.
In File S2, we investigate how linkage disequilibrium is affected if we alter g and λ while fixing the product Linkage disequilibrium decays more rapidly for higher g values with lower λ as there are more gene conversion events that break apart coalescent histories between individual sites.
Effect of population subdivision
Measurements of linkage disequilibrium are known to increase under population structure with obligate sex (Wakeley and Lessard 2003), as polymorphisms that only appear in specific regions will naturally be in disequilibrium, increasing Facultatively sexual organisms are known to show strong geographic differentiation (Arnaud-Haond et al. 2007). Hence we examined the effects of population structure in facultatively sexual organisms. We assumed an island model, consisting of four demes with a scaled migration rate between them (for the total population size across all demes). A total of 50 paired samples were simulated, with 13 samples taken from two demes, and 12 from the other two. Population-scaled parameters are subsequently defined relative to [i.e., ].
For high-sex cases () and low-sex cases [] where mitotic gene conversion is present, results are qualitatively similar to those observed for a single population (File S2). For the low-sex case with meiotic crossing over, we ran simulations with and equal to 20, 2, or 0.2 and compared them to an obligate-sex case with the same crossover rate with different rates of migration. With high migration (), the results are similar to what is observed without population structure, with disequilibrium visually decaying along the genome sample for Yet values are lower than in the panmictic case (compare the red line in Figure 8A with Figure 5). With lower migration (), disequilibrium values are unexpectedly reduced as the probability of sex decreases (Figure 8B). The reason for this unintuitive result is due to the partitioning of low-frequency polymorphisms under both low sex and population structure. With low migration rates, strong population structure is present, so polymorphisms are localized to specific demes. Low frequencies of sex further partition polymorphisms within demes on diverged haplotypes (Figure 5E in Hartfield et al. 2016). Hence the presence of rare sex, alongside high population structure, creates more polymorphisms at lower frequencies compared to populations with higher probabilities of sex (Figure 8, C and D). These polymorphisms tend to have small values for thereby reducing the average value. After removing polymorphisms with minor allele frequency <15%, estimates of become similar for all rates of sex, although results are still slightly lower than other cases for (Figure J in File S2).
Figure 8 (A and B).
Decay of linkage disequilibrium over 90,000 sites from samples taken over a subdivided population, as a function of the rescaled recombination rate (plotted on a natural log scale). Different colors denote individual rates of sex, as shown in the legend. Solid line is the mean value over 1000 simulations; fainter curves represent 95% confidence intervals. A total of 50 paired samples were simulated (100 samples in total) over four demes, scaled mutation rate scaled crossover rate over entire ancestral tract scaled migration rate is either (A) or (B) Black dashed line is equivalent obligate sex simulation run using ms with 100 samples. is shown for distances between 2500 and 87,500 sites apart. (C and D) Histogram of minor allele frequencies, with the bin frequency measured over all 1000 simulations. Bar colors correspond to the same rates of sex as used in (A and B).
Discussion
Summary of results
Existing single-locus theory for facultatively sexual organisms shows behavior distinct from sexual cases only with extremely low frequencies of sex [] (Bengtsson 2003; Ceplitis 2003; Hartfield et al. 2016). In this article, we provide novel analytical and simulation results to investigate how correlations in genetic diversity across loci are affected by facultative sex. We also provide an updated version of a simulation package and explain how existing crossover (Hudson 1983) and multi-site gene conversion routines (Wiuf and Hein 2000) can be included in facultative-sex coalescent processes, to investigate how they affect gene genealogies. This program can be used to simulate ancestral recombination graphs of facultatively sexual organisms.
When the frequency of sex is high (), we observe that the breakdown in linkage disequilibrium in a genetic sample is similar to that observed in an obligate sex model using an effective crossover probability (Figure 3A and Figure 4). This result reflects similar behavior in partially self-fertilizing organisms (Nordborg 2000), where the effective crossover rate is equal to for inbreeding rate F (although this scaling breaks down with high self-fertilization and crossover rates; Padhukasahasram et al. 2008; Roze 2009, 2016).
Hence if there exists knowledge of meiotic crossover rates, then one can use linkage disequilibrium data to estimate the overall frequency of sex. The situation becomes more complicated if mitotic recombination is present as it also breaks down linkage disequilibrium, even under low frequencies of sex. If sex is frequent but crossing over is rare, mitotic gene conversion principally affects linkage disequilibrium (Figure 6A). Once crossing over probabilities become high, then these principally break down linkage disequilibrium, so the effective crossover rate scaling still holds (Figure 6B).
When rates of sex become low [], the decay in linkage disequilibrium can no longer be captured by rescaling as the distribution of genealogies becomes fundamentally different than when sex is common (Figure 3, B–D). In the absence of gene conversion, becomes elevated with low rates of sex, reflecting more linked polymorphisms present at intermediate frequencies (Figure 5). If mitotic gene conversion is present, the ratio between rates of sex and gene conversion φ becomes a strong determinant of linkage disequilibrium, with unexpected behavior arising if gene conversion occurs at high rates relative to sex. Increasing gene conversion will first reduce overall disequilibrium values due to gene exchange breaking down associations between sites. Yet very high rates of gene conversion then cause elevated linkage disequilibrium values, which is a consequence of how gene conversion changes the distribution of coalescence times. Adding mitotic crossovers reduces the minimum observed linkage disequilibrium, unless mitotic gene conversion occurs at much higher rates (Figure 3, C and D, and Figure 7). Finally, low sex combined with low migration rates in subdivided populations also reduces values due to more low-frequency polymorphisms being present within demes (Figure 8). These nonintuitive effects illustrate the value of explicitly modeling genetic diversity under low rates of sex when considering genomic data for facultatively sexual organisms.
Future directions
The creation of the new coalescent algorithm that accounts for facultative sex, crossing over, and gene conversion can be used as a basis for inferring these processes from genomic data. This can be achieved by using coalescent simulations to create likelihood profiles over two loci (Hudson 2001; McVean et al. 2002; Wall 2004; Auton and McVean 2007). An alternative approach would be to use approximate Bayesian computation to recurrently simulate different outcomes, each time comparing them to the real data, and keeping those that match sufficiently well to build a pseudolikelihood (Sunnåker et al. 2013). Simulation results also suggest that it is important to jointly consider both genome-wide diversity and linkage disequilibrium if we wish to infer the effects of sex, meiotic crossovers, and gene conversion, especially if mitotic gene conversion is pervasive (Figure 7).
We anticipate that the FacSexCoalescent simulation can be expanded upon in the future to account for more complex scenarios. The only population structure we considered is an island model, although bottlenecks or unequally sized subpopulations are common (Pool and Aquadro 2006; Veeramah and Hammer 2014; Frantz et al. 2016). The gene conversion model can also be expanded upon to consider context-dependent events (for example, GC-biased gene conversion; Duret and Galtier 2009). Given ongoing debates on how gene conversion potentially affects genetic diversity and fitness in facultatively sexual organisms (Mancera et al. 2008; Flot et al. 2013; Tucker et al. 2013), a deeper understanding of how gene conversion affects the distribution of genetic diversity can shed further insight into what processes influence genetic evolution in facultatively sexual organisms.
Acknowledgments
We thank two anonymous reviewers and John Wakeley for providing constructive comments on the manuscript. M.H. was supported by a Marie Curie International Outgoing Fellowship, grant number MC-IOF-622936 (project SEXSEL), and an European Research Council (ERC) grant (FP7/20072013, ERC grant 311341) awarded to Thomas Bataillon. This work was also supported by Discovery Grants (A.F.A. and S.I.W.) from the Natural Sciences and Engineering Research Council of Canada.
Appendix: Implementing Recombination into the Facultative-Sex Simulation Algorithm
Overview of Basic Coalescent Simulation
Here we outline the implementation of meiotic and mitotic recombination events in the facultative-sex coalescent simulation routine (Hartfield et al. 2016). We describe the probability that set events occur per generation; that is, both the time in the past to the next event and resolution of events are based on unscaled probabilities (as opposed to rates, where a probability is multiplied by the population size to give the expected number of events per generation). We define as the probability that none of the x paired samples are split by sex, and as the probability of any event (e.g., coalescence, recombination) given that none of the paired samples are affected by sex. The absolute time to the next event is drawn from a geometric distribution with parameter this time is rescaled by so that it is on a coalescent timescale. It is subsequently determined whether any and, if so, how many of the x paired samples segregate into different individuals due to sexual reproduction. If k of x paired samples are produced via sex, then new unpaired samples are created. The total probability of any other event occurring is then recalculated, conditional on this updated sample configuration. It is determined whether any such event occurs, and which type of event if one does arise; the sample configuration is then updated appropriately. Note that if sex is common, the first term in is large and all paired samples are rapidly split by sex, so the model then behaves like a haploid process. If the population is structured as an island model, the logic is similar but we instead track paired and unpaired haplotypes in deme i, and consider total haplotypes over all subpopulations. We refer the reader to Hartfield et al. (2016) for further details of the basic coalescent simulation.
Implementing Meiotic and Mitotic Crossing Over
We outline the probability of either a crossover or gene conversion event occurring each generation and then implement these probabilities into the calculation of as described above. As with the single-locus routines, we assume that sexual reproduction occurs first, followed by subsequent gene exchange events. Let be the absolute meiotic crossover probability between any two adjacent sites, conditional on sex having occurred; is the mitotic crossover probability (which is not conditional on the reproductive mode); and L is the number of sites that the genetic samples cover. Assuming and are small, the total meiotic crossover probability in each individual at the start of the process is We assume that the total recombination probability is low [i.e., ] so we do not consider outcomes where more than one crossover event occurs per generation.
Following sexual reproduction, crossovers act on unpaired samples with probability The quantity is the “effective” crossover length summed over all y unpaired samples. We include this term to ensure that unnecessary crossover events are not considered, thus speeding up the routine (Hein et al. 2005). is defined as follows: let be the first ancestral site in unpaired sample i, and let be the last ancestral site. Then, equals the total number of breakpoints where a crossover can create two new samples, each carrying ancestral material. Note that any sites within individual haplotypes that have reached their most recent common ancestor are converted into nonancestral material (Hein et al. 2005). Then, This crossover event creates two new samples, with each part carrying ancestral material (Figure 1A).
If k out of the x paired samples segregate via sex into new unpaired samples, then the crossover probability is increased by adding on an extra term. Here is the effective crossover length over the new unpaired samples, defined in a similar manner to . The samples are a transitory class of unpaired haplotypes, created through sexual reproduction segregating paired samples into distinct individuals (see also Figure 1, B and C). Because they are already determined to have been created by sex by an earlier step in the algorithm, there is no factor σ contributing to their probability of experiencing meiotic crossing over. Those that do not undergo crossing over become regular unpaired samples (Figure 1B); those that do are transformed into regular paired samples (Figure 1C).
Mitotic crossing over can act on the remaining paired samples that do not undergo sexual reproduction. This event occurs with probability with being the effective crossover length measured over both arms within the remaining paired samples. is measured in a different manner than for unpaired samples. Let i be an individual where both haplotypes and are sampled. Define as the first ancestral site in each of these samples and as the last ancestral sites. Then, the first ancestral site at which mitotic crossing over is valid in individual i is similarly, Then, and Mitotic crossing over exchanges genetic material between the two samples within an individual (Figure 1D).
These probabilities are considered alongside other events to determine whether the next event involves a meiotic crossover. If it is chosen, then one of the appropriate samples is picked at random (weighing by the length of extant breakpoints present in each sample), and the appropriate outcome is enacted. Note that if the potential for crossing over is high (i.e., if the probability of sex and crossing over is high and there are a large number of samples) then the net recombination probability can exceed one, as the assumption that only up to one recombination event occurring per generation is violated, causing the algorithm to terminate. Hence large crossover probabilities should be avoided.
Implementing Meiotic and Mitotic Gene Conversion
To account for both meiotic and mitotic gene conversion events (Figure 1, E–G), up to four additional parameters are specified. Two new parameters are and g, the probabilities of either meiotic or mitotic gene conversion occurring with its leftmost boundary arising on the recipient homolog at a given site. We also define the average length of gene conversion events, denoted for meiotic gene conversion and λ for mitotic gene conversion. We implement and extend the algorithm of Wiuf and Hein (2000) to calculate the probability of either type of gene conversion event occurring each generation. Here, the length of gene conversion events (scaled by the total number of breakpoints) is drawn from an exponential distribution with parameter the number of breakpoints in units of average gene conversion length (Wiuf and Hein 2000). We define distinct for meiotic and mitotic gene conversion events. Further details of the mathematical derivations are in Section B of File S1.
There also exists a special class of gene conversion events, where conversion initiates outside the ancestral tract and extends completely over ancestral material (Figure 1H). If there exist pairs after k of them are split by sex, then the probability of this event happening equals (a full derivation is presented in Deriving Probability of “Complete” Gene Conversion below and in Section C of File S1).
Determining the Type of Gene Conversion (Meiotic or Mitotic)
To understand how the different events (meiotic and mitotic gene conversion) are considered, it is easiest to relate calculations to the obligate-sex case with a single type of gene conversion event. Here, the product of the gene conversion probability (using to differentiate this general gene conversion probability from the mitotic gene conversion notation) and the number of breakpoints is such that Then, the probability of a disruptive gene conversion event in a sample of length L is where is the probability that the leftmost edge of a gene conversion tract is at a given site and
| (A1) |
is the number of breakpoints in units of average gene conversion length (here, too, we use and to define this general gene conversion process). accounts for gene conversion events that only partly lie in ancestral material (i.e., only one end of the gene conversion lies in ancestral material) as well as those that lie entirely within this region (i.e., both breakpoints lie within ancestral material). Equation A1 assumes that the length of gene conversion events (scaled by the total number of breakpoints) is drawn from an exponential distribution with parameter (Wiuf and Hein 2000). Equation A1 also disregards possible edge effects (e.g., if the ancestral tract lies near the chromosome edge). In the facultative-sex coalescent, we can partition this probability depending on the type of conversion event (meiotic or mitotic) and the number of each type of sample (paired or unpaired) present at the time. Let there be paired samples after k of them have split after sex, making haplotypes in total; y unpaired samples; and new unpaired samples following genetic segregation. After partitioning over all possible outcomes, the total probability of disruptive gene conversion equals:
| (A2) |
Here, and are equal to above, with parameters and for mitotic and meiotic gene conversion, respectively. As segregation has already been resolved, the remaining paired samples reproduce asexually so only they can be subject to mitotic gene conversion. Unpaired samples can be subject to both meiotic and mitotic gene conversion; hence for each unpaired sample (y in total) we also have to consider the probability of sex σ. Note that there is no σ term when considering the new unpaired samples, as they have already undergone sex by this point in the algorithm. In contrast to the crossover procedure, we do not weigh samples by the number of breakpoints within ancestral material; gene conversion events affecting only nonancestral material are allowed to occur.
When a disruptive gene conversion event occurs, it is first determined if it acts on unpaired or paired samples. The probability that gene conversion acts on a paired sample is where is given by Equation A2, and one minus this probability is the chance it acts on unpaired samples. If acting on a paired sample, then only mitotic gene conversion can occur. If acting on unpaired samples, a further random draw is made to determine whether the gene conversion event is meiotic or mitotic. Let  be the probability of a gene conversion event that occurs on an unpaired sample. If an unpaired sample undergoes conversion, the probability that the event is mitotic equals
be the probability of a gene conversion event that occurs on an unpaired sample. If an unpaired sample undergoes conversion, the probability that the event is mitotic equals  ; a similar calculation can be made for meiotic gene conversion.
; a similar calculation can be made for meiotic gene conversion.
Drawing Start and End Breakpoints Following Gene Conversion
The scaling terms and account for the fact that gene conversion does not necessarily take place entirely within the gene tract, but may only partially overlap with it. We follow the logic outlined in Wiuf and Hein (2000) to accurately model the relative frequency of each of these events. Given the tract length in units of conversion events (which can be either Q or ), is the probability that if gene conversion starts in the sample, it will also end within it (Wiuf and Hein 2000, Equation 2). One can then define the probability that both breakpoints occur within the sample (Wiuf and Hein 2000, Equation 11):
| (A3) |
The probability that only one breakpoint falls within the sample equals (Wiuf and Hein 2000, Equation 12). We first choose whether one or both breakpoints lie within the sample, as determined by Equation A3. The appropriate start and end points are then chosen from the relevant probability distributions. Wiuf and Hein (2000) determined how the distribution of breakpoints depends on whether one or both breakpoints lie within the genome tract. For example, if only one breakpoint lies in the tract then it is likelier to occur closer to one of its edges. When choosing gene conversion breakpoints, they are selected by calculating the cumulative distribution function (CDF) for the event, drawing an initial start or end point from a uniform distribution, and then plugging this uniform draw into the inverse CDF to obtain the true start or end point. The CDFs are obtained from the relevant probability distribution functions outlined by Wiuf and Hein (2000). Note that the resulting outputs are continuous variables lying between zero and one, while the simulation program assumes discrete breakpoints. Hence after the relevant breakpoint locations have been found, it is then converted into the appropriate discrete value lying between 1 and including these values. Further details on the following derivations are provided in Section B of File S1.
If two breakpoints are chosen, the joint probability distribution of start points s and end points t equals (Wiuf and Hein 2000, Equation 4). By integrating out t from s to 1, one obtains the marginal density of start points, (Wiuf and Hein 2000, caption of figure 4). The CDF of s can then be calculated as:
| (A4) |
To choose a start point, we draw a value between 0 and 1 from a uniform distribution and plug it into which equals:
| (A5) |
where W is the Lambert function (Abramowitz and Stegun 1970). To draw the respective end point, we first need to determine the distribution i.e., the density of end points given a starting point s. This function is also equal to From this function, we obtain the CDF of T given s as well as the inverse CDF:
| (A6) |
| (A7) |
Equation A7 is then used to determine the end point of the gene conversion event, which automatically lies within the length of the genetic sample. If the chosen end point is the same as the start point, then another end point is chosen so that they are distinct.
If one breakpoint is chosen, it can be the start or end of gene conversion with equal probability (Wiuf and Hein 2000, Equation 7). If it is chosen to be the end point of gene conversion initiating outside the tract, then the start point is set to zero (i.e., the far-left edge of the tract). The probability density of end points t is (Wiuf and Hein 2000, Equation 8). This function is left skewed; end points are likely to be near the left-hand side of the genetic sample. The CDF and inverse CDF can be calculated as:
| (A8) |
| (A9) |
If the single breakpoint is instead a start point, then the end point is set to the extreme right side of the sample. The probability density of start points is given by (Wiuf and Hein 2000, Equation 6). This function is right skewed; start points are likely to appear toward the end of the sampled genome. The CDF and inverse CDF equal:
| (A10) |
| (A11) |
Before gene conversion is carried through, it is first checked whether it would result in a sample that does not carry any ancestral material. These fully nonancestral samples can arise if either (1) conversion acts on an unpaired sample, in a region spanning entirely nonancestral material; or (2) conversion acts over all remaining ancestral material in a paired sample, rendering it nonancestral. In case (1), the action stops without creating this “ghost” sample. In case (2), gene conversion causes a within-individual coalescent event, converting the paired sample into an unpaired sample. The recipient sample becomes nonancestral and is no longer tracked.
Deriving Probability of “Complete” Gene Conversion
Let Q be the mean scaled length of mitotic gene conversion events. Following Wiuf and Hein (2000), the length of gene conversion events can be drawn from an exponential distribution with parameter Q. Let a gene conversion event start at a distance x from the focal sequence (where distances are scaled by the number of breakpoints ). The gene conversion event will therefore cover the focal sequence with probability The probability of a complete gene conversion occurring over all paired haplotypes [of which there exist ], and over the entire density of conversion breakpoints [of which there exists per length of focal sequence] equals Solving the integral gives the probability
Note that if then this probability goes to infinity as In this case, the average gene conversion length is much larger than the genetic sample being simulated (i.e., ), so any gene conversion event is likely to affect the entire genetic region. The reason this discontinuity arises is because the coalescent process assumes that no more than one event occurs per generation. Wiuf and Hein (2000) ensures this logic is maintained by assuming Furthermore, a small Q value would invalidate the assumption used to compute specifically, conversion events that initiate outside the sample but end within it only do so in regions near to the genetic sample [since the probability of these events equals if initiating breakpoints away from the sample]. Hence, while the simulation can be run with very small Q values, it is inadvisable to do so as erroneous genealogies may be produced.
Footnotes
Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6949877.
Communicating editor: J. Wakeley
Literature Cited
- Abramowitz M., Stegun I., 1970. Handbook of Mathematical Functions. Dover Publications, New York. [Google Scholar]
- Arnaud-Haond S., Duarte C. M., Alberto F., Serrão E. A., 2007. Standardizing methods to address clonality in population studies. Mol. Ecol. 16: 5115–5139. 10.1111/j.1365-294X.2007.03535.x [DOI] [PubMed] [Google Scholar]
- Auton A., McVean G., 2007. Recombination rate estimation in the presence of hotspots. Genome Res. 17: 1219–1227. 10.1101/gr.6386707 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Balloux F., Lehmann L., de Meeûs T., 2003. The population genetics of clonal and partially clonal diploids. Genetics 164: 1635–1644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bengtsson B. O., 2003. Genetic variation in organisms with sexual and asexual reproduction. J. Evol. Biol. 16: 189–199. 10.1046/j.1420-9101.2003.00523.x [DOI] [PubMed] [Google Scholar]
- Brookfield J. F. Y., 1992. DNA fingerprinting in clonal organisms. Mol. Ecol. 1: 21–26. 10.1111/j.1365-294X.1992.tb00151.x [DOI] [Google Scholar]
- Burt A., Carter D. A., Koenig G. L., White T. J., Taylor J. W., 1996. Molecular markers reveal cryptic sex in the human pathogen Coccidioides immitis. Proc. Natl. Acad. Sci. USA 93: 770–773. 10.1073/pnas.93.2.770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Butlin R., 2002. The costs and benefits of sex: new insights from old asexual lineages. Nat. Rev. Genet. 3: 311–317. 10.1038/nrg749 [DOI] [PubMed] [Google Scholar]
- Ceplitis A., 2003. Coalescence times and the Meselson effect in asexual eukaryotes. Genet. Res. 82: 183–190. 10.1017/S0016672303006487 [DOI] [PubMed] [Google Scholar]
- Crease T. J., Lynch M., 1991. Ribosomal DNA variation in Daphnia pulex. Mol. Biol. Evol. 8: 620–640. [Google Scholar]
- Duret L., Galtier N., 2009. Biased gene conversion and the evolution of mammalian genomic landscapes. Annu. Rev. Genomics Hum. Genet. 10: 285–311. 10.1146/annurev-genom-082908-150001 [DOI] [PubMed] [Google Scholar]
- Flot J.-F., Hespeels B., Li X., Noel B., Arkhipova I., et al. , 2013. Genomic evidence for ameiotic evolution in the bdelloid rotifer Adineta vaga. Nature 500: 453–457. 10.1038/nature12326 [DOI] [PubMed] [Google Scholar]
- Frantz L. A. F., Mullin V. E., Pionnier-Capitan M., Lebrasseur O., Ollivier M., et al. , 2016. Genomic and archaeological evidence suggest a dual origin of domestic dogs. Science 352: 1228–1231. 10.1126/science.aaf3161 [DOI] [PubMed] [Google Scholar]
- Griffiths R. C., 1981. Neutral two-locus multiple allele models with recombination. Theor. Popul. Biol. 19: 169–186. 10.1016/0040-5809(81)90016-2 [DOI] [Google Scholar]
- Haag C. R., McTaggart S. J., Didier A., Little T. J., Charlesworth D., 2009. Nucleotide polymorphism and within-gene recombination in Daphnia magna and D. pulex, two cyclical parthenogens. Genetics 182: 313–323. 10.1534/genetics.109.101147 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartfield M., 2016. Evolutionary genetic consequences of facultative sex and outcrossing. J. Evol. Biol. 29: 5–22. 10.1111/jeb.12770 [DOI] [PubMed] [Google Scholar]
- Hartfield M., Wright S. I., Agrawal A. F., 2016. Coalescent times and patterns of genetic diversity in species with facultative sex: effects of gene conversion, population structure, and heterogeneity. Genetics 202: 297–312. 10.1534/genetics.115.178004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hein J., Schierup M. H., Wiuf C., 2005. Gene Genealogies, Variation and Evolution: A Primer in Coalescent Theory. Oxford University Press, Oxford. [Google Scholar]
- Hill W. G., Robertson A., 1968. Linkage disequilibrium in finite populations. Theor. Appl. Genet. 38: 226–231. 10.1007/BF01245622 [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 1983. Properties of a neutral allele model with intragenic recombination. Theor. Popul. Biol. 23: 183–201. 10.1016/0040-5809(83)90013-8 [DOI] [PubMed] [Google Scholar]
- Hudson R. R., 1990. Gene genealogies and the coalescent process, pp. 1–42 in Oxford Surveys in Evolutionary Biology, Vol. 7, edited by Futuyma D. J., Antonovics J. Oxford University Press, Oxford. [Google Scholar]
- Hudson R. R., 2001. Two-locus sampling distributions and their application. Genetics 159: 1805–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson R. R., Kaplan N. L., 1985. Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111: 147–164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaquiéry J., Stoeckel S., Rispe C., Mieuzet L., Legeai F., et al. , 2012. Accelerated evolution of sex chromosomes in aphids, an X0 system. Mol. Biol. Evol. 29: 837–847. 10.1093/molbev/msr252 [DOI] [PubMed] [Google Scholar]
- Judd S. R., Petes T. D., 1988. Physical lengths of meiotic and mitotic gene conversion tracts in Saccharomyces Cerevisiae. Genetics 118: 401–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kingman J. F. C., 1982. On the genealogy of large populations. J. Appl. Probab. 19: 27–43. 10.2307/3213548 [DOI] [Google Scholar]
- Lynch M., Gutenkunst R., Ackerman M., Spitze K., Ye Z., et al. , 2017. Population genomics of Daphnia pulex. Genetics 206: 315–332. 10.1534/genetics.116.190611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mancera E., Bourgon R., Brozzi A., Huber W., Steinmetz L. M., 2008. High-resolution mapping of meiotic crossovers and non-crossovers in yeast. Nature 454: 479–485. 10.1038/nature07135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mark Welch D. B., Meselson M., 2000. Evidence for the evolution of bdelloid rotifers without sexual reproduction or genetic exchange. Science 288: 1211–1215. 10.1126/science.288.5469.1211 [DOI] [PubMed] [Google Scholar]
- Martini E., Borde V., Legendre M., Audic S., Regnault B., et al. , 2011. Genome-wide analysis of heteroduplex DNA in mismatch repair-deficient yeast cells reveals novel properties of meiotic recombination pathways. PLoS Genet. 7: e1002305 10.1371/journal.pgen.1002305 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean G. A. T., 2002. A genealogical interpretation of linkage disequilibrium. Genetics 162: 987–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McVean G. A. T., Awadalla P., Fearnhead P., 2002. A coalescent-based method for detecting and estimating recombination from gene sequences. Genetics 160: 1231–1241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Möhle M., 1998. A convergence theorem for Markov chains arising in population genetics and the coalescent with selfing. Adv. Appl. Probab. 30: 493–512. 10.1239/aap/1035228080 [DOI] [Google Scholar]
- Nordborg M., 1997. Structured coalescent processes on different time scales. Genetics 146: 1501–1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M., 2000. Linkage disequilibrium, gene trees and selfing: an ancestral recombination graph with partial self-fertilization. Genetics 154: 923–929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg M., Donnelly P., 1997. The coalescent process with selfing. Genetics 146: 1185–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nordborg, M., and S. M. Krone, 2002 Separation of time scales and convergence to the coalescent in structured populations, pp. 194–232 in Modern Developments in Theoretical Population Genetics: The Legacy of Gustave Malécot, edited by M. Slatkin and M. Veuille. Oxford University Press, Oxford. [Google Scholar]
- Normark B. B., 1999. Evolution in a putatively ancient asexual aphid lineage: recombination and rapid karyotype change. Evolution 53: 1458–1469. [DOI] [PubMed] [Google Scholar]
- Ohta T., Kimura M., 1971. Linkage disequilibrium between two segregating nucleotide sites under the steady flux of mutations in a finite population. Genetics 68: 571–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Padhukasahasram B., Marjoram P., Wall J. D., Bustamante C. D., Nordborg M., 2008. Exploring population genetic models with recombination using efficient forward-time simulations. Genetics 178: 2417–2427. 10.1534/genetics.107.085332 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pool J. E., Aquadro C. F., 2006. History and structure of Sub-Saharan populations of Drosophila melanogaster. Genetics 174: 915–929. 10.1534/genetics.106.058693 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg N. A., Nordborg M., 2002. Genealogical trees, coalescent theory and the analysis of genetic polymorphisms. Nat. Rev. Genet. 3: 380–390. 10.1038/nrg795 [DOI] [PubMed] [Google Scholar]
- Roze D., 2009. Diploidy, population structure, and the evolution of recombination. Am. Nat. 174: S79–S94. 10.1086/599083 [DOI] [PubMed] [Google Scholar]
- Roze D., 2016. Background selection in partially selfing populations. Genetics 203: 937–957. 10.1534/genetics.116.187955 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schön I., Martens K., 2003. No slave to sex. Proc. Biol. Sci. 270: 827–833. 10.1098/rspb.2002.2314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schön I., Butlin R. K., Griffiths H. I., Martens K., 1998. Slow molecular evolution in an ancient asexual ostracod. Proc. Biol. Sci. 265: 235–242. 10.1098/rspb.1998.0287 [DOI] [Google Scholar]
- Simonsen K. L., Churchill G. A., 1997. A markov chain model of coalescence with recombination. Theor. Popul. Biol. 52: 43–59. 10.1006/tpbi.1997.1307 [DOI] [PubMed] [Google Scholar]
- Sunnåker M., Busetto A. G., Numminen E., Corander J., Foll M., et al. , 2013. Approximate Bayesian computation. PLOS Comput. Biol. 9: e1002803 10.1371/journal.pcbi.1002803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai I. J., Bensasson D., Burt A., Koufopanou V., 2008. Population genomics of the wild yeast Saccharomyces paradoxus: quantifying the life cycle. Proc. Natl. Acad. Sci. USA 105: 4957–4962. 10.1073/pnas.0707314105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tucker A. E., Ackerman M. S., Eads B. D., Xu S., Lynch M., 2013. Population-genomic insights into the evolutionary origin and fate of obligately asexual Daphnia pulex. Proc. Natl. Acad. Sci. USA 110: 15740–15745. 10.1073/pnas.1313388110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veeramah K. R., Hammer M. F., 2014. The impact of whole-genome sequencing on the reconstruction of human population history. Nat. Rev. Genet. 15: 149–162. 10.1038/nrg3625 [DOI] [PubMed] [Google Scholar]
- Wakeley J., 2009. Coalescent Theory: An Introduction, Vol. 1 Roberts & Company Publishers, Greenwood Village, CO. [Google Scholar]
- Wakeley J., Lessard S., 2003. Theory of the effects of population structure and sampling on patterns of linkage disequilibrium applied to genomic data from humans. Genetics 164: 1043–1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall J. D., 2004. Estimating recombination rates using three-site likelihoods. Genetics 167: 1461–1473. 10.1534/genetics.103.025742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weir B. S., Hill W. G., 1986. Nonuniform recombination within the human beta-globin gene cluster. Am. J. Hum. Genet. 38: 776–781. [PMC free article] [PubMed] [Google Scholar]
- Wiuf C., Hein J., 2000. The coalescent with gene conversion. Genetics 155: 451–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The new simulation program, FacSexCoalescent, along with documentation is available at http://github.com/MattHartfield/FacSexCoalescent. We first rebuilt the single-locus simulation program in C to greatly increase execution speed, before adding the crossover and gene conversion routines. As with the previous version of the simulation, FacSexCoalescent uses a timescale of generations while ms uses generations. The documentation specifies other cases where FacSexCoalescent inputs and outputs differ from other coalescent simulations. We performed various tests of the simulation as described in Section B of File S2.
File S1 is a Mathematica notebook of analytical derivations. File S2 contains additional results and figures. File S3 is a copy of the simulation code and manual. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.6949877.