Density-dependent adult recruitment in a low-density tropical tree

Significance

An important class of negative feedbacks in population dynamics is the activity of host-specific enemies that disproportionately kill individuals in locations where they are common. This mechanism, called the Janzen–Connell hypothesis, has been proposed as a determinant of the large number of species in tropical forests. A critical but untested assumption of the hypothesis is that density-dependent mortality among juvenile trees reduces the probability of adult recruitment. Here, we show that adult recruitment is negatively density dependent in a low-density tree population using time series from high-resolution remote sensing. However, this density dependence was not strong enough to stabilize the size of the adult population, which increased significantly in size.

Abstract

The Janzen–Connell hypothesis is a well-known explanation for why tropical forests have large numbers of tree species. A fundamental prediction of the hypothesis is that the probability of adult recruitment is less in regions of high conspecific adult density, a pattern mediated by density-dependent mortality in juvenile life stages. Although there is strong evidence in many tree species that seeds, seedlings, and saplings suffer conspecific density-dependent mortality, no study has shown that adult tree recruitment is negatively density dependent. Density-dependent adult recruitment is necessary for the Janzen–Connell mechanism to regulate tree populations. Here, we report density-dependent adult recruitment in the population of Handroanthus guayacan, a wind-dispersed Neotropical canopy tree species. We use data from high-resolution remote sensing to track individual trees with proven capacity to flower in a lowland moist forest landscape in Panama and analyze these data in a Bayesian framework similar to capture–recapture analysis. We independently quantify probabilities of adult tree recruitment and detection and show that adult recruitment is negatively density dependent. The annualized probability of adult recruitment was 3.03% ⋅ year⁻¹. Despite the detection of negative density dependence in adult recruitment, it was insufficient to stabilize the adult population of H. guayacan, which increased significantly in size over the decade of observation.

The Janzen–Connell hypothesis is a well-known explanation for why tropical forests have high tree species richness (1, 2). It is based on the assumption that tree species suffer sufficiently high density-dependent mortality of seeds, seedlings, and saplings near reproductive adults that no species is likely to replace itself in the same location in the next generation. There is strong empirical evidence that most seeds disperse close to parent trees, where seeds and seedlings suffer high density-dependent mortality from predators and pathogens (3–7). Other studies have shown that animal dispersers can move seeds to areas of low conspecific density and that seed survival increases in these areas (8). Two investigations have mapped spatial distributions of conspecific adults and shown that negative density dependence among the earliest tree life stages is strongest where conspecific adults are common (9, 10).

However, density dependence among the earliest life stages in tree communities is usually extremely local, detectable to a distance typically of only a few meters beyond the radius of the parent tree crown (7, 11). Most of this density dependence is among locally dispersed progeny of single maternal parents (12). Density-dependent mortality restricted to these within-sibling cohorts beneath single mother trees reduces individual tree fecundity but cannot by itself regulate the size of the adult population, because an individual that replaces its maternal parent has no net impact on the size of the adult population. Although the prediction of density-dependent seed and seedling mortality has been strongly supported, no study has shown that per capita recruitment of new adult trees decreases with conspecific adult density, a central prediction of the hypothesis and requirement for the Janzen–Connell mechanism to regulate tree populations (1).

There are at least two reasons why it has not been possible to directly test whether adult tree recruitment is density dependent. First, characterizing adult recruitment requires long-term observations of individuals to discover when a tree becomes reproductive for the first time (13). Second, adult densities for most tree species in species-rich tropical forests are <1 individual · ha⁻¹, and populations of adult trees have low demographic rates (14, 15). These facts require searching impractically large areas to identify adult recruits. For example, if the rate of adult recruitment for a given species is 2% ⋅ y⁻¹ and adult density is 1 individual · ha⁻¹, a 50-ha sample of forest will contain just 1 recruit · y⁻¹ on average. Because juvenile densities for most species can be orders of magnitude greater than the densities of conspecific adults and most juvenile trees do not survive to adulthood, finding new adult recruits is a needle-in-a-haystack problem. These impediments require a new approach to measure the vital rates of adult tree populations.

Here, we report on a method to quantify demographic rates in tree populations using time series remote sensing, and we apply this method to Handroanthus guayacan, a wind-dispersed Neotropical canopy tree species (16–19). Our approach takes advantage of conspicuous and highly synchronous annual flowering in this species to track individuals through time (Fig. 1) (17). We previously showed that the annual probability of adult mortality in this species is 0.2% ⋅ y⁻¹ (17). Here, we follow 989 individual trees in the adult population of H. guayacan distributed over the entirety of the 15.4-km² area of Barro Colorado Island, Panama (BCI). Because every tree in this sample has shown capacity to flower and is, therefore, a member of the adult population, our sample defines the subset of proven survivors that have persisted over many years through earlier life stages to reach a position in the forest canopy as a member of the adult population (20). We develop models in a Bayesian framework similar to capture–recapture analysis to analyze these observations in reverse time (21–24). These models allow us to quantify the annual probability of adult recruitment and to identify new recruits to the adult population. We used this reverse time, retrospective analysis over a 10-y observation period to answer two questions. (i) Is the per capita number of newly recruited adult trees a negative function of the density of conspecific adults at the beginning of the study (negative density dependence)? (ii) If so, does the density-dependent adult recruitment stabilize the size of the adult population when combined with our previous estimate (17) of the mortality rate?

Fig. 1.

Sampling adult H. guayacan using high-resolution satellite data. The image shows a 1 × 2-km subset of BCI on March 29, 2002 (A) and March 21, 2004 (B). C shows the spatial distribution of 84 adult H. guayacan identified within this 2-km² area overlaid on a lidar digital terrain model. The white boxes illustrate one tree that was observed flowering in 2004 but not in 2002. It either was an adult that was not flowering in 2002 or had not yet recruited to the adult population. (Scale bar: 500 m.)

We tested for negative density dependence in adult recruitment by fitting the model $R=a{A}^b$, where $R$ is the number of adult recruits per unit area and $A$ is the number of conspecific adults in the same unit area at the beginning of the study. Whenever the coefficient b is <1, a given increase in the number of adults $A$ results in a less than proportional increase in number of recruits $R$, and $R$ is negatively density dependent. We quantified this relationship within square cells of 1–100 ha by sequentially stepping the length of cell sides in increments of 100 m.

Results and Discussion

Density-Dependent Adult Recruitment.

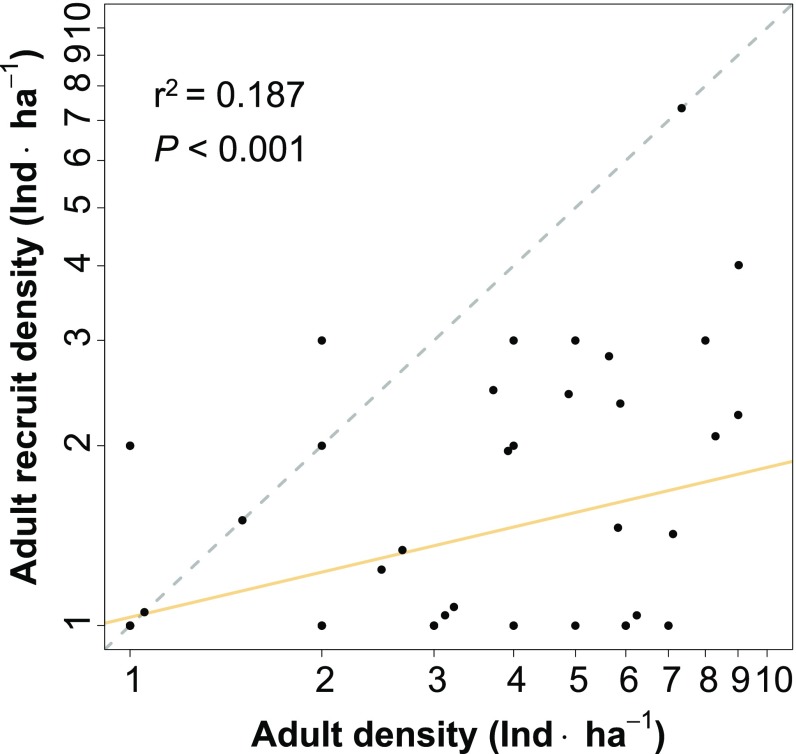
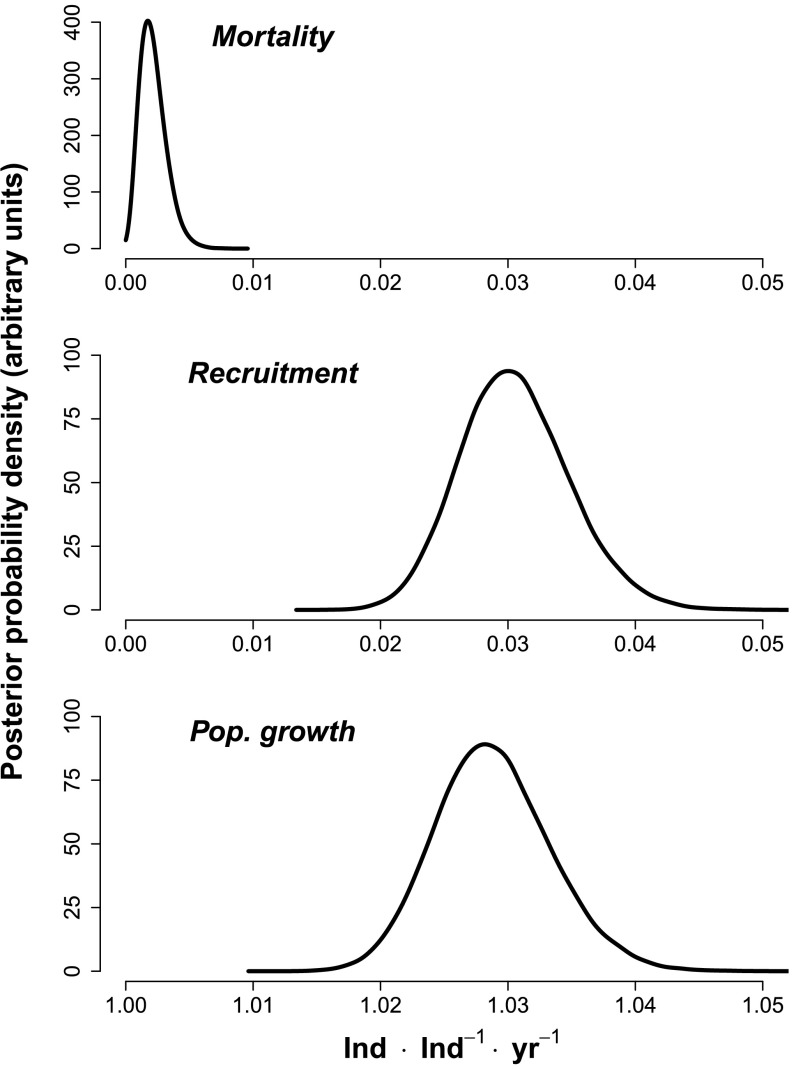
Adult recruitment was negatively density dependent (Figs. 2 and 3). The estimate of b within 1-ha cells was 0.25 (SE = 0.06, 95% CI = 0.14–0.37). The strength of this density dependence diminished as cell size increased and was significantly <1 for cell side lengths ≤700 m, which corresponds to an area of 49 ha (SI Appendix, Table S1). This finding indicates that conspecific density dependence is not limited just to very small neighborhoods around single maternal parents but can significantly influence adult recruitment over much larger areas. The annualized rate of adult recruitment was 3.03% ⋅ y⁻¹ (SE = 0.43, 95% CI = 2.27–3.96) (Fig. 4). We identified 186 adult recruits during the 10-y study using posterior prediction, corresponding to a mean density of 0.012 adult recruits · ha⁻¹ · y⁻¹ (SE = 0.001, 95% CI = 0.009–0.014). The smallness of this number underscores the challenge of quantifying adult recruitment in low-density tree populations.

Fig. 2.

The relationship between adult density and adult recruit density in H. guayacan. The axes are on a logarithmic scale (base 10). The dashed gray line is the one-to-one (density-independent) relationship. The slope of the relationship between adult density and adult recruit density is 0.25 and significantly <1. This indicates that adult recruitment is negatively density dependent.

Fig. 3.

Spatial distribution of the number of adults at the beginning of the study (A) and the number of adult recruits over the subsequent 10 y (B) in the population of H. guayacan on BCI. Cells are 100 × 100 m. (Scale bar: 1 km.)

Fig. 4.

Posterior distributions of (Top) mortality, (Middle) recruitment, and (Bottom) the realized population growth rate for adult H. guayacan on BCI.

The negative density dependence observed in our data shows that the per capita probability of adult recruitment is less in regions of high conspecific adult density and greater in regions of low conspecific adult density. This is true despite the fact that the absolute number of adult recruits increased with conspecific adult density (Fig. 2), a finding similarly reported for the seed to seedling transition (6). However, this negative density dependence in adult recruitment was not sufficiently strong to stabilize the size of the adult population during the 10-y study period. We combined the posterior distribution of the probability of adult recruitment with an estimate of the mortality rate obtained from a forward-time analysis of these data (17) to quantify the realized population growth rate using the equation $\lambda =e^{\left(r-m\right)}$, where $r$ is the probability of adult recruitment estimated by this study and $m$ is our previous estimate of the annual adult mortality rate (17). The annualized population growth rate is 1.03 (SE < 0.01, 95% CI = 1.02–1.04). This annualized rate indicates that the adult population of H. guayacan increased in abundance by 3% ⋅ y⁻¹ over the 10-y observation interval.

Estimates of adult recruitment are from 989 individuals detected for the first time after the first sampling occasion using high-resolution remote sensing (Materials and Methods). These 989 trees were detected 2,579 times in 5,008 observation attempts in 11 sampling occasions. There were 426 observation attempts that resulted in missing data due to cloud cover or incomplete spatial coverage of remote sensing data. The remaining 2,003 observation attempts resulted in no detections, because individuals were not flowering. Probabilities of adult recruitment and detection varied through time (SI Appendix, Tables S2 and S3).

Population Density and Size.

We detected 1,006 individual adult H. guayacan throughout the 15.4-km² landscape, corresponding to a mean density of 0.65 individuals · ha⁻¹. The mean conspecific adult density within edge-corrected 1-ha neighborhoods centered on each adult H. guayacan was 2.7 individuals · ha⁻¹, a value 4.1 times larger than the landscape mean density (range = 0–19.0 individuals · ha⁻¹). This indicates that the population is spatially aggregated and that the range in conspecific adult density is about one order of magnitude.

We quantified the size of the adult population using parameter-expanded data augmentation (PXDA) (Materials and Methods). This analysis allows us to estimate the total number of individuals in the adult population of H. guayacan throughout the 15.4-km² landscape, including individuals never detected by remote sensing. Our analysis indicates that the adult population contained 1,075 individuals (SE = 10, 95% CI = 1,058–1,095) during the 10-y study period. The sample of 1,006 trees, therefore, contains 93.6% of the adult population of this species on BCI (SE = 0.8, 95% CI = 91.9–95.1%). We located 123 trees in the field without prior knowledge of whether they had been detected by remote sensing data. These 123 trees define an independent sample against which we can evaluate trees detected remotely. Of these 123 trees, there were 109 (88.6%) individuals detected by remote sensing data and 14 (11.4%) that were not. There was no significant difference in diameter or height between the individuals that were detected and those that were not (P = 0.193 and P = 0.766, respectively) (SI Appendix, Table S4). Combined with the large percentage of the adult population in our sample, we conclude that the 1,006 adult H. guayacan obtained using remotely sensed data are unbiased and nearly a complete census.

Conclusion.

The findings reported here add to an emerging consensus that time series observations from high-resolution remote sensing contain information about demographic rates in tree populations (17, 25, 26). Extracting vital rates from these data requires models that can accommodate variable detection and missing observations (17). This analysis brings together estimates of mortality, recruitment, and the realized population growth rate, and it shows that adult recruitment is negatively density dependent.

The method is applicable to many other canopy tree species, including those with asynchronous reproduction or other phenology syndromes (27). Taking advantage of conspicuous phenology will increase detection probabilities and is likely to reduce commission errors, but capture–recapture methods can be applied to any sample of individuals that can be detected repeatedly (28), for example, using imaging spectroscopy (29, 30) or measurements from low-altitude drones.

Materials and Methods

Our study is based on a time series of 11 sampling occasions from high-resolution satellite remote sensing and 1 sampling occasion from airborne remote sensing during a 10-y interval. Data acquisitions were timed to observe the annual flowering event of adult H. guayacan, which is highly synchronous (31). We used these observations to produce a detection history for each individual tree. This history is a time series record of whether a given tree was detected or not on each sampling occasion (17). Some adult trees were not detected due to cloud cover, due to incomplete coverage of remote sensing data, or because they did not flower at the time of data acquisition. From these detection histories, it is possible to independently quantify probabilities of adult recruitment and detection (21) and whether adult recruitment is negatively density dependent.

Quantifying Adult Recruitment.

Consider a tree that is observed or not on three sampling occasions, each of which is an acquisition date of high-resolution remote sensing (Fig. 1). Between two sampling occasions when the individual is observed flowering, we know it is a living member of the adult population. There is uncertainty before the date of the first observation, because we do not know whether the tree was an adult that was not flowering or had not yet recruited to the adult population. Using these data to quantify adult recruitment requires a statistical framework that can handle intermittent detection and missing data. Here, we use the Bayesian state–space model, which decomposes observations of flowering trees into components that represent the partially observable true states (whether a given tree has recruited to the adult population) and the detections given the true states (24).

The detection history is a series of zeros and ones that describes the observations for each individual. A tree that was observed on the third occasion of a three-occasion study but not before the third occasion has detection history x = [0, 0, 1], and a tree that was observed on the first and third occasions has detection history x = [1, 0, 1]. Let $\gamma$ be the probability of transition between sampling occasions, and let p be the detection probability given that the individual is a member of the adult population. The transition probability, $\gamma$, is called the seniority probability (21). It describes the probability that an adult member of the population at time $t+1$ was also a member of the adult population at time $t$. We assume that a member of the adult population cannot transition out of the adult population, except by death. The complement to the seniority rate, $1-\gamma$, is the probability of adult recruitment. To quantify recruitment, we write a complete data likelihood that describes the series of observations in reverse order conditioned on the last detection. For the tree that was observed on the first and third occasions, the likelihood is proportional to

$$L={\gamma }_2\times \left(1-p_2\right)\times {\gamma }_1\times p_1.$$ [1]

Because this likelihood is computed in reverse time, it eliminates the need to deal with probabilities of tree survival. Given that the individual was detected on the third occasion, the expression says that this individual was an adult on the second occasion $\left({\gamma }_2\right)$ and was not detected $\left(1-p_2\right)$. It was also an adult on the first occasion $\left({\gamma }_1\right)$ and detected on the first occasion with probability $p_1$. We distinguish between observed states, denoted by the vector x, and true states, indicated by the vector z. The true states are only partially observable and describe whether a given individual is a living member of the adult population. Our knowledge about the true states for this individual is certain, and its true state history is z = [1, 1, 1]. Now consider an individual observed for the first time on the third sampling occasion and not observed before the third occasion, which shows the partially observable nature of the true states

$$L=\left[{\gamma }_2\times \left(1-p_2\right)\times {\gamma }_1\times \left(1-p_1\right)\right]+\hspace{0.17em}\left[{\gamma }_2\times \left(1-p_2\right)\times \left(1-{\gamma }_1\right)\right]+\left[\left(1-{\gamma }_2\right)\right].$$ [2]

This likelihood exhaustively describes the three possibilities that could produce the detection history x = [0, 0, 1]. It was an adult that was not detected on the first and second occasions $\left[{\gamma }_2\times \left(1-p_2\right)\times {\gamma }_1\times \left(1-p_1\right)\right]$, corresponding to true state history z = [1, 1, 1]; it was an adult that was not detected on the second sampling occasion and recruited between the second and first occasions $\left[{\gamma }_2\times \left(1-p_2\right)\times \left(1-{\gamma }_1\right)\right]$, corresponding to true state history z = [0, 1, 1]; or it recruited between the third and second occasions $\left[\left(1-{\gamma }_2\right)\right]$ and has true state history z = [0, 0, 1]. Each of these terms is a hypothesis about the true states and recruitment history for this individual.

Model Specification.

Following the notation in ref. 32, the indicator u_i,t describes whether individual i was detected (u_i,t = 1) or was not detected but known to be a member of the adult population (u_i,t = 0) on sample date t and not observed for the last time on sample date t. The expression below excludes the date of the last observation for each individual, because the reverse time analysis is conditioned on the last detection under the Cormack–Jolly–Seber framework (21, 22). The time-dependent probability of detection, p_t, is proportional to

$${\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{t=t_i-1}^1}{p}_t^{I\left(u_{i,t}=\hspace{0.17em}1\right)}{\left(1-p_t\right)}^{I\left(u_{i,t}=\hspace{0.17em}0\right)}.$$ [3]

Here, n is the number of individuals, t_i is the sampling occasion corresponding to the last detection for individual i, and I is the indicator function, which takes a value of one if its argument is true and zero otherwise. The second product iterates from the index immediately before the last detection for individual i to the first sampling occasion.

The indicator w_i,t describes whether individual i was a member of the adult population over the interval $t+1$ to t (w_i,t = 1) or recruited during this interval (w_i,t = 0). The likelihood for the probabilities of seniority is proportional to

$${\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{t=t_i-1}^1}{\gamma }_t^{I\left(w_{i,t}\hspace{0.17em}=\hspace{0.17em}1\right)}{\left(1-{\gamma }_t\right)}^{I\left(w_{i,t}=\hspace{0.17em}0\right)}.$$ [4]

Combining the detection and seniority probabilities and adopting conjugate beta priors, the time-dependent likelihood function is proportional to

$$\begin{array}{l}p\left(x,z|\gamma ,p\right)\propto {\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{t=t_i-1}^1}{p}_t^{I\left(u_{i,t}=1\right)}{\left(1\hspace{0.17em}-p_t\right)}^{I\left(u_{i,t}=0\right)}{\displaystyle \prod _{i=1}^n}{\displaystyle \prod _{t=t_i-1}^1}{\gamma }_t^{I\left(w_{i,t}=1\right)}{\left(1-{\gamma }_t\right)}^{I\left(w_{i,t}=0\right)}\\ \times {\displaystyle \prod _{t=T-1}^1}Beta\left(p_t\right|{\alpha }_{p_1},{\alpha }_{p_2}){\displaystyle \prod _{t=T-1}^1}Beta\left({\gamma }_t\right|{\alpha }_{g_1},{\alpha }_{g_2}).\end{array}$$ [5]

Quantifying the Annualized Probability of Adult Recruitment.

We report the annualized probability of recruitment over the entire time series. This number is

$$1-\exp \left[\raisebox{1ex}{$\text{ln}\left({{\displaystyle \prod }}_{t=1}^T{\gamma }_t\right)$}\!\left/ \!\raisebox{-1ex}{$10$}\right.\right].$$ [6]

The product is computed over all T transition intervals. The denominator is the length of the study in years. The time-varying (not annualized) estimates of recruitment are provided in SI Appendix, Table S2, and the time-varying estimates of detection are in SI Appendix, Table S3.

Handling Missing Data.

Missing observations happen when individuals cannot be detected. In our data, this occurs because of cloud cover and incomplete spatial coverage. Previously, we described missing data methods under the Bayesian state–space model applied to capture–recapture data (17). Here, we assume that individuals are missing at random, and we impute missing observations within the Markov-chain Monte Carlo framework using a generative model (33, 34). When a given observation is missing, we simulate it using the estimate of the probability of detection from the current iteration of the Gibbs sampler for that sampling occasion conditioned on the true state for individual i. Imputing missing data contributes additional information to the analysis by allowing detection histories that contain missing observations to be retained in the analysis. These detection histories would otherwise be omitted. In the SI Appendix, we provide code that shows the statistical models on simulated and real data.

Quantifying the Size of the Adult Population.

We used PXDA to quantify the size of the adult population of H. guayacan (34–36). The method was developed by casting the problem as an analysis of occupancy. In occupancy modeling, sites are observed on some sequence of occasions. Individuals are either detected or not on each occasion. One can develop a binomial model, where the number of successes is the number of occasions when individuals were detected, the number of trials is the total number of occasions, and the binomial probability $\psi$ is the occupancy rate.

When occupancy models are applied to sites, all sites that can be occupied are known, and unoccupied sites are observed. However, in the capture–recapture framework, we do not have a priori knowledge of the number of trees that were never detected. This number can be estimated by augmenting the real data with all-zero observation histories, called structural zeros (35). For each of these all-zero histories, we compute the probability that it represents a real individual exposed to sampling that was never detected:

$$\frac{\psi {\left(1-d\right)}^T}{\psi {\left(1-d\right)}^T+\left(1-\psi \right)}.$$ [7]

This states that the probability of an all-zero observation history is equal to the probability that the all-zero history represents a real individual exposed to sampling that was never detected $\left[\psi {\left(1-d\right)}^T\right]$ normalized by the probability that it is a real individual exposed to sampling that was never detected plus the probability that the all-zero history does not represent a real individual $\left(1-\psi \right)$. Normally, the detection probability is denoted $p$. However, we denote it $d$ to avoid confusion with the detection probability estimated in the analysis of adult recruitment, because these are not the same quantity. The superscript denotes the number of sampling occasions for which an individual was exposed to sampling. This number is straightforward to compute as the number of occasions when the individual was a member of the adult population less missing observations. The best estimate of this number is the conditional posterior distribution of simulated state histories from the Bayesian state–space model (the true state vector z). Before the first observation, we use simulated state histories from the recruitment analysis described above. After the last observation, we use simulated state histories from a forward-time analysis of the data described in ref. 17. Because these state histories predict whether an individual was living or dead on each sampling occasion, they allow us to integrate over the uncertainty in the number of sampling occasions for each individual. A previous analysis showed that this model produces unbiased estimates of population size (35).

Field Validation.

We located 274 adult trees that were distributed throughout the BCI forest (SI Appendix, Fig. S1). These investigations were conducted in March and April 2007 and July and August 2011. We measured stem diameter (centimeters) at breast height for 160 trees. We measured height, using a handheld laser range finder, for 137 trees. There were 123 adult trees that we located without prior knowledge of whether they had been detected by remote sensing data. We knew that these trees were reproductive, because we observed them flowering. These 123 trees define an independent sample against which we evaluated trees that were detected remotely (17). We compared the mean stem diameter and height between trees that were detected and trees that were not using dummy-variables regression.

Model Fitting.

We developed code in R to fit the Bayesian state–space model and PXDA analysis described above and distributed this code to 500 nodes on a research computing cluster at Brown University using a simple Bash script. The Markov chain on each node was independently initialized. We computed each chain for 10,000 iterations. We discarded the first 5,000 iterations from each chain and thinned by 25. This resulted in 200 iterations per chain and a total of 100,000 posterior samples. The raw data and code are available in SI Appendix.

Testing the Hypothesis of Density-Dependent Adult Recruitment.

To test the hypothesis that adult recruitment is negatively density dependent, we need to know the number of adult trees at the beginning of the study and the number of adult recruits over the subsequent 10 y within regions of varying conspecific adult density. We used posterior predictive distributions of the recruitment history for each tree to quantify both of these numbers within square cells of 100-m side length (Fig. 3). For each of the 100,000 posterior samples, we have a prediction for each tree that indicates whether it recruited to the adult population during the 10-y study. We used these predictions coupled with the geographic coordinates for each tree to count the number of adult recruits in each 1-ha grid cell where recruitment occurred and repeated this process for all 100,000 posterior samples. To determine whether adult recruitment is density dependent, we quantified the relationship $R=a{A}^b$, where $R$ is the median edge-corrected density of adult recruits over all 100,000 posterior samples in each grid cell, $A$ is edge-corrected adult density at the beginning of the study, and $a$ and $b$ are fitted coefficients. To compute adult density at the beginning of the study, we subtracted the posterior median number of adult recruits from the total number of adult H. guayacan in each grid cell. When the parameter $b$ is <1, a given change in $A$ results in a less than proportional increase in $R$. Thus, testing whether $b$ is significantly <1 is a test of the hypothesis that adult recruitment is negatively density dependent.

To determine how the strength of negative density dependence changed with the size of grid cells, we quantified the relationship $R=a{A}^b$ within grid cells of 100-, 200-, 300-, 400-, 500-, 600-, 700-, 800-, 900-, and 1000-m side length. These correspond to 1, 4, 9, 16, 25, 36, 49, 64, 81, and 100 ha, respectively. Within each grid cell, we computed the posterior median recruit density and corresponding adult density at the beginning of the study as described above, and we used these data to determine how the strength of negative density dependence changed as the sample area increased. The digital terrain model shown as a background in Fig. 1C was produced using airborne lidar acquired by ref. 37.