Significance
Artificial neural networks can suffer from catastrophic forgetting, in which learning a new task causes the network to forget how to perform previous tasks. While previous studies have proposed various methods that can alleviate forgetting over small numbers (10) of tasks, it is uncertain whether they can prevent forgetting across larger numbers of tasks. In this study, we propose a neuroscience-inspired scheme, called “context-dependent gating,” in which mostly nonoverlapping sets of units are active for any one task. Importantly, context-dependent gating has a straightforward implementation, requires little extra computational overhead, and when combined with previous methods to stabilize connection weights, can allow networks to maintain high performance across large numbers of sequentially presented tasks.
Keywords: catastrophic forgetting, continual learning, artificial intelligence, synaptic stabilization, context-dependent gating
Abstract
Humans and most animals can learn new tasks without forgetting old ones. However, training artificial neural networks (ANNs) on new tasks typically causes them to forget previously learned tasks. This phenomenon is the result of “catastrophic forgetting,” in which training an ANN disrupts connection weights that were important for solving previous tasks, degrading task performance. Several recent studies have proposed methods to stabilize connection weights of ANNs that are deemed most important for solving a task, which helps alleviate catastrophic forgetting. Here, drawing inspiration from algorithms that are believed to be implemented in vivo, we propose a complementary method: adding a context-dependent gating signal, such that only sparse, mostly nonoverlapping patterns of units are active for any one task. This method is easy to implement, requires little computational overhead, and allows ANNs to maintain high performance across large numbers of sequentially presented tasks, particularly when combined with weight stabilization. We show that this method works for both feedforward and recurrent network architectures, trained using either supervised or reinforcement-based learning. This suggests that using multiple, complementary methods, akin to what is believed to occur in the brain, can be a highly effective strategy to support continual learning.
Humans and other advanced animals are capable of learning large numbers of tasks during their lifetime, without necessarily forgetting previously learned information. This ability to learn and not forget past knowledge, referred to as continual learning, is a critical requirement to design artificial neural networks (ANNs) that can build upon previous knowledge to solve new tasks. However, when ANNs are trained on several tasks sequentially, they often suffer from “catastrophic forgetting,” wherein learning new tasks degrades performance on previously learned tasks. This occurs because learning a new task can alter connection weights away from optimal solutions to previous tasks.
Given that humans and other animals are capable of continual learning, it makes sense to look toward neuroscientific studies of the brain for possible solutions to catastrophic forgetting. Within the brain, most excitatory synaptic connections are located on dendritic spines (1), whose morphology shapes the strength of the synaptic connection (2, 3). This morphology, and hence the functional connectivity of the associated synapses, can be either dynamic or stable, with lifetimes ranging from seconds to years (2, 4, 5). Particularly, skill acquisition and retention is associated with the creation and stabilization of dendritic spines (6, 7). These results have inspired two recent modeling studies proposing methods that mimic spine stabilization to alleviate catastrophic forgetting (8, 9). Specifically, the authors propose methods to measure the importance of each connection and bias toward solving a task and then stabilize each according to its importance. Applying these stabilization techniques allows ANNs to learn several ( 10) sequentially trained tasks with only a small loss in accuracy.
However, humans and other animals will likely encounter large numbers (100) of different tasks and environments that must be learned and remembered, and it is uncertain whether synaptic stabilization alone can support continual learning across large numbers of tasks. Consistent with this notion, neuroscience studies have proposed that diverse mechanisms operating at the systems (10, 11), morphological (2, 4), and transcriptional (12) levels all act to stabilize learned information, raising the question as to whether several complementary algorithms are required to support continual learning in ANNs.
In this study, we examine whether another neuroscience-inspired solution, context-dependent gating (XdG), can further support continual learning. In the brain, switching between tasks can disinhibit sparse, highly nonoverlapping sets of dendritic branches (10). This allows synaptic changes to occur on a small set of dendritic branches for any one task, with minimal interference with synaptic changes that occurred for previous tasks on (mostly) different branches. In this study, we implement a simplified version of this XdG such that sparse and mostly nonoverlapping sets of units are active for any one task. The algorithm consists of an additional signal that is unique for each task, and that is projected onto all hidden neurons. Importantly, this algorithm is simple to implement and requires little extra computational overhead.
We tested our method on feedforward networks trained on 100 sequential MNIST permutations (13) and on the ImageNet dataset (14) split into 100 sequential tasks. XdG or synaptic stabilization (8, 9), when used alone, is partially effective at alleviating forgetting across the 100 tasks. However, when XdG is combined with synaptic stabilization, networks can successfully learn all 100 tasks with little forgetting. Furthermore, combining XdG with stabilization allows recurrent neural networks (RNNs), trained by using either supervised or reinforcement learning, to sequentially learn 20 tasks commonly used in cognitive and systems neuroscience experiments (15) with high accuracy. Hence, this neuroscience-inspired solution, XdG, when used in tandem with existing stabilization methods, dramatically increases the ability of ANNs to learn large numbers of tasks without forgetting previous knowledge.
Results
The goal of this study was to develop neuroscience-inspired methods to alleviate catastrophic forgetting in ANNs. Two previous studies have proposed one such method: stabilizing connection weights depending on their importance for solving a task (8, 9). This method, inspired by neuroscience research demonstrating that stabilization of dendritic spines is associated with task learning and retention (6, 7), has shown promising results when trained and tested on sequences of 10 tasks. However, it is uncertain how well these methods perform when trained on much larger numbers of sequential tasks.
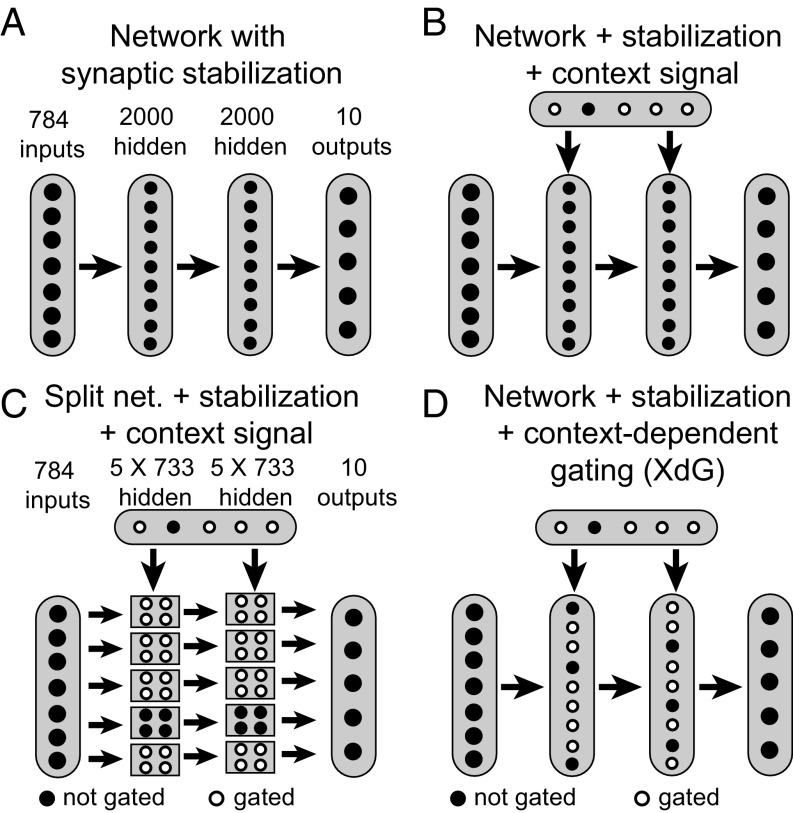
We first tested whether these methods can alleviate catastrophic forgetting by measuring performance on 100 sequentially presented digit classification tasks. Specifically, we tested a fully connected feedforward network with two hidden layers (2,000 units each; Fig. 1A) on the permuted MNIST digit classification task (13). This involved training the network on the MNIST task for 20 epochs, permuting the 784 pixels in all images with the same permutation, and then training the network on this new set of images. This test is a canonical example of an “input reformatting” problem, in which the input and output semantics (pixel intensities and digit identity, respectively) are identical across all tasks, but the input format (the spatial location of each pixel) changes between tasks (13).
Fig. 1.
Network architectures for the permuted MNIST task. The ReLu activation function was applied to all hidden units. (A) The baseline network consisted of a multilayer perceptron with two hidden layers consisting of 2,000 units each. (B) For some networks, a context signal indicating task identity projected onto the two hidden layers. The weights between the context signal and the hidden layers were trainable. (C) Split networks (net.) consisted of five independent subnetworks, with no connections between subnetworks. Each subnetwork consisted of two hidden layers with 733 units each, such that it contained the same amount of parameters as the full network described in A. Each subnetwork was trained and tested on 20% of tasks, implying that, for every task, four of the five subnetworks was set to zero (gated). A context signal, as described in B, projected onto the two hidden layers. (D) XdG consisted of multiplying the activity of a fixed percentage of hidden units by 0 (gated), while the rest were left unchanged (not gated). The results in Fig. 2D involve gating 80% of hidden units.
We sequentially trained the base ANN on 100 permutations of the image set. Without any synaptic stabilization, this network can classify digits with an accuracy of 98.5% for any single permutation, but mean classification accuracy falls to 52.5% after the network is trained on 10 permutations, and to 19.1% after training on 100 permutations.
Synaptic Stabilization.
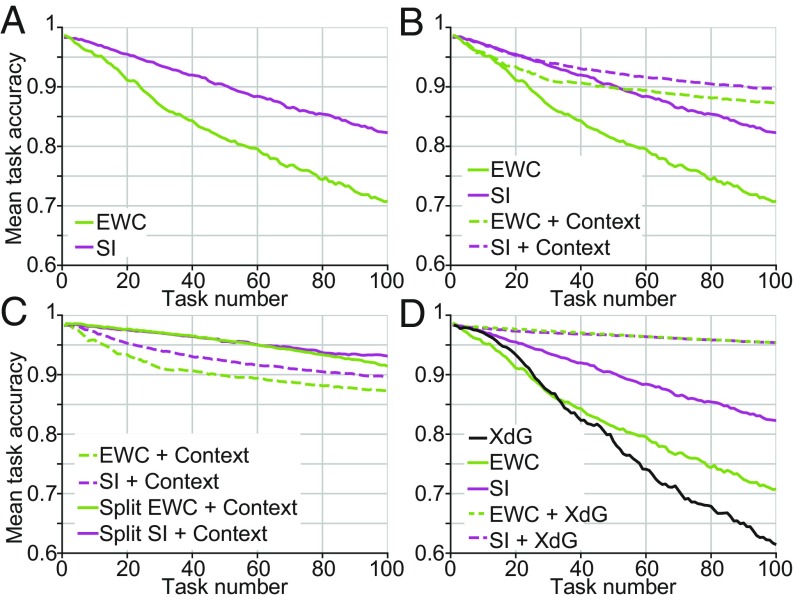
Given that this ANN rapidly forgets previously learned permutations of the MNIST task, we next asked how well two previously proposed synaptic stabilization methods, synaptic intelligence (8) and elastic weight consolidation (EWC) (9), alleviate catastrophic forgetting. Both methods work by applying a quadratic penalty term on adjusting synaptic values, multiplied by a value quantifying the importance of each connection weight and bias term toward solving previous tasks (Materials and Methods). We note that we use the term “synapse” to refer to both connection weights and bias terms. Briefly, EWC works by approximating how small changes to each parameter affect the network output, calculated after training on each task is completed, while synaptic intelligence works by calculating how the gradient of the loss function correlates with parameter updates, calculated during training. Both stabilization methods significantly alleviate catastrophic forgetting: Mean classification accuracies for networks with EWC (green curve, Fig. 2A) were 95.3% and 70.8% after 10 and 100 permutations, respectively, and mean classification accuracies for networks with synaptic intelligence (magenta curve, Fig. 2A) were 97.0% and 82.3% after 10 and 100 permutations, respectively. We note that we used the hyperparameters that produced the greatest mean accuracy across all 100 permutations, not just the first 10 permutations (Materials and Methods). Although both stabilization methods successfully mitigated forgetting, mean classification accuracy after 100 permutations was still far below single-task accuracy. This prompts the question of whether an additional, complementary method can raise performance even further.
Fig. 2.
Task accuracy on the permuted MNIST benchmark task. All curves show the mean classification accuracy as a function of the number of tasks the network was trained on, where each task corresponds to a different random permutation of the input pixels. (A) The green and magenta curves represent the mean accuracy for networks with EWC and with synaptic intelligence, respectively. (B) The solid green and magenta curves represent the mean accuracy for networks with EWC and with synaptic intelligence, respectively (same as in A), and the dashed green and dashed magenta curves represent the mean accuracy for networks with a context signal combined with EWC or synaptic intelligence, respectively. (C) The dashed green and magenta curves represent the mean accuracy for networks with a context signal combined with EWC or synaptic intelligence, respectively (same as in B), and the solid green and magenta curves represent the mean accuracy for split networks with a context signal combined with EWC or synaptic intelligence, respectively. (D) The solid green and magenta curves represent the mean accuracy for networks with EWC or synaptic intelligence, respectively (same as in A), the black curve represents the mean accuracy of networks with XdG used alone, and the dashed green and magenta curves represent the mean accuracy for networks with XdG combined with EWC or synaptic intelligence, respectively. SI, synaptic intelligence.
Context Signal.
One possible reason why classification accuracy decreased after many permutations was that ANNs were not informed as to what permutation, or context, was currently being tested. In contrast, context-dependent signals in the brain, likely originating from areas such as the prefrontal cortex, project to various cortical areas and allow neural circuits to process incoming information in a task-dependent manner (16–18). Thus, we tested whether such a context signal improves mean classification accuracy. Specifically, a one-hot vector (N-dimensional consisting of N − 1 zeros and 1 one), indicating task identity, projected onto the two hidden layers. The weights projecting the context signal could be trained by the network.
We found that networks including parameter stabilization combined with a context signal had greater mean classification accuracy (context signal with synaptic intelligence = 89.6%, with EWC = 87.3%; Fig. 2B) than synaptic stabilization alone. However, the mean classification accuracy after 100 tasks still falls short of single-task accuracy, suggesting that contextual information alone is insufficient to alleviate forgetting.
Split Network.
Recent neuroscience studies have highlighted how context-dependent signaling not only allows various cortical areas to process information in a context-dependent manner, but selectively inhibits large parts of the network (19, 20). This inhibition potentially alleviates catastrophic forgetting, provided that changes in synaptic weights only occur if their presynaptic and postsynaptic partners are active during the task, and are frozen otherwise.
To test this possibility, we split the network into five subnetworks of equal size (Fig. 2C). Each subnetwork contained 733 neurons in each hidden layer, so that the number of connection weights in this split network matched the number of free parameters in the full network. For each permutation, one subnetwork was activated, and the other four were fully inhibited. Furthermore, the context signal described in Fig. 2B projected onto the hidden layers. This architecture achieved greater mean classification accuracies (split networks with context signal and synaptic intelligence = 93.1% and EWC = 91.4%) than full networks with stabilization combined with a context signal.
XdG.
These results suggest that context-dependent inhibition can potentially allow networks to learn sequentially presented tasks with less forgetting. However, splitting networks into a fixed number of subnetworks a priori may be impractical for more real-world tasks. Furthermore, this method forces each subnetwork to learn multiple tasks, whereas greater classification accuracies might be possible if unique, partially overlapping sets of synapses are responsible for learning each new task. Thus, we tested a final method, XdG, in which the activity of X% of hidden units, randomly chosen, was multiplied by 0 (gated), while the activity of the other (1 − X)% was left unchanged. In this study, we gated 80% of hidden units per task. The identity of the gated units was fixed during training and testing for the specific permutation, and a different set of fully gated hidden units was chosen for each permutation. When XdG was used alone (black curve, Fig. 2D), mean accuracy was 97.1% after 10 tasks and 61.4% across all 100 permutations. However, when XdG was combined with synaptic intelligence or EWC, mean classification accuracy was 95.4% for both stabilization methods (dashed green and magenta lines), greater than any of the previous methods we tested. Thus, while XdG alone does not support continual learning, it becomes highly effective when paired with existing synaptic stabilization methods.
The optimal percentage of units to gate is a compromise between keeping a greater number of units active, increasing the network’s representational capacity, and keeping a greater number of units gated, which decreases the number of connection weight changes and forgetting between tasks. For the permuted MNIST task, we found that mean classification accuracy peaked when between 80% and 86.7% of units were gated (values of 95.4% and 95.5%, respectively) (SI Appendix, Fig. S1). We note that this optimal value depends on the network size and architecture and the number of tasks upon which the network is trained.
XdG combined with synaptic stabilization allowed networks to learn 100 sequentially trained tasks with minimal loss in performance, with accuracy dropping from 98.2% on the first task to a mean of 95.4% across all 100 tasks. This result raises the question of whether XdG allows networks to learn even more tasks with only a gradual loss in accuracy, or if they would instead reach a critical point where accuracy drops abruptly. Thus, we repeated our analysis for 500 sequentially trained tasks and found that XdG combined with stabilization allowed for continual learning with only a gradual loss of accuracy over 500 tasks (XdG combined with synaptic intelligence = 90.7%; SI Appendix, Fig. S2). In comparison, mean accuracy for stabilization alone decreased more severely (synaptic intelligence = 54.9%).
Analyzing the Interaction Between XdG and Synaptic Stabilization.
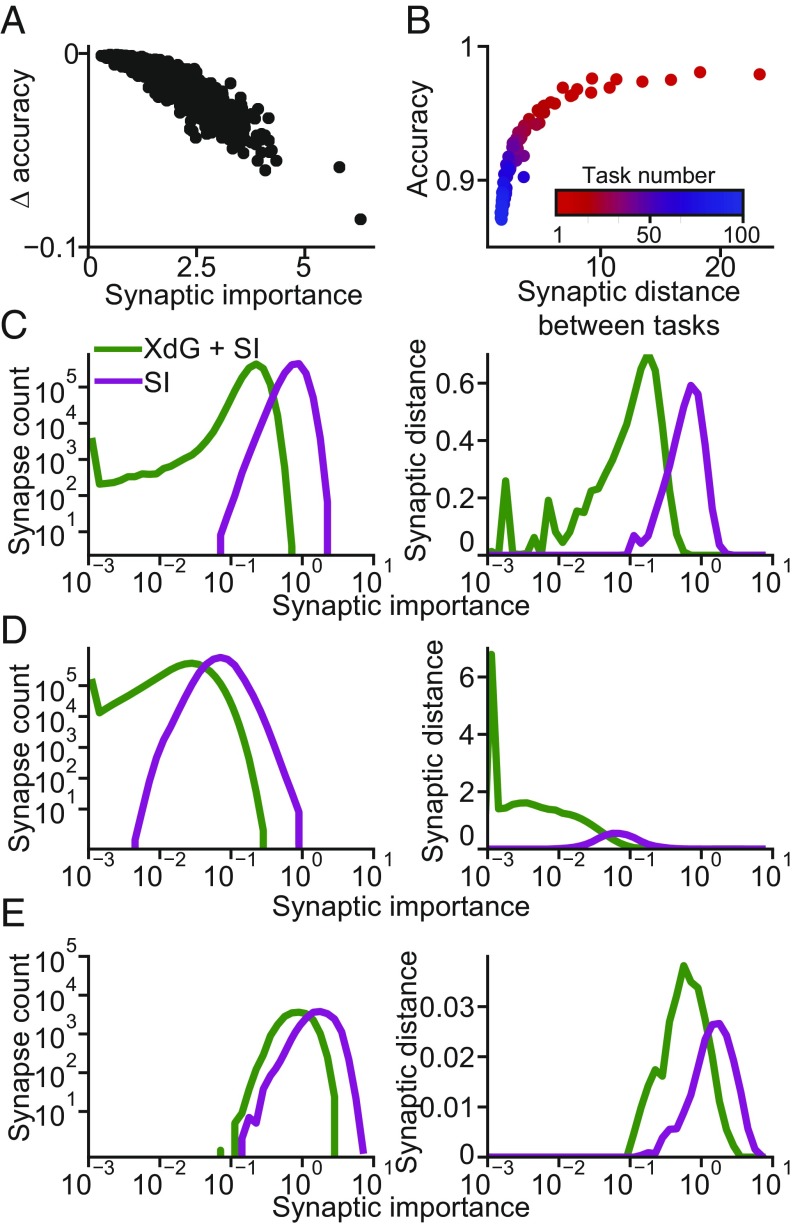
We would like to understand why XdG combined with synaptic stabilization better alleviates forgetting compared to stabilization alone. We hypothesize that to accurately learn many sequential tasks with little forgetting, the network must balance two competing demands: it must stabilize synapses that are deemed important for previous tasks, yet remain flexible so that it can adjust synaptic values by a sufficient amount to accurately learn new tasks. To demonstrate the first point, which is the basis for synaptic intelligence (8) and EWC (9), we trained a network with stabilization (synaptic intelligence) on 100 MNIST permutations and then measured the mean accuracy across all permutations after perturbing individual synaptic values (see Materials and Methods for details regarding analysis). As expected, perturbing more-important synapses degraded accuracy more than perturbing less-important synapses (R = −0.904; Fig. 3A).
Fig. 3.
Analyzing the interaction between XdG and synaptic stabilization. (A) The effect of perturbing synapses of various importance is shown for a network with synaptic intelligence that was sequentially trained on 100 MNIST permutations. Each dot represents the change in mean accuracy (y axis) after perturbing a single synapse, whose importance is indicated on the x axis. For visual clarity, we show the results from 1,000 randomly selected synapses chosen from the connection weights to the output layer. (B) Scatter plot showing the Euclidean distance in synaptic values measured before and after training on each MNIST permutation (x axis) vs. the accuracy the network achieved on each new permutation. The task number in the sequence of 100 MNIST permutations is indicated by the red to blue color progression. (C, Left) Histogram of synaptic importances from the connections between the input layer and the first hidden layer (layer 1), for networks with XdG (green curve) and without (magenta curve). (C, Right) Synaptic distance, measured before and after training on the 100th MNIST permutation, for groups of synapses binned by importance. (D) Same as C, except for the synapses connecting the first and second hidden layers (layer 2). (E) Same as C, except for the synapses connecting the second hidden layer and the output layer (layer 3).
To demonstrate that learning new tasks requires flexible synaptic values that can be adjusted sufficient amounts to learn new tasks, we show the network’s accuracy on each new MNIST permutation it learns (y axis, Fig. 3B) vs. the distance between the synaptic values measured before and after training on each MNIST permutation (x axis). For synaptic intelligence and EWC, synaptic importance values accumulate across tasks (Materials and Methods), leading to greater stabilization and less flexibility as more tasks are learned. For the first several tasks (red dots), synapses require less stabilization, allowing the network to adjust synapse values by relatively large amounts to accurately learn each new task. However, as the network learns increasing numbers of tasks (blue dots), synaptic importances, and hence stabilization, increases, preventing the network from adjusting synapse values large amounts between tasks, decreasing accuracy on each new task.
To help us understand why XdG combined with stabilization better satisfies this trade-off compared with stabilization alone, in Fig. 3 C–E, Left, we show the distribution of importance values for synapses connecting the input and first hidden layers (referred to as layer 1; Fig. 3C), connecting the first and second hidden layers (layer 2; Fig. 3D), and connecting the second hidden and output layers (layer 3; Fig. 3E). For all three layers, the mean importance values were lower for networks with XdG (layer 1, Fig. 3C: synaptic intelligence = 0.793, synaptic intelligence + XdG = 0.216; layer 2, Fig. 3D, synaptic intelligence = 0.076, SI + XdG = 0.026; layer 3, Fig. 3E, synaptic intelligence = 1.81, synaptic intelligence + XdG = 0.897). We hypothesized that having a larger number of synapses with low importance is beneficial, as the network could adjust those synapses to learn new tasks with minimal disruption to performance on previous tasks.
To confirm this, we binned the synapses by their importance and calculated the Euclidean distance in synaptic values measured before and after training on the 100th MNIST permutation (Fig. 3 C–E, Right). These images suggest that synaptic distances are greater for networks with XdG combined with synaptic intelligence and that larger changes in synaptic values are more confined to synapses with low importances.
To confirm, we calculated the synaptic distance using all synapses from each layer and found that it was greater for networks with XdG combined with synaptic intelligence (layer 1, Fig. 3C, synaptic intelligence = 1.21, synaptic intelligence + XdG = 1.65; layer 2, Fig. 3D, synaptic intelligence = 1.26, synaptic intelligence + XdG = 8.54; layer 3, Fig. 3E, synaptic intelligence = 0.06, synaptic intelligence + XdG = 0.09). Furthermore, the distance for each synaptic value multiplied by its importance was lower for networks with XdG combined with synaptic intelligence (layer 1, Fig. 3C, synaptic intelligence = 457.33, synaptic intelligence + XdG = 83.56; layer 2, Fig. 3D, synaptic intelligence = 109.75, synaptic intelligence + XdG = 17.83; layer 3, Fig. 3E, synaptic intelligence = 12.15, synaptic intelligence + XdG = 3.16). Thus, networks with XdG combined with stabilization can make larger adjustments to synapse values to accurately learn new tasks and simultaneously make smaller adjustments to synapses with high importance.
By gating 80% of hidden units, 96% of the weights connecting the two hidden layers and 80% of all other parameters are not used for any one task. This allows networks with XdG to maintain a reservoir of synapses that have not been previously used, or used sparingly, that can be adjusted by large amounts to learn new tasks without disrupting performance on previous tasks.
XdG on the ImageNet Dataset.
A simplifying feature of the permuted MNIST task is that the input and output semantics are identical between tasks. For example, output unit 1 is always associated with the digit 1, output unit 2 is always associated with the digit 2, etc. We wanted to ensure that our method generalizes to cases in which the output semantics are similar between tasks, but not identical. Thus, we tested our method on the ImageNet dataset, which comprises approximately 1.3 million images, with 1,000 class labels. For computational efficiency, we used images that were downscaled to 32 × 32 pixels from the more traditional resolution of 256 × 256 pixels. We divided the dataset into 100 sequential tasks, in which the first 10 labels of the ImageNet dataset were assigned to task 1, the next 10 labels were assigned to task 2, etc. The 10 class labels used in each of the 100 tasks are shown in SI Appendix, Table S1. Such a test can be considered an example of a “similar task” problem as defined by ref. 13.
We tested our model on the ImageNet tasks using two different output layer architectures. The first was a “multihead” output layer, which consisted of 1,000 units, one for each image class. The output activity of 990 output units not applicable to the current task was set to zero.
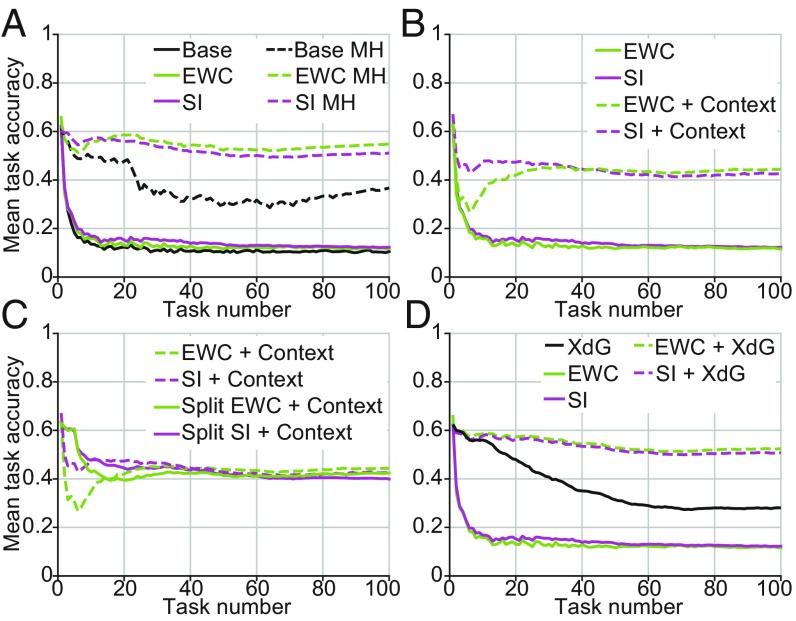
To measure the maximum obtainable accuracy our networks could achieve when sequentially trained on the 100 tasks, we trained and tested networks without stabilization and with resetting synaptic values between tasks and measured their accuracy at learning each new task. We disregarded accuracy on previous tasks. These networks achieved a mean accuracy of 56.5%, representing the maximum any network of this architecture could achieve across the sequence of 100 tasks. In comparison, mean accuracy across 100 sequentially trained tasks using the multihead output layer was 36.7% without synaptic stabilization, and adding synaptic stabilization almost fully alleviated forgetting (synaptic intelligence = 51.1%, EWC = 54.9%; Fig. 4A).
Fig. 4.
Similar to Fig. 2, except showing the mean image classification accuracy for the ImageNet dataset split into 100 sequentially trained sections. (A) The dashed black, green, and magenta curves represent the mean accuracies for multihead networks without synaptic stabilization, with EWC or synaptic intelligence, respectively. The solid black, green, and magenta curves represent the mean accuracies for nonmultihead networks without synaptic stabilization, with EWC or synaptic intelligence, respectively. All further results involve nonmultihead networks. (B) The solid green and magenta curves represent the mean accuracies for networks with EWC or synaptic intelligence, respectively (same as in A). The dashed green and magenta curves represent the mean accuracies for networks with a context signal combined with EWC or synaptic intelligence, respectively (C) The dashed green and magenta curves represent the mean accuracies for networks with a context signal combined with EWC or synaptic intelligence, respectively (same as in B). The solid green and magenta curves represent the mean accuracies for split networks, with a context signal combined with EWC or synaptic intelligence, respectively. (D) The black curve represents the mean accuracy for networks with XdG used alone. The solid green and magenta curves represent the mean accuracies for networks with EWC or synaptic intelligence, respectively (same as in A). The dashed green and magenta curves represent the mean accuracies for networks with XdG combined with EWC or synaptic intelligence, respectively. SI, synaptic intelligence.
The multiheaded network architecture, while potentially effective, can be impractical for real-world implementations, as it requires one output unit for each possible output class that the network might encounter, which might not be known a priori. Thus, we also tested a “single-head” output layer, which consisted of only 10 units, and the activity of these 10 units was associated with different image classes in different tasks. Mean classification accuracy for this more-challenging architecture was substantially lower (without stabilization = 10.5%, synaptic intelligence = 12.3%, EWC = 11.6%; Fig. 4A).
We wanted to know whether our method could alleviate forgetting for this more-challenging architecture, in which output units were associated with different image classes. Thus, we repeated our analysis used for Fig. 2 B–D. We found that adding a context signal substantially increased mean accuracy (context signal with synaptic intelligence = 42.7%, and with EWC = 44.4%; Fig. 4B). Splitting networks into five subnetworks did not lead to any improvement over using stabilization and a context signal alone (split networks with context signal and synaptic intelligence = 40.0%, and EWC = 42.5%; Fig. 4C). Next, we trained networks with XdG, in which we gated 80% of hidden units. Mean accuracy for XdG alone (black curve, Fig. 4D) was greater than synaptic intelligence or EWC used alone, but was less than networks with stabilization and a context signal or split networks (XdG = 28.1%). However, when XdG was combined with synaptic intelligence or EWC, networks could learn all 100 tasks with little forgetting (XdG with synaptic intelligence = 50.7%, with EWC = 52.4%; Fig. 4D). Thus, XdG used in tandem with synaptic stabilization can alleviate catastrophic forgetting, even when the output domain differs between tasks.
XdG of RNNs.
The sequential permuted MNIST and ImageNet tests demonstrated that XdG, combined with synaptic stabilization, can alleviate forgetting for feedforward networks performing classification tasks, trained through supervised learning. To demonstrate that our method generalizes and performs well in other task conditions, we trained RNNs on 20 sequentially presented cognitively demanding tasks (15). These 20 tasks are similar to those commonly used in neuroscience experiments and involve decision-making, working memory, categorization, and inhibitory control. In a physical setting, all tasks involve one or multiple visual motion stimuli, plus a fixation cue, that are presented to a subject, who reports their decisions by either maintaining gaze fixation (akin to withholding its response) or by performing a saccadic eye movement to one of several possible target locations.
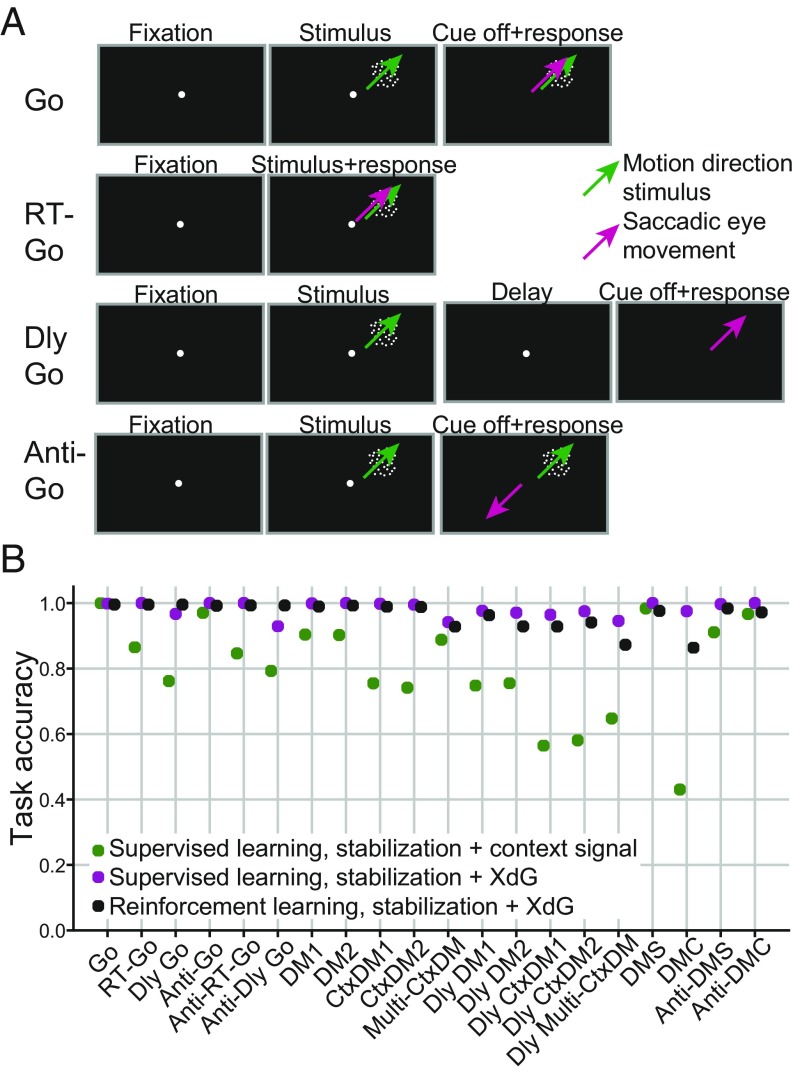
Schematics of the first four tasks are shown in Fig. 5A. In the Go task, trials begin with a fixation period lasting a random duration, followed by a motion direction stimulus (represented by a green arrow) that could occur in one of two locations. As soon as the fixation cue (white centrally located dot) disappears, the network should respond by moving in the dire the motion stimulus (represented by the magenta arrow). The RT-Go task is similar to the task above, except that crucially, the network should ignore the fixation cue and respond as soon as it is presented with the motion stimulus. In the Delay Go task, the motion stimulus is briefly presented, and the network must maintain the stimulus direction in short-term memory across a delay period until the fixation cue disappears, at which time it can respond. Lastly, the Anti-Go is similar to the Go task, except that the network must respond in the direction 180° opposite to the motion direction stimulus. Thus, to learn many tasks, the network must learn to ignore, or to actively work against, information it has learned in previous tasks. Full description of all 20 tasks is provided in Materials and Methods.
Fig. 5.
Task accuracy of recurrent networks sequentially trained on 20 cognitive-based tasks. (A) Schematics of the first four tasks. All trials involve a motion direction stimulus (represented by the white dot pattern and green motion direction arrow), a fixation cue (represented by the white centrally located dot), and an action response using an eye saccade (represented by a magenta arrow). (B) Green represents mean accuracy for networks with stabilization (synaptic intelligence) combined with a rule cue, trained by using supervised learning. Magenta dots represent the mean accuracy for networks with stabilization (synaptic intelligence) combined with XdG, trained by using supervised learning. Black dots represent the mean accuracy for networks with stabilization (synaptic intelligence) combined with XdG, trained by using reinforcement learning.
Our RNN consisted of 256 LSTM cells (21) that received input from 64 motion direction-tuned input units and 4 fixation-tuned units. It projected onto nine output units; one unit represented the choice to maintain fixation (i.e., withhold a response), and the other eight represented responses in eight different directions.
To assess how various methods can learn these tasks without forgetting, we trained networks on all tasks sequentially and then measured accuracy for each task. We first trained RNNs using standard supervised learning, in which the network parameters were adjusted to minimize the difference between the actual network output and the target output. By using this approach, RNNs equipped with synaptic stabilization (synaptic intelligence) and a context signal (green dots, Fig. 5B) achieved a mean task accuracy of 80.0%, with a range of 43.1–100.0%. In comparison, networks with stabilization combined with XdG (magenta dots) achieved a mean accuracy 98.2%, with a range of 92.9–100.0%.
The networks described above were all trained by using supervised learning. If our method is to work in more practical settings, and if something akin to this method is implemented in the brain, then it should be compatible with reinforcement-learning-based training. Thus, we repeated our test on networks with synaptic stabilization (using a modified version of synaptic intelligence compatible with reinforcement learning; Materials and Methods) combined with XdG (black dots). Mean accuracy across all 20 tasks was 96.4%, with a range of 86.4–100.0%. Thus, these results demonstrate that XdG, when combined with synaptic stabilization, can allow RNNs to learn a large sequence of cognitively demanding tasks and is compatible with supervised or reinforcement learning.
Discussion
In this study, we have shown that XdG, used in conjunction with previous methods to stabilize synapses, can alleviate catastrophic forgetting in feedforward and recurrent networks trained by using either supervised or reinforcement learning, on large numbers of sequentially presented tasks. This method is simple to implement and computationally inexpensive. Importantly, this study highlights the effectiveness of using multiple, complementary strategies to alleviate catastrophic forgetting, as opposed to relying on a single strategy. Such an approach would appear to be consistent with that used by the brain, which uses a diverse set of mechanisms to combat forgetting and promote consolidation (4, 6, 10, 11).
Transfer Learning.
Humans and other advanced animals can rapidly learn new rules or tasks, in contrast to the thousands of data points usually required for ANNs to accurately perform new tasks. This is because most new tasks are at least partially similar to tasks or contexts that have been previously encountered, and one can use past knowledge learned from these similar tasks to help learn the rules and contingencies of the new task. This process of using past knowledge to rapidly solve new tasks is referred to as transfer learning, and several groups have recently proposed how ANNs can implement this form of rapid learning (22–24).
Although the XdG method we have proposed in this study likely does not support transfer learning in its current form, one could speculate how such a signal could be modified to perform this function. Suppose that specific ensembles of units underlie the various cognitive processes, or building blocks, required to solve different tasks. Then, learning a new task would not require relearning entirely new sets of connection weights, but, rather, implementing a context-dependent signal that activates the necessary building blocks, and facilitates their interaction, to solve the new task. PathNet (24), a recent method in which a genetic algorithm selects a subset of the network to use for each task, is one prominent example of how selective gating can facilitate transfer. Although it is computationally intensive, requires freezing previously learned synapses, and has only demonstrated transfer between two sequential tasks, it clearly shows that gating specific network modules can allow the agent to reuse previously learned information, decreasing the time required to learn a new task.
We believe that further progress toward transfer learning will require progress along several fronts. First, as humans and other advanced animals can seamlessly switch between contexts, novel algorithms that can rapidly identify network modules applicable to the current task are needed. Second, algorithms that can identify the current task or context, compare it to previously learned contexts, and then perform the required gating based on this comparison are also required. The method proposed in this study clearly lacks this capability, and developing this ability is crucial if transfer learning is to be implemented in real-world scenarios.
Third, and perhaps most important, is that the network must represent learned information in a format to support the above two points. If learned information is located diffusely throughout the network, then activating the relevant circuits and facilitating their interaction might be impractical. Strategies that encourage the development of a modular representation, as is believed to occur in the brain (25), might be required to fully implement continual and transfer learning (26). We believe that in vivo studies examining how various cortical and subcortical areas underlie task learning will provide invaluable data to guide the design of novel algorithms that allow ANNs to rapidly learn new information in a wide range of contexts and environments.
Related Methods to Alleviate Catastrophic Forgetting.
The last several years have seen the development of several methods to alleviate catastrophic forgetting in neural networks. Earlier approaches, such as Progressive Neural Networks (27) and Learning Without Forgetting (28), achieved success by adding additional modules for each new task. Both methods include the use of a multihead output layer (Fig. 4A), and, while effective, in this study we were primarily interested in the more general case in which the network size cannot be augmented to support each additional task and in which the same output units must be shared between tasks.
Other studies are similar in spirit to synaptic intelligence (8) and EWC (9) in that they propose methods to stabilize important network weights and biases (29, 30) or to stabilize the linear space of parameters deemed important for solving previous tasks (31). While we did not test the performance of these methods, we note that, like EWC and synaptic intelligence, these algorithms could in theory also be combined with XdG to potentially further mitigate catastrophic forgetting.
Another class of studies has proposed similar methods that also gate parts of the network. Aside from PathNet (24) described above, recent methods have proposed gating network connection weights (32) or units (33) to alleviate forgetting. The two key differences between our method and theirs are: (i) Gating is defined a priori in our study, which increases computational efficiency, but potentially makes it less powerful; and (ii) we propose to combine gating with parameter stabilization, while their methods involve gating alone. We tested the Hard Attention to Task (HAT) method (33) and found that it could learn 100 sequential MNIST permutations with a mean accuracy of 93.0% (SI Appendix, Fig. S3), greater than networks with EWC or synaptic intelligence alone. That said, combining synaptic intelligence and XdG still outperforms HAT (95.8% when using the same number of training epochs as HAT; SI Appendix, Fig. 3) and is computationally less demanding. This further highlights the advantage of using complementary methods to alleviate forgetting, but also suggests that adding synaptic stabilization to HAT could allow it to further mitigate forgetting.
Summary.
Drawing inspiration from neuroscience, we propose that XdG, a simple-to-implement method with little computational overhead, can allow feedforward and recurrent networks, trained by using supervised or reinforcement learning, to learn large numbers of tasks with little forgetting when used in conjunction with synaptic stabilization. Future work will build upon this method so that it not only alleviates catastrophic forgetting, but can also support transfer learning between tasks.
Materials and Methods
Network training and testing was performed by using the machine-learning framework TensorFlow (34).
Feedforward Network Architecture.
For the MNIST task, we used a fully connected network consisting of 784 input units, two hidden layers of 2,000 hidden units each, and 10 outputs. We did not use a multihead output layer, and thus the same 10 output units were used for all permutations. The ReLU activation function and Dropout (35) with a 50% drop percentage was applied to all hidden units. The softmax nonlinearity was applied to the units in the output layer.
The ImageNet network included four convolutional layers. The first two layers used 32 filters with 3 × 3 kernel size and 1 × 1 stride, and the second two layers used 64 filters with the same kernel size and stride. Max pooling with a 2 × 2 stride was applied after layers two and four, along with a 25% drop rate. Gating was not applied to the convolutional layers. After the four convolutional layers were two full connected hidden layers of 2,000 units each. As described above, the ReLu activation function and a 50% drop rate was applied to the hidden units in the two fully connected layers. The softmax activation function was applied to the output layer. We primarily used a single-head output layer, with 10 units in the output layer that were used in all tasks (Fig. 4). For comparison, we also tested a multihead output layer (Fig. 4A) consisting of 1,000 output units wherein 990 of the units were masked for any one task.
For computational efficiency, we first trained the ImageNet network on a different, yet similar, dataset, which combined the 50,000 images of the CIFAR-10 dataset with the 50,000 images of the CIFAR-100 dataset. After training, we fixed the parameters in the convolutional layers and then trained the parameters in the fully connected (and not the convolutional) layers of the network on the 100 tasks of the ImageNet dataset.
Recurrent Network Architecture.
All RNNs consisted of 256 LSTM cells (21) that projected onto one unit representing the choice to maintain fixation (i.e., withhold a response) and eight units representing responses toward eight different directions. The softmax nonlinearity was applied to activity in the output layer. Input into the RNN consisted of four fixation-tuned units and two sets of 32 motion-direction-tuned units, in which each set represents visual motion input from one of two spatial locations. For RNNs that used a context signal (green dots, Fig. 5B), the input consisted of an additional one-hot vector of length 20 representing the current task.
Network Training and Testing.
For all networks, parameters were trained by using the Adam optimizer (36) (, , ). The optimizer state was reset between tasks.
When training the feedforward and recurrent networks using supervised learning, we used the cross-entropy loss function. We trained the networks for 20 epochs for each MNIST task, 40 epochs for each ImageNet task, and for 6,000 training batches on each cognitive-based task. We used a batch size of 256 and a learning rate of 0.001. We tested classification accuracy on each task using 10 batches; for the MNIST and ImageNet tasks, the test images were kept separate from the training images.
In addition to supervised learning, we also trained RNNs using the actor-critic reinforcement learning method (37), in which the network is trained to maximize the expected discounted future reward,
| [1] |
where is the discount factor and is the reward given at time . For this method, the RNN output consisted of a nine-dimensional policy vector that maps the activity of the RNN into a probability distribution over actions and a value scalar which estimates the future discounted reward. Specifically, we denote the policy output as , where represents the network parameters, the vector of possible actions at time , and as the output activity of the LSTM cells. We also denote the value output as . The loss function can be broken down into expressions related to the value output, the policy output, and an entropy term that encourages exploration. First, the network should minimize the mean squared error between the predicted and expected discounted future reward,
| [2] |
Second, the network should maximize the logarithm of choosing actions with large advantage values (defined below)
| [3] |
In this study, we use the generalized advantage estimation (38), which represents the difference between the expected and the actual reward:
| [4] |
We note that when calculating the gradient of the policy-loss function, one treats the advantage function as a fixed value (i.e., one does not compute the gradient of the advantage function).
We also include an entropy term that encourages exploration by penalizing overly confident actions:
| [5] |
We obtain the overall loss function by combining all three terms:
| [6] |
where and control how strongly the entropy and value loss functions, respectively, determine the gradient.
Synaptic Stabilization.
The XdG method proposed in this study was used in conjunction with one of two previously proposed methods to stabilize synapses: synaptic intelligence (8) and EWC (9). Both methods work by adding a quadratic penalty term to the loss function that penalizes weight changes away from their values before starting training on a new task:
| [7] |
where is the loss function of the current task , is a hyperparameter that scales the strength of the synaptic stabilization, represents the importance of each parameter toward solving the previous tasks, and is the parameter value at the end of the previous task.
For EWC, is calculated for each task as the diagonal elements of the Fisher information :
| [8] |
where the inputs are sampled from the data distribution for task , , and the labels are sampled from the model . We calculated the Fisher information using an additional 32 batches of 256 training data points after training on each task was completed.
For synaptic intelligence, for each task , we first calculated the product between the change in parameter values, , with the negative of the gradient of the loss function , summed across all training batches :
| [9] |
We then normalized this term by the total change in each parameter plus a damping term :
| [10] |
Finally, for both EWC and synaptic intelligence, the importance of each parameter at the start of task is the sum of across all completed tasks:
| [11] |
Parameter Stabilization for Reinforcement Learning.
The method described above to calculate synaptic intelligence is ill-suited for reinforcement learning, as the policy-loss function depends on the estimated discounted future reward, which can be inaccurate, especially early in training. Thus, we first calculate the product between the change in parameter values, , and the change in the mean reward obtained for each batch, , summed across all training batches :
| [12] |
To normalize, we first calculate the sum of the absolute value of this product that represents the maximum value the above equation can obtain if the sign of the change in parameter and the sign of the change in mean reward are always aligned:
| [13] |
We then divide these two terms, plus a damping term , and take the absolute value:
| [14] |
Hyperparameter Search.
We tested our networks on different sets of hyperparameters to determine which values yielded the greatest mean classification accuracy. When using synaptic intelligence, we tested networks with , and When using EWC, we tested networks with . Furthermore, for the MNIST dataset, we tested networks with and without a 20% drop rate in the input layer.
Once the optimal and (for synaptic intelligence) for each task were determined, we tested one additional value , where and were the two values generating the greatest mean accuracies ( and were always adjacent). The hyperparameters yielding the greatest mean classification accuracy across the 100 or 500 MNIST permutations, the 100 ImageNet tasks, or the 20 cognitive tasks were used for Figs. 2, 4, and 5.
Training the RNNs using reinforcement learning required additional hyperparameters, which we experimented with before settling on fixed values. We set the reward equal to −1 if the network broke fixation (i.e., did not choose the fixation action when required), equal to −0.01 when choosing the wrong output direction, and equal to when choosing the correct output direction. The reward was 0 for all other times, and the trial ended as soon as the network received a reward other than 0. The constant weighting the value loss function, , was set to 0.01. The discount factor, , was set to 0.9, although other values between 0 and 1 produced similar results. Lastly, the constant weighting the entropy loss function, was set to 0.0001, and the learning rate was set to 0.0005.
Analysis Methods.
For our analysis into the interaction between synaptic stabilization and XdG, we trained two networks, one with stabilization (synaptic intelligence) and one with stabilization combined with XdG, on 100 sequential MNIST permutations. After training, we tested the network with synaptic intelligence alone after perturbing single connection weights located between the last hidden layer and the output layer. Specifically, we randomly selected 1,000 connections weights one at a time, measured the mean accuracy on all 100 MNIST permutations after perturbing the weights by +10, and then by −10, and then compared the mean accuracy after perturbation to the mean accuracy without perturbation. Fig. 3A shows the scatter plot of the difference in mean accuracy before and after perturbation (y axis) with the synaptic importance (x axis) calculated using Eq. 11.
For Fig. 3B, we wanted to compare network flexibility (how much its connection weights and biases could be adjusted during training) and the network’s accuracy on each new task. Thus, we calculated the Euclidean distance between the values of the connection weights and biases before and after training on each task and compared this value with the network’s accuracy on the new task (Fig. 3B). This was done for the entire sequence of 100 MNIST permutations.
For the comparison between synaptic importance and their change in value when learning a new task (Fig. 3 C–E, Right), we binned the connection weights based on their importance using 80 evenly spaced bins on the logarithmic scale between 0.001 and 10 (same bins as used for histograms in Fig. 3 C–E, Left). For display purposes, we set the minimum importance value to 0.001. Then, for all connection weights in a bin, we calculated their Euclidean distance before and after training on the 100th MNIST permutation. This was calculated for networks with synaptic intelligence only (magenta curves) and with synaptic intelligence combined with XdG (green curves).
Supplementary Material
Acknowledgments
This work was supported by National Institutes of Health Grants R01EY019041 and R01MH092927 and National Science Foundation Grant NCS 1631571.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
Data deposition: All code is available at https://github.com/nmasse/Context-Dependent-Gating.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1803839115/-/DCSupplemental.
References
- 1.Peters A. The Fine Structure of the Nervous System: Neurons and Their Supporting Cells. Oxford Univ Press; Oxford: 1991. [Google Scholar]
- 2.Kasai H, Matsuzaki M, Noguchi J, Yasumatsu N, Nakahara H. Structure–stability–function relationships of dendritic spines. Trends Neurosci. 2003;26:360–368. doi: 10.1016/S0166-2236(03)00162-0. [DOI] [PubMed] [Google Scholar]
- 3.Yuste R, Bonhoeffer T. Morphological changes in dendritic spines associated with long-term synaptic plasticity. Annu Rev Neurosci. 2001;24:1071–1089. doi: 10.1146/annurev.neuro.24.1.1071. [DOI] [PubMed] [Google Scholar]
- 4.Yoshihara Y, De Roo M, Muller D. Dendritic spine formation and stabilization. Curr Opin Neurobiol. 2009;19:146–153. doi: 10.1016/j.conb.2009.05.013. [DOI] [PubMed] [Google Scholar]
- 5.Fischer M, Kaech S, Knutti D, Matus A. Rapid actin-based plasticity in dendritic spines. Neuron. 1998;20:847–854. doi: 10.1016/s0896-6273(00)80467-5. [DOI] [PubMed] [Google Scholar]
- 6.Yang G, Pan F, Gan W-B. Stably maintained dendritic spines are associated with lifelong memories. Nature. 2009;462:920–924. doi: 10.1038/nature08577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Xu T, et al. Rapid formation and selective stabilization of synapses for enduring motor memories. Nature. 2009;462:915–919. doi: 10.1038/nature08389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zenke F, Poole B, Ganguli S. International Conference on Machine Learning. International Machine Learning Society; Princeton: 2017. Continual learning through synaptic intelligence; pp. 3987–3995. [PMC free article] [PubMed] [Google Scholar]
- 9.Kirkpatrick J, et al. Overcoming catastrophic forgetting in neural networks. Proc Natl Acad Sci USA. 2017;114:3521–3526. doi: 10.1073/pnas.1611835114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cichon J, Gan W-B. Branch-specific dendritic Ca2+ spikes cause persistent synaptic plasticity. Nature. 2015;520:180–185. doi: 10.1038/nature14251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tononi G, Cirelli C. Sleep and the price of plasticity: From synaptic and cellular homeostasis to memory consolidation and integration. Neuron. 2014;81:12–34. doi: 10.1016/j.neuron.2013.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kukushkin NV, Carew TJ. Memory takes time. Neuron. 2017;95:259–279. doi: 10.1016/j.neuron.2017.05.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goodfellow IJ, Mirza M, Xiao Da, Courville A, Bengio Y. 2013. An empirical investigation of catastrophic forgetting in gradient-based neural networks. arXiv:1312.6211.
- 14.Deng J, et al. Imagenet: A large-scale hierarchical image database. IEEE Conference on Computer Vision and Pattern Recognition. 2009:248–255. [Google Scholar]
- 15.Robert Yang G, Francis Song H, Newsome WT, Wang X-J. 2017. Clustering and compositionality of task representations in a neural network trained to perform many cognitive tasks, bioRxiv:183632.
- 16.Engel AK, Fries P, Singer W. Dynamic predictions: Oscillations and synchrony in top-down processing. Nat Rev Neurosci. 2001;2:704–716. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
- 17.Johnston K, Levin HM, Koval MJ, Everling S. Top-down control-signal dynamics in anterior cingulate and prefrontal cortex neurons following task switching. Neuron. 2007;53:453–462. doi: 10.1016/j.neuron.2006.12.023. [DOI] [PubMed] [Google Scholar]
- 18.Miller EK, Cohen JD. An integrative theory of prefrontal cortex function. Annu Rev Neurosci. 2001;24:167–202. doi: 10.1146/annurev.neuro.24.1.167. [DOI] [PubMed] [Google Scholar]
- 19.Kuchibhotla KV, et al. Parallel processing by cortical inhibition enables context-dependent behavior. Nat Neurosci. 2017;20:62–71. doi: 10.1038/nn.4436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Otazu GH, Tai L-H, Yang Y, Zador AM. Engaging in an auditory task suppresses responses in auditory cortex. Nat Neurosci. 2009;12:646–654. doi: 10.1038/nn.2306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hochreiter S, Schmidhuber J. Long short-term memory. Neural Comput. 1997;9:1735–1780. doi: 10.1162/neco.1997.9.8.1735. [DOI] [PubMed] [Google Scholar]
- 22.Santoro A, Bartunov S, Botvinick M, Wierstra D, Lillicrap T. 2016. One-shot learning with memory-augmented neural networks. arXiv:1605.06065.
- 23.Lake BM, Salakhutdinov RR, Tenenbaum J. One-shot learning by inverting a compositional causal process. In: Burges CJC, Bottou L, Welling M, Ghahramani Z, Weinberger KQ, editors. Advances in Neural Information Processing Systems. Curran Assoc; Red Hook, NY: 2013. pp. 2526–2534. [Google Scholar]
- 24.Fernando C, et al. 2017. PathNet: Evolution channels gradient descent in super neural networks. arXiv:1701.08734.
- 25.Bassett DS, et al. Dynamic reconfiguration of human brain networks during learning. Proc Natl Acad Sci USA. 2011;108:7641–7646. doi: 10.1073/pnas.1018985108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Velez R, Clune J. 2017. Diffusion-based neuromodulation can eliminate catastrophic forgetting in simple neural networks. arXiv:1705.07241.
- 27.Rusu AA, et al. 2016. Progressive neural networks. arXiv:1606.04671.
- 28.Li Z, Hoiem D. Learning without forgetting. IEEE Trans Pattern Anal Mach Intell. 2018 doi: 10.1109/TPAMI.2017.2773081. [DOI] [PubMed] [Google Scholar]
- 29.Aljundi R, Babiloni F, Elhoseiny M, Rohrbach M, Tuytelaars T. 2017. Memory aware synapses: Learning what (not) to forget. arXiv:1711.09601.
- 30.Nguyen CV, Li Y, Bui TD, Turner RE. 2017. Variational continual learning. arXiv:1710.10628.
- 31.He X, Jaeger H. 2017. Overcoming catastrophic interference by conceptors. arXiv:1707.04853.
- 32.Mallya A, Lazebnik S. 2017. Packnet: Adding multiple tasks to a single network by iterative pruning. arXiv:1711.05769.
- 33.Serrà J, Surís D, Miron M, Karatzoglou A. 2018. Overcoming catastrophic forgetting with hard attention to the task. arXiv:1801.01423.
- 34.Abadi M, et al. 2016. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv:1603.04467.
- 35.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. J Machine Learn Res. 2014;15:1929–1958. [Google Scholar]
- 36.Kingma D, Ba J. 2014. Adam: A method for stochastic optimization. arXiv:1412.6980.
- 37.Barto AG, Sutton RS, Anderson CW. Neuronlike adaptive elements that can solve difficult learning control problems. IEEE Trans Syst Man Cybernetics. 1983;5:834–846. [Google Scholar]
- 38.Schulman J, Moritz P, Levine S, Jordan M, Abbeel P. 2015. High-dimensional continuous control using generalized advantage estimation. arXiv:1506.02438.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.