Multistability of model and real dryland ecosystems through spatial self-organization

Significance

Today, vast areas of drylands in semiarid climates face the dangers of desertification. To understand the driving mechanisms behind this effect, many theoretical models have been created. These models provide insight into the resilience of dryland ecosystems. However, until now, comparisons with reality were merely visual. In this article, a systematic comparison is performed using data on wavenumber, biomass, and migration speed of vegetation patterns in Somalia. In agreement with reaction–diffusion models, a wide distribution of regular pattern wavenumbers was found in the data. This highlights the potential for extrapolating predictions of those models to real ecosystems, including those that elucidate how spatial self-organization of vegetation enhances ecosystem resilience.

Abstract

Spatial self-organization of dryland vegetation constitutes one of the most promising indicators for an ecosystem’s proximity to desertification. This insight is based on studies of reaction–diffusion models that reproduce visual characteristics of vegetation patterns observed on aerial photographs. However, until now, the development of reliable early warning systems has been hampered by the lack of more in-depth comparisons between model predictions and real ecosystem patterns. In this paper, we combined topographical data, (remotely sensed) optical data, and in situ biomass measurements from two sites in Somalia to generate a multilevel description of dryland vegetation patterns. We performed an in-depth comparison between these observed vegetation pattern characteristics and predictions made by the extended-Klausmeier model for dryland vegetation patterning. Consistent with model predictions, we found that for a given topography, there is multistability of ecosystem states with different pattern wavenumbers. Furthermore, observations corroborated model predictions regarding the relationships between pattern wavenumber, total biomass, and maximum biomass. In contrast, model predictions regarding the role of slope angles were not corroborated by the empirical data, suggesting that inclusion of small-scale topographical heterogeneity is a promising avenue for future model development. Our findings suggest that patterned dryland ecosystems may be more resilient to environmental change than previously anticipated, but this enhanced resilience crucially depends on the adaptive capacity of vegetation patterns.

A key aim of ecological modeling is to generate an understanding of the mechanisms driving observed patterns (1). A significant challenge in this pursuit, however, is that multiple alternative processes may generate the same emergent outcome (1–4), a phenomenon also referred to as equifinality (5, 6). As a result, modeling efforts may reveal that a particular ecological pattern can be explained by a suite of alternative driver mechanisms. Therefore, a match between a pattern simulated with a mechanistic model and a pattern observed in a real ecosystem may constitute only limited support for the modeled mechanism being its true driver (2, 5, 6).

Pattern-oriented modeling (2, 7) aims to address the challenge of equifinality of alternative model formulations. In this approach, model assessment is based on the degree to which the output corresponds to observed patterns. A distinction is made between strong and weak patterns. Strong patterns are the dominant emergent features a model should reproduce, such as the cycles within predator and prey population sizes, or a spatial distribution of vegetation patches (6, 7). Weak patterns are typically qualitative relationships, such as the existence of a population over a specific timespan or a positive association between one state variable and another (6, 7). Rather than comparing model output to a single strong pattern, additional comparisons to multiple weak patterns, at different scales or levels of organization, provide more power to model validation and selection procedures (2, 6, 7).

A specific type of ecological patterns that has received considerable attention is regular spatial patterning of sessile biota (8). On flat terrain, the reported patterns are gaps, labyrinths, and spots (9, 10). On sloping grounds banded patterns form, their regular spacing enabling a description of the characteristic band–interband period and wavenumber. Evidence is accumulating that these patterns are self-organized, meaning that the larger-scale patterning is driven by internal ecosystem processes operating at smaller scales (8, 11). The crucial component in this self-organization process is a long-range negative effect of biota on itself, either directly or through modulation of resource availability. In cases where this long-range negative feedback is coupled to a locally positive feedback, the mechanism creating pattern formation may be linked to the existence of alternative stable states, as well as the possibility of so-called catastrophic shifts between these states (11). This phenomenon has been most prominently studied in (semi)arid ecosystems, where decreases in resource availability or increases in grazing pressure may trigger catastrophic shifts from vegetated states to desert states without vegetation (12–14). In this context, the formation of regular spatial vegetation patterns may indicate proximity to a threshold of catastrophic change (11).

There is a long tradition in the scientific literature of explaining regular spatial patterning with reaction–diffusion models (15–17). In line with this work, a variety of reaction–diffusion models have been applied to investigate self-organization in (semi)arid ecosystems (9, 10, 18, 19). Despite the broad support for the findings obtained with these models and their implications for (semi)arid ecosystem functioning, comparisons of model results with empirical data have mainly been limited to comparison of a single strong pattern, namely the spatial distribution of vegetation patches. Until now, the few studies considering additional weak patterns have shown that reaction–diffusion model simulations successfully reproduce associations between pattern shape and aridity and associations between pattern shape and slope of the terrain (20). In addition, models that account for sloped terrain also seem to capture the observed migration of the location of banded patterns in an uphill direction (21). Despite these promising agreements between model results and empirical data, a more systematic comparison between model results and data, based on multiple patterns at different levels of organization (2, 7), was still lacking.

Advanced model analyses that have recently been applied to ecological models have yielded a number of findings which, when confronted with high-quality remote sensing products, make a more systematic comparison possible. More specifically, recent theoretical studies have shown that for a given environmental condition (i.e., a given parameter combination), not a single ecosystem state, but multiple ecosystem states with patterns spanning a range of wavenumbers may be stable and hence observable (22–24). The range of observable patterns, across a range of environmental conditions, forms a bounded region in (parameter, wavenumber) space. This region is referred to as the Busse balloon, after F. H. Busse, who studied similar phenomena in the field of fluid dynamics (25). Although the patterned ecosystem states in the Busse balloon are defined by their wavenumber, other properties, like migration speed and spatially averaged biomass, have also been studied (26) and are suggested to depend on the position of a system within the Busse balloon. These theoretical findings provide multiple additional weak patterns that can be compared with empirical data, providing opportunities for more powerful tests of the validity of the developed reaction–diffusion models to describe dryland ecosystems.

The aim of this study was to confront theoretical findings regarding pattern wavenumber, biomass, and migration speed with the same pattern properties derived from aerial imagery and remote sensing products of banded vegetation patterns in the Horn of Africa, a location with prominent undisturbed presence of vegetation pattern formation. Hence, a multilevel comparison between theory and data in line with the pattern-oriented modeling approach was conducted (2, 6, 7).

1. Theory

Model Description.

Multiple reaction–diffusion models of dryland vegetation dynamics include a mechanism in which vegetation acts as an ecosystem engineer, locally increasing the influx of available water (9, 10, 18, 19). Despite the different nuances between these models, a number of predictions can be robustly derived from these frameworks. One of the simplest of these ecosystem models—and the archetype considered in this article—is an extended version of the dryland ecosystem model by Klausmeier (18, 22), which we refer to as the extended-Klausmeier model. This model describes the interaction between water, $w$, and plant biomass, $n$. A nondimensional version of this model is used for the purposes of this article. A dimensional version of the model and the physical meaning of its parameters are in SI Appendix, section 1. The model is given by the equations

$$\left\{\begin{array}{cc}\frac{\partial w}{\partial t}\hfill & =e\frac{{\partial }^{2}w}{\partial x^2}+\frac{\partial \left(vw\right)}{\partial x}+a-w-w{n}^2,\hfill \\ \frac{\partial n}{\partial t}\hfill & =\frac{{\partial }^{2}n}{\partial x^2}-mn+w{n}^2.\hfill \end{array}\right.$$ [1]

The reaction terms model the change in water as a combined effect of rainfall ($+a$), evaporation ($-w$), and uptake by plants ($-w{n}^2$). The change of plant biomass comes from mortality ($-mn$) and plant growth ($+w{n}^2$). Dispersion by plants is modeled as diffusion and the movement of water as a combined effect of diffusion and advection. The latter is due to gradients in the terrain, which are proportional to the slope parameter $v$.

Theoretical Outcomes.

Multistability of patterned states.

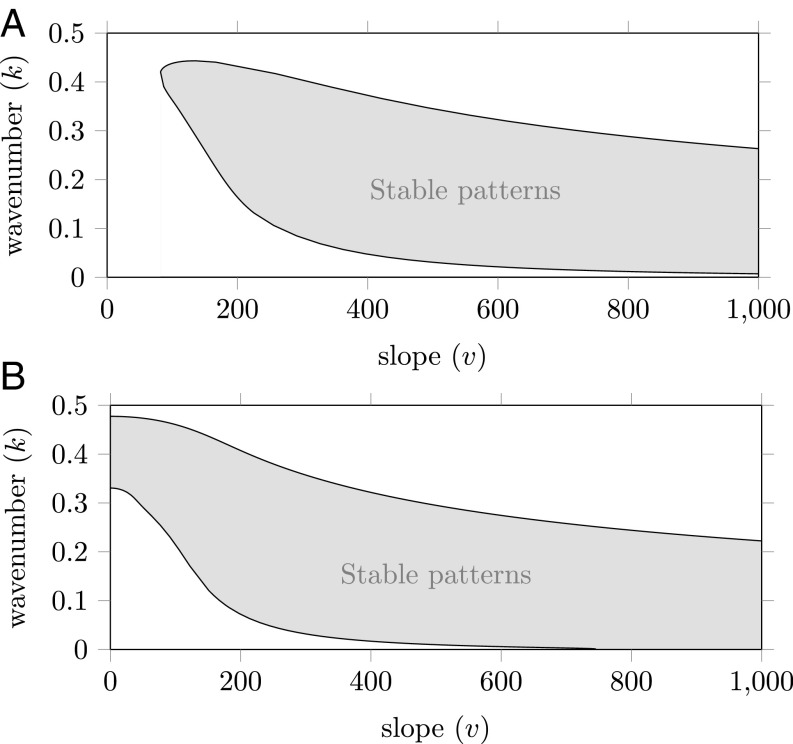
Reaction–advection–diffusion equations in general—and the extended-Klausmeier model in particular—exhibit a vast variety of spatial patterns (27, 28). However, not all feasible patterns are stable solutions of these models. Which patterned states are stable (hence, observable) depends on the combination of the model parameters. For regular patterns, the concept of the Busse balloon can help to illustrate this dependency (25). A Busse balloon is a model-dependent shape in the (parameter, wavenumber) space that indicates all combinations of parameter and wavenumber that represent stable solutions of the model. If, for a given set of model parameters, a wavenumber $k$ lies within the Busse balloon, then regular patterns with wavenumber $k$ are observable. So, in measurements, all (nontransient) patterns are expected to be present in the Busse balloon.

Typically, the Busse balloon is a high-dimensional structure due to the number of parameters in a system. Therefore, usually, only one parameter is varied when a Busse balloon is visualized. This produces a 2D slice of the full Busse balloon. In the context of desertification research, the straightforward choice would be to vary the rainfall (23). However, mean annual rainfall was relatively constant in our study sites during the observation period considered. Instead, topography (i.e., the slope gradient) comprised the main source of environmental variation within our study areas. Thus, relevant theoretical predictions for our study sites can be generated by varying the slope parameter $v$ (while keeping rainfall constant). Here, we present two of such 2D Busse balloon slices for the extended-Klausmeier model (Fig. 1), which were constructed by tracking the boundary of the Busse balloon using numerical continuation methods (23, 24, 29, 30). The shaded region in Fig. 1 A and B indicates the combinations of pattern wavenumber $k$ and slope $v$ for which stable solutions exist. Thus, the model shows multistability; a given slope $v$ can sustain a continuous range of wavenumbers $k$. That is, knowing all current parameter values of a system is not enough to predict the pattern, but gives only a range of possible wavenumbers—as indicated by the Busse balloon. For patterns with wavenumbers above this range, there are too few resources to sustain all bands; below this range, there is an abundance of resources that leads to the formation of additional vegetation bands.

Fig. 1.

(Slope, wavenumber)-Busse balloon slices for the extended-Klausmeier model for two different values of the rainfall parameter $a$. A banded pattern solution to the extended-Klausmeier model with slope $v$ and wavenumber $k$ is stable if the $\left(v,k\right)$ combination lies inside the Busse balloon. This indicates that a wide spread of $\left(v,k\right)$ combinations yields stable banded patterns. The latter are therefore expected for a broad range of wavenumbers—and not for specific $\left(v,k\right)$ choices only. The shape of a Busse balloon can change between models and between parameter values. This is illustrated in A and B, which were computed for different $a$ values. Model parameters used are $e=500,m=0.45,$ and $a=3.0\left(A\right)$ or $a=2.5\left(B\right)$.

It is in general not possible to predict which of these wavenumbers is selected at a specific location; small changes in the (entire) history of environmental changes can have large impacts on the wavenumber that is currently selected (26, 31). To understand these hysteretic dynamics, it is vital to acknowledge that model patterns do not change their wavenumber unless they have to (23, 30): If an environmental change forces the system outside of the Busse balloon, the current pattern has become unstable and will need to adapt into a new pattern that is again stable—and thus part of the Busse balloon. During this (fast) adaptation, only part of the vegetation bands are lost, while the remaining bands increase in volume; these adaptations thus have limited effect on the total biomass in the system (23). Hence, multiple wavenumber adaptations are expected to occur after each other that will, gradually, lead to a complete desertification of the system (23). Both the moment of a destabilization and the then-occurring wavenumber adaptation can be vastly different, depending on (historical) environmental conditions (26, 31, 32). Thus, indeed, precisely which wavenumber $k$ gets selected at each of these destabilizations is difficult to predict.

Numerical simulations help to get an insight into the kind of wavenumber distribution one ought to expect in observations. To illustrate the typical spread in wavenumber, a total of 200 simulations on a flat terrain ($v=0$) were run, where the rainfall parameter was slowly decreased from $a=3$ to $a=0.5$. The initial configurations for these runs were chosen randomly, but close to the equilibrium state of uniform biomass before the onset of patterns (between 90% and 110% of the uniform vegetated equilibrium state). At the end of each simulation—after several pattern selections—the wavenumber of the remaining pattern was measured. This gives a snapshot of the wavenumber distribution, similar to the snapshots acquired from observations. Note that a similar experiment was done before, albeit on a much smaller scale (30). The histogram of the resulting wavenumbers is shown in SI Appendix, Fig. S1. It shows a substantial spread, which goes from a wavenumber of 0.08 to 0.16 (a difference of 100%).

Biomass and migration speed.

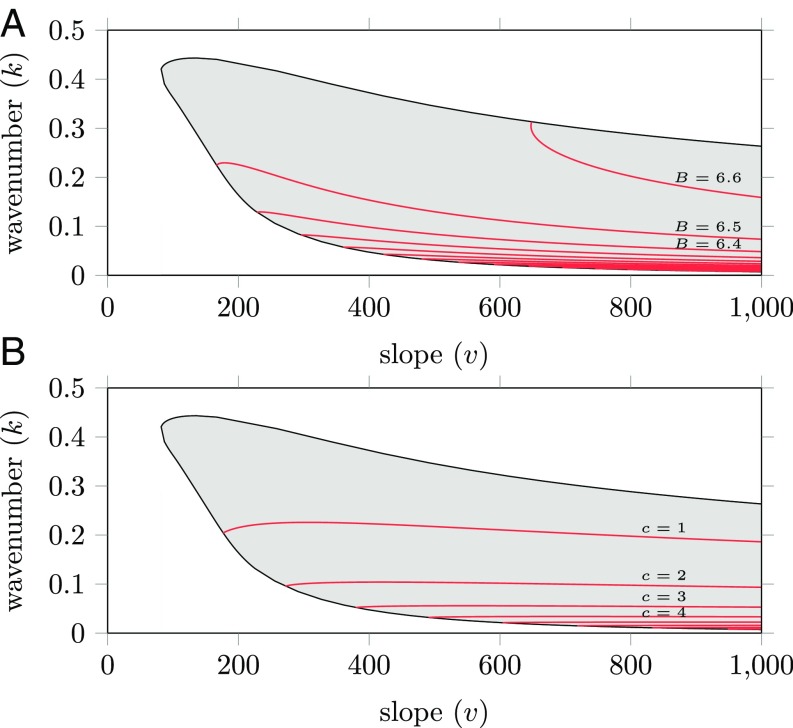
Besides a wavenumber, each ecosystem state also has a specific biomass and a specific pattern migration speed. The biomass of regular patterned states has been studied using numerical simulations (23) and more general formulas have been derived for patterns with small wavenumber (32). Both indicate that the biomass (per unit area) is positively correlated with both the wavenumber $k$ of the pattern and the slope parameter $v$ (23) (Fig. 2A). This has a physical interpretation: Both steeper slopes and higher wavenumbers (lower wavelengths) reduce the time it takes for water to reach vegetation bands and thereby reduce water losses during the transportation process. As a result, the vegetation will be able to harvest water from the uphill interbands more effectively. The biomass per wavelength is also of interest. The same studies indicate that the band biomass (per wavelength) is increased when the wavenumber $k$ is decreased and when the slope $v$ is increased. Hence, vegetation bands are expected to have more biomass when other vegetation is farther away, because of the larger (upslope) interband area water can be collected from.

Fig. 2.

(A and B) (Slope, wavenumber)-Busse balloon slices for the extended-Klausmeier model that include contours for the total biomass (per area) $B$ (A) and the migration speed $c$ (B). Biomass (per area) is positively correlated with both wavenumber $k$ and slope $v$; the migration speed is negatively correlated with the wavenumber $k$. Model parameters used: $a=3$, $m=0.45$, $e=500$.

The theoretical predictions for migration speed (of a pattern’s location) are a bit more subtle. For terrains with a constant slope, numerical simulations have been done (33, 34) and general formulas have been determined for patterns with small wavenumber (32, 35). In these idealized limit cases, migration speed is negatively correlated with wavenumber $k$ and positively correlated with slope $v$. However, beyond these idealizations, numerical computations show the contour lines are slightly humped (Fig. 2B). This indicates a (slightly) negative correlation between speed and slope $v$ for large slopes.

Testable Predictions.

The theoretical findings in this section lead to predictions that can be confronted with the field data. First of all, the model possesses a Busse balloon, which should lead to a wide spread in observable pattern wavenumbers (Fig. 1 and SI Appendix, Fig. S1). Moreover, biomass and migration speed are affected by pattern wavenumber. The biomass (per unit area) is expected to be positively correlated with both the wavenumber and the slope of the terrain (Fig. 2A). Migration speed is expected to decrease as a function of pattern wavenumber; the effect of slope on the migration speed is context specific, as it can be either positive or negative, depending on the specific topographical and environmental conditions (Fig. 2B).

2. Data Acquisition and Processing

For this comparison study, two sites were selected in Somalia. The first one ($8°0\prime 14″$–$8°15\prime 11″$N; $47°11\prime 54″$–$47°31\prime 4″$E) is located in the Haud pastoral region, which is referred to as the “Haud” site. The other site ($9°18\prime 49″$–$9°34\prime 34″$N; $48°8\prime 15″$–$48°43\prime 15″$E) is located in the Sool-Plateau pastoral area and is called the “Sool” site. Both sites mainly exhibit banded vegetation and have ground slopes ranging from $0\%$ to $1\%$. Vegetation mainly is composed of perennial grasses, which typically have an average lifetime of 1–7 y (36–38). A more detailed description of these sites is in SI Appendix, section 2; a map with the location of these sites along with the mean annual rainfall in these areas is shown in SI Appendix, Fig. S2.

To study the pattern properties in these study areas, each site was divided into square windows (of size $750\hspace{0.17em}\mathrm{m}\times 750\hspace{0.17em}\mathrm{m}$ for the Haud site and of size $\mathrm{1,010}\hspace{0.17em}\mathrm{m}\times \mathrm{1,010}\hspace{0.17em}\mathrm{m}$ for the Sool site). As has been done in previous studies, the type of pattern (e.g., bare soil, banded vegetation), along with its wavenumber, was determined using spectral analysis (20, 39–41). Only those windows were kept that exhibited banded vegetation with a wavenumber that could be determined with enough certainty (i.e., between 0.4 and 2.5 cycles per $100\hspace{0.17em}\mathrm{m}$). Moreover, windows with a too large curvature were ignored, because the theoretical predictions apply only to terrains with a constant slope. To obtain data on the migration speed of the banded vegetation, a cross-spectral analysis was performed, along the lines of previous studies (21, 42, 43). A more in-depth explanation of the processing steps is in SI Appendix, section 4.

The topographical data used in this article were derived from the Advanced Land Observation Satellite (ALOS) World 3D (AW3D) digital raster elevation model; biomass data for the Haud site were retrieved from a recently made map on (aboveground) biomass of African savannahs and woodlands (44) (no reliable data for the Sool site were available). Finally, optical data were acquired from various sources: Three multispectral WorldView-2 images were mosaicked and used as a reference for the Haud site; a panchromatic Ikonos “Geo” Imagery was acquired for the same site. For the Sool site, six WorldView-2 images were used and a panchromatic Satellite Pour l’Observation de la Terre (SPOT) 4 image preprocessed to level 2A was used as reference layer (Cnes 2004; Spot Image distribution). Moreover, two 7-$\mathrm{\mu }$m digitized panchromatic declassified Corona spy satellite images, national intelligence reconnaissance system, available from the US Geological Survey, were obtained for the Haud and Sool sites. More information about these datasets is in SI Appendix, section 3.

3. Results

Empirical Busse Balloon.

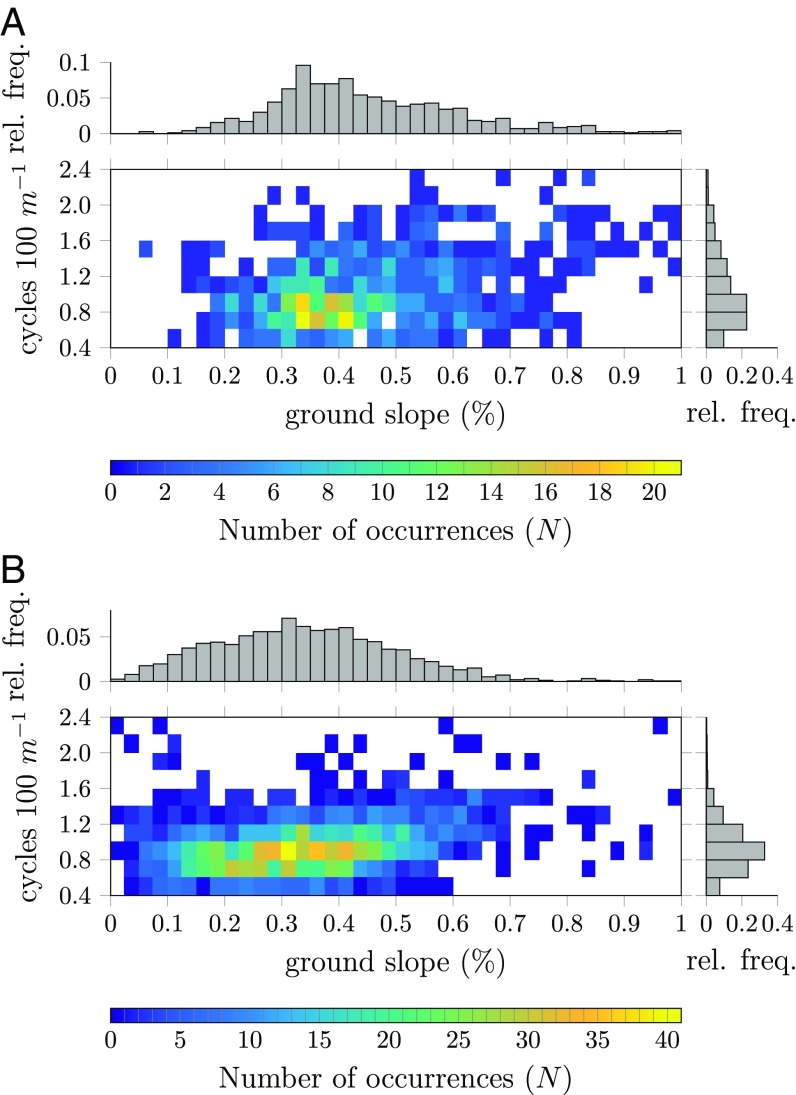
The most prominent pattern property studied in this article is the pattern wavenumber, which was derived from aerial imagery. The resulting distribution of wavenumbers is reported in Fig. 3 (a map with the spatial distribution of wavenumbers over the study sites is shown in SI Appendix, Fig. S3). Fig. 3 A and B shows the number of windows that have a particular slope–wavenumber combination. Also given is the relative frequency that indicates the spread of wavenumbers across all windows. The data display banded vegetation with wavenumbers roughly between 0.4 and 2.0 cycles per 100m. Importantly, this large spread is present for all of the ground-slope values which had a representative sample size and could not be explained by present heterogeneities in elevation or rainfall. This shows that for a given environmental condition not a single wavenumber pattern, but rather multiple patterns spanning a sizable range of wavenumbers are observable. Additionally, measurements used to determine the migration speed show barely any changes in wavenumber over the scope of 39 y (consistent with ref. 43), indicating that these patterns are in fact quite stable. Therefore, the observations are in agreement with the existence of a Busse balloon in the real ecosystem.

Fig. 3.

(A and B) Frequency distribution of banded patterns as function of ground slope and wavenumber (number of cycles per 100 m) for the Haud site (A) and the Sool site (B). The distribution on the right indicates the relative frequency of banded vegetation with corresponding wavenumber. The color gradient indicates the amount of windows ($N$).

Biomass and Migration Speed.

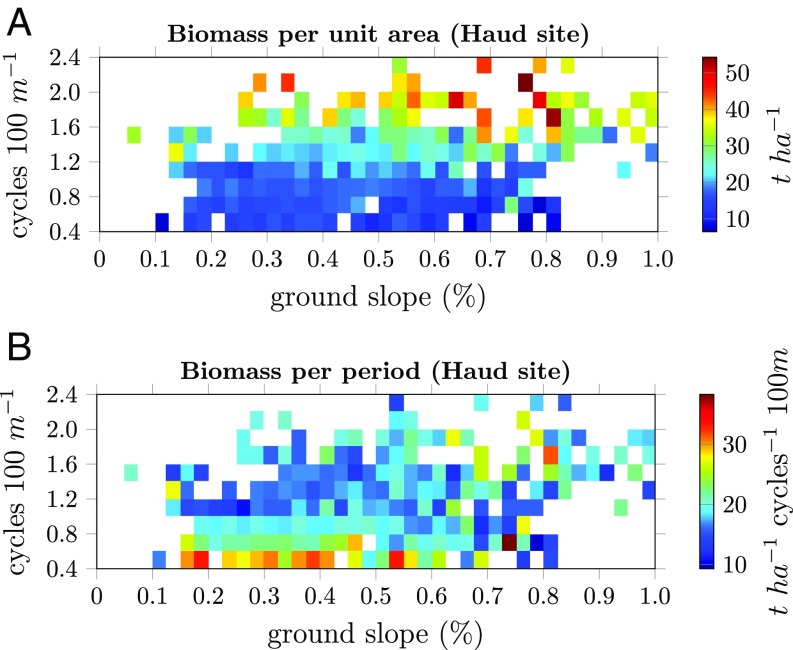
The processed biomass data for the Haud site are shown in Fig. 4. In Fig. 4A the relation between biomass per area (in $t\cdot {\mathrm{h}\mathrm{a}}^{-1}$) is plotted against the ground slope and the wavenumber. From the same data the biomass per period is computed—which is biomass per area divided by the window’s wavenumber. The resulting plot is given in Fig. 4B. The measurements of biomass show agreement with theoretical predictions of model studies; in both, the total biomass increases (all slopes: $r^2=0.64$, $n=714$, $P<0.001$; linear regression) and the biomass per period decreases when the wavenumber increases (all slopes: $r^2=0.09$, $n=714$, $P<0.001$; linear regression). However, a more in-depth inspection reveals disagreements. For one, the effect of ground slope is not strongly present in the data, although its effect is clear in the extended-Klausmeier model (Fig. 2A). Additionally, the more refined details of wavenumber dependence also differ (it is concave in the theoretical model and convex in the real-life data).

Fig. 4.

(A and B) Biomass distribution per area (A) and per period (B) as a function of ground slope and wavenumber (cycles per 100 m) for the Haud site. The color gradient indicates the amount of biomass measured for a particular (slope, wavenumber) combination.

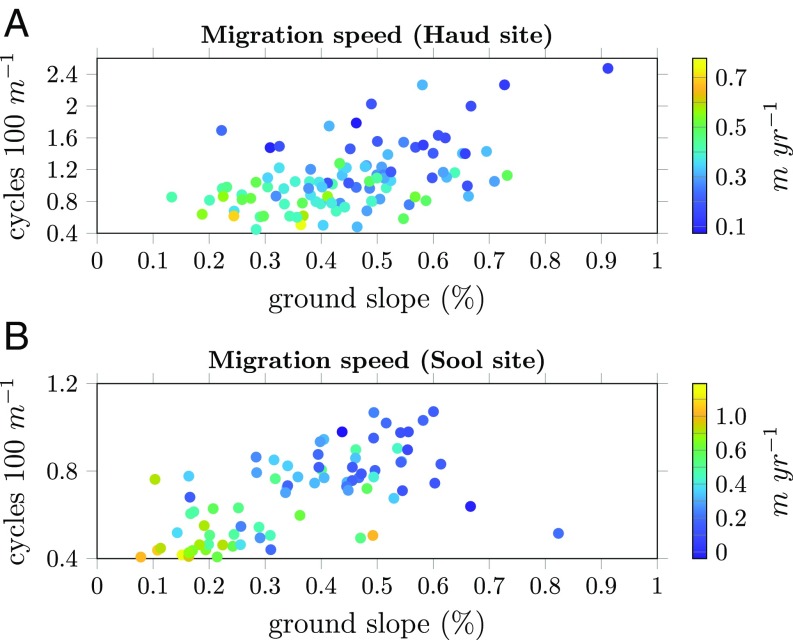
The migration speed is plotted in Fig. 5 for both the Haud and the Sool sites. These measurements show an increase in speed when the wavenumber decreases (Haud, $r^2=0.43$, $n=104$, $P<0.001$; Sool, $r^2=0.45$, $n=79$, $P<0.001$; linear regression), corroborating theoretical predictions (Fig. 2B).

Fig. 5.

(A and B) Observed (average) migration speed of vegetation bands in the Haud (A) and Sool (B) sites over the course of 39 y as a function of ground slope and wavenumber (cycles per 100 m). The color gradient indicates the migration speed for a particular (slope, wavenumber) combination. The sign indicates the direction of migration relative to the slope, with positive and negative values indicating upslope and downslope migration, respectively.

Discussion

Leading ecological frameworks emphasize the potential role of regular spatial vegetation patterns as indicators for proximity to catastrophic ecosystem shifts (11, 45). In these frameworks, however, monostability of patterns is implicitly assumed, suggesting that for a given environmental condition there is only one stable vegetated state, i.e., a single pattern with a specific wavelength (11, 45). Subsequent theoretical insights have challenged this view, highlighting the possibility of multistability of patterns, bounded by the so-called Busse balloon. In this study, we provide empirical evidence corroborating the existence of a Busse balloon for stable vegetation patterns in dryland ecosystems. Specifically, our two study sites in Somalia revealed the sustained (i.e., over a 39-y period) co-occurrence of banded vegetation with wavenumbers varying over a substantial range. Our findings have major implications for the way in which vegetation patterns indicate ecosystem resilience and mediate ecosystem responses to environmental change.

Specifically, the existence of a Busse balloon implies that an ecosystem’s resilience can no longer merely be defined by the magnitude of environmental change it can cope with (46). In these systems there is not one tipping point, but a cascade of destabilizations—indicated by the boundary of the Busse balloon. When environmental changes push a patterned ecosystem beyond the boundary of the Busse balloon, a wavelength adaptation occurs, and typically parts of the vegetation patches are lost, while the remaining patches grow in size. The extent of these adaptations depends on the rate of environmental change (23, 26, 47, 48). Moreover, human activities or natural variations can cause local disturbances, diminishing the regularity of ecosystem patterns. The recovery process from such disturbances may involve a rearrangement of patches in the landscape (23, 32). Again, the extent to which such recovery is possible depends on the rate of environmental change that the ecosystem is exposed to (47). Hence, the existence of a Busse balloon of stable dryland vegetation patterns suggests that adaptability of patches to changing environmental conditions provides a more comprehensive indicator for the ecosystem’s resilience than the shape of the pattern itself, as suggested in current leading frameworks (11, 45). To fully comprehend the consequences of this, it is necessary to provide a more thorough understanding of what determines the spatial rearrangement of vegetation patches resulting from disturbances, environmental changes, and spatial heterogeneities in the landscape.

The pattern-oriented modeling approach was mainly developed to aid model development and design, but the approach can also be used to evaluate the success of existing models to explain multiple strong and weak patterns observed (7). This so-called “reverse pattern-oriented modeling” approach (7) was used in the current study. Such systematic comparisons between model predictions and empirical data can be part of an iterative process toward further model improvement (5, 6). In this context, it is interesting to note the discrepancy that we observed between model predictions and field measurements of the influence of the ground slope on pattern migration speeds. Because topography critically changes the distribution of water within ecosystems, it also alters the migration speed of patterns. Therefore, it is of interest to determine the effects of more complex topographies for dryland ecosystem dynamics.

Moreover, the available empirical data align with theoretical predictions on both strong and weak patterns. However, environmental conditions were characterized by differences in slope gradient only. Although, indeed, the topography comprised the main source of environmental variation, other less pronounced heterogeneities are present and can cause spreads in wavenumber. The observed spread could not be attributed to variation in rainfall or elevation, but the role of other heterogeneities (e.g., soil composition and grazing activity) could not be fully determined for lack of precise and accurate datasets. When these become more readily available, further research might infer to which extent the observed wavenumber spread is explained by these environmental drivers.

Since their appearance on aerial photographs in the 1950s (49), the origin of regular vegetation patterns in dryland ecosystems has been a topic of fascination within the scientific community. The study of these patterns through reaction–diffusion modeling subsequently highlighted the importance of these patterns for the functioning of dryland ecosystems and their response to environmental change. The recent increase in the availability of optical and topographical data provides unprecedented opportunities to confront model predictions with empirical data (6, 31). In this study, we combined these data sources with in situ measurements of biomass, enabling the comparison of multiple pattern characteristics of Somalia drylands with predictions derived from reaction–diffusion modeling. The empirical evidence corroborates theories of multistability of patterned vegetation states, improving our understanding of these systems’ resilience to environmental changes. In addition, our results call for more detailed investigations of the role of small-scale topographic variability in pattern formation and migration.