Relation between blood pressure and pulse wave velocity for human arteries

Significance

Continuous, cuffless, and noninvasive blood pressure monitoring by measuring the pulse wave velocity is generally considered to be a promising technique for noninvasive measurements. Previously reported relations between blood pressure and pulse wave velocity relation involve unrealistic assumptions that do not hold for human arteries, and also rely on empirical expressions without any theoretical basis. Here, an analytical model without such assumptions or empirical expressions is established to yield a relation between blood pressure and pulse wave velocity that has general utility for future work in continuous, cuffless, and noninvasive blood pressure monitoring.

Abstract

Continuous monitoring of blood pressure, an essential measure of health status, typically requires complex, costly, and invasive techniques that can expose patients to risks of complications. Continuous, cuffless, and noninvasive blood pressure monitoring methods that correlate measured pulse wave velocity (PWV) to the blood pressure via the Moens−Korteweg (MK) and Hughes Equations, offer promising alternatives. The MK Equation, however, involves two assumptions that do not hold for human arteries, and the Hughes Equation is empirical, without any theoretical basis. The results presented here establish a relation between the blood pressure P and PWV that does not rely on the Hughes Equation nor on the assumptions used in the MK Equation. This relation degenerates to the MK Equation under extremely low blood pressures, and it accurately captures the results of in vitro experiments using artificial blood vessels at comparatively high pressures. For human arteries, which are well characterized by the Fung hyperelastic model, a simple formula between P and PWV is established within the range of human blood pressures. This formula is validated by literature data as well as by experiments on human subjects, with applicability in the determination of blood pressure from PWV in continuous, cuffless, and noninvasive blood pressure monitoring systems.

Blood pressure is a critical and highly elusive vital sign that varies depending on emotional state, physical activity, and health status. Low and high blood pressures correspond to two disease states called hypotension and hypertension (1–3), respectively. Roughly 30% of the population has hypertension-related health issues (4). The traditional method to measure blood pressure relies on an inflating cuff (5) that imparts an external pressure to the arm to stop the blood flow. Releasing this external pressure allows determination of the systolic and diastolic blood pressure, as pressures that correspond to stages of initiation and unimpeded flow of blood, respectively. Ambulatory blood pressure monitoring (6) based on this scheme requires an inflating cuff and oscillometric measurement (7, 8). The possibility for tissue damage due to the repeated blocking of blood flow in such approaches limits the interval of measurement to between 15 min and 30 min (9, 10). This sampling frequency fails to offer the time resolution necessary to detect fluctuations in blood pressure caused by, for example, exercise or mood swings. Continuous blood pressure monitoring is also essential for the care of critically ill patients and is typically achieved using invasive techniques based on intraarterial pressure measurements (11). Although considered the gold standard for beat-to-beat blood pressure monitoring, such methods expose patients to risks of complications and require intensive care monitoring (12).

Continuous, cuff less, and noninvasive blood pressure monitoring by measuring the pulse wave velocity (PWV) is generally considered to be a promising technique for continuous noninvasive measurements (13–16). PWV is defined as the velocity of the propagation for the pulse wave in the artery. The Moens−Korteweg (MK) (17) + Hughes (18) Equations are generally used to relate PWV to the blood pressure P,

$$\text{MK}\hspace{0.17em}\text{Equation}:\text{PWV}=\sqrt{\frac{E{h}_0}{2\rho {\mathit{R}}_0},}$$ [1a]

$$\text{Hughes}\hspace{0.17em}\text{Equation}:E=E_0\exp \left(\zeta P\right),$$ [1b]

where E, $h_0$, and $R_0$ are the elastic (tangent) modulus at blood pressure P and thickness and radius of the artery, respectively, $\rho$ is the blood density, $E_0$ is the elastic modulus at zero blood pressure, and $\zeta$ is a material coefficient of the artery. As the blood pressure P increases, the artery stiffens (i.e., increase of the tangent modulus E based on Eq. 1b), leading to an increase in PWV according to Eq. 1a. The MK Equation [1a] involves two assumptions: (i) The artery wall is thin such that it can be modeled as a thin shell, and (ii) the thickness and radius of the artery remain fixed as the blood pressure changes. For human arteries, however, these two assumptions may not hold, since the thickness-to-radius ratio $h_0/R_0$ = 0.08 to ∼0.22 (19) is beyond the limit $h_0/R_0$ < 0.05 (20) for a thin shell, and the change of the radius of a human artery can reach ∼30% due to blood pressure (19, 21). In addition, the Hughes Equation [1b] is completely empirical, without any theoretical foundation.

This paper aims to establish a relation between the PWV and blood pressure without the two assumptions involved in the MK Equation [1a], nor the empirical Hughes Equation [1b], which is replaced by the linear or nonlinear constitutive models for the artery. The results are validated by in vitro experiments using thin walled tubes of polydimethylsiloxane (PDMS), as a linear elastic material, for an artificial blood vessel. For human artery, which is well represented by the Fung hyperelastic model (21), the newly established relation between the PWV and blood pressure is much more accurate than the MK + Hughes Equations, leading to an improved understanding of the connections between blood pressure and PWV, with relevance in continuous, cuffless, and noninvasive blood pressure monitoring.

Results

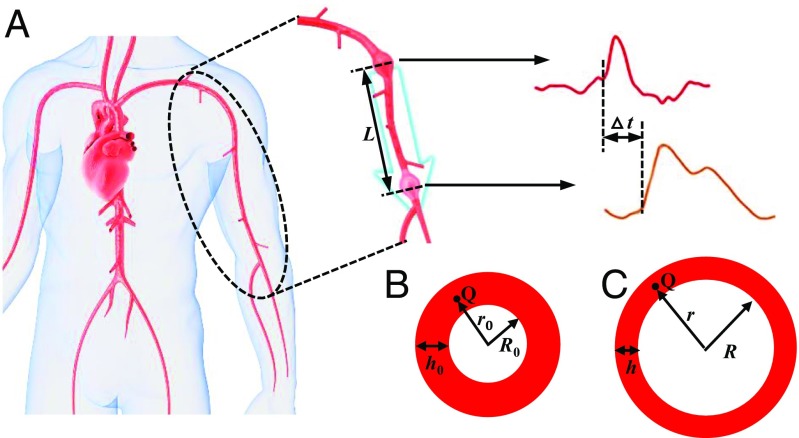
The schematic diagrams in Fig. 1 show the pulse wave propagation in a human artery. The disturbances caused by beating of the heart propagate as waves along the artery at a finite velocity. For a long and straight tube (artery) containing incompressible and nonviscous blood, the PWV is related to P, the inner area of the artery (A), and $\rho$ by (19)

$$\text{PWV}=\sqrt{\frac{A}{\rho }\frac{dP}{dA}}.$$ [2]

Fig. 1 B and C illustrates the cross-section of the artery before (initial thickness $h_0$ and radius of $R_0$) and after (thickness h and radius of R) the deformation induced by the blood pressure. Assumption ii in the MK Equation stated above gives the inner area of the artery fixed at $A=\pi R_0^2$. The two assumptions i and ii in the MK Equation, together with the equilibrium of force in the artery wall, yield $dP/dA=E{h}_0/\left(2\pi R_0^3\right)$, and its substitution in Eq. 2 leads to the MK Equation [1a]. In the following, a P−A relation is established without the two assumptions in the MK Equation.

Fig. 1.

(A) Schematic diagram of pulse wave propagation in a human artery. (B and C) The cross-sectional dimensions of the artery (B) before and (C) after deformation due to the blood pressure.

Equilibrium of force in the artery wall in the cylindrical coordinates {$r$,$\theta$,$z$} along the artery wall requires

$$\frac{d{\sigma }_{rr}}{dr}+\frac{1}{r}\left({\sigma }_{rr}-{\sigma }_{\theta \theta }\right)=0,$$ [3]

where the stresses ${\sigma }_{rr}$ and ${\sigma }_{\theta \theta }$ in the radial and circumferential directions are no longer uniform after assumption i in the MK Equation is relaxed; they are related to the corresponding strains via a constitutive model, such as the Fung hyperelastic model (21) for the human artery. After assumption ii in the MK Equation is relaxed, the (logarithmic) strains are obtained in terms of the (change of) inner area of the artery A. The pressure (P) can be obtained by integrating Eq. 3 from the inner radius $r=R$ to the outer radius $r=R+h$ after the deformation, i.e.,

$$P={\displaystyle {\int }_{-P}^{0}d{\sigma }_{rr}}={\displaystyle {\int }_R^{R+h}\frac{1}{r}\left({\sigma }_{\theta \theta }-{\sigma }_{rr}\right)dr}.$$ [4]

This equation, together with the constitutive model of the artery, gives the relation between P and A (see SI Appendix, Note 1 for details). Its substitution into Eq. 2 yields the relation between the blood pressure (P) and PWV, which is given separately in Eqs. 6, 7, 9, and 10 for the linear elastic model and Fung hyperelastic model of the artery, and is validated by the in vitro experiments.

In Vitro Experiments.

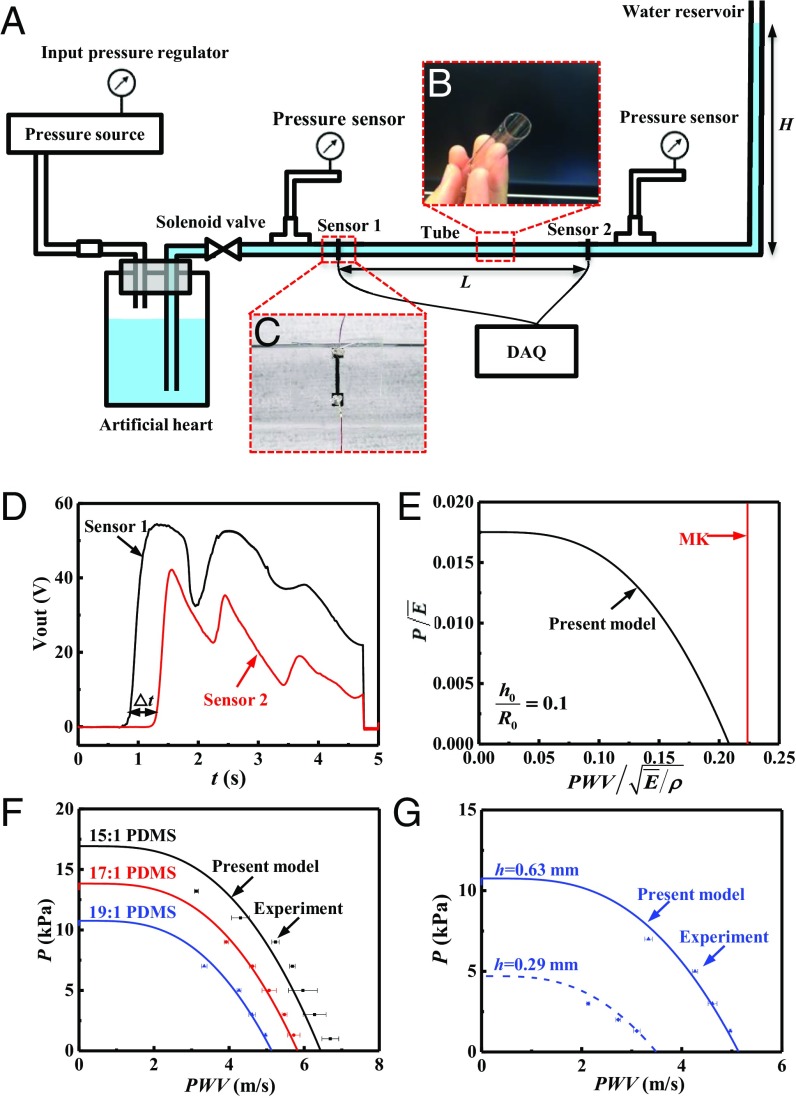
An in vitro hemodynamic simulator is developed, as shown in Fig. 2A, to verify the theory. The simulator includes a pulsatile flow generator, an artificial blood vessel, strain sensors, pressure sensors, and a water reservoir to define the base pressure on the tube. Pressurized water controlled by solenoid valve provides pulsatile flow, while the height of the water reservoir determines the diastolic pressure in the tube. Thin PDMS tubes with various wall thicknesses and elastic properties (controlled by changing the base to curing agent mixing ratio) provide artificial blood vessels with linear elastic properties within the range of deformations studied (Fig. 2B). Two strain sensors made of carbon black-doped PDMS (CB-PDMS) (22) detect the pulses at two different positions along the tube. The time difference $\mathrm{\Delta }t$ between the arrival of the pulse at each sensor position together with the distance L between the two sensors allows calculation of PWV (Fig. 2C). Fig. 2D shows the voltage signal of the two sensors with the distance L, which gives the PWV (23)

$$\text{PWV}=\frac{L}{\mathrm{\Delta }t}.$$ [5]

PDMS (base polymer: curing agent = 15:1, 17:1, and 19:1) is used to fabricate the tube for the in vitro experiment. SI Appendix, Fig. S1 shows the storage and loss moduli ($E\prime$ and $E″$) of the 17:1 PDMS measured by dynamic mechanical analysis at frequencies between 0.1 Hz and ∼10 Hz. The dynamic modulus is $\sqrt{E{\prime }^2+E{″}^2}$. The moduli of the 15:1, 17:1, and 19:1 PDMS at 10 Hz are 650, 540, and 420 kPa, respectively, for the samples used in the experiment shown in Fig. 2F. SI Appendix, Fig. S2 shows the relation between the true stress and logarithmic strain of the 17:1 PDMS measured by tensile testing, which displays good linearity for strain less than 30%. The tube in the in vitro experiment is, therefore, linear elastic with the modulus of E (i.e., the dynamic modulus $\sqrt{E{\prime }^2+E{″}^2}$ at 0 Hz).

Fig. 2.

(A) Schematic diagram of the in vitro experimental setup. (B and C) Experimental image of (B) the PDMS tube and (C) the strain sensor. (D) Signals from the two sensors. (E) Comparison of normalized pressure versus normalized PWV for linear elastic behavior of the tube between the present model and the MK Equation. (F and G) Comparison between the present model and the in vitro experiment, without any parameter fitting, for (F) different materials and (G) different tube thickness.

The Relation Between Pressure and PWV for Linear Elastic Tube Walls.

The linear stress−strain relation for the PDMS tubes, together with Eq. 4, gives the relation between the pressure P and inner area A as (see SI Appendix, Note 1 for details)

$$P=\frac{\overline{E}}{4}\left[\text{dilog}\left(\frac{A+A_{wall}}{A_0+A_{wall}}\right)-\text{dilog}\left(\frac{A}{A_0}\right)\right]+\frac{\overline{E}}{8}\left[\text{ln}{\left(\frac{A+A_{wall}}{A_0+A_{wall}}\right)}^2-\text{ln}{\left(\frac{A}{A_0}\right)}^2\right],$$ [6]

where $\overline{E}=E/\left(1-{\nu }^2\right)$ is the plane strain modulus; $\nu$ = 0.5 is the Poisson’s ratio for PDMS; $A_0=\pi R_0^2$ and $A_{wall}=\pi {\left(R_0+h_0\right)}^2-\pi R_0^2$ are the inner area of the artery and the area of artery wall, respectively, without pressure; and $\text{dilog}$ is the dilogarithm function (24). Substitution of Eq. 6 into Eq. 2 gives the PWV as

$$\text{PWV}=\sqrt{\frac{\overline{E}A}{4\rho }\left[\frac{A_0}{A\left(A-A_0\right)}\ln \frac{A}{A_0}-\frac{A_0+A_{wall}}{\left(A+A_{wall}\right)\left(A-A_0\right)}\ln \left(\frac{A+A_{wall}}{A_0+A_{wall}}\right)\right]}.$$ [7]

Eqs. 6 and 7 are parametric equations for the relation between the pulse wave velocity PWV and pressure P; elimination of the intermediate variable A yields the following scaling law between the normalized PWV and pressure P:

$$\frac{\text{PWV}}{\sqrt{\frac{\overline{E}}{\rho }}}=g\left(\frac{P}{\overline{E}},\frac{h_0}{R_0}\right),$$ [8]

where g is a nondimensional function shown in Fig. 2E. It is clear that PWV displays a strong dependence on P. For comparison, the MK Equation [1a] predicts a constant PWV (independent of the pressure), and is also shown in Fig. 2E. Fig. 2F indicates that, without any parameter fitting, the relation between PWV and P obtained from Eq. 8 agrees well with the in vitro experiments for 15:1, 17:1, and 19:1 PDMS and fixed $R_0$ = 6.3 mm, $h_0$ = 0.63 mm, and $\rho$ = 1,000 kg/m³ for water. The effect of liquid viscosity is shown in SI Appendix, Note 2 and Fig. S3. Similarly, Fig. 2G shows excellent agreement with experimental results for two thicknesses ($h_0$ = 0.63 and 0.29 mm) of the tube made of 19:1 PDMS and fixed $R_0$ = 6.3 mm, and $\rho$ = 1,000 kg/m³, without any parameter fitting. The experimental data all display strong dependence on the pressure, which clearly do not support the MK + Hughes Equations.

The Relation Between Blood Pressure and PWV for Human Artery Walls.

The human artery walls are well characterized by the Fung hyperelastic model (21), which has the strain energy density

$$W=\frac{C}{2}{\mathrm{e}}^{a_1{E}_{\theta \theta }^2+a_2{E}_{zz}^2}-\frac{C}{2},$$ [9]

where $E_{\theta \theta }$ and $E_{zz}$ are the Green strains in the circumferential and axial directions of the artery, respectively, and $a_1$, $a_2$, and $C$ are the material parameters, which are related to the elastic modulus (at zero pressure) by $E_0=C{a}_1$. Following the same analysis, but with the linear elastic model replaced by the Fung hyperelastic model for human arteries, yields parametric equations for the relation between the pulse wave velocity and pressure, similar to Eqs. 6 and 7, as (see SI Appendix, Note 1 for details)

$$P=\frac{1}{4}C{\text{e}}^{a_2{E}_{zz}^2}\sqrt{\pi a_1}\left\{\mathrm{erfi}\left(\frac{A-A_0}{2A_0}\sqrt{a_1}\right)-\mathrm{erfi}\left[\frac{A-A_0}{2\left(A_0+A_{wall}\right)}\sqrt{a_1}\right]\right\},$$ [10]

$$\text{PWV}=\sqrt{\frac{C{e}^{a_2{E}_{zz}^2}{a}_{1}A}{4\rho }\left[\frac{1}{A_0}{e}^{\frac{a_1{(A-A_0)}^2}{4A_0^2}}-\frac{1}{A_0+A_{wall}}{e}^{\frac{a_1{(A-A_0)}^2}{4{(A_0+A_{wall})}^2}}\right]}.$$ [11]

where $\mathrm{erfi}$ is the imaginary error function (25). Elimination of the intermediate variable A in Eqs. 10 and 11 yields the following scaling law between the normalized pulse wave velocity PWV and blood pressure P:

$$\frac{\text{PWV}}{\sqrt{\frac{C{\mathrm{e}}^{a_2{E}_{zz}^2}}{\rho }}}=f\left(\frac{P}{C{\mathrm{e}}^{a_2{E}_{zz}^2}},a_1,\frac{h_0}{R_0}\right),$$ [12]

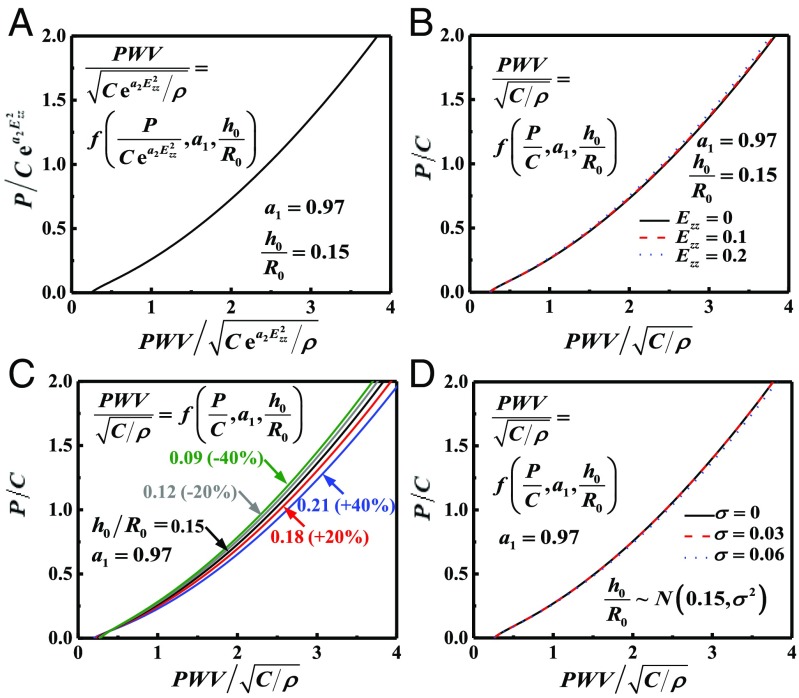
where f is a nondimensional function, and is shown in Fig. 3A for $a_1$ = 0.97 (26) and $h_0/R_0$ = 0.15 (19) for the human artery. Fig. 3B examines the effect of artery stretching $E_{zz}$ by comparing the limit $E_{zz}$ = 0 of Eq. 12, which takes the form

$$\frac{\text{PWV}}{\sqrt{\frac{C}{\rho }}}=f\left(\frac{P}{C},a_1,\frac{h_0}{R_0}\right),$$ [13]

to the scaling law in Eqs. 10 and 11 for a representative $a_2$ = 2.69 (21) and $E_{zz}$ = 0.1 and 0.2. The effect of artery stretching is negligible even for 20% stretching.

Fig. 3.

(A) Normalized blood pressure P versus normalized PWV for the human artery characterized by the Fung hyperelastic model. (B–D) Normalized P versus normalized PWV for (B) different axial stretching of the artery, (C) different thickness-to-radius ratio $h_0/R_0$ of the artery, and (D) different SD $\sigma$ for a normal distribution of $h_0/R_0$.

The scaling law in Eq. 13 degenerates to the MK Equation [1a] in the limit of low blood pressure, which gives $A\to A_0$; therefore $e^{a_1{\left(A-A_0\right)}^2/\left(4A_0^2\right)}=\sim 1$ and $e^{a_1{\left(A-A_0\right)}^2/\left[4{\left(A_0+A_{wall}\right)}^2\right]}=\sim 1$. Eq. 11, at the limit $E_{zz}$ = 0, then becomes $\text{PWV}=\sqrt{C{a}_1{A}_{wall}/\left[4\rho \left(A_0+A_{wall}\right)\right]}$, which is identical to the MK Equation [1a] for a thin artery wall [i.e., $A_{wall}/\left(A_0+A_{wall}\right)=\sim 2h_0/R_0$] at zero blood pressure.

The artery thickness, in general, is not a constant even for the same human artery; the thickness-to-radius ratio $h_0/R_0$ has an average of 0.15 and a variation of 40% (19). Fig. 3C shows the normalized pressure $P/C$ versus $\text{PWV}/\sqrt{C/\rho }$ for $h_0/R_0$ = 0.09, 0.12, 0.15, 0.18, and 0.21, corresponding to ±20% and ±40% variations of $h_0/R_0$ = 0.15. Even for 40% variations, the curves in Fig. 3C are different by only ∼6%. For $a_1$ = 0.97 and a normal distribution of $h_0/R_0$ with the mean 0.15 and SD $\sigma$, the mean PWV is obtained as

$$\frac{\text{PWV}}{\sqrt{\frac{C}{\rho }}}=f\left[\frac{P}{C},a_1=0.97,\frac{h_0}{R_0}\sim N\left(0.15,{\sigma }^2\right)\right],$$ [14]

and is shown in Fig. 3D for several values of $\sigma$. The curve based on the mean $h_0/R_0$ gives an accurate relation between the PWV and blood pressure.

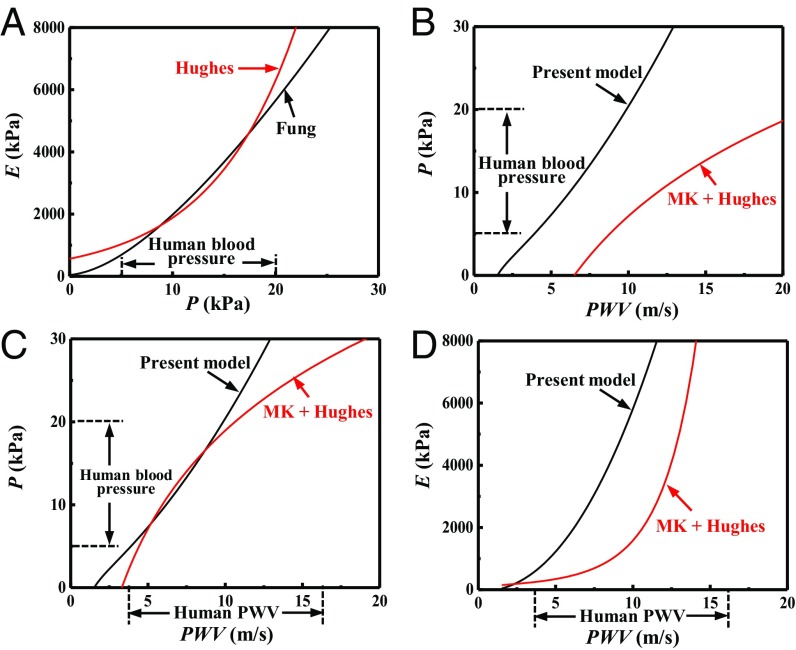
Fig. 4 A and B compares the present model (in Eq. 13) to the classical MK + Hughes Equations (in Eqs. 1a and 1b) for a human artery characterized by the Fung hyperelastic model with C = 39 kPa, $a_1$ = 0.97, and $h_0/R_0$ = 0.15 (19, 26). The arterial stiffness, or the equivalent tangent modulus E, is shown in Fig. 4A versus the blood pressure P. In the range of human blood pressure (5 kPa to ∼20 kPa), the arterial stiffness is used to determine the material parameters in the Hughes Equation [1b] as $E_0$ = 563 kPa and $\zeta$ = 0.121 kPa⁻¹, which yields good agreement between the Hughes Equation and the present model. However, for the same range of blood pressure, Fig. 4B shows that the MK + Hughes Equations overestimate the PWV by a factor of ∼2 compared with the present model. This large discrepancy results from the large change of radius and thickness of the artery wall (>50%), which is neglected in the MK Equations (due to assumption ii) but is accounted for in the present model.

Fig. 4.

(A) The arterial stiffness (equivalent modulus) E versus the blood pressure P for a human artery characterized by the Fung hyperelastic model; the Hughes Equation is also shown, where its parameters $E_0$ and $\zeta$ are determined by fitting the arterial stiffness within the range of human blood pressure (5 kPa to ∼20 kPa). (B) The blood pressure P versus the PWV of the human artery, given by the present model and by the MK + Hughes Equations, where the parameters $E_0$ and $\zeta$ are determined from A. (C) The blood pressure P versus the PWV for the human artery characterized by the Fung hyperelastic model; the MK + Hughes Equations are also shown, where the parameters $E_0$ and $\zeta$ in the Hughes Equation are determined by fitting within the range of human blood pressure (5 kPa to ∼20 kPa). (D) The artery stiffness (equivalent modulus) E versus the PWV of the human artery, given by the present model and by the Hughes Equation, where the parameters $E_0$ and $\zeta$ are determined from C.

Another important clinical application of PWV is to determine the arterial stiffness (equivalent tangent modulus) of the artery wall as the elastic properties of arteries are affected by aging and cardiovascular diseases, therefore providing useful prognostic information (27). The blood pressure P is shown in Fig. 4C versus the PWV. In the range of human blood pressure (5 kPa to ∼20 kPa), the pressure−PWV relation is used to determine the material parameters in the Hughes + MK Equations (Eqs. 1a and 1b) as $E_0$ = 145 kPa and $\zeta$ = 0.117 kPa⁻¹, which yields good agreement between the MK + Hughes Equations and the present model. However, for the same range of PWV, Fig. 4D shows that the MK + Hughes Equations significantly underestimate the equivalent tangent modulus by a factor of ∼3 compared with the present model. The main reason for this large discrepancy is the same as that shown in Fig. 4 A and B.

For the human artery characterized by the Fung hyperelastic model with C = 39 kPa, $a_1$ = 0.97, and $h_0/R_0$ = 0.15 (19, 26), the range of human blood pressure (5 kPa to ∼20 kPa) gives $A/A_0$ = 2.46 to ∼3.55, which is relatively large such that the function erfi in Eq. 10 can be approximated by $\mathrm{erfi}\left(x\right)\approx e^{x^2}/\left(\sqrt{\pi }x\right)$ (28). Eqs. 10 and 11, at the limit $E_{zz}$ = 0, have the asymptotes for large $A/A_0$ (see SI Appendix, Note 3 for details),

$$P\approx \frac{C}{2}\frac{A_0}{A-A_0}{e}^{\frac{a_1{(A-A_0)}^2}{4A_0^2}},$$ [15]

$${\text{PWV}}^2\approx \frac{C{a}_1}{4\rho }\frac{A}{A_0}{e}^{\frac{a_1{(A-A_0)}^2}{4A_0^2}}.$$ [16]

Eliminating the variable A yields the following relation (see SI Appendix, Note 3 for details):

$$\ln \frac{P}{C}+\ln \left(\sqrt{1+\frac{8\rho }{a_1}\frac{{\text{PWV}}^2}{P}}-1\right)=\frac{a_1}{16}{\left(\sqrt{1+\frac{8\rho }{a_1}\frac{{\text{PWV}}^2}{P}}-1\right)}^2,$$ [17]

which, as shown in Fig. 5A, is in reasonable agreement with the P versus PWV curve at large pressure, and their difference is approximately a constant (i.e., a shift along the vertical axis). The above equation suggests that the blood pressure scales with PWV², i.e., $P\approx \alpha {\text{PWV}}^2$, and the scaling coefficient $\alpha$ is approximately a constant since the logarithmic term $\ln \left(P/C\right)$ has a very weak dependence on the pressure. Accordingly, the relation between P and PWV can be represented by

$$P=\alpha {\text{PWV}}^2+\beta ,$$ [18]

where $\beta$ represents the constant shift between the two curves in Fig. 5A, and $\alpha$ and $\beta$ depend on the material properties and geometry of the artery ($C$, $a_1$, $\rho$, $R_0$, and $h_0$) and are to be determined from the experiments.

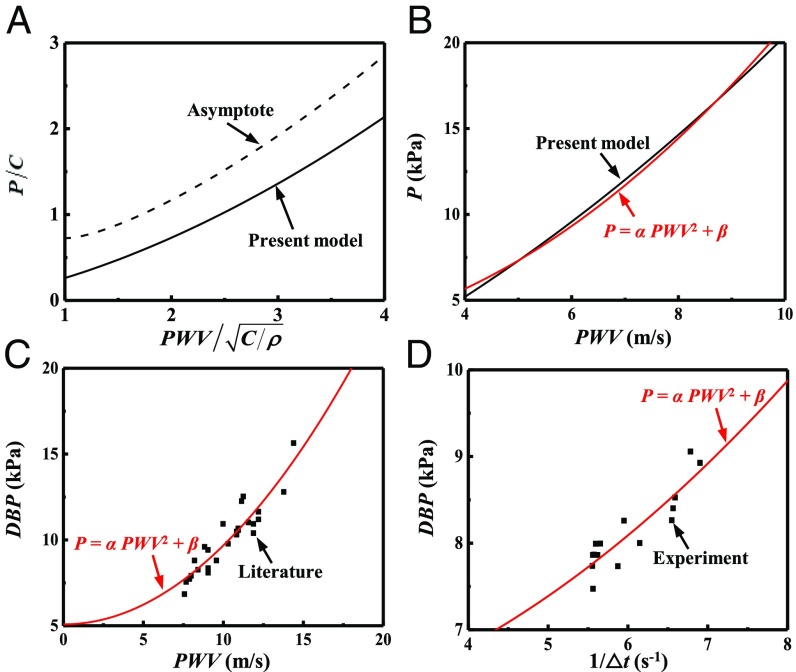
Fig. 5.

(A) The normalized blood pressure P versus the normalized PWV given by the present model (in Eqs. 10 and 11) and its asymptote (in Eq. 17). (B and C) Comparison of $P=\alpha {\text{PWV}}^2+\beta$ to (B) the present model (Eqs. 10 and 11) and (C) literature data (29). (D) Comparison of $P=\alpha L^2/\mathrm{\Delta }{t}^2+\beta$ to the experiments of blood pressure P versus $1/\mathrm{\Delta }t$, where $\mathrm{\Delta }t$ is pulse arrival time.

For the human artery characterized by the Fung hyperelastic model with C = 39 kPa, $a_1$ = 0.97, and $h_0/R_0$ = 0.15 (19, 26), the constants are $\alpha$ = 0.18 kPa·s²⋅m⁻² and $\beta$ = 2.7 kPa, which show excellent agreement (Fig. 5B) with the P versus PWV relation obtained from Eqs. 10 and 11 in the range of human blood pressure (5 kPa to ∼20 kPa). Fig. 5C further compares Eq. 18 with literature data (29) of the experimental diastolic blood pressure (DBP, measured by an invasive method) versus PWV (obtained from the ear and toe pulses) during and after anesthesia for surgery. For $\alpha$ = 0.046 kPa·s²⋅m⁻² and $\beta$ = 5.1 kPa, Eq. 18 agrees reasonably well with the experimental data.

SI Appendix, Fig. S4A, Inset shows a multimodal wearable sensor called the BioStamp (MC10 Inc.) (30), which contains electrodes and an optical sensor for collection of electrocardiogram (ECG) (31) and photoplethysmograph (PPG) (32) signals simultaneously. The BioStamp mounts on the torso in the subclavicular region (SI Appendix, Fig. S4A) or, alternatively, on the posterior side overlaying the scapula (SI Appendix, Fig. S4B). These two positions allow collection of ECG and PPG signals concurrently, and exploit the temporal relationship between these two signals to compute pulse arrival times ($\text{PVW}=L/\mathrm{\Delta }t$: pulse arrival distance, L, pulse arrival time, $\mathrm{\Delta }t$). Evaluations of the correlations between these $\mathrm{\Delta }t$ measurements and blood pressure rely on episodic measurements of blood pressure with a conventional cuff device with the subject instrumented with the BioStamp. The $\mathrm{\Delta }t$ and DBP versus time are measured during the postexercise period. The $1/\mathrm{\Delta }t$ and DBP both decrease during the first 300 s (after sprinting), then approach a stable resting value as shown in SI Appendix, Fig. S5. Their relation can be described by substituting Eq. 5 into Eq. 18,

$$P=\alpha \frac{L^2}{\mathrm{\Delta }{t}^2}+\beta .$$ [19]

The $1/\mathrm{\Delta }t$ and DBP response during the first 300 s are shown in Fig. 5D, together with Eq. 19 and $\alpha L^2$ = 0.064 kPa·s² and $\beta$ = 5.8 kPa, which shows reasonable agreement with the experimental data. In general, once $\beta$ and $\alpha$ in Eq. 18 (or $\alpha L^2$ in Eq. 19) are determined, then the continuous, cuffless, and noninvasive blood pressure can be monitored by measuring the PWV.

Conclusions

This paper establishes a relation between the blood pressure P and pulse wave velocity PWV that does not rely on the Hughes Equation or on assumptions in the MK Equation. This relation degenerates to the MK Equation in a regime of extremely low blood pressures. An in vitro hemodynamic simulator is developed to collect PWV and pressure data using liquid flow through a PDMS (with linear stress−strain relation) tube. These in vitro experiments show that the PWV depends strongly on pressure, unlike expectations based on the MK equation but in excellent, quantitative agreement with the newly established relation without any parameter fitting. For human arteries, which are well characterized by the Fung hyperelastic model, a simple formula $P=\alpha {\text{PWV}}^2+\beta$ is established within the range of human blood pressure. This formula is validated by literature data as well as by experiments on human subjects, and can be used to determine the blood pressure from the measured PWV in continuous, cuffless, and noninvasive blood pressure monitoring.

Methods

Hemodynamic Simulator.

A pressurized bottle filled with water driven by a 12-V solenoid valve (Adafruit Industries) produced pulse wave flow by opening of a given repeatable pressure in the water reservoir. Two factory-calibrated pressure sensors (HHP886; OMEGA Engineering) with measurement accuracy of ±1.5% were located before strain sensor #1 and after strain sensor #2 as shown in Fig. 2A. Strain sensors were placed on the surface of a PDMS tube at a specific distance. Resistance difference during pulse wave by data acquisition system at 1-kHz sampling rate (Powerlab 8/35; ADInstruments) provided the detection of the peak of resistance change from strain sensors. The water reservoir controlled the diastolic pressure in the tube by adjusting the water height. The water generated from the pulse generator flowed out from the tube to maintain the pressure in the tube before and after pulse generation.

Fabrication of Thin CB-PDMS Strain Sensor.

Spin coating 30:1 PDMS (Sylgard 184 Silicone Elastomer; Dow Corning) at 1,000 rpm on a Si wafer generated a substrate. Spin coating polyimide (PI2545; HD Microsystems) at 3,000 rpm for 30 s followed by baking at 110 °C for 1 min, 150 °C for 4 min, and 250 °C for 5 min produced a thin layer. Spin coating AZ4620 (AZ Electronic Materials) at 2,000 rpm for 30 s and developing generated a mold for the strain sensor. Fabrication of thin CB-PDMS began with mixing 25 wt% carbon black (VULCAN XC72R; Cabot Corporation) and 30:1 PDMS. A doctor blade method formed a thin CB-PDMS layer in the opening region in the mold. After baking at 70 °C for 2 h, immersion in acetone removed the photoresist to leave only the patterned CB-PDMS on a PI layer. Spin coating and baking at 70 °C for 2 h of 30:1 PDMS generated a uniform encapsulation layer.

Fabrication of Thin PDMS Tube.

Pouring a precursor to PDMS (Sylgard 184 Silicone Elastomer; Dow Corning) with a specific mixing ratio into the inside of clear poly(ethylene terephthalate)-glycol tube with 12.7-mm inner diameter (McMaster-Carr) to cover all of the inside of the tube and curing it overnight while held in a vertical position at room temperature at 20 °C generated one layer of thin PDMS. The tube was then reversed before pouring a second layer to reach an approximately homogeneous thickness along the length of the tube (thickness variation is less than 10%). The number of repetitions of this process determined the thickness of the tubing. A week of additional curing process reached a stable state of the PDMS in terms of elastic properties.

Measurement of Elastic Properties.

Elastic properties of each PDMS tube were measured using a RSA3 dynamic mechanical analyzer, within a few hours after the pulse wave velocity measurement to avoid any aging effect.