Transport and trapping of nanosheets via hydrodynamic forces and curvature-induced capillary quadrupolar interactions

Abstract

Hypothesis

The manipulation of nanosheets on a fluid-fluid interface remains a significant challenge. At this interface, hydrodynamic forces can be used for long-range transport (>1× capillary length) but are difficult to utilize for accurate and repeatable positioning. While capillary multipole interactions have been used for particle trapping, how these interactions manifest on large but thin objects, i.e., nanosheets, remains an open question. Hence, we posit hydrodynamic forces in conjunction with capillary multipole interactions can be used for nanosheet transport and trapping.

Experiments

We designed and characterized a fluidic device for transporting and trapping nanosheets on the water-air interface. Analytical models were compared against optical measurements of the nanosheet behavior to investigate capillary multipole interactions. Energy-based modeling and dimensional analysis were used to study trapping stability.

Findings

Hydrodynamic forces and capillary interactions successfully transported and trapped nanosheets at a designated trapping location with a repeatability of 10% of the nanosheet’s length and 12% of its width (length = 1500 μm, width = 1000 μm) and an accuracy of 20% of their length and width. Additionally, this is the first report that surface tension forces acting upon nanoscale-thick objects manifest as capillary quadrupolar interactions and can be used for precision manipulation of nanosheets.

Graphical Abstract

1. Introduction

Two-dimensional nanomaterials, also called “nanosheets”, feature thicknesses on the order of nanometers, with lengths and widths on the order of micrometers to millimeters. The fabrication and manipulation of nanosheets, as well as their integration with substrates and devices, remains a significant challenge, despite its relevance to a broad range of fields, from nanotechnology, to neuroscience, to materials science.^[1–10] Nanosheets hold promise to bring significant advances in thin-film transistor, actuator, energy harvesting/power generating, and opto-electronic technologies.^[1–5] In recent years, methods of nanosheet fabrication involving self-assembly of nanomaterials at liquid-air interfaces have been shown to be reliable for nanosheet manufacturing.^[7–10] However, objects on liquid-air interfaces are subject to a complex combination of capillary and hydrodynamic forces.^[11–22]

Thus, while the ability to fabricate nanosheets has been well established, the manipulation of nanosheets remains an unsolved problem. Within a single fluid, there are many options for particle manipulation, ranging from optical, magnetic, electrokinetic, closed-loop microfluidic hydrodynamic, and acoustic systems.^[23–29] Yet, at fluid-fluid interfaces, options are largely limited to hydrodynamic and capillary forces. Curvature-induced capillary multipole interactions at the fluid-fluid interface are able to manipulate a variety of particles but typically across distances less than one capillary length.^[11–22] From prior literature, the dominant multipole interaction that facilitates particle movement varies depending on the geometry of the object: quadrupolar capillary interactions are known to facilitate the attraction of small (r ~ 1 μm) particles, while monopolar capillary interactions are known to facilitate the attraction of large (r ~ 1 mm) isometric objects.^[11–22] For extremely anisotropic materials with aspect ratios much greater than one—e.g., nanosheets—it remains unclear which multipole capillary interaction is the dominant term. Nonetheless, for distances greater than one capillary length, multipole capillary interactions are generally impractical for rapid manipulation of nanosheets. Conversely, hydrodynamic forces are effective for long-range transportation at the air-water interface but are difficult to utilize for trapping.

Ultimately, we present an approach that combines hydrodynamic and curvature-induced capillary interactions in a device for the transport and trapping of nanosheets at a liquid-air interface. In our device, the hydrodynamic forces, produced by bulk fluid motion, enable long-range (> 1× capillary length) transport while the capillary interactions, produced by a curvature-inducing trapping feature, enable short-range (< 1× capillary length), accurate and repeatable trapping thereby passively manipulating nanosheets on the liquid-air interface. Additionally, we demonstrate, with modeling and experiment, the interactions of nanosheets via quadrupolar capillary interactions.

2. Materials and Methods

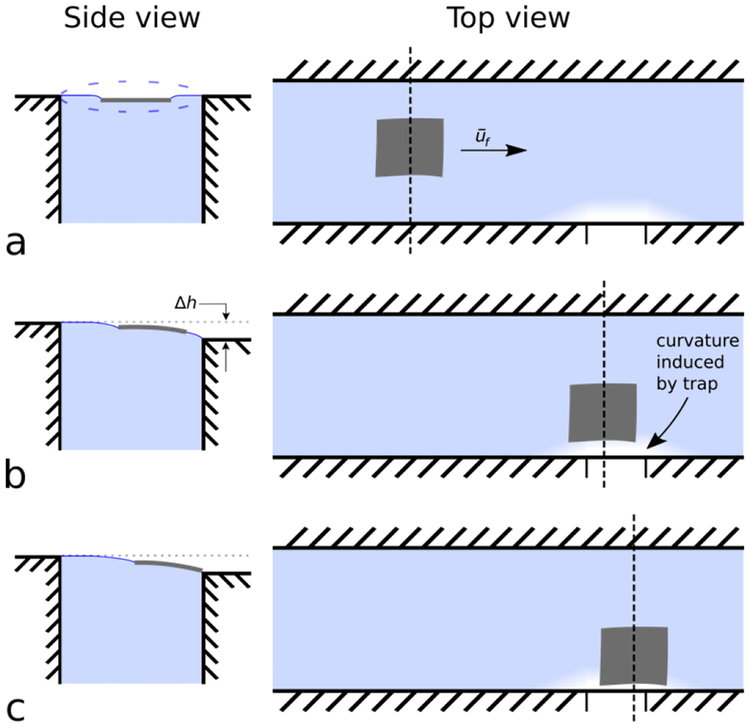
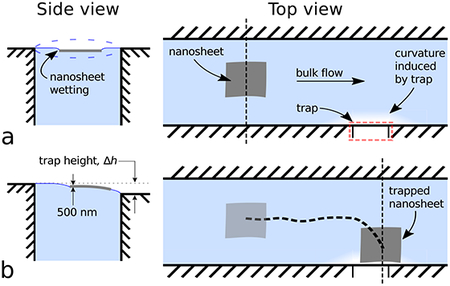
A schematic of our device is shown in Figure 1. Initially, a nanosheet is placed onto a flat water-air interface, thus deforming the water surface around itself. Due to surface tension forces, the nanosheet remains trapped at the water-air interface. Bulk flow is produced within the channel, and the nanosheet is transported “downstream” via hydrodynamic forces, as indicated in Figure 1a, right. Further downstream, a trap is created from a micro-machined notch in the channel wall, which induces curvature on the water-air interface, shown in Figure 1b. As the nanosheet approaches the trap, the curvature induced by the nanosheet interacts with the curvature induced by the trap, attracting the nanosheet towards the trap. Ultimately, the nanosheet comes to rest at the trap, as shown in Figure 1c. For further illustration, a video of nanosheet manipulation is shown in Supplemental Movie 1.

Figure 1.

The nanosheet trapping device comprises a water-filled, open millifluidic channel with a notch (i.e., trap) along one edge. As a nanosheet flows through the channel, it comes to rest in contact with the trap. The device works by using a combination of hydrodynamic forces far from the trap (view a) and curvature-induced capillary interactions close to the trap (views b, c) to transport and trap nanosheets, respectively. Top views illustrate the position of the nanosheet in the channel relative to the trap. Side views, at locations indicated by vertical dashed lines, illustrate curvature of water-air interface. (a, side view) The trap water height is set properly when the fluid level has minimal curvature. (a, top view) The water and nanosheet both flow with average velocity, ūf far from the trap (approximately 1–10× capillary length of the water-air interface, or equivalently 2.7 mm-27 mm). (b, side view) Near the trap (<1× capillary length (<2.7 mm) of the water-air interface), the nanosheet’s trajectory is influenced by water-air curvature arising from the trap’s height difference, Δh. (c, side view) The nanosheet comes to rest at the trap where the water-air interface surface energy is minimized.

2.1. Device design and fabrication.

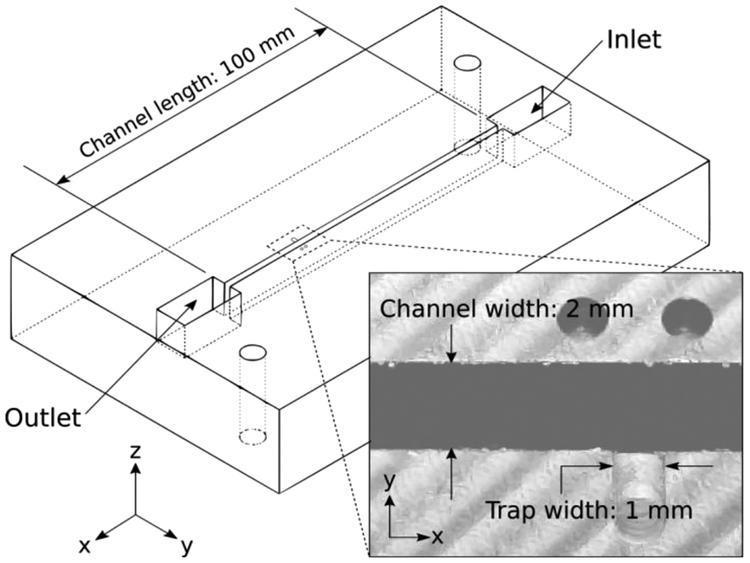
We designed and fabricated a device for nanosheet transport and trapping, shown in Figure 2. The device was designed in computer aided design software (SolidWORKS); G-code was generated using computer-aided manufacturing software (HSMWorks). The device was fabricated using a CNC mill (Haas Office Mill, Model OM-1A) from black Delrin®. Delrin was chosen due to its ease of machining; the black color enables optical contrast via thin film interference for observation. The channel length was 100 mm with a width and depth of 2 mm and 10 mm, respectively. The trap consists of a 1 mm wide, 100 μm-deep milled feature in the channel wall on one side (Figure 2, inset). The depth of the trapping feature was verified using surface profilometry (Veeco Dektak 150). Two 1 mm holes were added near each trap as fiducial marks for video registration during data processing. The device is open to atmospheric pressure and is not enclosed within any pressurized chamber.

Figure 2:

SolidWORKS wireframe model of device. Channel length is 100 mm, with the trapping feature positioned 90 mm from the inlet to ensure that the flow is fully developed. Inset: Field of view of camera for all experiments. The nanosheet trapping feature i s shown, milled into the side of the channel. Trapping feature width is 1 mm; trapping feature depth is 100 μm, confirmed by profilometry. Channel width is 2 mm; channel depth is 10 mm.

2.2. Experiment methods

The device was secured to an optical breadboard (THORLABS) for all experiments. A syringe pump (Harvard Apparatus), with two 60 mL syringes filled with deionized water, was used to produce a combined flow rate of 12 mL/min (2 × 10⁻⁷ m³/s). The two syringes were connected with a T-junction, luer-lock fitting to merge the two streams. Plastic tubing with 6.35 mm outer diameter and 4.35 inner diameter was used. By using two syringes, we were able to perform six trials without refilling, using 20 mL each. The inlet tube was positioned in the device using an articulating arm. We attached one end of an outlet tube (6.35 mm outer diameter and 4.35 mm inner diameter) to the device outlet. The other end was attached to a vertically oriented (along the z-direction, as shown in Figure 2) linear stage with coupled micrometer (THORLABS), enabling us to position the outlet tube with micrometer resolution. The water level was adjusted with the syringe pump running at the specified flow rate until there was no observed water surface deformation in the main channel. This was performed by illuminating the water surface with a white light LED lamp and observing the edges of the water channel to see if the water meniscus was convex, concave, or flat. (See Supplemental Movie 1, t = 0.0s – 5.0s for examples of water-air interface deformation). The outlet tube was placed into a waste beaker. Water was not reused to avoid contamination. The entire experimental setup was placed inside an acrylic box to shield from ambient air currents and temperature fluctuations due to the building heating and air conditioning system.

A USB camera (Veho, VMS-004) was manually positioned with an articulating arm, 100 mm from the trap feature, and at 20 degrees from vertical to allow sufficient thin-film interference to see the nanosheets. Videos were recorded at a frame rate of 6.25 fps using the MATLAB Image Acquisition Toolbox (MATLAB 2015b). Nanosheets were cut using an ultramicrotome (Leica UC7), at 500 nm thickness, using a diamond knife (Diatome). Nanosheets were cut from an epoxy resin block (EPON 812, ρ = 1.22 g/cm³) that was trimmed manually to a cross section of roughly 1 mm × 1.5 mm. Nanosheets were transferred manually from the ultramicrotome to the device using a commercial tool (Perfect Loop, Electron Microscopy Supplies).

The Reynolds number of the main channel, Re, was calculated as

$$Re=\frac{{\rho }_{\text{water}}\frac{Q}{A_{\text{channel}}}{R}_h}{\mu },\text{where}$$

A_channel is the channel cross-sectional area, defined as

$$A_{\text{channel}}=w_{\text{channel}}{d}_{\text{channel}},$$

ρ_water is the density of water at 25°C, Q is the volumetric flow rate in the channel, w_channel is the channel width, d_channel is the channel depth, R_h is the hydraulic radius, defined as

$$R_h=\frac{A_{\text{channel}}}{2d_{\text{channel}}+w_{\text{channel}}}$$

for open channel flow, and μ is the dynamic viscosity of water at 25°C. With the calculated Reynolds number of the channel (Re ~ 10), we assumed primarily laminar flow. Additionally, we calculated the nanosheet Reynolds number, Re_nanosheet, to access the effect of inertial forces relative to that of viscous forces, with Re_nanosheet defined as

$$R{e}_{\text{nanosheet}}=\frac{{\rho }_{\text{nanosheet}}\frac{Q}{A_{\text{channel}}}{L}_c}{\mu },$$

where ρ_nanosheet is the density of the nanosheet (ρ = 1.22 g/cm³), Q is the volumetric flow rate in the channel, A_channel is the channel cross-sectional area, L_c is the nanosheet characteristic length, defined as

$$L_c=\sqrt{w^2+l^2+t^2},$$

(w, l, and t, are the width, length, and thickness of the nanosheet, respectively), and μ is the dynamic viscosity of water at 25°C. We calculate Re_nanosheet ~ 10⁻³, indicating inertial forces to be negligible to viscous forces exerted by the water upon the nanosheet.

Furthermore, we assessed the effects of gravity versus surface tension forces by calculating the Bond number and the effects of inertial versus surface tension forces by calculating the Weber number. The equation for the Bond number and the Weber number are

$$Bo=\frac{\Delta \rho g{L}_c^2}{\gamma }\text{and\hspace{0.17em}}We=\frac{\Delta \rho v^2{L}_c}{\gamma },\text{\hspace{0.17em}respectively},$$

where L_c is the nanosheet characteristic length, Δρ is the difference in density between the nanosheet and water at 25°C, g is the acceleration due to gravity, v is the average fluid velocity, and γ is the surface tension coefficient of the water-air interface at 25°C. With the calculated Bond number (Bo ~ 10⁻²) and Weber number (We ~ 10⁻¹⁰), we assumed gravitational forces and inertial forces on the nanosheet to be negligible relative to capillary interactions.

Prior to an experiment, a nanosheet was positioned in the flow channel at a starting position–approximately 20 mm upstream of the trap–using air puffs from a syringe with an attached, 31-gauge needle tip (Becton Dickinson). Syringe pump flow and video recording were manually initiated for each trial (i.e., a single nanosheet transport and trapping measurement). Between trials, the nanosheet was manually reset to its initial starting position using the same air-filled syringe. Trials were repeated with the same nanosheet as many times as possible, up to ten, within one hour to minimize any effect of water evaporation. Sets of trials were performed on ten nanosheets in total. We assumed all nanosheets investigated were of the same size and did not vary significantly between trials. Additionally, we assumed that the nanosheet is neither significantly deformed nor physically changed due to the trap. Results from the trials were used to compute accuracy and repeatability of the nanosheet position in the trap and to compare with a mathematical model. For the trap, the repeatability was computed as the standard deviation of the nanosheet centroid final positions, and the accuracy was computed as the Euclidian distance between each nanosheet centroid final position and a specified reference position. Accuracy of the trap was computed relative to the trap’s downstream corner, subtracting an offset of ½ of the mean nanosheet width, for each nanosheet measured.

2.3. Data analysis methods

Raw video files (.avi format) were imported into a custom MATLAB script. In each frame, the following basic steps were used to locate the nanosheet: video length trimming, image cropping, image binary filtering, noise removal, background subtraction, and objection detection via blob analysis. Fixed pixel count metrics were used to eliminate false-positives, and all nanosheet centroid paths were manually verified. Videos were corrected and aligned via coordinate transformations using the fiducial marks in each video.

From these videos, we obtained the nanosheet’s centroid-to-trap distance over time. The x-direction, y-direction, and root-mean-square (RMS) centroid-to-trap distances were calculated as

$$\Delta x_i=\left|x_i-x_f\right|$$ (1),

$$\Delta y_i=\left|y_i-y_f\right|$$ (2),

$$r_i=\sqrt{{\left(x_i-x_f\right)}^2+{\left(y_i-y_f\right)}^2}$$ (3),

respectively, where x_i is the current nanosheet position along the x-direction, x_f is the final nanosheet position in the x-direction, y_i is the current nanosheet position along the y-direction, and y_f is the final nanosheet position in the y-direction. For coordinate axes, see Figure 2, inset. As a choice of convention, time, τ, is defined as

$$\tau =t_i-t_f$$ (4),

where t_i is the current time and t_f is the time at which the nanosheet comes to rest. In analyzing the nanosheet centroid-to-trap distances, we decomposed the nanosheet centroid-to-trap distances into their x- and y-direction components and plotted them as a function of time. We analyzed trials that were longer than 8s; this corresponded to trials whose initial RMS centroid-to-trap distance was greater than or equal to twice the capillary length of the water-air interface. This criterion was imposed to minimize the effect of system dynamics (e.g., starting and stopping of the syringe pump). In addition, we analyzed Δy > 0.42 mm; this lower bound was obtained by multiplying the resolution limit of our camera (0.14 mm/px) by a factor of three, representing an imposed minimum signal-to-noise ratio of 3.

3. Results and Discussion

A total of 94 individual trials were recorded using 10, 500 nm-thick nanosheets. A representative transport and trapping trial is given in Supplemental Movie 1. For most experiments, 10 trials were possible during the one-hour evaporation limit (7 out of 10 experiments). In all trials, the nanosheets were successfully transported down the channel and trapped at the trapping feature.

3.1. Mechanisms of nanosheet transport and trapping

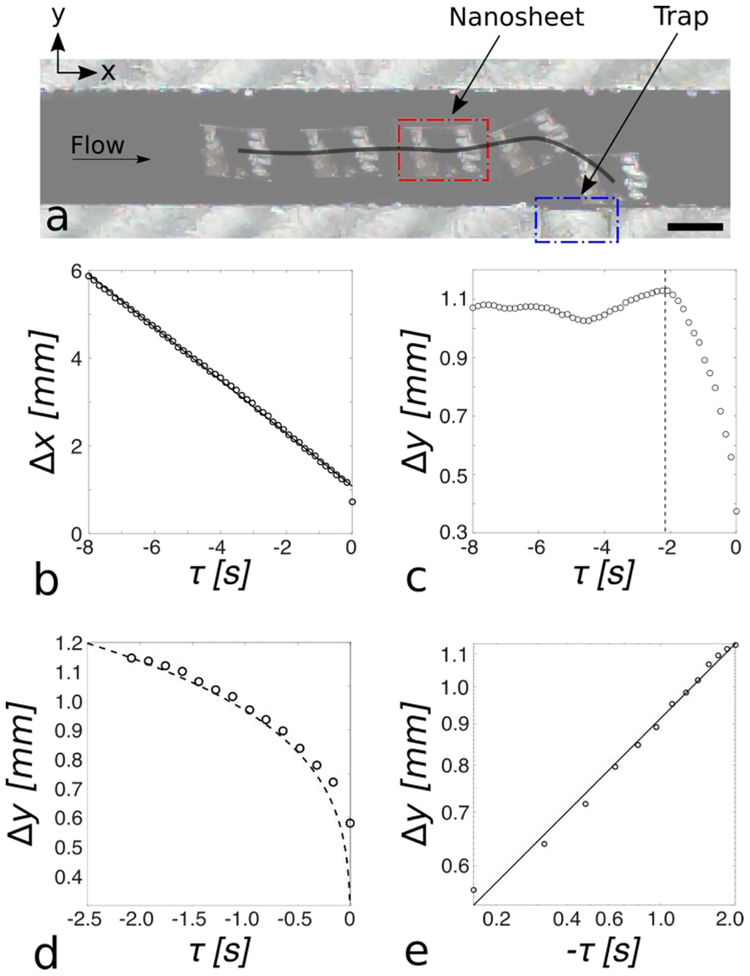
To determine the transportation mechanisms along the channel and into the trap, we analyzed individual nanosheet trajectories. A typical nanosheet trajectory from a single trial is shown in Figure 3a. Of the 94 trials, 48 of the trials fulfilled our criteria for further trajectory analysis (see Section 2.3 for details).

Figure 3.

(a) A typical nanosheet trajectory is shown (black line). A nanosheet (red outline) travels downstream (positive x-direction) towards the trap (blue outline). As the nanosheet approaches the trap, it is attracted towards the trap and comes to rest with one edge mated against the channel wall. Scale bar: 1 mm. (b) Mean (n=48 trials) x-direction nanosheet centroid-to-trap distance plotted as a function of time (black circles) with linear regression line overlayed (solid black line). The x-direction centroid-to-trap distance is linear as a function of time (r2 = 0.99), indicating steady-state hydrodynamic transport. (c) Mean (n=48 trials) y-direction nanosheet centroid-to-trap distance plotted as a function of time (black circles). The black dashed line indicates the time at which the nanosheet RMS centroid-to-trap distance is equal to the capillary length of water (2.7 mm). (d) Experimental, mean (n = 48), y-direction centroid-to-trap distance plotted as a function of time (black circles) after the nanosheet is within one capillary length of the trap with overlayed mathematical model (dashed black line), root mean square error (RMSE), 0.28 mm. The experiment data shows good alignment with a mathematical quadrupole-monopole capillary interaction model. (e) y-direction centroidto-trap distance plotted vs. time on a log-log scale (black circles), with overlayed linear regression line (solid black line, α = 0.29, r2 = 0.99). The nanosheet’s y-direction centroid-to-trap distance as a function of time is well described by a power law (i.e., y ~ tα), with α = 0.29, indicating trapping of nanosheets via capillary quadrupolar interactions.

We first examined the x-direction behavior. The x-direction centroid-to-trap distance as a function of time is shown in Figure 3b (black circles), with an overlaid linear regression line (black line, slope = −0.6 mm/s, r² = 0.99). The x-direction centroid-to-trap distance is linear with respect to time, indicating steady-state hydrodynamic transport. The y-direction centroid-to-trap distance as a function of time is shown in Figure 3c (black circles). The black dashed line indicates the time at which the RMS centroid-to-trap distance (see Equation 3) is equal to the capillary length of the water-air interface (2.7 mm), which we define as tCL. We observe far from the trap, the y-direction centroid-to-trap distance remains relatively constant, indicating that only hydrodynamic transport in the x-direction is occurring. To the right of the black dashed line (i.e., τ > t_CL), the y-direction centroid-to-trap distance rapidly decreases until the nanosheet comes to rest, at time τ = 0 s. The shape of this decline is non-linear, as shown in Figure 3d (black circles), giving evidence that another force is responsible for the trapping of the nanosheets. Prior literature discussing micro-particle self-assembly via capillary quadrupolar interactions found that the particle’s position, r, as a function of time, t, is well described by the power law r~t^1/4.^[18] Therefore, we extended the prior analytical model of capillary quadrupole-monopole interactions to our geometry and studied the effects of capillary multipole interactions on the nanosheets.^{[12, 18]}

From the work of Cavallaro, et. al., a quadrupole capillary deformation is produced by a cylindrical particle trapped at a fluid-fluid interface, while the capillary monopole is produced by a microfabricated micro-post, which pins the fluid-fluid interface at a particular height.^[18] The interaction energy between the capillary quadrupole and monopole is given as

$$E=\gamma \nabla \nabla h_0:\Pi$$ (5)

where ∇∇h₀ is the curvature tensor of the undisturbed host interface, h₀, evaluated at the particle position, and represents contributions due to externally imposed curvature gradient. Π is the quadrupole moment tensor, which represents the contribution due to interfacial deformations resulting from the object trapped at the fluid-fluid interface. γ is the surface tension of the fluid-fluid interface.

In the case of capillary quadrupole-monopole interactions, Equation 5 can be simplified to

$$E\left(r\right)=-\pi \gamma H_p{R}_p^2\frac{1}{r^2}\text{\hspace{0.17em}cos\hspace{0.17em}}2\left({\phi }_p-\phi \right)$$ (6)

where r particle position, φ is the particle orientation angle, H_p is the deformation amplitude, R_p is the particle radius, and φ_p is the orientation of the quadrupolar rise axis.

The interaction force between the capillary quadrupole and monopolar can be written as

$$F=\frac{\delta E}{\delta r}=\pi \gamma H_p{R}_p^2\frac{2}{r^3};$$ (7)

in our one-dimensional model, we assume φ_p = φ, resulting in the cosine term equating to one. We equate the capillary interaction force to the drag force experienced by the nanosheet, written as

$$F_{\text{capillary}}=\pi \gamma H_p{R}_p^2\frac{2}{r^3}=b\frac{dr}{dt}=F_{\text{drag}},$$ (8)

where b is equal to 4πμR_p, μ is the dynamic viscosity of the fluid, and R_p is the particle radius.^[32]

In solving the ordinary differential equation given in Equation 8, we are left with an explicit analytical expression of the nanosheet position, r, as a function of time, t:

$$r_{\text{model}}\left(t\right)={\left(\frac{2\gamma H_p{R}_p}{\mu }\right)}^{\frac{1}{4}}{t}^{\frac{1}{4}}+c_1\cdot$$ (9)

In our model, we used H_p = 50 nm. From prior work, the deformation amplitude has been shown to be roughly 10% of the particle radius for a sphere; thus is our case, we use 10% of the nanosheet thickness.^[11] In addition, we used R_p = 500 nm for the nanosheet thickness, γ = 72 mN/m for surface tension at the water-air interface (at 25°C), and μ = 0.89 mPa*s for the dynamic viscosity of water at 25°C. In solving for c₁, we imposed the boundary condition r_model(t = −2.0 s) = r_experiment(t = −2.0 s); thus, for our model, c₁ = −0.304.^[20]

We find good alignment (RMSE = 0.28 mm) between our mathematical model (Figure 3d, dashed black line) and experiment data (Figure 3d, black circles) without any fitted parameters; suggesting that the behavior of the nanosheets is governed by capillary quadrupole-monopole interactions. Small discrepancies between our mathematical model and the experimental data may be explained by variation in the deformation amplitude, variation in the effective particle radius, or rotational effects.

For further investigation, the y-direction centroid-to-trap distance as a function of time for τ > t_CL was plotted on a log-log scale (black circles), as shown in Figure 3e. The best-fit line is plotted on top of the data (solid black line). From the linear regression model, we report an ordinary r-squared value of 0.99 and slope, α, of 0.29. Our measured power-law model exponent (α = 0.29) is consistent with previously reported values for capillary quadrupolar interactions, as opposed to monopolar interactions, which would have an expected exponent of ~0.5.^{[12, 18, 20–22]}

Interestingly, despite the large characteristic length of the nanosheets relative to the capillary length, capillary quadrupolar interactions remain the dominant capillary multipole interaction. This finding is contrary to prior work investigating large objects trapped at a fluid-fluid interface, which typically interact via capillary monopolar interactions.^[20–22] However, while our nanosheets may be large in lateral dimensions, they exhibit a small Bond number (Bo ~10⁻²). Therefore it is not entirely unexpected for capillary monopole interactions to be negligible.

The mechanism by which the nanosheets create a capillary quadrupolar deformation remains an open question. For nanosheets to create a capillary quadrupolar deformation via their geometry, as in the case of cylindrical micro-particles, significant distortion in the water-air interface as well as bending in the nanosheet would be required. Thus, due to their thickness, it is likely an undulated contact line, or an “irregular meniscus,” with a dominant quadrupole term that manifests the capillary quadrupole deformation.^[11]

In Figure 3b, the x-direction centroid-to-trap distance versus time for τ > t_CL does not appear to deviate from its linear relationship. This gives evidence that the hydrodynamic forces and curvature-induced capillary quadrupolar interactions are acting independent from one another and that their effects may be linearly superimposed.

While a power-law model fits our data, there is a small discrepancy between our reported power-law model exponent and that of published literature. We assert this difference may be explained by the different experimental conditions: Prior literature investigated the attraction of two micro-scale particles, moving towards one another in one-dimension without rotation. In our system, the nanosheets are attracted towards a fixed trap, are moving in two-dimensions, and are free to rotate. Additionally, we acknowledge 46 of the 94 trials were not included in our trajectory analysis due to our stated criteria but, in all 94 trials, the nanosheets were transported and trapped. Therefore, we do not expect a different rationale for the observed behavior in these trials.

3.2. Nanosheet trapping stability

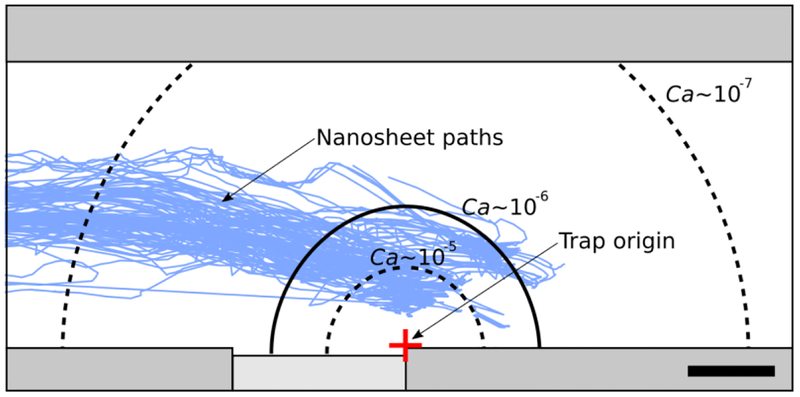
To analyze nanosheet trapping stability within our device, we first generated a stability diagram in terms of a dimensionless grouping, the capillary number (Ca), shown in Figure 4.

Figure 4.

Diagram of stable trapping regions as a function of the capillary number, Ca, with overlayed nanosheet paths (solid blue lines, n = 94). The stability regions are shown with respect to our trap origin (red crosshair), defined as the right edge of the trap where the water and channel wall meet. Our system, which has Ca ~ 10⁻⁶, contains a stable trapping region with a calculated maximum radius (r_max) of 1.2 mm (solid black line). Lowering Ca by an order of magnitude results in r_max = 2.5 mm (outer, black dashed line) while increasing Ca by an order of magnitude results in r_max = 0.5 mm (inner, black dashed line). Scale bar: 500 μm.

In expressing the nanosheet position as a function of the capillary number (Ca = μv/γ), Equation 8 can be written as

$$\left(\frac{H_p{R}_p}{2r_{\text{max}}^3}\right)=Ca=\frac{\mu }{\gamma },$$ (10)

using values for H_p, R_p, μ, and γ previously given, and v, the average fluid velocity, equal to 0.6 mm/s, taken from the slope of the x-direction centroid-to-trap distance as a function of time plot in Figure 3b. Using these values, we report Ca = 7.42 × 10⁻⁶. The small capillary number gives evidence that surface tension forces play a much larger role in the transport of the nanosheet, resulting in nanosheet trapping. Further experiments could be performed by modulating capillary number to access trapping behavior: it is likely that, as the capillary number approaches unity, the efficiency of this trap would decrease.

In Equation 10, we replace the nanosheet position, r, with r_max since this equation represents the maximum distance at which trapping will occur. We measure r_max relative to the right edge of the trap, where the water and channel wall meet (Figure 4, red crosshair), since the interaction energy is maximized at this location (see Equation 6). Thus, in solving for r_max, we are able to show “stability regions” (defined mathematically as 0 < r(t) < r_max), i.e., areas where a nanosheet would be successfully pulled towards and come to rest at the trap. We see that in Equation 10, r_max³ ~ Ca, indicating that relatively small changes in the capillary number result in large changes in r_max.

For our system, using Equation 10 to solve for r_max, we obtain r_max = 1.19 mm. This stability region is outlined in Figure 4 (solid black line). Interestingly, we find this value aligns well with the mean y-direction centroid-to-trap distance at which the RMS centroid-to-trap distance is equal to the capillary length of the water-air interface (Figure 4, black dashed line). At this distance, the edge of the nanosheet interacts with the capillary monopole created by the trap, thereby attracting the nanosheet. We see that for our device, all nanosheet paths (Figure 4, solid blue lines, n = 94) cross the calculated r_max threshold and subsequently are trapped, as predicted. Given that the stability region is radially symmetric, it is possible for nanosheets to overshoot the trap in the x-direction and still be trapped as long as the nanosheet is within the stable region, as we observe in some of the nanosheet paths.

Furthermore, we mathematically modulate the capillary number to observe how the stability region changes. Experimentally, these changes in capillary number could be accomplished by varying the fluid velocity, the fluid dynamic viscosity, and/or the surface tension coefficient. Increasing the capillary number by an order of magnitude results in r_max = 0.55 mm (Figure 4, inner dashed black line); a dramatically smaller trapping region. In contrast, decreasing the capillary number by an order of magnitude results in r_max = 2.56 mm (Figure 4, outer dashed black line), which would encapsulate the entire channel width. While encompassing the entire channel width may guarantee nanosheet trapping, there may be negative trade-offs. For example, lowering the fluid velocity would increase trapping time, and changing the surface tension coefficient or the fluid viscosities could introduce fluids that are chemically incompatible with the nanosheet. As encapsulated in Equation 10, changing the object of interest would change H_p and R_p, thereby affecting r_max. Future experiment could be conducted to investigate stability regions for other objects.

While multi-nanosheet experiments are beyond the scope of this work, we postulate developing a multiplexed device, that incorporates our findings here, is possible. Future work may investigate a single-fluid device that modulates the fluid velocity via channel stenosis; thereby locally changing the capillary number to switch between trapping stability regimes. Further investigation would be needed to study the effects of multi-body interactions.

The interaction between two nanosheets remains unclear, particularly if one is already trapped and the other is freely moving. We speculate that multi-nanosheet interactions are likely capillary quadrupole-quadrupole interactions, as opposed to the capillary quadrupole-monopole interaction we observe between the nanosheet and the trap. From prior literature, capillary quadrupole-quadrupole interactions have lower interactions energy than that of monopole-monopole interactions. Therefore, it is plausible that the trap acts in a binary fashion: when unoccupied by a nanosheet, it will attract any nanosheet within its stability region via capillary quadrupole-monopole interactions. When occupied, the nanosheet becomes the interacting body since it is physically blocking the trap, thus lowering the interaction energy.^[17,20] If the capillary number is tuned properly, the approaching nanosheet could pass the trapped nanosheet and continue further downstream.

3.3. Nanosheet trapping accuracy and repeatability

We analyzed the accuracy and repeatability of the nanosheet trapping data. The final centroid position of all 94 nanosheets is shown in Figure 5. The repeatability is the standard deviation of the centroid positions. We computed this for all 94 trials in both the x-direction and y-direction. The repeatability was 350 μm in the x-direction and 224 μm in the y-direction. We posit that the repeatability is better in the y-direction because the nanosheets are reliably constrained by the channel wall. Small rotational differences of the nanosheet, at the trap, between trials adversely affect repeatability.

Figure 5:

(top) Photograph of the device showing trapped nanosheet centroids for all trials, n = 94 (red). Detailed view (bottom) shows the distribution of the centroids. The blue crosshair indicates the desired centroid position, which is aligned with the corner of the trap in the xdirection and offset half a nanosheet’s width from the trap wall in the y-direction, as shown. Scale bars: (top) 1 mm (bottom) 500 μm.

Within each set of trials, we also calculated the standard deviation of the centroid position and computed an average standard deviation; weighted by the number of trials per set of trials. With this method, we computed a repeatability of 150 μm and 120 μm in the x- and y-direction, respectively. Thus, intra-set repeatability (with the same nanosheet) is greater than inter-set repeatability (using different nanosheets). In fact, some nanosheets exhibited repeatability as low as ~3% of their length. Thus, we posit that the manner in which the water pins to each nanosheet may vary between nanosheets but does not change between trials, attributable to variations during the fabrication process or inhomogeneity in the bulk resin block from which nanosheets are cut.

The average accuracy was 300 μm in the x-direction and 200 μm in the y-direction. In our accuracy calculations, we offset the target by half the width (the short edge, ~1 mm wide) of each nanosheet (See Figure 5, blue cross-hair). The accuracy of the device may be limited by several factors, such as nanosheet imperfections, the out of plane stiffness of the nanosheet counteracting the surface energy of the water, or higher-order multipole interactions. The accuracy and repeatability of this device exceeds that required for mounting a nanosheet onto a copper transmission electron microscopy grid with 1 mm × 2 mm aperture, a common inspection technique following nanosheet fabrication.^{[1,3,6,7,32–35]} Beyond engineering applications, this technology may have relevance for biological applications, such as serial section electron microscopy-based tomography, array tomography, or x-ray microscopy, all of which require the manipulation of nano- to micro-scale thickness slices of biological tissue in preparation for analysis. ^[6,36,37]

During trials, we found that nanosheets exhibited rotation as well as translation. We observe, in all but one trial, the nanosheet’s long edge (~1.5 mm) came to rest against the channel wall, indicating our device’s ability to orient the nanosheets. Future work may explore the trap geometry parameter-space to increase our device’s accuracy and repeatability. From early experiments, we found that we could trap thinner nanosheets, but the time required for these nanosheets to pin to the trap was very long (on the order of tens of minutes). From these preliminary results, we surmise there exists a relationship between nanosheet thickness and trapping time. For 500 nm-thick nanosheets used in this work, our throughput was one section transported and trapped every 23 seconds on average with a standard deviation of 16 seconds. Future work to scale this technology to even thinner nanosheets (e.g., ~1–10 nm) may provide a useful, non-contact tool for the manipulation of two-dimensional materials.^[1–5]

4. Conclusions

Expanding upon prior particle transport and trapping methods, we demonstrate that hydrodynamic forces in conjunction with capillary quadrupolar-monopolar interactions can be used for long-range transport (>1× capillary length) and accurate and repeatable trapping, respectively, for nanosheets on the water-air interface.^{[11–20, 27, 28]} Capillary quadrupolar interactions have been shown to manifest on nanoscale colloidal particles while capillary monopolar interactions have been observed for millimeter-scale particle interactions; therefore, it remains unknown how nanosheets, which feature millimeter-scale in-plane dimensions and nanoscale thicknesses, interact with their surroundings on the water-air interface.^{[11, 12, 21]} We confirm via mathematical modeling and experiment that nanosheets interact via capillary quadrupolar interactions. Furthermore, we demonstrate that our hybridized methodology enables the controlled manipulation of nanosheets on a water-air interface over distances greater than those of methods solely using capillary multipole interactions.^{[11, 12, 18]} In quantifying our device, we show that the accuracy and repeatability of this device exceeds that required for mounting a nanosheet onto a transmission electron microscopy grid, a common inspection technique following nanosheet fabrication.^{[1,3,6,7,32–35]} We envisage our methodology to be used in conjunction with techniques for functional nanosheet fabrication—which are typically created on a water-air interface—to enable accurate and repeatable device integration and manufacturing.^[1–5] Additionally, this technology may have relevance for biological applications, such as serial section electron microscopy-based tomography, array tomography, or x-ray microscopy, all of which require the manipulation of nano- to micro-scale thickness slices of biological tissue on a water-air interface in preparation for ultrastructural analysis.^[6,36,37] From our stability diagram, we show the trapping stability is dependent upon the capillary number; moving forward, device multiplexing via capillary number modulation could be used to facilitate high-throughput nanosheet manipulation. Ultimately, this device demonstrates an application of capillary quadrupolar interactions in conjunction with hydrodynamic forces to overcome the challenge of nanosheet manipulation, an important problem in the fields of nanotechnology, biosciences, and material science.