Energy Renormalization for Coarse-Graining the Dynamics of a Model Glass-Forming Liquid

Abstract

Coarse-grained modeling achieves the enhanced computational efficiency required to model glass-forming materials by integrating out “unessential” molecular degrees of freedom, but no effective temperature transferable coarse-graining method currently exists to capture dynamics. We address this fundamental problem through an energy-renormalization scheme, in conjunction with the localization model of relaxation relating the Debye–Waller factor ⟨u²⟩ to the structural relaxation time τ. Taking ortho-terphenyl as a model small-molecule glass-forming liquid, we show that preserving ⟨u²⟩ (at picosecond time scale) under coarse-graining by renormalizing the cohesive interaction strength allows for quantitative prediction of both short- and long-time dynamics covering the entire temperature range of glass formation. Our findings provide physical insights into the dynamics of cooled liquids and make progress for building temperature-transferable coarse-grained models that predict key properties of glass-forming materials.

INTRODUCTION

The bottom-up prediction of the dynamics of glass-forming (GF) liquids is a long-standing challenge, as their properties are strongly dependent on temperature.¹ Classical molecular dynamics (MD) simulations have emerged as one of the most powerful methods to study complex GF liquids, but it is inherently challenging to simulate these materials with MD simulations due to the limited time and length scales accessible for all-atomistic (AA) models of fluids. Multiscale modeling techniques, such as coarse-grained (CG) modeling approaches derived from atomistic molecules, have been used to overcome the spatiotemporal limitations of AA MD simulations.² These coarse-graining methods achieve computational efficiency by integrating out degrees of freedom to remove “unessential” atomistic features.^3,4 Despite tremendous efforts in this direction, no systematic technique currently exists that allows for the prediction of the temperature-dependent GF properties of the AA model to a good approximation. This has limited CG modeling to identifying qualitative rather than quantitative trend in the properties of GF fluids.

Several coarse-graining methodologies have previously been proposed, including the inverse Boltzmann method (IBM),^5,6 optimized relative entropy,⁷ force matching,^8,9 inverse Monte-Carlo method,¹⁰ and other approaches based on statistical mechanics principles.^11–14 These methods have been shown to preserve key equilibrium properties of the AA systems, such as static structure factor. However, these approaches to coarsegraining often do not perform well in reproducing the dynamics of the GF materials. For instance, the CG models derived through the IBM often exhibit artificially fast dynamics compared to the AA counterpart.^3,6 These changes in the dynamics of cooled liquids can be largely attributed to the reduction of the fluid configurational entropy s_c, as the degrees of freedom are integrated out upon coarse-graining.^7,11,12,15 This artificially fast dynamics of the CG models can be useful for some purposes, e.g., fast achieving equilibrium to capture static structural and thermodynamic properties. However, in applications that are aimed at quantitative modeling and predicting dynamic properties, the artificial speed-up of dynamics becomes a serious problem. Although recent studies have shown that it is possible for CG modeling to reproduce the AA dynamics by introducing nonconservative forces (e.g., frictional and dissipative forces),^12,15–20 temperature transferability^2,21 remains a significant hurdle to overcome due to a lack of understanding of the strong temperature dependence of the molecular friction and relaxation properties of GF materials.

To address this fundamental problem, we recently proposed a coarse-graining strategy, namely the energy-renormalization (ER) method, which preserves both density and dynamic properties of the GF polymer (polystyrene).²² This approach borrows ideas from the Adam–Gibbs (AG) theory²³ and the more recent generalized entropy theory (GET) of glass formation,²⁴ both of which emphasize the critical role of s_c in the dynamics of cooled liquids. We hypothesize that as the system’s s_c decreases under coarse-graining, we may compensate for this effect by correspondingly renormalizing the enthalpy (based on the established “entropy–enthalpy compensation” effect)^25–27 by tuning the molecular cohesive interaction strength, often parametrically related to the Lennard-Jones (LJ) energetic parameter, ε. This parameter has a strong influence on their dynamics and mechanical response of the materials through its influence on s_c.^28,29 By renormalizing ε as a function of temperature, we aim to “correct” for the activation free energy and thus preserve the dynamics of the CG melt upon approaching the glass transition.

However, our original formulation of coarse-graining polymer dynamics based on the ER method required extensive MD simulation of diffusion and relaxation over a large temperature range, making the application of the method somewhat computationally intensive. In this study, we present a more computationally efficient formulation of the ER method based on a single readily computed and measurable property, the Debye–Waller factor ⟨u²⟩. Specifically, we are interested here in whether the ER strategy can be applied to a classic model small-molecule GF liquid, ortho-terphenyl (OTP). Our simulation results demonstrate the success of the proposed ER method for the development of the CG model, which can quantitatively reproduce the dynamics of the GF liquid over a wide temperature range.

COARSE-GRAINING STRATEGY

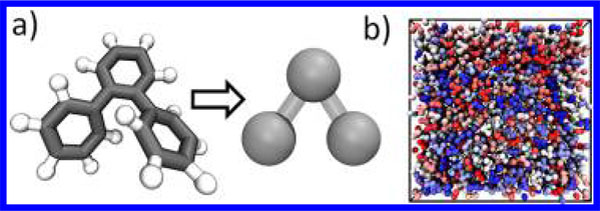
To coarse-grain the atomistic OTP model, each phenyl ring is grouped into one CG bead with the force center located at the center of mass of each ring, resulting in three consecutive CG beads per molecule (Figure 1). This mapping preserves essential degrees of freedom of this molecule under coarse-graining and is consistent with earlier CG treatment of OTP.³⁰ The bond and angle interactions of the CG model are derived from the probability distributions of the AA system using the IBM, which can be captured by harmonic potential forms (Figure S1 in the Supporting Information (SI)). For the nonbonded interaction, we employ a commonly applied 12–6 LJ potential for our CG modeling: $U(r)=4\epsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right]$ where σ governs the effective van der Waals radius and marks the distance at which U is 0 and ε is the depth of the potential well associated with the cohesive interaction strength of the materials. The cutoff distance of the LJ potential is 1.5 nm. To achieve temperature transferability, we take the CG model parameters σ and ε to be temperature dependent, i.e., σ(T) and ε(T). As shown in our earlier work,^22,31 σ(T) can be readily determined by demanding the AA density to be consistent with the CG model, yielding a linear dependence of σ on temperature (Figure S2 in the SI). The functional forms and bonded parameters of the CG potentials are listed in Table S1 in the SI. Our study is then focused on deriving temperaturedependent ε(T) through a consideration of a fast dynamics property, the Debye–Waller factor ⟨u²⟩, which can be readily determined by experimental measurement and short-time simulation of the materials.

Figure 1.

(a) Mapping from the AA model (left) to the CG model (right) of OTP. The force centers of the CG beads are located at the center of mass of the phenyl ring. (b) The snapshot of the simulation box consisting of CG molecules (each molecule is colored differently).

Previous studies have indicated that ⟨u²⟩ quantifies the molecular “free volume” and “stiffness” in the picosecond time scale over which the molecules are caged by their neighbors.^32,33 Based on the random first-order transition theory, Hall and Wolynes (HW)³⁴ argued that the structural relaxation time τ of a GF liquid should obey the relation with ⟨u²⟩ via $\langle u^2\rangle \text{ via }\tau ~\exp \left(u_0^2/\langle u^2\rangle \right)$ with $u_0^2$ as an adjustable constant. This result is consistent with the heuristic idea that the activation barrier for condensed matter relaxation should increase with material stiffness. This scaling relationship was also deduced by Schweizer and co-workers^35–37 based on a mode-coupling approach to predicting liquid dynamics. This relationship also accords in spirit with the “shoving” model of Dyre and co-workers,^38,39 where the activation barrier for transport properties is identified with the glassy shear modulus G of the material. More recently, Simmons and co-workers⁴⁰ introduced the localization model (LM), which indicates a relation between τ and ⟨u²⟩ based on the free volume model of fluid dynamics, $\tau ~\exp \left[{\left(u_0^2/\langle u^2\rangle \right)}^{\alpha /2}\right]$, where the exponent α is related to the shape of the free volume (i.e., regions explored by the center of mass of a rattling particle in the fluid). Betancourt et al.²⁶ made a significant step forward in the predictive nature of this kind of relationship by reducing ⟨u²⟩ by its value $u_{\text{A}}^2\equiv \langle u^2\left(T_{\text{A}}\right)\rangle$ at the onset temperature T_A for molecular caging, and by fixing the prefactor in the τ–⟨u²⟩ relation by the observed value of τ in T_A, τ(T_A) ≡ τ_A, leading to the relation:

$$\tau (T)={\tau }_{\text{A}}\exp \left[{\left(u_{\text{A}}^2/\langle u^2(T)\rangle \right)}^{\alpha /2}-1\right]$$ (1)

In this present work, we take this LM relation, i.e., eq 1, as the basis of a strategy for coarse-graining the dynamics of OTP. We hypothesize that by preserving ⟨u²⟩ of the AA system via renormalizing ε, we can recover the temperature-dependent GF dynamics of the full atomistic model of OTP by its CG analogue.

RESULTS AND DISCUSSION

To check our hypothesis based on the LM relation, we first evaluate the influence of cohesive interaction ε on the magnitude of ⟨u²⟩. We determine ⟨u²⟩ from the segmental mean-squared displacements (MSD) ⟨r²(t)⟩ at around t_c ≈ 3 ps, which is estimated from the caging time scale from our simulations. As shown in Figure S3 in the SI, ⟨u²⟩ increases nonlinearly with T for the AA and CG systems with varying ε. The lower value of ⟨u²⟩ of the CG model with increasing ε indicates that increasing the intermolecular cohesive interaction strength leads to a suppressed segmental mobility. For each ε, ⟨u²⟩ of the CG model intersects with the AA ⟨u²⟩ at a different temperature, demonstrating the necessity of renormalizing ε at different temperatures to preserve the AA ⟨u²⟩. This is consistent with Shell’s general observation⁴² that the intermolecular potential parameters of the CG model describing the atomistic system are generally state dependent. Accordingly, ε(T) can be determined by demanding that the ⟨u²⟩ of the CG system must equal ⟨u²⟩ of the atomistic model at each temperature (inset in Figure 2), leading to a sigmoidal variation in ε(T):

$$\epsilon (T)=\left({\epsilon }_{\text{A}}-{\epsilon }_{\text{g}}\right)\Phi +{\epsilon }_{\text{g}}$$ (2)

where ε_g and ε_A refer to the ε values in the low-T glassy and high-T Arrhenius regimes, respectively; Φ is a two-state crossover function having the form: Φ = 1/[1 + exp(–k(T – T_T))], where k is a parameter related to the temperature breadth of the transition and T_T (≈ 475 K) describes the crossover point of this sigmoidal function. These parameters are summarized in Table S2 in the SI.

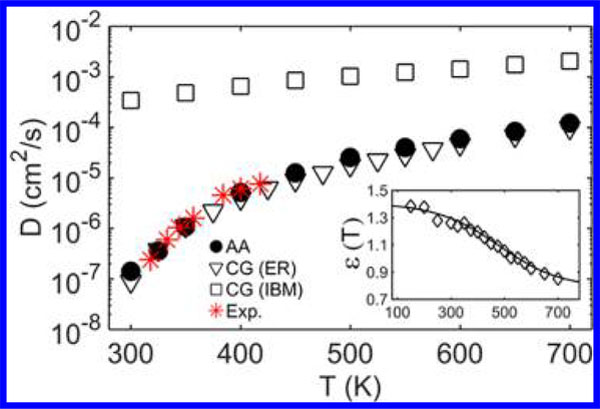
Figure 2.

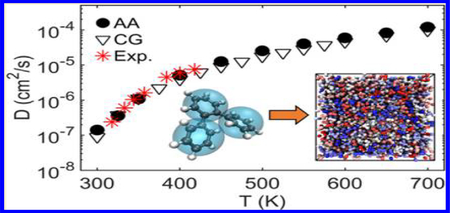
Self-diffusion coefficient D of molecules for the AA and CG models using both ER and IBM at varying temperatures, and their comparison with the experimental data from ref 41. (Inset) The cohesive interaction strength ε(T) (in kcal/mol) for the CG model determined by matching the T-dependent Debye–Waller factor ⟨u²⟩ of the AA model to the CG model.

In the high-T Arrhenius and low-T glassy regimes, ε(T) tends to be plateau values, where ε(T) has a greater magnitude in the glassy low-temperature regime. However, in the non-Arrhenius regime at intermediate temperatures between the glassy and Arrhenius regimes, ε(T) strongly varies with T. The sigmoidal dependence of ε on T can be understood from the GET and AG theory, which predict that ΔG(T) of GF liquids increases with decreasing T as s_c decreases upon cooling, but this quantity saturates at both high- and low-T limits.^23,24 Many of these features have been confirmed by the recent molecular simulations.^43,44 Therefore, the ΔG(T) of the CG model (without ER) should follow a similar T-dependence of the AA model, but with different magnitudes due to their reduced s_c and cohesive interaction. By implementing the ε(T) based on the condition that ⟨u²⟩ is preserved under coarse-graining, we observe that the T-dependence of the self-diffusivity D of the AA model is well described by the CG model via our ER approach, which also agrees well with the experimental observation (Figure 2).⁴¹ For comparison, the D of the CG model derived from the IBM (Figure S4 in the SI) is significantly larger than that of the AA model (by 1–4 orders of magnitude depending on T). This dramatic speed-up of dynamics necessitates ER under coarse-graining to preserve the AA dynamics over a wide T range.

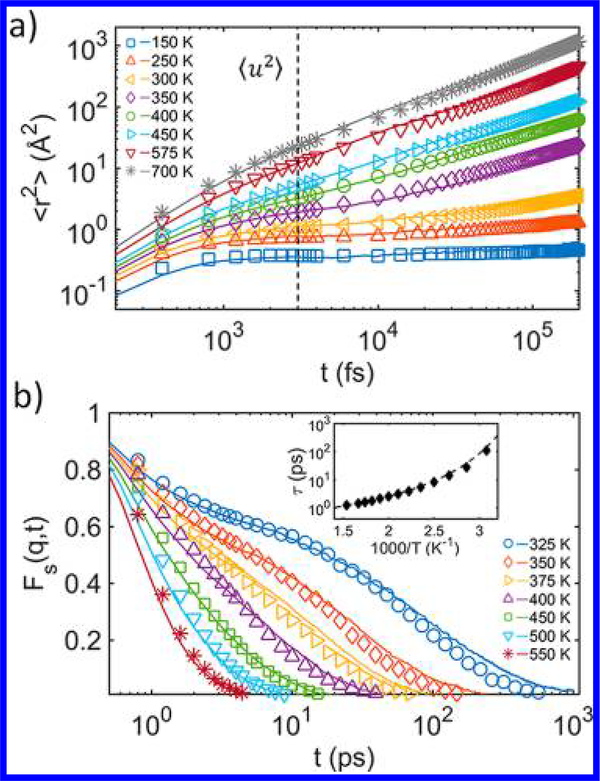
We next examine the segmental dynamics by evaluating timedependent segmental ⟨r²(t)⟩ and the intermediate scattering function F_s(q,t) of the AA and CG models. Figure 3a shows the comparison of ⟨r²(t)⟩ for the AA and CG models at varying T. Remarkably, by preserving the AA values of ⟨u²⟩ (marked by the vertical dashed line in Figure 3a) through renormalizing ε and σ, the CG model can reproduce nearly the entire MSD curves of the AA system at different T spanning from glassy to melt regimes. The wave number q (= 14 nm⁻¹) for calculating F_s(q,t) is chosen from the first peak of the static structure factor S(q), consistent with previous studies.⁴⁵ Figure 3b shows an excellent agreement of F_s(q,t) between the AA and CG models over a wide temperature range. From the calculation of F_s(q,t), we can evaluate the structural relaxation time τ and characteristic temperatures associated with the glass formation for the OTP. The inset in Figure 3b shows the temperature-dependent τ for both AA (dashed line) and CG (symbol) models, which can be well described by the Vogel–Fulcher– Tammann (VFT) relation:^46–48, $\tau (T)={\tau }_0\exp \left(\frac{B}{T-T_0}\right)$ where τ₀, B, and T₀ are the fitting parameters associated with the glass formation process.

Figure 3.

(a) Segmental MSD ⟨r²⟩ vs time for the AA (lines) and CG (symbols) models. (b) Comparison of F_s(q,t) for the AA (lines) and (symbols) the CG models. The Debye–Waller factor ⟨u²⟩ (obtained from the ⟨r²⟩ at t_c ≈ 3 ps) shows a good agreement between the AA and CG models. Inset shows the temperature-dependent structural relaxation time τ for the AA (line) and for the CG (symbol) model.

From the VFT relation, the Vogel temperature T₀, which roughly indicates the “end” of glass transition, is determined to be about 234 K for both the AA and CG systems. The glasstransition temperature (T_g) is estimated by extrapolating the relaxation data to the empirical observation time scale, τ(T_g) ≈ 100 s, where we find T_g to be about 250 K for the AA and CG models. The estimated onset temperature T_A (≈ 500 K) from the τ data is slightly higher than the experimental value 455 K from the viscosity measurement,⁴⁹ which can be possibly attributed to the different measurement methods. We also estimate the crossover temperature T_c by fitting the τ data with the mode-coupling inspired relationship, τ∼ (T – T_c)^–γ, where γ is an adjustable parameter.^24,50 The resulting T_c is estimated to be around 291 K for our models of OTP. These characteristic temperatures from our model predictions agree reasonably well with the literature values^49,51,52 (summarized in Table S3 in the SI). We also note that T_T (≈ 475 K), the empirical transition point in ε(T) derived from our ER procedure, characteristically lies between T_A and T_g, confirming that the temperature-dependent rescaling of the cohesive interaction is related to the GF processes of the CG model.

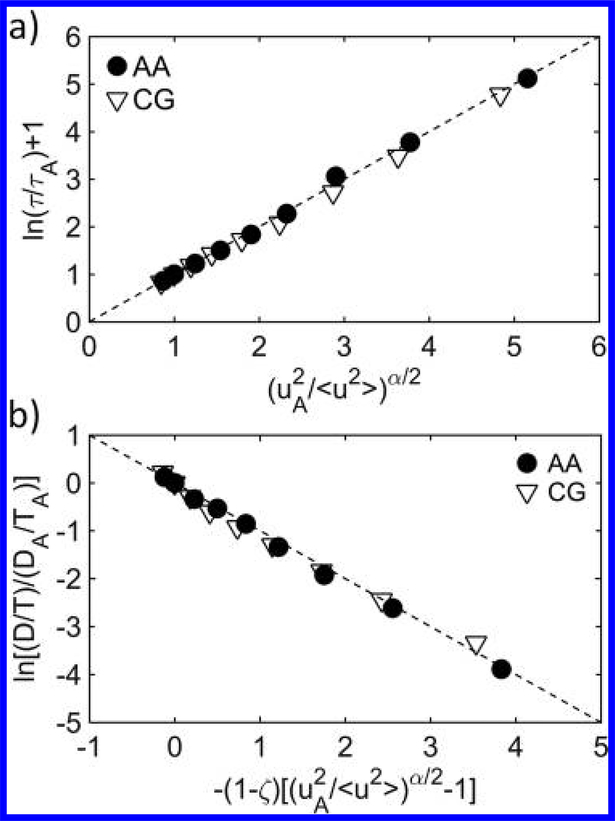
We proceed to test the quantitative scaling relationship (eq 1), as described by the LM for the AA and CG models. Remarkably, our ER approach is able to closely reproduce the scaling relationship between the ⟨u²⟩ and τ for the AA model over a wide temperature range (Figure 4a). The exponent α is determined to be about 1.9 from the best fit of the data for both AA and CG models, which is consistent with the HW model prediction with numerical uncertainty,³⁴ and other models and experiments also indicate α ≈ 2.⁵³ However, the specific value of α in the LM should depend on the geometry of free volume, which can be different for varying material systems. For instance, in the case of Cu–Zr metallic glass alloys, the free volume geometry is expected to be more isotropic, leading to α ≈ 3, which has been confirmed by simulations.⁵⁴ Our result also suggests that the developed CG model can not only predict the dynamics but also the anisotropic geometry of the segmental free volume.

Figure 4.

(a) Test of the localization model predictions of τ (eq 1) for the AA and CG models. (b) Quantitative relationship between D and ⟨u²⟩ predicted from the modified localization model in conjunction with the decoupling relation: D/T ∼ (1/τ)^1–ζ for the AA and CG models. The dashed lines in (a) and (b) show the predictions of data from the localization model in comparison to simulation results.

Recent studies have shown that the diffusion coefficient D of metallic alloys can be linked to τ via a fractional Stokes– Einstein (FSE) relation (i.e., an extension of the Stokes– Einstein relation):^54,55 D/T ∼ (1/τ)^1–ζ, where ζ is a decoupling exponent that is usually nonzero for most GF liquids; ζ LM in conjunction with the FSE relation, the D can be quantitatively estimated from ⟨u²⟩ by the relation:

$$\ln \frac{D}{T}=\ln \frac{D_{\text{A}}}{T_{\text{A}}}-(1-\zeta )\left[{\left(u_{\text{A}}^2/\langle u^2(T)\rangle \right)}^{\alpha /2}-1\right]$$ (3)

where D_A is the D at T_A. Figure 4b shows the scaling relation of D and ⟨u²⟩ for the AA and CG models by normalizing its value at T_A, which is well predicted from the LM. We estimated ζ to be equal to 0.1 for our models, suggesting a relatively weak decoupling for the OTP compared to metallic glasses.⁵⁴

Earlier studies have shown that rescaling the time⁵⁶ or introducing the dynamic scaling factor (i.e., the ratio of CG to AA diffusivities)⁶ for the CG models allows for the estimate of AA diffusion at higher temperatures because the systems enter the diffusive regime very rapidly. However, at a lower temperature, using such methods is expected to fail to capture the entire MSD curves due to the existence of an extended “caging” regime. The CG model via our ER approach, however, is able to recover the entire atomistic MSD curves encompassing different regimes over temperatures. We also note that whereas the ER approach allows us to effectively estimate the characteristic temperatures of glass formation, relaxation dynamics, and self-diffusion of the AA model, the CG model overpredicts the AA rotational diffusivity (D_r) that quantifies the rotational motion of the molecules (Figure S5a in the SI). The calculated D_r differs by a factor of around 7.7 between the AA and CG models over a wide T range. This speeding up of D_r might be attributed to the idealization of the spherical shape of the CG bead that represents each flat phenyl ring and its isotropic (nondirectional) potential adopted in our study. However, we find that we can account for this factor, associated with the change of the OTP hydrodynamic volume under coarse-graining, by normalizing D_r by its value at T_A (Figure S5a in the SI). A similar procedure can be applied to the calculation of the isothermal compressibility κ_T, a basic fluid thermodynamic property, where again a good consistency exists between the AA and CG models when the results are compared with the reduced form (Figure S5b in the SI). It is thus important to report simulation results of CG models in terms of appropriate reduced variables relating to molecular size and characteristic temperatures to achieve an optimal correspondence between both simulation models and experiment.

Our result demonstrates the success of using ⟨u²⟩, a shorttime (i.e., picosecond) measurable quantity, as a suitable property to determine the cohesive energy renormalization required to preserve the long-time dynamics under coarsegraining spanning over a wide range of temperature. Although we perform the AA simulations to derive the CG model, our approach should also be applicable without AA calculations using the experimental data for ⟨u²⟩. We should note that the ER approach to coarse-graining is mainly aimed at capturing the T-dependent dynamics of the AA model, which is different from the methods based on the statistical mechanics that attempt to preserve the thermodynamic properties. Capturing both dynamics and thermodynamics, as well as achieving temperature transferability within a single CG model, still remains to be improved in future investigations. Although we focus on the renormalization of ε as its primary influence on the fluid dynamics, preserving the density through renormalization of σ is also important for reproducing the dynamic and thermodynamic properties of the fluid.⁵⁷ Therefore, our ER approach in conjunction with the LM model appears to largely correct the usual shortcomings of single state-point derived CG models of their dynamics (i.e., faster dynamics and a lack of T transferability).

CONCLUSIONS

In summary, we have established a unified framework that builds upon the energy-renormalization approach and glass formation theories to achieve a temperature transferrable coarse-graining of OTP. By exploiting the localization model (LM), the cohesive interaction parameter ε(T) of the CG OTP model from the ⟨u²⟩ analysis exhibits a sigmoidal temperature dependence with a higher magnitude upon cooling. We find that our ER approach, in conjunction with the LM, can quantitatively predict the dynamics of the AA system over a wide temperature range from high-T Arrhenius melt to the non-Arrhenius regime of incipient of glass formation and low-T nonequilibrium glassy regime. Although we here focus on coarse-graining a small-molecule glass former, the ER approach should also be applicable to more complex GF molecules, such as polymers. Our findings demonstrate the effectiveness of the ER approach toward building a temperature-transferable CG modeling framework for the GF materials and highlight the critical role of caging dynamics in predicting the GF properties.