Can Deep Learning Improve Genomic Prediction of Complex Human Traits?

The current excitement around artificial intelligence and the renewed interest in “deep learning” (DL) have been applied to the genetic analysis of complex traits; however, the performance of DL for genomic prediction of complex...

Abstract

The genetic analysis of complex traits does not escape the current excitement around artificial intelligence, including a renewed interest in “deep learning” (DL) techniques such as Multilayer Perceptrons (MLPs) and Convolutional Neural Networks (CNNs). However, the performance of DL for genomic prediction of complex human traits has not been comprehensively tested. To provide an evaluation of MLPs and CNNs, we used data from distantly related white Caucasian individuals (n ∼100k individuals, m ∼500k SNPs, and k = 1000) of the interim release of the UK Biobank. We analyzed a total of five phenotypes: height, bone heel mineral density, body mass index, systolic blood pressure, and waist–hip ratio, with genomic heritabilities ranging from ∼0.20 to 0.70. After hyperparameter optimization using a genetic algorithm, we considered several configurations, from shallow to deep learners, and compared the predictive performance of MLPs and CNNs with that of Bayesian linear regressions across sets of SNPs (from 10k to 50k) that were preselected using single-marker regression analyses. For height, a highly heritable phenotype, all methods performed similarly, although CNNs were slightly but consistently worse. For the rest of the phenotypes, the performance of some CNNs was comparable or slightly better than linear methods. Performance of MLPs was highly dependent on SNP set and phenotype. In all, over the range of traits evaluated in this study, CNN performance was competitive to linear models, but we did not find any case where DL outperformed the linear model by a sizable margin. We suggest that more research is needed to adapt CNN methodology, originally motivated by image analysis, to genetic-based problems in order for CNNs to be competitive with linear models.

A major challenge of modern genetics is to predict an individual’s phenotype (or disease risk) from the knowledge of molecular information such as genotyping arrays or even complete sequences. Applications of genomic prediction range from the assessment of disease risk in humans (e.g., de los Campos et al. 2010) to breeding value prediction in animal and plant breeding (e.g., Meuwissen et al. 2013). Understanding how DNA sequences translate into disease risk is certainly a central problem in medicine (Lee et al. 2011; Stranger et al. 2011).

Genome-wide association studies (GWAS) have been used extensively to uncover variants associated with many important human traits and diseases. However, for the majority of complex human traits and diseases, GWAS-significant SNPs explain only a small fraction of the interindividual differences in genetic risk (Maher 2008). Whole-Genome Regression (WGR), a methodology originally proposed by Meuwissen et al. (2001), can be used to confront the missing heritability problem. In a WGR, phenotypes are regressed on potentially hundreds of thousands of SNPs concurrently. This approach has been successfully adopted in plant and animal breeding (e.g., de los Campos et al. 2013), and has more recently received increased attention in the analysis and prediction of complex human traits (e.g., Yang et al. 2010; Kim et al. 2017).

Most of the applications of WGRs in human genetics use linear models. These models have multiple appealing features and have proven to be effective for the prediction of complex traits in multiple applications. Recent developments in machine learning enable the implementation of high-dimensional regressions using nonlinear methods that have been shown to be effective in uncovering complex patterns relating inputs (SNPs in our case) and outputs (phenotypes). Among the many machine learning methods available, deep learning (DL) methods such as Multilayer Perceptrons (MLPs) have emerged as one of the most powerful pattern-recognition methods (Goodfellow et al. 2016). DL has demonstrated its utility in disparate fields such as computer vision, machine translation, and automatic driving, among others. It has also been applied to genomic problems using Convolutional Neural Networks (CNNs) to learn the functional activity of DNA sequences (Kelley et al. 2016), predict the effects of noncoding DNA (Zhou and Troyanskaya 2015), investigate the regulatory role of RNA-binding proteins in alternative splicing (Alipanahi et al. 2015), or infer gene expression patterns, among others.

Shallow neural networks (NNs, e.g., single-layer networks) have been considered for nonparametric prediction of complex traits in plant and animal breeding (Gianola et al. 2011; González-Camacho et al. 2012; Pérez-Rodríguez et al. 2012). Some of these studies suggest that NNs can achieve reasonably high prediction accuracy; however, there has not been consistent evidence indicating that NNs can outperform linear models in prediction. Perhaps most importantly, most of the available studies were based on relatively small sample sizes and limited numbers of SNPs. So far, the application of NNs for genomic prediction of complex traits has been limited, with only a few studies published in animal (e.g., Okut et al. 2011) and plant breeding (e.g., González-Camacho et al. 2016).

In this study, we present an application of DL for the prediction of complex human traits using data from distantly related individuals. Achieving high prediction accuracy with MLPs or CNNs requires using very large data sets for model training (TRN). Until recently, such data sets were not available in human genetics. Fortunately, this situation has changed as very large biomedical data sets from biobanks become available. Here, we use data from the interim release of the UK Biobank (http://www.ukbiobank.ac.uk/), and compare the predictive performance of various MLPs and CNNs with commonly used linear regression methods [BayesB and Bayesian Ridge Regression (BRR)] using five complex human traits.

Materials and Methods

Data set

The UK Biobank (www.ukbiobank.ac.uk) is a prospective cohort including half a million participants aged between 40 and 69 years who were recruited between 2006 and 2010. From the subjects whose genotypes and phenotypes were provided, we used data from those that were white Caucasians (self-identified and confirmed with SNP-derived principle components) and were distantly related (genomic relationships < 0.03). For comparison purposes, we use the same data set and the same TRN testing (TST) partition as the one used by Kim et al. (2017). The final data set consists of a total of 102,221 distantly related white Caucasian individuals. The TRN set contains 80,000 subjects and the TST set, the remaining 22,221 individuals. Further details about sample inclusion criteria and quality control are provided in Kim et al. (2017).

As in Kim et al. (2017), we also analyzed human height because it is a highly heritable trait with a very complex genetic architecture and a common human model trait in quantitative genetic studies (Visscher et al. 2010). However, because human height is known to be a trait with high narrow-sense heritability, we expect that a large fraction of phenotypic variance could be captured with a linear model. Therefore, to contemplate traits for which nonadditive effects may be more relevant, we also considered bone heel mineral density (BHMD), body mass index (BMI), systolic blood pressure (SBP), and waist–hip ratio (WHR). Not all phenotypes were available for all individuals. The numbers of records available for each trait are given in Table 1. Phenotypes were all precorrected by sex, age, the center where phenotypes were collected, and with the top-10 SNP-derived principal components.

Table 1. Number of phenotypes available and genetic parameters.

Trait	No. of samples TRN set	No. of samples TST set	$h_A^2$ (SD)	$h_D^2$ (SD)
Height	80,000	22,221	0.67 (0.04)	0.07 (0.02)
Bone heel mineral density	71,529	19,784	0.32 (0.04)	0.11 (0.03)
Body mass index	79,915	22,192	0.29 (0.04)	0.09 (0.02)
Waist–hip ratio	79,962	22,214	0.20 (0.03)	0.10 (0.02)
Systolic blood pressure	74,560	20,687	0.18 (0.03)	0.09 (0.02)

${\mathit{h}}_{\mathit{A}}^2\mathit{ }$: Posterior density median and SD of genomic heritability. ${\mathit{h}}_{\mathit{D}}^2\mathbf{:}$ Posterior density median and SD of genomic dominance variance (% of phenotypic variance). ${\mathit{h}}_{\mathit{A}}^2\mathit{ }$ and ${\mathit{h}}_{\mathit{D}}^2\mathit{ }$were estimated from 10k individuals from the TRN set using all markers via a Bayesian Ridge Regression algorithm. No., number; TRN, training; TST, testing.

Genotypes

The UK Biobank’s participants were genotyped with a custom Affymetrix Axiom array containing ∼820k (k = 1000) SNPs (http://www.ukbiobank.ac.uk/scientists-3/uk-biobank-axiom-array/). Here, SNP filtering followed the criteria used in Kim et al. (2017). Briefly, SNPs with a minor allele frequency < 0.1% and a missing rate > 3% were filtered out using PLINK 1.9 (Chang et al. 2015). Mitochondrial and sex chromosome SNPs were also removed, except those in pseudoautosomal regions, yielding a total of 567,867 used SNPs.

For each of the prediction methods described below, we evaluated performance with SNP sets of 10k and 50k SNPs. In set “BEST,” the 10k or 50k top most-associated SNPs, i.e., those with the lowest P-values in a GWAS on the TRN set for each trait, were chosen. In set “UNIF,” the genome was split in windows of equal physical length and the most-associated SNP within each window was chosen. This criterion was chosen to accommodate the philosophy of CNNs, which are designed to utilize the correlation between physically adjacent input variables (see below). Windows were 309- and 61-kb long in the 10k and 50k SNP UNIF sets, respectively.

Variance components analyses

We estimated the proportion of variance that could be explained by additive and dominance effects using a genomic best linear unbiased prediction (GBLUP) model (VanRaden 2008). The additive genomic relationship matrix for additive effects was computed as in VanRaden’s equation

$$G=\frac{X{X}^{’}}{2{{\displaystyle \sum }}_{j=1}^m{q}_j (1-q_j)},$$

where X is an n × m matrix (n individuals and m markers) that contains the centered individual genotype values, i.e., −2q_j, 1−2q_j, and 2−2q_j when genotypes are coded as 0, 1, and 2, with q_j being the allele frequency of alternative allele “1” at j-th SNP. The dominance relationship matrix was calculated as proposed in Vitezica et al. (2013):

$$D=\frac{M{M}^{’}}{4{{\displaystyle \sum }}_{j=1}^m{[q_j (1-q_j)]}^2},$$

where the elements of matrix M_nxm are −2q_j², 2q_j(1−q_j), and −2(1−q_j)² for genotypes 0, 1, and 2, respectively. Due to computational constraints, 10,000 random individuals from the TRN set were used to build the genomic relationship matrices, although with all markers.

Bayesian linear models

BayesB (Meuwissen et al. 2001) and Bayesian Ridge Regression (also called BLUP in the animal breeding literature, Henderson 1984) are two widely used genomic linear prediction methods; thus, we used these two methods as benchmarks against which we compare DL techniques. In these models, the phenotype of the i-th individual can be expressed as:

$$y_i=b_0+{\mathit{x}}_i^{’}\mathit{b}+e_i,$$

where b is a vector with regression coefficients on marker genotypes x_i and e, a residual term. The likelihood is written as:

$$p\left(\theta \text{|}\mathit{y}\right)= \prod _{i=1}^{n}N\left(y_i- b_0-{\mathit{x}}_i^{’}\mathit{b},{\sigma }_e^2\right) p(\theta )$$

The difference between BRR and BayesB lies in the prior specification $p(\theta ).$ In BayesB, the parameters θ include the probability π of a given SNP being included in the model, and this probability in turn is also sampled according to a β binomial distribution, whereas all markers enter into the model for BRR (see, e.g., Pérez and de Los Campos (2014) for further details).

MLPs

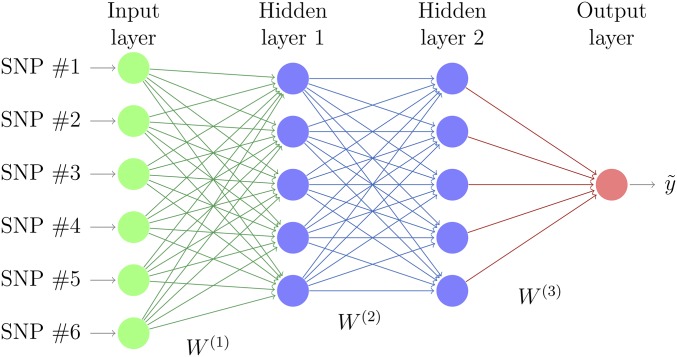
MLPs, also called fully connected feed-forward NNs, are commonly used for DL. An MLP consists of at least three layers of nodes (Figure 1). The first layer, known as the input layer, consists of a set of neurons (x_i, j = 1, m) representing the input features (SNP genotypes). Each neuron in the hidden layer transforms the values from the previous layer with a weighted linear summation, i.e., for the first layer and l-th neuron $a_l^{(1)}={\displaystyle {\sum }_{j=1}^m{w}_{lj}^{(1)}{\mathit{x}}_j+b_0^{(1)}},$ where $w_{lj}^{(1)}$ is the weight of l-th neuron to j-th input in the first layer, b₀ is the intercept (called “bias” in machine learning literature), followed by a nonlinear activation function f($a_l$) that results in neuron’s output. Subsequent layers receive the values from the previous layers and the last hidden layer transforms them into output values. Learning occurs in the MLP by changing weights (w) after each piece of data is processed, such that the loss function is minimized. This process is carried out through back-propagation, a generalization of the least squares algorithm in the linear perceptron (Rosenblatt 1961; Rumelhart et al. 1986; LeCun et al. 1998a). The multiple layers and nonlinear activation distinguish an MLP from a linear perceptron and make them far more versatile for representing complex outputs. An issue with MLPs is the need to optimize the neuron architecture, which depends on numerous parameters: activation function, dropout rate (i.e., the rate at which a random neuron is removed from the model, Srivastava et al. 2014), and the number of layers and neurons per layer. See section Hyperparameter optimization below.

Figure 1.

Representation of a Multilayer Perceptron. Each layer is connected to the previous one by a weighted linear summation, here represented by weight matrices W⁽ⁱ⁾, and a (non)linear transformation. Redrawn from http://www.texample.net/tikz/examples/neural-network/.

In the standard variable coding, the values of each SNP genotype are considered as numeric values, say 0, 1, and 2 for each genotype. This assumes additivity. To allow explicitly for dominance, we used the so-called one-hot encoding (Wan et al. 2010) in a subset of analyses, where each genotype is coded as a set of three binary variables instead of a number taking values 0, 1, and 2 for the three genotypes, as we did for the rest of the MLPs and CNNs described below.

CNNs

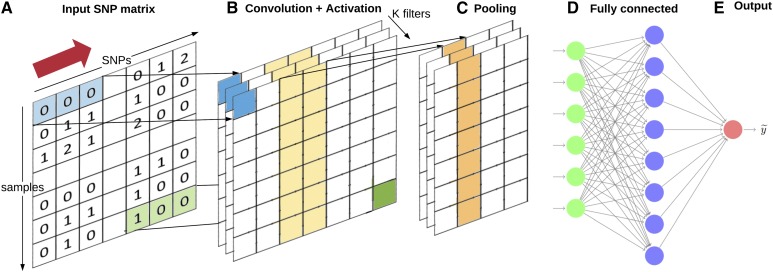
CNNs (LeCun and Bengio 1995; LeCun et al. 1998b) are a specialized kind of NN for data, where inputs are associated with each other and exploit that fact. The hidden layers of a CNN typically consist of convolutional layers, pooling layers, fully connected layers, and normalization layers. CNNs combine several layers of convolutions with nonlinear activation functions. Figure 2 shows a general diagram of a CNN. During the training phase, a CNN automatically learns the coefficients of the so called “filters.” A filter is defined as a combination of the input values where the weights are the same for all input windows (e.g., SNP windows). For example, in image classification, a CNN may learn to detect edges from raw pixels in the first layer, and then use the edges to detect simple shapes (say circles) in the second layer. Then, these shapes can be used by the next layer to detect even more complex features, say facial shapes. Finally, the last layer is then a classifier that uses these high-level features. These learnt filters are then used across all input variables. However, to make them slightly invariant to small translations of the input, a pooling step is added. CNNs have shown great success in computer vision, where pixel intensities of images are locally correlated. In the genomic prediction context, adjacent SNP genotypes are expected to be correlated due to linkage disequilibrium. In this case, it makes sense to use one-dimensional kernels, as opposed to two-dimensional kernels used for images. This means that sliding sets of s consecutive SNPs are used for each filter (Figure 2), instead of squares of pixels.

Figure 2.

Representation of a Convolutional Neural Network. (a) The input layer consists of the SNP matrix. The convolution filters are the same through all different SNPs; we slide these filters horizontally with a stride of “s” SNPs, i.e., the number of SNPs that the filter is moved to compute the next output. (b) Neuron outputs of convolutional layer with K dimensions (outlined as blue and green squares) are computed from inputs of input layer, which fall within their receptive field (here consecutive sets of three SNPs) in the layer below (shown as blue- and green-colored rectangles). (c) Convolutional networks usually include pooling layers, combining the output of the previous layer at certain locations into a single neuron (here, a 1 × 2 pooling is outlined in yellow). (d) Fully connected layers connect every neuron in one layer to every neuron in another layer. It is the same as traditional MLPs, finally obtaining an estimated output (e). Partly redrawn using code in http://www.texample.net/tikz/examples/neural-network/.

Hyperparameter optimization

Hyperparameter optimization is a fundamental step for DL implementation since it can critically influence the predictive performance of MLPs and CNNs. Here, we applied a modified genetic algorithm as implemented in DeepEvolve (Liphardt 2017) to evolve a population of MLPs or CNNs with the goal of achieving optimized hyperparameters in a faster manner than with traditional grid or random searches. The algorithm is described in Supplemental Material, Figure S1 and the different parameters optimized together with their theoretical effects on the model capacity are presented at Table S1. This optimization was done for each trait independently using the TRN set and the 10k BEST SNP set in two steps. In the first step, we selected the best five architectures for each of the five traits independently. Next, all 25 solutions were evaluated for the remaining traits. Finally, we selected the best three MLPs and CNNs that performed uniformly best across traits.

Assessment of prediction accuracy

For all prediction methods, parameters were estimated by regressing the adjusted phenotypes on SNPs set using data from the TRN set. Subsequently, we applied the fitted model to genotypes of the TST data set and evaluated prediction accuracy by correlating (R) the SNP-derived predicted phenotype with the adjusted phenotype in the TST set. Since the MLP or CNN depends, to an extent, on initialization values, we ran each case six times and we retained the best learner in the TRN stage, i.e., using only the TRN set. Approximate lower-bound SE’s of R were obtained from $\sqrt{(1-R^2)/(n-2),}$ n being the TST data size.

Software

GWAS and phenotype adjustment analyses were performed with the BGData R package (de Los Campos and Grueneberg 2017). BayesB and BRR were fitted with the BGLR R package (Pérez and de Los Campos 2014) using default parameters. A Bayesian GBLUP using BRR prior and eigenvalue decomposition of G and D was employed to estimate genomic heritabilities with the BGLR package [see Forneris et al. (2017) for an application of this model]. Genomic matrices were computed with a Fortran program that employs Basic Linear Algebra Subroutines (BLAS) (Dongarra et al. 1990, www.netlib.org/blas/) for efficient parallelization, available at https://github.com/miguelperezenciso/dogrm. The rest of the analyses were implemented in python using scikit (Pedregosa et al. 2011, www.scikit-learn.org), pandas (pandas.pydata.org), and numpy (www.numpy.org/) among other libraries for the processing and analysis of the data. To implement machine learning methods, we used the Keras API (Chollet 2015, www.keras.io), which provides a high-level NN API on top of Tensorflow (Abadi et al. 2015, www.tensorflow.org) libraries. Software and pipelines are available at https://github.com/paubellot/DL-Biobank.

Data availability

This research has been conducted using the UK Biobank Resource under project identification number 15326. The data are available for all bona fide researchers and can be acquired by applying at http://www.ukbiobank.ac.uk/register-apply/. The Institutional Review Board (IRB) of Michigan State University has approved this research with the IRB number 15–745. The three authors completed IRB TRN. Lists of SNPs and P-values are available at https://github.com/paubellot/DL-Biobank. Supplemental material contains a summary of main DL parameters, a description of the genetic algorithm used for hyperparameter optimization, and additional MLP and CNN results. Supplemental material available at Figshare: https://doi.org/10.6084/m9.figshare.7035866.

Results

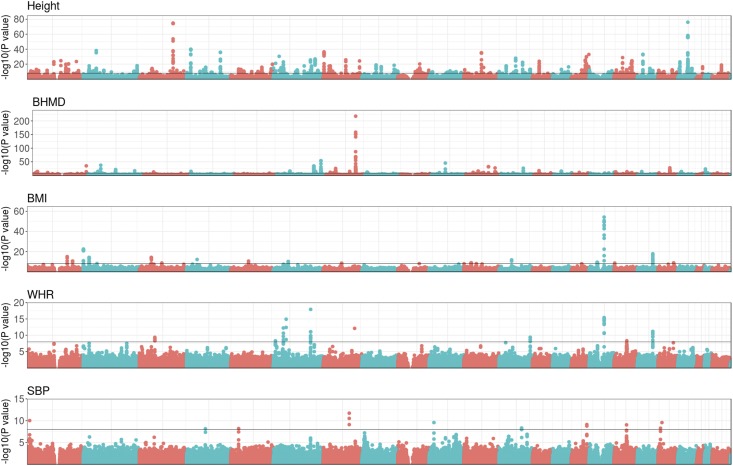
The five phenotypes analyzed span a wide range of genetic profiles, as the GWAS in Figure 3 and heritabilities in Table 1 show. Height is a well-studied phenotype in the field of human quantitative genetics and, in agreement with the literature (e.g., Yang et al. 2010), the GWAS does show numerous and highly significant peaks scattered throughout the genome: 946 SNPs had a P-value < 10⁻⁸, the tentative genome-wide significance level. Height was also the trait with highest genomic heritability: $h_A^2$ = 0.67 (Table 1). Genomic heritabilities were markedly lower for the rest of the phenotypes. As expected, the dominance variance for height was small relative to the additive variance; however, the estimates of dominance variance were between one-half and one-third of that of the additive variance for the other four traits.

Figure 3.

Genome-wide association study of traits analyzed. Each dot represents the P-value (−log10 scale) of a single SNP. SNPs from different chromosomes are represented by alternating colors, starting with chromosome 1 on the left. The horizontal line indicates the tentative genome-wide significance level (P-value = 10⁻⁸). BHMD, bone heel mineral density; BMI, body mass index; SBP, systolic blood pressure; WHR, waist–hip ratio.

Although numerous peaks were detected for all traits, the major locus for BHMD in chromosome 7 (Hsa7: 120,945,328–121,018,579 bp) is striking. Nguyen et al. (2003) already predicted the presence of a major gene for BHMD and Kemp et al. (2017) previously identified the WNT16 gene as the most likely candidate for this QTL, which was the most significant region in a GWAS on a larger subset of the biobank data set. As for BMI and WHR phenotypes, they shared some peaks but they were more significant for BMI. Perhaps related to this, the genomic heritability of BMI was 50% larger than that of WHR (0.29 vs. 0.20, respectively, Table 1). The heritability of SBP was mildly lower than that of WHR and QTL peaks were concordantly less significant. We only found 15 SNPs with a P-value <10⁻⁸ in SBP vs. 56 SNPs in WHR.

The retained MLPs and CNNs that performed uniformly best across traits are shown in Table 2. MLP1, MLP2, and MLP3 differ mainly in the number of layers: 1, 2, and 5, respectively. For CNNs, the optimum SNP window was very small with maximum overlap (stride = 1), but they differed in activation function, number of neurons, and on number of filters. For one-hot encoding, we evaluated only one MLP. Overall, the chosen regularization, as inferred from the genetic algorithm, was very small for either MLPs or CNNs (Table 2).

Table 2. Main features of chosen MLPs and CNNs.

Model	Activationa	No. of fully connected layers (neurons)	No. of convolutional layers (filters)	No. SNPs/window (stride)	Dropout (weight regularization)
MLP1	Elu	1 (32)	NA	NA	0.01 (0.0)
MLP2	Elu	2 (64)	NA	NA	0.03 (0.0)
MLP3	Softplus	5 (32)	NA	NA	0.01 (0.0)
MLP-hot	Elu	4 (128)	NA	NA	0.03 (0.01)
CNN1	Linear	1 (32)	1 (16)	3 (1)	0.01 (0.0)
CNN2	Elu	3 (32)	1 (32)	2 (1)	0.01 (0.0)
CNN3	Softplus	3 (64)	1 (16)	2 (1)	0.01 (0.0)

No., number; MLP, Multilayer Perceptron; Elu, exponential linear unit; CNN, Convolutional Neural Network.

^aElu: f(x) = c (e^x−1) x < 0, f(x) = x, x > 0; SoftPlus: f(x) = ln(1+e^x); and Linear: f(x) = c x.

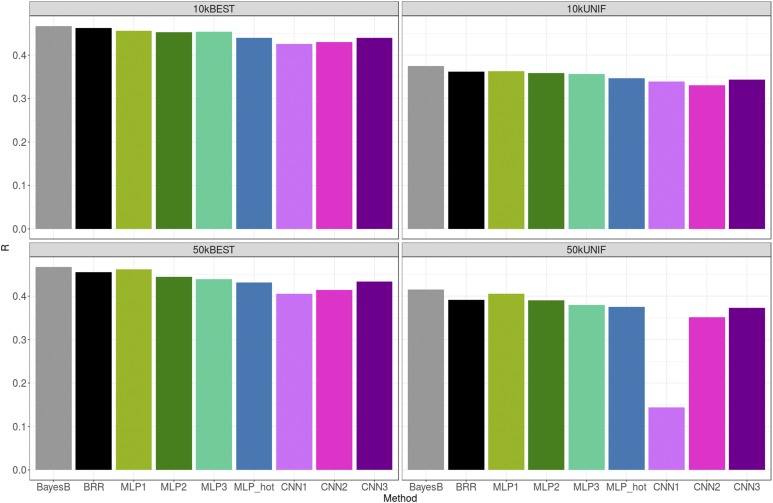
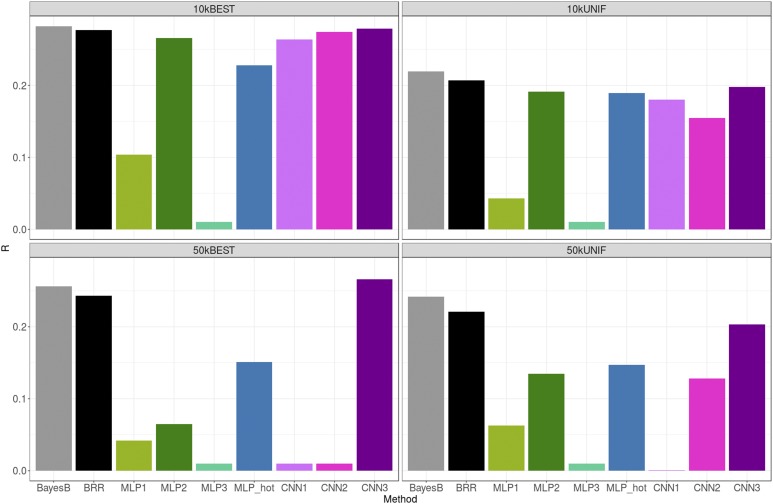
Figure 4 shows the TST correlation (R) between predicted and adjusted height for each of the methods and SNP sets. Overall, all methods performed similarly, although CNN models were slightly worse. Prediction correlations with the linear model were very similar to those reported in Kim et al. (2017), as expected because we used the same data set. Selecting SNPs based only on unrestricted GWAS P-values (BEST set) was systematically better than setting a restriction on the distance between retained SNPs (UNIF set), especially — and paradoxically — for CNNs. Penalized linear methods were not so sensitive to SNP choice, in particular when the total number of SNPs was large (50k). We did not observe a clear improvement in prediction accuracy for any of the methods when increasing the number of SNPs from 10k to 50k. For some CNNs (CNN3), adding SNPs was even detrimental when using the UNIF set.

Figure 4.

Prediction performance across methods and SNP sets for height. Gray, green, blue, and magenta bars correspond to linear, MLP, one-hot encoding MLP, and CNN methods, respectively. Average SE of R’s were ∼3 × 10⁻³. BEST, set with the 10k or 50k top most-associated SNPs; BRR, Bayesian Ridge Regression; CNN, Convolutional Neural Network; MLP, Multilayer Perceptron; UNIF, set in which the genome was split in windows of equal physical length and the most-associated SNP within each window was chosen.

Figure 5 shows the correlation between predicted and adjusted BHMD in the TST set, which displays a different picture from that obtained with height (Figure 4). For this phenotype, CNNs performed better overall than MLPs, especially for 10k SNP sets. In particular, CNN3 configuration was comparable or slightly better than Bayesian linear methods. Consistent with the height phenotype though, methods performed better with the BEST SNP set than with the UNIF set. For some MLPs and CNNs with the 50k sets, we observed some convergence problems that persisted even after several reinitializations of the algorithm. This is likely due to the exponential increase in parameters to be learnt in nonlinear methods with large SNP data sets and to the reduced predictive ability, compared to height. However, these issues were not observed with linear methods.

Figure 5.

Prediction performance across methods and SNP sets for bone heel mineral density. Gray, green, blue, and magenta bars correspond to linear, MLP, one-hot encoding MLP, and CNN methods, respectively. Very low bar means method not converging. Average SE of R’s were ∼3 × 10⁻³. BEST, set with the 10k or 50k top most-associated SNPs; BRR, Bayesian Ridge Regression; CNN, Convolutional Neural Network; MLP, Multilayer Perceptron; UNIF, set in which the genome was split in windows of equal physical length and the most-associated SNP within each window was chosen.

For the rest of the phenotypes, predictive accuracies were lower than for height or BHMD (Figure S2). Similar to what we observed for BHMD, in the case of BMI, WHR and SBP Bayesian linear methods, and the CNN3, were consistently the best methods overall. In some instances though, e.g., BMI, one-hot encoding or MLP2 could be preferred. Differences between top methods were never very large. In general, performance of MLPs or CNNs was sensitive to the specified network architecture, and highly dependent on the phenotype analyzed (Figure 5 and Figure S2). This was not so much the case for Bayesian linear methods, which were far more stable.

CNNs are designed to exploit a spatially local correlation by enforcing a putative connectivity pattern between nearby inputs. This fact motivated the usage of equally spaced SNP sets (UNIF sets). However, simply selecting SNPs on absolute significance (BEST sets) was a better option across all analyses. This indicates that systematic controlling for linkage disequilibrium does not necessarily improve, and can even harm, prediction accuracy. Furthermore, CNN hyperparameter optimization suggested that maximum overlapping (stride = 1) between very small windows (2–3 SNPs) was the optimum configuration for CNNs (Table 2). To further investigate the effect of SNP spacing and stride on CNNs, we fitted CNN3 for height phenotype varying the overlap (maximum vs. no overlap) and SNP window size (2–10 SNPs). We observed that overlapping between windows was better than no overlapping, and small windows (2–3 SNPs) should be preferred to large ones when using the BEST criterion (Table S2). In the case of uniformly distributed SNPs, differences between criteria were relatively small.

Discussion

With this work, we aim to stimulate debate and research on the use of DL techniques for genomic prediction. DL is prevailing in areas such as computer vision (LeCun et al. 2015), in part due to its ability to extract useful features (i.e., to learn a hierarchical-modular feature space from visual space) and the ability of DL to map from these derived features into outputs (either a quantitative outcome or a set of labels). In these problems, the label is usually perfectly known and the input visual space consists of complex features, sometimes of mixed types, whose values vary over wide ranges but are locally correlated. The natures of complex trait analyses using SNP data are very different. First, the attribute (the expected value of a trait or genetic risk) is not observable. Rather, we observe a noisy version of it, which is a function of both DNA-sequence and environmental factors. Moreover, the inputs used in genomic prediction are much simpler (SNP genotypes can take only three values) and much more structured than the ones used in computer vision or other areas where DL has thrived. Furthermore, since allele frequencies of SNP genotypes are highly unbalanced, a large number of SNP genotypes can be considered as simple 0/1 bits. The complex and noisy nature of the phenotypes, and the relatively simple nature of the input data, may explain why DNA-based prediction linear models perform similarly, and in many cases better, than DL.

The relative performance of DL vs. linear methods depended on the trait analyzed but also on the DL network architecture. For height, a highly polygenic trait with a predominant additive genetic basis, there were no large differences between methods, although linear methods prevailed. This was not likely due to a limitation in the size of the data but to the nature of the problem, which apparently can be approximated rather well with a linear model. CNNs were the worst-performing method in height, whereas the performance of the simplest MLP (MLP1) was nearly undistinguishable from BayesB or BRR (Figure 4). In contrast, some CNNs were comparable or slightly outperformed linear methods for BHMD, WHR, and SBP in some instances (Figure 5 and Figure S2).

The predictive accuracy of Bayesian linear methods depended highly on heritability. An interesting observation is that this was not the only factor in MLPs and CNNs. For instance, BHMD and BMI had similar heritabilities, yet the performance of the several MLPs and CNNs varied. This may be due to the very different distribution of QTL effects, as shown in the GWAS profiles of Figure 3. Despite of the fact that the estimated dominance variance was sizable for some of the traits (WHR and SBP), using one-hot encoding did not improve prediction in general. Given that dominance variance could be ≤ 50% of additive variance in some traits (Table 1), this suggests that DLs using one-hot encoding may not efficiently capture dominance (compared to other methods). The highly skewed distribution of allele frequencies makes it difficult to accurately consider all three genotype effects. Note also that one-hot encoding results in an increase in the number of parameters, increasing the risk of overfitting.

MLPs and CNNs are actually highly heterogeneous classes of predictors. Depending on the configuration (e.g., on the number of layers, number of neurons per layer, or the activation function used, Table S1), very different models can be obtained. In addition to selecting the network configuration, hyperparameters that control regularization need to be estimated as well. Finding an optimal configuration for an MLP or CNN can be challenging. Here, we used a genetic algorithm to perform this optimization. Genetic algorithms are a well-known (e.g., Mitchell 1998) approach for maximizing complex functions in cases such as the one considered here, where optimum hyperparameter values are highly dependent between them. The complexity of DL methods contrasts with the frugality of penalized linear regressions, where the search is constrained to the class of linear models and the only estimation problem consists of finding weights associated with each of the inputs.

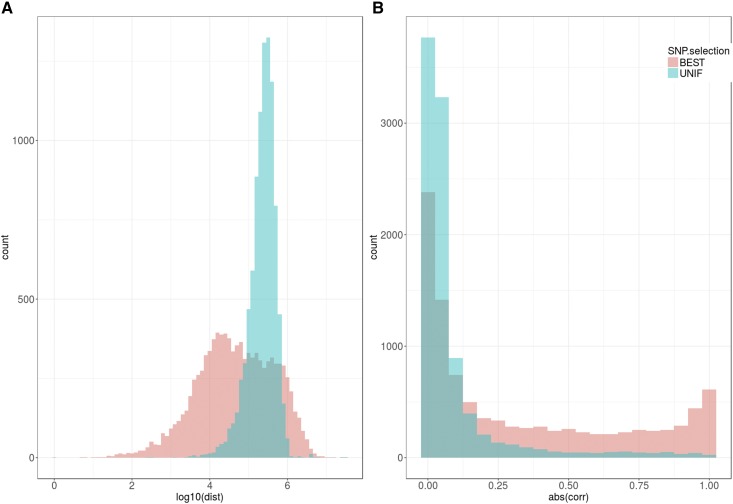
It was computationally impossible to fit all ∼500k SNPs with 100k subjects in an MLP or a CNN, and some feature selection was needed. The GWAS top P-value was the best and simplest criterion of those evaluated, although it is not guaranteed to be uniformly the best choice. Although autocorrelation between features may be a hindrance to prediction, we did not find that limiting disequilibrium between SNPs improved performance, in agreement with previous results in the same data set (Kim et al. 2017). CNNs are designed to exploit correlation between adjacent features, which in our context translates into disequilibrium between markers. We expected then that uniformly selecting the best SNPs would be preferred over selection only on P-value; however, our analyses showed the opposite (Figure 4, Figure 5, and Figure S2). We argue that this is due to the presence of clusters of associated SNPs together with large genome “deserts,” for which markers are not useful for prediction. To investigate this, we plotted the distances and disequilibrium between the top pairs of consecutive SNPs for BHMD in Figure 6 (plots for height were very similar and are not shown). Figure 6a shows that, as expected, the distribution of distances in the BEST set is much broader than that in the UNIF set. Far more interesting, an important fraction (74%) of consecutive distances in the BEST set were actually smaller than those in the UNIF set median, a clear consequence of BEST set SNPs not being randomly distributed but clustered in specific regions (see GWAS profiles in Figure 3). In terms of linkage disequilibrium (measured as correlation between genotype values at two SNPs), the differences were dramatic since LD was very low genome-wide (UNIF set), whereas LD was much higher in the BEST sets (Figure 6b). In summary, choosing SNPs based only on individual P-values resulted in groups of clustered SNPs, the structures of which were better exploited by CNNs than when SNPs were chosen at equal intervals. As a result, CNNs performed better than some MLPs for BHMD or other traits (Figure 5 and Figure S2).

Figure 6.

Histogram of distances and correlations between consecutive SNPs in the 10k BEST (the 10k top most-associated SNPs) and UNIF (the genome was split in windows of equal physical length and the most-associated SNP within each window was chosen) sets. (a) Distances (dist) in base pairs (log10 units) between consecutive SNPs, within the same chromosome. (b) Absolute value of correlation [abs(corr)] between genotype values of consecutive SNPs when each genotype is coded as 0, 1, or 2.

Our analyses show that CNNs performed comparatively better as narrow-sense heritability decreased and the contribution of dominance increased. Therefore, in our opinion, future efforts in DL research for genomic prediction should aim at improving mapping functions to overcome linear constraints that relate genotype to phenotype. For CNNs, methods for optimum exploitation of SNP disequilibrium in CNNs are also needed. A major problem here is that LD varies along the genome and therefore optimum SNP window sizes are not constant. This problem is similar to that found in learning from text, where the length of each document varies. Therefore, each individual word cannot be used as an input feature, because long documents and words would require different input spaces to shorter ones. Researchers in text machine learning have proposed several methods to address those issues such as classical “bag of words” (BOW, Salton and McGill 1983) or more recent word2vec (Mikolov et al. 2013) algorithms. The basic idea of both methods is to represent documents or words with numbers, turning text into a numerical form that DL can understand. BOW is based on the frequency of words, whereas word2vec maps every word into a vector, so similar words are closer. To use genotypes in CNNs more efficiently, a similar approach could be explored. This representation should be smaller and length-independent, and yet able to encode the SNPs’ information. To the best of our knowledge, CNNs have not been applied to human genetic prediction so far, but here we show that they are promising tools that deserve future research.