Scaling of G1 Duration with Population Doubling Time by a Cyclin in Saccharomyces cerevisiae

Abstract

The longer cells stay in particular phases of the cell cycle, the longer it will take these cell populations to increase. However, the above qualitative description has very little predictive value, unless it can be codified mathematically. A quantitative relation that defines the population doubling time (T_d) as a function of the time eukaryotic cells spend in specific cell cycle phases would be instrumental for estimating rates of cell proliferation and for evaluating introduced perturbations. Here, we show that in human cells, the length of the G1 phase (T_G1) regressed on T_d with a slope of ≈0.75, while in the yeast Saccharomyces cerevisiae, the slope was slightly smaller, at ≈0.60. On the other hand, cell size was not strongly associated with T_d or T_G1 in cell cultures that were proliferating at different rates. Furthermore, we show that levels of the yeast G1 cyclin Cln3p were positively associated with rates of cell proliferation over a broad range, at least in part through translational control mediated by a short upstream ORF (uORF) in the CLN3 transcript. Cln3p was also necessary for the proper scaling between T_G1 and T_d. In contrast, yeast lacking the Whi5p transcriptional repressor maintained the scaling between T_G1 and T_d. These data reveal fundamental scaling relationships between the duration of eukaryotic cell cycle phases and rates of cell proliferation, point to the necessary role of Cln3p in these relationships in yeast, and provide a mechanistic basis linking Cln3p levels to proliferation rates and the scaling of G1 with doubling time.

RECURRING shapes and patterns in nature are sometimes described by mathematical relationships. As a result, these natural processes can be predicted and understood better. Regarding patterns of eukaryotic cell division, one could ask: how are the lengths of eukaryotic cell cycle phases related to each other and to the total doubling time of the population? Can such relationships be described mathematically, in the form of a scaling formula? If so, what are the molecular mechanisms that govern the scaling? A scaling relationship that describes eukaryotic cell division would be a significant advance. For example, it could serve as a point of reference against which the effects of genetic or other perturbations can be evaluated.

The “textbook” view in the coordination of growth and division in the eukaryotic cell cycle [e.g., see figures 10–26 in Morgan (2007)] is that expansion of the G1 phase of the eukaryotic cell cycle accounts for most, if not all, of the lengthening of the cell cycle in slower-proliferating cells in budding yeast (Johnston et al. 1977; Brauer et al. 2008) or humans (Baserga 1985; Fisher 2016). However, there is no report in the literature of a quantitative relationship that defines the doubling time (T_d) as a function of the time that yeast or human cells spend in the G1 phase (T_G1). Here, based on all the available data for budding yeast and human cell populations, we derived for the first time in the field scaling relationships between T_G1 and T_d. These scaling relationships also allowed us to critically evaluate the role of cell cycle regulators in yeast cells proliferating at different rates.

Two key regulators of the length of the G1 phase in Saccharomyces cerevisiae are the Cln3p and Whi5p proteins. The G1 cyclin Cln3p promotes the initiation of DNA replication (Cross 1988; Nash et al. 1988). In contrast, the transcriptional repressor Whi5p acts analogously to the retinoblastoma gene product in animals to inhibit the G1/S transition (Costanzo et al. 2004; de Bruin et al. 2004; Palumbo et al. 2016). It has been reported that while synthesis of Cln3p parallels cell size, the synthesis of Whi5p is independent of cell size (Schmoller et al. 2015), arguing that dilution of Whi5p as cells get bigger in G1 governs the length of the G1 phase (Schmoller and Skotheim 2015; Schmoller et al. 2015).

Here, we obtained the first measurements of Cln3p and Whi5p levels as a function of proliferation rates in steady-state cultures. The levels of Cln3p varied over a broad range, due to an upstream ORF (uORF) affecting translation of CLN3. Our data also show that loss of Whi5p does not significantly affect the scaling relationship between T_d and T_G1. Instead, we provide strong evidence for the functional and molecular basis of the necessary role of Cln3p in this process.

Materials and Methods

Strains

Unless stated otherwise, S. cerevisiae wild-type, cln3Δ, and whi5Δ strains were in the BY4741 background [National Center for Biotechnology Information (NCBI) Taxonomy 559292; MATa, his3Δ1, leu2Δ0, ura3Δ0, met15Δ0), and they have been described previously (Soma et al. 2014). For protein surveillance, we constructed an otherwise wild-type strain that carried epitope-tagged WHI5 and CLN3 alleles at their endogenous chromosome locations. First, a commercially available WHI5-TAP::HIS3 strain (BY4741 otherwise; GE Healthcare) was backcrossed three times into the W303 background (NCBI Taxonomy 580240; MATα leu2-3,112 trp1-1 can1-100 ura3-1 ade2-1 his3-11,15). Then, it was crossed with an otherwise wild-type strain carrying a CLN3-13MYC allele (W303 background), described elsewhere (Thorburn et al. 2013), and kindly provided by A. Amon (Massachusetts Institute of Technology and Howard Hughes Medical Institute). The resulting diploid was sporulated and dissected to obtain MATa haploid segregants carrying both the epitope-tagged WHI5 and CLN3 alleles (strains HB94/97; MATa CLN3-13MYC::TRP⁺WHI5-TAP::HIS⁺leu2ura3met15), which were used in the experiments shown in Figure 4. We verified expression of Whi5p-TAP and Cln3p-(Myc)₁₃ in this strain (see Supplemental Material, File S1), and their absence in whi5Δ or cln3Δ strains, respectively. We also generated a derivative of this strain, which lacks the uORF in the 5′-leader of the CLN3 mRNA. To this end, we used plasmid A-315T-pMT10, which we have described previously (Polymenis and Schmidt 1997), as a template in a PCR reaction with forward (5′-CAAGAACTACCATTCGACAGG-3′) and reverse primers (5′-CGTACAGAAAGCGTATCAAA-3′) to generate a product that carries the URA3-marked A-315T mutation, which inactivates the uORF, in the 5′-leader of CLN3. We then used this PCR product to transform strain HB94 (WHI5-TAP and CLN3-13MYC). Genomic DNA of transformants was sequenced to verify the presence of the A-315T mutation. Confirmed A-315T mutants were then backcrossed with wild-type cells (W303) to segregate away possible secondary mutations at other loci. The resulting heterozygote was sporulated and dissected to isolate a WHI5-TAP, A-315T-CLN3-13MYC segregant (HB104), which was used in the experiments shown in Figure 4.

Figure 4.

The levels of the G1 cyclin Cln3p vary over a broad range as a function of T_d, due to an upstream ORF (uORF) affecting translation of CLN3. Scatter plots of the relative abundance (y-axis) of Cln3p-(Myc)₁₃ and Whi5p-TAP in otherwise wild-type CLN3-13MYC, WHI5-TAP cells (A) or CLN3 uORF (A-315T-CLN3) mutant cells (B), against T_d (x-axis). Each data point in the scatter plots is the average of immunoblot signal intensities run in duplicate, and detected with antibodies against the Myc or TAP epitopes (see Materials and Methods). All the raw immunoblots used to quantify protein levels are shown in the source data (File S1). Before averaging, each individual signal intensity value was normalized against loading in the corresponding immunoblot lane (visualized with Ponceau staining, see File S1 and Materials and Methods). For each Cln3p-(Myc)₁₃ or Whi5p-TAP relative unit (r.u.) shown in the scatterplots (A and B), the normalized, averaged intensities were scaled by the lowest value (set to 1) for each protein in the given chemostat experiment run at different dilution rates. Scatter plots of the relationship of cell size (x-axis) and T_d (y-axis) in the indicated strains, cultured under glucose (C) or leucine (D) limitation, from the same cultures described in (A) and (B).

Data sets for population-based cell cycle parameters

All the obtained variables that we report here represent population averages. They do not resolve intergenerational differences in cell cycle progression of the same cells in successive cell cycles. In the context of this study, population averages hold significant advantages: first, they are easily obtained; second, they are ubiquitously used and reported in the literature; and third, they allow straightforward comparisons between different systems, for example between yeast and human cells (see Figure 1).

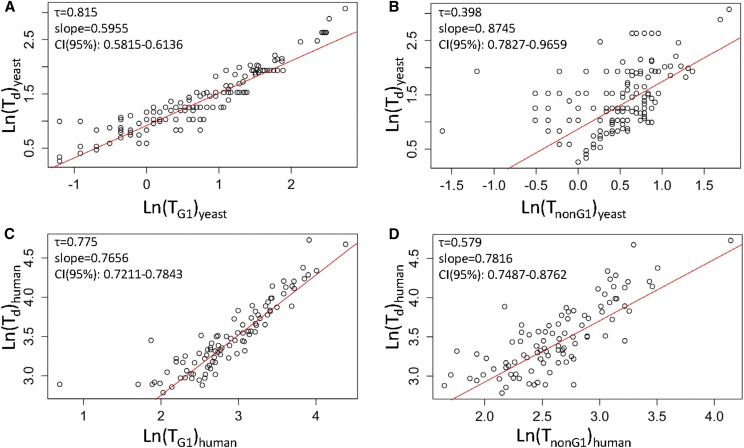
Figure 1.

Linking the length of the G1 phase with population doubling time. Scatter plots of T_G1 (A and C) or T_nonG1 (B and D) values on the x-axis, against T_d values (y-axis). All plots used the natural logarithms (Ln) of the values for yeast (A and B) and human (C and D) cells from Tables S1 and S2, respectively. The Kendall’s (τ) rank correlation coefficient is shown in each case. In red are regression lines of the Siegel repeated medians. The slope and the associated 95% C.I.s of the linear model are shown in each case. Additional statistical parameters associated with these plots are shown in Table 1.

For yeast, the data we collected (Table S1) were from wild-type strains from various backgrounds, except in the few cases where they carried temperature-sensitive alleles, such as cdc mutations (Jagadish and Carter 1977), to estimate the length of the G1 phase upon transfer to the nonpermissive temperature. The methods used to calculate the fraction of G1 cells included: measurements of the DNA content of the cells by flow cytometry (Slater et al. 1977; Johnston et al. 1980; Guo et al. 2004; Brauer et al. 2008; Henry et al. 2010); budding (Tyson et al. 1979; Rivin and Fangman 1980), sensitivity to cell cycle arrest before DNA replication by pheromone (Hartwell and Unger 1977; Jagadish and Carter 1977), or cdc (Jagadish and Carter 1977) mutations. In this study, to obtain the fraction of G1 cells (e.g., see Figure 3 and Figure 4), we used DNA content measurements by flow cytometry, as described previously (Hoose et al. 2012, 2013).

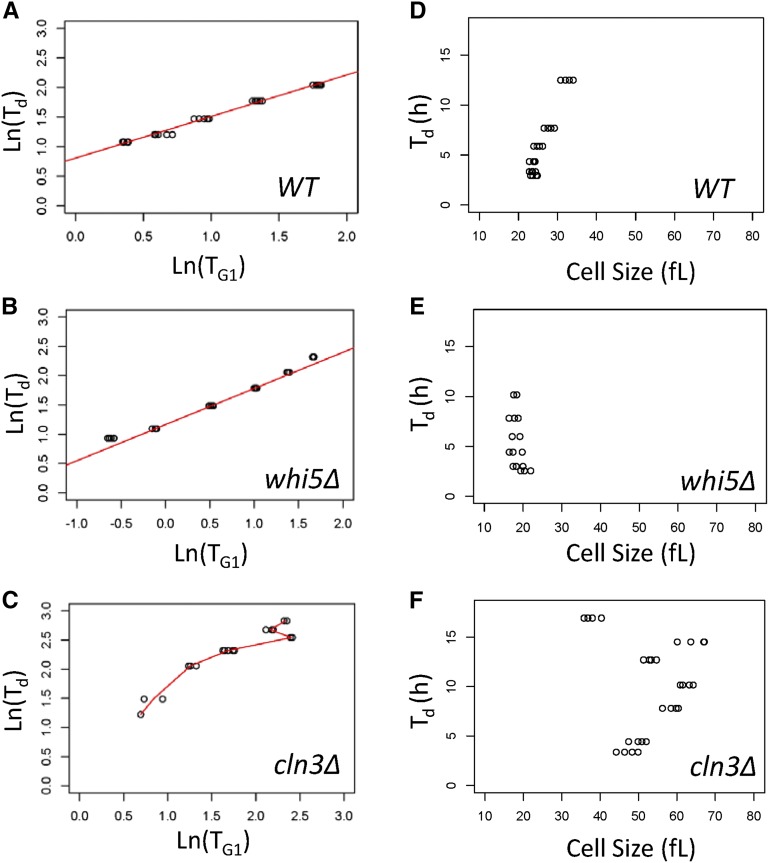
Figure 3.

Cln3p, but not Whi5p, imposes the proper relationship between T_G1 and T_d. Scatter plots of T_G1 values on the x-axis against T_d values (y-axis). All plots used the natural logarithms (Ln) of the values for wild-type (WT) (A), whi5∆ (B), or cln3∆ (C) cells, sampled from chemostat cultures several times at each dilution rate, as indicated. For WT and whi5∆ cells, regression lines of the Siegel repeated medians are in red and the slope of the linear models are shown (additional statistical parameters are in Table 1). For cln3∆ cells, the red line shown simply connects the average values at each dilution rate. There is no regression line because the relationship between T_d and T_G1 breaks down, especially at longer generation times. Scatter plots of the relationship of cell size and T_d in WT (D) or cells lacking Whip5 (E) or Cln3p (F), with cell size values (x-axis) plotted against T_d (y-axis) from the same cultures described in (A–C). All the strains were in the BY4741 background (see Materials and Methods).

For human cells, earlier studies employed ³H-thymidine pulses or division waves after thymidine block (Baserga 1985). The doubling times of the NCI-60 human cancer cell lines that we included in Table S2 are known (Ross et al. 2000; Scherf et al. 2000; Polymenis 2017), but there was no quantitative cell cycle data for most of the cell lines. However, images of DNA content profiles for the NCI-60 panel, albeit with no quantification, have been published (Garner and Eastman 2011). We requested and obtained high-resolution files of these images from Alan Eastman (Geisel School of Medicine, Dartmouth College). From the entire DNA content histogram, to quantify the fraction of cells in G1, we used imaging software to measure the area on the left side of the G1 peak (from peak to valley) and multiplied this area by two, as has been described previously (Johnston et al. 1980). This approach avoids complications from heavy right-side tails due to S phase cells and yields an acceptable estimate of the relative G1 length as a fraction of total cell cycle time. We then combined these values with all others available from human cells, cancerous and normal (Sisken and Kinosita 1961; Defendi and Manson 1963; Lennartz and Maurer 1964; Aoki and Moore 1970; Baserga 1985; Kumei et al. 1989; Brons et al. 1992; Luciani et al. 2001; Hahn et al. 2009), to compile a data set of 96 values for G1 length (T_G1) and doubling time (T_d) for human cells, shown in Table S2.

Estimates of G1 length

The values we show in Tables S1 and S2 were obtained from studies reporting on the relative duration of the G1 phase. To estimate the absolute length of the G1 phase, T_G1, we multiplied the relative G1 length by T_d (Tables S1 and S2). This simple equation is the appropriate one to use with chemostat data when as many cells are removed as are being produced in the culture (Hoffman 1949). Subtracting T_G1 from T_d yields the duration of the rest of the cell cycle phases (T_nonG1). For nonchemostat data, other more elaborate equations could be used, especially for the asymmetric patterns of division of budding yeast (Hartwell and Unger 1977; Johnston et al. 1980). However, for simplicity and ease of comparison across systems, we uniformly applied the simple equation mentioned above. Furthermore, inaccuracies in the absolute values of T_G1 may only affect the intercept of the linear relationship between T_d and T_G1, but not the slope that describes the fundamental scaling between T_d and T_G1, or any of our conclusions. Indeed, when we plotted in the same manner as in Figure 1 only the chemostat values in Table S1 (94 data points), the slope of LnT_d $\propto$ LnT_G1 was 0.6107. For the remaining, nonchemostat values (55 data points), the slope of LnT_d $\propto$ LnT_G1 was 0.6074.

Lastly, a limitation of the nonchemostat data in yeast and all the data from human cells is that it is assumed that cell death contributes negligibly to the doubling time of the population. This assumption is reasonable in yeast because young cells vastly outnumber older ones approaching senescence. However, it may be of concern in mammalian culture systems. Hence, our data with human cells should be interpreted with caution, because the fraction of growing cells in the culture may be significantly lower than one. Also, although we are looking at trends that seemingly hold across a multitude of human cell types, the data were overwhelmingly derived from cancer cell lines, which in many cases have altered cell cycles.

Chemostat cultures

The experiments were done using a New Brunswick BioFlo (BF-110) reactor with a working volume of 880 ml. The reactor was run at room temperature, as described earlier (Henry et al. 2010). In each experiment and at each dilution rate, the reactor was sampled several times to measure protein levels by immunoblots, the DNA content with flow cytometry, and the cell size and cell density of the culture using a Beckman Z2 channelyzer (Henry et al. 2010; Hoose et al. 2012), as indicated. We measured the cell density at every sampling to ensure that we never reached “wash-out” conditions at the high dilution rates. In every experiment, the cell density remained > 1E+07 cells/ml, and did not vary more than threefold between the lowest and highest dilution rates.

Protein surveillance

Proteins were resolved onto 4–12% Tris-glycine gels (catalog number: XP04125BOX; Thermo Scientific). Cln3p-(Myc)₁₃ was detected with an anti-Myc antibody (catalog number: ab13836; Abcam). All other procedures for TAP-tagged protein detection, extract preparation for immunoblots, and their analysis have been described elsewhere (Blank et al. 2017).

Statistical analysis

Data were analyzed and displayed with R language packages. All R functions, the corresponding packages, and their use are listed in Table S3. To build the linear models we described using the values for the yeast (Table S1) and human (Table S2) data sets, we first examined if the assumptions for building simple, linear parametric models were satisfied. The diagnostic residual plots evaluating whether the errors were independent of each other, normally distributed around a mean of zero and equal variance, are shown in Figure S2. In both the yeast and human data sets, the existence of a few outlier points appeared to violate the necessary assumptions [Figure S2; P < 0.05 for assessment of the assumptions using the global test on four d.f. (Peña and Slate 2006)]. Hence, we opted for nonparametric, robust linear regression models based on Siegel repeated medians (Table 1). For the meta-analysis of cell size data (see Figure 2) we used the metafor R language package (Viechtbauer 2010). Briefly, the correlation coefficients from each study were transformed using Fisher’s z transformation. An unbiased random effects analysis, as opposed to a fixed effects one, was then performed using this index, and the summary values were converted back to correlations and displayed as such with “forest” plots (Figure 2 and Table S3).

Table 1. Statistical parameters of linear relationships.

Variables		Coefficientsa		Confidence intervals (level = 0.95)				τb	rc
Y	X	Intercept	Slope	Intercept		Slope
(Td)yeast	(TG1)yeast	1.429	1.091	1.3817	1.5049	1.0598	1.1133	0.815	0.938
(Td)yeast	(TnonG1)yeast	0.36	1.75	0.1900	0.8712	1.6244	2.0278	0.398	0.532
Ln(Td)yeast	Ln(TG1)yeast	0.9168	0.5955	0.9047	0.9418	0.5815	0.6136	0.815	0.938
Ln(Td)yeast	Ln(TnonG1)yeast	0.8682	0.8745	0.7764	0.9128	0.7827	0.9659	0.398	0.532
(Td)human	(TG1)human	7.558	1.279	6.8401	8.5971	1.2433	1.3339	0.775	0.921
(Td)human	(TnonG1)human	6.838	1.738	3.6212	7.3905	1.6919	2.0059	0.579	0.762
Ln(Td)human	Ln(TG1)human	1.2202	0.7656	1.1770	1.3663	0.7211	0.7843	0.775	0.921
Ln(Td)human	Ln(TnonG1)human	1.3608	0.7816	1.1374	1.4674	0.7487	0.8762	0.579	0.762
Ln(Td)whi5Δd	Ln(TG1)whi5Δd	1.1654	0.6166	1.1613	1.1910	0.6083	0.6362	0.928	0.987
Ln(Td)HB94/7e	Ln(TG1)HB94/7	0.9691	0.6848	0.9031	0.9843	0.6588	0.7461	0.765	0.918
Ln(Td)HB104f	Ln(TG1)HB104	0.9913	0.7048	0.9902	1.0074	0.6930	0.7120	0.934	0.989

T_d, population doubling time; T_G1, length of the G1 phase; T_nonG1, length of the cell cycle excluding G1 phase; LN, natural logarithm.

^aFrom the linear fit of Siegel repeated medians.

^bKendall’s (τ) rank correlation coefficient.

^cSpearman’s (r) rank correlation coefficient.

^dThe values for whi5Δ cells were from the experiment shown in Figure 3B.

^eThe values for HB94/7 cells (CLN3-13MYC, WHI5-TAP) were from the experiments in Figure 4A.

^fThe values for HB104 cells (A-315T-CLN3-13MYC, WHI5-TAP) were from the experiments in Figure 4B.

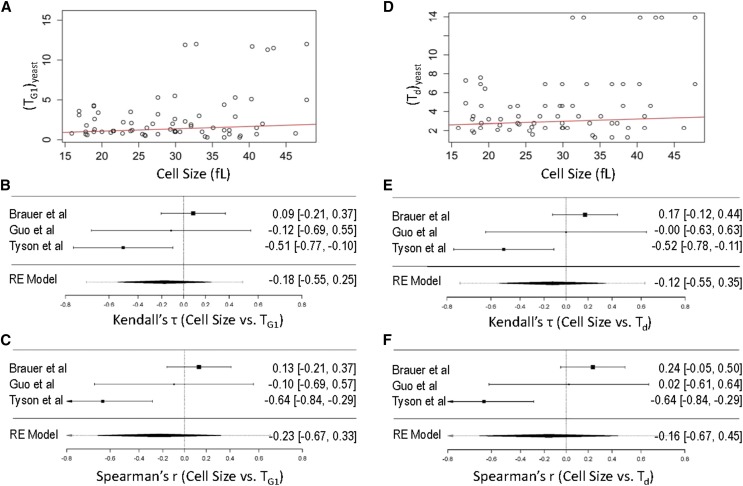
Figure 2.

Cell size does not correlate with T_d or T_G1 in yeast. Scatter plots of cell size values (x-axis) against T_d (A) or T_G1 (D) values (y-axis) from the data shown in Table S1. In red are regression lines of the Siegel repeated medians. Forest plots of the measure of effect for each of the studies included in the analysis (Tyson et al. 1979; Guo et al. 2004; Brauer et al. 2008), based on the Kendall’s (τ) rank correlation coefficients (B and E) or Spearman’s (r) rank correlation coefficients (C and F), are shown in each case, for cell size vs. T_G1 (B and C) and cell size vs. T_d (E and F). The C.I.s from each study are shown in parentheses and represented by horizontal whisker lines. In the studies in which the confidence intervals overlap with the vertical line at the 0 point on the x-axis, their effect sizes do not differ from no effect. The meta-analyzed measure of the effect is shown at the bottom of each plot, based on random effects (RE) models.

Data availability

Strains and plasmids are available upon request. The authors affirm that all data necessary for confirming the conclusions of the article are present within the article, figures, and tables. Figure S1 shows goodness-of-fit plots for lognormal distribution of yeast and human T_G1 values. Figure S2 shows diagnostic plots of simple linear regression models for T_d and T_G1 values of yeast and human cells. Figure S3 shows additional chemostat experiments with whi5∆ and cln3∆ cells. Table S1 lists all the cell cycle values for yeast cells from the literature. Table S2 lists all the cell cycle values for human cells from the literature. Table S3 lists all R functions, the corresponding packages, and their use. File S1 contains all raw immunoblot images generated and used in this study. Supplemental material available at Figshare: https://figshare.com/articles/Supplemental_Data/7011275.

Results

Rationale

The rationale for the experiments we describe was the following. First, use all the available values from the literature to derive a quantitative relationship of the population doubling time (T_d) as a function of the time eukaryotic cells spend in the G1 phase of the cell cycle (T_G1) (Figure 1). Second, based on the same data sets and analyses, examine if cell size is also related to T_d or T_G1, because cell size is often used as a proxy for the control of cell division by nutrients (Figure 2). Third, use the linear relationship linking T_d and T_G1 as a metric to evaluate the contributions of Whi5p and Cln3p, two proteins that govern the G1/S transition in budding yeast (Figure 3). Fourth, if Cln3p or Whi5p impinges on the relationship between T_d and T_G1, then provide a mechanistic understanding of its role (Figure 4).

T_G1 values are distributed lognormally, consistent with exponential patterns of growth

We compiled the available values for T_d and T_G1 from the literature for budding yeast (Table S1) and human (Table S2) cells (see Materials and Methods). With the data set of T_G1 values at hand, we next examined their distribution. Knowing how the T_G1 values are distributed will inform how to better model T_G1 against T_d and offer some insight into the processes that determine G1 length. We found that T_G1 values were not normally distributed for yeast (P = 4.434E−14, Shapiro–Wilk test) or human cells (P = 1.039E−07, Shapiro–Wilk test). Instead, T_G1 values fit a lognormal distribution better. For example, for yeast T_G1 values, the Anderson–Darling statistic was the lowest for the lognormal distribution (0.347) compared to other distributions (Weibull: 1.693; γ: 1.521; exponential: 2.462). As expected for lognormal distributions, log-transformed values of T_G1 were normally distributed for yeast (Figure S1, A–D, P = 0.1871, Shapiro–Wilk test) and human cells (Figure S1, E–H, P = 0.3099, Shapiro–Wilk test). The apparent lognormal distribution of T_G1 values is consistent with a multiplicative process of many, positive, independent random variables that determine the G1 length (Koch 1966). Lognormal distributions are very common in biological growth processes (Mosimann and Campbell 1988). In cell proliferation, lognormality has been proposed to reflect exponential patterns of growth in mass. Despite fluctuations in the growth rate constant, the growth of the overwhelming majority of cellular components is influenced similarly, leading to lognormality (Koch and Schaechter 1962; Koch 1966). In budding yeast and other cell types, there is evidence for exponential patterns of protein synthesis (Elliott and McLaughlin 1978; Di Talia et al. 2007; Tzur et al. 2009) and increase in mass in the cell cycle (Bryan et al. 2012; Son et al. 2012). Such considerations accommodate the lognormality of T_G1 values we describe here.

Strong association between T_G1 and T_d, but non-G1 phases also expand in lower proliferation rates

To test for association between T_G1 and T_d, we used the distribution-free Spearman’s and Kendall’s tests for independence based on ranks. We used these nonparametric, distribution-free tests because of the existence of outliers even in log-transformed T_G1 values (e.g., see Figure S1). The high values (> 0.75) of the rank correlation coefficients (τ for Kendall’s and r for Spearman’s; see Table 1) show a strong positive association between T_G1 and T_d, for both yeast (Figure 1A) and human (Figure 1C) cells. However, interestingly, the duration of the non-G1 phases (T_nonG1) of the cell cycle were also positively correlated with T_d (Figure 1, B and D and Table 1) in both organisms, albeit less so in yeast (τ = 0.398; Figure 1B) than in human cells (τ = 0.579; Figure 1D). Overall, our data document the strong association between T_G1 and T_d (Figure 1, A and C). Additionally, they suggest that growth requirements for cell division are not registered exclusively in G1, but also later in the cell cycle (see Figure 1, B and D), in agreement with observations from other groups (Anastasia et al. 2012; Ferrezuelo et al. 2012; Dowling et al. 2014; Soifer and Barkai 2014; Cerulus et al. 2016; Mayhew et al. 2017; Garmendia-Torres et al. 2018).

A scaling relationship between T_G1 and T_d

To estimate a predictive and quantitative relationship between T_G1 and T_d, we derived nonparametric, robust linear regression models using the Siegel repeated median estimates (Siegel 1982) (Figure 1 and Table 1; see also Materials and Methods). The intercepts of the linear T_G1 vs. T_d plots reflect the apparent minimum duration of the S+G2+M phases in yeast (1.4 hr; Table 1) and human (7.6 hr; Table 1) cells. The slopes in the linear relationships indicate how much T_d is affected by T_G1 or T_nonG1. For example, if non-G1 phases were not expanding in slower-proliferating cells, then one would expect a vertical line parallel to the y-axis in T_nonG1 vs. T_d plots. We noticed that the slope of the regression of T_G1 on T_d appeared to slightly differ between the yeast and human data sets (Figure 1 and Table 1). Applying the nonparametric Sen–Adichie test for parallelism confirmed that the difference in the slopes of the regression lines of T_G1 on T_d between yeast and human cells was statistically significant (V statistic = 7.324, P-value = 0.007). Although the T_G1 distributions themselves are lognormal, log-transformation is not necessary for any of our conclusions, since we used a nonparametric, ordinal-based analysis in all our statistical tests. Nonetheless, we display regression plots using log-transformed data to improve visualization, because data points appear more evenly on these graphs. Furthermore, log-transformed values are often incorporated in scaling relationships between the measured variables in the literature (Chan and Marshall 2010). The quantitative relationships that we identified linking T_G1 with T_d are significant because they provide a framework to interpret experimental perturbations in cell cycle progression and cell proliferation, as we will describe for yeast cells.

Nutrient-specific, but not growth rate-dependent, association between cell size and T_G1, or T_d

Control of cell size has frequently been used synonymously with growth control of G1 transit in the cell cycle, especially in budding yeast. Daughter cells of S. cerevisiae are born smaller than their mother is, and they will not initiate a new round of cell division until they reach a size characteristic of the culture medium. The rate at which daughter cells increase in volume has been reported to contribute to the size at which they will initiate a new round of cell division (Ferrezuelo et al. 2012). Note that unless indicated otherwise, here we use the term growth rate to describe the rate at which cells proliferate and not the rate at which they increase in size in a given cell cycle. As the cell cycle is prolonged in poor nutrients, it is also widely assumed that the cells get smaller [e.g., see figures 10–26 in Morgan (2007)]. To test the strength of the association between cell size and T_G1, or T_d, we combined the available data from previous studies (Tyson et al. 1979; Guo et al. 2004; Brauer et al. 2008; see Table S1). From such an unbiased but unweighted analysis (Figure 2, A and D), it appeared that the size of yeast cells was not significantly associated with T_d (P-value = 0.171, based on Kendall’s test; Figure 2A) or T_G1 (P-value = 0.2449, based on Kendall’s test; Figure 2D).

Unlike the strong association of T_G1 with T_d, which was consistent across studies (see Figure 1 and Materials and Methods), the association between cell size and T_G1, or T_d, appeared to vary among the relevant studies. Given the different number of samples analyzed in each study and their associated variance, we calculated the effect sizes from each study separately, based on the nonparametric Spearman’s and Kendall’s correlation coefficients. These study-specific correlation coefficients then served as the effect size index, to standardize the different studies and arrive at a summary correlation (Borenstein 2009). The results were visualized in typical forest plots (Figure 2, B, C, E, and F). A negative association between size and rates of cell proliferation, with cells getting smaller with larger T_d values, was only evident at a moderate level in batch cultures (τ = −0.52, r = −0.64; see Figure 2, E and F), where different nutrients were used to achieve different doubling times (Tyson et al. 1979). In contrast, in other studies (Guo et al. 2004; Brauer et al. 2008), which employed chemostats to alter the population doubling time independently of the limiting nutrient, there was no correlation between cell size and T_d, or T_G1 (Figure 2). Importantly, within these chemostat studies, cell size measurements were internally calibrated. Hence, the lack of any correlation between cell size and T_d, or T_G1 cannot be attributed to experimental variabilities of different studies incorporated in our meta-analysis of the literature. Lastly, the lack of a significant association between T_G1 and cell size agrees with a genome-wide survey of single-gene deletions (Hoose et al. 2012), which found no pattern of correlation between cell size and the relative duration of the G1 phase. Hence, although cell size can be modulated by changes in nutrient composition in yeast (Tyson et al. 1979; Soma et al. 2014; and others), our data suggest that it is more likely that these are nutrient-specific effects, not causally linked to changes in cell proliferation rates.

Cln3p, but not Whi5p, is required for the strong association between T_G1 and T_d

To understand how the relationship between the length of the G1 phase and doubling time is established in budding yeast, we next examined the role of the Cln3p and Whi5p proteins, which regulate the G1/S transition in this organism. It has been proposed that dilution of Whi5p as cells get bigger in G1 is the key event controlling the timing of the G1/S transition (Schmoller and Skotheim 2015; Schmoller et al. 2015). Since in cells proliferating at different rates there is not a significant correlation with cell size (Figure 2 and Table S1), it is not clear how the inhibitor dilution model would apply to the conditions we examined in this study. To our knowledge, the kinetics of cell cycle progression in cells lacking Cln3p or Whi5p have not been examined previously in steady-state cultures proliferating at different rates. To test the role of Cln3p and Whi5p in the relationship between T_G1 and T_d, we examined the cell cycle profile of cln3Δ or whi5∆ cells in continuous, steady-state chemostat cultures. We measured T_G1 in cln3∆ or whi5∆ cells from the DNA content of the cultures under glucose (0.08% ^w/_v) limitation and at different dilution rates (0.038–0.348 hr⁻¹; corresponding to T_d values between 18 and 2 hr, respectively). As expected, cells lacking Whi5p were very small (≈18 fl) and their size did not change significantly as a function of T_d (Figure 3E and Figure S3D). Furthermore, the intercept of the linear fit between the log-transformed T_d and T_G1 values of whi5Δ cells was significantly higher than the intercept of the linear fit of these parameters in wild-type cells (1.17 vs. 0.92; see Table 1), consistent with the shortened G1 phase of whi5Δ cells. The slope of the linear relationship between T_d and T_G1 in whi5∆ cells (Figure 3B) was similar to what we observed in the aggregate analysis of wild-type cells (Figure 1A and Table 1; Sen–Adichie V statistic = 1.775, P-value = 0.183), albeit slightly smaller than the slope of wild-type cells from a separate, independent experiment performed in this study [0.6723 in wild-type (Figure 3A) vs. 0.6166 in whi5∆ cells (Figure 3B)]. These data suggest that in different physiological states, and despite their shortened G1 phase and small size, whi5∆ cells nonetheless remain responsive to different environments, displaying minimal changes in their scaling of the expected proportional changes between T_d and T_G1.

In contrast, cells lacking Cln3p had an abnormal behavior. In three independent experiments (Figure 3C and Figure S3, B and C), T_G1 did not even have a straightforward linear relationship with T_d in cultures of cln3Δ cells. At shorter division times (T_d < 5 hr), the T_d and T_G1 values of cln3Δ cultures were related linearly, albeit with a higher slope (e.g., Figure S3C; slope = 0.7685). More importantly, in all three independent experiments, the linear relationship breaks down in slower-proliferating cln3Δ cultures (Figure 3C and Figure S3, B and C). Even when combining all data points from the individual experiments for each strain, we found that at all doubling times tested the linear relationship between T_d, and that T_G1 remains strong for whi5Δ cells (τ > 0.8, based on Kendall’s nonparametric test). The same is true for cln3Δ cells at values of LnT_d < 1.5 (corresponding to T_d values <4.5 hr). In contrast, the linear relationship between T_d and T_G1 is significantly weaker (τ < 0.5) for slower-proliferating cln3Δ cells (LnT_d > 1.5). These data suggest that Cln3p is more important than Whi5p for imposing the proper scaling relationship of T_d $\propto$T_G1 in wild-type cells.

Cln3p levels are strongly and positively associated with cell proliferation rates

Given the important role of Cln3p in establishing the proper relationship between T_d and T_G1 (Figure 3 and Figure S3), we sought to measure the levels of Cln3p and Whi5p as a function of T_d. There are no reports of the steady-state levels of Cln3p or Whi5p in cell populations proliferating at different rates in chemostats. To measure Whi5p and Cln3p levels from the same cells, we generated a strain that carries WHI5-TAP and CLN3-13MYC alleles, providing the only source of these gene products in the cells, expressed from their endogenous chromosomal locations (Figure 4A, see Materials and Methods). The expressed proteins were epitope-tagged, but otherwise unmutated, wild-type Whi5p-TAP and Cln3p-(Myc)₁₃. These cells were then cultured in continuous, steady-state chemostat cultures under glucose (0.08% ^w/_v) or leucine (0.0015% ^w/_v) limitation. Although the CLN3-13MYC allele provides the means for reliable detection of otherwise wild-type Cln3p, it is known to be slightly hypermorphic, stabilizing the Cln3p protein somewhat and shortening the G1 phase of the cell cycle (Thorburn et al. 2013). Indeed, the intercept of the linear fit between the log-transformed T_d and T_G1 values of this strain (HB94; WHI5-TAP and CLN3-13MYC) was slightly higher than the intercept of the linear fit of these parameters in wild-type cells (0.97 vs. 0.92; see Table 1), consistent with a shortened G1 phase. The slope of the linear relationship between the log-transformed values of T_d and T_G1 was increased somewhat for these cells compared to the aggregate analysis of wild-type cells (0.68 vs. 0.6; see Table 1). Importantly, these cells still displayed a strong, linear, positive association between T_d and T_G1 (τ = 0.77; r = 0.92; see Table 1) at all dilution rates we tested. Hence, we concluded that the relationship between T_d and T_G1 was only minimally affected in this strain, and we proceeded to quantify the levels of both Whi5p-TAP and Cln3p-(Myc)₁₃ from separate chemostat experiments under glucose or leucine limitation, each run at ≥ 5 dilution rates (Figure 4; see Materials and Methods).

The levels of Whi5p-TAP were not increased in slower-proliferating cells (Figure 4, A and B). Previously, (Liu et al. 2015) reported that Whi5p abundance increases around threefold in cells growing in poorer carbon sources, although this was not seen in a more recent study by Dorsey et al. (2018). In any case, several variables were different between the Liu et al. (2015) study and ours, which could account for the disagreement in the findings. First, different epitope-tagged alleles were used (WHI5-tdTomato vs. WHI5-TAP). Second, different detection methods were applied (fluorescence live cell imaging vs. immunoblots). Third, Liu et al. (2015) used cells in the W303 background, which are larger than cells of the BY background that we use here, possibly leading to differences in cell size regulation. Fourth, and most significantly, nutrient-specific effects could not be separated from growth rate-specific ones in Liu et al. (2015). As we discussed earlier (see Figure 2), chemostats provide the only experimental approach for properly studying how rates of cell proliferation may affect a given output, separately from any effects unique to particular nutrients.

We observed a significant and disproportionate reduction of Cln3p-(Myc)₁₃ levels in slower-proliferating cells (Figure 4, A and B). With Cln3p-(Myc)₁₃ levels normalized against the total cellular protein content, the fastest-proliferating populations had > 10-fold higher levels of Cln3p-(Myc)₁₃ compared to the slowest-proliferating cells (Figure 4, A and B). Furthermore, because these estimates rely on the hypermorphic CLN3-13MYC allele, which produces a slightly stabilized Cln3p protein (Thorburn et al. 2013), the dynamic range of Cln3p levels as a function of doubling time is likely even broader.

A uORF in CLN3 adjusts the levels of Cln3p at different cell proliferation rates

What is the mechanism that underpins the growth-dependent control of Cln3p abundance? We had predicted that a uORF in CLN3 could inhibit its translational efficiency in poor media disproportionately (Polymenis and Schmidt 1997). However, predictions of a growth-dependent role of the uORF had not been accompanied with measurements of Cln3p levels. A kinetic model of protein synthesis (Lodish 1974) forecasts that removing the uORF would derepress synthesis of Cln3p in slowly dividing cells when the ribosome content of the cell is low. In contrast, removing the CLN3 uORF would have minimal effects in cells that proliferate quickly when the ribosome content is high. To test this model, we introduced an A-315T substitution that mutates the start codon of the uORF in CLN3 without affecting CLN3 mRNA levels (Polymenis and Schmidt 1997), in the strain that expresses otherwise wild-type Whi5p-TAP and Cln3p-(Myc)₁₃ (see Materials and Methods). Note also that in chemostat conditions very similar to the ones we used here, the levels of wild-type CLN3 mRNA do not change significantly as a function of growth rate (Brauer et al. 2008).

The effects of the uORF were evident in slower-proliferating cultures (T_d > 4 hr), where the dynamic range of Cln3p levels was much narrower (three–fourfold) in A-315T cells, very different from the range of Cln3p levels (10-fold) in their wild-type counterparts at these longer doubling times (P = 0.03648, based on the nonparametric Kolmogorov–Smirnov test), and indistinguishable from the range of Whi5p levels (Figure 4, A and B and File S1). We note that although the range of Cln3p levels is narrower in slower-proliferating CLN3 uORF mutant cells (Figure 4), it is not flattened, arguing for additional mechanisms that could adjust the levels of Cln3p at different growth rates. Nonetheless, an independent piece of functional evidence further strengthened a growth-dependent role of the CLN3 uORF. A hallmark phenotypic readout of gain-of-function CLN3 alleles is a reduction in cell size (Nash et al. 1988). Cells that lack the CLN3 uORF were smaller than their wild-type counterparts were, and this effect was T_d-dependent (see Figure 4, C and D). Especially in leucine-limited cells, which displayed pronounced enlargement as they proliferated slower, removing the CLN3 uORF reduced their size substantially (Figure 4D). These results are consistent with a derepression of Cln3p synthesis upon removal of the CLN3 uORF.

These data argue that translational control contributes to the disproportionate reduction of Cln3p levels as a function of T_d. Note also that loss of Cln3p severely perturbs the linear relationship between T_d and T_G1 (Figure 3 and Figure S3). In summary, our results underscore the critical role of the G1 cyclin Cln3p in the physiological coupling between growth and division.

Discussion

The scaling relationships between G1 length and population time in yeast and human cells that we report are significant for several reasons. First, if the duration of G1 is estimated, they allow predictions of proliferation rates, which could be useful in diverse settings, such as in tissues at an organismal level. Second, they serve as benchmarks against which the effects of genetic or other perturbations can be evaluated, as we demonstrated for Whi5p and Cln3p, two cell cycle regulators in yeast. Third, scaling relationships of cellular physiology may ultimately point to general, physical mechanisms that organize life at the cellular level. In the next paragraphs, we discuss our findings in relation to current models of how cell division is controlled by cellular biosynthetic capacity, with emphasis on the roles of Whi5p and Cln3p.

What is the context of this study in relation to others?

Our results pertain to cell cycle kinetics of steady-state cultures that proliferate at different rates, not to cell cycle adjustments immediately after nutrient shifts (Tokiwa et al. 1994; Leitao and Kellogg 2017). We also did not examine G1 progression in a particular cell cycle, where small daughter cells will not initiate a new round of cell division until they reach a size characteristic of the culture medium (Hartwell and Unger 1977; Johnston et al. 1977). Hence, the scaling of G1 duration between populations with different doubling times may not necessarily be controlled by the same mechanism that controls how G1 duration is regulated to maintain size homeostasis within a population of cells that proliferates at a given rate. This interpretation is consistent with the findings that cell size is not associated with rates of cell proliferation (Figure 2), at least in experimental settings of steady-state chemostat cultures, which separate nutrient-specific effects from the impact of different rates of cell proliferation. For example, note the very different sizes of cells in glucose- vs. leucine-limited cultures at the same dilution rate (compare Figure 4, C and D), offering yet another demonstration of how particular nutrients may affect cell size independently of any changes in rates of cell proliferation. Furthermore, in leucine-limited cultures, the cells were not only bigger than cells in glucose-limited chemostats at all dilution rates tested, but they also got even bigger as they divided slower (Figure 4). These observations argue against the widely held assumptions that cells get smaller the slower they proliferate. Instead, they support the notion that nutrient effects on cell size may be particular to specific nutrients, and not associated with changes in rates of cell proliferation.

How do our results mesh with models of G1 control?

As we noted above, our data were from cells dividing at different rates, which was not addressed in the Whi5p dilution model of Schmoller et al. (2015). Hence, the two studies are not directly comparable. However, the Whi5p dilution model was constructed on the basis that while Whi5p levels were disproportionately lower than expected from cell growth, Cln3p levels were roughly constant and proportional to the increase in size from birth to START (Schmoller et al. 2015). Given the disproportionate dependency of Cln3p levels on cell proliferation rates that we reported here and had predicted earlier (Polymenis and Schmidt 1997), could the uORF-mediated translational control of CLN3 affect Cln3p synthesis in the G1 phase from birth to START? We think this is unlikely because the uORF-mediated translational control we described operates when the concentration of active ribosomes in the cell changes (Lodish 1974), for example in poor vs. rich nutrients. Hence, while such translational control mechanisms provide excellent conduits to disproportionately alter gene expression and communicate growth-related inputs to downstream mRNA targets, to our knowledge, there is no report of cell cycle-dependent changes in ribosome content. Other mechanisms, not due to changes in the translational efficiency of CLN3, may contribute to significant, periodic changes in Cln3p abundance in G1, within a given cell cycle.

There are conflicting reports in the literature about whether Cln3p cycles in the cell cycle. Cln3p is of such low abundance that it could not be properly measured in the single-cell microscopy methods of Schmoller et al. (2015), because mutant CLN3 alleles had to be used, producing extremely stabilized and dysfunctional Cln3p protein that accumulates at very high, but nonphysiological, levels so that it can be visible with microscopy. The initial report claiming that Cln3p-HA levels were constant in the cell cycle did not interrogate the early G1 phase (Tyers et al. 1993). In that report, although early G1, small (25 fl), elutriated daughter cells were collected, Cln3p levels were not measured until much later in G1 [at 35 fl, when by 40 fl, 25% of the cells were already budded in that experiment; see figure 4 in Tyers et al. (1993)]. Based on that result, it had been assumed for decades that Cln3p levels were constant in the cell cycle. However, two independent studies by the Amon (Thorburn et al. 2013) and Kellogg (Zapata et al. 2014) laboratories recently assayed elutriated synchronous cells carrying epitope-tagged, but otherwise wild-type, CLN3 alleles. Both studies showed that Cln3p levels change > 10-fold in G1. Cln3p is absent in early G1 cells, while it rises dramatically before START. We also used the same CLN3-13MYC allele to monitor Cln3p levels at different rates of cell proliferation (see Figure 4). The CLN3-13MYC allele is known to produce a slightly stabilized Cln3p protein (Thorburn et al. 2013). Note that, on the face of the slight stabilization of the Cln3p-(Myc)₁₃, the dynamic range of Cln3p levels as a function of growth rate that we report is likely even broader, not narrower. Hence, our conclusions are strengthened, not weakened, by the slight stabilization of the Cln3p-Myc we used. For the same reasons, the changes in Cln3p levels in G1 observed previously (Thorburn et al. 2013; Zapata et al. 2014) are likely even greater than indicated in these reports.

Overall, although a twofold dilution of Whi5p is observed in G1 (Schmoller et al. 2015), the changes in Cln3p levels are likely more pronounced (Thorburn et al. 2013; Zapata et al. 2014), through transcriptional (Zapata et al. 2014) or other mechanisms. In this context, it is perhaps unsurprising that we found Cln3p to be more important than Whi5p in the relationship between T_d and T_G1. However, it is important to stress that any changes of Cln3p levels in G1 do not affect the key aspect of the inhibitor dilution model, namely that Whi5p levels are reduced by cell growth. Hence, we may be dealing with a more complex, “mixed” model of inhibitor dilution and activator accumulation. It is possible that the levels of additional proteins may behave analogously to Cln3p and Whi5p, contributing to a broader network of factors whose antagonistic relationships control the timing of initiation of cell division. Regardless of the identity of those proteins, in yeast and other models, the fundamental relationship between T_G1 and T_d we describe in this report will serve as a useful metric to evaluate the role of these protein(s) in the control of cell division by growth inputs.