Revisiting the structure of low-Mach number, low-beta, quasi-perpendicular shocks

Abstract

A study of the structure of 145 low-Mach number (M ≤ 3), low-beta (β ≤ 1), quasi-perpendicular interplanetary collisionless shock waves observed by the Wind spacecraft has provided strong evidence that these shocks have large-amplitude whistler precursors. The common occurrence and large amplitudes of the precursors raise doubts about the standard assumption that such shocks can be classified as laminar structures. This directly contradicts standard models. In 113 of the 145 shocks (~78%), we observe clear evidence of magnetosonic-whistler precursor fluctuations with frequencies ~0.1–7 Hz. We find no dependence on the upstream plasma beta, or any other shock parameter, for the presence or absence of precursors. The majority (~66%) of the precursors propagate at ≤45° with respect to the upstream average magnetic field and most (~87%) propagate ≥30° from the shock normal vector. Further, most (~79%) of the waves propagate at least 20° from the coplanarity plane. The peak-to-peak wave amplitudes (δB_pk-pk) are large with a range of maximum values for the 113 precursors of ~0.4–13 nT with an average of ~2 nT. When we normalize the wave amplitudes to the upstream averaged magnetic field and the shock ramp amplitude, we find average values of ~40% and ~220%, respectively.

Plain Language Summary

We present new results that suggest that the magnetic structure of collisionless shock waves is not a smooth, step-like transition but rather riddled with large-amplitude waves as large or larger than the shock itself. These results have implications for the dynamics of weak shocks from propagation and evolution to particle acceleration and heating.

1. Background and Motivation

The macroscopic dynamics of collisionless shock waves have long been thought to be regulated by the upstream fast mode Mach number, 〈M_f〉_up, shock normal angle, θ_Bn—the angle between the average upstream quasi-static magnetic field, 〈B_o〉_up and the shock normal vector, $\widehat{\mathbf{n}}$—and the average upstream plasma beta, 〈β〉_up—ratio of thermal to magnetic energy density [e.g, Sagdeev, 1966; Coroniti, 1970a; Tidman and Krall, 1971; Kennel et al., 1985]. By dynamics we are referring to the evolution, propagation, and thickness of the shock ramp—the spatial gradient scale length of the magnetic transition region.

Collisionless shock waves are generally separated into multiple categories including quasi-perpendicular (θ_Bn ≥ 45°) and quasi-parallel (θ_Bn < 45°); low (〈M_f〉_up ≲ 2.5) and high (〈M_f〉_up > 2.5) Mach number; and low (〈β〉_up ≤ 0.5–1.0) and high (〈β〉_up > 1.0) beta shocks [e.g., Sagdeev, 1966; Coroniti, 1970a; Tidman and Krall, 1971; Kennel et al., 1985]. The physical significance of the categories lies in the different predicted energy dissipation mechanisms—the processes by which the shock converts bulk flow kinetic energy into other forms like heating and/or accelerating particles.

Early theoretical models described quasi-perpendicular collisionless shock waves as dispersive nonlinear wave trains forming from an initial step-like function in the magnetic field [e.g., Galeev and Karpman, 1963; Karpman, 1964]. These types of shocks are said to be regulated by dispersive radiation [e.g., Decker and Robson, 1972; Galeev and Karpman, 1963; Mellott and Greenstadt, 1984; Morton, 1964; Sagdeev, 1966; Stringer, 1963; Tidman and Northrop, 1968], which has been supported by some recent observations [e.g., Sundkvist et al., 2012; Wilson III et al., 2009, 2012, 2014a, 2014b]. Shocks that dissipate energy through dispersive radiation do so by emitting/radiating a magnetosonic whistler precursor—a right-hand polarized and obliquely propagating (both with respect to the quasi-static magnetic field, B_o) electromagnetic wave that is compressive (i.e., the magnetic fluctuations, δB, oscillate in phase with density fluctuations, δn). Whistler mode waves are dispersive—phase speed depends upon the frequency/wavenumber—which results in a train of coherent oscillations extending into the upstream with the highest (shortest) frequency(wave length) farthest away from the ramp [e.g., see Wilson, 2016, and references therein]. We will refer to these modes as whistler precursors or just precursors for brevity. In observational studies, one often observes both the decreasing (with decreasing distance to shock ramp) and constant frequency whistler precursors. The precursors with nearly constant frequency have been shown to be those that have a group velocity sufficiently large to allow them to escape the shock into the upstream [e.g., Orlowski et al., 1990; Orlowski and Russell, 1991]. Thus, the dispersive precursors are generally observed closer to the shock ramp than the nearly constant frequency precursors.

As previously mentioned, dissipation mechanisms control the shock structure which means that the detailed properties of precursors can be important. When investigating the properties of precursors, two propagation angles are computed; one between the wave vector, $\widehat{\mathbf{k}}$, and B_o, θ_kB, and one between $\widehat{\mathbf{k}}$ and $\widehat{\mathbf{n}}$ (shock normal vector), θ_kn. The former angle is important for interactions between the waves and particles while the latter is relevant for its interaction with the shock [e.g., Biskamp, 1973; Decker and Robson, 1972; Sagdeev, 1966; Tidman and Krall, 1971]. Most precursors observed at quasi-perpendicular interplanetary shocks satisfy θ_kB ≲ 30°–45° and θ_kn ≳ 20°–45° [e.g., Aguilar-Rodriguez et al., 2011; Blanco-Cano et al., 2016; Kajdič et al., 2012; Ramírez Vélez et al., 2012; Wilson III et al., 2009]. Similar results have been found for quasi-perpendicular bow shocks [see, e.g., Wilson, 2016, and references therein].

Some other observations, however, show a different magnetic profile exhibiting a sharp, almost step function ramp, which was first described in theoretical models as dissipative transition rather than a dispersive one [e.g., Galeev, 1976; Sagdeev, 1966]. Dissipative shocks are regulated by wave-particle interactions [e.g., Coroniti, 1970a; Gary, 1981; Papadopoulos, 1985; Sagdeev, 1966], which has also been supported by recent observations [e.g., Breneman et al., 2013; Wilson III et al., 2007,2010,2012,2014a, 2014b]. The question then becomes which, if either, dominates and ultimately controls the macroscopic structure of low-Mach number (〈M_f〉_up ≲ 2.5), quasi-perpendicular collisionless shocks.

Early work further parameterized the magnetic profiles of collisionless shocks into the following categories: “laminar,” “quasi-laminar,” “turbulent,” and “quasi-turbulent” based upon the upstream average values of 〈M_f〉_up and 〈β〉_up [e.g., see Greenstadt, 1985; Mellott, 1985, and references therein]. The terms laminar and turbulent are meant to be intuitive in their descriptiveness, but it is important to note that a laminar shock may still exhibit upstream fluctuations [e.g., Gary and Mellott, 1985]. The original use of the term laminar implied that coherent, linear, or nonlinear oscillations could be used to describe the profile of the shock without resorting to turbulence theory [e.g., Galeev and Karpman, 1963; Karpman, 1964; Sagdeev, 1966]. However, in practice the term has become synonymous with a step function-like magnetic profile where the transition from upstream to downstream occurs almost entirely within the shock ramp.

The separation between laminar and turbulent generally fell into the regime where the former applied to low-Mach number (〈M_f〉_up ≲ 2–3), low-beta (〈β〉_up ≤ 0.5–1.0), quasi-perpendicular shocks based on theory [e.g., Biskamp, 1973; Galeev and Karpman, 1963; Karpman, 1964; Sagdeev, 1966; Tidman and Krall, 1971], and supported by observations [e.g., Farris et al., 1993, 1973a; Greenstadt et al., 1975; Mellott and Greenstadt, 1984; Mellott, 1985]. In contrast, the latter applied to high 〈β〉_up (≳1.0) and/or high 〈M_f〉_up (≳3) based on theory [e.g., Coroniti, 1970b; Formisano and Hedgecock, 1973a, 1973b, 1975; Kennel and Sagdeev, 1967a, 1967b; Sagdeev, 1966] and again supported by observations [e.g., Formisano and Hedgecock, 1973a, 1973b; Formisano et al., 1975; Kennel and Sagdeev, 1967a, 1967b; Wilson III et al., 2012]. Given that some early observations supported this laminar-turbulent separation based upon 〈M_f〉_up and 〈β〉_up, it was assumed that low-Mach number, low-beta, quasi-perpendicular shocks were simple and well-understood phenomena. Thus, most subsequent work has focused on the high 〈M_f〉_up and/or high 〈β〉_up shocks.

However, some recent observations showed that precursor amplitudes, δB, can be comparable to the shock ramp amplitude, ΔΒ (= 〈B_o〉_dn - 〈B_o〉_up) [e.g., Goncharov et al., 2014; Wilson III et al., 2009, 2012, 2014a, 2014b]. A few studies even showed that precursors at interplanetary shocks can cause strong heating and stochastic acceleration in ions and electrons in addition to significantly perturbing the incident bulk flow and density [e.g., Goncharov et al., 2014; Wilson III et al., 2012]. Further, several past studies have shown that the separation between shocks with and without precursors is often a result of undersampling rather than a physical difference [e.g., Newbury et al., 1998; Russell, 1988; Wilson III et al., 2012].

Nearly all of the quasi-perpendicular shocks examined to date satisfy 〈M_f〉_up ≥ 3 and/or 〈β〉_up ≥ 1.0, mostly because Earth’s bow shock typically satisfies these criteria. There have been no statistical studies of the structure of low-Mach number, low-beta, quasi-perpendicular shocks. There have been a few studies [e.g., Farris et al., 1993; Greenstadt et al., 1975; Fairfield and Feldman, 1975] that explicitly examined quasi-perpendicular shocks satisfying 〈M_f〉_up < 3 and 〈β〉_up < 1.0, but they only examined a small number of events and most lacked the higher time resolution of more modern instruments. This raises several questions: Does the assumed laminar, step-like magnetic profile of these shocks match the observed profile when higher-resolution data are examined? Can one define a single magnetic profile for these shocks from a statistically significant set of observations? Are these shocks dissipative or dispersive? To answer these questions, we analyze the large database of interplanetary shocks observed by the Wind spacecraft.

In this paper we describe a statistical analysis of low-Mach number, low-beta, quasi-perpendicular shocks to determine whether the structure can be described as “laminar” or “turbulent,” i.e., does the shock exhibit large-amplitude (i.e., δB/B > 10%) whistler fluctuations (turbulent) or not (laminar). The paper is outlined as follows; section 2 introduces the data sets and databases used herein; section 3 describes the analysis and methodology; section 4 discusses the analysis of the observed precursors; and section 5 summarizes our discussion and conclusions. We also include several appendices that provide additional details for the reader of our parameter definitions (Appendix A), properties, and methodology for parameterizing the precursors (Appendix B), and summary of the adaptive interval software utilized (Appendix C).

2. Definitions and Data Sets

In this section we introduce the instrument data sets and shock database used to examine the interplanetary shocks examined herein. All data were measured by instruments on board the Wind spacecraft [Harten and Clark, 1995]. Details about our symbol/parameter definitions can be found in Appendix A.

All shock parameters used herein were taken from the Harvard Smithsonian Center for Astrophysics’ Wind shock database, which can be found at https://www.cfa.harvard.edu/shocks/wi_data/.

Hereafter, we will refer to this database as WSDB for brevity. Note that the purpose of this work is not to evaluate the solutions obtained from the WSDB. We also used the suggested solution method on each event page regardless of whether it may actually be the most physically consistent solution. See Appendix A for more details and definitions of the parameters used.

Quasi-static magnetic field measurements were taken from the Wind/MFI dual, triaxial fluxgate magnetometers [Lepping et al., 1995]. The instrument returns three component vectors sampled at ~5, ~11, or ~22 samples per second (sps), depending upon the instrument mode and spacecraft location relative to Earth. The plasma parameters used to construct the WSDB relied upon the two Wind/SWE Faraday Cups (FCs) [Ogilvie et al., 1995], with a ~92 s cadence.

3. Analysis and Methodology

In this section we discuss how we analyzed and quantified the whistler precursor parameters.

At the time of writing this manuscript, there were 430 fast forward (i.e., antisunward propagating in plasma rest frame) shocks in the WSDB, of which 250 were quasi-perpendicular shocks. We define low-Mach number, low-beta, quasi-perpendicular shocks as those satisfying the following constraints: 〈M_f〉_up ≥ 1; 1 ≤ 〈M_A〉_up ≤ 3; 〈β〉_up ≤ 1; 1 ≤ ℛ ≤ 3; and θ_Bn ≥ 45°, where ℛ is the shock compression ratio defined as 〈n_i〉_down/〈n_i〉_up. Of the 250 quasi-perpendicular fast mode shocks in the WSDB, 145 satisfied this criteria. For the rest of this paper, we will only refer to these 145 events unless otherwise specified.

The statistical properties of these shocks are shown in Table 1. For the 145 shocks examined, we observed 〈β〉_up ~ 0.018–0.94, θ_Bn ~ 45.5°–88.1°, 〈M_A〉_up ~ 1.15–2.98, and 〈M_f〉_up ~ 1.02–2.52. Note that 107/145 (or ~71 %) of these shocks satisfy 〈β〉_up ≤ 0.5, thus, most events satisfy the low-beta, low-Mach number criteria cited in Mellott [1985] to be classified as laminar. We found no dependence of the precursor amplitude on 〈β〉_up, or any other shock parameter for that matter. The full list of shock parameters, including critical Mach numbers, can be found in the supporting information [e.g., Abraham-Shrauner and Yun, 1976; Edmiston and Kennel, 1984; Kennel et al., 1985; Koval and Szabo, 2008; Krall and Trivelpiece, 1973; Krasnoselskikh et al., 2002; Russell et al., 1983; Szabo, 1994; Vinas and Scudder, 1986].

Table 1.

Average IP Shock Parameters

Parameter	Xming	Xmaxh	$\overline{X}$i	$\tilde{X}$j	σxk
250 Shocks Satisfying:
〈Mf〉up ≥ 1; 〈MA〉up ≥ 1; ℛ ≥ 1; and θBn ≥ 45°
〈β〉up (N/A)a	0.02	3.86	0.54	0.40	0.53
θBn [°]b	45	90	68	68	13
〈Mf〉up (N/A)c	1.02	6.39	2.20	1.92	1.05
〈MA〉up (N/A)c	1.15	15.61	2.95	2.47	1.79
〈|Vshn|〉up (km s−1)d	9	1164	490	461	169
〈|Ushn|〉up(km s−1)e	37	550	142	109	97
〈|Bo|〉up (nT)	1.0	19.0	5.9	5.5	2.9
〈ni〉up (cm−3)	0.6	35.5	8.6	7.0	5.8
Δ|Bo| [nT]f	0.4	28.5	6.0	4.6	4.5
145 Shocks Satisfying:
〈Mf〉up ≥ 1; 1 ≤ 〈MA〉up ≤ 3 〈β〉up ≤ 1; 1 ≤ ℛ ≤ 3; and θBn ≥ 45°
〈β〉up (N/A)	0.02	0.94	0.35	0.34	0.21
θBn (deg)	46	88	68	68	12
〈Mf〉up (N/A)	1.02	2.52	1.64	1.61	0.36
〈MA〉up (N/A)	1.15	2.98	2.01	2.01	0.49
〈|Vshn|〉up (km s−1)	9	976	452	433	124
〈|Ushn|〉up (km s−1)	39	275	108	98	50
〈|Bo|〉up (nT)	2.1	17.4	6.4	5.8	2.8
〈ni〉up (cm−3)	1.0	29.5	8.3	6.9	5.5
Δ|Bo| (nT)	0.4	21.4	4.8	3.8	3.3
113 Shocks With Precursors Satisfying:
〈Mf〉up ≥ 1; 1 ≤ 〈MA〉up ≤ 3 〈β〉up ≤ 1; 1 ≤ ℛ ≥ 3; and θBn ≥ 45°
〈β〉up (N/A)	0.02	0.82	0.32	0.30	0.20
θBn (deg)	46	88	66	67	12
〈Mf〉up (N/A)	1.02	2.52	1.66	1.68	0.37
〈MA〉up (N/A)	1.15	2.95	2.00	2.01	0.51
〈|Vshn|〉up (km s−1)	9	908	451	438	123
〈|Ushn|〉up(km s−1)	39	275	112	99	52
〈|Bo|〉up (nT)	2.1	17.4	6.7	6.0	3.0
〈ni〉up (cm−3)	1.0	29.5	8.4	6.6	5.6
Δ|Bo| (nT)	0.4	21.4	5.2	4.4	3.4

^a”Total” plasma beta ≡ (3/5)$C_s^2/V_A^2$.

^bShock normal angles ≡ ${\cos }^{-1}({\langle {\widehat{B}}_o\rangle }_{\mathrm{up}}\cdot \widehat{\mathbf{n}})$.

^cUpstream α Mach number ≡ 〈|U_shn|〉_up/〈V_α〉_up.

^dShock normal speed in SCF.

^eUpstream flow speed along shock normal In SHF.

^fΔQ ≡ 〈Q〉_dn - 〈Q〉_up.

^gMinimum.

^hMaximum.

ⁱMean or average;

^jMedian.

^kStandard deviation.

3.1. Shock Characterization

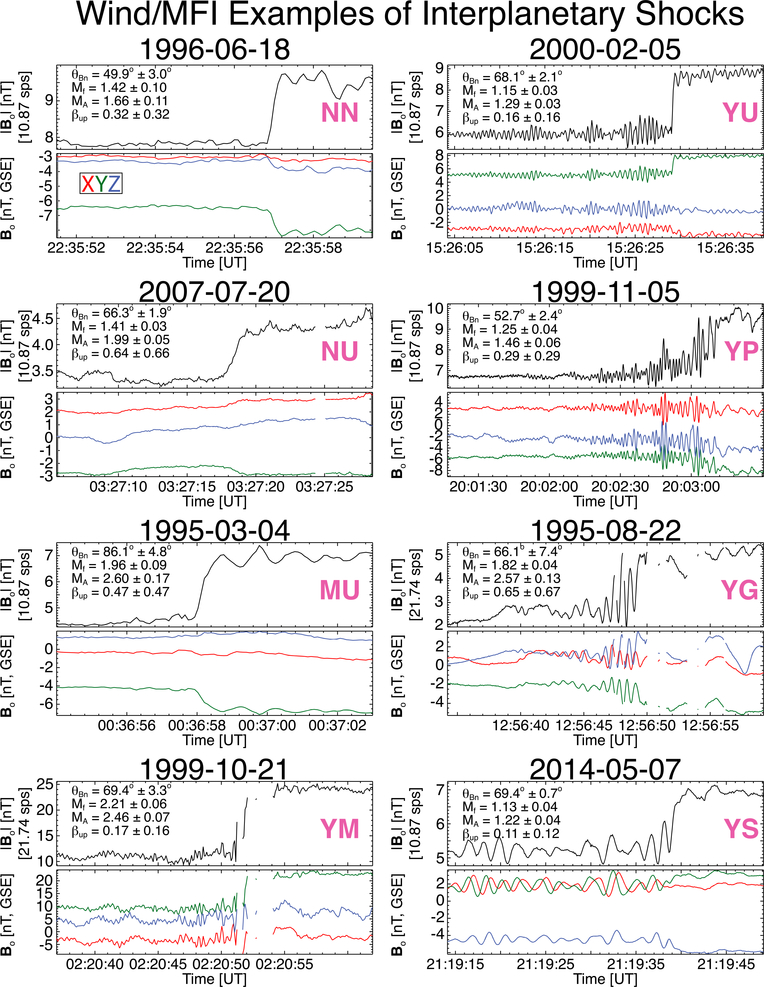
We examined the high time resolution Wind/MFI data for all 145 good events “by eye” to determine whether they exhibited clear whistler precursor fluctuations immediately adjacent to the shock ramp. We examined the ramp region and/or whistler precursor fluctuations to determine whether the data were well resolved (i.e., smooth, continuous transitions between points) or underresolved (i.e., spiky, discontinuous transitions between points). To parameterize these properties, we categorized every shock with a two-letter code. The code is summarized as follows:

1. First Letter

   1. Y = yes, a whistler precursor is clearly observed;
   2. N = no, nothing is observed; and
   3. M = maybe/unclear
2. Second Letter

   1. S = data are resolved or sampled well enough (e.g., precursor appears as smooth modulated sine wave);
   2. U = fluctuation(s) present but underresolved (e.g., looks like triangle or sawtooth wave);
   3. P = data are at least partially or mostly resolved but still a little spiky (e.g., some of the precursor is smooth but some parts are triangle wave-like);
   4. G = data gap is present within the precursor time interval but data are still well resolved;
   5. M = data gap is present within the precursor time interval and data are underresolved (similar comments as above); and
   6. N = nothing is observed.

The full list of two-letter codes can be found in the supporting information.

The two-letter code is only meant to qualitatively distinguish shocks with and without clear precursor fluctuations for further analysis. A summary of the statistics for the two-letter codes is shown in Table 2 for all 145 events (top part), 132 events observed at ~11 sps (middle part), and 12 events observed at ~22 sps (bottom part). Only one event (on 31 January 2002) was observed at ~5 sps and was classified as YU.

Table 2.

Summary of Two-Letter Code Stats

All shocks below satisfy:
〈Mf〉up ≥ 1; 1 ≤ 〈MA〉up ≤ 3; 〈β〉up ≤ 1;
1 ≤ ℛ ≤ 3; and θBn ≥ 45°
	Second Letter
First Letter	S	P	U	G	M	N	Total
	Stats for All 145 Shocks Examined
Y	11	33	59	2	8	0	113
N	0	0	1	0	0	16	17
M	0	0	15	0	0	0	15
Total	11	33	75	2	8	16	145
	Stats for 132 Shocks Observed at ~11 sps
Y	11	29	56	1	8	0	105
N	0	0	1	0	0	13	14
M	0	0	13	0	0	0	13
Total	11	29	70	1	8	13	132
	Stats for 12 Shocks Observed at ~22 sps
Y	0	4	2	1	8	0	7
N	0	0	0	0	0	3	3
M	0	0	2	0	0	0	2
Total	0	4	4	1	8	3	12

Figure 1 shows illustrative examples of each of the eight unique two-letter shock types observed in the 145 interplanetary shocks examined. Note that the character codes associated with data gaps are only applied if the gap occurs within the precursor time interval, thus the NU designation for the shown example does not directly reflect the data gap found downstream of the ramp.

Figure 1.

Example interplanetary shock crossings observed by the Wind spacecraft illustrating the two-letter code morphology. For each event there are two panels showing (top) |B_o| (nT, ~11 —22 sps) and (bottom) the GSE components of B_o (nT, ~11 −22 sps). The vector component color code legend Is shown in the upper left-hand example. In each event, we also show the following upstream shock parameters and associated uncertainties: shock normal angle, θ_Bn (deg); fast mode Mach number, 〈M_f〉_up; Alfvénic Mach number, 〈M_A〉_up; and plasma beta, 〈β〉_up.

Given that several past studies have shown that the separation between shocks with and without precursors is often a result of undersampling rather than a physical difference [e.g., Newbury et al., 1998; Russell, 1988; Wilson III et al., 2012], it is possible that the remaining 32(~22%) of the 145 events examined do exhibit a precursor but are not resolved by the fluxgate data. We found 67/113 shocks with precursors were underresolved (i.e, YU or YM) and 46/113 shocks with precursors were at least partially resolved (i.e., YS or YG or YP). We examined the upstream average shock parameters to look for dependencies in the whistler precursor parameters. The statistics of these results are shown in Table 3. In general, the shocks with clearly resolved precursors have slightly lower average (and median) values of θ_Bn, 〈M_f〉_up, 〈M_A〉_up, 〈|V_shn|〉_up, 〈|U_shn|〉_up, 〈|B_o|〉_up, and 〈n_i〉_up. These results are somewhat expected as previous work found that the frequency of these waves directly scaled with |B_o| [see, e.g., Wilson, 2016, and references therein] and Doppler effects would increase the spacecraft frame frequencies for higher Mach numbers and 〈|V_shn|〉_up. However, there appears to be no dependence on 〈β〉_up for whether or not precursors are observed.

Table 3.

Average IP Shock Parameters for Resolved and Unresolved Precursors

All Shocks Below Satisfy:
〈Mf〉up ≥ 1; 1 ≤ 〈MA〉up ≤ 3; 〈β〉up ≤ 1;
1 ≤ ℛ ≤ 3; and θBn ≥ 45°
Parameter	Xmin	Xmax	$\overline{X}$	$\tilde{X}$	σx
67/113 Shocks With Underresolved Precursorsa
〈β〉up (N/A)	0.02	0.82	0.32	0.30	0.22
θBn (deg)	46	88	69	69	11
〈Mf〉up (N/A)	1.04	2.52	1.72	1.76	0.39
〈MA〉up (N/A)	1.15	2.95	2.08	2.14	0.53
〈|Vshn|〉up (km s−1)	86	908	465	455	119
〈|Ushn|〉up (km s−1)	39	275	121	109	55
〈|Bo|〉up (nT)	2.4	17.4	7.4	6.7	3.0
〈ni〉up (cm−3)	1.6	27.8	9.3	7.6	5.8
46/113 Shocks With Resolved Precursorsb
〈β〉up (N/A)	0.04	0.66	0.32	0.36	0.17
θBn (deg)	46	88	62	61	11
〈Mf〉up (N/A)	1.02	2.22	1.57	1.59	0.33
〈MA〉up (N/A)	1.15	2.80	1.89	1.93	0.47
〈|Vshn|〉up (km s−1)	9	701	430	418	127
〈|Ushn|〉up (km s−1)	43	259	98	87	45
〈|Bo|〉up (nT)	2.1	15.6	5.7	5.1	2.5
〈ni〉up (cm−3)	1.0	29.5	7.0	6.1	5.2

^aShocks designated as YU or YM.

^bShocks designated as YS or YG or YP.

4. Whistler Precursors

4.1. Properties

In this section we show several examples to illustrate the general properties of whistler precursors. For a summary of specific details about their properties, see Appendix B.

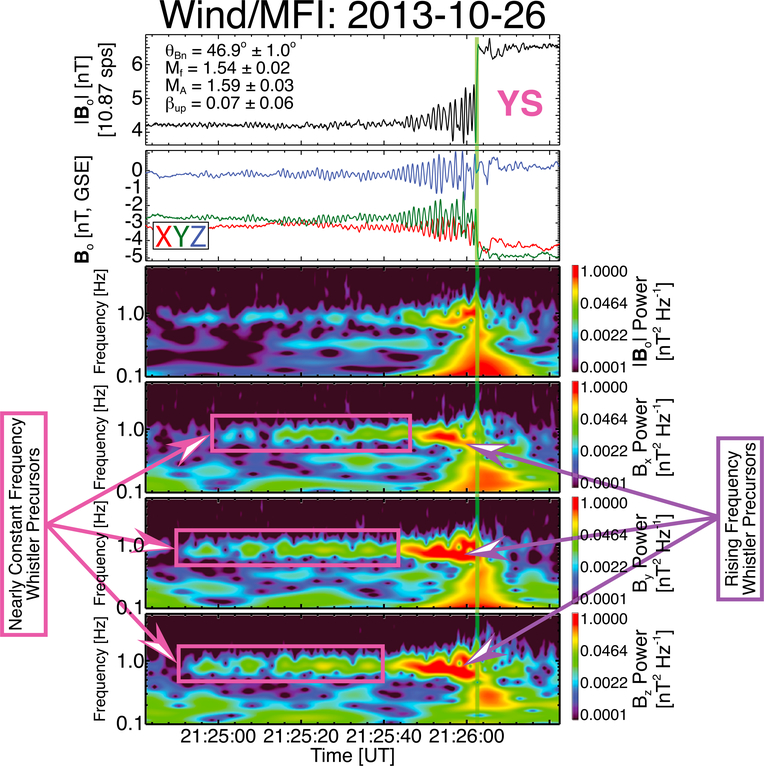
Figure 2 shows an illustrative example of an interplanetary shock with both a dispersive and nearly constant frequency whistler precursors. The Morlet wavelet transforms [e.g., Morlet et al., 1982; Morlet, 1982] show the characteristic dispersive nature of these modes—the highest frequencies observed first (i.e., farthest from ramp) with a slow decrease in frequency with increasing time (i.e., decreasing distance to ramp)—indicated with purple arrows. The wavelets also show a nearly constant frequency precursor farther upstream. Previous studies have shown these to be whistlers with a large enough group velocity to escape the shock into the upstream [see, e.g., Wilson, 2016, and references therein]. Note that the horn-shaped wavelet enhancement centered on the shock ramp (i.e., vertical green line) is a consequence of the transform and can give the impression of a locally rising frequency. Any time variation occurring on an interval shorter than the smallest wavelet scale for the chosen basis (e.g., Morlet) will produce a similar signal [see, e.g., Lau and Weng, 1995, Figure 4]. Below we provide more examples of events with different precursor durations, normalized amplitudes, and appearance.

Figure 2.

An illustrative example of an interplanetary shock exhibiting both a dispersive (purple arrows) and nearly constant frequency (magenta arrows and boxes) whistler precursors observed by the Wind spacecraft, (first and second panels) The same format as Figure 1. Shown are the Morlet wavelet transforms [Torrence and Compo, 1998], from top-to-bottom, of (third panel) |B_o|, (fourth panel) B_ox, (fifth panel) B_oy, and (sixth panel) B_oz, with wavelet power range shown to the right as color bars. Figure 2 (first panel) shows the same upstream shock parameters as in Figure 1. Finally, the green vertical line denotes the separation between upstream (to left) and downstream (to right) regions.

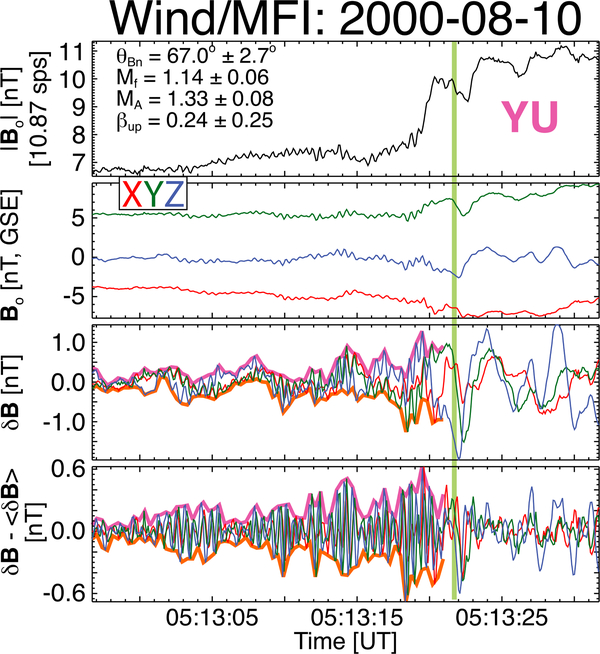
Figure 4.

Example interplanetary shock observed by the Wind spacecraft illustrating the use of the outer waveform envelope to parameterize the precursor amplitude statistics, (first and second panels) Same format as in Figure 1. (third panel) The high-pass filtered GSE components of B_o. (fourth panel) The same high-pass filtered data, but has been detrended—removed low-frequency contaminants using a 10 point boxcar averaging window—to isolate the precursor oscillations. The upper (magenta) and lower (orange) bounds of the outer waveform envelope are shown in Figures 4 (third panel) and 4 (fourth panel). The green vertical line denotes the separation between upstream (to left) and downstream (to right) regions.

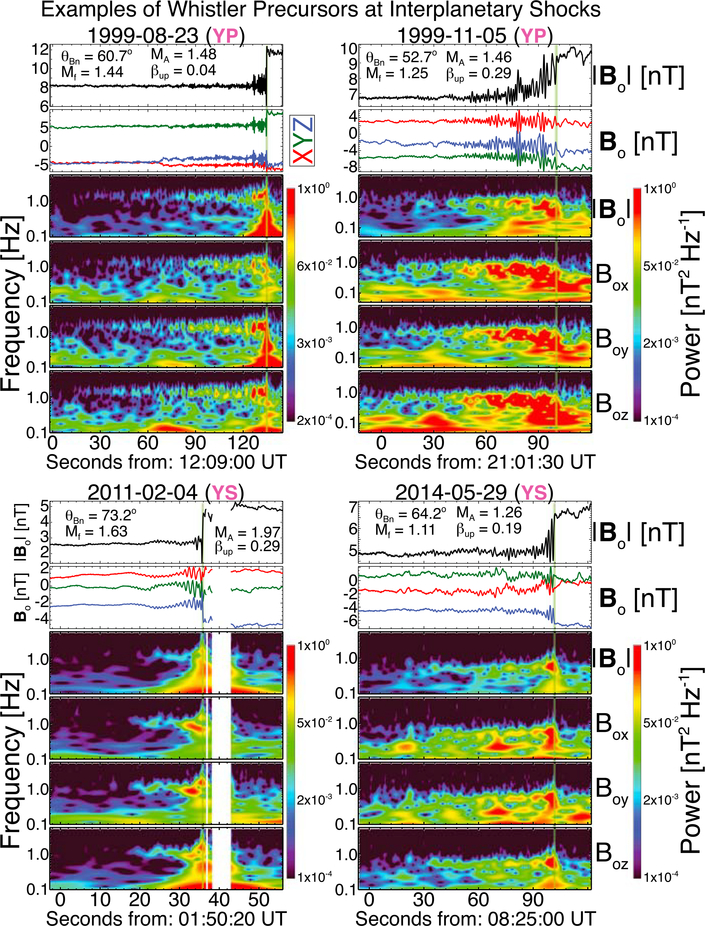
Figure 3 shows four more illustrative examples of whistler precursors and Morlet wavelet transforms at interplanetary shocks. Each event was chosen to highlight common features of precursors. The 23 August 1999 event shows a relatively small amplitude precursor with a waveform appearance that is commonly observed followed by a well-defined/sharp shock ramp [e.g., Aguilar-Rodriguez et al., 2011; Blanco-Cano et al., 2016; Kajdič et al., 2012; Ramírez Vélez et al., 2012; Wilson III et al., 2009]. The 4 February 2011 event also shows a relatively small amplitude precursor, but frequency dispersion is more obvious and there is a sharp dip in the magnetic field magnitude (i.e., well below 〈|B_o|〉_up) immediately preceding the shock ramp. The 29 May 2014 event shows a small amplitude precursor upstream that smoothly transitions into a large-amplitude precursor. Finally, the 5 November 1999 event shows a more dramatic, large-amplitude precursor with unipolar pulses in the field magnitude.

Figure 3.

Four interplanetary shocks showing illustrative examples of whistler precursors observed by the Wind spacecraft. Each shock has six panels with the same format as those in Figure 2.

There are also differences in the waveform appearance between the small- and large-amplitude precursors. The left-hand column shows fluctuations that can be described as sinusoidal oscillations about some mean value for both the magnitude and each vector component. The right-hand column, however, shows that fluctuations do not oscillate symmetrically about some mean value but rather are unipolar (i.e., more obvious in the field magnitude than components). Further, these oscillations are comparable in amplitude to the main shock ramp. From the appearance of the precursor waveforms compared to previous studies [e.g., Balikhin et al., 1989], those in the left-hand column could be described as linear while those in the right-hand column as nonlinear. Further, the unipolar pulses are similar in appearance to the soliton-like pulses described in previous bow shock observations [e.g., Lefebvre et al., 2009; Lobzin et al., 2007; Walker et al., 1999] and theory/simulation [e.g., Hellinger et al., 2007; Krasnoselskikh et al., 2002; Scholer and Burgess, 2007] as evidence of nonstationarity.

There is no obvious dependence of the shock structure on the upstream shock parameters, in disagreement with theory [e.g., Biskamp, 1973; Gary and Mellott, 1985; Gedalin, 2016; Hellinger, 2003; Ofman et al., 2009]. For instance, the 23 August 1999 event has a much smaller 〈β〉_up and comparable 〈M_A〉_up to the 5 November 1999 event, but the latter is more turbulent and the precursors are nonlinear. The difference cannot be attributed to a larger θ_Bn either after one compares the 23 August 1999 event to the shock structure for the 29 May 2014 event.

4.2. Amplitudes

To parameterize the amplitudes of the whistler precursors observed upstream of the 113 of the 145 interplanetary shocks studied, we performed several operations to isolate the oscillations from the background and to define the amplitude, as discussed in Appendix B.

Figure 4 shows an example of the aforementioned procedure. The top two panels share the same format as Figure 1. The convex hull is calculated in the standard way using a four-point sliding window and is shown in the third and fourth panels as the orange (lower bound) and magenta (upper bound) lines. The δB_pk-pk/Δ|B_o| and δB_pk-pk/〈|B_o|〉^up values for this event ranged from ~0.009 to 0.24 and from ~0.006 to 0.16, respectively, with average values ~0.06 and ~0.04. The δB_pk-pk values for this event ranged from ~0.04 to 1.0 nT, with average (median) values ~0.3 (~0.2) nT.

Table 4 shows the statistics of the amplitude statistics. As shown in Figure 4, each precursor will have an array of δB_pk-pk values. The full list of wave amplitudes (both absolute and normalized values) for each precursor interval can be found in the supporting information. Table 4 represents the one-variable statistics on the full lists of amplitude statistics found in the supporting information. For instance, there are 113 values of X_max of the δB_pk-pk/〈|B_o|〉_up parameter. Therefore, to get the second column in the second part of Table 4, we perform one-variable statistics on these 113 values of X_max of the δB_pk-pk/〈|B_o|〉_up parameter. Thus, each column heading in Table 4 defines the parameter from the list of 113 values and the row headings define the one-variable statistics of those parameters.

Table 4.

Whistler Precursor Amplitude Statistics

All Shocks Below Satisfy:
〈Mf〉up ≥ 1; 1 ≤ 〈MA〉up ≤ 3; 〈β〉up ≤ 1;
1 ≤ ℛ ≤ 3;and θBn ≥ 45°
Statisticsa	Xmin	Xmax	$\overline{X}$	$\tilde{X}$	σx
Statistics of δ Bpk-pk(nT) for the 113 Shocks With Precursors
Yminb	0.01	0.4	0.08	0.05	0.07
Ymaxc	0.2	13.0	3.0	2.3	2.5
$\overline{Y}$d	0.07	1.9	0.5	0.4	0.4
$\tilde{Y}$e	0.07	1.3	0.3	0.3	0.3
σyf	0.03	2.5	0.6	0.4	0.5
Statistics of δBpk-pk/〈|Bo|〉upfor the 113 Shocks With Precursors
Ymin	0.003	0.04	0.01	0.01	0.008
Ymax	0.03	1.6	0.5	0.4	0.3
$\overline{Y}$	0.01	0.4	0.08	0.07	0.06
$\tilde{Y}$	0.01	0.3	0.05	0.04	0.04
σy	0.004	0.5	0.09	0.06	0.08
Statistics of δBpk-pk/Δ|B0|for the 113 Shocks With Precursors
Ymin	0.004	0.2	0.02	0.01	0.02
Ymax	0.04	15.3	0.8	0.5	1.5
$\overline{Y}$	0.01	2.2	0.1	0.09	0.2
$\tilde{Y}$	0.01	1.1	0.08	0.06	0.1
σy	0.006	2.7	0.2	0.08	0.3

^aThe array of 113 values, one for each precursor interval.

^bMinimum of each parameter defined by column heading (implied for rest of row headings).

^cMaximum.

^dMean or average.

^eMedian.

^fStandard deviation.

Notice that the maximum values of δB_pk-pk/〈|B_o|〉_up for all good events (i.e., X_max column in second part of Table 4) range from ~0.04 to 1.6 (i.e., from Y_min and Y_max rows), with the average (i.e., $\overline{\mathbf{Y}}$ row) and median (i.e., $\tilde{\mathbf{Y}}$ row) of these values being ~0.4 and ~0.3, respectively. The average whistler precursor amplitudes are ~40% of the upstream average magnetic field magnitudes. The maximum values of δB_pk-pk/Δ|B_o| (i.e., X_max column in third part of Table 4) range from ~0.2 to 15.3 with the average (median) of these values being ~2.2 (~1.1). Thus, on average, the whistler precursor amplitudes for low-Mach number, low-beta, quasi-perpendicular collisionless shocks are ~220% of the shock ramp amplitudes.

We examined the upstream shock parameters to determine if they could serve as indicators of the shock structure by correlating them with the precursor amplitudes. We observed no correlation between any of the three presentations of precursor amplitudes in Table 4 with any upstream shock parameter. The only shock parameter that appeared to show any influence over the magnetic profile of the shocks was θ_Bn. The magnetic profile of shocks satisfying θ_Bn > 70° generally had a well-defined/sharp magnetic ramp clearly separate from the whistler precursor. Some of the shocks satisfying θ_Bn ≲ 70° showed large-amplitude precursors preceding and within the magnetic ramp blurring the separation between upstream and downstream. Further, previous studies of higher-Mach number shocks with θ_Bn > 70° have found large-amplitude precursors pervading the magnetic ramp and magnetic profiles not well described by the traditional step function-like appearance [e.g., Holzer et al., 1972; Wilson III et al., 2012,2014a, 2014b]. For instance, Wilson III et al., [2012] presented a highly oblique (θ_Bn ~ 82°), strong (〈M_f〉_up ~ 5) shock that appeared laminar in the fluxgate magnetometer data (at ~11 sps) but they observed δB_pk-pk > 25 nT precursor in the search coil magnetometer data (at ~1875 sps). Thus, the above separation depending upon θ_Bn may only result from sample rate limitations.

Some theoretical work implies that whistler precursors should not play a significant role in the bulk dynamics of the plasma as it crosses the shock [e.g., Ofman et al., 2009; Gedalin, 2016,2017]. However, the assumption that the precursor does not affect the incident flow is problematic when the precursor amplitude, δB, becomes comparable to the shock ramp amplitude, ΔB. Precursors have been shown to cause strong heating and stochastic acceleration at strong (i.e., 〈M_f〉_up ~ 4.7) interplanetary shocks [e.g., Wilson III et al., 2012], but they have also been found to significantly perturb the incident bulk flow (δV/〈V〉_up ≲ 13%) and density (δn/〈n〉_up ≲ 75%) at weak (i.e., 〈M_f〉_up ~ 1.3) interplanetary shocks as well [e.g., Goncharov et al., 2014]. These results suggest that large-amplitude precursors should not be neglected when considering macroscopic shock dynamics.

4.3. Propagation Statistics

In this section we discuss our analysis of the wave propagation directions using minimum variance analysis (MVA).The details of the analysis can be found in Appendix B. Of the ~8.8 million total MVA intervals analyzed, only 2189 satisfied our stringent constraints and 1996 had a ≥0.9° of polarization.

The 1996 good MVA intervals were not evenly distributed among the 113 shocks with precursors. In the following we will use N_MVA to represent the number of good MVA intervals. Of the 113 shocks with precursors, we found 1 (~0.9%) satisfied N_MVA = 0, 107 (~95%) satisfied N_MVA ≥ 2, 50 (~44%) satisfied 1 ≤ N_MVA ≤ 10, 62 (~55%) satisfied N_MVA ≥ 11, and 36 (~32%) satisfied N_MVA ≥ 20.

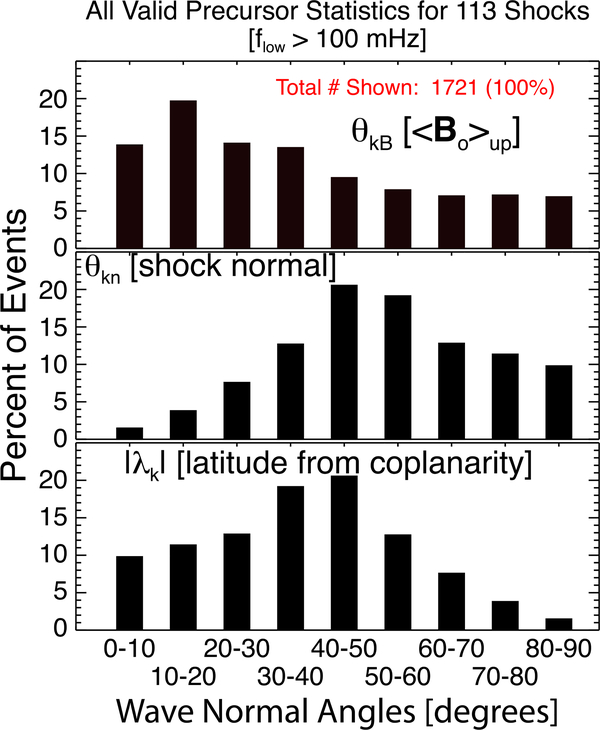
We limit the following discussion to those results with a lower frequency bound greater than 100 mHz to avoid contamination by lower frequency modes leaving 1721 good MVA subintervals. There were 332 filter ranges with valid MVA results for the 113 shocks with precursors, 278 of which have a lower bound >100 mHz. We define the angle between the wave vector, $\widehat{\mathbf{k}}$, and 〈B_o〉_up as θ_kB, between $\widehat{\mathbf{k}}$ and $\widehat{\mathbf{n}}$ as θ_kn, and between $\widehat{\mathbf{k}}$ and the plane formed by $\widehat{\mathbf{n}}$ (i.e., the shock normal vector) and 〈B_o〉_up—called the coplanarity plane—as λ_k. Note that we show and discuss all angles as magnitudes ranging from 0° to +90° due to the ambiguity in the sign of $\widehat{\mathbf{k}}$ even though θ_kB and θ_kn range from 0° to +180° and λ_k ranges from −90° to +90°.

Figure 5 shows histograms of the angles θ_kB (top), θ_kn (middle), and |λ_k| (bottom) for the 1721 good intervals analyzed. We find that ~66% of the best subintervals satisfy θ_kB ≤ 45° and ~87% satisfy θ_kn ≥ 30°, consistent with previous observations [e.g., Aguilar-Rodriguez et al., 2011; Blanco-Cano et al., 2016; Kajdič et al., 2012; Ramírez Vélez et al., 2012; Wilson III et al., 2009; Hull et al., 2012; Wilson III et al., 2012]. For the wave vector latitude, we find that most precursors propagate out of this plane, not within it. For instance, of the 1721 good precursor intervals, 1643 (~95%) satisfy |λ_k| ≥ 5°, 1551 (~90%) satisfy |λ_k| ≥ 10°, 1354 (~79%) satisfy |λ_k| ≥ 20°, and 1132 (~66%) satisfy |λ_k| ≥ 30°. These results are consistent with some previous studies [e.g., Wilson III et al., 2009, 2012], but inconsistent with the work by Hull et al., [2012], The difference is likely due to the nearly perpendicular geometry and potential influence of reflected-ion instabilities of the high-Mach number bow shock crossing examined by Hull et al., [2012], In contrast, most of the interplanetary shocks presented herein are more oblique and much lower Mach number, which should produce fewer reflected ions and thus are less likely to excite the modified two-stream instabilities discussed by Hull et al., [2012].

Figure 5.

Wave normal angle statistics for the best MVA subintervals examined for the 113 precursors. The histograms show the percentage of all results versus the angle bins, where the total number of MVA subintervals is shown in Figure 5 (top). The panels show, (top) the angle between $\widehat{\mathbf{k}}$ and 〈B_o〉_up (θ_kB), (middle) $\widehat{\mathbf{k}}$ and $\widehat{\mathbf{n}}$ (θ_kn), and (bottom) the magnitude of the latitude of $\widehat{\mathbf{k}}$ from the coplanarity plane (|λ_k|).

Finally, we examined the polarization of the magnetic fields of the waves with respect to 〈B_o〉_up. Of the 1721 good precursor intervals, 1256 (465) or ~73% (~27%) exhibited a right- (left-)hand polarization in the spacecraft frame of reference. These results are consistent with previous observations [see, e.g., Wilson, 2016, and references therein].

4.4. Rest Frame Properties

In this section we summarize our estimates of the rest frame parameters of the precursors following the methods outlined in Wilson III and other [2013]. See Appendix A for symbol definitions and Appendix B3 for methodology. The range of spacecraft frame frequencies (i.e., range of band-pass filter frequencies) used is 0.11–7.0 Flz. The median values of the lower and upper bounds are 0.6 Hz and 1.2 Hz, respectively. We impose the following constraints based upon previous results [see, e.g., Wilson, 2016, and references therein] on the numerical solutions to equation (B1): $\Re [\overline{k}]>0$; 0° ≤ θ_kB ≤ 90°; 0° ≤ θ_kV ≤ 180°; and 〈Ω_cp〉_up ≤ ω ≤ 〈ω_lh〉_up.

We find that the precursors have the following ranges of rest frame parameters: 0.02 ≲ $\overline{k}$ ≲ 5.9; 0.003 ≲ k(ρ_ce)_up ≲ 2.7; 2 km ≲ λ ≲ 1040 km (where λ is the wavelength); 0.04 Hz ≲ f ≲ 8 Hz; and 6 km/s ≲ ω/k ≲ 590 km/s. Note that the upper (lower) frequency(wavelength) bound is limited by the sample rate of the magnetic field measurements. These results are consistent with previous studies [see, e.g., Wilson, 2016, and references therein].

5. Discussion and Conclusions

We have presented a statistical survey of 145 low-Mach number (〈M_f〉_up ≥ 1 and 1 ≤ 〈M_A〉_up ≤ 3), low-beta (〈β〉_up ≤ 1), quasi-perpendicular (θ_Bn ≥ 45°) interplanetary shocks observed by the Wind spacecraft. Seventy-eight percent (113) of the 145 shocks showed clear evidence of magnetosonic-whistler precursor fluctuations. An explanation for the fact that some shocks did not have precursors in previous work was often a result of undersampling rather a physical difference [e.g., Newbury et al., 1998; Russell, 1988; Wilson III et al., 2012], suggesting that the 32 (~22%) shocks without clear precursors may just be unresolved. We found no relationship between the presence or absence of precursors on 〈β〉_up (or any other shock parameter), contrary to theory [e.g., Biskamp, 1973; Gary and Mellott, 1985; Gedalin, 2016; Hellinger, 2003; Ofman et al., 2009].

We examined the precursor propagation directions using minimum variance analysis (MVA). The majority (~66%) of the waves propagate within 45° of 〈B_o〉_up and most (~87%) propagate at more than 30° from $\widehat{\mathbf{n}}$. We also found that most (~79%) propagated at 20° or more from the coplanarity plane. Finally, the majority (~73%) of the precursors were right-hand polarized with respect to the magnetic field in the spacecraft frame of reference.

The precursors have rest frame frequencies of 0.04 Hz ≲ f ≲ 8 Hz, phase speeds 6 km/s ≲ ω/k ≲ 590 km/s, and wavelengths of 2 km ≲ λ ≲ 1040 km, i.e., the waves span from the electron-to-ion scales and can propagate from below the Alfvén speed to nearly that of the bulk solar wind flow. The large phase speeds have implications for studies that assume the so-called “Taylor hypothesis”—temporal variations are assumed to be spatial variations convected with the bulk flow of the solar wind under certain limits—because the spacecraft frame frequencies ranged from ~0.11–7.0 Hz. Thus, spacecraft frame frequencies above ~0.1 Hz can violate the Taylor approximation in the presence of magnetosonic-whistler mode waves.

When we examined the statistics of the precursor amplitudes, we found that maximum values of δB_pk-pk/〈|B_o|〉_up for all 113 events range from ~0.04 to 1.6 with the average (median) of these values being ~0.4 (~0.3). If we instead compare the precursor amplitude with the shock ramp amplitude, we find maximum values of δB_pk-pk/Δ|B_o| range from ~0.2 to 15.3 with the average (median) of these values being ~2.2 (~1.1). Thus, even for low-Mach number, low-beta, quasi-perpendicular interplanetary shocks the average values of δB_pk-pk/〈|B_o|〉_up and δB_pk-pk/Δ|B_o| are ~40% and ~220%.

Such large normalized amplitudes raise doubts about whether such shocks can be classified as laminar, as has been traditionally done [e.g., see Mellott, 1985, and references therein]. These values also exceed the typical approximations for the separation between linear and nonlinear oscillations (e.g., δB/B ~ 0.1) [e.g., Yoon et al., 2014]. Previous work has found that precursors can stochastically accelerate the hot/halo particles [e.g., Wilson III et al., 2012] and significantly deflect and modulate the cold/core particles [e.g., Goncharov et al., 2014]. All of these factors raise doubts about the assumption that the precursors do not play an important role in the transformation of the incident bulk flow kinetic energy into other forms. Therefore, we argue that the term “laminar” should not be broadly assumed for low-Mach number, low-beta, quasi-perpendicular collisionless shocks.

In summary, magnetosonic-whistler precursor waves appear to be a ubiquitous feature of quasiperpendicular shocks, regardless of Mach number or plasma beta. We further find that their amplitudes are large enough to question the traditional assumption that low-Mach number, low-beta, quasi-perpendicular collisionless shocks are “laminar” structures. Finally, regardless of their generation mechanism it is clear that magnetosonic-whistler precursor waves are a critical feature of collisionless shock wave structure and evolution.

Key Points:

• Low-Mach number, low-beta, quasi-perpendicular shocks are not laminar, step-like, magnetic structures

• Whistler precursor amplitudes are on average 50% and 80% of the upstream average magnetic field and shock ramp amplitude, respectively

• Whistler precursors propagate obliquely to the upstream magnetic field, shock normal vector, and coplanarity plane

Erratum.

In the originally published version of this article, some values from Table 4 were misquoted when referenced in the text, specifically, in the last sentence of the Abstract, in the fourth paragraph of section 4.2, and in the fourth paragraph of section 5. The correct values are now properly referenced in these places in the article text, and the current version may be considered the authoritative version record.

Appendix A: Definitions

First, we list our symbol notations. We use the following notations for any quantity, Q, throughout this paper: Q_o, δQ, and 〈Q〉_j, where Q_o is any quasi-static quantity, δQ is any fluctuating or high-pass filtered quantity, ΔQ = 〈Q〉_dn - 〈Q〉_up, and 〈Q〉_j is the time average of any quantity over region j = upstream (up) or downstream (dn). Note that Q_o is not the same as 〈Q〉_j in this context. We differentiate scalars and vectors using regular and bold face text, respectively. All vectors presented herein are shown in the geocentric solar ecliptic (GSE) coordinate basis.

We use the following symbols in reference to the standard one-variable statistics: minimums ≡ X_min, maximum ≡ X_max, mean ≡ $\overline{X}$, median ≡ $\tilde{X}$, standard deviation ≡ σ_x, and standard deviation of the mean ≡ ${\sigma }_x/\sqrt{N}$.

Throughout the paper we use the following parameter definitions: $c=1/\sqrt{{\epsilon }_o{\mu }_o}$ is the speed of light in vacuum and ε_o and μ_o are the permittivity and permeability of free space; B_o is the quasi-static magnetic field vector (nT); V_bulk is the bulk flow velocity vector (km s⁻¹); n_s is the number density of species s (cm⁻³); m_s is the mass of species s (kg); q_s is the charge of species s (C); T_s is the scalar temperature of species s (eV); $W_s=\sqrt{k_B{T}_s/m_s}$ is the RMS thermal speed of a one-dimensional ideal gas of species s; Ω_cs = q_s B_o/m_s is the angular cyclotron frequency of species s (rad s⁻¹); ${\omega }_{\text{ps}}=\sqrt{n_{\text{s}}{q}_s^2/{\epsilon }_o{m}_s}$ is the angular plasma frequency of species s (rad s⁻¹); ${\omega }_{\mathrm{lh}}=\sqrt{{\mathrm{\Omega }}_{\mathrm{ce}}{\mathrm{\Omega }}_{\mathrm{cp}}}$ is the lower hybrid resonance frequency assuming only protons and electrons (rad s⁻¹); ρ_cs = W_s/Ω_cs is the thermal gyroradius of species s (km); λ_s = c/ω_ps is the inertial length (or skin depth) of species s (km); $V_A=B_o/\sqrt{{\mu }_o{m}_i{n}_i}$ is the Alfvén speed (km s⁻¹); δB is the filtered fluctuating magnetic field due to a whistler precursor (nT); Δ|Β_o| is the change in the magnetic field magnitude across a shock ramp (nT); SCF is the spacecraft rest frame; and SHF is the shock rest frame.

We define the angle between a wave unit vector, $\widehat{\mathbf{k}}$, and an arbitrary unit vector, $\widehat{\mathbf{u}}$, as θ_ku. Due to the ambiguity in the sign of $\widehat{\mathbf{k}}$, these angles are presented as the smaller of two supplementary angles (i.e., ranging from 0° to 90°). The plane formed by the vectors $\widehat{\mathbf{n}}$ and 〈B_o〉_up is called the coplanarity plane. We define the angle between $\widehat{\mathbf{k}}$ and this plane as −90° ≤ λ_k ≤ +90°. We define the rest frame wavenumber and frequency as k and ω, respectively.

Below we define several parameter definitions that were taken from the Harvard Smithsonian Center for Astrophysics’ Wind shock database (WSDB), which can be found at https://www.cfa.harvard.edu/shocks/wi_data/.

The WSDB provides tables of numerical solutions to the Rankine-Hugoniot relations [e.g., Vinas and Scudder, 1986; Koval and Szabo, 2008] for eight different methods. The WSDB analysis methods were briefly described in Pulupa et al. [2010]. The first table, titled General Information, on each event webpage lists the selected best method from which we take the values for all events examined herein. Note that the selected best method may not correspond to the most physically consistent solution. For instance, in some cases the selected best method suggests that the Mach number is less than one, while all other methods show greater than unity, and the plasma parameters are consistent with a fast forward shock. However, the purpose of this work is not to evaluate the WSDB but to illustrate the ubiquity of whistler precursors at low-Mach number, low-beta, quasi-perpendicular collisionless shocks.

In the tables that follow on each event webpage, some parameters are listed by name while others use symbols or abbreviations on the WSDB. In the following we will state our definition followed by the WSDB equivalent label in parentheses and italicized text. Rather than repeatedly state that 〈Q〉_j corresponds to the quantity Q averaged over the jth region, we will simply imply it for brevity. These parameters we used are as follows: 〈W_s〉_j (Ws) is the RMS thermal speed of a one-dimensional ideal gas of species s (km s⁻¹); 〈V_A〉_j (Alfven Speed) is the Alfvén speed averaged (km s⁻¹); 〈C_s〉_j (Sound Speed) is the sound or ion-acoustic sound speed, defined on the WSDB as $\sqrt{\frac{5}{3}}{\langle W_i\rangle }_j;{\langle \beta \rangle }_j$ (Plasma Beta) is the “total” plasma beta, defined on the WSDB as $(3/5)C_s^2/V_A^2;\widehat{\mathbf{n}}$ (Nx, Ny, and Nz) is the shock normal unit vector [GSE]; ℛ (Compression) is the shock density compression ratio, defined as 〈n_i〉_down/〈n_i〉_up; θ_Bn (ThetaBn) is the shock normal angle, defined as the acute reference angle between 〈B_o〉_up and $\widehat{\mathbf{n}}$; 〈|V_shn|〉_up (Shock Speed) is the upstream shock normal speed in the SCF; 〈|U_shn|〉_j (dV) flow speed along shock normal in the SHF (km s⁻¹); 〈M_A〉_j(not shown) is the Alfvénic Mach number, defined as 〈|U_shn|〉_j/〈V_A〉_j; and 〈M_f〉_j (Fast Mach) is the fast mode Mach number, defined as 〈|U_shn|〉_j/〈V_f〉_j where V_f is the MHD fast mode phase speed.

Note that since we are using shock parameters from the WSDB, which relies entirely upon the Wind SWE Faraday cup measurements, we assume T_e = T_i; thus, thermal speeds differ by the square root of the mass ratio. Again, the purpose of this study is not to evaluate the WSDB but this assumption will affect our estimates for parameters depending upon (ρ_ce)_up.

Appendix B: Parameterizing Precursors

In this appendix we introduce the general properties and theory of whistler precursors, discuss our calculation of the wave amplitude, and finally describe our analysis of the wave propagation directions.

Magnetosonic-whistler precursors are generated through dispersive radiation—the emission of a mode from the time-varying currents in the shock ramp [e.g., Mellott and Greenstadt, 1984; Morton, 1964; Sagdeev, 1966; Stringer, 1963; Tidman and Northrop, 1968], similar to the emission from an antenna. It is worth noting that theoretical/simulation studies [e.g., Comişel et al., 2011; Hellinger et al., 2007; Riquelme and Spitkovsky, 2011; Wu et al., 1983] and observations [e.g., Dimmock et al., 2013; Hull et al., 2012; Wilson III et al., 2012] have found evidence that whistler precursors can be generated (and/or enhanced) by instabilities, with similar properties to the dispersively radiated ones, as well.

Whistler precursors are intrinsically right-hand polarized (with respect to B_o) with rest frame frequencies from below the ion cyclotron frequency, f_ci, up to the lower hybrid resonance frequency, f_lh. Whistler precursors are dispersive in nature, thus their phase velocity depends upon their frequency/wavenumber. Thus, dispersively radiated precursors are often observed as train of coherent oscillations extending away from the shock ramp, with the highest (shortest) frequency (wave length) farthest away from the ramp (see, e.g., Biskamp [1973], Kennel et al., [1985], Krasnoselskikh et al. [2002], Mellott [1984,1985], Tidman and Krall [1971], and Wilson III [2016] for more detailed discussions).

Whistler precursors are observed as compressive, quasi-sinusoidal oscillations in both the magnetic field components and magnitude with spacecraft frame frequencies from approximately a few mHz to ~10 Hz. In the spacecraft frame, they can exhibit both left- and right-hand polarizations with respect to B_o, but they are intrinsically right-hand polarized (i.e., in the plasma rest frame the fluctuating fields rotate in a counterclockwise sense about the quasi-static magnetic field). They can exhibit a broad range of propagation angles relative to the quasi-static magnetic field (θ_kB ~ 30°–88°) and macroscopic shock normal vector (θ_kn ~ 3°–90°), but most exhibit θ_kB ≲ 45° and θ_kn ≳ 20°. Thus, most precursors do not phase stand in the shock rest frame (i.e., θ_kn ≠ 0°). Their rest frame phase speeds and wavelengths, respectively, range from approximately tens to hundreds of km/s and from approximately tens to thousands of kilometers (i.e., from electron-to-ion scales). Finally, their phase speed is proportional to their rest frame frequency, producing a wave train where the higher (shorter) frequency (wavelength) modes are observed farther from the shock ramp than the lower (longer) frequency (wavelength) modes [see, e.g., Wilson, 2016, and references therein].

B1. Quantifying Amplitudes

To quantify the amplitude of the observed whistler precursors, we performed several operations to isolate the oscillations and minimize contamination from other effects. The details of this procedure are outlined below.

For every shock exhibiting a clear whistler precursor, we

1. defined a 2 h interval centered on the shock ramp (reasons for time range discussed below);

2. performed a standard Fourier high-pass filter (above 100 mHz for all events) on the entire 2 h interval of high time resolution magnetic field data;

3. defined the time interval of the whistler precursor;

4. detrended the high-pass filtered data using a 10-point box car average to remove offsets due to the shock ramp;

5. calculated the convex hull (i.e., outer envelope) of the filtered three-component waveform (e.g., see Figure 4) using a four-point sliding window;

6. determined the peak-to-peak precursor amplitude, δB_pk-pk, for every pair of points from the convex hull (i.e., the peak-to-peak amplitude of the outer wave envelope);

7. calculated the standard one-variable statistics (i.e., X_min, X_max, $\overline{X},\tilde{X}$, σ_x, and ${\sigma }_x/\sqrt{N}$) on all the δB_pk-pk, δB_pk-pk/Δ|B_o|, and δB_pk-pk/〈|B_o|〉_up values within every precursor interval; and

8. calculated the standard one-variable statistics on each one-variable statistic from the previous step, e.g., calculate X_min, X_max, $\overline{X},\tilde{X}$, σ_x, and ${\sigma }_x/\sqrt{N}$ all the minimum values for all events.

We chose a 2 h interval to have a sufficient number of input points to reduce edge effects [e.g., Harris, 1978] for the amplitude estimates. The results are shown in Table 4. The full list of normalized wave amplitudes can be found in the supporting information.

B2. Minimum Variance Analysis

Next we explain the steps involved to determine the propagation direction of the precursors. To determine the plane orthogonal to an electromagnetic wave vector, k, we can use minimum variance analysis (MVA) [e.g., Khrabrov and Sonnerup, 1998] on selected time intervals to calculate the minimum variance eigenvector. This unit vector is parallel or antiparallel to $\widehat{\mathbf{k}}$, where the sign ambiguity cannot be resolved without at least one electric field component. Prior to any MVA analysis, we performed a standard box Fourier band-pass filter on a 12 h time window centered on the shock ramp. To determine the frequency ranges for each filter, we examined a standard Fourier power spectrum (i.e., power versus frequency) for each precursor interval. We then defined frequency ranges based upon the observed frequency peaks for each interval. There were 332 filter ranges for the 113 shocks with precursors, 278 of which had a lower bound >100 mHz. The range of frequencies used for these 278 is 0.11–7.0 Hz, with median values of 0.6 Hz and 1.2 Hz for the lower and upper bounds, respectively.

The use of such a large time window relative to the typical precursor duration (i.e., approximately a few to tens of seconds) is to reduce edge effects and increase Fourier frequency bin resolution [e.g., Harris, 1978]. We follow a similar method to that used by Wilson, et al. [2013] for selecting the best time intervals. However, here we use between one and five frequency filters per precursor interval, an adaptive interval selection software (see Appendix C for details) to define time intervals for MVA and impose the following constraint λ_mid/λ_min ≥ and λ_max/λ_mid ≤ 3, where the max, mid, and min subscripts correspond, respectively, to the maximum, intermediate, and minimum eigenvalues of the magnetic field spectral matrix.

Only the “best” intervals were kept, which are defined as those that maximize λ_mid/λ_min and minimize λ_max/λ_mid in addition to requiring that no two subintervals overlap by more than 55%. Of the ~8.8 million total MVA intervals analyzed, only 2189 satisfied our stringent constraints and 1996 had a ≥0.9° of polarization. Finally, though we performed analysis on precursors using filters below 100 mHz, we only present results using filters where the lower frequency bound was greater than 100 mHz to avoid comparison with lower frequency modes.

B3. Doppler Shift Results

In this appendix we discuss our estimates of the rest frame parameters of the precursors following the methods outlined in Appendix A of Wilson, et al. [2013]. Below we will use the following definitions $\overline{k}=k{\lambda }_e=kc/{\omega }_{\text{pe}}$ (where k is the rest frame wavenumber), $\tilde{\omega }=\omega /{\mathrm{\Omega }}_{\text{ce}}$ (where ω is the rest frame frequency), and $\tilde{V}=V_{\text{bulk}}\cos {\theta }_{\text{kV}}/{\lambda }_e{\mathrm{\Omega }}_{ce}$ (where θ_kV is the angle between $\widehat{\mathbf{k}}$ and 〈V_bulk〉_up). Any parameter that depends upon density, temperature, or magnetic field can be assumed to be the upstream average values in this study (i.e., we did not explicitly show 〈Q〉_up for each parameter for brevity). For spacecraft frame measurements, we will use a subscript SC.

To determine k and ω, we numerically solve equation (A3) from Wilson, et al. [2013] given by

$$0=\tilde{V}{\overline{k}}^3+\left(\cos {\theta }_{\text{kB}}-{\tilde{\omega }}_{\text{SC}}\right){\overline{k}}^2+\tilde{V}\overline{k}-{\tilde{\omega }}_{\text{SC}}$$ (B1)

for $\overline{k}$ and then insert the results into the cold plasma whistler dispersion relation, equation (A1) from Wilson, et al. [2013], given by

$$n^2=\frac{k^2{c}^2}{{\omega }^2}=\frac{{\omega }_{\text{pe}}^2}{\omega \left({\mathrm{\Omega }}_{\text{ce}}\cos {\theta }_{\text{kB}}-\omega \right)}$$ (B2)

to find ω. The n² here refers to the index of refraction.

More recently, Stansby et al., [2016] performed a more accurate analysis on whistler mode wave packets in the solar wind to determine rest frame parameters and found that the cold plasma approximation is qualitatively okay for low wavenumbers (kρ_ce ≲ 0.3) butthermal effects begin to play an important role at higher wavenumbers (kρ_ce ≳ 0.3). Narita et al. [2016] used the four Magnetospheric Multiscale mission (MMS) spacecraft to examine the rest frame properties of broadband whistler turbulence finding their observations consistent with cold plasma approximations for $\overline{k}$ ≲ 0.3. Thus, while thermal effects will likely alter our rest frame estimates from the cold plasma approximation, these and other studies support our use of this assumption.

Appendix C: Adaptive Interval Software

The adaptive interval selection software is a simple set of routines created to automate the process of applying the minimum variance analysis (MVA) [e.g., Khrabrov and Sonnerup, 1998] technique described by Wilson et al. [2009] and Wilson, et al. [2013]; whereby one applies multiple band-pass frequency filters then iteratively zooms-in and zooms-out to find the best subintervals. Below we summarize the basic algorithm used by the software.

The software is a simple set of routines that break an input time interval, composed of N_int time steps, into an integer number of time windows, N_win, each composed of N_sub subintervals. Each time window is N_max time steps in length, with the start of each adjacent time window offset from the preceding one by AW_win. The subinterval length varies from N_min to N_max time steps, with the difference in length between any two consecutive subintervals equal to ΔN_sub. The software imposes the following constraints N_win ≥ 1, N_sub ≥ 1, 7 ≤ N_min ≤ N_max ≤ N_int, ΔN_win ≥ 0, ΔN_sub ≥ 0, and several others that are case specific. Each of the above parameters optional inputs, which can be automatically defined by the software using default values and modification to adjust to the specific constraints of the input time series. Thus, the first part of the algorithm is effectively a binning procedure to define the array indices for later use.

The software then applies a standard box Fourier band-pass filter, from user-defined frequencies, on the entire input time series. It is generally a good idea to input a much larger time range of data than the interval upon which MVA will be applied to reduce edge effects and increase Fourier frequency bin resolution [e.g., Harris, 1978]. The time range for the interval to be analyzed, another required input, defines where to clip the filtered data. The clipped data now contains N_int time steps.

The software then performs MVA on every subinterval within every time window (i.e., brute force approach). After completion, the “best” intervals are defined as those that maximize λ_mid/λ_min and minimize λ_max/λ_mid in addition to requiring that no two subintervals overlap by more than a user-defined threshold (we used 55%). The user can also impose an additional requirement that the best intervals also satisfy λ_mid/λ_min ≥ 10 and λ_max/λ_mid ≤ 3. In practice, circularly polarized plane waves generally satisfy λ_mid/λ_min ≫ 1 and λ_mid/λ_min ~ 1.

While the initial approach is one of brute force and rather simple, the output returns only the best intervals which satisfy all the user-defined criteria and does so orders of magnitude faster than can be done “by hand.” The more commonly used automated software by the community applies a fixed time window for decomposing a time series into a superposition of eigenstates, as described by Samson and Olson [1980]. The major limitation here is that the fixed time window is defined independent of the wave/fluctuation properties. One adverse side effect of this was illustrated by Santolík et al. [2014], where the wave normal angles estimated from the fixed time window method were, on average, much smaller than the instantaneous values.

In contrast, the software described here adjusts the duration of the time window to the wave being analyzed, resulting in λ_mid/λ_min often exceeding several hundreds, much larger than the typical values of a few tens reported in previous studies of whistler precursors [e.g., Aguilar-Rodriguez et al., 2011; Blanco-Cano et al., 2016; Kajdič et al., 2012; Ramírez Vélez et al., 2012]. The primary reasons for the difference are the use of a band-pass filter and subinterval selection on individual wave packets rather than analyzing the entire wave interval.

The adaptive interval and other analysis software can be found at https://github.com/lynnbwilsoniii/wind_3dp_pros.