Nebulin stabilizes the thin filament and regulates force generation in skeletal muscle, but its precise role is not understood. Using conditional knockout mice, Kawai et al. demonstrate that nebulin functions to increase the force per cross-bridge in skinned slow-twitch soleus muscle fibers.
Abstract
Nebulin (Neb) is associated with the thin filament in skeletal muscle cells, but its functions are not well understood. For this goal, we study skinned slow-twitch soleus muscle fibers from wild-type (Neb+) and conditional Neb knockout (Neb−) mice. We characterize cross-bridge (CB) kinetics and the elementary steps of the CB cycle by sinusoidal analysis during full Ca2+ activation and observe that Neb increases active tension 1.9-fold, active stiffness 2.7-fold, and rigor stiffness 3.0-fold. The ratio of stiffness during activation and rigor states is 62% in Neb+ fibers and 68% in Neb− fibers. These are approximately proportionate to the number of strongly attached CBs during activation. Because the thin filament length is 15% shorter in Neb− fibers than in Neb+ fibers, the increase in force per CB in the presence of Neb is ∼1.5 fold. The equilibrium constant of the CB detachment step (K2), its rate (k2), and the rate of the reverse force generation step (k−4) are larger in Neb+ fibers than in Neb− fibers. The rates of the force generation step (k4) and the reversal detachment step (k−2) change in the opposite direction. These effects can be explained by Le Chatelier’s principle: Increased CB strain promotes less force-generating state(s) and/or detached state(s). Further, when CB distributions among the six states are calculated, there is no significant difference in the number of strongly attached CBs between fibers with and without Neb. These results demonstrate that Neb increases force per CB. We also confirm that force is generated by isomerization of actomyosin (AM) from the AM.ADP.Pi state (ADP, adenosine diphophate; Pi, phosphate) to the AM*ADP.Pi state, where the same force is maintained after Pi release to result in the AM*ADP state. We propose that Neb changes the actin (and myosin) conformation for better ionic and hydrophobic/stereospecific AM interaction, and that the effect of Neb is similar to that of tropomyosin.
Introduction
Nebulin (Neb) is a giant protein (mol wt, 700–900 kD; Wang, 1982; Donner et al., 2004) that is known to be associated with the thin filament in skeletal muscles (Wright et al., 1993; Ottenheijm et al., 2012). Neb’s functions are incompletely understood (Labeit and Kolmerer, 1995; Pappas et al., 2011), except that it may function as a stabilizer of the thin filament (Bang et al., 2006; Witt et al., 2006; Pappas et al., 2010) and regulator of active force generation (Root and Wang, 2001; Bang et al., 2009; Chandra et al., 2009; Labeit et al., 2011). Neb has 185 “simple Neb repeats” with ∼35 amino acid residues each (Labeit and Kolmerer, 1995) that are likely to interact with monomeric actin in the thin filament (Jin and Wang, 1991a; Trinick, 1992), much like tropomyosin (Tpm)’s quasi repeat interacts with monomeric actin (Parry, 1975; McLachlan and Stewart, 1976). It has been known that Neb mutations cause nemaline myopathy, supporting the idea that Neb plays an important role in skeletal muscle function (Lehtokari et al., 2011; Li et al., 2015). Studies on Neb− fibers demonstrated a significant reduction of active force (Chandra et al., 2009; Ottenheijm et al., 2010, 2013; Ochala et al., 2011; Li et al., 2015). Neb is not found in cardiac muscles, except for its smaller counterpart, nebulette (mol wt, 107 kD), which is likely to play a role in and near the Z-disk (Moncman and Wang, 1995; Bang and Chen, 2015; Lin et al., 2017).
Previously created Neb knockout mouse models did not survive beyond a few days postnatally (Bang et al., 2006; Witt et al., 2006) and cannot be used to study adult muscle. For this reason, we created a Neb conditional knockout (cKO) mouse model that survives into adulthood and that can be used for investigating the effects of Neb on contractility in adult muscle (Li et al., 2015). For the present study, we used this model and we focused on soleus muscle. While soleus muscle is categorized as a slow-twitch red muscle with type I myosin heavy chain (MHC), it also contains fast-twitch muscle fibers with type IIA MHC both in rabbits (Wang and Kawai, 1996; Galler et al., 2005) and in mice (Li et al., 2015). In the Neb cKO (Neb−) mice, almost all fibers become slow-twitch fibers (Li et al., 2015), and we focused on this fiber type. Previously, a decrease in kTR has been observed in Neb− myofibrils compared with Neb+ myofibrils (Ottenheijm et al., 2013). We characterized the cross-bridge (CB) kinetics and the elementary steps of the CB cycle by sinusoidal analysis and compared the results with those from Neb+ mice. This comparison demonstrates that Neb stiffens the thin filament, modifies elementary steps of the CB cycle, and increases both force and force/CB at maximal activation (pCa 4.55, where pCa = −log10[Ca2+]).
Materials and methods
Animal protocol
The treatment of animals used in this study followed the guidelines approved by the Institutional Animal Care and Use Committee of the University of Arizona. Mice used in this study were handled to minimize pain in compliance with the guideline of the National Academy of Sciences’s Guide for the Care and Use of Laboratory Animals. Neb cKO mice were created at the University of Arizona as described (Li et al., 2015). In brief, the mouse model was created by floxing the start codon of the NEB gene, which was deleted by the MCK-Cre. About half of the mice die within 3 mo postnatally, but the other half survives into adulthood. Mice were used that were 4–6 mo old when Neb expression is ∼2% of that in wild-type mice.
Muscle fiber preparations
At the University of Arizona, soleus muscles were skinned and then dissected into small fiber bundles that were shipped overnight on ice to the University of Iowa (storage solution: 50% glycerol, 50% relaxing solution by volume), where they were stored at ‒20°C. The relaxing solution composition is listed in Table 1 of Wang et al. (2014b). A small bundle consisting of 1–4 fibers (∼100 µm in diameter and ∼1 mm in length) was dissected under the stereomicroscope and mounted to the experimental apparatus with two ends fixed with a minute quantity of nail polish to two hooks made of stainless steel wires. One hook was connected to the length driver, and the other was connected to the tension transducer. The sarcomere length was adjusted to 2.5 µm by optical diffraction. After the experiments, fibers were removed from the experimental apparatus, dissolved in solubilization buffer, frozen, and then shipped back to the University of Arizona for the identification of MHC isoforms. Only fibers that expressed 95–100% MHC-I (slow-twitch, type I fibers) were used for this report. Four female mice were used for Neb+ preparations, and four female mice were used for Neb− preparations. There were no systematic variations with respect to the individual mice from the same genotype.
SDS-PAGE and identification of MHC isoforms
To determine MHC isoform composition, MHC isoforms were separated on 8% SDS gels as described (Agbulut et al., 2003). Gels were stained with Coomassie blue G-250 and imaged, and the percentage of myosin isoforms was determined using ImageJ software. Examples of the MHC expression profile of fiber bundles that were used in this study are shown in Fig. 1.
Figure 1.
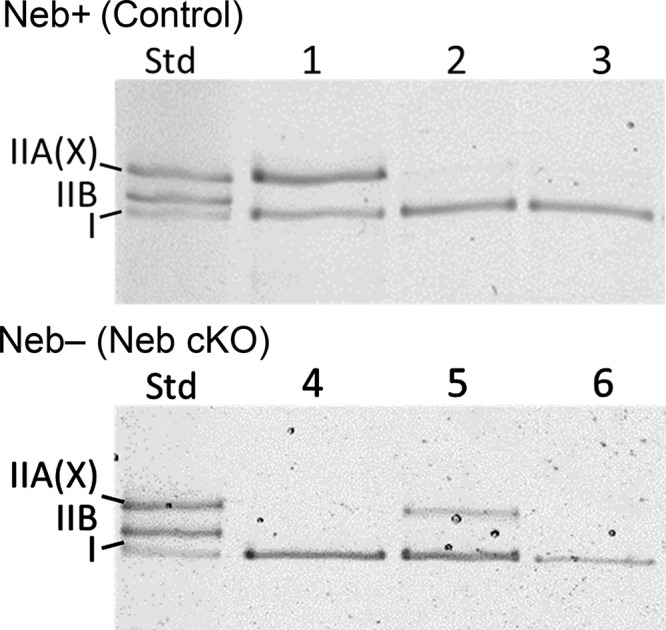
MHC isoform expression analysis with SDS-PAGE. MHC isoform composition of fiber bundles dissected from skinned soleus muscle from Neb-expressing control muscle (top) and Neb-deficient muscle (bottom). The left lane is a standard (Std) that was made by mixing soleus and tibialis cranialis muscle lysate, revealing type I, IIB and IIA(X) MHC bands; note that this electrophoresis system is unable to separate IIA and IIX MHC isoforms. Lanes 1 and 5 are examples of bundles that contained both type I and IIA(X) MHC; these were not used in the present study. Lanes 2, 3, 4, and 6 contain solely type I MHC, and they are examples of fiber bundles that were entered in the present work.
Solutions and experimental protocol
The experiments included the standard activation study, the rigor study, the ATP study, the ADP study, and the phosphate (Pi) study. All experiments were performed at 25°C. The solution compositions used for these studies are listed in Table 1 of Wang et al. (2014b). In brief, all activating solutions contained 6 mM CaEGTA, and pCa was ≤4.55 ([Ca2+] ≥ 28 µM). Acetate (Ac) was the major anion because it preserves muscle fibers well (Andrews et al., 1991). Na+ concentration was maintained at 55 mM, and most Na+ was added as Na2H2ATP and Na2CP. [KAc] was adjusted to result the ionic strength to be at 200 mM. 10 mM 3-(N-morpholino)-propanesulfonic acid (MOPS) was used for the pH buffer, and all experimental solutions were adjusted to pH 7.00. The solutions of the ATP and Pi studies contained 15 mM phosphocreatine (PC) and 80 U/ml creatine kinase (CK); in the ADP study, these were replaced with 0.1 mM P1,P5-di(adenosine-5′-) pentaphosphate (A2P5), which inhibits adenyl kinase.
Fibers were initially tested with the standard activating solution (5 mM MgATP2−, 8 mM Pi, 1 mM Mg2+, 6 mM CaH2EGTA, 79 mM KAc, 13 mM NaAc, 15 mM Na2PC, 80 U/ml CK, 10 mM MOPS, pCa 4.55) at the beginning and in the end of experiments. 5 mM MgATP2- was chosen because this is close to the physiological concentration (Godt and Maughan, 1988) and increases step 2 transition (Scheme 1) so that signal (process C) from this step is enhanced. 8 mM Pi was chosen because this is close to the physiological concentration in slow-twitch fibers (Kushmerick et al., 1992) and increases step 4 transition (Scheme 1) so that signal (process B) from this step is enhanced. Solutions containing varied [ATP], [ADP], or [Pi] were applied subsequently. For the ATP study, [MgATP] was changed as 0.05, 0.1, 0.2, 0.5, 1, 2, 5, and 10 mM, in the presence of 8 mM Pi. For the Pi study, [Pi] was changed as 0, 2, 4, 8, 16, and 30 mM, in the presence of 5 mM MgATP. For the ADP study, [MgADP] was changed as 0, 1, 2, and 3 mM in the presence of 2 mM MgATP and 8 mM Pi. In the rigor study, the standard activating solution was first applied, which was followed by two changes of the rigor solution that did not contain ATP, PC, CK, or A2P5.
Scheme 1.
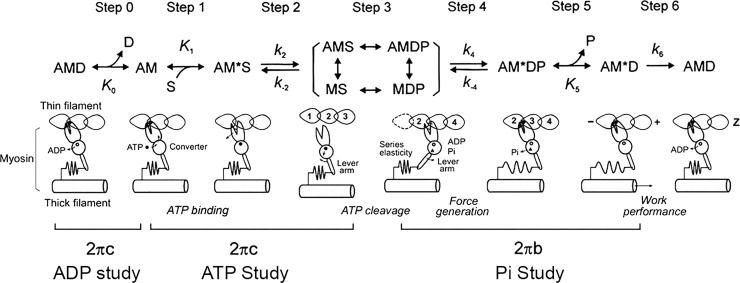
The six-state CB model that was used in the present study. A, actin; M, myosin; D, MgADP; S, MgATP; and P, Pi, phosphate. Upper-case letters K indicate equilibrium constants (including association constants), and lower-case letters k indicate rate constants of the elementary steps of the CB cycle. These are as a whole called “kinetic constants.” z, direction of the Z-line; +, direction of the + end; −, direction of the − end.
Sinusoidal analysis
As soon as a steady tension was developed, sinusoidal analysis was performed to record the tension time course as previously described (Kawai and Brandt, 1980; Kawai and Zhao, 1993). The length of the fibers were oscillated in sine waves of varying frequencies (f): 0.13, 0.25, 0.35, 0.5, 0.7, 1, 2, 3.1, 5, 7, 11, 17, 25, 35, 50, 70, and 100 Hz; this frequency range corresponds to 1.6 ms–1.2 s (=1/(2πf)) in the time domain and is adequate for slow-twitch fibers. The amplitude was 0.125%, or ±1.6 nm/(half sarcomere), which is less than the CB step size (5–10 nm). If this is larger than the step size, the elementary steps could not be resolved, because CB cycles, hence the time course, are limited by the slowest reaction of the cycle. The complex modulus Y(f) was calculated as the ratio of stress to strain at each frequency. Y(f) is a transfer function relating the length change (strain) to the tension change (stress) expressed in the frequency domain, and shown in complex numbers: their real part is called (Young’s) elastic modulus, and the imaginary part is called the viscous modulus. To determine the apparent (measured) rate constants, the complex modulus data were fitted to Eq. 1, which consists of four exponential processes A, B, C, and D; these processes represent the kinetics of actively cycling CBs (Kawai and Brandt, 1980; Zhao and Kawai, 1993), and have been previously used to fit complex modulus of rabbit soleus slow-twitch fibers (Wang and Kawai, 1996, 1997):
| (1) |
where ; a, b, c, and d (a < b < c < d) are the characteristic frequencies of processes A, B, C, and D, respectively; and 2πa, 2πb, 2πc, and 2πd are their respective apparent rate constants. Processes C and D are high frequency–exponential advances (fast tension recovery), where the muscle absorbs work; process B is a medium frequency–exponential delay (delayed tension), where the muscle generates oscillatory work on the length driver; process A is a low frequency–exponential advance (slow tension recovery), where the muscle absorbs work. A, B, C, and D are their respective magnitudes, and H is a constant. The four exponential processes are absent in relaxed fibers, or in fibers in which rigor is induced (Kawai and Brandt, 1980; Kawai et al., 1993; Wang and Kawai, 1997), hence the exponential processes are signatures of cycling CBs.
From Eq. 1, the modulus extrapolated to the infinite frequency (f → ∞) is
| (2) |
which is loosely called “stiffness” in muscle mechanics literature. In step analysis, Y∞ corresponds to phase 1, processes C and D to phase 2, process B to phase 3, and process A to phase 4 (Heinl et al., 1974; Huxley, 1974; Kawai and Brandt, 1980; Kawai and Halvorson, 2007).
Stiffness of the rigor state was measured at 100 Hz. The complex modulus of the rigor state consists mostly of the elastic modulus with minimal viscous modulus, and the complex modulus is only a weak function of frequency (Kawai and Brandt, 1980; Wang and Kawai, 1997).
Elementary steps of the CB cycle
The apparent rate constants 2πb and 2πc were studied as functions of [MgATP], [MgADP], and [Pi] at full activation (pCa ≤ 4.55), and the results were interpreted in terms of Scheme 1 (Kawai and Halvorson, 1991; Kawai and Zhao, 1993), which has six identifiable states based on muscle fiber studies, and six transitions (steps) between them. Our purpose is to characterize these steps together with active tension per CB in Neb− and Neb+ fibers. Step 1 is the ATP binding to the myosin head with the ATP association constant K1. Step 2 is a rapid detachment of myosin from actin that follows the ATP binding, and k2 and k−2 are its forward and reversal rate constants, respectively. Step 3 is the ATP cleavage step, but CBs are weakly attached or detached, hence there is not much signal derived from this step. Consequently these states are combined and called “detached” (Det) state, and they are included in […] in Scheme 1. Step 4 is a conformational change of the Pi bound state, and force is generated in this step as observed in skinned fiber studies (Fortune et al., 1991; Kawai and Halvorson, 1991; Dantzig et al., 1992). The rate constant of its forward step is termed as k4, and its reversal step is termed as k−4. Step 5 is the Pi release step, which itself does not change the force supported by a CB. The Pi binding is its reversal step, and its association constant is K5. Step 6 is isomerization of the ADP bound state, is very slow in muscle fiber studies, and limits the ATP hydrolysis rate. Its rate constant is k6. This step is practically irreversible with the equilibrium constant ∼50 as found in solution studies (Sleep and Hutton, 1980). Step 0 is the ADP release step, which is characterized by the ADP association constant (K0), which is the reversal of step 0. Step 0 is characterized by the ADP study, steps 1 and 2 by the ATP study, steps 4 and 5 by the Pi study, and step 6 by the ATP hydrolysis rate study (Kawai et al., 1987; Zhao and Kawai, 1994).
The result of the ATP and ADP studies were fitted to Eq. 3 (Kawai and Halvorson, 1989) to find K0, K1, k2, and k−2, where S = [MgATP] and D = [MgADP]. K2 = k2/k−2 is defined in the usual way.
| (3) |
For the ATP study, D∼0.01 mM in the presence of PC/CK, and K0D∼0.1, hence K0D is much smaller than (1 + K1S), therefore, this term was omitted from Eq. 2.
The results of the Pi study were fitted to Eq. 4 (Kawai and Halvorson, 1991) to find k4, k−4, and K5, where P = [phosphate], σ is calculated as in Eq. 5 with K1 and K2 deduced from the ATP study and S = 5 mM (experimental condition). Eq. 4 is modified by σ, because there are rapid equilibria to the left of step 4. These equilibria must be faster than step 4 because of the ATP sensitivity of the apparent rate constant 2πb (Kawai and Zhao, 1993).
| (4) |
| (5) |
Tension is fitted to Eq. 6 (Kawai and Zhao, 1993):
| (6) |
where T56 represents fiber tension when all the CBs are in the AM*DP and/or AM*D states, and scales with force/CB when multiplied by the total number of CBs interacting with actin. Because a recent report based on crystallographic evidence of myosin subfragment-1 proposed that force is developed after Pi is released (Sweeney and Houdusse, 2010), we also derived the projected tension based on this assumption (Eq. 7):
| (7) |
In this case, T5 = 0, and T6 is the fiber tension when all the CBs are in the AM*D state.
Statistical analysis
All the data were presented as mean ± SEM. Because two populations were compared, Student’s t test was performed to calculate the probability of identity (P value). 0.01 < P ≤ 0.05 is considered to be significantly different and is indicated by *. P ≤ 0.01 is considered to be highly significantly different and is indicated by **.
Results
Tension and stiffness
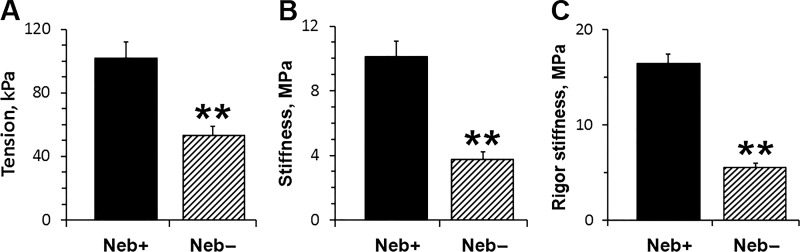
Fig. 2 compares active tension (Fig. 2 A) and stiffness (Fig. 2 B) of Neb+ (control) fibers and Neb− (mutant) fibers that were maximally activated under standard activating conditions. Both isometric tension and dynamic stiffness are significantly reduced (P < 0.01) in Neb− fibers: tension by 48% and stiffness by 63%. After the activation, ATP was washed out to induce the rigor state, and rigor stiffness was determined. Rigor stiffness was 68% less in Neb− fibers compared with that of Neb+ fibers (Fig. 2 C). During the rigor induction, stiffness was lower by 66% for Neb‒ fibers compared with that of Neb+ fibers. The ratio of active stiffness to rigor stiffness, which is an estimate of the number of attached CBs during maximal activation compared with the rigor state, is 62% in Neb+ fibers and 68% in Neb− fibers. These results suggest an approximate equal number of CBs participating during active contraction in Neb+ and Neb− fibers.
Figure 2.
Effect of nebulin on tension and stiffness. (A) Tension and (B) stiffness in standard activation solution (pCa 4.55, 8 mM Pi, 5 mM MgATP, 200 mM ionic strength) at 25°C. n = 14 for Neb+ fibers and n = 22 for Neb− fibers. (C) Rigor stiffness measured at 100 Hz. Fibers were brought to the rigor condition directly from the standard activation solution by washing out ATP. n = 13 (Neb+ fibers) and n = 21 (Neb− fibers). In this and the other figures, data are shown as the mean and SEM.
CB kinetics at the standard activation
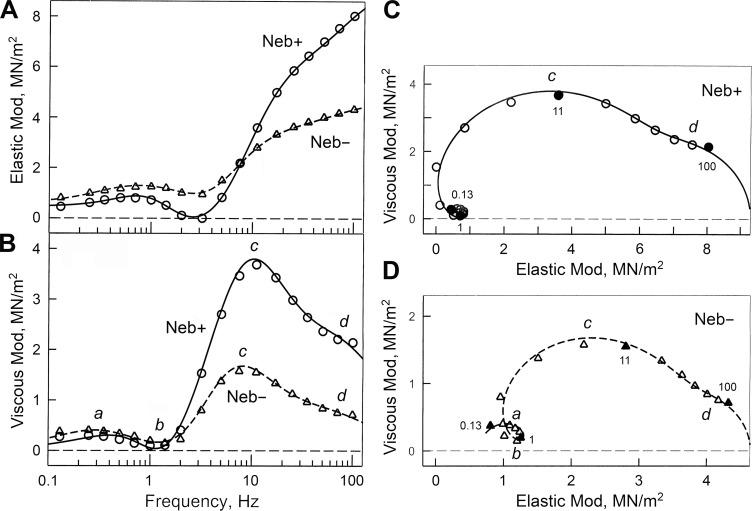
To characterize CB kinetics, a sinusoidal analysis was performed, and complex modulus data Y(f) were obtained during the standard activating conditions (Fig. 3, discrete data points). Fig. 3 A plots elastic moduli versus frequency, and Fig. 3 B plots viscous moduli versus frequency. These are standardized elasticity and viscosity, respectively, and are not expected to change with the physical size of the preparation. Fig. 3, C and D, are Nyquist plots of the same data: Fig. 3 C for Neb+ and Fig. 3 D for Neb− fibers. The complex modulus Y(f) was fitted to Eq. 1 to determine the apparent rate constants (2πa, 2πb, 2πc, and 2πd), which index how fast tension change occurs with time. Because they are absent in relaxed or rigor fibers (Kawai and Brandt, 1980), they represent kinetic properties of actively cycling CBs. The best fit results are shown in Fig. 3 by continuous (Neb+) and broken (Neb−) lines. As seen in all panels of Fig. 3, the data fit well to Eq. 1, demonstrating the appropriateness of Eq. 1 to extract exponential processes.
Figure 3.
Comparison of complex moduli of Neb+ and Neb− fibers. (A and B) Elastic modulus (Mod; A), and viscous modulus (B), plotted as functions of frequency. (C and D) The same data are plotted in Nyquist plots. In B‒D, a, b, c, and d indicate characteristic frequencies, identifying individual exponential processes. These are defined in Eq. 1 and represent the speed (kinetics) of force transients. Discrete points represent the measured data, and curves represent best fits to Eq. 1. The unit of moduli is MN/m2 = MPa, where M = mega = 106, N = Newton, and Pa = Pascal.
The elastic moduli (Fig. 3 A) increased with frequency and peaked at 0.5‒1 Hz, then decreased to assume a local minimum at ∼3 Hz (this is often referred to as fmin by other investigators), then increased again for higher frequencies. At frequencies <7 Hz, the elastic moduli were larger in Neb− fibers than in Neb+ fibers, but they coincided at 7 Hz, and the elastic moduli of Neb− fibers were about half of that of Neb+ fibers for frequencies >7 Hz. There are no differences between the frequencies that produce maximum and minimum elastic moduli.
The viscous moduli (Fig. 3 B) have a local peak at 0.25‒0.35 Hz representing process A, a local minimum at 1‒1.4 Hz representing process B, and a local maximum at 7‒11 Hz representing process C. Process D is represented by a shoulder at around 70 Hz. The viscous moduli are larger in Neb− fibers than Neb+ fibers for frequencies ≤1.4 Hz, but their order reversed for frequencies ≥2 Hz. There are subtle effects in the maximum and minimum frequency points. In Neb− fibers, both maxima occurred at lower frequencies compared with Neb+ fibers, but the minimum frequency occurred at a higher frequency.
The Nyquist plot (Fig. 3, C and D) is a plot of the elastic moduli on the abscissa, and the viscous moduli on the ordinate with the frequency (f) as an intervening parameter. It can be seen that each plot consists of four hemicircles, centered at 0.25‒0.35 Hz (process A), at 1‒1.4 Hz (process B), at 7‒10 Hz (process C), and at the high-frequency end (∼70 Hz; process D). Process D is exhibited only as a shoulder because of its small magnitude. The hemicircles of processes A, C, and D are open downward, and that of process B is open upward. This determines the polarity of each process as shown in Eq. 1. The Nyquist plot of Neb− fibers (Fig. 3 D) are scaled down to about half of the Nyquist plot of Neb+ fibers (Fig. 3 C): notice the change of axis values (both abscissa and ordinate) in Fig. 3 (C and D). This is related to the decrease of active tension and stiffness to about half in Neb− fibers (Fig. 2, A and B).
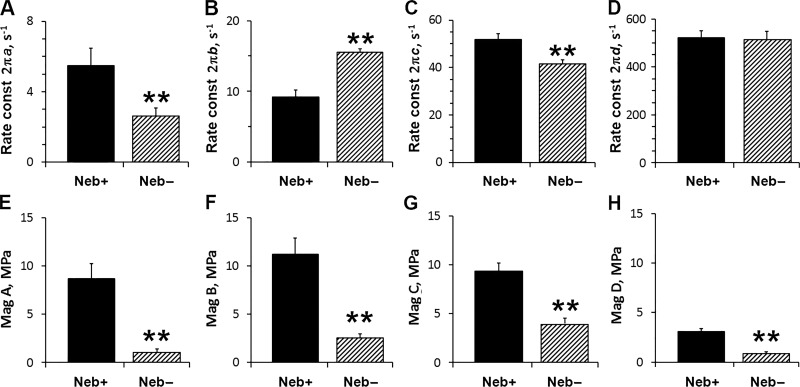
Fig. 4 plots parameters of exponential processes during the standard activation. This figure demonstrates that, in Neb− fibers, 2πa decreased by 52% compared with Neb+ fibers (Fig. 4 A). Similarly, 2πc decreased by 20% in Neb− fibers (Fig. 4 C). In contrast, 2πb increased by 73% in Neb− fibers (Fig. 4 B). There was no change in 2πd between with and without Neb fibers (Fig. 4 D). The magnitude parameters of Neb+ fibers (Fig. 4, E‒H) are comparable for processes A–C at ∼10 MPa, but smaller for process D at 3 MPa. All magnitude parameters decreased significantly by 60–87% in Neb− fibers compared with Neb+ fibers (Fig. 4, E‒H). This is related to the 63% decrease of active stiffness in Neb− fibers (Fig. 2 B).
Figure 4.
Parameters of exponential processes. (A–D) The apparent rate constants (const; in s−1) are plotted for Neb+ and Neb− fibers during the standard activation (pCa 4.55, 8 mM Pi, 5 mM MgATP, 200 mM IS) at 25°C. (E–H) Respective magnitudes (Mag; amplitudes) of the exponential processes are plotted (in MPa). n = 13 for Neb+ fibers, and n = 21 for Neb− fibers.
Elementary steps of the CB cycle
Studying one particular activating condition (such as the standard activation as described above) is not sufficient for characterizing elementary steps of the CB cycle. The characterization is achieved by studying the effects of varying ATP, ADP, and Pi concentrations on the apparent rate constants. The ATP study characterizes ATP binding step 1 and rapid CB detachment step 2, which follows the binding step, and the ADP study characterizes the ADP release step 0 (Kawai and Halvorson, 1989); 2πc is sensitive to steps 0‒2. The Pi study characterizes the Pi-release step 5 and the force-generation step 4, which precedes the Pi-release step (Kawai and Halvorson, 1991); 2πb is sensitive to steps 4 and 5. The results are analyzed in terms of Scheme 1, which is based on six CB states, and which has been successfully used for characterizing rabbit fast-twitch muscle fibers (Kawai and Halvorson, 1991; Kawai and Zhao, 1993; Galler et al., 2005), rabbit slow-twitch muscle fibers (Wang and Kawai, 1996, 1997), and cardiac muscle fibers from rodents (Wang et al., 2013, 2014a; Kawai et al., 2016) and large mammals (Zhao and Kawai, 1996; Fujita et al., 2002).
ATP and ADP studies
Fig. 5 plots the effect of ATP on the apparent rate constant 2πc on a linear scale (Fig. 5 A) and a semi-log scale (Fig. 5 B). Fig. 5 A demonstrates that 2πc increases rapidly with [MgATP] until reaching ∼2 mM and then approaches saturation. The saturation level is lower in Neb− fibers than in Neb+ fibers. The result (discrete data points) was fitted to Eq. 3. From this fitting, we deduced the ATP association constant (K1), the rate constant of the CB detachment step (k2), and the rate constant of its reversal step (k−2), also referred to as “kinetic constants of the elementary steps.” In Fig. 5, the continuous lines represent theoretical projections of Eq. 3 based on best fit parameters; the closeness of the fit demonstrates the appropriateness of the use of Eq. 3 and its associated CB model’s steps 1 and 2 (Scheme 1).
Figure 5.
Effect of ATP on the rate constant. (A and B) Effect of ATP on 2πc in linear plot (A), and semi-log plot (B). Average and SEM are shown for n = 7 (Neb+ fibers) and n = 9 (Neb− fibers). Continuous lines represent best fit curves to Eq. 3. c is the characteristic frequency of the fast exponential advance, and 2πc is its rate constant as defined in Eq. 1.
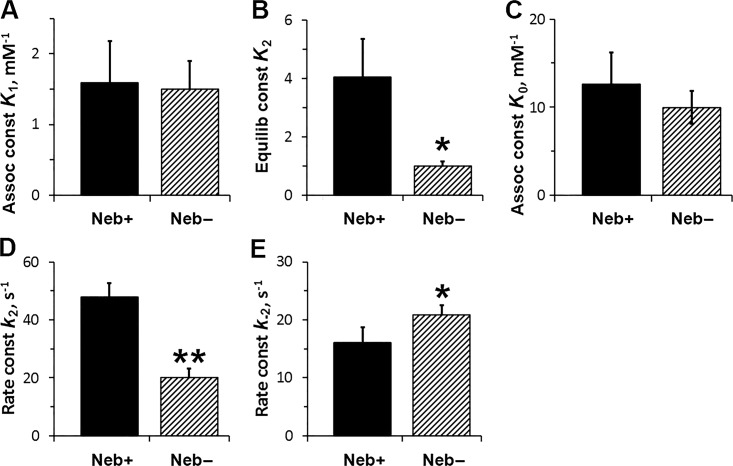
Fig. 6 plots the kinetic constants of the elementary steps. Fig. 6 A shows that K1 is not different between Neb− and Neb+ fibers. Fig. 6 B demonstrates that K2 (equilibrium constant of the CB detachment step) is much reduced (by 74%) in Neb− fibers compared with Neb+ fibers. Fig. 6 D demonstrates that k2 is reduced by 60% in Neb− fibers compared with Neb+ fibers, and Fig. 6 E demonstrates that k−2 is increased by 28%.
Figure 6.
The kinetic constants of steps 0, 1, and 2, deduced from the effects of ATP and ADP on 2πc. For the ATP study (in A, B, D, and E), n = 7 for Neb+ fibers, and n = 9 for the Neb− fibers. For the ADP study (C), n = 10 for Neb+ fibers and n = 5 for Neb− fibers. K2 = k2/k−2. Assoc, Association; Equilib, Equilibrium; const, constant.
The ADP study was performed in the absence of PC/CK, and in the presence of 0.1 mM A2P5 (adenylate kinase inhibitor) to find K0 as previously described (Kawai and Halvorson, 1989). The results are plotted in Fig. 6 C, and they demonstrate that there is no effect of Neb on the ADP association constant. The ADP association constant is about eightfold larger than K1, as found in rabbit soleus slow-twitch fibers (Wang and Kawai, 1996), demonstrating a need to remove ADP as soon as it is formed, because ADP is a competitive inhibitor of ATP (Kawai and Halvorson, 1989) in the actomyosin system.
Pi study
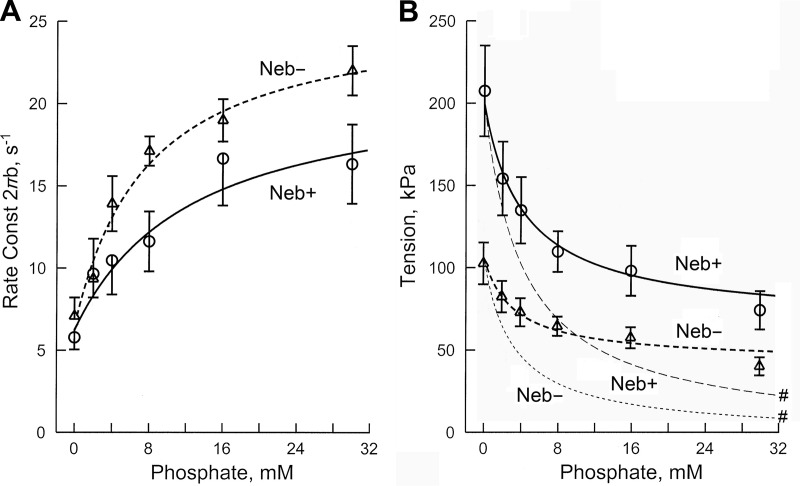
Fig. 7 (discrete data points) shows the effect of Pi (0–30 mM) on the apparent rate constant 2πb and active tension. Fig. 7 A shows that 2πb increased in the low millimolar range of Pi, and approached saturation in the high millimolar range. Fig. 7 B shows that active tension was maximum at no added Pi, and decreased and saturated as [Pi] (P in Eq. 1) was increased. The rate constant results were fitted to Eq. 4, and the tension results were fitted to Eq. 6. In Fig. 7, A and B, the continuous thick lines represent theoretical projections based on Eqs. 4 and 6, respectively, and their best fit parameters. Whereas Eq. 6 is based on the fact that tension develops before Pi is released (T56 = T5 = T6), a recent report suggested that tension develops after Pi is released (Sweeney and Houdusse, 2010), and Eq. 7 is its mathematical representation. The best fit to this equation is plotted in Fig. 7 B with thin broken lines marked with #. The same kinetic constants as obtained from Fig. 7 A were used together with the assumption that T5 = 0 and T6 = T56. The tension data do not fit to Eq. 7, demonstrating that force is unlikely to develop after Pi release. In contrast, the data fit well to Eq. 4, demonstrating the appropriateness of Eqs. 4 and 6 and their associated CB model in Scheme 1 (steps 4 and 5) and supporting that tension develops before Pi is released.
Figure 7.
Effect of Pi on 2πb and active tension. n = 9 (Neb+ fibers), and n = 8 (Neb− fibers). Thick continuous curves represent theoretical projections based on Eqs. 4 and 6 and their best-fit parameters. Thin continuous curves (# in B) represent theoretical projections based on Eq. 7. b is the characteristic frequency of the medium speed exponential delay, and 2πb is its rate constant as defined in Eq. 1.
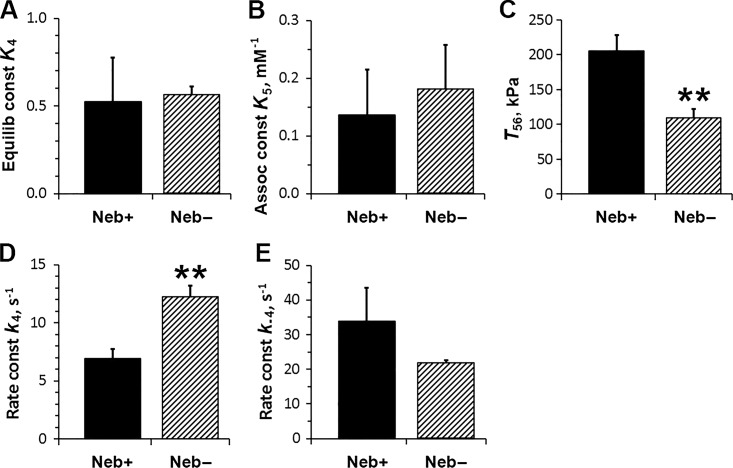
Fig. 8, A and B, plot the equilibrium constant of step 4 (K4), and the association constant of Pi to CBs (K5, reversal of step 5), respectively; these results reveal that there is no significant Neb effect on these equilibrium constants. Fig. 8, D and E, plot the rate constants of the force generation step (k4) and its reversal step (k−4), respectively. This plot shows that the forward rate constant increased significantly in Neb− fibers, but the change in the reversal rate constant was not significant. Fig. 8 C plots T56, which is the force if all CBs are in the tension-generating states, AM*DP and AM*D. This plot demonstrates a 50% reduction in T56 in Neb− fibers compared with Neb+ fibers. This value scales with force/CB and the total number of CBs mobilized to cycle.
Figure 8.
The kinetic constants of steps 4 and 5, and T56, deduced from the effect of Pi on 2πb and tension. (A) K4 is the equilibrium constant of the force generation step 4. (B) K5 is Pi association constant (step 5). (C) T56 is fiber tension when all CBs are either at AM*DP or AM*D states, and scales with force/CB. (D) k4 is the forward rate constant of the force generation step 4. (E) k−4 is its backward rate constant. n = 7 for Neb+ fibers, and n = 8 for Neb− fibers. Assoc, Association; Equilib, Equilibrium; const, constant.
CB distribution
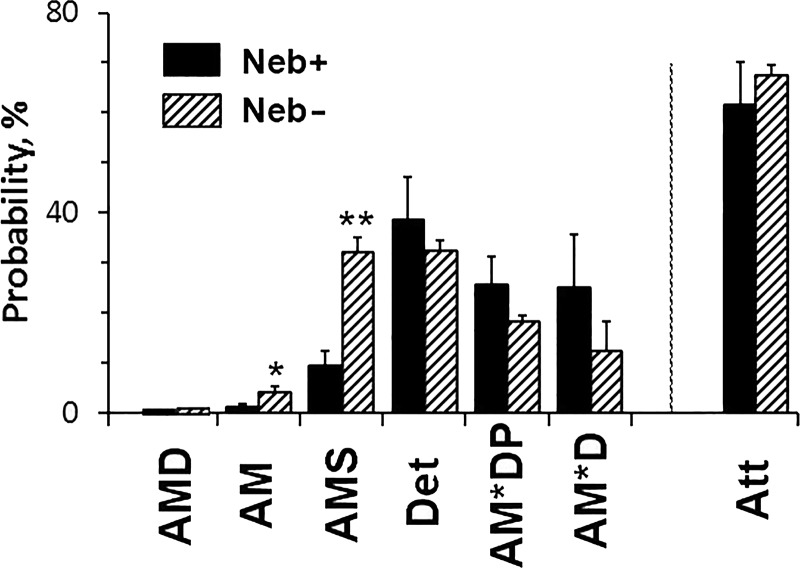
The CB distributions among states were calculated based on the kinetic constants, ligand concentrations (S, D, P), and Eqs. 8‒14 of Zhao and Kawai (1996) for the standard activation (5 mM MgATP, 0.01 mM MgADP, and 8 mM Pi), respectively, and plotted in Fig. 9. [MgADP] is estimated to be 0.01 mM in the presence of PC/CK (Kushmerick et al., 1992). We also added the value for the strongly attached states (Att), which generate or support force. There are significant increases in the AM and AM*S in Neb− fibers. However, the distribution of strongly attached (force-generating) CBs is not significantly different between Neb− and Neb+ fibers. The fraction of CBs in the AMD state is small (<2%) because of the low concentration of [MgADP] in the presence of PC/CK. It is also caused by the small fraction of CBs in the AM state.
Figure 9.
Distribution of CBs among six states. The CB distribution among six states at 8 mM Pi, 5 mM MgATP, and 0.01 mM MgADP is calculated. These were calculated based on the equilibrium constants, ligand concentrations (S = 5 mM, D = 0.01 mM, P = 8 mM), and Eqs. 8‒14 of Zhao and Kawai (1996). The sum of all strongly attached (tension generating) CBs is also included and labeled as Att, where Att = AMD+AM+AM*S+AM*DP+AM*D = 1─Det. Det includes all detached states (MS and MDP) and weakly attached states (AMS and AMDP).
The effect of Neb and comparison with Tpm
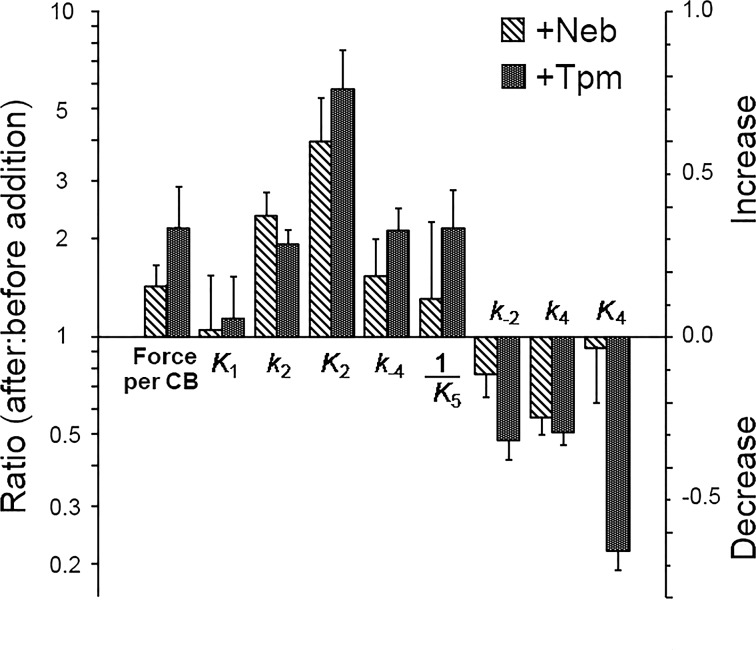
Because we noticed that the effect of Neb addition is reminiscent of the effect of Tpm addition reported earlier (Fujita et al., 2002), we made a comparison of the tension/CB and the eight kinetic constants. Fig. 10 plots the results. The ratio after the addition to before the addition on each parameter is first calculated (left ordinate), then its common log (log10) was taken (right ordinate). With this plot, if the effect is an increase, then log10 is positive, whereas if the effect is a decrease, then log10 is negative. The results of Fig. 10 indicates that the Tpm effect on force/CB is larger than that of Neb, and the same holds true for most parameters, except k2, which is not significantly different. Fig. 10 also implies that the effect is mostly a decrease in the number of attached CBs.
Figure 10.
Comparison of the effect of Neb versus the effect of Tpm (in the presence of the troponin complex and Ca2+) on active tension and the kinetic constants. The ratio (after:before Neb or Tpm addition) of the parameters indicated are plotted (left ordinate). The right ordinate is log10 of the ratio. Active tension for Neb− fibers was corrected for the thin-filament length difference before the ratio was taken. Errors are propagated. K5 is the Pi association constant, hence 1/K5 is used to describe the Pi dissociation step 5. The data on Tpm were taken from Fujita et al. (2002).
Repeated activation–relaxation cycles
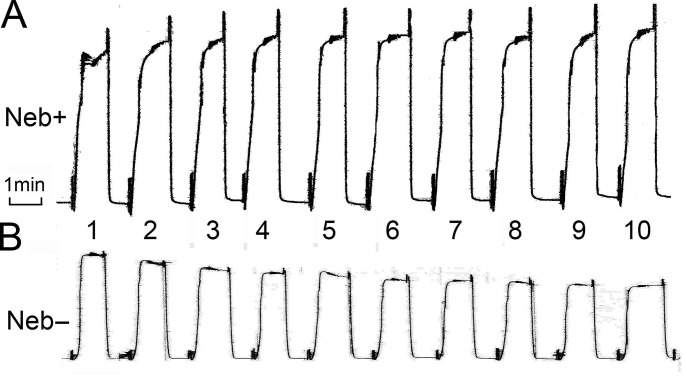
The rigor experiments (Fig. 2 C) indicate that series stiffness is decreased significantly in Neb− fibers, which suggests weakening of the thin filament or its attachment to the Z-disk. Because of this, we tested reproducibility of isometric tension under the two activating conditions: in the presence of 8 mM Pi and in its absence (Figs. 11 and 12). Each activation lasted for 1 min, and 10 of the same activations were repeated (Fig. 11); 10 fibers for each condition were examined. The data were normalized to the initial tension, and the averages are plotted in Fig. 12. In the presence of 8 mM Pi (Fig. 12 B), the isometric tension did not vary much and stayed approximately the same in both Neb+ and Neb− fibers. In contrast, in the absence of Pi (Fig. 12 A), the isometric tension of Neb− fibers declined steadily and significantly with repeated activations (this can also be observed in the example experiment shown in Fig. 11 B). In Neb+ fibers, (Fig. 11 A) this decline was absent, indicating no alterations in the sarcomere structure. The weakening of the preparation is likely caused by the larger tension in the absence of Pi (Fig. 12 A). Because of this rundown with Neb− fibers, the 8-mM Pi turned out to be a better condition to study this preparation.
Figure 11.
Isometric tension of repeated activations at 0 mM Pi and 5 mM MgATP. (A and B) Neb+ fibers (A) and Neb− fibers (B). Small vibration on tension trace is the result of sinusoidal oscillations of the length of the fibers.
Figure 12.
The change of tension with repeated activations comparing Neb+ and Neb− fibers at 25°C. n = 10 for each curve. (A) In the absence of Pi. (B) In the presence of 8 mM Pi (standard activation). The data were individually normalized to the isometric tension of the first activation, then averaged, and plotted against the number of activations, each lasting ∼1 min.
Discussion
In this study, we mechanically characterized type I fibers from mice deficient in the thin filament protein Neb and compared them to type I fibers from mice that express normal amounts of Neb. Large differences were found in both tension and stiffness during maximal activation and during rigor. Measurements during rigor, a state in which CB attachment to the thin filament is maximized, revealed a stiffness value in Neb− fibers that was 0.34 of that of Neb+ fibers (Fig. 2 C). Some of this is likely due to the shorter thin filaments of Neb− fibers (0.97 µm compared with 1.14 µm in Neb+ fibers, including 1/2 width of the Z-line [Li et al., 2015]), whereas the thick filament length is 1.60 µm with a central bare zone of 0.16 µm. At the sarcomere length of 2.50 µm, at which our study was performed, the length of the thick-and-thin filament overlap region is 0.52 µm (= 0.97 + 1.60/2 ‒ 2.50/2) in Neb− fibers, and 0.69 µm (= 1.14 + 1.60/2 ‒ 2.50/2) in Neb+ fibers (the thin filament does not reach the bare zone). As a consequence, the overlap region of Neb− fibers is 0.754 (= 0.52/0.69) of that of Neb+ fibers, indicating only 75.4% of CBs are generating force in Neb− fibers compared with Neb+ fibers. Therefore, some quantities measured with Neb− fibers must be multiplied by 1.327 (= 0.69/0.52) for equal overlap comparison; the corrections apply to the data in Figs. 2; 3; 4, E–H; 7 B; and 8 C. This correction results in a 0.45 (= 0.34 × 1.327)–fold difference in the rigor stiffness, or an increase of rigor stiffness by 2.2 (= 1/0.45)–fold when Neb is added. Although it has been known for some time that thin filaments are compliant in skeletal muscle (Huxley et al., 1994; Wakabayashi et al., 1994), with thin filament accounting for approximately half of the rigor stiffness (Higuchi et al., 1995), our work for the first time provides mechanical evidence that, in the absence of Neb, thin filament compliance is greatly increased. In cardiac muscles, Neb is absent. Instead, its related protein nebulette is present (Bang and Chen, 2015; Lin et al., 2017), but it is a small protein that cannot reach far along the thin filament and is unlikely to strengthen the full thin filament.
We observed that active tension is reduced to 52% (69% with the overlap correction) in Neb− fibers compared with Neb+ fibers (Fig. 2 A). This result is consistent with earlier observations (Ottenheijm et al., 2010, 2013; Ochala et al., 2011; Li et al., 2015). The reduction in tension in Neb− fibers is unlikely due to the increased thin filament compliance, because CBs can cycle many times (at the expense of increased ATP hydrolysis) to strain the series elasticity to the extent that the force generated by CBs and the force in thin filament due to its strain are balanced. The effect of thin filament compliance on isometric tension has also been evaluated in several mathematical modeling studies. A recent study (Fenwick et al., 2017) predicted that a 10-fold increase in the thin filament compliance results in an ∼10% decline in isometric tension (their Fig. 5). In our present study, the estimated compliance increase is ∼2.2-fold based on the rigor study, which, according to this model, predicts a 2.2% (= 10% x 2.2/10) force decrease with the linear extrapolation, which is very much less than the 31% (= 100 – 69%) reduction that we measured. In another modeling study (Daniel et al., 1998), a 10-fold increase in thin filament compliance resulted in a 28% (= (16.18 – 12.68)/12.68) increase in isometric tension (Table 1 of Daniel et al., 1998), which predicts a 6% (= 28% × 2.2/10) increase in tension in our experiments. Thus the modeling studies provide conflicting results, and, furthermore, the predicted effects of the compliance increase on tension are much less than measured in the present study.
With regard to the role of CBs in force, there are two mechanisms that can account for the force reduction. In mechanism 1, the force per CB is reduced without changing the number of force-generating CBs. In mechanism 2, the number of force-generating CB is reduced without changing the force generated by each CB. Because the observed T56 is the product of force/CB and the number of cycling (activated) CBs, T56 alone is not able to differentiate these two possibilities, hence other methods must be sought. For this purpose, rigor stiffness can be used. It is a good indicator of stiffness when all available CBs interact with actin, regardless of the condition of the thin filament. By taking the ratio of active stiffness (Y∞) to rigor stiffness, one can obtain an approximate estimate of the number of CBs attached during activation (the presence of series compliance precludes great precision: Wang and Kawai, 1997). The ratio was found to be 70 ± 5% in Neb− fibers, and 61 ± 9% in Neb+ fibers (the difference is not significant). Hence, mechanism 2 is unlikely. Therefore, we conclude that mechanism 1 is likely to explain our results: force generated in each CB is reduced in Neb− fibers compared with Neb+ fibers.
Based on this conclusion, the measured difference in T56 (Fig. 8 C) between the two kinds of fibers (189 ± 22 kPa for Neb+ fibers, and 146 ± 16 kPa for Neb− fibers with the overlap correction) supports that force generated by a CB increases when Neb is present. Similarly, if we divide the isometric tension by the probability of strongly attached CBs, higher force/CB values are obtained for Neb+ fibers (164 kPa versus 119 kPa for Neb− fibers with the correction).
As seen in plots in Fig. 7, the fits of the data to Eqs. 4 and 6 are satisfactory, demonstrating the appropriateness of these equations and their associated CB model in Scheme 1 (steps 4 and 5), and confirming the earlier reports that tension develops before Pi is released (Fortune et al., 1991; Kawai and Halvorson, 1991; Dantzig et al., 1992; Kawai and Zhao, 1993; Wang and Kawai, 1997). In this case, T5 = T6 = T56; T5 is the force associated with the AM*DP state, and T6 with the AM*D state. A recent report suggested that tension develops after Pi is released based on crystallographic evidence on myosin (Sweeney and Houdusse, 2010). Eq. 7 is its mathematical representation, which is plotted in Fig. 7 B with broken thin lines (marked with #). In this case, T5 = 0 and T6 = T56. As seen in Fig. 7 B, the tension data do not fit to Eq. 7, demonstrating that force does not develop after Pi is released. It is possible that the presence of actin, Tpm, and Neb change the shape of actin and myosin conformations. The crystallographic results were obtained in the absence of these thin filament proteins and in the absence of tension measurement. Hence the results may be different from skinned fiber studies that were performed in the presence of all the contractile proteins, in physiological solutions, and while tension was generated. It has been known for some time that the myosin ATP hydrolysis rate increases dramatically in the presence of actin (Bremel and Weber, 1972; Taylor, 1979) and further increases in the presence of Tpm (Murray et al., 1982); a similar increase in isometric tension is present as actin filament is added and as Tpm, Tn, and Ca2+ are added in skinned fiber experiments (Fujita et al., 2002), suggesting significant conformational changes of myosin when actin and Tpm, Ca2+, and possibly Neb are present.
Our results also show that Neb affects elementary steps of the CB cycle (Figs. 6 and 8), particularly in k2, K2, k−2, k−4, and k4: k2 is the rate of CB detachment step, k−2 is the rate of its reversal, K2 is its equilibrium constant, k4 is the rate of the force generation step, and k−4 is its reversal step. Their changes are coupled with the change in force/CB, because it has been known that these kinetic constants are strain-sensitive, and an increase in the strain promotes the detached states (or low force states), and a decrease in the strain promotes the attached states (or high force states). This is in accordance with Le Chatelier’s principle as it is applied to the muscle system (Kawai and Halvorson, 2007). Although Le Chatelier’s principle applies for the equilibrium condition, it can be extended to the steady-state condition if one does not focus on the rate-limiting step (slowest step in the CB cycle), which is step 6. Because we apply this principle on faster steps 0, 1, 2, 4, and 5, which are nearly at equilibria, the use of Le Chatelier’s principle is justified. When force/CB (strain) is increased as Neb is added, K2, k2, and k−4 increase, and k−2 and k4 decrease, as predicted based on Le Chatelier’s principle and as observed (Figs. 6 and 8). The changes in the kinetic constants could not be predicted by mechanism 2, because in this mechanism, there should be no difference in the strain between Neb− and Neb+ fibers at the CB level, hence the kinetic constants are not predicted to change with the addition of Neb. The strain sensitivity of the kinetic constants has long been assumed and modeled (Huxley, 1957; Huxley and Simmons, 1971; Smith and Geeves, 1995a,b; Kawai and Halvorson, 2007), and we provide direct supportive evidence that this is the case. No effect of Neb on ligand association constants (K0 for ADP, K1 for ATP, and K5 for Pi) is detected (Figs. 6, A and C; and Fig. 8 B), indicating that CB force change is minimal with these steps. This is because step 1 and the reversal of steps 0 and 5 consist of a diffusion-limited (instantaneous) collision complex formation, which itself does not change force, and the force change occurs subsequently with a conformational change (Kawai and Zhao, 1993) with a detectable time course.
We noticed that the effects of Neb on the elementary steps of the CB cycle are similar to those previously published for Tpm (see Fig. 10 for comparison). The effect of Tpm was studied previously in actin filament reconstituted fibers and the results were compared with the thin filament reconstituted fibers from bovine myocardium (Fujita et al., 2002). The addition of Tpm (together with the troponin complex and Ca2+) increased force/CB by 2.1-fold, and Neb by 1.91-fold (1.45-fold with the overlap correction). They do not have an effect on the ATP binding step (K1). When force/CB (strain) is increased with addition of Neb or Tpm, k2, K2, and k−4 increase, and k−2 and k4 decrease (Fig. 10), as predicted based on Le Chatelier’s principle, because these changes promote lower force states. K5 is the Pi association constant, hence its reciprocal value is plotted in Fig. 10 to emphasize the Pi release step. This step increases with Tpm, but the increase is not significant with Neb because of a scatter in the data. Once again, this observation supports the idea that force is not increased with the Pi release step; if force is generated with this step, 1/K5 should decrease when Neb or Tpm is added, and this is the opposite of what is observed (Fig. 10). The K4 reduction is different for Neb and Tpm, which indicates that Neb and Tpm may have different functional roles in this step.
Because the steady-state CB distribution primarily depends on the equilibrium constants, only the AM and AMS states are increased in Neb− fibers, owing to the decrease in K2, but changes in other states are not significant (Fig. 9). This resulted in a slightly greater number of strongly attached CBs in Neb− fibers (68 ± 2%) than Neb+ fibers (62 ± 9%), but this difference is not significant (Fig. 9). These results nicely complement the estimates of attached CBs based on the stiffness ratio of active:rigor states (70 ± 5% in Neb− fibers, and 61 ± 9% in Neb+ fibers).
Now let us consider what happens at the molecular level. Neb has a “simple Neb repeat” structure with 185 repeats that contain ∼35 amino acid residues each (Labeit and Kolmerer, 1995). Each repeat is likely to interact with an actin monomer (Jin and Wang, 1991b), similar to how Tpm’s quasi repeats interact with actin monomers (Parry, 1975; McLachlan and Stewart, 1976). Thus, it is possible that Neb functions similar to Tpm. It has been shown that, in the presence of troponin and Ca2+, Tpm allosterically affects actin so that it has a better stereospecific and hydrophobic match with myosin that can now generate a larger force/CB (Fujita et al., 2002; Fujita and Kawai, 2002). Interestingly, Neb–Tpm interaction has been demonstrated (Ogut et al., 2003; Marttila et al., 2014), and structural data suggest that both Neb and Tpm can move around on the thin filament (Lukoyanova et al., 2002). Thus, it is possible that both Tpm and Neb are part of the cooperative unit. Here it is important to note that, in both Neb and Tpm, force/CB increases in spite of the fact that Neb and Tpm are physically placed between actin and myosin, which might sterically hinder the actomyosin interaction. Thus, their effect on actin may be steric blocking at low calcium levels, but allosteric enhancement at high calcium levels. However, our observations and intuitions derived from them are based on muscle fiber studies under the isometric contraction in physiological solutions with high protein concentrations, and it may not apply to the unloaded conditions in low ionic strength solutions such as used in the in vitro motility assays (Gordon et al., 1998; Homsher et al., 2000; Schoffstall et al., 2011) with low protein concentrations.
How does Neb alter the conformation of actin? We speculate that, similar to Tpm (Zhao and Kawai, 1994; Lu et al., 2005; Wang et al., 2017), Neb interacts with actin to expose ionic and hydrophobic amino acid residues on the surface of actin, and these are important for myosin interaction. The electrostatic interaction takes place for a long distance (7 Å at 200 mM ionic strength [Wang et al., 2015]), and is considered to be the first event in actomyosin interaction (Sutoh, 1982; Sutoh et al., 1991; Furch et al., 1998; Wang et al., 2017). This is followed by the hydrophobic and stereospecific interactions that take place at a short distance (∼1 Å), resulting in force generation (Zhao and Kawai, 1994); it appears that the electrostatic interaction promotes the hydrophobic interaction (Lu et al., 2005). In the absence of Neb, actin’s ionic/hydrophobic residues may be less exposed, hence myosin may not interact with actin as much as it does in the presence of Neb, resulting in a lowered activation of myosin, which in turn results in less force generation.
There has been a concern that a change in series compliance may alter the rate constants being measured (Luo et al., 1993, 1994; Martyn et al., 2002; Labeit et al., 2011). To address this concern, we previously altered the length of the thin filament in the I-band (changing series compliance as a result) by varying the sarcomere length in the 1.8–2.4-µm range in rabbit psoas fibers, and found that the apparent rate constants 2πb and 2πc are not altered by changing the series compliance (Wang et al., 1999). In contrast, increased series compliance lessens the slow-rate constant kTR measured by a quick release and restretch experiment as observed by Li et al. (2015), and as predicted from the new model proposed by Wang and Kawai (2013). Thus, it appears that the series compliance alters the slow-rate constant, including kTR, but it does not affect the fast-rate constants, such as 2πb and 2πc, used in this report.
Finally, interesting results were also revealed when fibers were repeatedly activated (Figs. 11 and 12). We tested two conditions: absence of added Pi (Figs. 11 and 12) and 8 mM Pi added to the activating solution (Fig. 12). Adding 8 mM Pi lowered active tension by about half of that with 0 mM Pi (Fig. 7 B), hence this may be considered a more gentle condition. In the presence of Pi, isometric tension did not change much during repeated activations either in the presence or absence of Neb (Fig. 12 B). In the absence of added Pi, isometric tension decreased when Neb was absent, but the isometric tension remained the same when Neb was present (Figs. 11 and 12 A). These experiments demonstrate that muscle fibers are weak in the absence of Neb, in particular when large tension develops, which may structurally damage the thin filament when Neb is absent. Thus, we propose that Neb adds to the tensile strength of the thin filament in addition to increasing its stiffness.
Conclusions
Neb functions to strengthen the thin filament and increase its stiffness. Active tension and stiffness are reduced in Neb− fibers compared with Neb+ fibers, caused by a 29% decrease in force generated per CB. Some elementary steps are modified, the effects are similar to Tpm, and follow Le Chatelier’s principle. No significant change is found in strongly attached CB numbers between Neb− and Neb+ fibers. Neb− fibers are weaker than Neb+ fibers for repeated activations when Pi is absent, most likely because active tensions exceed the tensile strength of the Neb-deficient thin filament.
Acknowledgments
This work was supported by grants from the American Heart Association (13GRNT16810043 to M. Kawai) and the National Institute of Arthritis and Musculoskeletal and Skin Diseases of the National Institutes of Health (R01AR053897 to H.L. Granzier).
The authors declare no competing financial interests.
Author contributions: Planning of the experiments was done by M. Kawai and H.L. Granzier. Mechanical experiments were done by T.S. Karam, and gel analysis was done by J. Kolb. Supervision of experiments were done by M. Kawai, L. Wang, and H.L. Granzier. Analyses of the results were done by all authors. Manuscript was drafted by M. Kawai and extensively modified by H.L. Granzier, followed by proofreading by all authors.
Richard L. Moss served as guest editor.
References
- Agbulut O., Noirez P., Beaumont F., and Butler-Browne G.. 2003. Myosin heavy chain isoforms in postnatal muscle development of mice. Biol. Cell. 95:399–406. 10.1016/S0248-4900(03)00087-X [DOI] [PubMed] [Google Scholar]
- Andrews M.A., Maughan D.W., Nosek T.M., and Godt R.E.. 1991. Ion-specific and general ionic effects on contraction of skinned fast-twitch skeletal muscle from the rabbit. J. Gen. Physiol. 98:1105–1125. 10.1085/jgp.98.6.1105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bang M.L., and Chen J.. 2015. Roles of Nebulin Family Members in the Heart. Circ. J. 79:2081–2087. 10.1253/circj.CJ-15-0854 [DOI] [PubMed] [Google Scholar]
- Bang M.L., Li X., Littlefield R., Bremner S., Thor A., Knowlton K.U., Lieber R.L., and Chen J.. 2006. Nebulin-deficient mice exhibit shorter thin filament lengths and reduced contractile function in skeletal muscle. J. Cell Biol. 173:905–916. 10.1083/jcb.200603119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bang M.L., Caremani M., Brunello E., Littlefield R., Lieber R.L., Chen J., Lombardi V., and Linari M.. 2009. Nebulin plays a direct role in promoting strong actin-myosin interactions. FASEB J. 23:4117–4125. 10.1096/fj.09-137729 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bremel R.D., and Weber A.. 1972. Cooperation within actin filament in vertebrate skeletal muscle. Nat. New Biol. 238:97–101. 10.1038/newbio238097a0 [DOI] [PubMed] [Google Scholar]
- Chandra M., Mamidi R., Ford S., Hidalgo C., Witt C., Ottenheijm C., Labeit S., and Granzier H.. 2009. Nebulin alters cross-bridge cycling kinetics and increases thin filament activation: a novel mechanism for increasing tension and reducing tension cost. J. Biol. Chem. 284:30889–30896. 10.1074/jbc.M109.049718 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Daniel T.L., Trimble A.C., and Chase P.B.. 1998. Compliant realignment of binding sites in muscle: transient behavior and mechanical tuning. Biophys. J. 74:1611–1621. 10.1016/S0006-3495(98)77875-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dantzig J.A., Goldman Y.E., Millar N.C., Lacktis J., and Homsher E.. 1992. Reversal of the cross-bridge force-generating transition by photogeneration of phosphate in rabbit psoas muscle fibres. J. Physiol. 451:247–278. 10.1113/jphysiol.1992.sp019163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donner K., Sandbacka M., Lehtokari V.L., Wallgren-Pettersson C., and Pelin K.. 2004. Complete genomic structure of the human nebulin gene and identification of alternatively spliced transcripts. Eur. J. Hum. Genet. 12:744–751. 10.1038/sj.ejhg.5201242 [DOI] [PubMed] [Google Scholar]
- Fenwick A.J., Wood A.M., and Tanner B.C.W.. 2017. Effects of cross-bridge compliance on the force-velocity relationship and muscle power output. PLoS One. 12:e0190335 10.1371/journal.pone.0190335 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fortune N.S., Geeves M.A., and Ranatunga K.W.. 1991. Tension responses to rapid pressure release in glycerinated rabbit muscle fibers. Proc. Natl. Acad. Sci. USA. 88:7323–7327. 10.1073/pnas.88.16.7323 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujita H., and Kawai M.. 2002. Temperature effect on isometric tension is mediated by regulatory proteins tropomyosin and troponin in bovine myocardium. J. Physiol. 539:267–276. 10.1113/jphysiol.2001.013220 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fujita H., Sasaki D., Ishiwata S., and Kawai M.. 2002. Elementary steps of the cross-bridge cycle in bovine myocardium with and without regulatory proteins. Biophys. J. 82:915–928. 10.1016/S0006-3495(02)75453-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Furch M., Geeves M.A., and Manstein D.J.. 1998. Modulation of actin affinity and actomyosin adenosine triphosphatase by charge changes in the myosin motor domain. Biochemistry. 37:6317–6326. 10.1021/bi972851y [DOI] [PubMed] [Google Scholar]
- Galler S., Wang B.G., and Kawai M.. 2005. Elementary steps of the cross-bridge cycle in fast-twitch fiber types from rabbit skeletal muscles. Biophys. J. 89:3248–3260. 10.1529/biophysj.104.056614 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Godt R.E., and Maughan D.W.. 1988. On the composition of the cytosol of relaxed skeletal muscle of the frog. Am. J. Physiol. 254:C591–C604. 10.1152/ajpcell.1988.254.5.C591 [DOI] [PubMed] [Google Scholar]
- Gordon A.M., Chen Y., Liang B., LaMadrid M., Luo Z., and Chase P.B.. 1998. Skeletal muscle regulatory proteins enhance F-actin in vitro motility. Adv Exp Med Biol. 453:187–196; discussion 196–187. [DOI] [PubMed] [Google Scholar]
- Heinl P., Kuhn H.J., and Rüegg J.C.. 1974. Tension responses to quick length changes of glycerinated skeletal muscle fibres from the frog and tortoise. J. Physiol. 237:243–258. 10.1113/jphysiol.1974.sp010480 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Higuchi H., Yanagida T., and Goldman Y.E.. 1995. Compliance of thin filaments in skinned fibers of rabbit skeletal muscle. Biophys. J. 69:1000–1010. 10.1016/S0006-3495(95)79975-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homsher E., Lee D.M., Morris C., Pavlov D., and Tobacman L.S.. 2000. Regulation of force and unloaded sliding speed in single thin filaments: effects of regulatory proteins and calcium. J. Physiol. 524:233–243. 10.1111/j.1469-7793.2000.00233.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley A.F. 1957. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 7:255–318. 10.1016/S0096-4174(18)30128-8 [DOI] [PubMed] [Google Scholar]
- Huxley A.F. 1974. Muscular contraction. J. Physiol. 243:1–43. 10.1113/jphysiol.1974.sp010740 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huxley A.F., and Simmons R.M.. 1971. Proposed mechanism of force generation in striated muscle. Nature. 233:533–538. 10.1038/233533a0 [DOI] [PubMed] [Google Scholar]
- Huxley H.E., Stewart A., Sosa H., and Irving T.. 1994. X-ray diffraction measurements of the extensibility of actin and myosin filaments in contracting muscle. Biophys. J. 67:2411–2421. 10.1016/S0006-3495(94)80728-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jin J.P., and Wang K.. 1991a Cloning, expression, and protein interaction of human nebulin fragments composed of varying numbers of sequence modules. J. Biol. Chem. 266:21215–21223. [PubMed] [Google Scholar]
- Jin J.P., and Wang K.. 1991b Nebulin as a giant actin-binding template protein in skeletal muscle sarcomere. Interaction of actin and cloned human nebulin fragments. FEBS Lett. 281:93–96. 10.1016/0014-5793(91)80366-B [DOI] [PubMed] [Google Scholar]
- Kawai M., and Brandt P.W.. 1980. Sinusoidal analysis: a high resolution method for correlating biochemical reactions with physiological processes in activated skeletal muscles of rabbit, frog and crayfish. J. Muscle Res. Cell Motil. 1:279–303. 10.1007/BF00711932 [DOI] [PubMed] [Google Scholar]
- Kawai M., and Halvorson H.R.. 1989. Role of MgATP and MgADP in the cross-bridge kinetics in chemically skinned rabbit psoas fibers. Study of a fast exponential process (C). Biophys. J. 55:595–603. 10.1016/S0006-3495(89)82857-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M., and Halvorson H.R.. 1991. Two step mechanism of phosphate release and the mechanism of force generation in chemically skinned fibers of rabbit psoas muscle. Biophys. J. 59:329–342. 10.1016/S0006-3495(91)82227-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M., and Halvorson H.R.. 2007. Force transients and minimum cross-bridge models in muscular contraction. J. Muscle Res. Cell Motil. 28:371–395. 10.1007/s10974-008-9131-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M., and Zhao Y.. 1993. Cross-bridge scheme and force per cross-bridge state in skinned rabbit psoas muscle fibers. Biophys. J. 65:638–651. 10.1016/S0006-3495(93)81109-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawai M., Güth K., Winnikes K., Haist C., and Rüegg J.C.. 1987. The effect of inorganic phosphate on the ATP hydrolysis rate and the tension transients in chemically skinned rabbit psoas fibers. Pflugers Arch. 408:1–9. 10.1007/BF00581833 [DOI] [PubMed] [Google Scholar]
- Kawai M., Saeki Y., and Zhao Y.. 1993. Crossbridge scheme and the kinetic constants of elementary steps deduced from chemically skinned papillary and trabecular muscles of the ferret. Circ. Res. 73:35–50. 10.1161/01.RES.73.1.35 [DOI] [PubMed] [Google Scholar]
- Kawai M., Karam T.S., Michael J.J., Wang L., and Chandra M.. 2016. Comparison of elementary steps of the cross-bridge cycle in rat papillary muscle fibers expressing α- and β-myosin heavy chain with sinusoidal analysis. J. Muscle Res. Cell Motil. 37:203–214. 10.1007/s10974-016-9456-2 [DOI] [PubMed] [Google Scholar]
- Kushmerick M.J., Moerland T.S., and Wiseman R.W.. 1992. Mammalian skeletal muscle fibers distinguished by contents of phosphocreatine, ATP, and Pi. Proc. Natl. Acad. Sci. USA. 89:7521–7525. 10.1073/pnas.89.16.7521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Labeit S., and Kolmerer B.. 1995. The complete primary structure of human nebulin and its correlation to muscle structure. J. Mol. Biol. 248:308–315. 10.1016/S0022-2836(95)80052-2 [DOI] [PubMed] [Google Scholar]
- Labeit S., Ottenheijm C.A., and Granzier H.. 2011. Nebulin, a major player in muscle health and disease. FASEB J. 25:822–829. 10.1096/fj.10-157412 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lehtokari V.L., Pelin K., Herczegfalvi A., Karcagi V., Pouget J., Franques J., Pellissier J.F., Figarella-Branger D., von der Hagen M., Huebner A., et al. . 2011. Nemaline myopathy caused by mutations in the nebulin gene may present as a distal myopathy. Neuromuscul. Disord. 21:556–562. 10.1016/j.nmd.2011.05.012 [DOI] [PubMed] [Google Scholar]
- Li F., Buck D., De Winter J., Kolb J., Meng H., Birch C., Slater R., Escobar Y.N., Smith J.E. III, Yang L., et al. . 2015. Nebulin deficiency in adult muscle causes sarcomere defects and muscle-type-dependent changes in trophicity: novel insights in nemaline myopathy. Hum. Mol. Genet. 24:5219–5233. 10.1093/hmg/ddv243 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin B.L., Song T., and Sadayappan S.. 2017. Myofilaments: Movers and Rulers of the Sarcomere. Compr. Physiol. 7:675–692. 10.1002/cphy.c160026 [DOI] [PubMed] [Google Scholar]
- Lu X., Bryant M.K., Bryan K.E., Rubenstein P.A., and Kawai M.. 2005. Role of the N-terminal negative charges of actin in force generation and cross-bridge kinetics in reconstituted bovine cardiac muscle fibres. J. Physiol. 564:65–82. 10.1113/jphysiol.2004.078055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lukoyanova N., VanLoock M.S., Orlova A., Galkin V.E., Wang K., and Egelman E.H.. 2002. Each actin subunit has three nebulin binding sites: implications for steric blocking. Curr. Biol. 12:383–388. 10.1016/S0960-9822(02)00678-4 [DOI] [PubMed] [Google Scholar]
- Luo Y., Cooke R., and Pate E.. 1993. A model of stress relaxation in cross-bridge systems: effect of a series elastic element. Am. J. Physiol. 265:C279–C288. 10.1152/ajpcell.1993.265.1.C279 [DOI] [PubMed] [Google Scholar]
- Luo Y., Cooke R., and Pate E.. 1994. Effect of series elasticity on delay in development of tension relative to stiffness during muscle activation. Am. J. Physiol. 267:C1598–C1606. 10.1152/ajpcell.1994.267.6.C1598 [DOI] [PubMed] [Google Scholar]
- Marttila M., Hanif M., Lemola E., Nowak K.J., Laitila J., Grönholm M., Wallgren-Pettersson C., and Pelin K.. 2014. Nebulin interactions with actin and tropomyosin are altered by disease-causing mutations. Skelet. Muscle. 4:15 10.1186/2044-5040-4-15 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martyn D.A., Chase P.B., Regnier M., and Gordon A.M.. 2002. A simple model with myofilament compliance predicts activation-dependent crossbridge kinetics in skinned skeletal fibers. Biophys. J. 83:3425–3434. 10.1016/S0006-3495(02)75342-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McLachlan A.D., and Stewart M.. 1976. The 14-fold periodicity in alpha-tropomyosin and the interaction with actin. J. Mol. Biol. 103:271–298. 10.1016/0022-2836(76)90313-2 [DOI] [PubMed] [Google Scholar]
- Moncman C.L., and Wang K.. 1995. Nebulette: a 107 kD nebulin-like protein in cardiac muscle. Cell Motil. Cytoskeleton. 32:205–225. 10.1002/cm.970320305 [DOI] [PubMed] [Google Scholar]
- Murray J.M., Knox M.K., Trueblood C.E., and Weber A.. 1982. Potentiated state of the tropomyosin actin filament and nucleotide-containing myosin subfragment 1. Biochemistry. 21:906–915. 10.1021/bi00534a015 [DOI] [PubMed] [Google Scholar]
- Ochala J., Lehtokari V.L., Iwamoto H., Li M., Feng H.Z., Jin J.P., Yagi N., Wallgren-Pettersson C., Pénisson-Besnier I., and Larsson L.. 2011. Disrupted myosin cross-bridge cycling kinetics triggers muscle weakness in nebulin-related myopathy. FASEB J. 25:1903–1913. 10.1096/fj.10-176727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ogut O., Hossain M.M., and Jin J.P.. 2003. Interactions between nebulin-like motifs and thin filament regulatory proteins. J. Biol. Chem. 278:3089–3097. 10.1074/jbc.M205853200 [DOI] [PubMed] [Google Scholar]
- Ottenheijm C.A., Hooijman P., DeChene E.T., Stienen G.J., Beggs A.H., and Granzier H.. 2010. Altered myofilament function depresses force generation in patients with nebulin-based nemaline myopathy (NEM2). J. Struct. Biol. 170:334–343. 10.1016/j.jsb.2009.11.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottenheijm C.A., Granzier H., and Labeit S.. 2012. The sarcomeric protein nebulin: another multifunctional giant in charge of muscle strength optimization. Front. Physiol. 3:37 10.3389/fphys.2012.00037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ottenheijm C.A., Buck D., de Winter J.M., Ferrara C., Piroddi N., Tesi C., Jasper J.R., Malik F.I., Meng H., Stienen G.J., et al. . 2013. Deleting exon 55 from the nebulin gene induces severe muscle weakness in a mouse model for nemaline myopathy. Brain. 136:1718–1731. 10.1093/brain/awt113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pappas C.T., Krieg P.A., and Gregorio C.C.. 2010. Nebulin regulates actin filament lengths by a stabilization mechanism. J. Cell Biol. 189:859–870. 10.1083/jcb.201001043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pappas C.T., Bliss K.T., Zieseniss A., and Gregorio C.C.. 2011. The Nebulin family: an actin support group. Trends Cell Biol. 21:29–37. 10.1016/j.tcb.2010.09.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parry D.A. 1975. Analysis of the primary sequence of alpha-tropomyosin from rabbit skeletal muscle. J. Mol. Biol. 98:519–535. 10.1016/S0022-2836(75)80084-2 [DOI] [PubMed] [Google Scholar]
- Root D.D., and Wang K.. 2001. High-affinity actin-binding nebulin fragments influence the actoS1 complex. Biochemistry. 40:1171–1186. 10.1021/bi0015010 [DOI] [PubMed] [Google Scholar]
- Schoffstall B., LaBarbera V.A., Brunet N.M., Gavino B.J., Herring L., Heshmati S., Kraft B.H., Inchausti V., Meyer N.L., Moonoo D., et al. . 2011. Interaction between troponin and myosin enhances contractile activity of myosin in cardiac muscle. DNA Cell Biol. 30:653–659. 10.1089/dna.2010.1163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sleep J.A., and Hutton R.L.. 1980. Exchange between inorganic phosphate and adenosine 5′-triphosphate in the medium by actomyosin subfragment 1. Biochemistry. 19:1276–1283. 10.1021/bi00548a002 [DOI] [PubMed] [Google Scholar]
- Smith D.A., and Geeves M.A.. 1995a Strain-dependent cross-bridge cycle for muscle. Biophys. J. 69:524–537. 10.1016/S0006-3495(95)79926-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith D.A., and Geeves M.A.. 1995b Strain-dependent cross-bridge cycle for muscle. II. Steady-state behavior. Biophys. J. 69:538–552. 10.1016/S0006-3495(95)79927-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutoh K. 1982. Identification of myosin-binding sites on the actin sequence. Biochemistry. 21:3654–3661. 10.1021/bi00258a020 [DOI] [PubMed] [Google Scholar]
- Sutoh K., Ando M., Sutoh K., and Toyoshima Y.Y.. 1991. Site-directed mutations of Dictyostelium actin: disruption of a negative charge cluster at the N terminus. Proc. Natl. Acad. Sci. USA. 88:7711–7714. 10.1073/pnas.88.17.7711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweeney H.L., and Houdusse A.. 2010. Structural and functional insights into the Myosin motor mechanism. Annu. Rev. Biophys. 39:539–557. 10.1146/annurev.biophys.050708.133751 [DOI] [PubMed] [Google Scholar]
- Taylor E.W. 1979. Mechanism of actomyosin ATPase and the problem of muscle contraction. CRC Crit. Rev. Biochem. 6:103–164. 10.3109/10409237909102562 [DOI] [PubMed] [Google Scholar]
- Trinick J. 1992. Understanding the functions of titin and nebulin. FEBS Lett. 307:44–48. 10.1016/0014-5793(92)80899-R [DOI] [PubMed] [Google Scholar]
- Wakabayashi K., Sugimoto Y., Tanaka H., Ueno Y., Takezawa Y., and Amemiya Y.. 1994. X-ray diffraction evidence for the extensibility of actin and myosin filaments during muscle contraction. Biophys. J. 67:2422–2435. 10.1016/S0006-3495(94)80729-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang K.1982. Purification of titin and nebulin. Methods Enzymol. 85(pt B):264–274. [DOI] [PubMed]
- Wang G., and Kawai M.. 1996. Effects of MgATP and MgADP on the cross-bridge kinetics of rabbit soleus slow-twitch muscle fibers. Biophys. J. 71:1450–1461. 10.1016/S0006-3495(96)79346-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G., and Kawai M.. 1997. Force generation and phosphate release steps in skinned rabbit soleus slow-twitch muscle fibers. Biophys. J. 73:878–894. 10.1016/S0006-3495(97)78121-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., and Kawai M.. 2013. A re-interpretation of the rate of tension redevelopment (k(TR)) in active muscle. J. Muscle Res. Cell Motil. 34:407–415. 10.1007/s10974-013-9366-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang G., Ding W., and Kawai M.. 1999. Does thin filament compliance diminish the cross-bridge kinetics? A study in rabbit psoas fibers. Biophys. J. 76:978–984. 10.1016/S0006-3495(99)77261-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Muthu P., Szczesna-Cordary D., and Kawai M.. 2013. Diversity and similarity of motor function and cross-bridge kinetics in papillary muscles of transgenic mice carrying myosin regulatory light chain mutations D166V and R58Q. J. Mol. Cell. Cardiol. 62:153–163. 10.1016/j.yjmcc.2013.05.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Ji X., Barefield D., Sadayappan S., and Kawai M.. 2014a Phosphorylation of cMyBP-C affects contractile mechanisms in a site-specific manner. Biophys. J. 106:1112–1122. 10.1016/j.bpj.2014.01.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Sadayappan S., and Kawai M.. 2014b Cardiac myosin binding protein C phosphorylation affects cross-bridge cycle’s elementary steps in a site-specific manner. PLoS One. 9:e113417 10.1371/journal.pone.0113417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Bahadir A., and Kawai M.. 2015. High ionic strength depresses muscle contractility by decreasing both force per cross-bridge and the number of strongly attached cross-bridges. J. Muscle Res. Cell Motil. 36:227–241. 10.1007/s10974-015-9412-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Bai F., Zhang Q., Song W., Messer A., and Kawai M.. 2017. Development of apical hypertrophic cardiomyopathy with age in a transgenic mouse model carrying the cardiac actin E99K mutation. J. Muscle Res. Cell Motil. 38:421–435. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witt C.C., Burkart C., Labeit D., McNabb M., Wu Y., Granzier H., and Labeit S.. 2006. Nebulin regulates thin filament length, contractility, and Z-disk structure in vivo. EMBO J. 25:3843–3855. 10.1038/sj.emboj.7601242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright J., Huang Q.Q., and Wang K.. 1993. Nebulin is a full-length template of actin filaments in the skeletal muscle sarcomere: an immunoelectron microscopic study of its orientation and span with site-specific monoclonal antibodies. J. Muscle Res. Cell Motil. 14:476–483. 10.1007/BF00297210 [DOI] [PubMed] [Google Scholar]
- Zhao Y., and Kawai M.. 1993. The effect of the lattice spacing change on cross-bridge kinetics in chemically skinned rabbit psoas muscle fibers. II. Elementary steps affected by the spacing change. Biophys. J. 64:197–210. 10.1016/S0006-3495(93)81357-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., and Kawai M.. 1994. Kinetic and thermodynamic studies of the cross-bridge cycle in rabbit psoas muscle fibers. Biophys. J. 67:1655–1668. 10.1016/S0006-3495(94)80638-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y., and Kawai M.. 1996. Inotropic agent EMD-53998 weakens nucleotide and phosphate binding to cross bridges in porcine myocardium. Am. J. Physiol. 271:H1394–H1406. [DOI] [PubMed] [Google Scholar]