Finite-Size Effects in Metasurface Lasers Based on Resonant Dark States

Abstract

The quest for subwavelength coherent light sources has recently led to the exploration of dark-mode based surface lasers, which allow for independent adjustment of the lasing state and its coherent radiation output. To understand how this unique design performs in real experiments, we need to consider systems of finite size and quantify finite-size effects not present in the infinite dark-mode surface laser model. Here we find that, depending on the size of the system, distinct and even counterintuitive behavior of the lasing state is possible, determined by a balanced competition between multiple loss channels, including dissipation, intentional out-coupling of coherent radiation, and leakage from the edges of the finite system. The conclusions are crucial for the design of future experiments that will enable the realization of ultrathin coherent light sources.

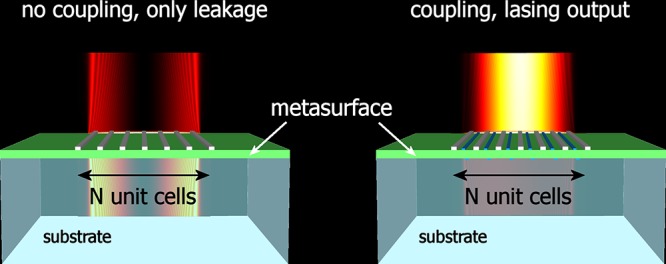
Dark states are localized, resonant electromagnetic modes that do not radiate.¹ This individual feature is what makes them ideal for energy storage and, in particular, laser resonators.^2,3 In comparison to other existing laser systems, such as dielectric-based designs⁴⁻⁹ that are efficient but not subwavelength or metal (plasmon)-based designs¹⁰⁻¹⁶ that are indeed subwavelength but not efficient, the lasing dark surface mode concept overcomes this apparent dead end; it allows for independent adjustment of the resonant state and its coherent radiation output, and significantly high Q factors can therefore be sustained even when the system size becomes subwavelength.^2,3

A simple numerical realization was demonstrated in refs (2 and 3) in which the system was assumed infinite, accounting for realistic systems of sufficiently large numbers of unit cells. But, how many unit cells make a “sufficiently large” system, is not straightforward. In general, very few publications related to photonic crystal systems,¹⁷⁻²⁰ metamaterials,^21,22 certain disordered systems,²³⁻²⁵ and nanolasers,^26,27 have considered this aspect.

In this work, we investigate aspects that arise when metasurface lasers of finite size are considered, as is necessary to understand in real experiments. We find that the overall performance depends on the balanced competition between all existing loss channels, including dissipation, intentional out-coupling of coherent radiation, and leakage from the edges of the finite system, in a nontrivial way. As it turns out, the size of the aperture (metasurface size) plays a crucial role, as it can qualitatively alter the physical behavior of the system, leading to distinct regimes of operation, which in some cases are counterintuitive. To relate the performance of finite-sized systems with their infinitely large counterparts we introduce a metric based on energy balance. To facilitate the experimental identification of the lasing mode we also propose how far-field imaging techniques can be utilized in a configuration suitable for experimental demonstration in the near-infrared.

Principle of Operation

The principle of operation of dark-mode metasurface lasers was previously introduced in ref (2). A thin dielectric slab that supports a (dark) waveguide mode with continuous dispersion (red line in Figure 1b) is periodically interrupted by a subwavelength grating of silver scatterers of uniform thickness d and a certain periodicity a (Figure 1a), in order to spatially quantize the modes and to achieve a spectrally discrete set of resonant dark states with (in-surface) wave vectors that are multiples of π/a. In practice, a band structure emerges, splitting the modes at the edge of the Brillouin zone into two distinct categories: those modes that are located at the bottom of each gap (filled blue dots in Figure 1b), having their E-field minima (nodes) overlap with the metal inclusions and those modes that are located at the top of each gap (open blue dots in Figure 1b), which are spatially shifted by quarter unit cell, thus overlapping at E-field maxima. Therefore, the former have significantly higher Q factors than their latter, π/2-phase shifted counterparts. Embedding the dielectric region with an appropriate gain material that supports stimulated emission at the frequency of the desired dark mode (Figure 1c), the composite system becomes a dark mode resonator. When the gain medium is pumped above the lasing threshold, the pump power stores electromagnetic energy in the dark mode, because dissipative loss in the dielectric is low and radiative damping is suppressed as the mode is dark; the system lases, that is, builds macroscopic photon population in the dark state, but does not radiate.² In order to deliver the stored energy to radiation, a small dielectric scatterer is placed on the surface at distance δx from the unit cell boundary such that the stored power can be subsequently outcoupled as E_z-polarized waves, with a controllable small amount of radiative damping of the lasing mode. The system is periodic and, hence, the scatterer is placed periodically as well, forming a passive metasurface that serves as a vehicle for outcoupling.²⁸⁻³¹ In Figure 1, a design for operation at 1.5 μm is illustrated, utilizing the second of the quantized TE₀^(even) modes (red circle in Figure 1b), which has an antisymmetric electric field profile with respect to the center of the slab. The periodicity is a = 960 nm, the width of silver is 2w_m = 100 nm, and the thickness of the overall metasheet is d = 60 nm, which is thin enough to be subwavelength, but still can accommodate a gain material, such as a single quantum well.^32,33 In our system we have assumed a gain slab of (unpumped) permittivity ε_r,slab = 12.1 and a Drude silver of permittivity based on Johnson and Christy data.^34,35 Our system is examined with full-wave vectorial Finite Element Method (FEM) eigenfrequency simulations, utilizing the commercial software COMSOL Multiphysics (see Supporting Information for additional details). To understand the macroscopically observable behavior of the system when it lases and how that depends on the finite size, here we calculate quantities, such as the mode structure (eigenmodes) and the balance between loss channels (Q factors), which are present even when the system is not lasing, that is, in the simulations, the system is unpumped. For our study, this is a satisfactory approximation, as our independent calculations for the lasing thresholds using self-consistent FDTD calculations that consider the full, nonlinear gain system^2,3 verify that the pump induces only a slight change of the host refractive index (of the order of 0.1%).

Figure 1.

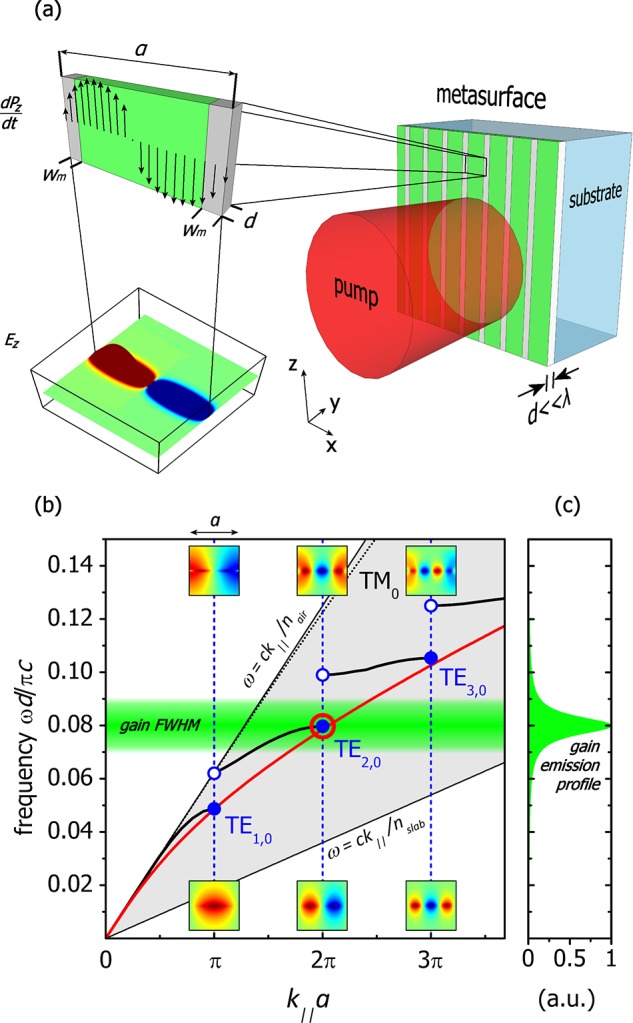
Dark-mode metasurface laser. (a) Perspective view of the unit cell, illustrating the spatial distribution of the dark mode, with which we work throughout this study (its operation point is marked in (b) with a red circle). A schematic of the laser containing 7 unit cells is shown as well. (b) TE₀ branch of dispersion relation for the unpumped uniform dielectric slab of thickness d (red line) and band structure for the composite dielectric-metal system (connected dots). The TM₀ branch is also shown as a dotted line. The electric field distribution (E_z) within the unit cell is shown at the bandedges, which are denoted with the open and filled dots. The shaded region is bounded by the air- and slab- lightlines and the gradient zone depicts the line width of the gain material. (c) Spectral emission profile of gain material.

Effects of Finite Size

Because the system is infinite along the x axis, the in-plane wavenumber k_∥ changes continuously, approaching multiples of k_a = π/a at the Brillouin-zone edge. For a finite version with N unit cells (a finite radiating aperture of the metasurface) the total length L = N × a of the metasurface introduces an additional in-plane wavenumber k_L = π/L due to the boundary conditions at the far edges of the finite structure, which now forces k_∥ to change in discrete steps m of k_L (k_L ≪ k_a because L ≫ a). In essence, making the system finite, makes the Bloch momentum discrete; the smaller the system, the more sparsely it becomes spectrally discretized. A direct consequence is that the Bloch waves are modulated to have an additional sine-like envelope of periodicity 2π/mk_L = 2L/m.^36,37

Due to this fact, the Bloch momentum cannot be situated exactly at the Brillouin edge anymore, but the closest available Bloch wave (m = 1) is k_L units away from the edge, the second (m = 2) 2k_L, the third (m = 3) 3k_L, and so on. This is the first fundamental difference between the infinite system and its finite counterparts. For example, in Figure 2, the first three modal envelopes (m = 1, 2, 3) closest to k_∥ = 2π/a are shown for a system with N = 30 unit cells (length L = 30a). The TE_2,0 dark mode, which is expected at this band edge for the infinite system, can be clearly seen within each unit cell of the finite system and is now modulated according to an overall envelope with periodicity 2 × 30a/m (m = 1 top, m = 2 middle, and m = 3 bottom figure). In the infinite system, for k_∥ = 2π/a all unit cells oscillate in phase. However, in the finite system this holds only for m = 1. For higher orders the envelopes split into groups that oscillate π-out of phase, as can be seen in Figure 2 (two groups of N/2 unit cells for m = 2, three groups of N/3 unit cells for m = 3, etc.³⁸).

Figure 2.

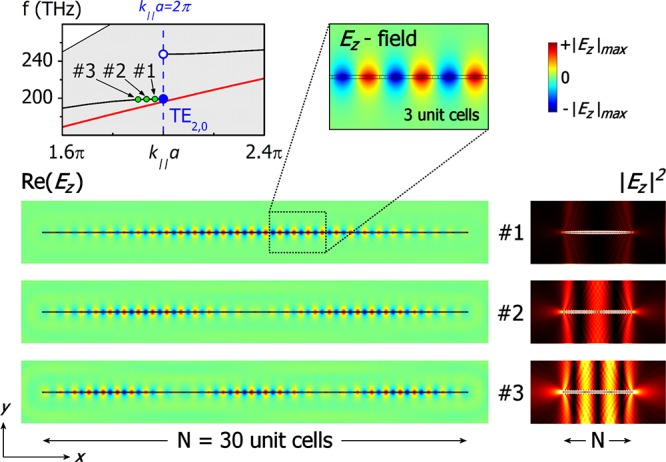
Example of the discretized dispersion due to finite size, for a system with N = 30 unit cells (detail of dispersion diagram close to the 2nd bandgap). The first three discretized modes are marked with the green dots (identified with #1, #2, and #3), where the dispersion of the infinite system (interrupted black line) and of the homogeneous dielectric slab (continuous red line) are shown as well. The spatial distributions of Re(E_z) and |E_z|² for the three modes are shown below. In the intensity plots on the right panel, a narrow range is shown from 0 (black) to ∼1.7 × 10^–3 |E_z|²_max, to emphasize the leaked over the stored energy.

Due to the overall modulation, the dark mode amplitude acquires a minimum (maximum) at those unit cells that are situated at the nodes (antinodes) of the envelope. This modulation leaves residual radiating moments that lead to leakage, even without any scatterer present. The more rapid the modulation, the stronger the residual moments and the more intense the leakage. As the envelope follows a sine-like form, the maximum slope is located at its zeros and this is why radiation is expected to be stronger at the nodes of the envelope and especially at the edges where the system is sharply terminated. This can be clearly seen in |E_z|² in Figure 2, where the intensity range is shown from 0 (black) to ∼1.7 × 10^–3 |E_z|²_max, to emphasize the leaked power over the much stronger energy density in the local fields due to the stored energy. From this plot it is also evident that the weakest leakage is associated with the m = 1 envelope order (which contains the minimum amount of nodes) and we will therefore focus on this wave for the rest of the analysis (information about the other orders can be found in the Supporting Information).

Leakage competes against two other loss channels to dissipate the modal energy, namely (undesired), dissipation due to material absorption and (intended) outcoupling due to the scatterers, once they are introduced. All three loss channels constitute the total Q factor:

1

where the last two terms comprise the purely radiative part, that is, Q_leak^–1 + Q_scat ≡ Q_rad^–1. Q_leak does not depend on the scatterers, but is a function of N that acquires finite values for finite N and diverges as N → ∞ (when leakage is suppressed). In the absence of any scatterer, that is, when Q_scat → ∞ (and, hence, Q_rad ≡ Q_leak), the amount of the leaked energy (W, leak) over the total modal energy (W, mode) follows a ∼L^–2 dependence, as depicted in Figure 3a (left panel, filled connected dots) and repeated calculations with the metal loss artificially set to zero verify that material absorption does not interfere with this effect (open connected dots). The competition between leakage and dissipation is shown in Figure 3a (right panel) and, although dissipation does not depend on the system size, the radiative part clearly follows a ∼L² law. The system size N for which Q_leak = Q_diss separates this plot into two regions, rendering the total Q factor leakage dominated for Q_leak < Q_diss and dissipation dominated for Q_leak > Q_diss. The more our system lies within the dissipation dominated region, the more its behavior approaches that of its infinite counterpart. On the other hand, Q_scat does not depend on N, but is a function of the scatterer’s position, δx, material, and geometry. In the absence of any leakage, that is, when the system is infinitely large and consequently Q_leak → ∞ (and, hence, Q_rad ≡ Q_scat), as we scan δx, Q_scat acquires finite values except when δx/a = 0, 0.5, and 1, where it diverges, as no power is outcoupled.^2,3Q_scat varies within a [Q_scat,∞) range (Q_scat^min is the minimum Q_scat and is marked with the blue dashed line in Figure 3a,b), spanning Q_total accordingly, as shown in the shaded region of Figure 3b, for which a scatterer with a permittivity of 12.1 and a rectangular cross section of 30 nm × 60 nm has been considered (as in ref (2)). Finally, when both contributions are combined (finite system with scatterer), the total Q_rad varies within the range [(1/Q_leak(N) + 1/Q_scat)⁻¹,Q_leak(N)], spanning Q_total accordingly [shaded area in Figure 3a (right panel)].

Figure 3.

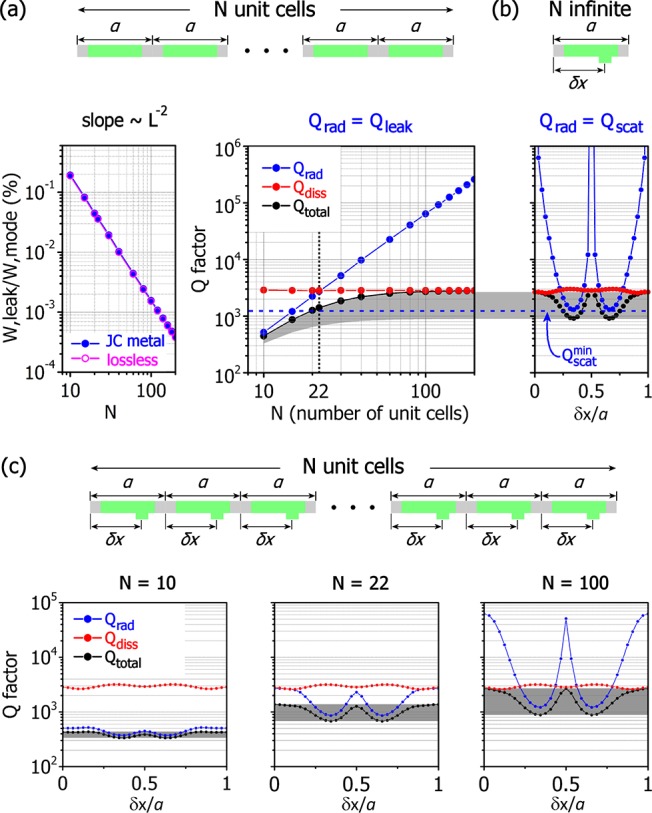
Competition between edge radiation and intended operation. (a) Finite system (metasurface with finite radiating aperture size) without scatterer (Q_scat → ∞). Amount of modal energy radiated (left) and Q factors (right) as a function of the system size. The dotted line denotes Q_leak = Q_diss, indicating the transition from leakage dominated behavior of the finite system to outcoupling dominated behavior equivalent to the infinite system. The limit of the infinite system is reached very soon (for as few as 100 unit cells). (b) Infinite system (unbound radiating metasurface with infinite aperture size) with scatterer (Q_leak → ∞); Q factors as a function of the scatterer position. The dashed line denotes Q_scat^min, that is, the strongest outcoupling achievable with the chosen scatterer. (c) Finite system with scatterer. Q factors as a function of the scatterer position, for systems with 10 (strong leakage), 22, and 100 (weak leakage) unit cells.

The system is designed to maximize the intended outcoupling when the scatterer is placed at positions where the fields are the strongest. At those positions the polarization currents induced on the scatterer by the dark mode are the strongest and hence outcoupling becomes maximum.^2,3 For infinite (Figure 3b) or very large systems (N = 100, Figure 3c, right panel), which lie in the dissipation dominated regime (Q_diss < Q_leak), the total Q factor is characterized by a double dip with respect to the scatterer’s position, as the dark mode that we have worked with exhibits two maxima along the unit cell. However, as the system size approaches and eventually enters the leakage dominated regime, things may change dramatically. The reason is that in this region Q_diss and Q_leak can become strongly coupled and consequently the double-dip behavior of Q_total, which is expected when leakage is absent or decoupled from dissipation may change or even disappear entirely, exhibiting counterintuitive features. In particular, if the scatterer is strong (Q_scat^min < Q_diss, Q_leak), the double-dip pattern of the total Q factor can be still observed, as the strong outcoupling obscures any interplay between Q_diss and Q_leak. However, due to the coupling between Q_leak and Q_diss, new features might appear, as shown in Figure 3c (left panel) for N = 10. There, one can observe that besides the double-dip pattern, the total Q factor rises and then drops again as we approach the unit cell boundaries, which is something that cannot be observed in large systems. If, on the other hand, the scatterer is weak (Q_scat > Q_diss, Q_leak), then Q_total is dominated by the interplay between Q_diss and Q_leak, and may exhibit nonexpected features, such as inverted or multiple dips (see Supporting Information for examples). In Figure 3c, besides the two extreme cases of N = 10 where leakage is particularly strong (left panel) and N = 100 where leakage is highly suppressed (right panel), the intermediate case of N = 22 (middle panel), where leakage becomes equal to dissipation, is also shown.

The chosen scatterer induces stronger radiation damping than leakage for a broad range of system sizes (down to N = 15). However, this condition alone is not sufficient to guarantee the tunability of the total Q factor; this is ensured by the condition Q_diss > Q_scat^min. In fact, if dissipation becomes significantly stronger than outcoupling from the scatterer (Q_diss ≪ Q_scat), then this tunability may cease, both for the leakage and the dissipation dominated regimes. In other words, the scatterer cannot be arbitrarily weak if we wish that it has an effect.

Observable Far-Field

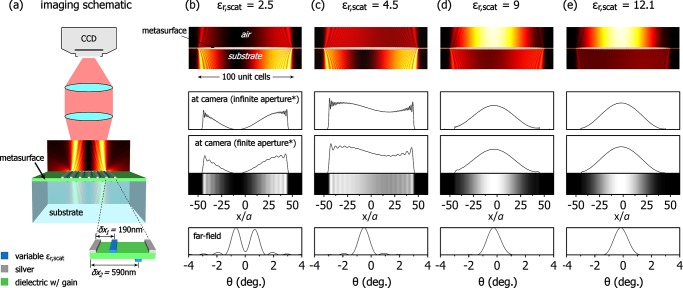
Already without the scatterer, the particular way light leaks out of the finite structure implies that a simple plane wave is not to be expected (see, for example, intensity plots in Figure 2). Depending on the mode order different interference patterns appear, leading to distinct near- and far-field formations. These are expected to be altered when a scatterer is present, so it is important to be able to identify whether an observed field is due to the scatterer or to the leakage. In Figure 4 intensity patterns of the m = 1 order TE₂₀ mode are shown for a system with N = 100 unit cells, as the outcoupling strength increases. For this example, we have introduced a more realistic version of the system examined so far, which is now mechanically supported by a glass substrate of 1.5 refractive index and has (reduced) periodicity a = 860 nm, to maintain the operation point at 1.5 μm (the 60 nm × 100 nm metal scatterers have also been transferred on top of the slab, to simplify fabrication). To enable full control over the emission direction, we have incorporated a second scatterer below the gain slab;² to tune the outcoupling strength we have fixed the position of both scatterers as shown in Figure 4a and varied their permittivity instead. An increased permittivity leads to stronger polarization currents driven by the dark mode and therefore stronger radiation by the scatterers. As shown in Figure 4, it can pass from being weaker (Figure 4b) to being comparable (Figure 4c) and finally stronger (Figure 4d,e) than leakage, leading to distinct far-field formations. For absent or weak scatterers, the outcoupled light propagates in the far-field as two lobes in small off-normal angles (Figure 4b) dominated by leakage from the edges. When imaged by a camera, it is seen as two intense sharp edges with a node in between. As the scatterers become stronger, this distribution starts to become stronger in the middle, because the scatterers induce stronger propagating k’s normal to the surface (Figure 4c), which is the intended outcoupling. The two angular lobes start to merge as well, until for very strong scatterers a single lobe is observed in both far-field patterns (Figure 4d,e). In this limit, leakage becomes negligible and the finite system behaves very similar to the infinite surface. This behavior is very distinctive to the first order TE₂₀ dark mode, as compared to the rest orders or the equivalent TE₂₀ bright mode, which is located at the top of the bandgap (see Supporting Information for additional information).

Figure 4.

Intensity patterns due to leakage of the 1st order dark mode for a system with N = 100 unit cells, for different outcoupling strengths. The scatterers have a 30 nm × 60 nm rectangular cross section, fixed positions as shown and the outcoupling strength is tuned via their permittivity ε_r,scat, which is set to 2.5 in (b) (weak), 4.5 in (c) (moderate), 9 in (d) (strong), and 12.1 (e) (very strong). The top row shows |E_z|² at the vicinity of the metasurface, which is located horizontally in the middle of the panel. The far-field image seen with a camera is shown in the two middle rows, for ideally infinite aperture and realistically finite aperture of NA = 0.32 (shown as density plot as well). *Aperture here refers to the numerical aperture of the imaging lens, as opposed to the aperture size of the radiating metasurface. The bottom row shows the far-field angular distribution.

To calculate the far-field angular distribution, we take a cross-section of the E-field along the metasurface–air interface and we apply a Fourier Transform, which projects all propagating plane wave components with real wavevectors in the far-field (the evanescent components with complex wavevectors spatially decay away from the interface and, consequently, do not enter the calculation). Then we calculate the normalized intensity |E|² of the distribution and express it as a function of the angle, rather than a function of the in-plane component k of the wave vector (parallel to the interface). To retrieve the camera image we perform the inverse Fourier Transform on the far E-field calculated in the previous step, modeling the phase compensation introduced by a focusing camera lens. This gives the image that would be produced by an ideal, aberration free, focusing lens with infinite aperture. It should be noted that the result is different from the E-field distribution at the taken cross-section, as the inverse Fourier Transform restores only the propagating k’s, while the actual field at the metasurface-air interface contains both real and imaginary in-plane k’s. To be more realistic, we also take into account the finite numerical aperture (NA) of the lens, which collects only a subset of the propagating k’s (the use of “aperture” for the finite imaging lens should not be confused with the finite radiating aperture of the metasurface). Hence, in this case we first truncate the propagating k’s up to a maximum k before applying the inverse Fourier Transform, according to the lens aperture, which we have considered to be NA = 0.32.

The comparison between camera images with infinite and finite NA shows that the qualitatively different far-field profiles originate from the actual lasing mode and not from the particular imaging system. Experimentally, camera images can be retrieved if the source is imaged to a microscope objective, a schematic of which is shown in Figure 4a. The angular distribution can be measured by standard Fourier plane scanning techniques. As our simulations verify, the parity of the system (even or odd number of unit cells) does not play any role, neither in the Q factor nor in the field distributions. Leakage depends only on the actual size of the system, and the lasing mode can be therefore identified uniquely from the field patterns.

Conclusion

With this work we intend to guide future experiments, both in terms of fabrication and measurements. As our study reveals, the behavior will strongly depend on the size of the system, as the same lasing mode may manifest qualitatively differently in the far-field, depending on whether the leakage is weak or strong. This means that the observation of the experimental results will not give unambiguous information on the lasing, if there is not an a priori knowledge of the regime that the experiment actually operates. Our study provides the basis for interpreting the experimentally observable behavior for the finite aperture lasing metasurface. Quantitatively, our study demonstrates how to predict the amount of leakage as the system deviates from its infinite limit, providing guidelines as to how big a system and how strong the scatterers should be fabricated, in order to achieve the desired features. In addition, we propose convenient ways to identify which mode is lasing, that is, standard, well-established, and easy to perform far-field techniques, instead of involved near-field instrumentation. These necessary measurements will help lift any ambiguity on the origin of the emitted light, facilitating the design of further experiments. In this work we have shown how to tailor the amount of intentionally out-coupled coherent radiation over the leaked light and obtain control on the desired operation, thus, carving the path to the realization of subwavelength coherent light sources in realistic finite-aperture designs.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.8b00835.

• Calculation of the Q factors and further imaging calculations for related configurations. Proposed designs for experimental implementation in the visible and near-infrared (PDF)

The authors declare no competing financial interest.