Abstract
Chiral surface plasmon polaritons (SPPs) produced by plasmonic nanowires can be used to enhance molecular spectroscopy for biosensing applications. Nevertheless, the switchable stereoselectivity and detection of various analytes are limited by a lack of switchable, chiral SPPs. Using both finite-element method simulations and analytic calculations, we present a graphene-coated chalcogenide (GCC) nanowire that produces mid-infrared, chiral SPPs. The chiral SPPs can be reversibly switched between “on” (transparent) and “off” (opaque) by non-volatile structural state transitions in the dielectric constants of the chalcogenide glass Ge2Sb2Te5. Furthermore, by controlling the Fermi energy of the graphene-coating layer, the nanowire can output either non-chiral or chiral SPPs. A thermal-electric model was built to illustrate the possibility of ultrafast on/off switching of the SPPs at the terminus of the nanowire. Finally, we show that a selective, lateral sorting of sub-10-nm enantiomers can be achieved via the GCC nanowire. Chiral nanoparticles with opposite handedness experience transverse forces that differ in both their sign and magnitude. Our design may pave the way for plasmonic nanowire networks and tunable nanophotonic devices, which require the ultrafast switching of SPPs, and provide a possible approach for a compact, enantiopure synthesis.
Surface plasmon polaritons: sub 10 nm enantiomer separation with nanowires
Coating of phase change Ge2Sb2Te5 nanowires with graphene enables separation of sub-10 nm enantiomers. Surface plasmon polaritons in nanowires are known to be capable of generating optical forces in different directions for the separation of chiral objects of different sign. However, modulation and switching on/off of the polaritons has been limited by the choice of nanowire. A team in China led by Tun Cao now demonstrates theoretically a graphene-coated Ge2Sb2Te5 nanowire, where the known rapid and reversible phase change – between amorphous and crystalline structures—enables a wide range of polariton modes. This contributes to the observation of sub-10 nm chiral nanoparticles of opposite handedness being pushed in different directions. This study suggests the possibility of nanowire-based enantiomer separation with enhanced nanoparticle selectivity.
Introduction
Chiral recognition is crucial in chemical synthesis, especially in the manufacturing of pharmaceuticals1,2. However, the prevailing chemical methods produce redundant side products and have low discrimination3,4. Recently, enantiomer separation using chiral optical forces has attracted increased interest due to its advantages of being more efficient and less invasive than chemical schemes5–9. The idea of this optical enantiomer-selective separation is to create experimental conditions under which the chiral objects with chiral polarizabilities of opposite signs experience forces in different directions. To date, the separation of a sub-100-nm enantiomeric pair has only been numerically demonstrated using plasmonic nanostructures10,11, and the complicated fabrication of plasmonic nanostructures may pose limitations for further applications in the field12–17. Furthermore, the smallest chiral objects that have been separated thus far are much larger than the pharmaceutically relevant sub-10-nm biomolecules. It is desirable to extend this mechanism to sub-10-nm objects, e.g., chiral molecules in nature.
A recently developed metallic nanowire is a promising candidate for resolving these challenges18–34. The nanowire can produce chiral light and possesses a nanometer-sized geometry that is comparable to that of sub-10-nm chiral biomolecules. However, the metal component of the nanowire may result in high loss and poor biocompatibility35. In this regard, very recently, a graphene-coated dielectric nanowire that supports surface plasmon polariton (SPP) modes has been theoretically demonstrated36–38, and the SPP modes are tuned by varying the Fermi energy (EF) of the graphene coating39–43. The low loss and strong field confinement of the SPPs in the graphene-coated nanowire make it a better alternative than the metallic nanowire. Even so, the graphene-coated nanowires that have been investigated thus far use passive dielectric cores, such as Si and SiO2, which have a few disadvantages. First, little is known about actively switching the SPP waves on/off, which is an important requirement for biosensing. For example, even though the current schemes can identify the presence of chirality in molecules, the chiral expression, i.e., the magnitude of the asymmetry effects on the chemical and physical properties of the systems, is less conspicuous, which makes it more difficult to recognize, count, and modify44–46. Likewise, contriving biosensors capable of selectively detecting multiple analytes with different signals remains a formidable challenge. Detectors with chiroptical switches may solve this problem. Therefore, manipulating the magnitude of the chiral shape expression and related phenomena is of interest, especially if the manipulation yields an effect that can be turned “on” and “off” through external stimuli. The success of graphene-based plasmonic nanowires for manipulating SPP modes is empowered by creative designs and advanced nano-fabrications36–43, but very few of these studies have investigated the modulation rate of the SPP modes. It is crucial to recognize that these limitations can be avoided if the core of the nanowire has an ultrafast reconfigurability. Chalcogenide glass exhibits a remarkable portfolio of properties47, and Ge2Sb2Te5 (GST) is important due to its fast switching speed, excellent thermal stability, and high cyclability. In particular, the rapid and reversible phase transition of GST between amorphous and crystalline48,49 makes the material ideal for rapidly tunable photonic devices50–52. The GST nanowire has proved to be promising and useful for high-density memory devices since it has a low-power consumption and writing currents53–58. Our research extends the above knowledge into the field of chiral recognition, i.e., enantioselective optical separation.
In this work, we present lateral sorting of paired sub-10-nm enantiomers by combining chiral transverse forces with a graphene-coated GST (GCG) nanowire. First, we designed a GCG nanowire to produce chiral SPPs by introducing a coherent superposition of transverse magnetic (TM) and electromagnetic hybrid (EH) SPPs with right-/left-handed quasi-elliptically polarized (QEP) states at the input. By mismatching the mode-phase-matching (MPM) condition, the coherent superposition of the different SPP modes causes the light to propagate along a helical path, producing an unstable helix crescent light (chiral SPP). We show that the reversible phase transition between the amorphous GST and crystal provides a significant contrast in the real part of the permittivity and allows switching of the output chiral SPPs. The SPP modes can be interchanged between the chiral and non-chiral beam profiles via the Fermi energy (EF) of the graphene coating. Herein, EF varies in an appropriate region from 0.46 to 0.6 eV. The chiral SPP mode operates across a broad spectral range of 3 to 5 μm. The GST phase change material possesses a crystallization temperature of TC = 433 K and a melting temperature of TM = 873 K. The as-deposited amorphous GST can be crystallized by heating it beyond the TC instead of below the TM. A reverse re-amorphization process (from the crystalline to the amorphous state) can be obtained by rapidly increasing the local temperature above TM59. Our thermal-electric model shows that the temperature of the GST rod increased from room temperature to 433 K in 2.4 ns (8 ns) with a biasing voltage of Vg = 17 V (10 V), which can switch off the chiral (non-chiral) SPPs. The SPPs can be switched on again in 5 ns during the re-amorphization with Vg = 25 V. When the state of the GST core is amorphous and the MPM state is mismatched by EF = 0.6 eV, the sub-10-nm paired enantiomers placed 5 nm above the output plane of the nanowire experience an opposite, large chiral transverse force (~300 fN) under a low incident light intensity (~100 mW/μm2). This allows the chiral force to push chiral nanoparticles with opposite handedness in opposite directions. The emissive chiral light can be terminated by changing the GST from amorphous to crystalline, which disables the enantiomer separation.
Results
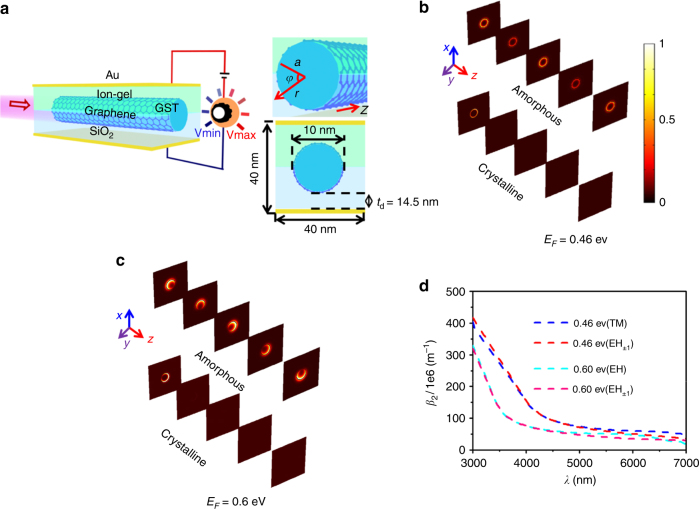
Figure 1a shows a sketch of a GCG nanowire with a radius of 5 nm (a = 5 nm) and a 0.5-nm-thick graphene coating (Tg = 0.5 nm). Vg was applied to the graphene coating via an ion gel with an index that matches that of the SiO2 (εgel = 2.25) layer. The EF was changed through a field effect transistor (FET)60, and a change in Vg of a few volts leads to a variation of 0.1 eV in EF. The change in EF can modulate the graphene permittivity, ε0. This controls the beam profile of the SPPs that propagate through the GCG nanowire. The graphene is defined as an atom-thick anisotropic sheet with , where σg represents the surface conductivity of graphene and ε0 the air permittivity61. The Kubo formula is used to express σg62. σg = σintra + σinter is composed of the intraband conductivity, , and the interband conductivity, , where the phenomenological scattering rate is Γ = 0.1 meV, T is the temperature, e is the electron charge, ħ is the reduced Planck’s constant, and kB is the Boltzmann constant, and fd(ε) = is the Fermi–Dirac distribution. EF is determined by the carrier density of graphene, , where vF = 9.5 × 105 m/s is the Fermi velocity. ns can also be expressed as ns = Vgεgelε0/etd, where td = 14.5 nm and εgel = 2.25 are the thickness and permittivity of the ion–gel layer, respectively63. Derived from the two different expressions of ns, the value of Vg in the dependence on EF can be obtained as . Figure S1 in the Supporting Information (SI) shows the complex dielectric constants of GST for both the amorphous (red line) and crystalline (blue line) states that were experimentally measured49. The radical change in the dielectric constant between the structural states is observed over a wide mid-infrared (M-IR) region; for example, εa-GST ≈ 16 + 0.05i, εc-GST ≈ 35 + 0.2i from 3 to 7 μm. εa-GST and εc-GST represent the GST permittivities for the amorphous and crystalline states, respectively.
Fig. 1.
a Sketch of the GCG nanowire. The nanowire described in a cylindrical coordinate system is shown in the top inset and its cross-section is shown in the bottom one. Switching “on” (top panel) and “off” (bottom panel) b non-chiral SPP modes at EF = 0.46 eV and c chiral SPP modes at EF = 0.6 eV by changing the GST phase from amorphous to crystalline. Fig. 1b,c share the same color bar. d Comparison of β2 for the EH±1 and TM SPP modes in the GCG nanowire with the crystalline GST core
The GCG nanowire can simultaneously produce and propagate the QEP EH, quasi-linearly polarized (QLP) EH, and TM plasmon modes, where the distributions of the time-averaged Poynting vectors of the plasmon modes, , are numerically demonstrated in Fig. S2 of the SI64. It is noteworthy that these plasmon modes can be experimentally produced by hybrid plasmonic waveguides65 and tapered graphene66. The analysis of the electromagnetic (EM)-field components for both the EH and TM SPPs is shown in S3 of the SI. The polarization properties of QEP EH−1 and QEP EH+1 and the QLP plasmon modes are analytically investigated in S4, where QEP EH+1 and QEP EH−1 represent the <S> of the right and left-handed QEP EH modes, respectively. As seen in Fig. S2 and S4, the polarization behaviors of the EH and TM plasmon modes propagating through the GCG nanowire are very different. Their coherent superposition leads to either constructive or destructive interference, which is related to the variation in the propagation constant. The propagation constant, β = β1 + β2i, of the SPP modes is strongly dependent on the interplay between the GST phase transition and the change in EF in the GCG nanowire. In the top panel of Fig. 1b, we show that the GCG can propagate a stable, non-chiral beam launched by the coherent superposition of the incident TM and QEP EH modes, where the state of the GST core is amorphous and Vg = 10 V, corresponding to EF = 0.46 eV. Herein, the TM and QEP EH modes possess identical values of β1. This causes the operation wavelength, λoper, to reach the MPM condition (λoper = λMPM = 4 μm). As a result, the coherent interference of the two modes can support a ring beam propagating along the GCG nanowire (see Fig. S5 and S3 of SI). A phase change of the GST from amorphous to crystalline can switch off the output ring beam (the bottom panel of Fig. 1b). In the top panel of Fig. 1c, we increase Vg to 17 V (EF = 0.6 eV), which is applied to the GCG nanowire with an amorphous GST core. This illustrates that the GCG nanowire can export a helix crescent light. This is because λoper = 4 μm is not located at the MPM point (λMPM = 3.5 μm) at EF = 0.6 eV, and the beam can be transported along a helical path (see S5 and Fig. S3 of the SI). Likewise, the output chiral beam with a helix crescent profile can be switched off by changing the GST state to crystalline (the bottom panel of Fig. 1c). Such a GCG nanowire acts as a reconfigurable SPP mode converter for the non-chiral and chiral states, which is mainly achieved by tuning the EF (Vg) of graphene, and exhibits a switchable function via the GST phase transition. In Fig. S3 of the SI, we calculate and discuss the complex propagation constants, β = β1 + β2i, of the TM and EH±1 SPPs propagating along the GCG nanowire at EF = 0.46 and 0.6 eV when the GST core is amorphous. Moreover, Fig. 1d further explains how the crystallization of the GST core switches off the output SPP modes. As seen, the values of β2 for the SPP modes propagating along the crystalline GCG nanowire are approximately two orders of magnitude greater than those of the amorphous one (Fig. S3(a) of the SI). This is particularly attractive because the larger β2 can considerably attenuate the SPP modes. Thus, by switching the state of GST between amorphous and crystalline, the SPPs can be either “on” (transparent) or “off” (opaque). This further explains the observation from Fig. 1b,c. A simulation was carried out using the commercial finite-element method package COMSOL. A detailed description of the model can be found in S6 of the SI. As an EF beyond 0.7 eV is difficult to achieve in a real experiment67, we controlled EF over a realistic range of 0.46 to 0.6 eV.
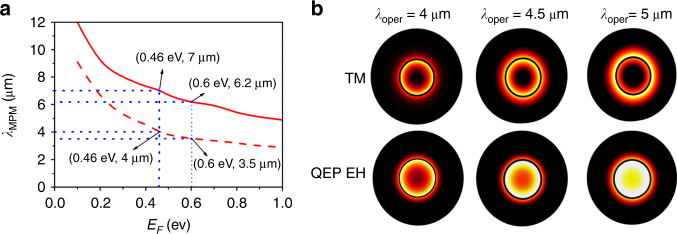
In Fig. 2a, we investigated the dependence of the MPM wavelengths on the EF for the GCG nanowire with amorphous GST, and the solid and dashed lines show the longer and shorter MPM wavelengths, respectively. At each given EF, we calculated the wavelength-dependent β1 spectra for both the TM and EH±1 modes (left column of Fig. S3(a) of the SI). Two MPM wavelengths are observed when the β1 values of the different modes are identical (right column of Fig. S3(a) of the SI). For example, the MPM wavelengths are λMPM = 4 and 7 μm at EF = 0.46 eV, but only the shorter wavelength of λMPM = 4 μm can be used. To further explore this concept, in Fig. 2b the values of <S> of the TM and QEP EH modes were examined at several wavelengths. As seen in the top panel of Fig. 2b, the <S> of the TM mode is approximately zero inside the GST core over a broad spectral region. However, the <S> of the QEP EH mode in the center increases with λoper (bottom panel of Fig. 2b). Therefore, field overlapping, which would produce a stable ring beam with λoper > 4.5 μm, is not achieved. Namely, the overlap of the TM and QEP EH modes can be efficiently preserved with λoper < 4.5 μm. This is because coincides with β2TM (namely, small) across a spectral region from 3 to 4.5 μm (right column of Fig. S3(b) of SI), which, in turn, provides strong mode interference.
Fig. 2.
a Spectra of λMPM versus EF for the GCG nanowire with amorphous GST, and the dashed and solid red lines represent the shorter and longer λMPM, respectively. b The <S> of the TM modes (top panel) and QEP EH modes (bottom panel) at the output of the GCG nanowire for λoper = 4 μm, λoper = 4.5 μm, and λoper = 5 μm
In Fig. S4 of the SI, we calculated the degree of circular polarization, 1, where δx – δz is the phase difference between the transverse E-field components Ex and Ez and <> denotes the time average. The calculation shows that the photons emitted by the GCG nanowire possess a relatively high C (C > 0.5) over most of the M-IR regime.
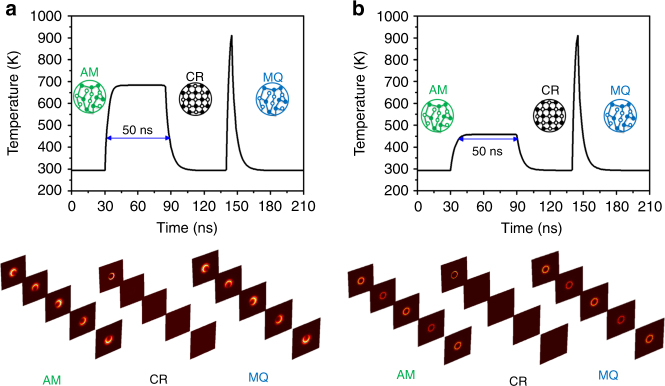
The structural state of GST changes from amorphous to crystalline (crystallization) upon heating to a temperature between the TC and TM. This phase transition is reversible (re-amorphization) if the local temperature is momentarily increased above the TM. Recently, it has been shown that the phase change speed of GST is faster than 100 ns68. In Fig. 3a,b, a heat transfer model was built to explore the temporal change in the temperature of the GST core at Vg = 17 and 10 V, respectively. In Table S1 of the SI, we summarize the material thermoelectric properties that were used to define the graphene, ion gel, and GST in the thermal-electric model. The temperature of the as-deposited amorphous GST rod rapidly increases with the time of loading Vg = 17 V (Fig. 3a), and the chiral SPP modes are excited due to EF = 0.6 eV. The temperature increases above TC = 433 K after 2.4 ns, crystallizing the GST. A subsequent annealing procedure is performed to maintain the temperature above TC but below TM for ~50 ns69. This can fully crystallize the GST and completely turn off the chiral SPP modes. The temperature of the crystalline GST core decreases to room temperature once Vg = 17 V is removed due to heat dissipation into the air. The re-amorphization of the GST can turn on the chiral SPP modes. To re-amorphize the GST, the crystal lattice needs to be molten and subsequently quenched to room temperature to avoid recrystallization of the atomic structure. A biasing time of 5 ns at Vg = 25 V was selected to re-amorphize the GST. Vg = 25 V can provide a high thermal energy that rapidly increases the temperature above the TM, melting the GST. By switching off Vg = 25 V, the subsequent fast cooling can quench the melt in an amorphous state. The chiral SPP mode was switched on again by setting Vg back to 17 V. Figure 3b shows the temporal variations in the GST temperature under Vg = 10 V (EF = 0.46 eV), and the reversible switching of non-chiral SPP modes was obtained. Moreover, videos 1 and 2 record the whole process of turning “on/off” the chiral and non-chiral SPP modes, respectively, which showed that our GCG nanowire exhibits an excellent performance for dynamically switchable functions.
Fig. 3.
a Switching the chiral SPP modes. The as-deposited amorphous (AM) GST core is electrically heated beyond TC = 433 K, allowing it to transform into crystalline (CR) GST under Vg = 17 V. Vg = 25 V is applied to heat the CR-GST beyond TM = 873 K. Subsequent quenching leads to the melt-quenched (MQ) state GST. b Switching of the non-chiral SPP modes, where the AM-GST rod is electrically heated above TC = 433 K by using Vg = 10 V
A nanometer-sized chiral specimen interfering with a monochromatic EM field can be characterized by oscillating magnetic and electric dipolar moments, M = Re[m(r)e−iωt] and P = Re[p(r)e−iωt], respectively. The dipolar moments m and p are proportional to the local magnetic, H, and electric, E, fields at the target object, which are expressed as:70,71
| 1 |
where μd and εdrepresent the permeability and permittivity of the surrounding medium, respectively. The magnetic, β, electric, α, and mixed magnetic-electric, χ, dipolar polarizabilities are complex scalars, where the sign (+,−) of χ is associated with the handedness of the enantiomers. It is noteworthy that β and α are the same for two enantiomers with opposite handedness, since they are quadratic forms of the magnetic and electric dipoles72. Therefore, our task is to distinguish the effect of the sign change of χ on the optical forces exerted on the chiral object. For a nanosphere, α, β, and χ can be represented as:73
| 2 |
| 3 |
| 4 |
μr = μ/μd and εr = ε/εd are the relative permeability and permittivity relating to the surrounding media, respectively; (ε, μ) provides the object’s refractive index, n; κ is the object’s chirality, and R is the object’s radius.
The time-averaged chiral force, Fχ, acting on a chiral specimen is composed of reactive () and dissipative () constituents, which are associated with the real and imaginary parts of the complex, χ, respectively:70,74
| 5 |
where , , is the Poynting vector, is the chirality density of the EM-field, and ω is the angular frequency of the EM wave.
The flow of the chirality is expressed by, where and . Herein, to simplify the calculation, we did not take into account the imaginary part, κ, of the chiral specimens by assuming that Im(κ) ≪ Re(κ)8,11. Therefore, can be ignored due to the absence of the Im[χ]of the chiral entity, and Fχ is mainly determined by the gradient of the optical chirality (∇K). Figure 4a schematically illustrates an enantiomer-selective separation of the chiral specimens with opposite handedness using the GCG nanowire, where λoper = 4 μm, EF = 0.6 eV, and the state of the GST core is amorphous. The radius of a chiral nanoparticle is R = 3 nm. The chirality is κ = ± 1, where ‘−’ and ‘+’ denote the left-handed and right-handed enantiomers, respectively. The paired enantiomers are located 5 nm above the output plane of the nanowire. The chiral molecules are in the air. The input light intensity of the nanowire is 100 mW/μm2. Upon illumination with the coherent superposition of the EH and TM SPP modes, we show the ∇K as arrows in Fig. 4b, and the direction and color of the arrows represent the direction and strength of ∇K, respectively. Figure 4c presents Fχ acting on the enantiomeric pair in the x–y plane. The left column of Fig. 4c shows that for a chiral specimen with κ = −1, Fχ mainly drags the specimen downwards. For a specimen with κ = + 1, Fχ mostly repels the particles upwards (right column of Fig. 4c). This is very close to the ideal experimental circumstance; i.e., sub-10-nm chiral molecules (R = 3 nm) with opposite handedness above the output plane of the nanowire can experience opposite and relatively large Fχ (~300 fN) under a low incident light intensity (~100 mW/μm2). That, in turn, pushes the chiral molecules with opposite handedness in different directions. However, the enantioselective separation of the chiral specimens is deactivated by crystallizing the GCG nanowire.
Fig. 4.
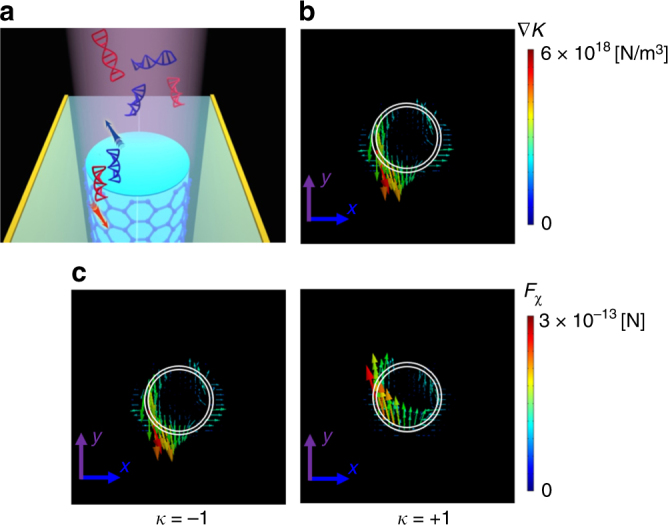
a Illustration of the GCG nanowire, where the enantiomeric pair is placed 5 nm above the output plane of the nanowire. The GCG nanowire is launched by a coherent superposition of the TM SPP and EH SPP modes at the input with an incident light intensity of 100 mW/μm2. b The distribution of ∇K at λoper = 4 μm. c Fχ exerted on the chiral nanoparticles (R = 3 nm) with κ = −1 (left column) and κ = + 1 (right column) at λoper = 4 μm. The white solid lines are used to outline the structure’s geometry. The direction and color of the arrows represent the direction and magnitude of ∇K and Fχ, respectively
Figure 5a–e schematically illustrate the fabrication process of the GCG nanowire. A graphene sheet was pulled away from Kish graphite using adhesive tape and adhered to the tape41. The GST nanowire was synthesized by a catalyst-mediated vapor–liquid–solid process and was placed on the graphene sheet using micromanipulation (Fig. 5a)54. Afterwards, the tape was attached to a silicon-on-insulator (SOI) wafer, and the side with the nanowire faced the wafer (Fig. 5b). We immersed the wafer in a 4-methyl-2-pentanone solution to dissolve the tape. Thus, a GCG nanowire on a SOI substrate was obtained (Fig. 5c). Then, a nanosecond laser beam propagating through a nanoscale tapered fiber was used to cut the graphene sheet along both sides of the nanowire on the substrate (Fig. 5d). Finally, the nanowire was removed from the substrate using the tapered fiber, and graphene spontaneously enfolded the nanowire to create a GCG nanowire (Fig. 5e).
Fig. 5. Schematic illustration of the GCG nanowire fabrication process.
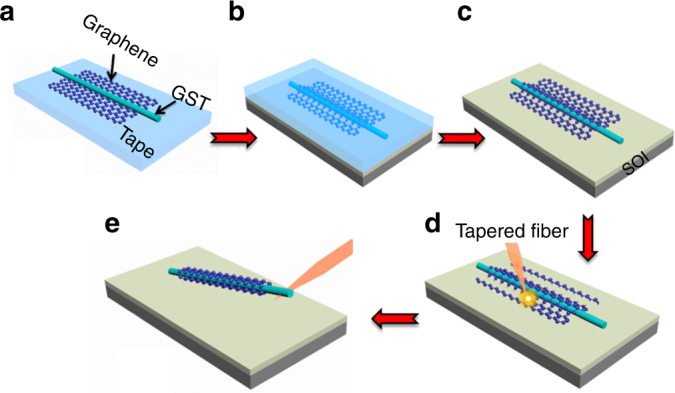
a A GST nanowire was placed above a graphene sheet on scotch tape. b The tape with the graphene and GST nanowire was attached to an SOI substrate. c By removing the tape in a 4-methyl-2-pentanone solution, a GCG nanowire on a SOI substrate was obtained. d The graphene sheet was cut along the nanowire by a nanosecond pulse laser propagating through the tapered fiber. e The GCG nanowire was removed from the wafer by the tapered fiber
Conclusions
This work has expanded the possibility of using GCG nanowire design to develop an optical separation process for sub-10-nm paired enantiomers. By introducing a nanowire with a coherent superposition of the TM and QEP EH modes, our proposed GCG nanowire can produce both an unstable helix crescent beam (chiral SPP) with EF = 0.6 eV and a stable ring beam (non-chiral SPP) with EF = 0.46 eV. In particular, the output chiral SPP modes will exert opposite chiral forces on the enantiomers at the boundary of the nanowire in opposite directions to obtain the enantioseparation. Our thermal model shows that this nanowire is dynamically reconfigurable, and the output SPP modes can be switched on/off by changing the phase of the GST core between amorphous and crystalline. Our findings suggest that the GCG nanowire can be used with a chiral source to separate sub-10-nm chiral molecules and integrated with a subwavelength photonic device to allow ultrafast optical switching, which may be a critical application for plasmonic nanowire networks.
Electronic supplementary material
Reconfigurable Graphene-Coated Chalcogenide Nanowire with Sub-10-nm Enantioselective Sorting Capability(DOCX 934 kb)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 61172059, 51302026), the International Science & Technology Cooperation Program of China (Grant No. 2015DFG12630), the Program for Liaoning Excellent Talents in University (Grant No. LJQ2015021), and the Fund Project for Shenzhen Fundamental Research Programme, China (Grant No. JCYJ20160308092830132).
Conflict of interest
The authors declare that they have no conflict of interest.
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41378-018-0008-3.
References
- 1.Zhang S, et al. Chiral surface plasmon polaritons on metallic nanowires. Phys. Rev. Lett. 2011;107:096801. doi: 10.1103/PhysRevLett.107.096801. [DOI] [PubMed] [Google Scholar]
- 2.Zhang W, et al. Amplification of the molecular chiroptical effect by low-loss dielectric nanoantennas. Nanoscale. 2017;9:5701–5707. doi: 10.1039/C7NR01527E. [DOI] [PubMed] [Google Scholar]
- 3.Ward TJ, Baker BA. Chiral separations. Anal. Chem. 2008;80:4363–4372. doi: 10.1021/ac800662y. [DOI] [PubMed] [Google Scholar]
- 4.Dobson CM. Protein folding and misfolding. Nature. 2003;426:884–890. doi: 10.1038/nature02261. [DOI] [PubMed] [Google Scholar]
- 5.Hayat A, Mueller JB, Capasso F. Lateral chirality sorting optical forces. Proc. Natl Acad. Sci. USA. 2015;112:13190–13194. doi: 10.1073/pnas.1516704112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Tkachenko G, Brasselet E. Optofluidic sorting of material chirality by chiral light. Nat. Commun. 2014;5:4577. doi: 10.1038/ncomms4577. [DOI] [PubMed] [Google Scholar]
- 7.Tkachenko G, Brasselet E. Helicity-dependent three-dimensional optical trapping of chiral microparticles. Nat. Commun. 2014;5:4491. doi: 10.1038/ncomms5491. [DOI] [PubMed] [Google Scholar]
- 8.Wang SB, Chan CT. Lateral optical force on chiral particles near a surface. Nat. Commun. 2014;5:4307. doi: 10.1038/ncomms4307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bradshaw DS, Andrews DL. Laser optical separation of chiral molecules. Opt. Lett. 2015;40:677–680. doi: 10.1364/OL.40.000677. [DOI] [PubMed] [Google Scholar]
- 10.Alizadeh MH, Reinhard BM. Plasmonically enhanced chiral optical fields and forces in achiral split ring resonators. ACS Photonics. 2015;2:361–368. doi: 10.1021/ph500399k. [DOI] [Google Scholar]
- 11.Zhao Y, Saleh AA, Dionne JA. Enantioselective optical trapping of chiral nanoparticles with plasmonic tweezers. ACS Photonics. 2016;3:304–309. doi: 10.1021/acsphotonics.5b00574. [DOI] [Google Scholar]
- 12.Giannini V, et al. Plasmonic nanoantennas: fundamentals and their use in controlling the radiative properties of nanoemitters. Chem. Rev. 2011;111:3888–3912. doi: 10.1021/cr1002672. [DOI] [PubMed] [Google Scholar]
- 13.Muskens OL, et al. Strong enhancement of the radiative decay rate of emitters by single plasmonic nanoantennas. Nano Lett. 2007;7:2871–2875. doi: 10.1021/nl0715847. [DOI] [PubMed] [Google Scholar]
- 14.Gansel JK, et al. Gold helix photonic metamaterial as broadband circular polarizer. Science. 2009;325:1513–1515. doi: 10.1126/science.1177031. [DOI] [PubMed] [Google Scholar]
- 15.Gorodetski Y, et al. Observation of the spin-based plasmonic effect in nanoscale structures. Phys. Rev. Lett. 2008;101:043903. doi: 10.1103/PhysRevLett.101.043903. [DOI] [PubMed] [Google Scholar]
- 16.Liu M, et al. Light-driven nanoscale plasmonic motors. Nat. Nanotech. 2010;5:570–573. doi: 10.1038/nnano.2010.128. [DOI] [PubMed] [Google Scholar]
- 17.Zhao X, et al. Voltage-tunable dual-layer terahertz metamaterials. Microsyst. Nanoeng. 2016;2:16025. doi: 10.1038/micronano.2016.25. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yao HZ, Zhong S. Frequency-dependent circular-polarization of terahertz chiral spoof surface plasmon polariton on helically grooved metallic wire. Opt. Commun. 2015;354:401–406. doi: 10.1016/j.optcom.2015.06.016. [DOI] [Google Scholar]
- 19.Huang Y, et al. Nanowire-supported plasmonic waveguide for remote excitation of surface-enhanced Raman scattering. Light Sci. Appl. 2014;3:e199. doi: 10.1038/lsa.2014.80. [DOI] [Google Scholar]
- 20.Wei H, et al. Polarization dependence of surface-enhanced Raman scattering in gold nanoparticle− nanowire systems. Nano Lett. 2008;8:2497–2502. doi: 10.1021/nl8015297. [DOI] [PubMed] [Google Scholar]
- 21.Day JK, et al. Standing wave plasmon modes interact in an antenna-coupled nanowire. Nano Lett. 2015;15:1324–1330. doi: 10.1021/nl5045428. [DOI] [PubMed] [Google Scholar]
- 22.Wei H, Xu H. Nanowire-based plasmonic waveguides and devices for integrated nanophotonic circuits. Nanophotonics. 2012;1:155–169. doi: 10.1515/nanoph-2012-0012. [DOI] [Google Scholar]
- 23.Lal S, et al. Noble metal nanowires: from plasmon waveguides to passive and active devices. Acc. Chem. Res. 2012;45:1887–1895. doi: 10.1021/ar300133j. [DOI] [PubMed] [Google Scholar]
- 24.Bian Y, Gong Q. Metallic nanowire-loaded plasmonic slot waveguide for highly confined light transport at telecom wavelength. IEEE J. Quantum Electron. 2013;49:870–876. doi: 10.1109/JQE.2013.2279906. [DOI] [Google Scholar]
- 25.Sun M, et al. Remotely excited Raman optical activity using chiral plasmon propagation in Ag nanowires. Light. Sci. Appl. 2013;2:e112. doi: 10.1038/lsa.2013.68. [DOI] [Google Scholar]
- 26.Tian XR, Tong LM, Xu HX. New progress of plasmonics in complex metal nanostructures. Sci. China Phys. Mech. Astron. 2013;56:2327–2336. doi: 10.1007/s11433-013-5339-3. [DOI] [Google Scholar]
- 27.Bian Y, Gong Q. Metallic-nanowire-loaded silicon-on-insulator structures: a route to low-loss plasmon waveguiding on the nanoscale. Nanoscale. 2015;7:4415–4422. doi: 10.1039/C4NR06890D. [DOI] [PubMed] [Google Scholar]
- 28.Pan D, et al. Mode conversion of propagating surface plasmons in nanophotonic networks induced by structural symmetry breaking. Sci. Rep. 2014;4:4993. doi: 10.1038/srep04993. [DOI] [Google Scholar]
- 29.Li Q, Qiu M. Plasmonic wave propagation in silver nanowires: guiding modes or not? Opt. Express. 2013;21:8587–8595. doi: 10.1364/OE.21.008587. [DOI] [PubMed] [Google Scholar]
- 30.Wei H, Pan D, Xu H. Routing of surface plasmons in silver nanowire networks controlled by polarization and coating. Nanoscale. 2015;7:19053–19059. doi: 10.1039/C5NR02511G. [DOI] [PubMed] [Google Scholar]
- 31.Wei H, et al. Highly tunable propagating surface plasmons on supported silver nanowires. Proc. Natl Acad. Sci. USA. 2013;110:4494–4499. doi: 10.1073/pnas.1217931110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wei H, Xu H. Controlling surface plasmon interference in branched silver nanowire structures. Nanoscale. 2012;4:7149–7154. doi: 10.1039/c2nr31551c. [DOI] [PubMed] [Google Scholar]
- 33.Peng Y, Kempa K. Controlling light propagation with nanowires. Appl. Phys. Lett. 2012;100:171903. doi: 10.1063/1.4704193. [DOI] [Google Scholar]
- 34.Anderson LJE, et al. A tunable plasmon resonance in gold nanobelts. Nano Lett. 2011;11:5034–5037. doi: 10.1021/nl203085t. [DOI] [PubMed] [Google Scholar]
- 35.Christensen J, et al. Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons. ACS Nano. 2011;6:431–440. doi: 10.1021/nn2037626. [DOI] [PubMed] [Google Scholar]
- 36.Davoyan AR, Engheta N. Salient features of deeply subwavelength guiding of terahertz radiation in graphene-coated fibers. ACS Photonics. 2016;3:737–742. doi: 10.1021/acsphotonics.5b00503. [DOI] [Google Scholar]
- 37.Gao Y, et al. Single-mode graphene-coated nanowire plasmonic waveguide. Opt. Lett. 2014;39:5909–5912. doi: 10.1364/OL.39.005909. [DOI] [PubMed] [Google Scholar]
- 38.Liang H, et al. Gate-programmable electro-optical addressing array of graphene-coated nanowires with sub-10 nm resolution. ACS Photonics. 2016;3:1847–1853. doi: 10.1021/acsphotonics.6b00365. [DOI] [Google Scholar]
- 39.Liu M, et al. A graphene-based broadband optical modulator. Nature. 2011;474:64–67. doi: 10.1038/nature10067. [DOI] [PubMed] [Google Scholar]
- 40.Lao J, et al. Tunable graphene‐based plasmonic waveguides: nano modulators and nano attenuators. Laser Photonics Rev. 2014;8:569–574. doi: 10.1002/lpor.201300199. [DOI] [Google Scholar]
- 41.Chen B, et al. Graphene coated ZnO nanowire optical waveguides. Opt. Express. 2014;22:24276–24285. doi: 10.1364/OE.22.024276. [DOI] [PubMed] [Google Scholar]
- 42.Yu S, et al. Graphene decorated microfiber for ultrafast optical modulation. Opt. Express. 2015;23:10764–10770. doi: 10.1364/OE.23.010764. [DOI] [PubMed] [Google Scholar]
- 43.Ansell D, et al. Hybrid graphene plasmonic waveguide modulators. Nat. Commun. 2015;6:9846. doi: 10.1038/ncomms9846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Feringa BL, et al. Chiroptical molecular switches. Chem. Rev. 2000;100:1789–1816. doi: 10.1021/cr9900228. [DOI] [PubMed] [Google Scholar]
- 45.Dai Z, Lee J, Zhang W. Chiroptical switches: applications in sensing and catalysis. Molecules. 2012;17:1247–1277. doi: 10.3390/molecules17021247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Asakawa M, et al. Switching “on” and “off” the expression of chirality in peptide rotaxanes. J. Am. Chem. Soc. 2002;124:2939–2950. doi: 10.1021/ja015995f. [DOI] [PubMed] [Google Scholar]
- 47.Wuttig M, Bhaskaran H, Taubner T. Phase-change materials for non-volatile photonic applications. Nat. Photon. 2017;11:465–476. doi: 10.1038/nphoton.2017.126. [DOI] [Google Scholar]
- 48.Wuttig M, Yamada N. Phase-change materials for rewriteable data storage. Nat. Mater. 2007;6:824–832. doi: 10.1038/nmat2009. [DOI] [PubMed] [Google Scholar]
- 49.Shportko K, et al. Resonant bonding in crystalline phase-change materials. Nat. Mater. 2008;7:653–658. doi: 10.1038/nmat2226. [DOI] [PubMed] [Google Scholar]
- 50.Wang Q, et al. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat. Photon. 2016;10:60–65. doi: 10.1038/nphoton.2015.247. [DOI] [Google Scholar]
- 51.Yin X, et al. Active chiral plasmonics. Nano Lett. 2015;15:4255–4260. doi: 10.1021/nl5042325. [DOI] [PubMed] [Google Scholar]
- 52.Li P, et al. Reversible optical switching of highly confined phonon-polaritons with an ultrathin phase-change material. Nat. Mater. 2016;15:870–875. doi: 10.1038/nmat4649. [DOI] [PubMed] [Google Scholar]
- 53.Jung Y, et al. Synthesis and characterization of Ge2Sb2Te5 nanowires with memory switching effect. J. Am. Chem. Soc. 2006;128:14026–14027. doi: 10.1021/ja065938s. [DOI] [PubMed] [Google Scholar]
- 54.Lee SH, Jung Y, Agarwal R. Highly scalable non-volatile and ultra-low-power phase-change nanowire memory. Nat. Nanotech. 2007;2:626–630. doi: 10.1038/nnano.2007.291. [DOI] [PubMed] [Google Scholar]
- 55.Lee SH, Jung Y, Agarwal R. Size-dependent surface-induced heterogeneous nucleation driven phase-change in Ge2Sb2Te5 nanowires. Nano Let. 2008;8:3303–3309. doi: 10.1021/nl801698h. [DOI] [PubMed] [Google Scholar]
- 56.Jung Y, et al. Core− shell heterostructured phase change nanowire multistate memory. Nano Lett. 2008;8:2056–2062. doi: 10.1021/nl801482z. [DOI] [PubMed] [Google Scholar]
- 57.Jung Y, et al. Phase-change Ge− Sb nanowires: synthesis, memory switching, and phase-instability. Nano Lett. 2009;9:2103–2108. doi: 10.1021/nl900620n. [DOI] [PubMed] [Google Scholar]
- 58.Park S, et al. Effect of the thermal conductivity on resistive switching in GeTe and Ge2Sb2Te5 nanowires. ACS Appl. Mater. Interfaces. 2015;7:21819–21827. doi: 10.1021/acsami.5b05703. [DOI] [PubMed] [Google Scholar]
- 59.Michel AKU, et al. Reversible optical switching of infrared antenna resonances with ultrathin phase-change layers using femtosecond laser pulses. ACS Photonics. 2014;1:833–839. doi: 10.1021/ph500121d. [DOI] [Google Scholar]
- 60.Ju L, et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotech. 2011;6:630–634. doi: 10.1038/nnano.2011.146. [DOI] [PubMed] [Google Scholar]
- 61.Cao T, et al. Tuning of giant 2D-chiroptical response using achiral metasurface integrated with graphene. Opt. Express. 2015;23:18620–18629. doi: 10.1364/OE.23.018620. [DOI] [PubMed] [Google Scholar]
- 62.Liang H, et al. Graphene surface plasmon polaritons with opposite in-plane electron oscillations along its two surfaces. Appl. Phys. Lett. 2015;107:091602. doi: 10.1063/1.4929886. [DOI] [Google Scholar]
- 63.Vakil A, Engheta N. Transformation optics using graphene. Science. 2011;332:1291–1294. doi: 10.1126/science.1202691. [DOI] [PubMed] [Google Scholar]
- 64.Sorger VJ, et al. Experimental demonstration of low-loss optical waveguiding at deep sub-wavelength scales. Nat. Commun. 2011;2:331. doi: 10.1038/ncomms1315. [DOI] [Google Scholar]
- 65.Chen J, et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature. 2012;487:77–81. doi: 10.1038/nature11254. [DOI] [PubMed] [Google Scholar]
- 66.Midrio M, et al. Graphene-based optical phase modulation of waveguide transverse electric modes. Photonics Res. 2014;2:A34–A40. doi: 10.1364/PRJ.2.000A34. [DOI] [Google Scholar]
- 67.Snitzer E. Cylindrical dielectric waveguide modes. J. Opt. Soc. Am. 1961;51:491–498. doi: 10.1364/JOSA.51.000491. [DOI] [Google Scholar]
- 68.Xiong F, et al. Low-power switching of phase-change materials with carbon nanotube electrodes. Science. 2011;332:568–570. doi: 10.1126/science.1201938. [DOI] [PubMed] [Google Scholar]
- 69.Yamada N, et al. High speed overwritable phase change optical disk material. Jpn. J. Appl. Phys. 1987;26:61. doi: 10.7567/JJAPS.26S4.61. [DOI] [Google Scholar]
- 70.Bliokh KY, Kivshar YS, Nori F. Magnetoelectric effects in local light-matter interactions. Phys. Rev. Lett. 2014;113:033601. doi: 10.1103/PhysRevLett.113.033601. [DOI] [PubMed] [Google Scholar]
- 71.Bliokh KY, Nori F. Characterizing optical chirality. Phys. Rev. A. 2011;83:021803. doi: 10.1103/PhysRevA.83.021803. [DOI] [Google Scholar]
- 72.Canaguier-Durand A, Genet C. Plasmonic lateral forces on chiral spheres. J. Opt. 2015;18:015007. doi: 10.1088/2040-8978/18/1/015007. [DOI] [Google Scholar]
- 73.Canaguier-Durand A, Genet C. Chiral route to pulling optical forces and left-handed optical torques. Phys. Rev. A. 2015;92:043823. doi: 10.1103/PhysRevA.92.043823. [DOI] [Google Scholar]
- 74.Canaguier-Durand A, et al. Mechanical separation of chiral dipoles by chiral light. New J. Phys. 2013;15:123037. doi: 10.1088/1367-2630/15/12/123037. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Reconfigurable Graphene-Coated Chalcogenide Nanowire with Sub-10-nm Enantioselective Sorting Capability(DOCX 934 kb)