Abstract
The potential research, policy and management applications of global burned area products place a high priority on rigorous, quantitative assessment of their accuracy. Such an assessment can be achieved by implementing validation methods employing design-based inference in which the independent reference data are selected via a probability sampling design. The majority of global burned area validation exercises use Landsat data to derive the independent reference data. This paper presents a three-dimensional sampling grid that allows for probability sampling of Landsat data in both space and time. To sample the globe in the spatial domain with non-overlapping sampling units, the Thiessen Scene Area (TSA) tessellation of the Landsat path/row geometry is used. The TSA grid is combined in time with the 16-day Landsat acquisition calendar to provide three-dimensional elements (voxels).This allows for implementation of stratified random sampling designs, where not only the location but also the time interval of the independent reference data is explicitly drawn by probability sampling. To illustrate this, we use a stratification methodology based on the Olson global ecoregion map and on the MODIS global active fire product. Using the global MODIS burned area product to establish a hypothetical population of reference data, we show that a sampling scheme based on the proposed stratification with equal sample allocation among strata is effective in reducing the standard errors of accuracy and area estimators compared to simple random sampling. Globally, the standard errors were reduced by 63%, 54%, 22% and 53% for overall accuracy, omission error, commission error and total burned area estimates respectively. By incorporating probability sampling in both the spatial and temporal domains, the present study establishes the foundation for rigorous design-based validation of global burned area products and, more generally, of terrestrial thematic products that have high temporal variability.
Keywords: Validation, Fire, Global Burned Area, Accuracy, Probability Sampling, MODI, Landsat
1 –. Introduction
The relevance of satellite derived burned area products for research, policy and management applications translates into the need for rigorous, transparent and repeatable product accuracy assessment (Morisette et al. 2006; Mouillot et al. 2014). Intercomparison of products made with different satellite data and/or algorithms provides an indication of gross differences and possibly insights into the reasons for any differences (Chang and Song 2009; Boschetti et al. 2004). However, product comparison with an independent reference data set, not used to generate the product, is needed to determine accuracy (Justice et al. 2000). Validation is the term used here, and more generally, to refer to the process of assessing accuracy by comparison with independent reference data (Roy and Boschetti 2009). Validation is required to provide accuracy information to help users decide if and perhaps how to use a product (Mouillot et al. 2014), and, combined with routine quality assessment (Roy et al. 2002), to identify any needed product improvements (Morisette et al. 2002). Burned area products generated with greater spatial and temporal coverage become increasingly difficult to validate in a statistically meaningful way. A number of global burned area products have been derived over the last two decades from coarse resolution satellite data including the GBA2000 (Global Burned Area 2000; Grégoire et al. 2003; Tansey et al. 2004), Globscar (Simon et al. 2004), GLOBCARBON (Plummer et al. 2006), L3JRC (Leicester, Louvain-la-Neuve, Lisbon & JRC, Tansey et al. 2008), Moderate Resolution Imaging Spectroradiometer (MODIS, Roy et al. 2005a; Roy et al. 2008; Giglio et al. 2009) and Fire CCI (Climate Change Initiative) (Alonso-Canas and Chuvieco 2015) burned area products.
Research to validate global burned area products in a statistically rigorous manner is still ongoing. Ground based burned area measurement is time consuming and difficult to undertake over large regions (Cardoso et al. 2005). Because it is unrealistic to collect a global sample of burned area independent reference data from ground measurements, independent reference data derived from remotely sensed data must be used instead. The Global Burned Area Satellite Validation Protocol (Boschetti et al. 2009) was endorsed by the Land Product Validation subgroup of the Committee on Earth Observation Satellites (CEOS, http://lpvs.gsfc.nasa.gov/) and is based on a protocol developed for validation of the MODIS burned area product (Roy et al. 2005b). It defines the requirements for the use of satellite data as independent reference data but does not include any recommendations regarding sampling and accuracy metrics (Boschetti et al. 2009). Globally, fire activity is usually concentrated in a relatively short season (from a few weeks to several months) even in places where a large percentage of the landscape burns annually (Csiszar et al. 2005; Giglio et al. 2006a; Boschetti and Roy 2008). Given the impermanent nature of many burned areas, with a spectral signal that can disappear in as little as a few weeks in certain savanna systems (Trigg and Flasse 2000), and conversely the persistence of the burned signal for several years in boreal systems (Sukhinin et al. 2004), the time period covered by the reference data must be the same as the time period of the satellite burned area product being validated. The CEOS validation protocol requires that global coarse resolution burned area products (250m – 1km spatial resolution) be validated using independent reference data derived from two or more Landsat-class images, allowing for comparison between the reference data and the burned areas detected by the global product in the period between acquisitions. The independent reference data must be derived with minimum error, either by visual interpretation (Roy et al. 2005b; Roy and Boschetti 2009; Giglio et al. 2009) or by application of a semi-automatic algorithm followed by visual checking and manual refinement (Boschetti et al. 2006; Padilla et al. 2014, 2015). The use of bi-temporal image pairs ensures that burned areas that occurred before the first acquisition date are not mistakenly mapped as having burned between the two acquisition dates. Furthermore, the use of two acquisitions provides several interpretative advantages over single date data for mapping burned areas. These include a reduction in the likelihood of confusion with spectrally similar static land cover types (e.g., water bodies or dark soil) and the option to interpret the data by mapping relative changes rather than using single image interpretation approaches (Chuvieco et al. 2002; Roy et al. 2005b).
The characteristics of the independent reference data influence the reliability and the degree to which validation results are representative of the product. Assuming good quality independent reference data, the CEOS endorsed the descriptive validation hierarchy proposed by Morisette et al. (2006) to provide a guide to the degree of reliability of validation reporting with respect to the independent reference data sampling characteristics:
-
–
Stage 1 Validation: Product accuracy has been estimated using a small number of measurements obtained from selected locations and time periods.
-
–
Stage 2 Validation: Product accuracy has been assessed over a widely distributed set of locations and time periods, representative of the full range of conditions present in the product.
-
–
Stage 3 Validation: Product accuracy has been assessed, and the uncertainties in the product established via independent measurements made in a statistically robust way that represents global conditions, and is characterized by the selection of reference data via a probability sampling i.e., design-based validation.
-
–
Stage 4 Validation: Validation results for Stage 3 are systematically updated when new product versions are released, or when the time coverage of existing products expands.
The majority of regional to global scale burned area product validation exercises have been Stage 1, using Landsat data selected on the basis of availability (e.g., Barbosa et al. 1999; Fraser et al. 2000; Silva et al. 2003). An early attempt at Stage 2 validation, where the reference dataset covered a range of representative conditions, was described by Roy et al. (2005b) and Roy and Boschetti (2009). They selected 11 Landsat bi-temporal image pairs distributed across Southern Africa to cover approximately the range of plant water availability conditions, that they considered to be a regionally controlling factor on the type and amount of vegetation, and so indirectly on human population density and land use, that together influence the regional distribution of burned areas (Archibald et al. 2009). Only a limited number of Stage 3 validation exercises have been undertaken and they have implemented spatially stratified sampling designs (Boschetti et al. 2006; Padilla et al. 2014).
In this paper, a stratified probability sampling design that encompasses both the spatial and temporal domain is proposed to achieve Stage 3 and Stage 4 validation criteria. Importantly, sampling of independent reference data with respect to both the spatial and temporal domains is shown to be necessary for statistically rigorous inferences derived from sample-based validation of global burned area products. The sampling design is tailored to the appropriate collection of bi-temporal Landsat images because of their aforementioned use for global coarse resolution burned area product validation, and because the Landsat satellites provide the longest, freely available, satellite record that is continuing with the availability of Landsat 8 data (Roy et al. 2014). The sampling units are defined with respect to the Landsat World-wide Reference System (WRS-2) path/row coordinates and Landsat 16-day acquisition calendar (Arvidson et al. 2001). Regional strata are constructed using a global ecoregion map (Olson et al. 2001) and the global MODIS active fire product is used to stratify the population based on the level of fire activity in each sampling unit. The sampling grid and the protocol for constructing the strata are fully independent from the burned area product that is being validated, and are therefore applicable to any of the current moderate resolution burned area products. To evaluate the performance of the proposed sampling design the global MODIS burned area product is used as a hypothetical population (census) of reference data. The stratified probability sampling design could be adapted for application using other Landsat class global frequent repeat coverage moderate resolution data and using other ecoregion maps to construct regional strata.
The paper is organized as follows. Section 2 describes the datasets used to demonstrate the proposed independent reference data sampling design. Section 3 describes the design, starting with a rigorous definition of the sampling elements for global burned area product validation, and presents formulae using the proposed sampling design for estimating (i) burned area product accuracy metrics and, (ii) total burned area estimates and associated standard errors. The formulae for optimal allocation of independent reference data that minimize the standard errors of (i) and (ii) using the design are presented. Section 4 demonstrates the proposed design by implementing the stratification using one year of the MODIS fire products, and computing the standard errors of the accuracy and area estimators using different sample allocation strategies. The efficiency of the proposed design is evaluated by computing the reduction of the standard errors compared to simple random sampling. The paper concludes with recommendations for future research and application.
2 –. Data
2.1. Fire Datasets
In this study MODIS products for all the globe from January to December 2008 were used. The year 2008 was selected as it has comparable average total global area burned compared to other years (Giglio et al. 2013) and also was the same year used to validate a number of other global burned area products (Padilla et al. 2014, 2015).
2.1.1. MODIS Active Fire Product
The global MODIS active fire product has been available since 2000 (Giglio et al. 2003) with continuity provided by the Visible Infrared Imaging Radiometer Suite (VIIRS) active fire product (Schroeder et al. 2014). It has been extensively validated with a reported commission error of approximately 3% globally (Morisette et al. 2005; Csiszar et al. 2006; Schroeder et al. 2008ab). The Collection 5, Level 3 8-day MODIS MOD14A1 (Terra) and MYD14A1 (Aqua) active fire detection summary products were used to take advantage of the different overpass times of the Terra and Aqua satellites (Giglio 2007). The Level 3 8-day MODIS fire products are defined in the standard MODIS Level 3 Land tile format in the sinusoidal projection and each tile has fixed earth-location and covers approximately 1200 × 1200 km (10° x 10° at the equator) (Wolfe et al. 1998). They contain 8 daily active fire detection summaries stored as separate bands, and for each 1 km pixel, one of the following is stored: 1) an active fire was detected within the 24 hour period; 2) no MODIS observations were obtained in the 24 hour period; 3) MODIS observations were obtained but no fires were detected; 4) some observation in the 24 hour period was cloudy, or if not cloudy if the surface was land or water (Giglio et al. 2003).
2.1.2. MODIS burned area product (population of hypothetical reference data)
The global MODIS Collection 5 burned area product (MCD45A1) for 2008 was used. The product is available as a monthly gridded 500m product that describes the approximate day of burning generated by consideration of temporal changes in reflectance without using the MODIS active fire product (Roy et al. 2005a). It is also produced in the standard MODIS Land tile format in the sinusoidal projection. Besides the approximate day of burning, the product describes for each pixel an extensive set of data that can be used to assess the reliability of the detection, or the presence of gaps in the time series, primarily due to cloud cover (Roy et al. 2008).
2.2. Landsat 5 image acquisition geometry and calendar
The Landsat acquisition geometry and calendar were used to help define a spatial and temporal sampling grid. The Landsat satellites have polar circular sun-synchronous orbits and beginning with Landsat 4 (launched in 1982) acquire data with a 16-day repeat cycle. Landsat data are provided in 185 km × 180 km scenes defined in the second World-wide Reference System (WRS-2) of scene path (ground track parallel) and row (latitude parallel) coordinates (Arvidson et al. 2001). Successive temporally overlapping Landsat missions (i.e., Landsat 4 and 5, Landsat 5 and 7, and Landsat 7 and 8) nominally together provide 8-day full Earth coverage. However, consistent global 8-day coverage was not obtained due to variable Landsat mission acquisition strategies and because of sensor, ground station and data communication issues (Goward et al. 2006; Kovalskyy and Roy 2013; Wulder et al. 2016). In 2008 both Landsat 5 and 7 were operating; the year 2008 Landsat 5 Thematic Mapper (TM) acquisition calendar was used to demonstrate the proposed sampling design. This is because the design can be applied in the future directly to a year of Landsat 8 data acquired from the same circular orbit and overpass time as the now decommissioned Landsat 5 satellite (Roy et al. 2014). The Landsat 8 Operational Land Imager (OLI) was launched in 2013 and has improved global acquisition coverage compared to previous Landsat missions and provides improved measurement of subtle variations in surface conditions, including burned areas, due to its superior calibration, signal to noise characteristics, higher radiometric resolution, and more precise geometry (Irons et al. 2012; Roy et al. 2014). The design could also be adapted to other Landsat-like satellite data and this along with issues concerning Landsat cloud cover and data availability are discussed in Section 5.
2.3. Biome map
A global biome map was used to define a spatial stratification and ensure that the independent reference data are distributed geographically across terrestrial land masses. In this study the Olson global ecoregion map (Olson et al. 2001) that defines 867 terrestrial ecoregions and 14 global biomes was used. In principle, any global vegetation map, such as the MODIS Global Landcover Product (Friedl et al. 2010), the MERIS Globcover product (Bontemps et al. 2011), or a fire zone characterization map such as the one presented by Giglio et al. (2006a), could be used.
3 –. Sampling design for burned area product validation
3.1. Statistical background
Using standard statistical terminology, sampling is the process of extracting of a subset of elements (the sample) from a population, typically with the objective of using the sample to draw inferences about the parameters of the population. A statistically rigorous sampling design and estimation protocol is defined as one that satisfies probability sampling design criteria and ensures that the estimators are consistent for the parameters of interest (Stehman 2001). This follows the design-based inference framework (Särndal et al. 1992, Section 13.6) which is the approach to inference implemented herein. The probability sampling design criteria are that (i) the inclusion probability of each element of the population is greater than zero, and (ii) the inclusion probabilities are known for the elements selected in each sample (Särndal et al. 1992, p.8; Stehman 2001). The inclusion probability for element u (denoted πu) is defined as the probability that element u will be included in the sample, defined as:
| [1] |
where p(s) is the probability of selecting sample s (which will depend on the sampling design) and the summation is over all the different samples that include element u (Särndal et al. 1992, p.31). The practical implication of requiring consistent estimators is that they must incorporate the inclusion probabilities associated with the sampling design (Särndal et al. 1992, Section 5.3; Stehman 2001). In this study the sampling elements are defined by a combined spatial and temporal sampling grid, which is defined by the Landsat orbits and acquisition calendar: this is described below.
3.2. Proposed sampling grid for selection of independent reference data
3.2.1. Spatial sampling grid
The Landsat orbits converge at the poles, resulting in an increasing overlap between scenes on neighboring paths further polewards. This overlap makes the Landsat WRS-2 grid undesirable as a sampling unit and complicates statistical estimation (Gallego 2006). Thiessen Scene Areas (TSAs) generated from the regular lattice of all the WRS-2 scene centroid latitude and longitude coordinates provide a global hexagonal tessellation that simplifies the sampling design and estimators of accuracy and area because the TSAs do not overlap and have no gaps (Gallego 2006; Cohen et al. 2010; Kennedy et al. 2010). As each TSA is a subset of a single WRS-2 scene, they are also a practical choice: once a TSA is selected it is simple to identify the corresponding Landsat WRS-2 scene for retrieval and processing. WRS path/rows and TSAs have been used previously as the spatial sampling unit for burned area product validation (Boschetti et al. 2006; Padilla et al. 2014).
3.2.2. Temporal sampling grid
Landsat data are acquired from each Landsat sensor with a 16-day repeat cycle thus providing a natural partition of time. Landsat WRS-2 path/row locations that are first overpassed between January 1 and January 13 (January 14 for leap years) are overpassed a total of 23 times per calendar year, while scenes first overpassed after January 14 (or January 15 for leap years) are overpassed 22 times per year. Therefore, each Landsat scene can be acquired a maximum of 22 or 23 times per year (Ju and Roy 2008).
3.2.3. Combined spatial and temporal voxel sampling grid
The combination of the TSA hexagons (spatial grid) with the Landsat 16-day acquisition calendar (temporal grid) results in a full partitioning of the space and time domain into a three dimensional sampling grid. Each sampling unit is a voxel uniquely identified by three coordinates {p,r, t}, where p is the WRS-2 path, r is the WRS-2 row, and t is the 16-day Landsat acquisition interval. For example, Figure 1 illustrates the voxels populated with a year of MODIS active fire detections over Western Eurasia and Western side of Africa. We show below that the voxel sampling unit provides the necessary structure to implement a statistically rigorous spatial and temporal Stage 3 probability sampling design, and allows for straightforward application of sampling formulas and derivation of unbiased burned area product accuracy metrics and total burned area estimates.
3.3. Proposed global stratification using the spatial and temporal voxel sampling grid
The selection of the voxels where independent reference data are collected is a sampling problem; in this paper a stratified random sampling design is proposed. Simple random sampling is appropriate when the cost of sampling is low (Stehman 2009), but for global burned area product validation only a limited sample of independent reference data can be collected given the need for an interpreter to either produce the reference data via visual interpretation or to evaluate and correct the results of a semi-automatic process. Moreover, simple random sampling is inefficient for burned area validation because fire occurs on only a minor fraction of the Earth’s surface, with a distinct fire season in different biomes and geographic regions. For example, Giglio et al. (2013) estimated an average of about 3.5 million km2 affected by fire every year during 1997–2011 corresponding to about 2.5% of the dry land masses of the planet, and most regions have a fire season that lasts less than six months (Boschetti and Roy 2008). If a global simple random sample is used to select an independent burned area reference dataset, then the great majority of the sample units would fall in areas and time periods where no burning occurs, potentially resulting in imprecise product accuracy estimates. When an independent reference data sampling design more efficient than simple random sampling is used, the same sample size results in lower standard errors of the accuracy and area estimators (Stehman 1997, 2007). Consequently, stratified random sampling has been proposed as a practical choice for global burned area product validation (Boschetti et al. 2006) and is adopted here. The proposed global stratification uses the spatial and temporal voxel sampling grid defined as below.
First, a spatial stratification is imposed based on the Olson biome map, assigning each voxel to the majority biome within its spatial footprint. As the biome map is static, all voxels at the same TSA location are assigned to the same spatial stratum. This spatial stratification ensures that the biomes are adequately represented in the sample of independent reference data. Some TSAs may fall across biome boundaries but given the much smaller area of a TSA relative to each of the Olson global biomes this would affect only a small fraction of the total number of TSAs. Moreover, it would be possible to split a TSA into several smaller sampling units where each unit belongs to its associated biome. This would create sampling units with more variable areas than the TSAs but otherwise no other changes in the protocol described in this paper would be needed.
Second, a temporal stratification is imposed by partioning the voxels in each biome into low and high fire activity strata, similarly to Padilla et al. (2014) but taking into account the timing of burning within the year. The purpose of this temporal stratification is to ensure an adequate sample size at the locations and times when burning occurs, thus reducing the standard errors of the accuracy and area estimators compared to simple random sampling. The active fire area in each voxel {p,r, t} is derived as the projected area of the MODIS active fire 1 km2 pixels detected within the voxel TSA hexagon {p,r} over the 16-day interval {t}. The cumulative distribution of the total annual active fire areas is derived for the year of voxels in the biome. Then a biome-specific threshold is used to separate the voxels in the biome into low or high fire activity strata. The threshold is set as the 20th quantile of the cumulative distribution. Thus, by definition the union of all low fire activity voxels comprises 20% of the active fire area defined over the year for the biome, and the union of the high fire activity voxels comprises the remaining 80% of the annual active fire area. Because fire is a relatively rare occurrence, the low fire activity voxels are usually far more numerous than the high fire activity ones; this is illustrated in detail in Section 4.1. The adoption of the voxel stratification in space and time takes into account the seasonality of fire distribution. Usually voxels acquired at the same TSA location will belong to the high fire activity stratum during the fire season and to the low fire activity stratum outside the fire season when no burning occurs. Figure 2 shows a cross section of the stratification represented in three dimensions. The red and grey cells represent high and low fire activity voxels respectively. The cross section is cut along Landsat WRS-2 path 175, and highlights the typical seasonality of fire in much of Africa (Archibald et al. 2010).
Figure 2:
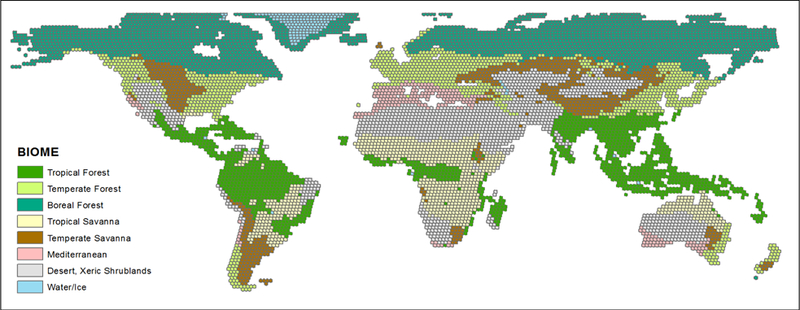
Biome stratification of the TSA hexagons of the Earth’s land masses between latitude 60°S and 75°N. The 14 ecoregions of Olson (2001) were aggregated into 7 general biomes, with an additional Water/Ice class not considered in the subsequent analysis.
3.4. Estimating accuracy and total burned area using the spatial and temporal voxel sampling grid
3.4.1. Confusion matrix
The confusion matrix represents the area agreement and disagreement between a classification and the reference data, often reported in terms of proportions by dividing the elements of the matrix by their sum (Congalton et al. 1983). For burned area products the confusion matrix is a two-way matrix composed of proportions of burned and unburned correspondences between the product and the independent reference data (Table 1). The confusion matrix elements may be used to generate product accuracy metrics and also for the calibration of area estimates (Foody 2002; Stehman 2013). All the formulae presented in this section assume that the two consecutive Landsat images are interpreted over the entire TSA hexagon (i.e., for the whole voxel). Selection of sub-units within the voxel would be a natural extension of the proposed method, but this topic is beyond the scope of the present paper.
Table 1.
Conventional confusion matrix used to assess burned area product accuracy, where the matrix elements describe the proportions of areal agreement and disagreement between the classified data, and the reference data, and the four elements sum to unity.
| Reference data | |||
|---|---|---|---|
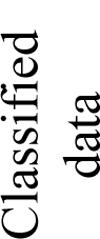 |
Burned | Unburned | |
| Burned | p11 | p12 | |
| Unburned | p21 | p22 | |
Each element of the confusion matrix can be defined in terms of the proposed voxel sampling grid. Recall that using standard statistical terminology, we refer to the limited set of independent reference data as a sample that is extracted from the population of all the possible independent reference data (i.e., all the voxels in space and time that define the burned area product); sample size is the number of elements of the sample, and population size is the number of elements of the population. Consider first a population of N voxels in which every voxel in space and time has independent reference data collected. The confusion matrix elements for the population are defined as:
| [2] |
| [3] |
where pij is element ij (i.e., row i and column j) of the confusion matrix, Au,ij defines the corresponding burned and/or unburned reference and product areas for voxel u, Au is the area (i.e. the spatial footprint) of voxel u (voxels are constructed from TSAs which may differ in area), A is the total area of all N voxels, and N is the population size. Because the voxel grid provides a tessellation in space and time (Figure 1), the total number of voxels N and the areas defined by Equations [2] and [3] are with respect to the spatial extent of the TSA hexagons and the number of 16-day temporal intervals. For example, if a validation was undertaken for a product defined by five TSA hexagons spatially, and each TSA had independent reference data for two 16-day periods, then the area A defined by Equation [3] would refer to the sum of the five TSA hexagon areas multiplied by two.
In most validation exercises, and certainly for global burned area product validation, only a limited amount of independent reference data are available. If the sample of independent reference data voxels is selected using a probability sampling design (as, for example, following a Stage 3 validation exercise) then the confusion matrix elements representing the whole population can be estimated from the sample using an unbiased estimator as:
| [4] |
where is an estimate of pij, n is the sample size, Au,ij defines the corresponding burned and/or unburned reference and product areas in voxel u, A is computed as [3], and πu is the inclusion probability of voxel u, which depends on the sampling design.
Under simple random sampling the inclusion probability (see Equation [1]) is constant for every voxel in the population and is defined as:
| [5] |
where n is the sample size and N is the population size.
Under stratified random sampling, such as proposed (Section 3.3), the inclusion probability is constant for any voxel within a stratum and is defined as:
| [6] |
where nh is the number of voxels sampled in stratum h, and Nh is the total number of voxels in stratum h.
3.4.2. Confusion matrix based product accuracy metrics
Three pixel-level accuracy metrics, widely used in burned area product validation and derived from the confusion matrix elements (Silva et al. 2002; Boschetti and Roy 2009; Padilla et al. 2014) are considered, namely the overall accuracy (OA), sometimes termed the percent correct when multiplied by 100, and the burned area omission error ratio (henceforth omission error, OE) and the commission error ratio (henceforth commission error, CE) that are estimated as:
| [7] |
| [8] |
| [9] |
where are elements of the confusion matrix (Table 1) estimated from the sampled voxels as [4].
The three accuracy estimators [7–9] belong to the general class of ratio estimators, where the parameter estimated is defined as
| [10] |
where R is the population ratio, and are the population means of the quantities x and y defined for each voxel u for the accuracy metrics [7–9] as follows:
Overall accuracy (OA):
| xu = Au (area of voxel u) |
| yu = Au,11 + Au,22 (area of agreement for voxel u) |
Omission error (OE):
| xu = Au,11 + Au,21 (area burned determined from the reference data for voxel u) |
| yu = Au,21 (area burned determined from the reference data but not mapped as burned in the classified product for voxel u) |
Commission error (CE):
| xu = Au,11 + Au,12 (area mapped as burned in the classified product for voxel u) |
| yu = Au,12 (area mapped as burned in the classified product but not burned as determined from the reference data for voxel u) |
For simple random sampling, the ratio R is estimated as:
| [11] |
where and are the sample means of y and x, determined from the n voxels belonging to the extracted sample.
The standard error (SE) of the ratio estimator under simple random sampling (Cochran 1977) is:
| [12] |
where N is the population size, n is the sample size, R is the population ratio calculated as in [10], and , are the population mean, variances and covariance over all N voxels of the quantities x and y defined above for the three accuracy estimators.
For a stratified population, the population ratio R can be expressed as:
| [13] |
where H is the total number of strata, Nh is the total number of voxels in stratum h, and and are the means in stratum h of the quantities x and y defined above for the three accuracy estimators. Thus, for stratified random sampling, the combined ratio estimator of R (Cochran 1977, Section 6.11) is:
| [14] |
where and are the sample means of x and y for stratum h.
The standard error of the ratio estimator under stratified random sampling (Cochran 1977) is:
| [15] |
where H is the number of strata, Nh is the population size in stratum h, nh is the sample size in stratum h, R is the population ratio calculated as in [13], and are the population mean and population variances of x and y in stratum h, and is the population covariance of x and y in stratum h.
3.4.3. Confusion matrix based total burned area estimation
The total area burned (units: km2) is a fundamental variable used for the computation of atmospheric emissions and is used for the analysis of fire regimes and for a variety of ecological and natural resource management applications (Trigg and Roy 2007; Bowman et al. 2009; Pechony & Schindell 2010; Giglio et al. 2013).
The total area burned can be estimated from the confusion matrix as:
| [16] |
where A is computed as [3], and are the elements of the first column of the confusion matrix, estimated from the sample of independent reference data as [4]. An equivalent formulation is:
| [17] |
where n is the sample size, bu is the burned area detected in voxel u by the independent reference data, and πu is the inclusion probability of voxel u, which depends on the sampling design as described by [5] and [6].
It follows that for simple random sampling the population total burned area B is estimated as:
| [18] |
where N is the population size and is the sample mean of bu.
For stratified random sampling:
| [19] |
where Nh is the population size in stratum h and is the sample mean burned area for stratum h.
The standard error of the burned area estimate under simple random sampling is (Cochran 1977):
| [20] |
where N is the population size, n is the sample size, bu is the burned area detected in voxel u, and is the population variance of bu.
The standard error of the burned area estimate under stratified random sampling is (Cochran 1977):
| [21] |
where H is the number of strata, Nh is the population size in stratum h, nh is the sample size in stratum h , and is the population variance of bu in stratum h.
3.4.4. Optimal stratified random sample allocation
As the total sample size of independent reference is limited due to resource constraints, the optimal allocation of sample size across strata is of interest. The optimal allocation under stratified random sampling minimizes the standard error of an estimator for a fixed total sample size n (Neyman 1934; Cochran 1977, Sec. 6.14). The optimal allocation can be computed for each of the accuracy estimators derived from the confusion matrix (Overall Accuracy, Omission Error, and Commission Error) and for the total burned area estimates as below.
To minimize the standard error of a stratified ratio estimator [14], the optimal sample size allocated to stratum h is:
| [22] |
where n is the total sample size (i.e. ), H is the number of strata, Nh and Nk are the population size in strata h and k respectively, R is the population ratio calculated as in [10], and are the population variances of x and y in strata h and k respectively,andare the population covariances of x and y in strata h and k, and x and y are defined in [10] for Overall Accuracy, Omission Error and Commission Error.
To minimize the standard error of the burned area estimate [19], the optimal sample size allocated to stratum h is:
| [23] |
where n is the total sample size, H is the number of strata, Nh and Nk are the population size in strata h and k respectively, and are the population standard deviations of bu in strata h and k respectively, bu is the burned area detected in voxel u.
4.0. Demonstration of the proposed stratified random sampling design
4.1. Stratification Implementation
The voxel grid was derived by combining the Thiessen Scene Areas (TSAs) generated from the regular lattice of all the Landsat WRS-2 scene centroid latitude and longitude coordinates with the 16-day periods of the Landsat 5 acquisition calendar for 2008. Only TSAs covering landmasses between 60°S and 75°N were included and higher latitudes were excluded because they are perennially snow covered and do not burn. Globally this provided a total of 7779 TSAs.
A spatial stratification of the TSAs was derived from the Olson (2001) global biome map by assigning each TSA to the majority biome class it encompassed. Several biomes have globally a disproportionately small areal extent. For example, the Mangrove and the Tropical and Subtropical Coniferous Forest Olson biomes are the majority biome for just 33 and 39 TSAs respectively. Consequently, the 14 original Olson biomes were generalized by merging the seven Olson biomes having the smallest areal extents with similar biomes resulting in seven aggregated biomes (Table 2). Water bodies and areas covered by perennial ice are not considered a biome, but are defined in the Olson map, and were not considered in the subsequent analysis as they do not burn. Figure 3 shows the resulting global spatial stratification.
Table 2:
Aggregation of the Olson (2001) biomes into seven biomes used for the present study.
| Olson (2001) Biomes | Aggregated Biomes | Biome class number |
|---|---|---|
| Tropical and subtropical moist broadleaf forests |
Tropical Forest | 1 |
| Tropical and subtropical dry broadleaf forests |
Tropical Forest | |
| Tropical and subtropical coniferous forests |
Tropical Forest | |
| Mangrove | Tropical Forest | |
| Temperate broadleaf and mixed forests |
Temperate Forest | 2 |
| Temperate coniferous forests | Temperate Forest | |
| Boreal forests/taiga | Boreal Forest and Tundra | 3 |
| Tundra | Boreal Forest and Tundra | |
| Tropical and subtropical grasslands, savannas, and shrublands |
Tropical Savanna | 4 |
| Temperate grasslands, savannas, and shrublands |
Temperate Savanna | 5 |
| Flooded grasslands and savannas | Tropical Savanna (latitude 23°S to 23°N) or Temperate Savanna (latitudes greater than 23°N or 23° S) |
4 / 5 |
| Montane grasslands and shrublands |
Temperate Savanna | 5 |
| Mediterranean forests, woodlands, and scrub or sclerophyll forests |
Mediterranean | 6 |
| Deserts and Xeric Shrublands | Deserts and Xeric Shrublands | 7 |
Figure 3:
Cumulative distribution of the active fire area globally and for the seven biomes for 2008. The x axis shows the number of voxels sorted in ascending order by active fire area and the y axis shows the normalized cumulative active fire area. The active fire areas are calculated using the 2008 MODIS active fire detections (Section 3.3). The vertical line indicates the 20th quantile of the active fire area cumulative distibution; 80% of the active fire area is detected in just 1% to 11% of the voxels, depending on the biome.
The temporal stratification was defined based on the MODIS active fire area in each voxel for 2008. To avoid incomplete Landsat 16-day intervals at either end of the year, 23 full 16-day intervals were used (368 days in total) starting, for each TSA hexagon, on the day of the first Landsat 5 overpass of the year. The cumulative distributions of the active fire area over all voxels in each biome were generated (Section 3.3) and are illustrated in Figure 4. To ease visualization the cumulative distributions are shown normalized to the total biome active fire area (obtained by summation over all the voxels of the biome for 2008). The majority of voxels are unaffected by fire because global fire activity is concentrated in only a small portion of the spatial and temporal domain. The vertical lines in Figure 4 mark the 20th quantile of each distribution and are used to define the biome-specific threshold separating the “low” and “high” fire activity strata. Table 3 reports for each biome the number of TSA hexagons and voxels, the total active fire area, the biome-specific “high” and “low” fire activity threshold, and the number of voxels assigned to the “high” and “low” fire activity stata. For example, in the Tropical Forest biome (Table 3, top row) there are 1352 TSA hexagons, 31096 voxels, and the total active fire area detected within the voxels for 2008 is 1262907 km2. The 20th quantile of the cumulative distribution of the total active fire area is 112 km2; thus, the union of all voxels with active fire areas lower than 112 km2 encompasss 20% of the total active fire area, and the union of all voxels with active fire area greater than 112 km2 encompasses 80% of the total active fire area of the biome. This is illustrated in Figure 4, top left, which shows the cumulative distribution of the active fire area in each biome as a function of all voxels of the biome sorted by acending active fire area. The horizontal line marks 20% of the total active fire area of the biome, which is reached by the summation of the 28763 voxels with the lowest active fire areas.
Figure 4:
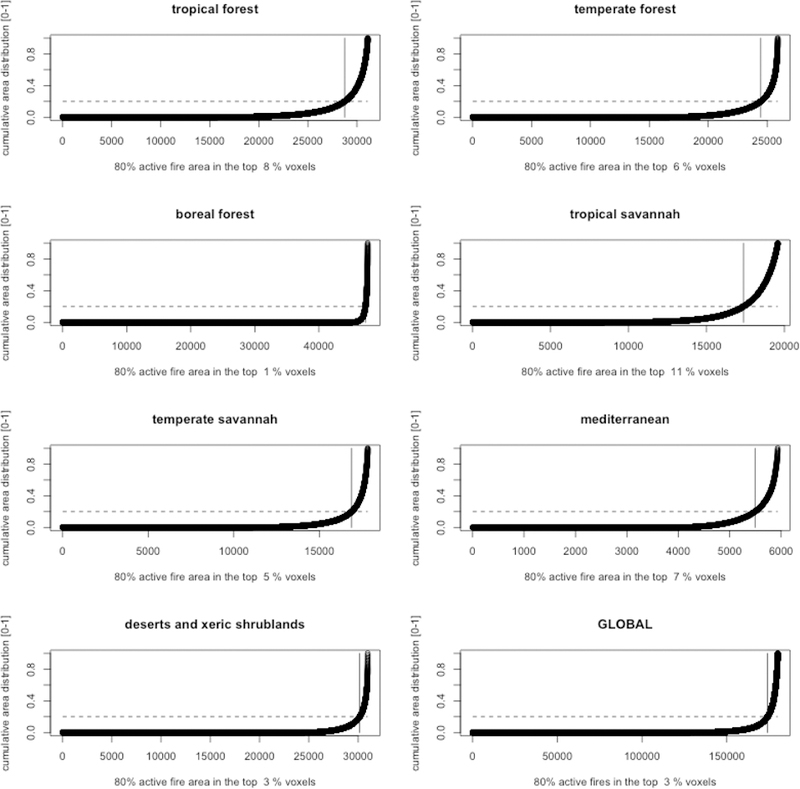
Global spatial distribution of the high fire activity voxels for 2008 obtained by applying the proposed two-level stratification. At each TSA location the map displays the number of voxels assigned to the high fire activity stratum based on the thresholds reported in Table 3.
Table 3:
Description of the geographic and fire activity strata for 2008 over the landmasses between 60°S and 75°N. The global total reports the sum of all the low and high fire activity strata of the seven biomes.
| Biome | Number of TSA hexagons |
Number of voxels |
Total active fire area [km2] |
High /Low fire activity threshold [km2] |
Number of high fire voxels (percent of all N voxels) |
Number of low fire voxels (percent of all N voxels) |
|---|---|---|---|---|---|---|
| Tropical Forest | 1352 | 31096 | 1262907 | 112 | 2333 (1.3%) |
28763 (16.1%) |
| Temperate Forest | 1126 | 25898 | 333222 | 39 | 1436 (0.8%) |
24462 (13.7%) |
| Boreal Forest | 2070 | 47610 | 135632 | 82 | 349 (0.2%) |
47261 (26.4%) |
| Tropical Savanna | 851 | 19573 | 4288425 | 517 | 2198 (1.2%) |
17375 (9.7%) |
| Temperate Savanna |
775 | 17825 | 472073 | 95 | 934 (0.5%) |
16891 (9.4%) |
| Mediterranean | 258 | 5934 | 41692 | 20 | 426 (0.2%) |
5508 (3.1%) |
| Deserts/Xeric Shrublands |
1347 | 30981 | 324360 | 61 | 813 (0.5%) |
30168 (16.9%) |
| Global Total | 7779 | 178917 | 6859727 | - | 8489 (4.7%) |
170428 (95.3%) |
Across the seven biomes 80% of the total active fire area occurs in only 1% (boreal forest biome) to 11% (tropical savanna biome) of the voxels (Figure 4). Globally (Table 3, bottom row) the union of the high fire activity strata of all the biomes encompasses 4.7% of the total number of voxels. This implies that if a global simple random sample is implemented for the selection of independent reference data then approximately 95% of the sampled voxels would be low fire activity voxels. With a limited sample size, this would likely result in a validation dataset that produces high standard errors of the accuracy and area estimators.
The spatial distribution of the voxels with high fire activity is illustrated in Figure 4, where the green-red colour scale indicates the number of high fire activity voxels within year 2008. The distribution of the high fire activity voxels broadly reflects the main global fire activity patterns observed in the literature (e.g., Giglio et al. 2006b, 2013; Chuvieco et al. 2008; Roy et al. 2008; Archibald et al. 2013).
4.2. Evaluation of the efficiency of the proposed stratification
The proposed stratification methodology was developed with the expectation that it will reduce the standard errors of the burned area product accuracy and area estimators relative to simple random sampling of the independent reference data. The magnitude of the reduction is indicative of the potential efficiency gain of the stratified design. To demonstrate this the statistical methods described in Section 3 were applied to the 2008 MODIS global burned area and active fire products, and the standard errors of the accuracy and area estimators under different stratification and sample allocation designs were calculated for each biome and globally. The optimal allocations that minimize the standard errors of each accuracy and area estimators, and practical allocations that can be used in actual validation exercises where the population parameters of the reference data are unknown are first described (Section 4.2.1) and then their standard errors are compared to the standard errors computed under simple random sampling of the MODIS fire products (Section 4.2.2).
The formulae defining the standard errors of the estimators as a function of the sample size (Section 3.4) require that the independent reference data population parameters are known. For the purposes of this analysis, the 2008 global burned area product (MCD45A1) was considered as the population of independent reference data. The 2008 global active fire product (MOD14A1/MYD14A1) was used to define the stratification into high and low fire activity strata and served as the product dataset that was validated. We note that the spatio-temporal relationship between satellite derived active fire locations and burned areas is complex, depending on factors including the satellite overpass time, cloud cover, the burning conditions and the algorithms used (Giglio et al. 2006a,b; Roy et al. 2008; Boschetti and Roy 2009; Hantson et al. 2013). In general, MODIS cumulative active fire detections underestimate the area burned in locations where the fire spreads rapidly relative to the satellite repeat cycle and overestimate the area in locations where fires are small relative to the 1km spatial resolution of the product. The actual accuracy of the MODIS fire products is not relevant here, however, as the objective of the present study is to use these two MODIS fire products to provide a case study evaluation of the potential reduction in standard errors of the accuracy and area estimates attributable to the stratified design. These analyses should not be construed as an assessment of the accuracy of either MODIS fire product.
4.2.1. Sample allocation to strata
The optimal allocation of sample size to the high fire and low fire activity strata of each biome for 2008 was computed for the accuracy and area estimators by using equation [22] for Overall Accuracy, Omission Error and Commission Error, and using equation [23] for the total burned area estimate. The optimal allocations constitute a benchmark for the performance of any alternative sample allocation, because by definition they result in the lowest possible standard errors of the estimators.
The optimal allocations are presented in Table 4 and are reported for each estimator and biome as percentages of the sample assigned to the high and low fire activity strata. Thus, for example, in the tropical forest biome encompassing 31096 voxels of which only 2333 are high fire activity in 2008 (Table 3), the allocation of 61% of the sample to the high fire activity stratum results in the lowest possible standard error of the Overall Accuracy estimator (Table 4). For each biome, among the four allocations the optimal allocations for the Commission Error (OPTCE) and the Omission Error (OPTOE) estimators assign the greatest and smallest percentages of the sample to the high fire activity strata respectively. Qualitatively, this behavior can be explained by considering that commission errors (for the purpose of the analysis, defined as areas detected as fires in the MOD14A1/MOD14A1 product but not in the MCD45A1 product) are more likely to occur in high fire activity voxels (which have, by design, a high number of active fire detections), while omission errors (for the purpose of the analysis defined as areas detected as fires in the in the MCD45A1 product but not in the MOD14A1/MOD14A1 product) are more likely to occur in low fire activity voxels. It is expected that if a different fire product were used as stratification variable, a different behavior would be observed. If for instance the product had no omission error, but large commission error, then the optimal allocation for the Commission Error would likely assign a smaller sample size to the high activity strata than the optimal allocation for Omission Error.
Table 4:
Optimal allocation of sample size across fire activity strata calculated using the 2008 MODIS active fire and burned area products. Optimal allocations for the Overall Accuracy (OPTOA), Commission Error (OPTCE), Omission Error (OPTOE), and Total Burned Area (OPTBA) are shown as percentages of the sample size allocated to the high fire activity stratum of each biome.
| Biome | Percentage of the sample allocated to the high fire activity and low fire activity stratum (in brackets) of each biome. |
|||
|---|---|---|---|---|
| OPTOA | OPTCE | OPTOE | OPTBA | |
| Tropical Forest | 61% (39%) | 81% (19%) | 34% (66%) | 50% (50%) |
| Temperate Forest |
66% (34%) | 85% (15%) | 41% (59%) | 60% (40%) |
| Boreal Forest | 30% (70%) | 37% (63%) | 16% (84%) | 27% (63%) |
| Tropical Savanna |
49% (51%) | 69% (31%) | 33% (67%) | 55% (45%) |
| Temperate Savanna |
52% (48%) | 70% (30%) | 37% (63%) | 48% (52%) |
| Mediterranean | 28% (72%) | 85% (15%) | 18% (82%) | 20% (80%) |
| Deserts/Xeric Shrublands |
66% (34%) | 68% (32%) | 40% (60%) | 54% (46%) |
In practical cases of validation the independent reference data are available for only a limited set of voxels and the population parameters required to compute the optimal allocations (Equations [22] and [23]) are unknown. Consequently, alternative sample allocations must be adopted, based on the data used to construct the strata. In this study three alternative allocations, which utilize the global voxel stratification but are not informed by the independent reference data, were considered:
-
-
Equal allocation (EQ): for each biome the sample is allocated equally among the low and high fire activity strata.
-
-
Proportional allocation (PROP): for each biome the sample is allocated proportionally to the total number of voxels in the low and high fire activity strata. The proportional allocation results are also useful because the standard errors for this allocation are approximately the same as would be achieved by post-stratified estimation in which the strata are used at the estimation stage following selection of a simple random sample (Cochran 1977, section 5A.9).
-
-
Active fire based allocation (AF): allocation obtained from [23] using the standard deviation of the active fire distribution, calculated over all the voxels of each stratum using the MOD14/MYD14 active fire product (the map used to construct the strata).
The percentage of the sample allocated to each high and low fire activity stratum is reported in Table 5. The EQ allocation simply divides the samples equally between the high and low fire activity stratum without considering any additional information. The PROP allocation reflects the proportion of high fire activity voxels in each biome (Figure 4, Table 3), therefore assigning only a small percentage of the sample (1% to 11%) to the high fire activity stratum. The AF allocation is informed by the population parameters of the dataset being validated (for this analysis, the active fire detections) which – unlike the population parameters of the independent reference data – are always known. The AF allocation is an approximation of the optimal OPTBA allocation if the standard deviation in each stratum of the dataset being validated is comparable to the standard deviation of the independent reference data. The results of Table 5 are referred to in the next section.
Table 5:
Sample allocations based on the active fire auxiliary variable used to define strata. Unlike the optimal allocations summarized in Table 4 the three sample allocations (EQ, PROP and AF) can be implemented in real validation exercises where the population parameters of the independent reference data are unknown. EQ is equal allocation where the sample size is equal in the high and low fire activity strata, PROP is proportional allocation where the sample is allocated proportionally to the total number of voxels in the stratum (Table 3), AF is the optimal allocation obtained through [22] using the population parameters of the dataset being validated (i.e., the map product used to construct the strata). Results for all allocations are reported as percentages of the sample size allocated to the high and low fire activity stratum of each biome.
| Biome | Percentage of the sample allocated to the high fire activity and to the low fire activity stratum (in brackets) of each biome |
||
|---|---|---|---|
| EQ | PROP | AF | |
| Tropical Forest | 50% (50%) | 8% (92%) | 66% (34%) |
| Temperate Forest | 50% (50%) | 6% (94%) | 74% (26%) |
| Boreal Forest | 50% (50%) | 1% (99%) | 36% (64%) |
| Tropical Savanna | 50% (50%) | 11% (79%) | 57% (43%) |
| Temperate Savanna | 50% (50%) | 5% (95%) | 64% (36%) |
| Mediterranean | 50% (50%) | 7% (93%) | 65% (35%) |
| Deserts/Xeric Shrublands |
50% (50%) | 3% (97%) | 72% (28%) |
4.2.2. Standard errors of the accuracy and area estimators
The ratio between the standard errors of the accuracy and burned area estimators calculated under stratified random sampling (provided by [15] and [21] respectively) and the corresponding standard errors calculated under simple random sampling (provided by [12] and [20]) allows for quantification of the reduction of the standard errors due to the stratified sampling design. Figure 4 shows the ratios for the confusion matrix based estimates (Overall Accuracy, Omission Error, and Commission Error) and for the total burned area estimate with respect to each biome and globally. The red dots show the ratios between the standard errors generated for the optimal sample allocations (Table 4) and the standard errors calculated under simple random sampling. The triangles show the ratios of the alternative practical sample allocations (Table 5) with respect to simple random sampling. Values less than 1.0 indicate a reduction in standard error attributable to the stratified design. Provided that the sample size is small compared to the population size (i.e., n << N and nh << Nh) as is generally the case in burned area validation exercises, the ratios plotted in Figure 4 are independent of sample size as the ratios [21]/[20] and [15]/[12] can be written as a function of nh/n allocated to each stratum (i.e., Tables 4 and 5).
The ratios obtained with the optimal allocations (red dots) are always smaller than 1.0, indicating that stratified random sampling always reduced the standard errors relative to simple random sampling for the case study population. Globally, the standard errors of the overall accuracy, omission error, commission error and total burned area estimates under stratified sampling with optimal allocation are 36%, 74%, 42% and 46% respectively of the standard errors calculated under simple random sampling. These ratios represent the theoretical upper bound of the reduction of standard error obtained by using the optimal allocation under the proposed stratification. The Equal (EQ) and Active Fire based (AF) allocations yield nearly similar results (the smallest biome, the Mediterranean, is the one exception) and globally the efficiency for these two practical allocations is only marginally lower than the theoretical upper bound. The standard error ratios for the global overall accuracy, omission error, commission error and total burned area estimates under stratified sampling are respectively 37%, 77%, 46%, 47% with the EQ allocation and 37%, 82%, 44%, 47% with the AF allocation.
While the EQ and AF allocations achieve a reduction of standard errors close to the upper bound values obtained with the optimal stratification, proportional allocation (PROP) provides a negligible reduction of standard errors compared to simple random sampling. This can be attributed to the fact that under the PROP allocation only a small percentage of the sample (Table 5) is allocated to the high activity fire strata, which encompass by design 80% of the active fire area. Thus, a sample extracted under proportional allocation will not include many of the voxels for which the majority of fires occur and this may translate to higher standard errors of the estimators. Given that the standard errors for proportional allocation approximate the standard errors for poststratified estimation, these results suggest that poststratified estimation applied to a simple random sample will not yield the magnitude of precision gains achievable by incorporating the strata information in the sampling design. At the individual biome level, both the EQ and AF allocations consistently reduce the standard errors of all estimators compared to simple random sampling. The only exception is the Mediterranean biome, where the standard errors of the omission error and total burned area estimators increase; this reflects the low agreement of the MCD45A1 and MOD14A1/MYD14A1 products in this biome, with the detection of burned areas in times and places where there are no active fire detections (i.e., omission errors). The stratification is consistently most effective at reducing the standard errors in the biomes (Deserts and Xeric Shrublands, Boreal Forest, Temperate Forest) where fire activity is concentrated in the smallest percentage of voxels (Figure 3). The standard errors for the EQ and AF allocations are close enough that either allocation could be used in practice. An advantage of the EQ allocation is that it is simpler to implement than the AF allocation. Furthermore, in the Mediterranean biome where the stratified design has the worst performance, the EQ allocation results in standard errors only marginally higher than simple random sampling.
5.0. Conclusions
Despite the number of available global satellite derived burned area products, there have been few rigorous assessments of their accuracy and limited development of systematic assessment methodologies. Product comparison studies have revealed large discrepancies in the area estimates, timing and location among satellite burned area products and highlight the need for systematic product validation (e.g., Korontzi et al. 2004; Boschetti et al. 2004; Roy and Boschetti 2009; Giglio et al. 2010; Padilla et al. 2015). Arguably this is attributable to lack of adequate independent reference datasets, resource limitations and the broad scope and complexity of the task, including the challenge of defining an appropriate independent reference data sampling methodology.
Satellite derived burned area has been identified by the Global Climate Observing System (GCOS) as one of the Essential Climate Variables (ECVs) needed in support of the United Nations Framework Convention on Climate Change (UNFCCC) (GCOS 2011). The Global Burned Area Satellite Validation Protocol, endorsed by the Committee on Earth Observation (CEOS) (Boschetti et al. 2009), defines the requirements for the use of satellite data as independent reference data but does not specify independent reference data sampling requirements. The methodology developed in this study is applicable for the validation of the current generation of coarse resolution burned area products, and contributes to the expansion of the CEOS protocol and is responsive to the needs expressed by the GCOS requirements for satellite products on climate which mandate a quantitative, statistically rigorous accuracy assessment of coarse resolution burned area products using Landsat-class independent reference data (GCOS 2011). Specifically, the present study complements the CEOS protocol, by proposing a sampling design for the extraction of Landsat data that are used to derive independent reference data. The novel aspect of this study is the definition of an unambiguous sampling unit encompassing both the spatial and the temporal domains. Although a few papers have addressed sampling strategies for burned area validation in the spatial domain (Boschetti et al. 2006; Padilla et al. 2014), none have incorporated a probability sampling design extending to the temporal aspect of the selection of reference data. Sampling of independent reference data with respect to both the spatial and temporal domains is necessary for statistically rigorous inferences from sample-based validation of global burned area products. By incorporating probability sampling in both the spatial and temporal domains, we establish a design-based foundation for inference applicable to validation of thematic terrestrial products that have high temporal variability. In addition to burned areas, the approach could be extended to the validation of other non-permanent disturbances and ephemeral phenomena (e.g. flooding, snow cover, clouds, or dynamic land/water masks).
The design of a sampling scheme inherently rests on empirical assumptions and subjective choices. Consequently, alternative stratifications to the proposed design, equally based on empirical assumptions, could be devised. Nonetheless, Stehman (1999, 2009) presented desirable criteria for a sampling scheme needed for the validation of thematic satellite products. In the absence of an objective manner to rank all possible alternative sampling designs the following six criteria allow for an evaluation of the proposed sampling design:
-
C1 –
satisfies the requirement of a probability sampling design,
-
C2 –
is practical to implement,
-
C3 –
resulting sample is spatially well distributed,
-
C4 –
standard errors of the accuracy estimators can be estimated without undue reliance on approximations other than those related to the sample size,
-
C5 –
change in the sample size can be accommodated at any step in the implementation of the sampling design,
-
C6 –
standard errors of the accuracy estimates should be small.
Criteria (C1) through (C5) are satisfied by the proposed voxel based stratified simple random sampling design as:
it is a probability sampling design (thus by definition satisfying C1),
it uses a spatial and temporal unit based on the Landsat WRS-2 acquisition grid and acquisition calendar in time (satisfying C2),
the spatial stratification by biomes ensures that the sample is well distributed geographically over the globe (satisfying C3),
the formulas for standard errors of the areal and pixel level accuracy estimators, discussed in Section 3.3, are a straightforward function of sample size (satisfying C4),
the stratified random sampling design ensures that additional sample voxels can be extracted to augment the reference sample at any point in the validation process (satisfying C5).
Assessment of C6 (standard errors of the accuracy estimates should be small) relies on a combination of stratified sampling theory as the basis of the result that stratification typically decreases standard errors relative to simple random sampling and numerical examples to illustrate the magnitude of the potential precision improvement.The stratification of voxels into low and high burned area strata follows the common recommendation to implement stratified sampling when the primary feature of interest is a rare feature of the landscape (Olofsson et al. 2014). For example, for the objective of estimating total area burned from the reference sample data, stratification will be most effective if the mean reference burned area differs between the low and high strata (Lohr 2010, p.91). Because the strata are constructed from the burned area product (map) being evaluated, the requirement for the strata to be effective is that the map is able to distinguish low burned area from high burned area voxels. These fundamental tenets of stratification provide the underlying theory supporting the general result that stratified sampling will improve precision relative to simple random sampling, sometimes greatly so as demonstrated by the results presented in Figure 4. Padilla et al. (2014) established a precedent for implementing this stratified approach in practice.
To examine quantitatively the potential reduction in standard errors of the estimators for the stratified design relative to simple random sampling, we conducted an analysis using the 2008 MODIS global fire products to represent hypothetical populations for the auxiliary (i.e., map product) and independent reference data. No Landsat scale global burned area products have been produced to date, despite the recent development of algorithms and regional to continental scale prototypes (Boschetti et al. 2015; Goodwin and Collett 2014; Eidenshink et al. 2007). Considering the 2008 MODIS fire products globally the standard errors of the overall accuracy, omission error, commission error and total burned area estimates under stratified sampling with equal allocation of the sample were 37%, 77%, 46%, 47% respectively of the standard errors calculated under simple random sampling. These values are very close to the theoretical upper bound performance of the optimal allocation based on a known reference population, which was 36%, 74%, 42%, and 46% for the same four estimators. The magnitude of these reductions will vary for different applications depending on the map product being evaluated and the accuracy of this map relative to the independent reference data Additional work will be needed to explore refinements of the methodology such as investigating the impact of different thresholds to define low and high fire activity and exploration of additional hypothetical populations to further establish the range of potential reductions in standard error achievable in practice by the stratified design.
The present work did not take into account the actual availability of Landsat data, implicitly assuming instead that all Landsat acquisitions are available and are unaffected by clouds. However, the global Landsat data archive has spatially and temporally variable acquisition coverage due to variable acquisition strategies and cloud cover (Kovalskyy and Roy 2013; Wulder et al. 2016). The global Landsat 8 acquisition coverage is much improved compared to previous Landsat missions due to improved onboard recording and satellite to ground transmission capabilities and the majority of the land WRS-2 paths/rows overpassed each day by Landsat 8 are acquired (Roy et al. 2014). Even using Landsat 8, though, the cloud cover at the time of satellite overpass may not be random in space or time, for example, in regions with stationary weather systems or orographic clouds (Roy et al. 2006; Sano et al. 2007; Kovalskyy and Roy 2015). Standard “non-response” statistical techniques will need to be implemented in the analysis to reliably address this missing data problem. For example, Särndal et al. (1992, Section 14.6.2) proposed an extended probability sampling approach to accommodate missing data that combines the randomization distribution of design-based inference with a model-based component of inference to address the non-sampling error attributable to missing data. Nonetheless, the underlying probability sampling structure described in this study provides a strong foundation for inference. The implementation of appropriate techniques to address the issue of missing Landsat data will be a priority for future research. This will be performed in the context of implementing the described stratified random sampling design for global scale (i.e., Stage 3) validation of the planned Collection 6 MODIS burned area product using a global sample of independent reference data derived from Landsat 8 images.
At regional to global scale the same sampling design could be applied to other coarse resolution burned area products to provide more reliable burned product accuracy and total area burned estimates using Landsat data. The proposed design is based on a sampling unit defined as a function of the Landsat WRS-2 grid and acquisition calendar (i.e., the voxel is defined as TSA for a 16-day Landsat interval). Future research can extend application of these design concepts to other Landsat-class moderate resolution satellite systems with systematic global acquisition and frequent repeat, such as those provided by the Sentinel 2 Multi Spectral Instrument (MSI) (Drusch et al., 2012).
Figure 1:
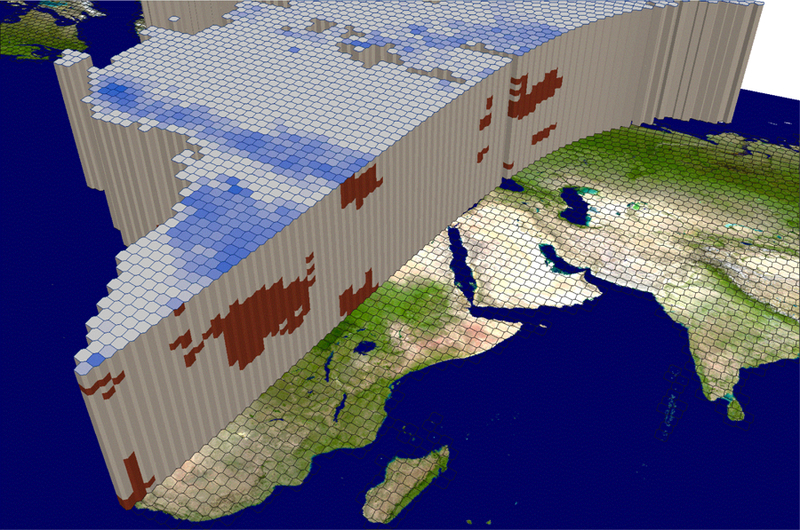
Three-dimensional voxel representation of the distribution of 2008 MODIS active fires in space and in time. Each voxel is defined spatially by a Thiessen Scene Area (TSA) generated from the regular lattice of all the WRS-2 scene centroid latitude and longitude coordinates and is defined temporally by a 16-day period. The red and gray cells represent high and low MODIS active fire activity in each voxel. The blue hexagons, on the upper surface, indicate the number of high fire activity voxels over the year. The details of the data and methods used to characterize the fire activity are discussed in Section 4
Figure 5:
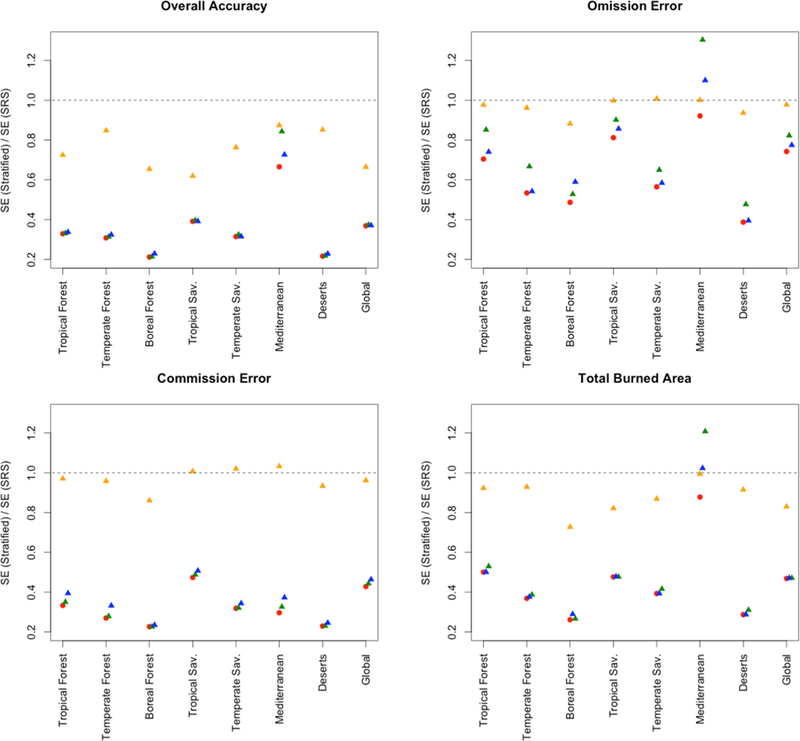
Standard error (SE) ratios under stratified sampling with respect to simple random sampling for the four estimators. For each estimator, the ratios obtained using the corresponding optimal sample allocation (OPTOA for Overall Accuracy, OPTCE for Commission Error, OPTOE for Commission Error and OPTBA for the Burned Area Total, Table 4) are plotted as red dots. The ratios obtained using the three candidate practical sample allocations (Table 5) are plotted as colored triangles: blue for equal allocation (EQ), orange for proportional allocation (PROP), and green for optimal allocation based on the active fire product used to create the stratification (AF). The red dots reflect the lowest standard errors that are attainable with the theoretically optimal allocation under the proposed stratification. The points below the horizontal dashed line indicate that stratified random sampling has a standard error lower than simple random sampling.
ACKNOWLEDGEMENTS
This research was funded by NASA grants number NNX14AI68G, NNX14AP70A, NNX11AF39G, and NNX13AP48G. The authors gratefully acknowledge the contribution by Michael Humber, Department of Geographical Sciences, University of Maryland, for his support to the GIS analysis of the datasets. We thank the three anonymous reviewers for constructive comments that helped improve the manuscript.
REFERENCES
- Alonso-Canas I, & Chuvieco E (2015). Global Burned Area Mapping from ENVISAT-MERIS and MODIS active fire data. Remote Sensing of Environment, 163, 140–152. [Google Scholar]
- Archibald S, Roy DP, Van Wilgen BW, and Scholes RJ 2009, What Limits Fire?: An examination of drivers of burnt area in sub-equatorial Africa, Global Change Biology special issue on Fire Ecology and Climate Change, 15, 613–630, 10.1111/j.1365-2486.2008.01754.x. [DOI] [Google Scholar]
- Archibald S, Scholes RJ, Roy DP, Roberts G, & Boschetti L (2010). Southern African fire regimes as revealed by remote sensing. International Journal of Wildland Fire, 19, 861–878. [Google Scholar]
- Archibald S, Lehmann CE, Gómez-Dans JL, & Bradstock RA (2013). Defining pyromes and global syndromes of fire regimes. Proceedings of the National Academy of Sciences, 110(16), 6442–6447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arvidson T, Goward SN, Gasch J, & Williams D (2006). Landsat-7 long-term acquisition plan: development and validation. Photogrammetric Engineering & Remote Sensing, 72, 1137–1146. [Google Scholar]
- Barbosa PM, Grégoire JM, & Pereira JMC (1999). An algorithm for extracting burned areas from time series of AVHRR GAC data applied at a continental scale. Remote Sensing of Environment, 69(3), 253–263. [Google Scholar]
- Bastarrika A, Alvarado M, Artano K, Martinez MP, Mesanza A, Torre L, … & Chuvieco E (2014). BAMS: A tool for supervised burned area mapping using Landsat data. Remote Sensing, 6(12), 12360–12380. [Google Scholar]
- Bontemps S, Defourny P, Bogaert EV, Arino O, Kalogirou V, & Perez JR (2011). GLOBCOVER 2009-Products description and validation report Retrieved from: http://due.esrin.esa.int/page_globcover.php (last accessed 3/11/2016)
- Boschetti L, Eva HD, Brivio PA, & Grégoire JM (2004). Lessons to be learned from the comparison of three satellite‐derived biomass burning products. Geophysical Research Letters, 31(21). [Google Scholar]
- Boschetti L, Brivio PA, Eva Hugh D., Gallego J, Baraldi A and Grégoire J-M (2006). A sampling method for the retrospective validation of global burned area products. IEEE-Transactions on Geoscience and Remote Sensing, 44, 1765 – 1773. [Google Scholar]
- Boschetti L, & Roy DP (2008). Defining a fire year for reporting and analysis of global interannual fire variability. Journal of Geophysical Research: Biogeosciences, 113, G03020. [Google Scholar]
- Boschetti L, Roy DP, & Justice C (2009). International global burned area satellite product validation protocol, CEOS-CalVal (Ed.), Part I—Production and standardization of validation reference data, Committee on Earth Observation Satellites, USA, pp. 1–11. [Google Scholar]
- Boschetti L, Roy DP, Justice CO, & Humber M (2015). MODIS-Landsat fusion for large area 30m burned area mapping. Remote Sensing of Environment, 161, 27–42. [Google Scholar]
- Bowman DM, Balch JK, Artaxo P, Bond WJ, Carlson JM, Cochrane MA, … & Pyne SJ (2009). Fire in the Earth system. Science, 324(5926), 481–484. [DOI] [PubMed] [Google Scholar]
- Cardoso MF, Hurtt GC, Moore B, Nobre CA, & Bain H (2005). Field work and statistical analyses for enhanced interpretation of satellite fire data. Remote Sensing of Environment, 96, 212–227. [Google Scholar]
- Chang D, & Song Y (2009). Comparison of L3JRC and MODIS global burned area products from 2000 to 2007. Journal of Geophysical Research: Atmospheres (1984–2012), 114(D16).
- Chuvieco E, Martín MP, & Palacios A (2002). Assessment of different spectral indices in the red-near-infrared spectral domain for burned land discrimination. International Journal of Remote Sensing, 23, 5103–5110. [Google Scholar]
- Chuvieco E, Giglio L, & Justice C (2008). Global characterization of fire activity: toward defining fire regimes from Earth observation data. Global Change Biology, 14(7), 1488–1502. [Google Scholar]
- Cochran WG (1977). Sampling Techniques (3rd edition). Wiley, New York, pp. 413. [Google Scholar]
- Cohen WB, Yang Z, & Kennedy R (2010). Detecting trends in forest disturbance and recovery using yearly Landsat time series: 2. TimeSync—Tools for calibration and validation. Remote Sensing of Environment, 114(12), 2911–2924. [Google Scholar]
- Congalton RG, Oderwald RG, & Mead RA, (1983), Assessing Landsat classification accuracy using discrete multivariate analysis statistical techniques. Photogrammetric Engineering & Remote Sensing, 49, 1671–1678. [Google Scholar]
- Csiszar IA, Morisette JT and Giglio L (2006) Validation of active fire detection from moderate-resolution satellite sensors: The MODIS example in northern Eurasia, IEEE Transactions on Geoscience and Remote Sensing 44(7), 1757–1764. 10.1109/Tgrs.2006.875941. [DOI] [Google Scholar]
- Drusch M, Del Bello U, Carlier S, Colin O, Fernandez V, Gascon F, … Bargellini P (2012). Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sensing of Environment, 120, 25–36. [Google Scholar]
- Eidenshink J, Schwind B, Brewer K, Zhu Z, Quayle B, & Howard S (2007). A project for monitoring trends in burn severity. Fire Ecology, 3, 3–21. [Google Scholar]
- Foody GM (2002). Status of land cover classification accuracy assessment. Remote sensing of Environment, 80(1), 185–201. [Google Scholar]
- Fraser RH, Li Z, & Landry R (2000). SPOT VEGETATION for characterizing boreal forest fires. International Journal of Remote Sensing, 21(18), 3525–3532. [Google Scholar]
- Friedl MA, Sulla-Menashe D, Tan B, Schneider A, Ramankutty N, Sibley A, & Huang X (2010). MODIS Collection 5 global land cover: Algorithm refinements and characterization of new datasets. Remote Sensing of Environment, 114(1), 168–182. [Google Scholar]
- GCOS (2011). Systematic Observation Requirements for Satellite-Based Data Products For Climate (2011 Update), retrieved from https://www.wmo.int/pages/prog/gcos/Publications/gcos-154.pdf (last accessed 20–11-2015).
- Gallego FJ (2005). Stratified sampling of satellite images with a systematic grid of points. ISPRS Journal of Photogrammetry and Remote Sensing, 59(6), 369–376. [Google Scholar]
- Giglio L, Descloitres J, Justice CO, & Kaufman YJ (2003). An enhanced contextual fire detection algorithm for MODIS. Remote Sensing of Environment, 87, 273–282. [Google Scholar]
- Giglio L, van der Werf GR, Randerson JT, Collatz GJ, & Kasibhatla P (2006a). Global estimation of burned area using MODIS active fire observations. Atmospheric Chemistry and Physics, 6, 957–974. [Google Scholar]
- Giglio L, Csiszar I, & Justice CO (2006b). Global distribution and seasonality of active fires as observed with the Terra and Aqua Moderate Resolution Imaging Spectroradiometer (MODIS) sensors. Journal of Geophysical Research-Biogeosciences, 111, G02016, 10.1029/2005JG000142 . [DOI] [Google Scholar]
- Giglio L (2007). Characterization of the tropical diurnal fire cycle using VIRS and MODIS observations. Remote Sensing of Environment, 108(4), 407–421. [Google Scholar]
- Giglio L, Loboda T, Roy DP, Quayle B, & Justice CO (2009). An active-fire based burned area mapping algorithm for the MODIS sensor. Remote Sensing of Environment, 113, 408–420. [Google Scholar]
- Giglio L, Randerson JT, van der Werf GR, Kasibhatla PS, Collatz GJ, Morton DC, & DeFries RS (2010). Assessing variability and long-term trends in burned area by merging multiple satellite fire products. Biogeosciences, 7, 1171–1186. [Google Scholar]
- Giglio Louis, Randerson James T., and Werf Guido R.. (2013). Analysis of daily, monthly, and annual burned area using the fourth‐generation global fire emissions database (GFED4). Journal of Geophysical Research: Biogeosciences, 1181: 317–328. [Google Scholar]
- Goodwin NR, & Collett LJ (2014). Development of an automated method for mapping fire history captured in Landsat TM and ETM+ time series across Queensland, Australia. Remote Sensing of Environment, 148, 206–221. [Google Scholar]
- Goward S, Arvidson T, Williams D, Faundeen J, Irons J, & Franks S (2006). Historical record of Landsat global coverage: Mission operations, NSLRSDA, and international cooperator stations. Photogrammetric Engineering and Remote Sensing, 72, 1155. [Google Scholar]
- Grégoire JM, Tansey K, & Silva JMN (2003). The GBA2000 initiative: developing a global burnt area database from SPOT-VEGETATION imagery. International Journal of Remote Sensing, 24(6), 1369–1376. [Google Scholar]
- Hantson S, Padilla M, Corti D, & Chuvieco E (2013). Strengths and weaknesses of MODIS hotspots to characterize global fire occurrence. Remote Sensing of Environment, 131, 152–159. [Google Scholar]
- Irons JR, Dwyer JL, Barsi JA (2012), The next Landsat satellite: The Landsat data continuity mission, Remote Sensing of Environment, 122, 11–21. [Google Scholar]
- Ju J and Roy DP, 2008, The Availability of Cloud-free Landsat ETM+ data over the Conterminous United States and Globally, Remote Sensing of Environment, 112:1196–1211. [Google Scholar]
- Justice C, Belward A, Morisette J, Lewis P, Privette J, & Baret F (2000). Developments in the ‘validation’ of satellite sensor products for the study of the land surface. International Journal of Remote Sensing, 21(17), 3383–3390. [Google Scholar]
- Kennedy RE, Yang Z, & Cohen WB (2010). Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sensing of Environment, 114(12), 2897–2910. [Google Scholar]
- Korontzi S, Roy DP, Justice CO, & Ward DE (2004). Modeling and sensitivity analysis of fire emissions in southern Africa during SAFARI 2000. Remote Sensing of Environment, 92(3), 376–396. [Google Scholar]
- Kovalskyy V & Roy DP (2013). The global availability of Landsat 5 TM and Landsat 7 ETM+ land surface observations and implications for global 30m Landsat data product generation. Remote Sensing of Environment, 130, 280–293. [Google Scholar]
- Kovalskyy V & Roy DP (2015). A one year Landsat 8 conterminous United States study of cirrus and non-cirrus clouds. Remote Sensing, 7, 564–578. [Google Scholar]
- Morisette JT, Privette JL, & Justice CO (2002). A framework for the validation of MODIS land products. Remote Sensing of Environment, 83, 77–96. [Google Scholar]
- Lohr SL (2010). Sampling: Design and Analysis (2nd edition). Brooks/Cole, Boston, MA. [Google Scholar]
- Morisette JT, Giglio L, Csiszar I & Justice CO (2005). Validation of the MODIS active fire product over Southern Africa with ASTER data. International Journal of Remote Sensing 26(19), 4239–4264. [Google Scholar]
- Morisette JT, Baret F, & Liang S (2006). Special issue on global land product validation. IEEE Transactions on Geoscience and Remote Sensing, 44(7), 1695–1697. [Google Scholar]
- Mouillot F, Schultz MG, Yue C, Cadule P, Tansey K, Ciais P, & Chuvieco E (2014). Ten years of global burned area products from spaceborne remote sensing—A review: Analysis of user needs and recommendations for future developments. International Journal of Applied Earth Observation and Geoinformation, 26, 64–79. [Google Scholar]
- Neyman J (1934). On the two different aspects of the representative method: the method of stratified sampling and the method of purposive selection. Journal of the Royal Statistical Society, 97, 558–625. [Google Scholar]
- Olofsson P, Foody GM, Herold M, Stehman SV, Woodcock CE, & Wulder MA (2014). Good practices for estimating area and assessing accuracy of land change. Remote Sensing of Environment, 148, 42–57. [Google Scholar]
- Olson DM, Dinerstein E, Wikramanayake ED, Burgess ND, Powell GV, Underwood EC, D’Amico JA, Itoua I, Strand HE, Morrison JC, Loucks CJ, Allnutt TF, Ricketts TH, Kura. Y, Lamoreux JF, Wettengel WW, Hedao P, & Kassem KR (2001). Terrestrial Ecoregions of the World: A New Map of Life on Earth A new global map of terrestrial ecoregions provides an innovative tool for conserving biodiversity. BioScience, 51(11), 933–938. [Google Scholar]
- Padilla M, Stehman SV, & Chuvieco E (2014). Validation of the 2008 MODIS-MCD45 global burned area product using stratified random sampling. Remote Sensing of Environment, 144, 187–196. [Google Scholar]
- Padilla M, Stehman SV, Ramo R, Corti D, Hantson S, Oliva P, Alonso-Canaz I, Bradley AV, Tansey K, Mota B, Pereira JM and Chuvieco E (2015). Comparing the accuracies of remote sensing global burned area products using stratified random sampling and estimation. Remote Sensing of Environment, 160, 114–121. [Google Scholar]
- Pechony O, & Shindell DT (2010). Driving forces of global wildfires over the past millennium and the forthcoming century. Proceedings of the National Academy of Sciences, 107(45), 19167–19170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy DP, Borak JS, Devadiga S, Wolfe RE, Zheng M, & Descloitres J (2002). The MODIS land product quality assessment approach. Remote Sensing of Environment, 83(1), 62–76. [Google Scholar]
- Roy DP, Jin Y, Lewis PE, & Justice CO (2005a). Prototyping a global algorithm for systematic fire-affected area mapping using MODIS time series data. Remote Sensing of Environment, 97(2), 137–162. [Google Scholar]
- Roy DP, Frost PGH, Justice CO, Landmann T, Le Roux JL, Gumbo K, Makungwa S, Dunham K, Du Toit R, Mhwandagara K, Zacarias A, Tacheba B, Dube OP, Pereira JMC, Mushove P, Morisette JT, Vannan SKS, Davies D (2005b). The Southern Africa Fire Network (SAFNet) regional burned-area product validation protocol. International Journal of Remote Sensing, 26, 4265–4292. [Google Scholar]
- Roy DP, Lewis P, Schaaf C, Devadiga S, & Boschetti L (2006). The global impact of cloud on the production of MODIS bi-directional reflectance model based composites for terrestrial monitoring. IEEE Geoscience & Remote Sensing Letters, 3, 452–456. [Google Scholar]
- Roy DP, Boschetti L, Justice CO, & Ju J (2008). The Collection 5 MODIS Burned Area Product - Global Evaluation by Comparison with the MODIS Active Fire Product. Remote Sensing of Environment,112, 3690–3707. [Google Scholar]
- Roy DP, & Boschetti L (2009). Southern Africa validation of the MODIS, L3JRC, and GlobCarbon Burned-Area Products. IEEE Transactions on Geoscience and Remote Sensing, 47, 1032–1044. [Google Scholar]
- Roy DP, Wulder MA, Loveland TR, Woodcock CE, Allen RG, Anderson MC, Helder D, Irons JR, Johnson DM, Kennedy R, Scambos TA, Schaaf CB, Schott JR, Sheng Y, Vermote EF, Belward AS, Bindschadler R, Cohen WB, Gao F, Hipple JD, Hostert P, Huntington J, Justice CO, Kilic A, Kovalskyy V, Lee ZP, Lymburner L, Masek JG, McCorkel J, Shuai Y, Trezza R, Vogelmann J, Wynne RH, & Zhu Z (2014). Landsat-8: science and product vision for terrestrial global change research. Remote Sensing of Environment, 145, 154–172. [Google Scholar]
- Sano EE, Ferreira LG, Asner GP, & Steinke ET (2007). Spatial and temporal probabilities of obtaining cloud-free Landsat images over the Brazilian tropical savanna. International Journal of Remote Sensing, 28, 2739–2752. [Google Scholar]
- Särndal C-E, Swensson B, and Wretman J (1992). Model-Assisted Survey Sampling, Springer-Verlag, New York, N.Y., 694 p. [Google Scholar]
- Schroeder W, Prins E, Giglio L, Csiszar I, Schmidt C, Morisette J and Morton D (2008a). Validation of GOES and MODIS active fire detection products using ASTER and ETM plus data. Remote Sensing of Environment, 112(5), 2711–2726. 10.1016/j.rse.2008.01.005. [DOI] [Google Scholar]
- Schroeder W, Ruminski M, Csiszar I, Giglio L, Prins E, Schmidt C & Morisette J (2008b). Validation analyses of an operational fire monitoring product: The Hazard Mapping System. International Journal of Remote Sensing, 29(20), 6059–6066. 10.1080/01431160802235845. [DOI] [Google Scholar]
- Schroeder W, Oliva P, Giglio L, Ivan A, & Csiszar IA (2014). The new VIIRS 375m active fire detection data product: Algorithm description and initial assessment. Remote Sensing of Environment, 143, 85–96. [Google Scholar]
- Silva J, Pereira J, Cabral AI, Sá AC, Vasconcelos MJ, Mota B, & Grégoire JM (2003). An estimate of the area burned in southern Africa during the 2000 dry season using SPOT-VEGETATION satellite data. Journal of Geophysical Research: Atmospheres (1984–2012), 108(D13).
- Simon M, Plummer S, Fierens F, Hoelzemann JJ, & Arino O (2004). Burnt area detection at global scale using ATSR-2: The GLOBSCAR products and their qualification. Journal of Geophysical Research: Atmospheres (1984–2012), 109(D14).
- Stehman SV (1997). Selecting and interpreting measures of thematic classification accuracy. Remote Sensing of Environment, 62, 77–89. [Google Scholar]
- Stehman SV (1999). Basic probability sampling designs for thematic map accuracy assessment. International Journal of Remote Sensing, 20, 2423–2441. [Google Scholar]
- Stehman SV (2000). Practical implications of design-based sampling inference for thematic map accuracy assessment. Remote Sensing of Environment, 72, 35–45. [Google Scholar]
- Stehman SV (2001). Statistical rigor and practical utility in thematic map accuracy assessment. Photogrammetric Engineering & Remote Sensing, 67, 727–734. [Google Scholar]
- Stehman SV (2009). Sampling designs for accuracy assessment of land cover. International Journal of Remote Sensing, 30, 5243–5272. [Google Scholar]
- Stehman SV (2013). Estimating area from an accuracy assessment error matrix. Remote Sensing of Environment, 132, 202–211. [Google Scholar]
- Sukhinin AI, French NH, Kasischke ES, Hewson JH, Soja AJ, Csiszar IA, … & Slinkina OA (2004). AVHRR-based mapping of fires in Russia: New products for fire management and carbon cycle studies. Remote Sensing of Environment, 93(4), 546–564. [Google Scholar]
- Tansey K, Gregoire JM, Stroppiana D, Sousa A, Silva J, Pereira JMC, Boschetti L, Maggi M, Brivio PA, Fraser R, Flasse S, Ershov D, Binaghi E, Graetz D, & Peduzzi P (2004). Vegetation burning in the year 2000: Global burned area estimates from SPOT VEGETATION data. Journal of Geophysical Research-Atmospheres, 109, 10.1029/2003JD003598. [DOI] [Google Scholar]
- Tansey K, Grégoire JM, Defourny P, Leigh R, Pekel JF, Van Bogaert E, & Bartholomé E (2008). A new, global, multi‐annual (2000–2007) burnt area product at 1 km resolution. Geophysical Research Letters, 35(1). [Google Scholar]
- Trigg S, & Flasse S (2000). Characterizing the spectral-temporal response of burned savannah using in situ spectroradiometry and infrared thermometry. International Journal of Remote Sensing, 21(16), 3161–3168. [Google Scholar]
- Trigg SN & Roy DP (2007). A focus group study of factors that promote and constrain the use of satellite derived fire products by resource managers in southern Africa. Journal of Environmental Management, 82, 95–110. [DOI] [PubMed] [Google Scholar]
- Wolfe RE, Nishihama M, Fleig AJ, Kuyper JA, Roy DP, Storey JC, & Patt FS (2002). Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sensing of Environment, 83, 31–49. [Google Scholar]
- Wulder MA, White JC, Loveland TR, Woodcock CE, Belward AS, Cohen WB, Fosnight G, Shaw J, Masek JG, Roy DP (2016). The global Landsat archive: Status, consolidation, and direction. Remote Sensing of Environment In Press 10.1016/j.rse.2015.11.032 [DOI]


