Microphysical and kinematic processes associated with anomalous charge structures in isolated convection

Abstract

Microphysical and kinematic characteristics of two storm populations, based on their macroscale charge structures, are investigated in an effort to increase our understanding of the processes that lead to anomalous (or inverted charge) structures. Nine normal polarity cases (mid-level negative charge) with dual-Doppler and polarimetric coverage that occurred in northern Alabama, and six anomalous polarity cases (mid-level positive charge) that occurred in northeastern Colorado are included in this study. The results show that even though anomalous polarity storms formed in environments with similar instability, they had significantly larger and stronger updrafts. Moreover, the anomalous polarity storms evidently have more robust mixed-phase microphysics, based on a variety of metrics. Anomalous polarity storms in Colorado have much higher cloud base heights and shallower warm cloud depths in this study, leading us to hypothesize that anomalous polarity storms have lower amounts of dilution and entrainment. We infer positively charged graupel, and therefore high supercooled water contents, in the mid-levels of the anomalous storms based on the relationship between colocations of graupel and inferred positive charge from Lightning Mapping Array data. Using representative updraft speeds and warm cloud depths, the time required for a parcel to traverse from cloud base to the freezing level was estimated for each storm observation. We suggest this metric is the key discriminator between the two storm populations and leads us to hypothesize that it strongly influences the amount of supercooled water and the probability of positive charge in the midlevels, leading to an anomalous charge structure.

1. Introduction

1.1. Thunderstorm charge structures

The non-inductive mechanism for cloud electrification is fairly well understood (e.g. Reynolds et al., 1957; Williams, 1985; Saunders et al., 2006; Takahashi et al., 2017). The basic premise is that charge separation occurs when ice crystals and graupel particles undergo rebounding collisions in the presence of supercooled liquid water (SCLW), followed by separation of these particles under the influence of gravity and convective motions (e.g. Simpson and Robinson, 1941; Williams, 1985; Bruning et al., 2010). Accordingly, charge structures and resultant lightning are directly linked to microphysical and kinematic processes (e.g. Smith et al., 2000; Williams et al., 2005; Carey and Buffalo, 2007). Consequently, the variability of storm-scale charge structures has been of interest for many years.

Most convective storms possess a “normal” polarity charge structure with mid-level (approximately −10 °C to −30 °C) negative charge between regions of upper- and lower-level positive charge (Wilson, 1920; Krehbiel, 1986; Williams, 1989). However, a class of storms, termed “inverted” or “anomalous”, have been observed and are thought to possess dominant mid-level positive charge (e.g. Lang et al., 2004; Rust et al., 2005; Wiens et al., 2005; MacGorman et al., 2008; Bruning et al., 2014; Fuchs et al., 2015).

Early lab studies conducted by Reynolds et al., (1957) and Takahashi (1978) determined that the polarity and magnitude of charge acquired by graupel depended on temperature and the amount of SCLW (e.g. Jayaratne, 1983; Saunders and Peck, 1998). Numerous laboratory studies investigating the charging of graupel have been conducted and while some differences exist, a common thread has emerged: cloud environments with warmer temperatures and larger SCLW contents promote positive graupel charging (e.g. Saunders et al., 2006). Additionally, the magnitude of charge transfer per collision is enhanced as SCLW increases. Baker and Dash (1989) hypothesized that the particle growing faster by deposition transfers mass (accompanied by negative charge) to the particle it collides with, thereby acquiring net positive charge. Additionally, Avila and Pereyra (2000) found that graupel was more likely to charge positively when the distribution of supercooled cloud droplets was shifted to smaller sizes.

Because the mixed-phase charging zone spans from ~ 0 °C to −40°C, this implies SCLW amounts may to first order determine the macroscale charge structure within a storm (Bruning et al., 2014). In normal polarity storms, graupel in the lower portion of the thunderstorm (temperatures between ~ 0 °C and −15 °C) acquires positive charge regardless of SCLW content, based on laboratory studies (e.g. Takahashi, 1978). In the mid-levels (~ −20 °C), however, the charge of graupel depends on SCLW amounts. The so-called charge reversal line, which separates positive and negative charging on graupel, ranges between 1–4 g m⁻³ in the mid-levels, depending on the particular laboratory study. In normal polarity storms, SCLW amounts in the mid-levels are below the reversal line, and thus graupel acquires negative charge. The ice crystals that acquire the corresponding positive charge from collisions with graupel are lofted to upper regions of the storm by the updraft comprising the upper-level positive charge.

If a storm has large SCLW contents that are above the reversal line in the mid-levels, graupel becomes positively charged in this region. Accordingly, ice crystals would acquire net negative charge, leading to upper-level negative charge region. Together, the mid-level positive charge and upper-level negative comprise an anomalous charge structure on the storm scale. Therefore, it follows that if the charge structure of a storm, particularly the charge of the mid-level graupel, can be determined or inferred, we can infer whether the SCLW is above (anomalous polarity) or below (normal polarity) the reversal line in the mid-levels. Note that the presence of a lower-level negative charge region in anomalous storms cannot be explained by a simple one-dimensional non-inductive charging model. As such, anomalous storms are not necessarily a mirror image of normal polarity storms. Indeed, Fuchs and Rutledge (2018) found that lightning occurs at lower altitudes in anomalous polarity storms compared to normal polarity storms.

1.2. Relation to storm processes

The dependence of charge structures on SCLW content has sparked interest in the dependence of SCLW on more fundamental storm processes. In this manner, charge structures can be used as a lens to study fundamental microphysical and kinematic processes in storms. Negatively charged mid-level graupel in normal polarity storms may be due to weaker vertical velocities or rapid liquid water depletion rates. Fallout of warm-phase precipitation from robust collision-coalescence processes and higher rates of entrainment have been observed for tropical convection that commonly have relatively narrow updraft widths (e.g. LeMone and Zipser, 1980; Bringi et al., 1997; Williams and Stanfill, 2002) and deep (~4 km) warm cloud depths (WCD; Atlas and Ulbrich, 2000; Stolz et al., 2015), resulting in rapid depletion of available cloud water and a shallow layer of positively charged graupel near the melting level (Figure 4 from Bruning et al., 2014).

Figure 4:

Distributions of (a) CAPE (J kg⁻¹), (b) NCAPE (m s⁻²), (c) LCL height (m AGL), (d) WCD (m), (e) adiabatic water content (g kg⁻¹), (f) precipitable water (mm), (g) surface temperature (C), (h) surface dew point (C), (i) average relative humidity (%) between 600–500 mb, (j) surface to 6 km shear (m s⁻¹), (k) CIN (J kg⁻¹), and (l) equilibrium height (m MSL) from attributed inflow soundings. The bars indicate the quantities associated with storm samples in this study. Median values of each quantity for both regions region and each study are indicated in each panel, in addition to the Spearman ranksum p value, which tests the null hypothesis by calculating the probability that both distributions are subsets of the same distribution.

Conversely, smaller liquid water depletion rates at warmer temperatures permit larger SCLW contents and increased likelihood of positively charged graupel at mid-levels. Williams et al. (2005) and Lang and Rutledge (2011) claimed instability promotes strong updrafts that in turn lead to large SCLW contents in the mixed-phase region and positive charging of graupel in anomalous storms. Slow depletion rates are expected in storms with shallow WCD (which are typically associated with elevated cloud base heights), allowing parcels to traverse the warm cloud region in a relatively short time, inhibiting warm-phase precipitation growth and fallout (Carey and Buffalo, 2007; Albrecht et al., 2011; Fuchs et al., 2015). Additionally, stronger and broader updrafts are thought to be less prone to entrainment, and are therefore less diluted which has the net effect of increasing SCLW contents (Williams and Stanfill, 2002; Williams et al., 2005; Bruning et al., 2014). In this case, the storm could contain a deep layer of positive charge underlying a region of negative charge (Figure 4 from Bruning et al., 2014). Note that this discussion is somewhat idealized because it assumes horizontally homogeneous charge regions and a single updraft. However, it should also be noted that the non-inductive charging mechanism is largely a one-dimensional process, since macroscale charge separation is carried out through updrafts and gravity.

In nature, charge structures can be much more complicated. Several updrafts and downdrafts may be simultaneously present leading to horizontally inhomogeneous charge regions, especially when convection is not isolated (e.g. mesoscale convective systems, Stolzenburg et al., 1998). Moreover, the charge structure of an isolated storm can evolve during the storm’s lifecycle, possibly due to changes in SCLW availability in the updraft, or by advection or sedimentation of charged particles, one example being the end of storm oscillation (Pawar and Kamra, 2007). For these reasons, this study is limited to isolated convection and each cell is treated individually at each timestep so that we may apply the simplified model to storm charge structures.

1.3. Inferring charge structures

Determining charge structures and supercooled water contents in nature is difficult. Therefore, researchers have been forced to rely on proxy data to infer charge structures within storms. Several studies have used the fraction of cloud-to-ground (CG) flashes that are positive polarity (+CG; e.g. Smith et al., 2000; Carey et al., 2003; Wiens et al., 2005). This is because most CG flashes originate in the midlevels (Krehbiel, 1986), so the polarity of CG flashes provides some information about the charge residing in the mid-levels of a storm.

In normal polarity storms with mid-level negative charge, nearly all the CG flashes are negative polarity (e.g. Krehbiel et al., 1979). In intense anomalous polarity storms, the fraction of +CG flashes is elevated, near 100% in some cases (e.g. Stolzenburg, 1994; Lang et al., 2004). However, there are other scenarios that can lead to increased production of +CG fractions such as precipitation unshielding (Carey and Rutledge, 1998; Pawar and Kamra, 2007) and the tilted dipole mechanism (Brook, 1982). Furthermore, intense anomalous polarity storms often produce relatively few CG flashes (e.g. Tessendorf et al., 2007; Fuchs et al., 2015), which can make it difficult to use CG polarity to infer storm polarity in some situations.

Our approach is to use Lightning Mapping Array (LMA) data to infer storm-scale charge structures, instead of CG polarity. LMAs detect VHF radiation produced by the discontinuous propagation of lightning channel breakdown (Rison et al., 1999; Krehbiel et al., 2000; Thomas et al., 2004). Negative breakdown into positive charge produces more VHF radiation than positive breakdown through negative charge, so the location of positive charge can be inferred from regions of high VHF source density (Wiens et al., 2005). Since LMAs detect the in-cloud component of lightning flashes, this method leverages the high fraction of intra-cloud flashes in storms (Boccippio et al., 2001; Zajac and Rutledge, 2001; Fuchs et al., 2015).

1.4. Study overview

Despite the extensive research into the variability of storm charge structures and graupel charging, understanding of the microphysical and kinematic processes that influence charge structures is incomplete. Many of the hypotheses about the connections between different processes are physically based, but have not yet been tested because of inadequate observations and datasets, including our inability to obtain in-situ measurements of microphysics and charge structures, especially in strong convection.

The goal of the present study is to leverage available radar-derived microphysical and kinematic data to investigate various hypotheses regarding the processes that lead to anomalous charge structures in thunderstorms by more directly investigating the links between environment, microphysics, kinematics and charge structure. This investigation will be carried out by comparing relevant microphysical and kinematic quantities between two storm populations: normal polarity storms (in northern Alabama) and anomalous polarity storms (in eastern Colorado). The study is organized as follows: section 2 will lay out the array of data sets and the methodology of the study, section 3 enumerates the environmental, microphysical and kinematic differences between the normal and anomalous polarity storms in the dataset, and section 4 discusses the insights that can be gained from this paper and the robustness of those insights.

2. Data and Methods

2.1. Radar

The majority of cases in this study are derived from the Deep Clouds and Convective Chemistry Experiment (DC3; Barth et al., 2015), which took place during the summer of 2012 in northern Alabama, eastern Colorado, central and western Oklahoma. One of the main objectives of DC3 was to understand the production and convective transport of various trace gasses from the boundary layer to the upper troposphere. Therefore, there are numerous DC3 cases with microphysical and three-dimensional kinematic data.

Polarimetric radar data in the Colorado region come from the CSU-CHILL polarimetric S-band radar (Brunkow et al., 2000; Bringi et al., 2011). Polarimetric data from the Alabama region comes from UAH ARMOR polarimetric C-band radar (Petersen et al., 2007). Both radars provided the standard polarimetric quantities: horizontal reflectivity (Z_H), differential reflectivity (Z_DR), cross-correlation coefficient at zero lag (ρ_HV) and differential phase (φ_dp). See Doviak and Zrnic (1993) and Bringi and Chandrasekar (2001) for more details about polarimetric radar. During DC3, CSU-CHILL operated in an alternating H/V mode allowing for the collection of linear depolarization ratio (LDR) in addition to the standard polarimetric quantities. Specific differential phase (K_dp) was calculated using the DROPS algorithm developed by Wang and Chandrasekar (2009). See Mecikalski et al. (2015) for more information regarding post-processing of ARMOR data. Before analysis, all CSU-CHILL (ARMOR) radar quantities were interpolated to a 0.5 km × 0.5 km × 0.5 km (1.0 km × 1.0 km × 1.0 km) Cartesian grid using the NCAR Sorted Position Radar INTerpolator (SPRINT; Mohr and Vaughan 1979; Miller et al., 1986). Prior to interpolation, the velocity data were manually unfolded with National Center for Atmospheric Research (NCAR) solo3 software (Oye and Case 1995).

Combinations of various polarimetric quantities provide information about hydrometeor shape, size, and phase, which can be used to estimate microphysical quantities of interest. Recently, a number of microphysical retrieval algorithms developed at CSU have been compiled in a Python-based package called CSU-Radartools, which is publicly available on Github (https://github.com/CSU-Radarmet/CSU_RadarTools; Lang et al., 2016; Mroz et al., 2017). The retrievals used in this study include fuzzy-logic inferred hydrometeor identification (HID; Dolan et al., 2013) and water/ice mass (Carey and Rutledge, 2000; Cifelli et al., 2002). While the ice mass derived in the aforementioned studies are comprised of both ice crystals and precipitation ice (graupel and hail), graupel dominates the retrieval, particularly in the mid-levels. Furthermore, our analysis is focused on tracking graupel in the mid-levels, so we will use large ice mass as a proxy for the presence of graupel (Carey and Rutledge, 2000). These calculations were carried out on the Cartesian grid after the data was quality controlled.

Dual-Doppler scanning for the CO cases was performed in coordination with the S-band CSU-PAWNEE Doppler radar (Lang et al., 2014, 2016; Basarab et al., 2015). For the AL cases, dual-Doppler scanning was performed in coordination with the S-band KHTX NEXRAD radar (Barth et al., 2015). For the DC3 field project, the majority of the scanning was done with a 5–6 minute dual-Doppler update time. The 3D wind synthesis from the Doppler radial velocities was performed with the NCAR Custom Editing and Display of Reduced formation in Cartesian Space (CEDRIC; Mohr et al., 1986). It should be noted that the errors in the vertical velocity (W) obtained by this methodology are typically on the order of 1–3 m s⁻¹, depending on the magnitude of vertical velocities and methods used to estimate the three-dimensional wind fields (e.g. Potvin et al., 2012; Calhoun et al., 2013). For further details of the DC3 dual-Doppler analysis and radar configurations, see Barth et al., (2015) and Basarab et al., (2015).

2.2. CSU Lightning, Environmental, Aerosol, and Radar (CLEAR) Framework

To synthesize the large amount of data from an array of data types and number of cases, we employ the CSU Lightning, Environmental, Aerosol, and Radar (CLEAR) automated case study framework (Lang and Rutledge, 2011; Fuchs et al., 2015). CLEAR begins by objectively identifying storm cells using contiguous regions of reflectivity based on multiple (tunable) reflectivity and size thresholds. In this study, the composite reflectivity field was queried for regions of 30 dBZ that were larger than 20 km², that also contained an area of 40 dBZ that larger than 10 km², following Fuchs et al., (2015). Each identified cell for each radar volume scan time is treated as an individual and independent storm observation for statistical purposes (Sec. 3.3). A convective cell was determined to be isolated if it was the only identified cell in a convective region using the Yuter and Houze (1998) algorithm (Figure 2 in Fuchs et al., 2015). Restricting the analysis to isolated convective cells increases the likelihood of charge structures adhering to our idealized model and avoids complicating factors such influences from nearby convection. Additionally, storm metrics, such as flash rates and updraft volumes, are easier to interpret if storms are isolated.

Figure 2:

Similar to Figure 1 but for the archetypal anomalous CO case study from 06 June 2012. Note that dual-Doppler data is not available between 2230Z and 2236Z due to a temporary issue with the PAWNEE radar.

Ellipses are fit to each identified cell, then cells are tracked by spatially matching ellipses in consecutive radar volumes. Once cells are identified and tracked, other types of data (such as lightning flash rates and environmental soundings) can be attributed to cells by spatial and temporal matching. Although each scan time is treated individually and independent, tracking is important for attribution of environmental properties and understanding the observations in a larger context for a deep-dive analysis into storm characteristics and temporal evolution (Sec. 3.2). Cell identification and tracking was performed on 6 days in Alabama and 5 days in Colorado. It should be noted that all cells included in this study were within dual-Doppler lobes and within 125 km of their respective LMA network. Once the other data types were attributed to the cells, a database was constructed based on inferred storm-scale charge structure (section 2.5).

2.3. Lightning Mapping Array (LMA)

This study utilizes the Lightning Mapping Array (LMA) networks in northern Alabama and northeastern Colorado. LMA networks are comprised of 6 or more receiving stations that detect and locate very high frequency (VHF) radiation produced by discontinuous breakdown of lightning channels (Rison et al., 1999; Thomas et al., 2004). During DC3, the northern Alabama network was comprised of 11 stations in an approximate circle centered near Huntsville, Alabama and 2 additional stations near Atlanta, Georgia. The northeastern Colorado network is comprised of 15 stations centered near the CSU-CHILL radar. Both networks have reliable detection and location of LMA sources and flashes to approximately 150 km from the respective network centers (Thomas et al., 2004; Koshak et al., 2004; Chmielewski and Bruning, 2016; Fuchs et al., 2016).

Since all identified cells are within 125 km of their respective network centers, there is little sensitivity to the locations of LMA sources or flashes with respect to the LMA center. To remove most of the noise from the LMA data, only sources that had at least 7 solution-contributing stations and a chi-squared fit value less than 1.0 were attributed to cells. LMA sources that satisfied filtering criteria were attributed to the appropriate cell if they were located within the spatial extent of the cell, defined by the composite reflectivity. LMA sources outside of any identified cells were attributed to the nearest cell if they were less than 10 km from a cell otherwise they were not considered in the analysis.

2.4. Flash clustering

LMA networks do not detect lightning flashes. Instead, LMAs detect VHF radiation sources produced by sub-flash processes (Rison et al., 1999). Therefore, further processing on VHF source data is required to obtain information about the physical lightning flashes detected by LMAs. This study uses the flash algorithm developed by Bruning (2013) and Fuchs et al., (2015, 2016), which clusters VHF sources that are close together in space and time. Due to high sensitivity of the Colorado LMA, the search radius for sources in a flash is set to be 3 km in space and 0.15 s in time. The Colorado LMA is more sensitive than the Alabama LMA because of newer technologies, more stations and lower background VHF noise levels (Fuchs et al., 2016; McCaul et al., 2004; Koshak et al., 2004). The search radius for sources in a flash is set to 6 km in Alabama. These values are consistent with McCaul et al. (2009) and Fuchs et al. (2015, 2016), which has been shown to produce realistic flash rates based on subjective analysis and comparisons with other algorithms, such as XLMA (Thomas et al., 2003).

Once VHF sources are initially clustered into flashes, some quality-control filtering is conducted. In the Colorado (Alabama) region, any analyzed flashes with less than 10 (2) sources are discarded from the analysis, following McCaul et al. (2009) and Fuchs et al., (2015, 2016). It should be noted that approximately 30% of flashes in Alabama storms were comprised fewer than 10 sources. However, the particular source threshold does not affect the conclusions of this study. Moreover, analysis of selected flashes (not shown) revealed that real flashes may have less than 10 sources in Alabama. The interested reader is referred to Fuchs et al. (2016) for more information on flash clustering criteria and sensitivities thereof.

Any flashes that are more than 10 km from any identified cells are discarded from the analysis, similar to the LMA source attribution. Once the flashes are filtered and attributed, information such as location, duration, and spatial extent of each flash can be estimated. Furthermore, statistics such as cell flash rate can be calculated.

2.5. Charge structure inference

In addition to flash-level information, LMA data can also be used to infer the charge structure within a thunderstorm, because LMA detection of leader propagation depends on polarity (Rison et al., 1999). Flashes typically initiate in regions of strong electric fields between positive and negative charge regions. Leaders of both polarities propagate away from the initiation point (MacGorman et al., 2001; Coleman et al., 2003; Maggio et al., 2005). Propagation of negative leaders into positive space charge is more discontinuous and produces stronger emissions than propagation of positive leaders into negative space charge (Rison et al., 1999). This normally results in more LMA-detected VHF sources from positive charge regions. Therefore, the height of dominant positive charge is inferred to be near the altitude of the LMA source density maximum within a storm (Wiens et al., 2005; Lang and Rutledge, 2011). By this method, the mode of LMA source density in a normal (anomalous) polarity storm is typically near −40 °C (−20 °C). Figure 2b in Fuchs et al., (2015) shows a schematic depiction of the relationship between charge structures and LMA source densities. It should be noted that since the negative leader propagation into positive charge produces more VHF radiation than positive leader propagation into negative charge, the LMA depiction of a flash is typically skewed towards the positive charge, it is difficult to know the precise location of the negative charge by this method (Wiens et al., 2005).

2.6. Environment

Hourly model reanalysis data was attributed to each identified cell for relevant environmental data and some polarimetric retrievals. Model data was used to attempt to capture spatial and temporal variability of the environment, particularly since many of the cases in Alabama occurred between 18Z and 21Z, several hours before the 00Z National Weather Service daily radiosonde launch. The Rapid Update Cycle (RUC; Benjamin et al., 2004) 13-km reanalysis was used for storms that occurred before 1 May 2012, thereafter the Rapid Refresh (RAP; Benjamin et al., 2006) 13-km reanalysis was used.

A representative inflow point for each storm was calculated by selecting the nearest grid point approximately 40 km from the storm along the low-level upwind vector, similar to Fuchs et al., (2015). All relevant quantities at that grid point were temporally interpolated to the radar volume scan time before being attributed to the cell (Lang and Rutledge, 2011). The reanalysis data includes fundamental atmospheric quantities such as temperature, wind, and pressure as well as standard calculated quantities such as freezing height and convective available potential energy (CAPE). Additional variables were calculated based on the fundamental quantities, such as normalized CAPE (NCAPE; Blanchard, 1998), CBH (Bradbury, 2000) and WCD (Carey and Buffalo, 2007).

3. Results

3.1. Overview

The analysis method in this study is to compare the environmental, electrical, microphysical, and kinematic characteristics of 73 electrically active (> 1 flash min⁻¹) individual radar volumes from 9 normal polarity cases from northern Alabama and 47 electrically active radar volumes from 6 anomalous polarity storms over northeast Colorado. The focus of this study is on isolated convective storms, since those are the easiest to interpret, adhere to the non-inductive charging model discussed in Section 1, and are not subject to interactions with adjacent cells. Recall that every storm at each radar volume time is treated as a separate individual cell. The macroscale charge structure was defined by the temperature corresponding to the LMA source density mode (Sec. 2). Normal polarity storms were defined to have an LMA modal temperature of < −30 °C. Storms with an LMA modal temperature > −25 °C were classified as anomalous. These classifications were adopted to simplify the analysis.

3.2. Case studies

3.2.1. Normal Alabama case study

The archetypal normal polarity case from Alabama occurred on 21 May 2012 during the DC3 field project. The storm developed around 2000Z, intensified between 2000–2030Z before dissipating around 2100Z. The storm was located about 70 km northeast of the ARMOR radar site located near Huntsville, AL and was located in the northern dual-Doppler lobe. Figure 1 shows a synopsis of the storm: both a snapshot during the mature phase of the storm at 2023Z (Figure 1a) and timeseries of the electrical, kinematic and microphysical characteristics of the storm (Figures 1b-d). Figure 1a shows an X-Z cross section of radar reflectivity along with updraft speeds and LMA source density. Maximum updrafts during the time of the cross section were approximately 12 m s⁻¹ and situated around 6 km MSL (−20 °C).

Figure 1:

Archetypal normal AL case study from 21 May 2012. (a) X-Z cross section of that case at 202341Z. Reflectivity values are shown in the color fill, following the colorbar on the right. Vectors show the U and W components of the wind, following the legend in the upper-right portion of the panel. Bilaterally smoothed two-dimensional LMA source density (within 1 km of the cross section) is shown in light contours. Each contour indicates 20%, 40%, 60%, 80%, and 100% of the maximum value for this case. Updraft speeds are shown in dark contours of 3, 5, 10, 20, and 30 m s⁻¹. A plan view of composite reflectivity is shown in the inset panel. The location of the X-Z cross section is illustrated by the black line. (b) Timeseries of vertical distribution of LMA source density (color fill), following the colorbar below the panel. The LMA modal height (green) follows the left axis, while the cell total flash rate (gray) following the right axis. (c) Timeseries of mean ice mass at each vertical level (color fill), following the colorbar below the panel. The mixed-phase 35 dBZ volume (gray) and the mixed-phase graupel volume (green) follow the right axis. The correlation coefficient between the vertical distributions of LMA source density and ice mass (gold dashed) follows the rightmost axis. (d) Timeseries of the 95^th percentile of updraft speed at each vertical level (color fill). Updraft volume > 5 m s⁻¹ (UV5) and > 10 m s⁻¹ (UV10) shown in the light and dark purple colors, respectively, and follow the right axis. The maximum updraft speed in the cell is shown in the dashed red line and follows the red axis on the far right. The time of the X-Z cross section and composite reflectivity is illustrated with a vertical line in panels b-d and the 0 °C, −20 °C and −40 °C levels are shown in dotted black lines in each panel.

The updraft remained strong to approximately 9 km MSL (equilibrium level was ~ 12 km MSL, not shown). Radar reflectivities in the main updraft ranged from 35–55 dBZ. Additionally, the updraft primarily contained large raindrops, hail, and high-density graupel as inferred by polarimetric radar observations (not shown). The LMA source density maximum, used as a proxy for positive charge location, was situated between −30 °C and −40 °C near the top of the updraft.

During the period from 2000 to 2016Z, the flash rate increased from 0 to 3 min⁻¹ (Figure 1b). The charge structure, as inferred from the vertical LMA source density, is noisy but suggests an active lower positive charge around 4–5 km MSL (Figure 1b). Mecikalski et al. (2015) and Carey et al. (2016) showed substantial –CG activity during this time, suggesting normal charge polarity. Updraft speeds are modest during this time, increasing from ~ 6 to 12 m s⁻¹ (Figure 1d). At 2008Z, the strongest updraft speeds were located below ~ 6 km, which is situated near the maximum of mean ice mass (Figure 1c). A simple metric representing the collocation of graupel and positive charge at lower levels is shown by the Pearson correlation coefficient relating the vertical distributions of LMA source density and mean ice mass (Figure 1c). The correlation is between 0.4 and 0.6 during the early stages of the storm.

An abrupt shift in charge structure occurs around 2022Z, when the dominant positive charge appears between 8–10 km MSL or approximately −35 °C. After the shift in storm charge structure to dominant upper positive charge, the maximum in mean ice mass remains below approximately 8 km MSL, which leads to an ice massLMA source correlation near 0 and suggests that graupel and positive charge are not collocated which implies graupel is the dominant carrier of negative charge. Maximum updrafts increase from ~ 12 m s⁻¹ at 2010Z to ~ 18 m s⁻¹ at 2025Z in concert with an increase in the altitude of maximum updraft strength. This updraft burst is coupled with an increase in the altitude of the maximum LMA source density, perhaps lofting the positively charged ice crystals to even greater heights. After 2033Z, the flash rates and mean ice mass decrease as updraft speeds weaken. The storm dissipated shortly thereafter. Additional details regarding the radar and lightning properties of this storm can be found in Mecikalski et al. (2015) and Carey et al. (2016).

3.2.2. Archetypal anomalous CO case

The presentation of the information about the archetypal anomalous CO case in Figure 2 follows the same format as Figure 1, facilitating direct comparisons between the cases. The storm was located approximately 60 km to the east-northeast of CSU-CHILL and was located in the eastern dual-Doppler lobe formed by CSU-CHILL and the CSU-Pawnee S-band radar. Figure 2a indicates the updraft is much stronger in this case, with peak values > 20 m s⁻¹. The updraft extends to about 13 km MSL, just above the sounding-derived equilibrium level (12.5 km MSL, not shown). The updraft contains largely rain below the melting level and low-density graupel above the freezing level (not shown), and reflectivities range from 20–40 dBZ, although much higher reflectivities exist just to the east of the main updraft. The maximum in LMA source density is located near 6 km MSL (~ −10 °C). The LMA source density maximum is located in a region of weak vertical motion, adjacent to the strong updraft.

This case was first identified by the tracking algorithm at 2155Z and quickly produced updrafts > 20 m s⁻¹. Quickly the storm became electrically active, as flash rates increased from ~ 2 flashes min⁻¹ to 20 flashes min⁻¹ at 2212Z. During this time, the dominant positive charge region was located in the mid-levels of the storm between 5–8 km MSL, collocated with a maximum in mean ice mass. This resulted in a high ice mass-LMA source correlation that ranges from 0.6 to 0.9 in the early and middle stages of the storm lifecycle. The high correlation indicates that graupel is collocated with positive charge, from which we infer that the mid-level graupel is the dominant carrier of positive charge. The storm remained intense with strong updrafts, high flash rates and mid-level positive charge until 2243Z.

There is an abrupt shift in the storm charge structure around 2243Z. The storm transitions from anomalous polarity to normal polarity, according to the definitions applied in this study. The dissipation of the mid-level positive charge is coincident with a dissipation in mid-level ice mass. Furthermore, as the upper-level positive charge becomes dominant, it is accompanied by the development of an upper-level ice mass maximum, which is indicated by the ice mass-LMA source correlation above 0.5. Perhaps this indicates that the positive charge above −30 °C is carried by graupel, which acquired its charge in situ or was transported upward from lower levels in the storm. This abrupt charge structure shift is accompanied by an increase in updraft strength at high altitudes, and a flash rate increase of ~ 100%. After 2243Z, the updrafts weakened considerably, coincident with the descent of upper positive charge, descent of the maximum in mean ice mass and decrease in storm flash rates.

This example illustrates the dynamic nature of storms, especially regarding storm-scale charge structure and further accentuates that point that charge structures in storms are fluid. However, treating each time step as an independent sample in this study allows us to only focus on the times when this storm was anomalous (before 2243Z), which results in a cleaner signal. It is for this reason we do not group CO storms with LMA modal temperatures colder than −30 °C together with normal polarity AL storms, because many of the CO cases behave in a similar manner to that described in Figure 2, namely they evolved from an anomalous polarity storm. In contrast, normal AL storms tend to possess normal polarity structures for nearly their entire lifecycle.

3.3. Statistical analysis

3.3.1. Electrical characteristics

To gain more insights regarding differences between normal and anomalous storms, we merge all observations (multiple storms, multiple sample times) for each charge structure classification and analyze them statistically. It is important to note that the observations are comprised of storms from the developing, mature and dissipating stages. However, the strict threshold imposed when identifying cells with the objective algorithm tend to favor cells near their mature phase (Fuchs et al., 2015). Moreover, in treating each storm observation separately, we can filter out complications, such as the charge structure transition highlighted in Figure 2.

The vertical distribution of LMA source densities from each storm observation of (AL) normal cases are shown in Figure 3a. By design, the peak of each distribution is < −30 °C. Note that few distributions have modal temperatures colder than −40 °C, and additionally that some profiles have a smaller, secondary maximum at warmer temperatures, consistent with a lower positive charge (Wiens et al., 2005), constituting a normal polarity tripole. The vertical distribution of LMA source densities from the anomalous (CO) cases are shown in Figure 3b. The spread in LMA modal temperatures is larger in these cases, with some distributions peaking around −25 °C and some around −10 °C. In fact, the distributions bear some resemblance to both schematics in the middle and right panels of Figure 2b from Fuchs et al., (2015). Bruning et al., (2014) argue that the charge structures exist in a continuum, rather than in the binary classifications of normal and inverted. Indeed, the storms in the middle and right panels of Figure 2b from Fuchs et al., (2015) may be the same, with the charge centers shifted vertically.

Figure 3:

(a) Vertical distribution of normalized LMA source densities for each normal AL storm, with temperature as the vertical coordinate. The red line indicates the −30 °C threshold bifurcating cells into normal or anomalous polarity. (b) Same as (a) but for each anomalous CO storm sample, red line indicates the −25 °C threshold. (c) Cumulative distribution of cell total flash rates for each storm sample.

The cell flash rates, derived from the number of attributed flashes and the radar update time, are shown in Figure 3c. Median cell flash rate (total lightning) for the normal AL samples is approximately 5 flashes min⁻¹, whereas the median cell flash rate from the anomalous CO samples is roughly 10 flashes min⁻¹. For both storm populations, approximately 80% of samples have cell flash rates < 20 min⁻¹. The maximum cell flash rate for the normal AL population is 45 min⁻¹; 75 min⁻¹ for the anomalous CO population. Note that the populations of cell sizes are not substantially different (Section 3.3.4). A comparison with the large statistical sample of isolated convective cells in Figure 7 of Fuchs et al., (2015) shows that an overwhelming majority of isolated convective cells in the vicinity of the northern Alabama LMA have LMA modal temperatures < −35 °C and an overwhelming majority of the CO events have LMA modal temperatures > −25 °C. Furthermore, the flash statistics in Fuchs et al., (2015, Figure 5a) shows that a cell flash rate of 5 flashes min⁻¹ is approximately the 70^th percentile of cell flash rates in the larger sample in northern Alabama. Cell flash rates of 10 min⁻¹ in northeast Colorado are about the 60^th percentile of flash rates from the larger Fuchs et al., (2015) sample. Hence, we argue the cells in this study are largely representative of their respective local climatologies based on the combination of cell flash rates and LMA modal temperatures compared with the larger Fuchs et al., (2015) dataset.

Figure 7:

(a) Fraction of total LMA sources collocated with a particular W bin at a particular height, averaged together for all normal AL storm samples. Contours show CFAD values of 1%, 10% and 30% of W. (b) Percentage of total LMA sources collocated with a particular bin of the horizontal gradient of W at a particular height for all normal AL storm samples. (c) Same as (a) but for the anomalous CO storm samples. (d) Same as (b) for the anomalous CO storm samples.

Figure 5:

(a) Composite contoured frequency by altitude diagram (CFAD) for all normal AL storm samples, following the log-scale color bar below the panel. The lines indicate the average updraft (red) and downdraft (blue) for all normal AL cases. (b) Same as (a) but for the anomalous CO storm samples. (c) Cumulative distribution of the maximum W (measured by the 99^th percentile) for both storm populations. (d) Cumulative distributions of updraft volume greater than 5 m/s (UV5; solid line) and updraft volume greater than 10 m/s (UV10; dashed line) for both storm populations.

3.3.2. Environmental characteristics

The environment influences storm kinematics and microphysics, which in turn, impact charge structures and lightning. Therefore, it is important to understand the environmental context of these storm populations. Figure 4 shows the distributions of relevant thermodynamic quantities from the present storm populations. Median CAPE and NCAPE values are both higher in the normal AL storms than the anomalous CO storms by about 40%. It should be noted that while the two-tailed p-value is less than 0.05 in both instability parameters, suggesting a statistically significant difference, some environmental conditions are autocorrelated on a much longer time scale than storm characteristics (Rudlosky and Fuelberg, 2013). Furthermore, model reanalaysis data is not able to capture all the small scale environmental features created by convection itself. Therefore, a 40% difference in instability may not be physically significant.

The CO storms have much shallower warm cloud depths (higher cloud base heights) in comparison to the AL samples. The precipitable water values are about 50% higher in AL storms than in the CO storms, consistent with climatology (Fuchs et al., 2015). It is perhaps somewhat surprising that the adiabatic water content is similar in both storm populations. This apparent inconsistency can be explained by the higher surface temperatures in anomalous CO cases in combination with similar surface dew points between the two populations. Higher surface temperatures with the same surface dew points will result in larger surface dew point depressions, which directly contributes to cloud base height (Bradbury, 2000; Williams et al., 2005). However, adiabatic water content depends only on surface dew point and pressure (Betts and Bartlo, 1991; Betts, 1994; Pruppacher and Klett, 1998). It is also surprising that mid-level relative humidity (as measured by average humidity between 600 mb and 500 mb) is higher in the CO samples. This may have implications for parcel dilution by entrainment. Surface to 6 km shear values are slightly larger in AL samples, but the values in both populations are modest, with respect to severe weather occurrence (Weisman and Klemp, 1982). The convective inhibition (CIN) is substantially larger in the CO samples, typically considered an ingredient for more intense convection (Riemann-Campe et al., 2009; Rasmussen and Houze, 2016). Finally, the equilibrium level heights are not significantly different between the two populations.

3.3.3. Kinematics

With the electrical and environmental characteristics providing context, we now examine the impacts of the environment on convective cell kinematics and the impacts of the overall cell kinematics on charge structures. Figures 5a,b show vertical motion composite contoured frequency by altitude diagrams (CFADs; Yuter and Houze, 1995) by averaging the CFAD for each observation in both storm populations. Probabilities corresponding to each W bin are color filled for each gridded altitude. Immediately apparent for each population is that most grid points have vertical velocities near zero at all altitudes, indicating that the majority of grid points within these storms are not associated with strongly rising or sinking air, consistent with previous studies (e.g. Yuter and Houze, 1995). One of the largest differences between the vertical velocities in the composite CFADs are that updrafts greater than 20 m s⁻¹ exist in the anomalous CO population, but are not present in the normal AL population. This indicates that the peak updrafts are stronger in the anomalous CO cases than they are in the normal AL cases, a signature evident in the maximum W cumulative distributions as well (Figure 5c).

The average updraft and downdraft profiles are shown in the line plots in Figures 5a,b. Average updrafts in the anomalous CO population are stronger than the normal AL population by approximately 100%. Furthermore, average updrafts and downdraft speeds in AL normal cases are nearly constant with height, while the average updrafts and downdrafts in anomalous CO cases show significant variations with height. The average updraft speed in anomalous CO storms peaks around 8 km MSL, which is also where peak updraft speeds are maximized.

Updraft volumes > 5 m s⁻¹ (UV5) and > 10 m s⁻¹ (UV10) are also much larger in the anomalous CO samples. The median value of UV5 is approximately a factor of three larger in the CO storms compared to the AL storms. The message of these comparison statistics is clear: the updrafts in the anomalous CO storms are stronger and larger in volume in comparison to the normal AL storms. Given that the instability in the normal AL storms is similar or larger than the values in the anomalous CO storms in this study, one might expect similar updraft speeds in both populations of storms based on simple parcel and buoyancy theory. These results (Figure 5) suggest that parcel theory alone is insufficient to explain the larger and stronger updrafts in anomalous CO storms. We suggest the higher CBHs and shallower WCDs in the anomalous CO cases reduce rainout loss of liquid water, which would allow for more robust mixed-phase processes and additional latent heat release. Since the updrafts in the anomalous CO storms are larger in volume, we would expect them to be wider as well, which may act to reduce dilution and entrainment.

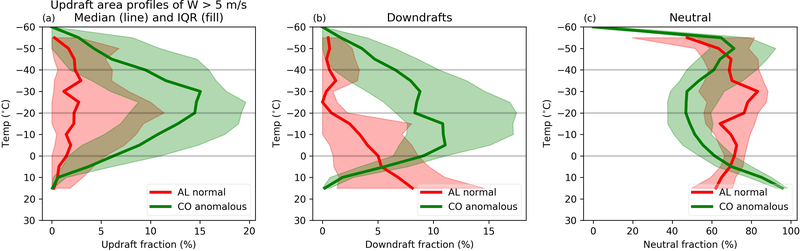
To investigate the issue of updraft width and potential impacts on entrainment, Figure 6 breaks down the areas of updrafts, downdrafts and neutral air with respect to temperature. Figure 6a shows the fraction of the storm area containing updrafts (defined here as W > 5 m s⁻¹) for each storm in both populations. Note that the results were not particularly sensitive to the W threshold choice (not shown). The thick line indicates the median value of updraft fraction for all storms in the population as a function of temperature, with the interquartile range filled. Stark differences in updraft area fraction exist between the populations at nearly every temperature level. Most notably, the anomalous CO storms have much wider updrafts than the normal AL storms. The areas of the updrafts in the anomalous CO storms increase from 0 °C to approximately −25 °C. This is perhaps some evidence of the thermal broadening hypothesis (Morton et al., 1956; Williams and Stanfill, 2002), since the updraft area increases with height. The fact that the updraft area is largest near −25 °C is interesting because that is typically in the mid-levels of the storm where graupel charge polarity is dependent on SCLW amounts, and we therefore expect this level to be consequential in determining the storm-scale charge structure. The −25 °C level also happens to be close to 8 km MSL in both storm populations, which is where the strongest average and peak updrafts are observed in the anomalous CO storms (Figure 5). In contrast, the median updraft fraction distribution in normal AL storms is nearly constant with height. Recall that the vertical mean updraft speed profile is nearly constant with height as well, suggesting updraft strength and updraft width may be related.

Figure 6:

(a) Median (line) and interquartile range (color fill) updraft area (W ≥ 5 m s⁻¹) for all storm samples at a particular temperature for each storm population. Converting radar heights to temperatures is done by interpolation using the attributed inflow sounding. (b) Same as (a) but for downdraft area (W < −3 m s⁻¹). (c) Same as (a) but for W between −3 and 5 m s⁻¹.

Figure 6b was compiled in an identical manner as Figure 6a, but shows the fraction of grid points with W < −3 m s⁻¹. Differences between the storm populations are evident, especially at lower altitudes. Downdraft fractions in normal AL storms are maximized near the base of the storm. In contrast, the largest downdraft areas in anomalous CO samples are found between −10 °C and −30 °C, overlapping with the largest updraft areas. The mechanisms for this mid-level downdraft maximum are not clear. Downdraft fractions near the base of the storm are a small fraction of the total area in anomalous CO cases. It is important to note that three-dimensional wind fields can only be calculated for regions where radar scatterers are present, so air motions outside of the storm radar echo cannot be retrieved. Figure 6c shows the remainder of the points at each level, which we classify as neutral because vertical motions are not particularly strong in either direction at these points. Note that most points are not located in significant updraft or downdraft regions as identified by this analysis, consistent with the CFADs in Figure 5.

It is essential to place the LMA sources within the content of the three-dimensional wind fields to understand how the kinematics may influence the inferred charge structures of these storms. Figure 7a shows the fraction of the storm total LMA sources in vertical motion bins for each radar grid height level, averaged over all AL storms. Most of the LMA sources (rough proxy for positive charge) are located around 10 km MSL in regions of weak vertical motion. Figure 7b was constructed in a similar manner, but the sources are collocated with the horizontal gradient of vertical motion. Large values of this gradient indicate LMA sources may be located near an updraft, downdraft or an updraft/downdraft interface (Dye et al., 1986). Figure 7b shows that the LMA sources (and positive charge) are not necessarily located near a strong updraft.

When paired with the results in Figure 7a, these results suggest that the positive charge is located at the top of the updraft, as was the case in the archetypal case shown in Figure 1. In contrast, Figure 7c shows that most of the LMA sources in the CO anomalous storms are located between 5–8 km MSL, but are located in regions of relatively weak vertical motion. However, many of the LMA sources occur in regions of moderate-to-strong horizontal gradients of vertical motion, indicating that the positive charge (and the breakdown process for lightning) in the anomalous CO storms is likely located near, but not in, the strongest updrafts. This phenomenon was observed in the archetypal case shown in Figure 2, but is confirmed on a larger scale here.

3.3.4. Microphysics

After elucidating some of the kinematic differences between the normal AL and anomalous CO storm populations, we will now contrast their microphysical characteristics. Figure 8 shows some relevant storm total metrics. Figure 8a shows the distributions of mixed-phase graupel volume (derived from the number of radar grid points between −5 °C and −40 C° with graupel or hail as the inferred dominant hydrometeor type) for both populations are very similar. Figure 8b shows that the mixed-phase 30 dBZ volumes (from grid points between −5 °C and −40 C° with reflectivity greater than 30 dBZ) are slightly larger for the normal AL cases compared to the anomalous CO cases. Figure 8c shows the distributions of maximum graupel height in both populations is quite similar, with median values differing by less than 1 km. Evidently the normal AL cases are just as tall and deep as the anomalous CO cases, at least for storms included in this dataset. Finally, the average mixed-phase ice mass is much larger in anomalous CO cases. Perhaps this is an indicator of more robust mixed-phase microphysical processes in the anomalous CO cases.

Figure 8:

Cumulative distributions of (a) mixed-phase graupel volume, (b) mixedphase 30 dBZ volume, (c) maximum graupel height (from inferred dominant hydrometeor type), (d) average mixed-phase graupel mass mixing ratio.

To further understand the differences in vertical structure between the two storm populations, Figure 9 shows the vertical profile of radar reflectivity (VPRR; Zipser and Lutz, 1994) for each population. Figures 9a,b shows the mean VPRR at each radar grid height for each normal AL storm (Figure 9a) and anomalous CO storm (Figure 9b), as well as an averaged composite for each population.

Figure 9:

(a) Mean vertical profile of radar reflectivity (VPRR) for each normal AL storm sample (light red lines) and the composite VPRR for the normal AL storm population (dark red line) and the composite VPRR for all anomalous CO storm population (dark green line). (b) Same as (a) but each thin green line is the mean VPRR for each individual anomalous CO storm sample. (c) Same as (a) but for max values instead of mean values in normal AL storm samples. (d) Same as (b) but for max values instead of mean values in anomalous CO storm samples.

Throughout a large depth (~ 2–12 km MSL), the average reflectivity is higher in the anomalous CO composite than in the normal AL composite. The magnitude of the difference varies from 0.5 dBZ near 12 km MSL to 5 dB at 7 km MSL, and is 3 dB or greater at most altitudes, which corresponds to a factor of roughly 25 larger ice mass, based on simple scaling arguments (Rutledge et al., 1992). Note that we are assuming Rayleigh scattering and perfect attenuation correction when making reflectivity and mass comparisons between radars with different wavelengths.

The reflectivity lapse rate between 5 km MSL and 8 km MSL (approximately 0 °C to −20 °C) is drastically different between the two populations. The average reflectivity difference in the anomalous CO composite is only 1.5 dB (0.5 dB km⁻¹), compared to ~6 dB (2 dB km⁻¹) in the normal AL composite. This difference is suggestive of more robust mixed-phase microphysics in the anomalous CO storms, which is consistent with stronger updrafts, precipitation ice growth, and potentially larger supercooled water contents.

The maximum vertical profiles of radar reflectivity are shown in Figures 9c,d. The composite average of each population is shown in the bold lines. Contrary to the mean profiles, the maximum profiles are more similar to each other. The maximum reflectivities are higher in normal AL cases above 10 km MSL. It is important to note, however, that the 5–8 km lapse rate difference is still intact. In the composite profile for the anomalous CO storms, the difference is 2.5 dB (0.8 dB km⁻¹), whereas the reflectivity difference in the normal AL storms is approximately 10 dB (3.3 dB km⁻¹). This difference is again indicative of stronger mixed-phase hydrometeor growth, particularly where graupel would be located in anomalous CO storms. The composite maximum reflectivity in normal AL storms is higher than anomalous CO cases below 5 km MSL, suggestive of more robust warm-phase precipitation processes in those storms.

It is important to place the LMA sources within the context of the storm microphysics to better understand how microphysical processes may influence the charge structures of these storms (as we did for the kinematic discussion earlier). The archetypal case from the normal AL population suggested that the graupel was not vertically collocated with the positive charge, as measured by the correlation between the vertical distributions of LMA sources and mean ice mass. Therefore, it was suggested that this was evidence for ice crystals being the carriers of positive charge in the upper-levels. Conversely, in the anomalous CO case, the maximum in LMA sources in the mid-levels was collocated with the maximum in graupel mass. This was used as evidence that graupel is the carrier of mid-level positive charge in the anomalous CO cases.

These correlations are further explored in Figure 10, which shows the distributions of the Pearson linear correlation coefficient, r, between the vertical distribution of LMA sources and the vertical distribution of average graupel mass. Figure 10a shows the correlation coefficient is less than 0 for nearly all of the normal AL cases, indicating that graupel is not collocated with positive charge and therefore likely carries negative charge in the mid-levels, according to the standard normal polarity charge model. However, in the anomalous CO cases, the majority of the samples have correlation coefficients greater than 0.75, indicating that graupel is collocated with positive charge, and may be the positive charge carrier in the midl-evels. If indeed this is the case, then the supercooled water contents in anomalous CO cases would have to be relatively large in accordance with laboratory charging studies.

Figure 10:

(a) Distributions of correlation coefficient between the vertical distribution of mean ice mass and the vertical distribution of LMA source density for every storm in both populations. (b) Same as (a) but correlations are computed between three-dimensional values of ice mass and LMA source density.

While the convective samples included in this study are limited to isolated convection, we acknowledge that a 1D correlation may be insufficient to claim whether graupel and positive charge are collocated. To address this concern, Figure 10b shows the full 3D correlation coefficient between LMA source density and mean ice mass. Since LMA source densities can be a noisy quantity, especially in lower flash rate storms, we would expect the 3D correlation coefficient to be closer to 0 regardless of the 1D correlation. Indeed, we do observe this in Figure 10b, with nearly all normal AL cases having a vanishingly small correlation coefficient. However, nearly all of the anomalous CO samples have a positive, nonzero correlation coefficient, suggesting graupel and positive charge are collocated. Hence graupel is likely the dominant charge carrier in the anomalous storms. Note that we have not discussed the possible role of hail as a charge carrier. This is because, radar-inferred dominant hydrometeor type (not shown) indicates the volume containing hail was a small fraction of overall storm sizes in both populations.

4. Summary and Discussion

This study used an automated and objective case study framework to compile a number of case studies from Colorado and Alabama in an effort to investigate the microphysical and kinematic processes that influence storm-scale charge structures. In particular, we wanted to understand and evaluate hypotheses that lead to anomalous charge structures in thunderstorms. LMA modal temperature was used to infer the storm charge structures, where storms with LMA modal temperatures < −30 °C (> −25 °C) were classified as normal (anomalous) polarity. We recognize that charge structures in isolated convective storms are continuous, but we have adopted these thresholds to simplify the analysis. Detailed analysis of case studies, similar to Figures 1–2, informed the relevant quantities to investigate in the statistical framework. Individual treatment of isolated updraft samples in the statistical framework allowed us to avoid complications such as transitions in storm-scale charge structures and therefore adhere to the simple charge-structure model described in Section 1.

The statistical analysis revealed that the inferred positive charge in normal polarity AL storms was located near the top of the updraft in regions of weak horizontal gradients of vertical motion. Furthermore, the low (and often negative) correlation coefficients between the vertical distributions of LMA sources (proxy for positive charge) and ice mass in normal AL storms indicate that positive charge and graupel are not collocated in those storms. This suggests, with reasonable confidence, that smaller ice crystals are the positive charge carriers in the upper levels of normal AL storms, conforming with the normal polarity charging model (e.g. Williams, 1985; Mansell et al., 2005).

It is more difficult to conclude with certainty that graupel in the mid-levels of those storms carries negative charge based on the LMA modal temperature methodology, but it would be a logical corollary to upper-level positively charged ice crystals. This seems reasonable, given that updrafts are weaker and narrower, coupled with the lower CBHs and deeper WCDs, all of which are expected to lead to less active mixed-phase microphysics and lower SCLW contents, despite having higher instability. Finally, note that the 6-km shear is stronger in the normal AL cases, but it is difficult to know what effect that may have had on the internal processes in the storms in this study.

In contrast, the positive charge in the anomalous CO storms was located at lower altitudes (and warmer temperatures) near regions of relatively strong updrafts. In addition, the high (often near 1) correlation coefficients between the vertical distributions of LMA sources and mean ice mass in anomalous CO storms indicate that positive charge and graupel were collocated in those storms. It is impossible, however, to conclude with certainty that the mid-level graupel is indeed the positive charge carrier because it is possible that ice crystals may be comingling with the graupel, yet the small ice crystals are obscured by the larger graupel particles (from a radar reflectivity perspective). If, however, graupel is the positive charge carrier in the mid-levels of anomalous CO storms, it would be logical to conclude that SCLW amounts are relatively high, based on laboratory studies. Recall that graupel charges positively (negatively) at relatively high (low) SCLW amounts at temperatures near −20 °C (e.g., Takahashi, 1978; Saunders and Peck, 1998). This seems reasonable when considering that updrafts in anomalous cases are broader and stronger compared to normal polarity storms. The larger ice mass and smaller mixed-phase reflectivity lapse rate suggest that mixed-phase microphysical processes are active and robust, which is consistent with high SCLW contents.

Fuchs et al., (2015) advanced the hypothesis that the majority of warm-season isolated convective storms in CO are anomalous polarity because of the short amount of time that parcels spend in the warm phase of the cloud, which we refer to here as the warm cloud residence time (WCT). With information about storm environment and kinematics in this study, we can test this hypothesis. Figure 11a shows the distributions of WCT for normal AL storms and anomalous CO storms. The WCT was calculated by dividing the WCD (distance) by a representative particle speed (difference between updraft and particle fall speed). Each box and whisker plot shows WCT calculations based on different representative W (speed) using different percentiles of vertical motion, below the melting layer. Each panel in Figure 11 shows the WCT calculations with a terminal fall velocity range of 0–6 m s⁻¹, which spans reasonable drop diameters (e.g. Gunn and Kinzer, 1949). If the terminal fall speed is larger than the representative updraft speed, the WCT is set to be 3600 s. This value is somewhat arbitrary and is employed to avoid negative values of WCT in cases where the particle fall speed exceeds the representative updraft speed. In these cases, particles would obviously never reach the mixed-phase region of the cloud.

Figure 11:

(a) Estimates of warm cloud residence time for each population using different values of W. No particle fall speeds are included in the calculation of warm cloud residence times. (b) Same as (a) but assuming a constant 2 m s⁻¹ particle fall speed. (c) Same as (a) assuming a constant 4 m s⁻¹ particle fall speed. (d) Same as (a) assuming a constant 6 m s⁻¹ particle fall speed. If particle fall speed is greater than representative updraft speed, warm cloud residence time is set to 3600 s.

Regardless of the W percentile choice or raindrop terminal fall speed, the WCTs are much longer for normal AL storms than for anomalous CO storms. At the 50^th percentile of W with no terminal fall speed (to represent cloud droplets), the median WCT for the normal AL population is approximately 9 minutes, while it is about 3 minutes for the anomalous CO population. To get a sense for the sensitivity of the WCT to particle fall speed, Figure 11b shows the same WCT calculation but includes a constant terminal fall speed of 2 m s⁻¹. The median of the distribution of the WCTs for the same 50^th percentile of W has increased from about 9 minutes to 20 minutes, well within the timeframe for warm rain processes to produce precipitation sized drops (e.g. Berry and Reinhardt, 1974; Lau and Wu, 2003). In contrast, the median value for the anomalous CO population has only increased from about 3 minutes to 5 minutes using the 50^th percentile of W. For larger raindrop terminal fall speeds, WCTs increase to the imposed limit of 60 minutes in normal AL cases for multiple W percentiles. WCTs only reach the imposed limit for anomalous CO cases for a terminal fall speed of 6 m s⁻¹.

Given that the normal cases in this study all came from Alabama and all the anomalous cases came from Colorado, we attempted to find and analyze an anomalous AL case, but were unable to find a storm with sufficient flash rates and a sustained region of dominant positive charge at warm temperatures. However, we did identify a case study in the Colorado region that resembled a normal polarity charge structure. Figure 12 shows a detailed analysis of the storm, similar to Figures 1–2. The important features of this storm are: 30–55 dBZ reflectivities in the updraft region, relatively low total flash rates of less than 5 min⁻¹ for its entire lifetime, an upper-level dominant positive charge near −40 °C for the first half hour of its lifetime when it was producing lightning, and maximum updraft speeds were approximately 10–15 m s⁻¹ for most of its lifetime. Roughly speaking, this storm resembles a normal polarity AL case. However, an inspection of the vertical distribution of mean ice mass reveals that in the first 5–10 minutes of storm development, the LMA source maximum near 10 km MSL is accompanied by relatively high mean ice mass at that same level, which leads to a correlation coefficient of 0.95. This suggests that the upper positive charge may be comprised of positively charged graupel. As the storm progresses, the correlation coefficient continuously decreases. During this time, the maximum in vertical LMA source density remains around 10 km MSL, while the majority of the mean ice mass is located below 8 km, much like the normal AL cases.

Figure 12:

Same as Figure 1, but for a normal polarity case in CO from 05 June 2012. VHF source distributions are not plotted from 2300Z to 2320Z because no lightning occurred within the cell during that time.

The local environmental conditions (not shown) for this case do not resemble a normal AL storm. CBH values are high, WCD values are low, CAPE values are ~500 J kg⁻¹, and the NCAPE is ~0.06 m s⁻². Interestingly, the estimated WCTs (using the 75^th W percentile and 2 m s⁻¹ terminal fall speed) for this case range from approximately 7 minutes during the development phase and increase to approximately 12 minutes after 2240Z, mainly due to the weaker updraft speeds. The WCTs in this case more closely resemble the normal AL storms than the anomalous CO storms.

With the different possible permutations of environmental quantities, it seems that WCT is perhaps the best discriminator between the normal AL storms and the anomalous CO storms in this study. Therefore, it is logical to argue that WCT influences SCLW contents (and charge structures) through the amount of liquid water loss via rainout in addition to average supercooled cloud droplet size. We argue these differences in WCTs between the populations control the loss of potential SCLW via warm phase precipitation processes. Simply speaking, the amount of warm-phase precipitation fallout is dependent on the ratio between WCT and the time required for large droplets to form. If this ratio is much less than 1, droplets that form in the warm phase of the updraft will not grow to sufficient sizes to permit fallout. On the other hand, if this ratio is at least 1, droplets may be able to grow large enough to fall out, depleting the parcel of liquid water and thus robbing the mixed phase region of potential supercooled water. We expect the drop formation ratio in anomalous storms to be much less than 1, placing the depletion of SCLW at a minimum. In addition, the broader updrafts observed in Figure 6 provides some observational evidence of a relationship between higher CBHs and broader updrafts. These broader updrafts would likely be less prone to entrainment and dilution of available liquid water, especially in the updraft core.

In normal polarity storms, longer warm cloud residence times result in the drop-formation ratio approaching or exceeding 1, resulting in warm phase precipitation that reduces SCLW in the mixed phase region. The narrower updraft widths in the normal polarity cases, which would make the updrafts more prone to entrainment and dilution, contribute to large liquid water depletion (Williams and Stanfill, 2002; Williams et al., 2005). Furthermore, since the cloud droplets spend more time in the warm phase of the cloud, we would expect the cloud droplets to be larger in normal polarity storms, which tends to result in graupel particles charging negatively in the mid-levels (Avila and Pereyra, 2000). Note that no physical mechanism for drop size impacting charge polarity was provided in the Avila and Pereyra study. Conversely, shorter WCTs in anomalous storms should lead to smaller supercooled cloud droplet sizes, which would increase the likelihood of positive graupel charging in the mid-levels.

In this study, we have directly investigated the relationships between environmental quantities and storm processes in addition to the relationships between storm processes and charge structures. The hypotheses relating to mixedphase microphysics (SCLW in particular) put forward based on the analysis in this study would help us better understand fundamental storm processes. However, without in situ observations of SCLW amounts, in addition to information about particle types and concentrations, it is impossible to test the hypotheses put forward in this study.

Main points.

• Positively charged mid-level graupel evident in anomalous polarity storms in concert with robust mixed-phase microphysics

• Anomalous storms in Colorado have stronger and wider updrafts than normal polarity storms

• Warm cloud residence time appears to be a key discriminator between normal polarity storms and anomalous polarity storms