Reducing Uncertainties in Carbonate Clumped Isotope Analysis Through Consistent Carbonate‐Based Standardization

Abstract

About a decade after its introduction, the field of carbonate clumped isotope thermometry is rapidly expanding because of the large number of possible applications and its potential to solve long‐standing questions in Earth Sciences. Major factors limiting the application of this method are the very high analytical precision required for meaningful interpretations, the relatively complex sample preparation procedures, and the mass spectrometric corrections needed. In this paper we first briefly review the evolution of the analytical and standardization procedures and discuss the major remaining sources of uncertainty. We propose that the use of carbonate standards to project the results to the carbon dioxide equilibrium scale can improve interlaboratory data comparability and help to solve long‐standing discrepancies between laboratories and temperature calibrations. The use of carbonates reduces uncertainties related to gas preparation and cleaning procedures and ensures equal treatment of samples and standards. We present a set of carbonate standards of diverse composition, discuss how they can be used to correct for mass spectrometric biases, and demonstrate that their use significantly improves the comparability among four laboratories. We propose that the use of these standards or of a similar set of carbonate standards will improve the comparability of data across laboratories.

Key Points

• Standardization and correction procedures for carbonate clumped isotopes are reviewed

• We propose a carbonate‐based standardization scheme to improve reproducibility

• We demonstrate improved interlaboratory comparability of clumped isotope measurements

1. Introduction

The carbonate clumped isotope thermometer is a relatively new geochemical method to determine the growth temperature of carbonate minerals. It is based on the determination of the temperature‐dependent excess abundance of ¹³C‐¹⁸O bonds in the carbonate lattice above a theoretical random distribution (Ghosh, Garzione, et al., 2006; Schauble et al., 2006). Unlike the conventional carbonate‐water isotopic thermometers, this novel method allows for the reconstruction of the formation temperature of carbonate minerals independent of the δ ¹⁸O of the fluid in which the mineral grew. Consequently, the δ ¹⁸O of these fluids can be reconstructed using clumped isotope data and the oxygen isotopic composition of the carbonate, which are measured simultaneously. Thus, the clumped isotope thermometer can provide unique information on geological samples and processes that are unobtainable with any other geochemical tool.

The carbonate clumped isotope thermometer has improved our understanding of long‐standing questions in Earth Sciences. For example, the temperature and oxygen isotope composition of ocean waters in deep time (Came et al., 2007; Cummins et al., 2014; Finnegan et al., 2011; Rodriguez‐Sanz et al., 2017), past changes in continental temperatures (Affek et al., 2008; Meckler et al., 2015; Passey et al., 2010; Snell et al., 2013; Zaarur et al., 2011, 2016), palaeoelevation and uplift rates of continents (Ghosh, Adkins, et al., 2006; Huntington et al., 2010; Quade et al., 2007), the diagenetic evolution of carbonate sequences (Bristow et al., 2011; Huntington et al., 2011; Loyd et al., 2012; Millan et al., 2016; Vandeginste et al., 2015, 2013), and formation of carbonate deposits during fault movement (Bergman et al., 2013; Huntington & Lechler, 2015). Given the broad range of applications, the field is expanding rapidly and the number of laboratories applying this technique is constantly growing.

Analytical challenges such as the relatively large sample sizes typically required, time‐consuming measurements, and complex correction procedures necessary to obtain accurate and reproducible results (Huntington et al., 2009) have initially limited the number of laboratories carrying out these measurements. However, in the last few years significant technical improvements such as full automatization of the extraction procedures (Passey et al., 2010; Schmid & Bernasconi, 2010), efforts to reduce the required sample sizes (Meckler et al., 2014; Müller, Fernandez, et al., 2017; Petersen & Schrag, 2014; Schmid & Bernasconi, 2010), and improved correction schemes for mass‐spectrometric artifacts (Bernasconi et al., 2013; Dennis et al., 2011; He et al., 2012; Meckler et al., 2014) are making this method more user friendly, leading to its implementation in a growing number of laboratories. With an increasing number of users, there is an urgent need for improved standardization to guarantee that data produced are comparable across different laboratories, to evaluate possible sources of uncertainties and, where possible, to simplify analytical procedures. Most analytical developments in the last 10 years focused on solving technical challenges and understanding the effect of technical differences among analytical approaches on the clumped isotope signal. Recently, an additional possible source of inconsistencies among laboratories has emerged, which is related to the parameters used for the ¹⁷O correction used in the calculation of Δ₄₇ (Daëron et al., 2016; Schauer et al., 2016). It is expected that with consistent use of the appropriate parameters, interlaboratory comparability can be improved significantly.

Here we review the evolution of correction schemes used in clumped isotope thermometry, discuss the most recent development in clumped isotope analytical techniques and data reduction methodologies, identify possible sources of discrepancies within and among laboratories, and provide guidelines and suggestions for improving analytical precision. We show that while recent technological developments are improving interlaboratory reproducibility, additional efforts are necessary to reach the accuracy needed for many (especially low temperature) applications, such as paleoclimate studies. After considering and assessing the importance of the largest analytical sources of uncertainty, we propose that currently the best avenue for improved interlaboratory comparability is to use a suite of carbonate standards across laboratories. These carbonate standards should be firmly anchored to the interlaboratory absolute standardization scheme or carbon dioxide equilibrium scale (CDES), which is a scale the clumped isotope community has developed to standardize clumped isotope values among laboratories (Dennis et al., 2011). In this study we demonstrate that a carbonate‐based standardization method allows for much better interlaboratory comparability than the current standardization based on heated and equilibrated gases.

2. Nomenclature and Isotopic Scales for Clumped Isotopes in Carbonate Minerals

The excess abundance of carbonate molecules containing both ¹³C and ¹⁸O (resulting in CO₂ molecules of mass 47) relative to the expected stochastic distribution of this combination is reported with the parameter Δ₄₇ that is defined as

$${\mathrm{\Delta }}_{47}\left(‰\right)=\left[\left(\frac{R^{47}}{R^{47*}}-1\right)-\left(\frac{R^{46}}{R^{46*}}-1\right)-\left(\frac{R^{45}}{R^{45*}}-1\right)\right]\times 1000,$$

where R ⁱ is the abundance of the minor isotopologues relative to the most abundant isotopologue with mass 44, and the expected stochastic ratios R ^i* are calculated using the measured abundance of ¹³C and ¹⁸O in the sample (Affek & Eiler, 2006). The measured abundance of isotopologues with m/z 47 in the sample with respect to the working gas (WG) in the mass spectrometer is reported in the traditional delta notation as

$${\mathit{\delta }}^{47}\left(‰\right)=\left[\left(\frac{{R^{47}}_{\text{sample}}}{{R^{47}}_{\text{working}\mathrm{gas}}}\right)-1\right]\times 1000.$$

The δ ⁴⁷ scale is a measure of the difference between the sample of interest and the WG used in the specific instrument; therefore, it cannot be compared across laboratories. Nevertheless, it is a very important measure because, as we will describe in more detail below, the corrections for mass spectrometric artifacts are not constant but depend on the difference in composition between WG and the sample of interest. A larger difference between the two requires larger corrections. This adds an additional degree of complexity to the corrections of clumped isotope measurements compared to the classic δ ¹³C and δ ¹⁸O measurements.

Clumped isotope compositions were initially reported on the Caltech or Ghosh scale (Ghosh, Adkins, et al., 2006), which was established with the development of the measurement methodology. The scale was based on the measurement of CO₂ heated to 1000°C to reach a nearly stochastic distribution of all isotopologues, which represents the zero point of the Δ₄₇ scale (Huntington et al., 2009). With the measurement of heated gases of different bulk isotope compositions (i.e., of variable δ ¹³C and δ ¹⁸O), it was observed that there is a dependence of the measured Δ₄₇ on the bulk isotope composition of the gas measured (Ghosh, Adkins, et al., 2006; Huntington et al., 2009). While the cause of this dependence was unknown at the time, by using gases of different bulk isotope composition it was possible to determine a heated gas line that could be used for correction of this nonlinearity effect, which is still commonly used by many laboratories to correct for mass spectrometric artifacts (Daëron et al., 2016; Schauer et al., 2016). Following the nonlinearity correction, observed variations in the compression of the Δ₄₇ scale were corrected by using the intercept of the heated gas line and relating it to the original value observed by Ghosh, Adkins, et al. (2006). This ratio was used to stretch the Δ₄₇ scale (Huntington et al., 2009; Schmid & Bernasconi, 2010).

Subsequent studies (Bernasconi et al., 2013; Fiebig et al., 2016; He et al., 2012) demonstrated that the apparent dependence of Δ₄₇ on δ ⁴⁷ (the heated gas line) is caused by negative backgrounds (also referred as negative pressure baseline) on the minor collectors (m/z 47, 48, and 49). This had already been shown by Yeung et al. (2012) to affect the measurements of O₂ and was confirmed also by Petrizzo and Young (2014). These backgrounds vary with time, instrument, and ion source conditions and show a strong negative correlation with the CO₂ pressure in the source (Bernasconi et al., 2013; Meckler et al., 2014). Because the magnitude of these backgrounds is controlled by the intensity of the m/z 44 ion beam, it affects the calculated δ ⁴⁷ ratio differently for different beam intensities, requiring an intensity‐proportional correction. Tests with a CO₂ gas containing 99.95% ¹²C and natural ¹⁸O abundance (Bernasconi, unpublished results) showed identical negative backgrounds on the m/z 47–49 as the WG with natural abundance of ¹³C. This occurred even though the intensity of the m/z 45 beam was almost 30 times less in the 99.95% ¹²CO₂ compared to the WG at a similar intensity of m/z 44. This suggests that the effect of the m/z 45 and 46 beams, if present, is negligible. The effect of the backgrounds on the calculated Δ₄₇ increases with the increasing difference in bulk isotope composition between the sample gas and the WG used in the mass spectrometer. The same background effects are also observed on m/z 48 and 49 and thus have to be corrected for when calculating Δ48 and Δ49. We also note that a proper background correction of the m/z 44, 45, and 46 is necessary, especially when the isotopic composition of the sample is far away from that of the WG (Meckler et al., 2014)

For a gas with the same bulk isotope composition as the WG, the presence of negative backgrounds has no influence on the calculated delta value because the relative amount of missing mass 47 signal is equal for both. However, for a sample with a low δ ⁴⁷ value (smaller m/z 47 signal than the WG), the effect of a negative background will be relatively more important than for the WG. This results in underestimation of Δ₄₇. For a sample with a positive δ ⁴⁷ value the relative proportion of the BG on the m/z 47 signal will be lower than that of the WG, thus leading to an overestimation of Δ₄₇. This is the origin of the slope of the heated gas line, and heated gases have been used to demonstrate that negative BGs can be properly corrected after independent determination of the background in the presence of gas (Bernasconi et al., 2013; He et al., 2012). The characterization of negative background, their effect on Δ₄₇ and correction procedures, has been described in detail in Bernasconi et al. (2013), He et al. (2012), and Müller, Fernandez, et al. (2017).

Initially, the only available anchor point to compare carbonate data among laboratories was the international carbonate standard NBS 19 which is distributed by the IAEA (International Atomic Energy Agency, Vienna). Using the assumption that the WG used at ETH had the same composition as the one at Caltech, Schmid and Bernasconi (2010) showed that it was possible to reproduce the composition of NBS 19, even with a very different analytical method. This situation was unsatisfactory, however, because a new laboratory would have only two anchor points consisting of a heated gas and a gas derived from NBS 19. Because NBS 19 is a marble, it was formed at high temperature and has a much lower Δ₄₇ than low‐temperature carbonates that are often the main targets of carbonate clumped isotope geochemistry.

3. The Absolute Reference Frame

A significant improvement was achieved with the establishment of the Absolute Reference Frame (ARF), also called the CDES (Dennis et al., 2011). The CDES is based on the measurement of gases of different composition heated to 1000°C or equilibrated with water at different temperatures (heated and equilibrated gases, respectively). The average slope of the heated and equilibrated gas lines is used for the nonlinearity correction, similar to before when only heated gases were measured. However, for the stretching correction, the intercept of both the heated gas and the equilibrated gas lines is now compared with the theoretically calculated Δ₄₇ of CO₂ equilibrated with water at different temperatures (Wang et al., 2004) to determine the (instrument‐specific) compression of the scale caused by processes in the source during ionization of the CO₂. These include isotope scrambling and molecule recombination or gas mixing, which are all poorly understood. This approach allows each laboratory to report their data to the CDES reference frame based on gases and theory, thereby making results more comparable among laboratories. Regular measurements of both heated and equilibrated gases are required to continuously monitor the mass spectrometer performance. Using this standardization method, the comparison of the Δ₄₇ composition of a set of four carbonate samples in four different laboratories resulted in maximum differences ranging between 0.018 and 0.031 (Dennis et al., 2011). If we consider that the temperature dependence of Δ₄₇ is about 0.0033‰/°C at temperatures below 50°C (Kele et al., 2015), these differences amount to differences of 5 to 10°C in calculated temperatures for the same sample measured in different laboratories. Such interlaboratory differences are even greater at higher temperatures as the temperature dependence of Δ₄₇ is a quadratic function of the form Δ₄₇ = a 10⁶/T ² + b (Ghosh, Adkins, et al., 2006). This accuracy may be sufficient for some applications but needs to be significantly improved if, for example, different laboratories aim to reconstruct climate variations on the order of a few degrees. It might in theory be possible to achieve this accuracy within an individual laboratory, but that requires that the temperature calibration is performed in the same laboratory using the same instrument and protocol.

The CDES scale is a significant improvement compared to the Caltech scale, because it allows for the correction of nonlinearities and scale compression caused by the mass spectrometer, which are variable among instruments and over time for each instrument. In addition, it standardizes the measurement to a scale (the CDES) based on theoretical predictions of the abundance of ¹³C‐¹⁸O bonds in gaseous CO₂ at thermodynamic equilibrium. The downside is that the procedure necessary to construct the reference frame is time consuming and difficult to automate. Both source scrambling and nonlinearity evolve with time and depend on other factors such as source tuning and, therefore, need to be continuously monitored, thereby effectively reducing the machine time available for measurement of unknowns. Dennis et al. (2011) proposed that laboratories could establish a secondary reference frame to monitor the evolution of the mass spectrometer through time once the CDES is established. This is generally done with in‐house carbonates or a mixture of gases and carbonates, depending on the laboratory.

One potential source of inconsistency with the establishment and implementation of the CDES in individual laboratories is the fact that sample preparation procedures for carbonates, heated and equilibrated gases, differ significantly among users. These procedures can be a potential source of artifacts. For example, one possible source of inconsistency is the purification of sample gases. This step is carried out in some laboratories by transferring the gas with a He‐flow through a gas chromatograph with a Porapak® column (e.g., Ghosh, Garzione, et al., 2006; Passey et al., 2010) or by forcing the CO₂ to diffuse through a tube filled with Porapak, via freezing from one cold finger to another (e.g., Dennis et al., 2011; Meckler et al., 2014). One possible issue is the temperature at which the Porapak trap is cooled. Petersen et al. (2016), for example, have shown that below −20°C, Δ₄₇ values decreased by 0.003–0.005‰/°C change in Porapak trap temperature. Although these authors suggest that this is not a problem if gases and samples are treated equally by passing through the same Porapak trap, it may become a significant issue if the Porapak system has to be changed and/or the temperature varies through time, or if carbonates are prepared in a system that cannot be used for gases, such as on a Kiel carbonate preparation device (Meckler et al., 2014; Schmid & Bernasconi, 2010), which requires a different setup for the gases. Although at ETH we have not observed any systematic drift in values related to the Porapak trap temperature mounted on the Kiel device, we observed that the Δ_47raw of two heated gases decreased from −0.635‰ ± 0.011 (n = 2) to −0.724 ± 0.011 (n = 3) after replacing the Porapak filling in the glass vacuum line used for offline gas purification. Both gases showed no sign of contamination based on the intensities of masses 48 and 49 (data not shown). We did not carry out enough measurements to identify the root cause of this difference, but this example highlights the potential to create artifacts during gas cleaning.

In addition to the potential influence of the gas cleaning procedure, the Δ₄₇ of heated or equilibrated gases can potentially be modified by user handling, adding another source of error. We therefore suspect that the exclusive use of heated and equilibrated gases might contribute to the significant differences observed among laboratories. The first issue is that standards and samples are not treated the same way, as gas processing does not involve acid digestion. This difference is aggravated if gases and samples are not passed through the same Porapak trap and the same capillary when fed into the source of the mass spectrometer. Additional uncertainties may arise from different laboratories creating and processing heated and equilibrated gases differently, including different protocols to remove water and noncondensable gases from the CO₂. Heated and equilibrated gases are often made regularly in small batches, and heated gases are usually cleaned manually on a glass vacuum line and heated in a high‐temperature furnace by individual users; thus, the potential is high to fractionate a gas or subtly change conditions during quenching. In addition, changes in phosphoric acid fractionation related to changes in the conditions of the reaction through time would go undetected.

The problems related with the establishment of the CDES scale in individual laboratories can be some of the causes for the observed discrepancies in the slopes of published calibrations of Δ₄₇ with precipitation temperatures (Defliese et al., 2015; Fernandez et al., 2014). Additional hypotheses have been advanced, including reaction temperature, acid quality (Zaruur et al., 2013), precipitation method for the carbonates, solution pH, or disequilibrium during precipitation (Hill et al., 2014). Three recent studies, however, have changed this view. Kelson et al. (2017) precipitated carbonates in the laboratory with several different methods and could show that precipitation mechanism and the temperature of phosphoric acid reaction cannot be the cause of discordant calibrations. They suggest that phosphoric acid preparation, CO₂ gas purification, and/or data reduction procedures are the remaining possible causes of the discrepancies. In particular they pointed out that the ¹⁷O correction procedure may be the greatest source of error. Based on their measurements they proposed that a universal calibration may exist. This was confirmed by Bonifacie et al. (2017) who compiled all Δ₄₇‐temperature calibrations produced at acid reaction temperatures of 70 to 90°C and demonstrated that when measurement errors are taken into account (e.g., by weighting the published data points by the number of replicates) most calibration data sets can be combined to calculate a single regression. Based on this reanalysis, Bonifacie et al. (2017) also suggested that there is a universal calibration for all carbonates, independent of mineralogy.

However, the data still show considerable scatter, which is much larger than what is predicted for the shot noise limit of clumped isotope measurements of about 0.009–0.015‰ (Hu et al., 2014; Huntington et al., 2009). Fernandez et al. (2017), using a more robust statistical analysis, have shown that the purported differences between calibrations are likely not real and can also be explained by the observation that analytical errors in Δ₄₇ are underestimated in most publications. Using error estimates at the 95% confidence level, they showed that, despite the large (2x) disagreement in temperature sensitivities among published calibrations, there is a close agreement in calibration slopes when only the experiments with the most statistically robust slopes are considered. They also showed that the discrepancies in slopes can be explained by (i) the limited temperature range covered by the samples used in many calibration studies, (ii) the low number of sample temperatures used, and (iii) the limited number of replicate analyses.

The study of Fernandez et al. (2017) focused on the precision (the confidence margin) and reproducibility of the measurements and their effect on the slope of a calibration. In the following we go a step further and discuss the accuracy of the method, identify the sources of differences in absolute values that cause discrepant intercepts of calibration curves, and propose solutions to improve the accuracy. In this respect, two recent publications have made a significant advance to improve interlaboratory data comparability by identifying a source of uncertainty in the choice of the parameters for calculating Δ₄₇ (Daëron et al., 2016; Schauer et al., 2016). However, as we show below, while the recalculation with these revised parameters reduces the differences, it does not solve all problems of interlaboratory comparability.

4. Calculation of Δ₄₇ and the Effect of the ¹⁷O Correction

One important source of inconsistency among laboratories is the parameters chosen for the correction of the ¹⁷O contribution to the m/z 45 and 47 beams (Daëron et al., 2016; Schauer et al., 2016). These include the λ values, which describes the proportionality in isotope fractionation between ¹⁷O and ¹⁸O (which has the form δ ¹⁷O = (1 + δ ¹⁸O)^λ − 1; Meijer & Li, 1998), and the numerical values for ¹³R, ¹⁸R, and ¹⁷R that define the absolute isotopic ratios in the Vienna Peedee belemnite (VPDB) and Vienna Standard Mean Ocean Water (VSMOW) standards. These recent studies have shown that using the λ value proposed by Meijer and Li (1998) and the absolute values for ¹⁷R_VPDB‐CO2 and ¹⁷R_VSMOW proposed by Assonov and Brenninkmeijer (2003) instead of those traditionally used by the clumped isotope community (summarized in Huntington et al., 2009) reconciles inconsistencies within individual and possibly also across laboratories. Because a detailed discussion of the derivation and choice of these parameters was published by Brand et al. (2010), the above authors refer to these parameters as the Brand parameters. For consistency we will keep this name here, although we recognize that this does not give credit to the original publications (Assonov & Brenninkmeijer, 2003; Meijer & Li, 1998). Below we discuss these improvements and show why the introduction of the new parameters is necessary but is not the ultimate solution for all problems of interlaboratory comparability.

Schauer et al. (2016) used two different WGs (FC and FF), one with a δ ¹³C of −10.5‰ (FC) and another with a δ ¹³C of −35.5‰ (FF) to construct two independent ARFs. They accomplished this by changing the δ ¹⁸O of the gases through equilibration with waters of different composition and subsequent heating to 1000°C (to reach a stochastic isotope distribution). Thus, the range in δ ⁴⁷ necessary for the construction of the reference frame was achieved by modifying the δ ¹⁸O of the gases only, while the δ ¹³C remained constant for either CDESs. With this experiment these authors showed that using the Huntington et al. (2009) parameters, the calculated Δ_47RAW of the heated and equilibrated gases, and thus the CDES could vary significantly depending on the δ ¹³C of the gas used (Figure 1a).

Figure 1.

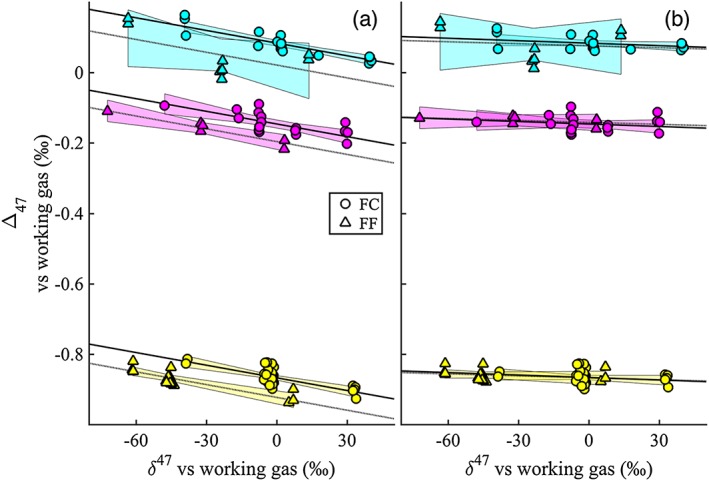
Reference frames obtained by Schauer et al. (2016) using two gases with different δ ¹³C (FF and FC), showing the effect of the calculations using the parameters as in Huntington et al. (2009) (a) and the Assonov and Brenninkmeijer (2003) ¹⁷R values and the λ value of Meijer and Li (1998) (b). Note that the differences disappear in Figure 1b. (Reproduced with permission from John Wiley & Sons, Inc.)

Consequently, the calculated Δ₄₇ (CDES) of an unknown carbonate could also vary by up to 0.06‰ depending if the FF or the FC reference frame was used when using the parameters as described in Huntington et al. (2009). Alternatively, when the Brand parameters were used, the differences between reference frames and calculated Δ₄₇ values for unknown samples disappeared (Figure 1b) and changed to a different value than those obtained with the Huntington calculations (see Table 3 in Schauer et al., 2016). Additionally, this study showed that the differences in slope and intercept observed in a large set of synthetic carbonates, precipitated at different temperatures using different methods for calibration purposes by Kelson et al. (2017), were greatly reduced when the Brand parameters were used. Finally, Schauer et al. (2016) concluded that the difference in Δ₄₇ between the ETH‐1 and ETH‐2 interlaboratory standards, which are expected to be identical as they were heated under identical conditions, disappeared when the calculations were performed with the Brand parameters. This confirms the work of Müller, Violay, et al. (2017) who showed these two standard carbonates to be identical in Δ₄₇ within analytical error (±0.002‰).

These results were confirmed in an independent study by Daëron et al. (2016) who additionally modeled quantitatively the impact of the different ¹⁷O correction parameters on Δ₄₇ for different δ ¹³C and δ ¹⁸O compositions. In particular, they showed that when using samples with uniform δ ¹³C a positive correlation is found between the δ ¹⁸O of the standard and the error in the calculated Δ₄₇, whereas a negative correlation is observed when using standards with constant δ ¹⁸O and variable δ ¹³C (Figure 2). They expressed this error as Δ (Δ₄₇) corresponding to the difference between the value obtained with the Assonov and Brenninkmeijer (2003) ¹⁷R values and the λ value of Meijer and Li (1998) and the parameters used in Huntington et al. (2009). When standards with random δ ¹³C and δ ¹⁸O are used, similar relationships are observed, but with more scatter (see Figure 6 in Daëron et al., 2016), as might be expected, because the two effects can either be additive or subtractive. Finally, Daëron et al. (2016) showed that also in their laboratory, the compositions of ETH‐1 and ETH‐2 are only identical when the Brand parameters were used, whereas they obtained significantly different compositions with the traditional parameters. The authors use this evidence to support the use of the Brand parameters to calculate Δ₄₇.

Figure 2.

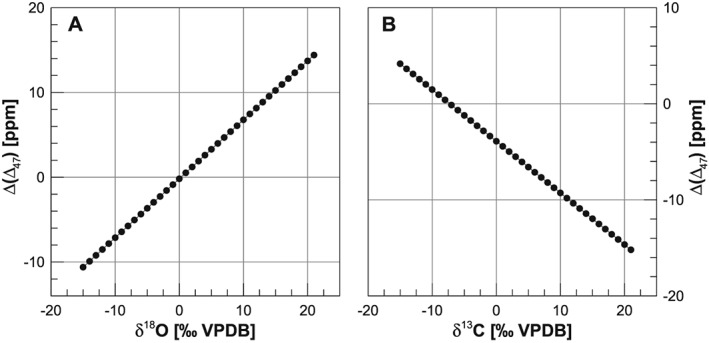
Difference in Δ₄₇ calculated as the difference between the value obtained using the Brand parameters and the one using the Huntington parameters, expressed as Δ (Δ₄₇) when fixing δ ¹³C and changing δ ¹⁸O (a) and fixing δ ¹⁸O but changing δ ¹³C (b). The diagrams are calculated for the composition of the ETH working gas using equation (10) in Daëron et al. (2016). Note the opposite effect in carbon versus oxygen isotope ratios. VPDB = Vienna Peedee belemnite.

One aspect of these observations that Daëron et al. (2016) could not explain was the fact that the values of ETH‐1 and ETH‐2 reported by Meckler et al. (2014) were identical within error, although these values were calculated with the parameters according to Huntington et al. (2009). The authors hypothesized that this could have been achieved if, for example, the heated gases at ETH had been prepared from ETH‐1 and ETH‐2; however, this is not the case.

At ETH the reference frame was not created using a single gas and modifying its δ ¹⁸O by water equilibration to achieve the range of compositions necessary to establish the heated gas line as outlined in Daëron et al. (2016) and Schauer et al. (2016). Instead, we used three different gases with variable δ ¹³C and δ ¹⁸O to achieve a broad spectrum of compositions for the heated gases. Only for the equilibrated gases did we modify the δ ¹⁸O of the gases using waters of different composition. In Table 1 we report the δ ¹³C and δ ¹⁸O of the three gases used for establishing the reference frame (WG, CARBA, and LINDE) of the four ETH standards and of the equilibrated gases that were used in 2013 to establish the accepted values for the ETH standards reported in Meckler et al. (2014). These values were subsequently used to standardize all data measured at ETH into the CDES (e.g., Meckler et al., 2015; Millan et al., 2016; Müller, Violay, et al., 2017; Thornalley et al., 2015). We also report the change in Δ_47raw (Table 1, column labeled Δ [Δ_47raw]) obtained by using equation 10 of Daëron et al. (2016) to determine the error caused by the use of the old parameters.

Table 1.

Carbon and Oxygen Isotope Compositions and Δ (Δ_47raw) Values of Gases Heated at 1000°C (HG; WG, CARBA, and LINDE), ETH Standards, and Gases Equilibrated at 25°C (EG) Used to Create the Reference Frame and Establish Accepted Values for the ETH Standards in 2013

Gas label	δ 13C (‰) (VPDB)	δ 18O (‰) (VPDB)	Δ (Δ47raw) (ppm)
WG, HG	−7.25	0.26	0
Carba, HG	−28.6	−17.68	−1.0
Linde, HG	−48.85	−23.87	5.6
ETH1	2.20	6.70	−0.6
ETH2	−10.0	−10.0	−5.7
ETH3	1.95	7.18	−0.1
ETH4	−10.0	−10.0	−5.7
EG WG + enriched	−6.96	29.40	20.1
EG WG + enriched	−6.97	30.73	21.0
EG WG + enriched	−7.03	31.02	21.3
EG Linde + tap	−47.97	−0.96	21.1
EG Linde + tap	−48.01	−1.05	21.0
EG Linde + tap	−47.94	−0.89	21.1
EG WG + tap	−6.06	1.84	0.5
EG WG + tap	−7.04	−0.23	−0.5

Note. The δ ¹⁸O values of the standards are given without a correction for the acid fractionation. Δ (Δ_47raw) is the change in Δ_47raw resulting from the use of the Brand parameters instead of the Huntington ones as calculated with equation (10) of Daëron et al. (2016). For explanations see text. VPDB = Vienna Peedee belemnite; WG = working gas.

First, we note that the Δ₄₇ of the three heated gases varies by very little, with a maximum of 5.6 ppm change for the most negative gas (Table 1). This is because oxygen and carbon isotope values of our heated gases are positively correlated so that the errors induced by changing both isotopic compositions almost completely cancel out. This is related to the positive correlation between δ ¹³C and Δ (Δ_47raw) and its negative correlation with δ ¹⁸O (Figure 2). Both Daëron et al. (2016) and Schauer et al. (2016) established their heated gas lines by varying only the δ ¹⁸O of their gases, which magnified deviations between the two calculation methods. In our case, a large difference is only observed for those gases that were equilibrated with water with much higher δ ¹⁸O (EG WG + enriched and EG Linde + enriched) that increased their oxygen isotope composition by 20 to 30‰, leading to an effect of the parameter choice on Δ₄₇ values of up to 21 ppm. This change is much greater than that calculated for the same gases with their original oxygen isotope composition (WG and Linde).

The choice of gases that were used for establishing the CDES at ETH explains why the values of the ETH‐1 and ETH‐2 standards published in Meckler et al. (2014) are indistinguishable within error, and why they do not change much with the new parameters. Establishing a reference frame with gases of variable δ ¹³C and δ ¹⁸O minimized the errors due to the opposite effects of carbon and oxygen compositions on Δ (Δ₄₇), leading to values closer to those calculated with the Brand parameters. We postulate that the corrections when changing to the revised parameters will be significantly larger for laboratories that have established a reference frame by only changing the δ ¹⁸O of the gas and are smaller for laboratories where gases with covarying δ ¹³C and δ ¹⁸O were used. If most laboratories have produced their reference frames using gases of covarying δ ¹⁸O and δ ¹³C, then this coincidence may also explain why many previous calibrations compiled by Bonifacie et al. (2017) are closer to the calibrations that are recalculated with the Brand parameters and do not show the very large differences expected from the Schauer et al. (2016) study. Caution, however, should still be used because differences on the order of 0.02 to 0.04‰ can still be observed. Evans et al. (2018), for example, reported that recalculation the Zaarur et al. (2013) calibration led to a change in the intercept of +0.021‰ and attributed this to the fact that synthetic samples used in that calibrations had very low carbon isotope values with δ ¹³C between −30 and −35‰ (VPDB). In contrast, the slope did not change significantly. In the following, we discuss in more detail the effect of the new parameters on the accepted values of the ETH standards and on Δ₄₇ of the Kele et al. (2015) calibration.

The redetermination of the accepted values of the four ETH standards by Müller, Violay, et al. (2017) with a full recalculation of the heated and equilibrated gases measured in 2013 with the Brand parameters results in new values (projected from a reaction temperature of 70°C to 25°C using an acid fractionation factor of 0.062‰) as reported in Table 2. The effect of the parameter choice on the reference frame impacts the different standards to a varying degree. Although most of the equilibrated gases changed by about 21 ppm, the influence on the composition of ETH‐1 and ETH‐2 is small, because their Δ₄₇ is closer to the values of the heated gases. Because of the influence of the equilibrated gases on the stretching factor, we found a slightly greater change in the composition of ETH‐3 and ETH‐4 compared to the other standards. The effect of the recalculation on the Kele et al. (2015) calibration with the Brand parameter, including the transfer to the CDES using the new accepted values of the ETH standards reported in Table 2, is small for the slope but significant for the intercept. The original calibration was

$${\mathrm{\Delta }}_{47}=0.044·\frac{{10}^6}{T^2}+0.205$$

Table 2.

Overview on the Δ₄₇ Values Reported From the ETH Laboratory Projected to 25 °C

Standard	Δ47 Meckler et al. (2014)	Full recalculation (this study)	Difference
ETH‐1	0.267	0.258	−0.009
ETH‐2	0.269	0.256	−0.013
ETH‐3	0.705	0.691	−0.014
ETH‐4	0.524	0.507	−0.017

Note. The recalculated values were obtained by recalculation of all measurements with the Brand parameters, including the heated and equilibrated gases used to establish the reference frame and the values of the standards as published in 2014.

The fully recalculated calibration normalized to the new ETH standard values is

$${\mathrm{\Delta }}_{47}=0.0449\left(\pm 0.001\right)·\frac{{10}^6}{T^2}+0.167\left(\pm 0.01\right)$$

where T is the temperature in Kelvin.

We note here that all individual replicates of the Δ₄₇‐T calibration published by Kele et al. (2015) were reevaluated with the Brand parameters. In addition, the temperature calibration now includes the three biogenic carbonates Arctica islandica, Dyscolia wyvillei, and Ostrich egg that were mentioned in the original publication but does not include the cave tufa sample Havasok due to its poor reproducibility. The change in intercept is solely due to the recalculation with the Brand parameters and to the calculation of the regression using all individual replicates rather than average values for each sample. The addition of three biogenic samples and omission of the tufa sample had no influence on slope and intercept. All data are reported in the supporting information (Table S1). The fully reevaluated Δ₄₇‐T calibration is extremely well constrained by a total of 758 individual replicates of 25 samples that cover a temperature range of 6 to 95°C. The δ ¹³C and δ ¹⁸O of the samples of this calibration cover a large range from −12.9 to +7.5‰ and from −24.8 to +3.6 (VPDB), respectively, with no correlation between them. This large compositional variability is due to the range of environments the samples were collected from. This example also shows that while the slope (i.e., the temperature sensitivity) of the calibration does not change significantly with the Brand parameters, the intercept shows a relatively large change −0.038‰, which is even greater than the case described by Evans et al. (2018).

We report the results projected to 25°C because this was the temperature originally used for the reaction, when the method was established and samples were measured manually (e.g., Ghosh, Garzione, et al., 2006). Because currently most laboratories use either custom built automatic extraction lines running at 90°C or commercially available sample preparation lines reacting at 70°C, we propose that in the future the projection to 25°C should be abandoned for either a 70°C or a 90°C reaction temperature. This would help reduce the uncertainties related to the temperature dependence of phosphoric acid reaction as the differences between 70 and 90°C reactions are much smaller (although still significant) and data produced at the same reaction temperature can be directly compared. The problem of uncertain phosphoric acid fractionation factors can also be completely circumvented if all measurements are normalized to the composition of a set of internationally accepted carbonate standards. This would completely eliminate the need for a precise knowledge of the phosphoric acid fractionation factor at different temperatures and for different preparation systems.

By comparing the ETH‐1 and ETH‐2 standards to calcites heated to 1000°C and by calculating all data with the Brand parameters, Müller, Violay, et al. (2017) demonstrated that the two standards should have the same Δ₄₇, with near‐stochastic composition. The absolute value for the phosphoric acid fractionation factor, determined by Müller, Violay, et al. (2017) is consistent with the theoretical value of Guo et al. (2009). We conclude that the new, revised values for ETH‐1 and ETH‐2 are probably very close to their true value. For the other two standards it is more difficult to determine if the measured values are close to their true value, but nevertheless, they can be used as reference points. Additional careful studies comparing heated gases with the carbonate standards in different laboratories are necessary to confirm our ETH‐3 and ETH‐4 values in the CDES. Until this is achieved, we advocate that these values could be accepted as a best approximation of their true value, and all data be normalized to them. If these values changed in the future because of more accurate determination of their true values, any old data can be easily recalculated with the newly revised value (see section 6). This guarantees the comparability of old and new data better than measurement based on heated and equilibrated gases alone. The same approach has been followed in conventional stable isotope geochemistry, where the certified composition of international standards has slightly changed through time, when more accurate values became available.

5. Does Use of the Brand Parameters Solve All Interlaboratory Inconsistencies?

The discussion above shows that the use of the CDES and the new Brand parameters for the ¹⁷O correction has led to significant improvements such as solving the previously inexplicable differences in composition between ETH‐1 and ETH‐2 in some laboratories. Still, the question remains if interlaboratory comparability has truly improved. Is it good enough for determining absolute temperatures with sufficient accuracy to be comparable across laboratories and for using temperature calibrations determined in other laboratories?

To date, there are only three studies that have published values for some or all of the four ETH carbonate standards calculated with the Brand parameters and transferred into the ARF on the basis of gas standards (Table 3). Table 3 suggests that some nonsystematic differences remain among the laboratories, despite the use of the most recent improvements in data analysis and processing. Apparently, the new Brand parameters are not the only reason for interlaboratory differences, the cause of which remains somewhat enigmatic. In particular, the offsets between the ETH‐1 and ETH‐2 values across laboratories are significant, on the order of up to 50 ppm. These might potentially be related to fractionations during gas purification, or other unknown factors related to sample preparation or corrections of the mass spectrometric nonlinearity, or to potential ¹⁷O anomalies in the gases used (Daëron et al., 2016).

Table 3.

Published Values of ETH Standards Projected to 25 °C, and Number in Parenthesis Is the Number of Replicates

Standard	This study: MAT 253, 70°C Kiel IV device Porapak without He flow. AFF: 0.062.	Daëron et al. (2016), Isoprime 100 common acid bath, 90°, Porapak trap with He flow. AFF 0.082	Schauer et al. (2016), MAT 253, 90° common acid bath, AFF: 0.082	Breitenbach et al. (2018), MAT 253, 70 °C Kiel IV device Porapak without He flow. AFF: 0.062.
ETH‐1	0.258 ± 0.003 (82)	0.311 ± 0.006 (18)	0.286 ± 0.006 (8)	0.265 ± 0.002 (279)
ETH‐2	0.256 ± 0.004 (83)	0.306 ± 0.007 (13)	0.282 ± 0.005 (12)	0.253 ± 0.002 (292)
ETH‐3	0.691 ± 0.004 (73)		0.695 ± 0.009 (6)	0.693 ± 0.002 (267)
ETH‐4	0.507 ± 0.004 (83)		0.537 ± 0.006 (7)	0.503 ± 0.003 (324)

Note. The different fractionation factors are due to the fact that Daëron et al. (2016) and Schauer et al. (2016) used a reaction temperature of 90°C, whereas Breitenbach et al. (2018) and this study reacted the carbonates at 70°C. AFF = acid fractionation factor used to project the results to 25°C.

We argue that improved reproducibility across laboratories will only be achieved if, in addition to identical constants, carbonate standards, rather than heated and equilibrated gases, are used for projecting the data into the CDES. In this context, we argue that trying to reconcile differences in clumped isotope calibrations from different laboratories will remain problematic because of the absence of consistent carbonate standards measured in each laboratory at the time the calibrations were established. In absence of such carbonates, there is no traceable substance to verify the comparability of the measurements. For this reason, comparison of data using old calibrations will inevitably retain a relatively large uncertainty related to potential interlaboratory differences, which cannot be resolved a posteriori.

In the following we first describe the set of carbonate standards that were developed at ETH with the goal of providing a set of standards to the clumped isotope community to improve interlaboratory consistency. We then demonstrate with three examples that their use for corrections instead of gases indeed does improve the reproducibility among laboratories.

These four standards were prepared in quantities exceeding 800 g and can be obtained on request from the corresponding author. Development of further standard materials is welcome, but, as the discussion below will show, we propose that these are currently the best possible suite of carbonate standards available.

6. Carbonate Standards for Optimized Data Correction and Linkage to the ARF

The multiple possible sources of uncertainty in clumped isotope analysis necessitate a set of carbonate standards with compositions carefully selected in order to best detect and correct for possible analytical problems. In addition, as described in more detail in section 2, errors in the correction procedures have effects of different magnitude and direction depending on the δ ¹³C and δ ¹⁸O of the sample and its relation to the composition of the WG. For this reason, it is vital to have a set of standards not only with variable Δ₄₇ but also with variable bulk isotope compositions. Finally, it is desirable to have standards that span the range in bulk compositions of the samples that are to be measured. The standards should allow a laboratory to (i) verify that the background correction is accurate and (ii) correct for variations in Δ₄₇ scale compression over time.

The two isotopically heavy standards (ETH‐1 and ETH‐3) were chosen to be close in isotopic composition to marine carbonates, while the light ones (ETH‐2 and ETH‐4) cover the range in negative δ ¹³C and δ ¹⁸O typically found in diagenetic cements and high‐temperature carbonates. In this context it is also important to consider the bulk isotopic composition of the WG used in the mass spectrometer because of its impact on the corrections. The WG at ETH has a δ ¹³C of −7.25‰ and δ ¹⁸O of +1.65‰ (VPDB). With such a bulk isotope composition of the WG two of the standards have a positive and two a negative δ ⁴⁷ value. Although we consider this an ideal condition, the standards are also suitable when the bulk composition of the WG is such that all four standards have a δ ⁴⁷ more positive or negative compared to the WG (see discussion below).

Low Δ₄₇ carbonates can be obtained by heating in a pressurized furnace, driving the Δ₄₇ value as close as possible to stochastic distribution as was done for ETH‐1 and ETH‐2, which are a Carrara marble and a synthetic carbonate, respectively (Müller, Violay, et al., 2017). Finding suitable high Δ₄₇ standards, however, is more challenging, partly because low‐temperature carbonates are either not available in large quantities (e.g., foraminifera that live at high latitudes), do not have a composition similar to marine sediments (e.g., diagenetic carbonate crusts from cold seeps at the ocean floor and continental speleothems), or are isotopically very heterogeneous (e.g., cold water corals). A synthetic carbonate (ETH‐4) and a chalk from the Cretaceous of Germany (ETH‐3) were the carbonates with the highest Δ₄₇ we could find that had a composition bracketing natural samples, were homogeneous, and were available in sufficient quantities. The chosen materials have compositions that, when plotted in Δ₄₇ versus δ⁴⁷ space, are indeed approximately symmetric with respect to the WG used in the ETH instrument.

The basic concept of using these four standards is equivalent to the use of heated (corresponding to ETH‐1 and ETH‐2) and equilibrated gases (corresponding to ETH‐3 and ETH‐4). Because ETH‐1 and ETH‐2 have the same absolute Δ₄₇ value and are close to scrambled (Müller, Violay, et al., 2017), they can be used to check for any remaining nonlinearity following a background correction as they should have the same Δ₄₇ value after proper background correction (Bernasconi et al., 2013). Additional samples such as the heated Merck Carbonate with very depleted carbon and oxygen isotope values, as used by Müller, Violay, et al. (2017), could be a useful additional standard for verifying the robustness of the corrections.

The problem with the negative backgrounds on many instruments is that their proper determination is not always straightforward (Meckler et al., 2014; Müller, Violay, et al., 2017); thus, it is important to be able to verify this correction. If the negative BG is overestimated, the calculated Δ₄₇ of the samples with negative δ ⁴⁷ will be overcorrected to give too high Δ₄₇, whereas those with a positive δ ⁴⁷ will give compositions that are lower than the accepted value (Figure 3, see also Table 7 and Figure 4 in Müller, Violay, et al., 2017). The opposite is true if the background is underestimated (Figure 3b). These overcorrections and undercorrections will have a larger effect the further the sample is positioned from the bulk composition of the WG. As shown by Müller, Violay, et al. (2017) the composition of calcites heated at 1000°C with a δ ⁴⁷ range from +13.7 to −42.8‰ gave identical Δ₄₇ values when the accuracy of the background correction was monitored with ETH‐1 (δ ⁴⁷ = +13.5) and ETH‐2 (δ ⁴⁷ = −15.30). This shows that the range in δ ⁴⁷ of 28.8‰ provides a robust extrapolation, provided a sufficient number of carbonate standards are measured together with the unknowns. By plotting the deviation of the measured from the accepted value of the standards, one can easily observe an overcorrection or undercorrection graphically and the pressure baseline correction can be modified accordingly. The advantage of the background correction over a heated gas correction is that the backgrounds can be determined at short intervals before and after each measurement (He et al., 2012) or daily (Meckler et al., 2014) so that the short‐term variations can be detected and corrected for.

Figure 3.

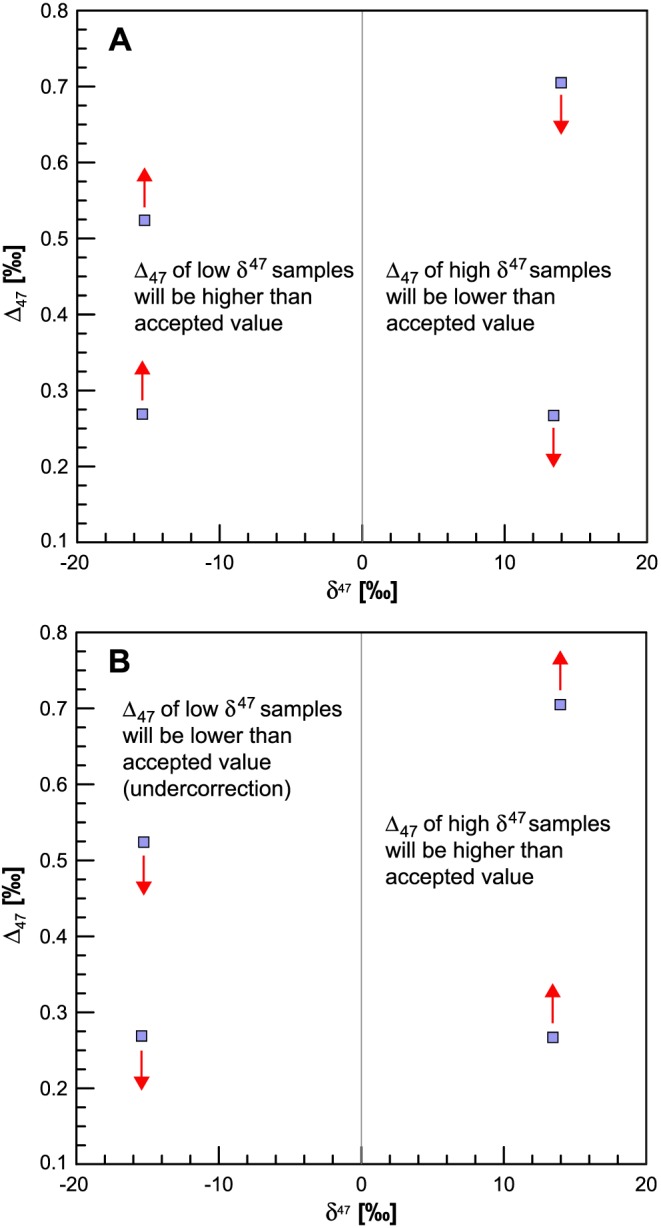
Schematic representation of the isotopic composition of the four ETH standards against a WG with δ ¹³C of −7.2‰ and δ ¹⁸O of 0.65‰ VPDB. The arrows show the change in composition that would be observed from erroneous (a) overcorrection or (b) undercorrection of the negative backgrounds. This is a very robust method to verify the quality of the correction. Contamination by isobaric interferences would increase the Δ₄₇ of all four standards. VPDB = Vienna Peedee belemnite; WG = working gas.

In some instruments with more complex cup configurations (Breitenbach et al., 2018) or with new instruments with specific clumped isotope collector designs (e.g., the ThermoFisher Scientific 253Plus) the background monitoring can also be done continuously using a half‐mass collector. The Nu Perspective (Nu Instruments, Wrexam, UK), on the other hand, does not show strongly negative backgrounds, but their absence needs to be verified regularly. In contrast, heated gas line‐based correction requires the averaging of measurements over multiple days or even weeks, as the construction of a heated gas line requires multiple measurements of heated gases with widely different compositions or of a large number of gases with variable compositions (e.g., Dennis et al., 2011; Huntington et al., 2009). Therefore, background changes cannot be immediately detected using heated gases.

After the pressure‐proportional background correction is carried out by adding the measured negative backgrounds to the measured beam intensities following Bernasconi et al. (2013), the bulk isotope composition and the stochastic isotope composition of the sample can be calculated according to the procedures described in detail in Huntington et al. (2009) but using the revised Brand parameters (Daëron et al., 2016; Schauer et al., 2016). From these calculations the Δ_47raw (i.e., the Δ₄₇ of the carbonate standard with respect to the WG in the mass spectrometer) is determined. If the Δ_47raw of the four standards is found to deviate in a systematic way from the expected values, the background correction is reevaluated. Once the background correction gives consistent Δ_47raw values for the four standards, and the same value for ETH‐1 and ETH‐2, the empirical transfer function (ETF) is determined by plotting the Δ_47raw of the four standards versus their accepted Δ₄₇ (CDES) value as in Dennis et al. (2011). The final Δ₄₇ (CDES) of an unknown sample is then calculated as

$${\mathrm{\Delta }}_{47}\left(\text{CDES}\right)=a\times D_{47\mathrm{raw}}+b$$

where a is the slope of the ETF and b its intercept.

The slope of this linear regression corrects for possible scale compression in the source of the mass spectrometer, and the intercept is the correction that accounts for the Δ₄₇ of the WG used in the specific mass spectrometer. This is the same approach used for scale normalization in the analysis of oxygen and hydrogen isotopes in water (Nelson, 2000) or for the normalization of δ ¹³C measurements to the VPDB scale (Coplen et al., 2006). The final step is to correct for the phosphoric acid fractionation factor that will depend on the digestion temperature. This carbonate‐based correction scheme is implemented in the community software Easotope (John & Bowen, 2016) that is routinely used at ETH‐Zürich, Massachusetts Institute of Technology (MIT), Cambridge and an increasing number of laboratories for data evaluation and archiving.

At ETH all 4 standards are measured at least 6 times in each batch of 46 samples that can be placed in the autosampler of the Kiel IV device. The measurement of a large number of standards is necessary for a robust determination of the ETF, the number being dependent on the standard deviation of the typical measurements. One of the reasons is that the difference in Δ₄₇ between the lowest and highest standards available is only 0.433‰, whereas the difference between a heated gas and a gas equilibrated with water at 25°C is 0.898 (Dennis et al., 2011). Because of the smaller range in Δ₄₇, the determination of the scale compression requires higher precision with carbonates. With a typical long‐term standard deviation on the order of ±0.025‰, each standard is determined with a standard error of about 0.01‰ with six replicates. This precision reached with multiple analyses is sufficient to compensate for the smaller difference in Δ₄₇ of the carbonates. The advantage of this approach is that short‐term fluctuations caused by the mass spectrometer in both slope and intercept of the ETF can be readily observed and corrected for. We demonstrate this in Figure 4, which shows the evolution of the slope and intercept of the ThermoFisher 253Plus instrument during approximately 5 weeks corresponding to the measurement period of the data discussed in Müller, Fernandez, et al. (2017). In contrast, typical measurement windows for laboratories using heated and equilibrated gases are on the order of a few weeks to months. For this reason, shorter‐term fluctuations in the mass spectrometer performance as shown in Figure 4 would go undetected. Depending on the standard deviation of the replicates, the number of standard measurements to reach the necessary precision can be adjusted to optimize the use of the instrument and measure only as many standards as needed. To verify the accuracy of the corrections through time, samples of known composition, but treated as unknowns, should be measured interspersed with the samples. At ETH a Carrara marble is used for this purpose.

Figure 4.

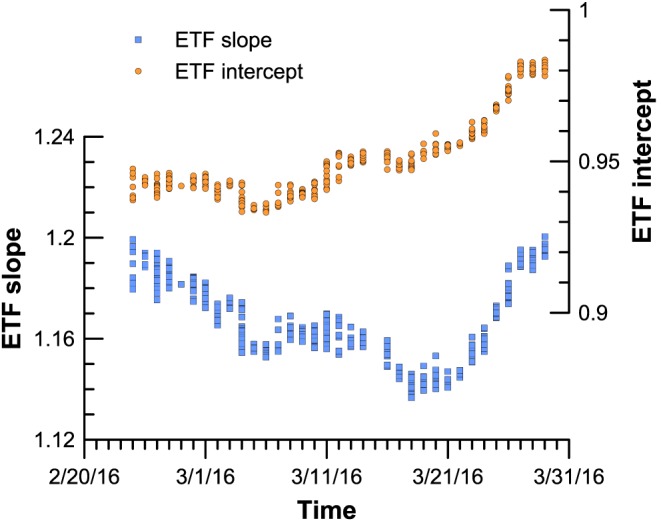
Evolution of the slope and intercept of the Thermo 253Plus at ETH between 24 February and 29 March 2016. Note the fluctuations in both slope and intercept that can be traced with a 2‐day resolution with the repeated measurements of the standards. ETF = empirical transfer function.

The direct conversion of the Δ_47raw values of samples via the accepted values of carbonate standards to the CDES has an additional advantage: it could effectively eliminate the uncertainties related to the phosphoric acid fractionation at the various reaction temperatures used in the different laboratories. Once a consensus value for the standards is reached by the community, all laboratories can simply normalize the results to the same value, independent of the temperature at which they digest the samples. This will remove an additional source of inconsistency between the laboratories, the uncertainties in the temperature dependence of the phosphoric acid fractionation factor. If improvements in future analytical methods require a revision of the accepted values of the standards used for normalization, all older data can be easily recalculated with a new ETF determined with a simple linear regression between accepted and measured values.

At present, only a few determinations of the true value of the four ETH standards have been published, but an interlaboratory calibration exercise is in progress to improve the situation. Even if the current values are not exact, for the reasons discussed above, we consider the ETH values (Table 3) to be close to the true values. What is the magnitude of the uncertainty if these values are inaccurate? We can estimate this by using the values published by other laboratories. For example, if we compare the values obtained at ETH with those published by Schauer et al. (2016), we note that the value of ETH‐3 differs by only 0.004‰ whereas the values of ETH‐1 and ETH‐2 differ on average by 0.027‰. As ETH‐3 represents the cold (approximately 20°C) and ETH‐1 and ETH‐2 the warm end of the scale (600°C) the difference in composition for actual samples on the CDES scale will be about 0.030‰ for high‐temperature samples reducing to 0.004‰ for samples formed at low temperatures. The situation is less clear for sample ETH 4 that also shows a difference of 0.03‰ between the laboratories, although it is closer in composition to ETH‐3 than ETH‐1 and ETH‐2. The cause of this discrepancy is currently unclear. In view of these differences, we definitely encourage the community to better constrain the true value of all four standards.

In the following we provide more detailed information on the four ETH standards and constraints on their bulk and clumped isotope composition.

ETH‐1 is a Carrara marble that was powdered to <60 μm in a disc mill. It was then filled in a steel tube in 10–20 g aliquots and pressed with a hydraulic press to remove as much air as possible. The steel tube was welded and subsequently heated to 600°C at 155 MPa pressure in a Hot Isostatic Press (Sinter‐HIP‐Kompaktanlage; ABRA Fluid AG, Switzerland) for 10 hr. Cooling of the sample to room temperature takes approximately 40 min. After cutting the metal open, the carbonate, which had completely recrystallized to a solid rock, was ground to <60 μm and homogenized in a disc mill.

ETH‐2 is a high‐purity synthetic carbonate (Riedel‐de Haen, calcium carbonate Puriss. p.a.; Lot No. 30800; same as ETH‐4) that was heated in the same HIP run as ETH‐1 and thus was exposed to the same P and T conditions for the same length of time. This sample also completely recrystallized to a solid rock.

ETH‐3 is a sample of Chalk of Campanian age (Upper Cretaceous), collected on the Island of Rügen, Northern Germany, and was ground and homogenized in the disc mill. It is composed principally of coccoliths with only minor impurities.

ETH‐4 is a synthetic carbonate (Riedel‐De Haën, now part of Sigma‐Aldrich Chemicals, St. Louis, MO, USA) Lot No. 30800. It is a pure calcium carbonate with <0.005% insoluble residue. The original material was homogenized by shaking and then transferred from the original plastic container into a glass bottle for long‐term storage.

X‐ray powder diffraction analysis of all samples revealed the presence of exclusively low magnesium calcite. All samples are available in an amount between 700 and 800 g. Samples are being distributed in 1‐g aliquots to interested laboratories.

6.1. Sample Homogeneity, Oxygen, and Carbon Isotope Composition

Before distribution to other laboratories, the samples were thoroughly evaluated for homogeneity in δ ¹³C and δ ¹⁸O at ETH Zürich, University of Bergen and Cambridge University. The δ ¹⁸O and δ ¹³C results of the homogeneity test are presented in Table 4. Samples from different aliquots filled in different vials from the glass bottle used to store the samples were repeatedly measured on both the Kiel IV carbonate device coupled to a MAT 253 routinely used for clumped isotope measurements (Meckler et al., 2014) and a Gasbench II coupled to a ThermoFisher Delta V with the methods described in Breitenbach and Bernasconi (2011) at ETH. In addition, different aliquots of these standards were measured at the stable isotope facility at the University of Bergen on two separate Kiel IV carbonate devices, coupled to a MAT 253 and a ThermoFisher 253 Plus, respectively, and at Cambridge University (CAM) on a Kiel IV‐MAT 253 system. The δ ¹³C and δ ¹⁸O were calibrated to the international standards NBS 19 and NBS18, as well as LSVEC in the case of ETH; thus, ETH‐1 to ETH‐4 can also be used to correct unknown δ ¹³C and δ ¹⁸O values.

Table 4.

Carbon and Oxygen Isotope Composition of the Carbonate Samples Versus VPDB

δ13C	ETH GB	ETH Kiel‐253Plus	UB Kiel‐MAT 253	UB Kiel‐253Plus	CAM Kiel‐MAT253	Average
ETH‐1	2.00	2.05	2.05	2.02	2.00	2.02
SD	0.05	0.03	0.01	0.01	0.05	0.03
N	27	21	5	10	279
ETH‐2	−10.20	−10.19	−10.17	−10.21	−10.06	−10.17
SD	0.05	0.02	0.01	0.02	0.07	0.06
N	29	21	5	10	292
ETH‐3	1.70	1.72	1.70	1.71	1.74	1.71
SD	0.04	0.02	0.02	0.03	0.05	0.02
N	28	21	5	10	267
ETH‐4	−10.22	−10.22	−10.18	−10.23	−10.17	−10.20
SD	0.03	0.01	0.01	0.01	0.04	0.03
N	28	21	5	10	324
δ 18O	ETH GB	ETH Kiel‐253Plus	UB Kiel‐MAT 253	UB Kiel‐253Plus	CAM
ETH‐1	−2.15	−2.15	−2.23	−2.21	−2.19	−2.19
SD	0.04	0.03	0.01	0.03	0.09	0.04
N	27	21	5	10	279
ETH‐2	−18.58	−18.66	−18.82	−18.80	−18.59	−18.69
SD	0.03	0.05	0.04	0.07	0.12	0.11
N	29	21	5	10	292
ETH‐3	−1.72	−1.75	−1.87	−1.75	−1.80	−1.78
SD	0.06	0.06	0.04	0.07	0.096	0.06
N	28	21	5	10	267
ETH‐4	−18.65	−18.80	−18.87	−18.89	−18.85	−18.81
SD	0.04	0.04	0.03	0.03	0.097	0.10
N	28	21	5	10	324

Note. The measurements are normalized to the accepted values of NBS 19, NBS18, and LSVEC in the case of ETH, NBS18, and NBS 19 for the measurements at University Bergen (UB) and NBS 19 at Cambridge University (CAM). SD = standard deviation.

The δ ¹⁸O and δ ¹³C results of the homogeneity test are presented in Table 4. The δ ¹⁸O and δ ¹³C are based on three different runs carried out on the Gasbench II (ETH GB) containing seven aliquots of 100–120 μg of each ETH standard and the international reference materials. Three runs on the ETH Kiel with seven aliquots of 100–120 μg each, and two runs with aliquots of 100–130 μg each at the two Bergen instruments, and > 90 runs over the course of approximately 11 months at CAM. These results demonstrate the homogeneity of these materials, whereby the reproducibility for ETH‐2 and ETH‐4 is slightly poorer compared to the other two, and they seem to have slightly less negative δ ¹⁸O values on the GB compared to the Kiel devices. The homogeneity of the four ETH standards with respect to Δ₄₇ was demonstrated by the long‐term reproducibility obtained over 15 months as reported in Meckler et al. (2014) and by the results presented in Müller, Fernandez, et al. (2017).

7. Examples of Carbonate‐Based Normalization Improving Interlaboratory Comparability

In the following section we illustrate the importance of carbonate normalization based on three examples: (I) a recalculation of the composition of the samples of the Kele et al. (2015) calibration using the values of the ETH standards reported by the University of Washington (Kelson et al., 2017; see also Table 3) instead of the accepted values used at ETH, (II) the new calibration of Breitenbach et al. (2018) based on subaqueous cave carbonates (cave pearls) obtained at CAM, and (III) a comparison of calcite and dolomite samples between ETH and MIT.

7.1. Case I

As a first example we show that normalization to the same values of the ETH carbonate standards significantly reduces the differences between independent calibration data sets in two different laboratories. To date, the only data available in the literature allowing such a comparison are from Breitenbach et al. (2018) that are discussed below, and from the University of Washington, which has published values for the four ETH carbonate standards (Schauer et al., 2016, see Table. 3). The latter laboratory has also produced an in‐house calibration based on synthetic carbonates, while processing all the data with the Brand parameters (Kelson et al., 2017) that is plotted as black line in Figure 5. This calibration is similar to the Kele et al. (2015) calibration produced at ETH using natural travertine samples (gray dashed line). However, significant differences are observed, increasing at higher temperatures. To demonstrate the effect of carbonate normalization, we recalculated the composition of the samples of Kele et al. (2015) with the Brand parameters and then transferred the results to the CDES assigning the values of Schauer et al. (2016) instead of the ETH ones to the four standards when constructing the ETF. This is consistent with our proposal of normalizing all data to common values of the ETH standards in all laboratories. The recalculated data set is plotted in green in Figure 5.

Figure 5.

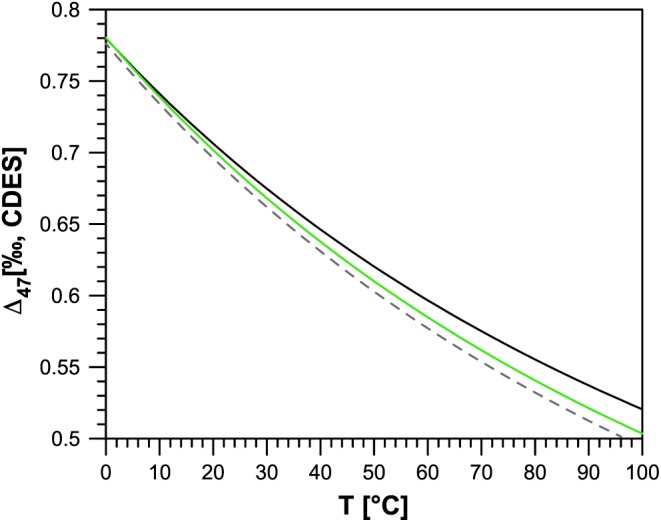
Comparison of the original Kele et al. (2015) calibration (gray dashed line) with the Kelson et al. (2017) calibration (black line) and the recalculated Kele et al. (2015) using the Brand parameters and projection of the data to the reference frame using the University of Washington values (Schauer et al., 2016) for the ETH standards (green line). CDES = carbon dioxide equilibrium scale.

It is clear that the difference between the two calibrations (Figure 5), which are based on completely different samples (natural travertines versus synthetic carbonates) and were measured with a Kiel IV device versus a traditional large‐sample common acid bath extraction line, become smaller after normalization to common carbonate standards. The difference between the two calibrations decreases from 0.013 to 0.001‰ at 5°C and from 0.028 to 0.014‰ at 80°C. This means that after normalization to the same carbonate standards both calibrations yield essentially the same temperatures in the range 0–35°C relevant for paleoclimatic studies and differences of less than 10°C at temperatures of up to 100°C. This is clearly an improvement compared to the differences of 3°C at low temperature and 17°C at higher temperatures before normalization.

7.2. Case II

The measurements for the calibration of Breitenbach et al. (2018) were carried out at the University of Cambridge on a MAT 253 instrument coupled to a Kiel IV carbonate device, a setup similar to the one at ETH, which is fully described in Breitenbach et al. (2018). The MAT 253 mass spectrometer has been retrofitted with a 10¹² Ω resistor on a Faraday cup at m/z 46.5 that allows continuous monitoring of the background during analysis. The laboratory established the composition of the ETH standards using heated and equilibrated gases (reported in Table 3). Subsequently, the carbonate standards were regularly measured to monitor the day‐to‐day performance of the mass spectrometer and to transfer the data into the CDES in a similar fashion as at ETH (see, e.g., Meckler et al., 2014). In Figure 6 we show a comparison of the Cambridge calibration with the data transferred to the CDES using the transfer function developed with heated and equilibrated gases (orange diamonds) and when the data are transferred to CDES using the carbonate standards with the ETH accepted values (blue dots). The black line represents the Kele et al. (2015) calibration recalculated with the Brand parameters. This example shows that the confidence interval of the calibration is reduced with the normalization to the values of the ETH standards compared to the use of a transfer function developed with equilibrated and heated gases. The smaller confidence interval can be attributed to a better monitoring of variations in slope and intercept of the ETF with the carbonates as shown in Figure 4 for the ETH instrument. Moreover, the larger variation can be attributed to fact that the heated and equilibrated gases were measured with the dual inlet through a different capillary than the carbonates, thus not capturing possible fractionation effects caused by the acid reaction and gas transfer and purification in the Kiel device. The Cambridge cave pearl calibration is statistically indistinguishable from the Kele et al. (2015).

Figure 6.

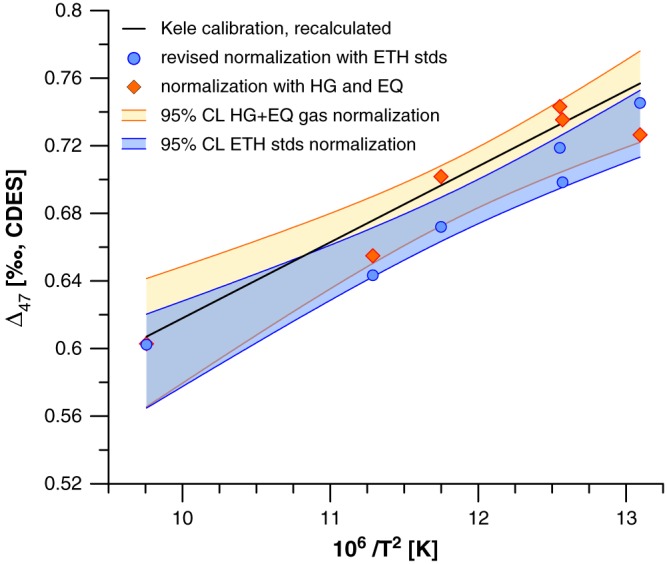
Comparison of the Cambridge calibration calculated with normalization to heated and equilibrated gases (orange diamonds) and the normalization against the ETH carbonate standards (Blue dots). Between 12 and 21 carbonate standards were measured with every batch of 46 samples that can be accommodated in the Kiel device. The black line is the Kele et al. (2015) calibration recalculated with the Brand parameters. CDES = carbon dioxide equilibrium scale.

7.3. Case III

We further validated the use of the ETH standards to correct the Δ₄₇ of unknowns into the CDES reference frame by comparing measurements of carbonate samples between MIT and ETH, which utilize very different setups and instruments for measuring Δ₄₇. The ETH setup of a Kiel IV device coupled to a ThermoFisher Scientific 253Plus is described above. The MIT lab uses a Nu Perspective coupled to a Nu Carb with a built‐in diffusive Porapak trap held at −30°C. The Nu Carb device acidifies ~400 μg of carbonate at 70°C using 150 μL of acid for 25 min. To best compare standard measurements between labs, MIT used the ETH‐1 to ETH‐3 accepted values of this study (Table 3) to standardize values into the CDES reference frame and used the Brand parameters for calculations. The data are reported for a reaction temperature of 70°C. Importantly, the MIT raw Δ₄₇ values with respect to the WG for ETH‐1 and ETH‐2 are indistinguishable, indicating no linearity issues (ETH‐1 = −0.693‰ ± 0.028 (1 standard deviation, SD), n = 38 and ETH‐2 = −0.693‰ ± 0.029, n = 38). The samples that are independently comparable are the calcites ETH‐4, IAEA C1, IAEA C2, NBS18 and NBS 19, and the dolomites Sansa and Rodolo (Table 5). The results of the calcites are very close for both laboratories, with a maximum difference of 0.007 and 0.008‰ for NBS18 and NBS 19, respectively, which can be attributed to the relative low number of measurements at MIT. All values are within error of those from the other laboratory, and clearly show the very high level of interlaboratory reproducibility that can be reached with carbonate standardization. The dolomite standard, Sansa, shows identical values in both laboratories while the dolomite Rodolo shows a difference of 0.014‰. We attribute this larger difference either to incomplete reaction of the dolomite or to possible inhomogeneity of the sample. Further studies are ongoing to understand the cause of the difference.

Table 5.

Comparison of the Results of Five Calcite and Two Dolomite Unknowns Between MIT and ETH

Sample	N	δ13C (VPDB)	SD	δ18O (VPDB)	SD	Δ47 (CDES)	SD	SE	Difference in Δ47 ETH‐MIT
MIT
ETH‐4	69	−10.24	0.02	−18.65	0.07	0.453	0.025	0.003	−0.004
IAEA C1	5	2.43	0.01	−2.31	0.03	0.287	0.025	0.011	0.000
IAEA C2	4	−8.26	0.02	−8.94	0.04	0.652	0.020	0.010	0.001
NBS18	2	−5.03	0.04	−23.03	0.04	0.369	0.020	0.014	0.007
NBS 19	6	1.91	0.02	−2.08	0.09	0.286	0.032	0.013	−0.008
Rodolo	10	−3.79	0.02	2.61	0.25	0.646	0.023	0.007	0.014
Sansa	12	1.43	0.04	−3.91	0.10	0.525	0.022	0.006	−0.001
ETH
ETH‐4	37	−10.23	0.05	−18.85	0.14	0.457	0.038	0.008
IAEA C1	6	2.47	0.01	−2.32	0.03	0.287	0.018	0.007
IAEA C2	11	−8.25	0.02	−9.00	0.05	0.650	0.022	0.007
NBS18	22	−5.00	0.07	−23.02	0.28	0.362	0.040	0.009
NBS 19	42	1.93	0.15	−2.19	0.13	0.294	0.035	0.005
Rodolo	151	−3.71	0.06	2.77	0.12	0.632	0.034	0.002
Sansa	19	1.45	0.09	−3.56	0.18	0.526	0.029	0.007

Note. N is the number of replicates, SD = standard deviation, and SE = standard error of the mean. The D₄₇ is reported for a reaction temperature of 70 °C. The last column shows the difference in Δ₄₇ between MIT and ETH. IAEA = International Atomic Energy Agency; VPDB = Vienna Peedee belemnite; CDES = carbon dioxide equilibrium scale; MIT = Massachusetts Institute of Technology.

8. Outlook

Based on the results presented above, the use of carbonates with carefully chosen bulk and clumped isotope compositions can significantly contribute to improved interlaboratory comparability. This is valid for analytical systems using small (100–400 μg) as well as large (>2 mg) samples, different acid reaction, and gas purification systems. The use of carbonate standards, which have a smaller range in Δ₄₇ than heated and equilibrated gases (~0.4‰ versus ~ 0.9‰), requires sufficient replication of the carbonates in order to determine an accurate scaling factor. The required number of replicates depends on the external reproducibility of the measurements and will be different for different laboratories/analytical systems (Fernandez et al., 2017). A carbonate‐based calibration poses an increased challenge on large‐sample systems with limited sample throughput, as it may require a greater number of replicates than is commonly measured with heated and equilibrated gases. However, even for these systems a carbonate‐based standardization is necessary in order to resolve interlaboratory inconsistencies. In this respect, the commercially available automated carbonate digestion systems using small samples (150–400 μg) have a distinct advantage. With typical reproducibilities of 0.02–0.030‰ these systems may require more replicates than what can be achieved in the best laboratories analyzing large samples of 3–10 mg with custom built lines (0.014–0.020‰; Fernandez et al., 2017). However, the speed of analysis and the small sample sizes used for each analysis allow precise and accurate measurements on total sample sizes of 1 to 2 mg (Müller, Fernandez, et al., 2017) as opposed to 10–15 mg or more for large‐sample systems. The ability of analyzing small samples opens new avenues of research that cannot be approached with the conventional large‐sample systems (e.g., analysis of foraminifera by Rodriguez‐Sanz et al., 2017).

We stress here that the proposed ETH standards are merely a way to improve data correction and normalization to the commonly accepted CDES and are not a new carbonate reference frame. As shown by the published values (Table 3), differences of up to 0.05‰ in the Δ₄₇ of these standards are still observed across laboratories when their composition is determined against heated and equilibrated gases. The magnitude of these differences is relatively large and needs to be addressed by the community in order to work toward accepted values of these standards. The next ongoing step in this direction is an interlaboratory comparison effort, named InterCarb, in which at least 30 laboratories are participating. The goals of this initiative are to determine accepted values for the ETH standards that could then be adopted by the clumped isotope community, as well as further test of our proposal that a carbonate‐based standardization will improve interlaboratory data comparability. This goal will be achieved by the analysis of three unknowns together with the ETH standards and by calculating their composition through carbonate standardization based on ETH‐1 to ETH‐3. Based on the results of this interlaboratory calibration, best practice strategies for data correction and analytical procedures will be formulated.

From the available data, we suggest that at least for automated instruments analyzing submilligram samples in microvolume mode, such as the Kiel IV‐253Plus system or the Nu Carb‐Nu Perspective systems, the carbonate standardization scheme is the best way forward, as it eliminates the uncertainties related to the different preparation of gases and carbonates. For systems using large samples, best strategies of correction will have to be established depending on the possible sample throughput. However, it will be imperative to report the results of internationally available standards in the publications in order to determine data comparability across laboratories. Efforts to produce additional standards with different mineralogy such as dolomites, aragonite, siderite, phosphate should continue to provide the community with a broader range of standards. In particular, samples with Δ₄₇ ≫ 0.700‰ would be a very welcomed addition to the available set.

9. Conclusions

• We reviewed the recent developments in carbonate clumped isotope data processing and correction schemes and identify possible sources of uncertainties.

• We confirm that the use of the Brand parameters is necessary to improve interlaboratory comparability, but it does not resolve all differences.

• We propose a set of four carbonate standards for the community to use to standardize measurements to the ARF based on the CDES.

• Normalization of measurements with common carbonate standards is expected to improve interlaboratory comparability to the level necessary for most applications of clumped isotope paleothermometry, especially paleoclimate reconstructions that require the highest standards of precision and accuracy.

Supporting information

Supporting Information S1

Table S1

Bernasconi, S. M. , Müller, I. A. , Bergmann, K. D. , Breitenbach, S. F. M. , Fernandez, A. , Hodell, D. A. , et al. (2018). Reducing uncertainties in carbonate clumped isotope analysis through consistent carbonate‐based standardization. Geochemistry, Geophysics, Geosystems, 19, 2895–2914. 10.1029/2017GC007385