The Conformation of the Mannopyranosyl Phosphate Repeating Unit of the Capsular Polysaccharide of Neisseria meningitidis Serogroup A and Its Carba‐Mimetic

Abstract

Neisseria meningitidis serogroup A (MenA) is an aerobic diplococcal Gram‐negative bacterium responsible for epidemic meningitis disease. Its capsular polysaccharide (CPS) has been identified as the primary virulence factor of MenA. This polysaccharide suffers from chemical lability in water. Thus, the design and synthesis of novel and hydrolytically stable structural analogues of MenA CPS may provide additional tools for the development of therapies against this disease. In this context, the structural features of the natural phosphorylated monomer have been analyzed and compared to those of its carba‐analogue, where the endocyclic oxygen has been replaced by a methylene moiety. The lowest energy geometries of the different molecules have been calculated using a combination of quantum mechanical techniques and molecular dynamics simulations. The predicted results have been compared and validated using NMR experiments. The results indicate that the more stable designed glycomimetics may adopt the conformation adopted by the natural monomer, although they display a wider flexibility around the torsional degrees of freedom.

Introduction

Most of the cases of meningococcal disease worldwide are caused by six serogroups (A, B, C, Y, W and X). Serogroup A, in particular, has been responsible for the largest and most devastating epidemic meningitis disease in developing countries in the first part of the twentieth century.1 Today the meningitis epidemics caused by MenA are rare in the US and Europe and especially afflict the sub‐Saharan region of Africa.2 The capsular polysaccharide (CPS), which covers the bacterial cell surface, is distinct within the different serogroups and has been identified as the primary virulence factor. The CPS of serogroup A (MenA) has a backbone formed by (1→6)‐linked 2‐acetamido‐2‐deoxy‐α‐d‐mannopyranosyl phosphate repeating units (Figure 1).3

Figure 1.

Natural monomer of Neisseria meningitidis. A capsular polysaccharide and carbasugar mimetics.6, 7

This polysaccharide suffers from poor stability of the anomeric linkage that tends to hydrolyze significantly in aqueous solutions and a high temperature (above 4 °C).4 The reason for this instability seems to be the presence of a phosphodiester linkage at the anomeric position together with the axially‐oriented N‐acetyl group at position 2 of the mannosamine moiety, which can assist the departure of the phosphomonoester group by facilitating the cleavage of the C1–O1 bond.4

Consequently, there is an increasing interest in the design and synthesis of novel and hydrolytically stable mimetic of MenA capsular polysaccharide. The hydrolysis of the glycosidic linkage can be avoided by chemical modification of the glycosyl 1‐O‐phosphate moiety using sugar mimicry, replacing the endo‐cyclic oxygen atom at the pyranose ring with a methylene group.5, 6 MenA carba‐analogues from monomer to trimer have been previously synthesized. Only the dimer was recognized by anti MenA PS antibodies5, 7, 8 and the CRM₁₉₇‐conjugated trimer was the sole neo‐glycoconjugate able to induce bactericidal antibodies, although at a lower level compared to a reference MenA CPS conjugate.5 It is well known that the three‐dimensional structure of the partners plays an essential role in antigen‐antibody molecular recognition processes. Herein, we describe the conformational analysis obtained by using a combination of quantum mechanical calculations and molecular dynamics (MD) simulations of the 2‐acetamido‐2‐deoxy‐α‐D‐mannopyranosyl derivatives 1a and 1b (with a methyl phosphodiester linked at the anomeric and primary hydroxyls, respectively) and their carba glycomimetics 2a and 2b (Figure 2). The results have been validated by NMR experiments, performed on the synthetized monosaccharides 1c and 1d and their corresponding carba‐analogues 2c and 2d (Figure 2).

Figure 2.

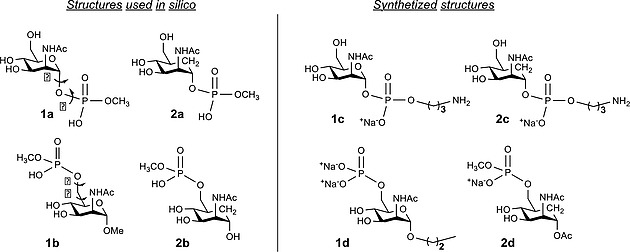
Schematic view of the structures of the studied compounds. Model compounds 1a and 1b and their C‐carba glycomimetics 2a and 2b were subjected to in silico studies. Synthetic compounds 1c and 1d and their corresponding carba‐analogues 2c and 2d were used for NMR studies. The torsion angles were defined as follows: φ = O5–C1–O–P for 1a and 1c and φ = C5a–C1–O–P for 2a and 2c, Ψ = C1–O–P–OMe, ω = O5–C5–C6–O6 for 1b and 1d and ω = C5a–C5–C6–O6 for 2b and 2d, and θ = C5–C6–O6–P.

Results and Discussion

Synthesis of the Natural and Mimetic Mannosamines

The 2‐acetamido‐2‐deoxy‐α‐D‐mannopyranosyl derivatives 1c, 1d and the carba‐glycomimetics 2c, 2d (structurally related to 1a, 1b and 2a, 2b used in the computational studies) were synthesized according to previously reported procedures (Figure 2 and Scheme 1 and Scheme 2, see Sup Info for details).7, 8 Mannosamine 1c and the carba‐analogue 2c were equipped with an α‐phoshopropylamine linker in order to resemble the phosphodiester linkage present in the natural MenA polysaccharide. The mannosamine 1d, structurally similar to 1b, was synthesized with the anomeric position blocked in α‐configuration by a propyl linker. The carba analogue 2d was obtained as phosphomethyl monoester counterpart of 2b.

Scheme 1.

Chemical synthesis of mannosamines 1c and 1d.

Scheme 2.

Chemical synthesis of the carba analogue, 2d.

The synthesis of 1c (Scheme 1) was achieved starting from the previously reported compound 3,9 which was subjected to phosphonation of the anomeric position with 2‐chloro‐1,3,2‐benzodioxaphosphorin‐4‐one, followed by condensation with benzyl N‐(3‐hydroxypropyl) carbamate to provide 5. Hydrogenation in the presence of Pd/C and methanolysis under Zemplen conditions gave the target molecule 1c, which was purified by size exclusion chromatography. For the synthesis of 1d (Scheme 1), allyl mannosamine 6 was silylated at the 6‐hydroxyl group and acetylated at positions 3 and 4. After removal of the tert‐butyldiphenylsilyl protection with HF in pyridine, the resulting alcohol 9 was phosphorylated with diphenylchlorophosphate in the presence of 4‐pyrrolidinopyridine/triethylamine to give 10, which was deprotected by PtO₂‐catalyzed hydrogenation and methanolysis to afford compound 1d, which was chromatographed on size exclusion column.

The carba‐analogue 2c was synthetized as previously reported by Qi Gao et al. Compound 2d was prepared starting from the previously reported intermediate 11 (Scheme 2),8 which was treated with 2‐chloro‐1,3,2‐benzodioxphosphorin‐4‐one to obtain hydrogen phosphonate 12. Due to its poor stability, compound 12 was promptly treated with pivaloyl chloride in pyridine and MeOH, followed by oxidation (I₂ in pyridine/water) to afford methyl phosphate 13. Removal of benzyl ethers via Pd/C hydrogenation, followed by ion exchange with Dowex 50W‐X8 resin gave the desired product 2d, which was isolated as a sodium salt.

Conformational Analysis

The conformational behavior of different glycomimetics, including carbasugars,10, 11 C‐glycosyl compounds12 and other mimetics13, 14 have been largely discussed. Their ability to mimic the binding features of the natural saccharides has also been subject of detailed investigations.15, 16 Generally speaking, for the glycomimetics, the lack of the stereoelectronic stabilization provided by the exo‐anomeric effect,17 provides additional flexibility around the glycosidic torsional angles of these molecules.18 Therefore, the knowledge of the geometrical and dynamic features of these molecules requires their detailed conformational analysis paying special attention to the different torsional degrees of freedom (glycosidic linkages and pendant groups) as well as the geometry of the six‐membered ring. The presence of the phosphate group poses additional structural complexity of these molecules compared with natural sugars. The conformational preferences of compounds 1a, 1b, 2a, and 2b (Figure 2) were evaluated using a combined theoretical (quantum mechanical and MD simulations) and experimental (NMR) approach. The latter was applied to the corresponding synthetic model compounds 1c, 1d, 2c, and 2d. Since 1a is not substituted at O6, the conformation around ω and θ was studied using compound 1b (see below).

The Conformation of the Natural Analogues 1a and 1c and their Carba‐Mimetics, 2a and 2c (Anomeric Phosphates)

For compound 1a, a long (1.5 µs) MD simulation (Figure 3a) was performed using the GLYCAM06 force field, specific for carbohydrate molecules, using explicit solvent molecules (water) and periodic boundary conditions. The results indicate that there is a highly preferred conformation for the glycosidic linkage in terms of φ/Ψ values. As expected for a natural sugar such as 1a, the φ value is consistent with the exo‐syn conformation (Figure 4). Indeed, the stereoelectronic contribution of the exo‐anomeric effect strongly stabilizes this geometry. For Ψ, the –60° value is largely populated. Obviously, there is certain motion around the corresponding global minimum, with minor excursions to other regions of the conformation map (Figure 3a).

Figure 3.

φ/ψ plots derived from 1.5 µs MD simulations in explicit water for a) 1a (GLYCAM06 force field) and b) 2a (GAFF).

Figure 4.

Representation of the exo‐syn, non‐exo, exo‐anti conformers for: compound 1a (A) and compound 2a (B).

A similar analysis was performed with 2a. However, in this case, the MD simulation of the carbasugar mimic, (Figure 3b) performed with the GAFF force field since GLYCAM06 does not contain parameters for carbasugars, suggested that the molecule is much more flexible, with a major contribution of the non‐exo form, which is not present in the natural compound. There is also a larger flexibility around Ψ torsion as evidenced in Figure 3b.

The energy profile for 1a around φ for the most stable Ψ value (–60°) was then evaluated quantum mechanically with B3LYP/6‐31++G(d,p) to estimate the relative stability of the different conformers. The relative energies and derived populations calculated for the three possible staggered rotamers are given in Table 1. In agreement with the MD simulations, the exo‐syn conformer is highly stabilized with respect to the non‐exoanomeric orientation for a natural sugar 1a, while for a carbasugar mimic 2a the contribution of the non‐exo form is greater. The exo‐anti geometry, which is highly destabilized due to steric hindrance (Figure 4), presents a high level of energy for both molecules. On the other hand, the quantum mechanics QM calculations for 2a showed that the exo‐syn and non‐exo conformations display very similar energy values (Table 1).

Table 1.

Relative energies (ΔE, in kcal mol^–1) and populations (%, in parentheses) at 298 K between the three staggered conformations around Φ: exo‐syn, non‐exo and exo‐anti conformations calculated with B3LYP/6‐31++g(d,p) for the natural compound 1a and its carba‐glycomimetic 2a

Conformation	ΔE (pop)	ΔE (pop)
	1a	2a
exo‐syn	0 (98 %)	1.5 (7 %)
non‐exo	2.3 (2 %)	0 (93 %)
exo‐anti	7.1 (0 %)	5.8 (0 %)

These theoretical predictions were validated through experimental NMR measurements obtained for 1c. Different NMR experiments (¹H, ¹H {³¹P}, ¹H‐³¹P COSY, ¹³C{¹H}, HSQC) were performed to obtain the key NMR parameters with conformational information that could be compared to the predictions. Special attention was paid to obtain the scalar coupling constants (J) defining the conformation around φ and Ψ torsion angles (Figure 2).

In particular the ³ J _H1,P, ³ J _P,C2, and ² J _P,C1 values were determined (Table 2) to deduce the preferred geometry of the glycosidic linkage around φ. The comparison between the experimental J‐couplings and the values calculated for the three conformations of 1a demonstrated that the exo‐syn conformation (Figure 4) is highly predominant for 1c in solution. In particular, ³ J _H1,P and ³ J _C2,P showed a clear preference for this geometry. The geminal ² J _P,C1 is also consistent with a major exo‐syn conformation.

Table 2.

Theoretical (calculated for 1a) and experimental (measured for 1c) J couplings (in Hz) for the three staggered orientations around φ. The theoretical values were calculated through the GIAO method at the B3LYP/6‐31++g(d,p) level. The agreement between the expected values for the exo‐syn conformer and the experimental values is remarkable. See also Figure S1

	3 J H1,P	3 J P,C2	2 J P,C1
Experiment (1c)	7.7	8.9	5.5
Calculated for exo‐syn (1a)	6.6	9.0	6.9
Calculated for non‐exo (1a)	0.9	0.4	3.3
Calculated for exo‐anti (1a)	19	4.2	12.3

A similar analysis was performed with the carba‐analogue 2c. The comparison between the experimental values for ³ _JH1,P, ³ J _P,C2, and ² J _P,C1 with those calculated quantum mechanically for the three considered conformations of 2a (Table 3) allowed defining the population of the different conformers of 2c in solution. Fittingly, in this case, the data supported the existence of two equal populations for the exo‐syn and non‐exo conformers around φ dihedral angle (Figure 4).

Table 3.

Theoretical (calculated for 2a) and experimental (measured for 2c) J‐couplings (in Hz) for the three staggered orientations around φ. The theoretical values were calculated through the GIAO method at the B3LYP/6‐31++g(d,p) level. See also Figure S4

	3 J PC,5′	3 J P,C2	2 J P,C1
Experiment (2c)	3.1	3.8	4.8
Calculated for 50 % exo‐syn + 50 % non‐exo (2a)	3.4	4.1	4.9
Calculated for exo‐syn (2a)	0.5	7.5	0.6
Calculated for non‐exo (2a)	6.3	0.8	9.2

The estimation fully agrees with the lack of exo‐anomeric stabilization for the carba‐analogue. In the absence of stereoelectronic effects, the expected steric interactions (Figure 4 and Figure S7) are fairly similar for the two possible orientations around φ.

The Conformation of the Natural Analogues 1b and 1d and Their Mimetics 2b and 2d (C6‐Phosphates)

The analysis of the 1.5 µs MD simulation performed for 1b (Figure 5a) using the GLYCAM06 force field indicated that this compound is rather rigid in terms of ω/θ. As expected for a natural sugar (Scheme 3), the dominant ω value corresponds to the gauche‐gauche (gg) conformation around C5–C6. For θ, there is a major conformation at ca. –120 °, while the anti geometry (180 °) is also present as a minor conformer, with certain flexibility around the corresponding minima (Figure 5a).

Figure 5.

ω/θ plots derived from 1.5 µs MD simulations in explicit water for a) 1b (GLYCAM06 force field) and b) 2b (GAFF).

Scheme 3.

Schematic representation of the gg, gt and tg orientations around the ω dihedral angle (ω = O5–C5–C6–O6) in a model α‐mannosamine molecule.

The analysis of the results of the long (1.5 µs) MD simulation for the carba‐analogue 2b (Figure 5b), performed using the GAFF force field, showed a conformational mixture of the gauche‐gauche (gg) and gauche‐trans (gt) orientations, with a very minor population of the trans‐gauche (tg) conformer, as indicated by the values ω (Figure S8). However, for θ, the anti‐geometry value is now the only populated conformational family.

The energy profile for 1b and 2b around ω for most stable θ value (–120° for 1b and 180° for 2b) was then evaluated quantum mechanically with B3LYP/6‐31++g(d,p) to estimate the relative stability of the different conformers. The relative energies and derived populations calculated for the three possible staggered rotamers (Figure S2 in the Supporting Information) of 1b and carba‐analogue 2b are given in Table 4. The DFT results also support that the gg conformer is highly stabilized with respect to the gt and tg orientations.

Table 4.

Relative energies (ΔE, in kcal mol^–1) and populations (%, in parentheses) at 298 K between the 3 staggered conformations around ω:gg, gt and tg conformations calculated with B3LYP/6‐31++g(d,p) for the natural compound 1b and its carba‐mimetic 2b

Conformation	ΔE [kcal/mol]	ΔE [kcal/mol]
	1b	2b
gg	0 (100 %)	0 (100 %)
gt	6.2 (0 %)	4.6 (0 %)
tg	14.2 (0 %)	4.5 (0 %)

Again, these theoretical results obtained for natural sugar 1b and carba‐analogue 2b were compared to those obtained through experimental NMR for compound 1d and carba‐analogue 2d, respectively. For 1d, in addition to the previously described NMR experiments, a J‐resolved experiment was performed to get key NMR parameters with conformational information. In particular, ³ J _H5,H6a and ³ J _H5,H6b values define ω, while ³ J _H6a,P, ² J _H6b,P, and ³ J _C5,P are related to θ torsion angle. The comparison between these experimental values with those estimated from DFT calculations for the 3 major conformers of 1b (Table 5) allowed assessing the existence of the gg rotamer as the sole conformation in solution for 1d. Regarding θ, the NMR spectroscopic data permitted to define that its major conformation corresponds to the anti form (θ = 180 °), while the eclipsed one (θ = 120 °) is also present in a minor amount.

Table 5.

Theoretical (1b) and experimental (1d) J couplings for the three major orientations of ω (³ J _H5,H6a,b) and θ (³ J _H6a,6bP, ³ J _C5,P) angles. The theoretical values have been calculated with B3LYP/6‐31++g(d,p) basis set and GIAO method. See also Figures S2 and S3

	3 J H5,H6a	3 J H5,H6b
Experiment (1d)	2.1	3.1
DFT calculation for gg (1b)	1.4	3.1
DFT calculation for gt (1b)	1.7	8
DFT calculation for tg (1b)	8.5	3.4
	3 J H6a,P	2 J H6b,P	3 J C5,P
Experiment (1d)	3	4.5	7.5
Calc. for 80 % anti + 20 % eclipsed (1b)	3.6	4.2	7.6
Calculated for θ 180 ° (1b)	1.8	2.2	9
Calculated for θ –120 ° (1b)	11	12	2

For compound 2d, the comparison between the experimental ³ J _H5,H6a and ³ J _H5,H6b values with those calculated quantum mechanically for 2b (Table 6) indeed supported the theoretical predictions and suggested populations in solution of around 60 % for gg and 40 % for gt for ω, respectively (Figure 6). Regarding θ (Table 7), the experimental data permitted to define that the populations in solution are 50 % of the anti geometry (θ = 180 °) and 50 % of the eclipsed one (θ = 120 °). Therefore, the mimetic molecules are rather flexible and may show a large variety of presentations to interact with the key receptors, including those present in the natural molecules.

Table 6.

Theoretical (calculated for 2b) and experimental (measured for 2d) J‐couplings (in Hz) for the three staggered orientations around ω. The theoretical values were calculated through the GIAO method at the B3LYP/6‐31++g(d,p) level. See also Figure S5

	3 J H5,H6a	3 J H5,H6b
Experiment (2d)	2.7	5.2
Calculated for 60 % gg + 40 % gt (2b)	2.9	5.1
Calculated for gg (2b)	2.4	2.2
Calculated for gt (2b)	3.8	9.6
Calculated for tg (2b)	9.5	4

Figure 6.

Different perspectives of the major conformation predicted for a natural trisaccharide, built by extension of the major exo‐anomeric conformers found for the natural monomers. On the right handside, a surface representation is provided indicating the presentation of the polar phosphate groups (in color orange) and apolar (in color green and white) methyl moieties.

Table 7.

Theoretical (calculated for 2b) and experimental (measured for 2d) J‐couplings (in Hz) for the three staggered orientations around θ. The theoretical values were calculated through the GIAO method at the B3LYP/6‐31++g(d,p) level. See also Figure S6

	3 J H6a,P	2 J H6b,P	3 J C5,P
Experiment (2d)	5	5.2	8
Calcd. for 50 % eclipsed + 50 % anti (2b)	5	5.2	5
Calculated for θ 180 ° (2b)	2.3	< 1	7.9
Calculated for θ –120 ° (2b)	7.8	9.4	2.1

Modelling of the Carba Trimer

For the natural monosaccharide (related to 1c), the extension of the major exo‐anomeric geometry leads to the trisaccharide structure shown in Figure 6. In this conformation, amphipathic presentation of alternative polar and lipophilic moieties would confer to the trimer a structure compatible with a helical arrangement with a pitch of six residues (Figure 7). In particular, both the polar phosphate groups and the nonpolar methyl moieties of the acetamide substituents, responsible of this amphiphilic character, are exposed to the solvent. Therefore, this alternate presentation of polar and nonpolar patches in the trisaccharide epitope may allow it to interact with the proper receptor architecture. The non‐natural carba‐analogue may also present a similar geometry (Figure 8), although given the presence of non‐exo‐anomeric conformers, more extended structures might also be present (see Figure S3 in the Supporting Information). Obviously, given the higher flexibility of the non‐natural oligosaccharide, the selection of the required conformer for receptor binding would impose a certain entropy penalty in the putative recognition process. However, given the small energy barriers among conformers, the unfavorable energy consequences for the use of the mimetic molecule would probably be largely overcome by the improved stability of the molecule provided by the carba motif.

Figure 7.

Schematic representation of a putative natural nonasaccharide, built by extension of the exo‐anomeric conformer. The amphiphilic molecule adopts a helix‐like structure, with a similar orientation every 6 residues. That is, the pyranose rings of 7, 8, and 9 adopt a similar presentation compared to 1, 2, and 3. In any case, the dynamic character of this structure should be highlighted.35

Figure 8.

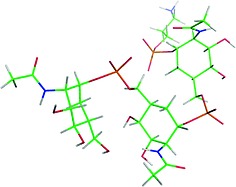
View of the major conformation predicted for a mimetic trisaccharide, built by extension of the exo‐anomeric conformer. This geometry resembles that predicted for the natural molecule. Obviously, given the intrinsinc flexibility of the different linkages of this molecule, the expected existence of this conformer is significantly smaller than that for the natural analogue.

Conclusions

Given the chemical and enzymatic lability of the phosphodiester linkages of the linear capsular homopolysaccharide of Neisseria meningitidis A, the corresponding carba analogues have been synthesized and studied as sugar mimics.5, 7, 8 In the present study, we have investigated the conformational behavior of the natural monosaccharide component of MenA CPS and its carbasugar mimetic, by using a combination of theoretical calculations and NMR spectroscopic experiments, using the chemically synthesized 1‐ or 6‐phophorylated mannosamines and their carba‐analogues as chemical probes. The data indicate that the natural sugar presents a well‐defined conformation around the different torsional degrees of freedom, especially at the glycosidic and lateral C5–C6 chain. In addition, we have observed that, given the absence of the anomeric effect, the 1‐ and 6‐phospho carba mannosamines display a higher conformational flexibility at the key pseudoglycosidic and aglyconic torsions compared to the native counterparts. Most importantly, one of the existing geometries corresponds to that adopted by the natural monomer. This result supports the capability of the carba mannosamine phosphate analogues to behave as conformational mimics of the natural MenA monosaccharide unit.

Experimental Section

Molecular Dynamics Simulations

The calculations were performed on 1a, 1b, 2a, 2b. Molecular Dynamics (MD) simulations were performed using the AMBER1219 with ff12SB and GLYCAM06j20 force fields for the natural saccharides (1a and 1b) and ff12SB and GAFF1121 for the carbasugar analogues (2a and 2b). Long MD simulations between 500 ns and 1.5 µs were employed to access to the conformational and dynamic information of these molecules. Additionally, MD simulations in water with the GLYCAM06 force field for performed the natural trimer and with the GAFF11 force field for the corresponding glycomimetic.

As first step, 1a and 1b were built using the GLYCAM carbohydrate builder web tool.22 The parameters and partial atomic charges for 2a and 2b were calculated with the antechamber module, using the GAFF force field and the AM1‐BCC method for estimating the atomic charges.23

The phosphate linkers were added using the xleap module of AMBER12 and the parameters and partial atomic charge were calculated with the antechamber module (derived from the DNA phosphodiester bond). Then, the resulting geometries were extensively minimized using conjugate gradients and then taken as starting structures for the MD simulations in explicit solvent. The molecules were solvated in a theoretical box of explicit TIP3P waters and the solute atoms were positioned at least at 10 Å from the solvent box edge. The equilibration phase consisted on energy minimization of the solvent followed by an energy minimization of the entire system without restraints. The system was then heated up to 300 K during 100 ps followed by 2 ns dynamics at constant temperature of 300 K, controlled by the Langevin thermostat, and constant pressure of 1 atm.

During the simulations, the SHAKE algorithm24 was turned on and applied to all hydrogen atoms. A cut‐off of 8 Å for all nonbonded interactions was adopted. An integration time step of 2 fs was employed and periodic boundaries conditions were applied throughout. During all simulations, the particle mesh Ewald (PME) method was used to compute long‐range electrostatic interactions.25, 26, 27, 28 Minimization, equilibration and production phases were carried out by the pmemd.cuda29, 30, 31 module of AMBER 12, while the analyses of the simulations were performed using cpptraj module from AMBERTOOLS 12. Data processing and 2D plots were carried out using GNUplot software.

Quantum Mechanical Calculations: The Gaussian 09 program32 as used for all DFT calculations. Geometries were optimized using the B3LYP33, 34 functional and the 6‐31++g(d,p) basis set with the IEF‐PCM implicit solvent model. Electronic energies were used to derive the energy profiles around different dihedral angles of interest (φ, ψ, and θ) Scalar coupling constants were computed for all the possible conformations (exo‐syn, non‐exo, and exo‐anti around φ and gg, gt, and tg around ω) using the GIAO method.

NMR Spectroscopic Experiments: All NMR spectroscopic data were acquired at 300 K with Avance 600 MHz spectrometers (Bruker) equipped with BBI probes. NMR samples (5 mm) were prepared in the sodium phosphate buffer (20 mm, pH 7.0) in D₂O. Spectra were processed and analyzed with TOPSPIN 2.0 (Bruker) software.

Supporting information

Supporting Information