Abstract
A fraction of chronic hepatitis C patients treated with direct‐acting antivirals (DAAs) achieved sustained virological responses (SVR), or cure, despite having detectable viremia at the end of treatment (EOT). This observation, termed EOT +/SVR, remains puzzling and precludes rational optimization of treatment durations. One hypothesis to explain EOT +/SVR, the immunologic hypothesis, argues that the viral decline induced by DAAs during treatment reverses the exhaustion of cytotoxic T lymphocytes (CTLs), which then clear the infection after treatment. Whether the hypothesis is consistent with data of viral load changes in patients who experienced EOT +/SVR is unknown. Here, we constructed a mathematical model of viral kinetics incorporating the immunologic hypothesis and compared its predictions with patient data. We found the predictions to be in quantitative agreement with patient data. Using the model, we unraveled an underlying bistability that gives rise to EOT +/SVR and presents a new avenue to optimize treatment durations. Infected cells trigger both activation and exhaustion of CTLs. CTLs in turn kill infected cells. Due to these competing interactions, two stable steady states, chronic infection and viral clearance, emerge, separated by an unstable steady state with intermediate viremia. When treatment during chronic infection drives viremia sufficiently below the unstable state, spontaneous viral clearance results post‐treatment, marking EOT +/SVR. The duration to achieve this desired reduction in viremia defines the minimum treatment duration required for ensuring SVR, which our model can quantify. Estimating parameters defining the CTL response of individuals to HCV infection would enable the application of our model to personalize treatment durations.
Keywords: Bistability, EOT+/SVR, mathematical model, sustained virological response, viral dynamics
Introduction
The treatment of chronic hepatitis C virus (HCV) infection is undergoing a paradigm shift with the long‐standing combination of pegylated interferon and ribavirin (PR) being replaced by direct‐acting antiviral agents (DAAs).1 Whereas PR required 24–48 weeks of therapy and cured about 50% of chronic HCV patients treated, DAA combinations elicit nearly 100% cure with 12 weeks or less of therapy.2 Significant efforts are ongoing now to reduce the duration of treatment with DAAs without compromising treatment outcomes.3, 4 Indeed, treatments as short as 3 weeks have been shown to succeed in select populations.4 A promising avenue for such reduction arises from the observation, made by several recent studies, that some patients treated with DAAs had detectable viremia at the end of treatment (EOT) but eventually attained a sustained virological response (SVR), or cure, without additional therapy.3, 5, 6, 7, 8, 9, 10, 11, 12 (Typically, SVR refers to undetectable viremia 12 weeks after the EOT.) For instance, in one study where 240 patients were treated with DAAs for 12 weeks, of the 86 patients available for follow‐up, 22 had detectable viremia at the EOT and 20 of the latter patients eventually achieved SVR.12 This observation is in striking contrast to PR treatment, where detectable viremia at the EOT typically implies treatment failure and results in viral rebound.13 The achievement of SVR despite detectable viremia at the EOT, a phenomenon termed EOT+/SVR, suggests that DAA treatments can be terminated much earlier than the currently prescribed duration of 12 weeks, even if virus is detectable, at least in some patient subpopulations. The benefits of reduced costs and toxicities are expected to be tremendous.14 Identifying suitable patient subpopulations and the corresponding reduced treatment durations requires an understanding of the mechanism(s) by which DAA treatments lead to EOT+/SVR.
Two hypotheses have been proposed to explain EOT+/SVR.9 According to the first hypothesis, termed the “virologic” hypothesis, DAAs are argued to render virions produced from infected cells increasingly non‐infectious, to a point where the virions detected at the EOT are incapable of establishing a sustained infection. The residual, predominantly non‐infectious virions would be cleared eventually, leading to SVR. Evidence for this hypothesis comes from studies that show a reduction in viral infectivity following exposure to DAAs, including a preferential targeting of infectious over non‐infectious virion production by some DAAs.15, 16, 17 Furthermore, mathematical models of viral kinetics that account for this mode of DAA action have been constructed and shown to describe data of viral load changes during therapy in patients who experience EOT+/SVR, as well as SVR rates elicited by certain DAA combinations.18, 19 The hypothesis, however, remains to be established conclusively. In patients who achieve EOT+/SVR, the virions detectable at the EOT are yet to be shown to be predominantly non‐infectious. The limit of detection with the current assays is 1–10 IU mL−1,3 which implies the presence of >104–105 virions, given the 15 L of fluid in an average human, at the EOT in patients displaying EOT+/SVR. SVR is thought to be achieved when the viral level reaches the “cure boundary” of 1 virion in 15 L.20, 21 A reduction in viral load of 4–5 log10 is thus necessary to achieve SVR following the EOT, which may require several weeks or more given the rate of viral load decline at the EOT.18, 19 The half‐life of DAAs is 1–2 days,22 indicating that the reduction occurs largely in the absence of DAAs. That any new virions produced from infected cells in the absence of DAAs past the EOT are also predominantly non‐infectious remains to be established.
The second hypothesis, termed the “immunologic” hypothesis, argues that treatment with DAAs lowers viral levels, which reverses the exhaustion of effector CD8+ T cells (CTLs) induced by chronic exposure to viral antigen, thereby allowing the immune system to clear the residual virus after the EOT. Multiple lines of evidence support this hypothesis: Ex vivo studies demonstrate increased exhaustion of CTLs in chronic HCV patients pre‐treatment compared to uninfected individuals and a reduction of this exhaustion accompanied by improved proliferative capacity and functionality of HCV‐specific CTLs during treatment.23, 24, 25 Interferon treatment is unable to induce this reversal,26 explaining the absence of EOT+/SVR with PR treatment, barring a few exceptions.27, 28, 29, 30 When the percentage of hepatocytes infected was reduced below a threshold, exhausted CTLs regained their functionality in a mouse model of HCV infection.31 Anti‐PD‐1 therapy, which prevents or reverses CTL exhaustion, has shown some success in HCV‐infected primates and humans.32, 33 Unlike the virologic hypothesis, however, whether the immunologic hypothesis is consistent with patient data of viral load changes during DAA treatments is unknown. No model of viral kinetics based on the immunologic hypothesis has yet been constructed.
In this study, we constructed a model of viral kinetics based on the immunologic hypothesis, examined its ability to describe published patient data, and assessed its implications for shortening treatment durations. Models of viral kinetics have been used widely to describe viral load changes in patients during treatment, have provided key insights into disease progression and guided treatments.21 Existing models, including the recent extensions based on the virologic hypothesis,18, 19 have focused primarily on describing the impact of drugs. The influence of the immune system in controlling HCV infection is rarely considered explicitly. Models of CTL dynamics and exhaustion have been constructed previously in the context of other chronic infections.34, 35, 36, 37 For instance, CTL exhaustion in chronic HIV‐1 infection and its reversal during antiretroviral treatment that leads to lasting post‐treatment control but not clearance of infection in a subset of infected individuals has recently been described using a mathematical model.36 Here, we integrated a formalism of CTL exhaustion, drawn from the latter models, with a basic model of HCV kinetics to elucidate the immunologic hypothesis underlying EOT+/SVR. We found that our model recapitulates data of viral load changes in patients experiencing EOT+/SVR, identifies an underlying bistability in the system as the origin of EOT+/SVR, and presents an avenue, exploiting the bistability, to estimate the minimum DAA treatment durations required to achieve SVR.
Results
Mathematical model
We constructed a model of HCV kinetics in a chronically infected individual under DAA therapy with CTL dynamics governed by the immunologic hypothesis (Figure 1). The following equations described the ensuing dynamics and predicted viral load changes in the individual during and after therapy:
| (1) |
| (2) |
| (3) |
| (4) |
Figure 1.
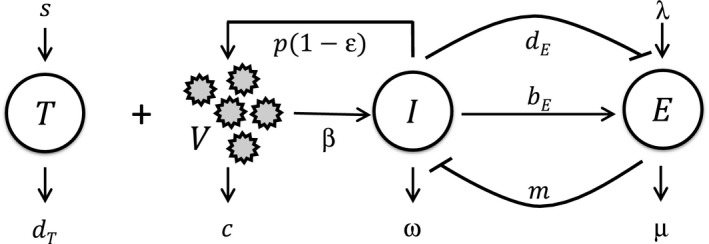
Schematic of the model. Target cells, T, are infected by free virions, V, to yield infected cells, I, which produce new virions. Treatment with DAAs lowers this production of new virions. I activate effector cells, E, which in turn control I. I, however, can also suppress E by inducing their exhaustion. The model parameters and equations governing the ensuing dynamics are described in the text.
Here, following the basic model of HCV kinetics,21 we let target cells, T, be produced at the rate s and lost with a first order rate constant d T. Free virions, V, infect target cells with the second order rate constant β, yielding infected cells, I. In the absence of treatment, infected cells produce virions at the rate p per cell. DAAs lower p by the factor 1‐ε(t), where ε(t) is the efficacy of treatment at time t following the start of treatment. For simplicity, we assumed that the efficacy is constant during treatment and rapidly vanishes after the EOT, so that ε(0 ≤ t ≤ τ d) = ε and ε(t>τ d) = 0, where τ d is the treatment duration. Virions are cleared with the rate constant c. Infected cells are killed by HCV‐specific CTLs, E, with the second order rate constant m. The loss of infected cells by mechanisms independent of E is assumed to occur with the first order rate constant ω. To describe CTL dynamics, we followed previous studies,34, 36 where CTLs are assumed to be produced at the rate λ and are lost with the first order rate constant μ. They are activated by contact with infected cells with the second order rate constant b E. This activation is saturable and is half‐maximal when I equals k B. Sustained stimulation or stimulation with high levels of antigen induces CTL exhaustion, which we described using a Hill function with the second order rate constant d E, the exponent n, and the half‐maximal value k D. As I increases from values much smaller to much larger than k D, the level of exhaustion rises from minimal to maximal. The larger the value of n, the sharper this rise is around k D.
The equations above present a model of HCV kinetics that incorporates the essential features of the immunologic hypothesis underlying EOT+/SVR. Incorporating additional features such as target and infected cell proliferation or cumulative antigenic stimulation leading to exhaustion did not alter our results (Supplementary text 1, Supplementary text 2, Supplementary figure 1, and Supplementary figure 2).
The immunologic hypothesis and EOT+/SVR
To examine whether the immunologic hypothesis yielded EOT+/SVR, we solved the above model equations with parameter values representative of chronic HCV patients (Table 1; Methods) and predicted viral load changes during and after therapy. We found that the model yielded EOT+/SVR (Figure 2). The viral load declined in a biphasic manner during therapy (Figure 2a), as observed in patients.10, 11 From the classical analysis of the basic model of viral kinetics,21, 38, 39 the first phase is attributed to the decreased production of virions from infected cells due to drug action, which destroys the pre‐treatment balance between viral production and clearance (pI 0 = cV 0) in the chronic phase of infection. The second phase is attributed to the resulting loss of infected cells (Figure 2b). Viral production and clearance are estimated to be fast relative to infected cell production and loss, leading to a pseudo steady state between virion and infected cell populations in the second phase [p(1‐ε)I ≈ cV].
Table 1.
Parameters and their values
| Parameter | Meaning | Value [95% CI] | Source | |
|---|---|---|---|---|
| s | Target cell production rate | 105 cells mL−1 day−1 | 14, 18 | |
| d T | Target cell death rate | 0.01 day−1 | 39 | |
| β | Infectivity | 1 × 10−8 mL cells−1 day−1 | 14, 18, 51 | |
| ω | Natural death rate of infected cells | 0.01 day−1 | ω = d T | |
| λ | Effector cell recruitment rate | 1 cells mL−1 day−1 | 36 | |
| b E | Antigen‐induced proliferation rate of effector cells | 1 day−1 | ||
| μ | Death rate of effector cells | 2 day−1 | ||
| k B | Hill function scaling for effector cell proliferation | 103 cells mL−1 | 35, 36 | |
| n | Hill coefficient for exhaustion | >1 | ||
| p | Production rate of virions by infected cells | 4.4 virions cell−1 day−1 |
|
|
| m | Killing rate of infected cells by effector cells | 0.244 mL cells−1 day−1 |
|
|
| δ | Death rate of infected cells | 0.059 [0.026–0.092] day−1 | Best‐fits (Figure 3a)a | |
| ε | Efficacy of drugs | 0.9991 [0.9988–0.9994] | ||
| c | Viral clearance rate | 6.3 [5.8–6.8] day−1 | ||
| d E | Antigen‐induced exhaustion rate of effector cells | 4 day−1 | ||
| k D | Hill function scaling for effector cell exhaustion | 2.7 × 104 cells mL−1 |
For the patient in Figure 3b, δ = 0.2 day−1, d E = 6 day−1, k D = 1.95 × 103 cells mL−1, p = 35.7 virions cell−1 day−1, and m = 1.36 mL cells−1 day−1.
Figure 2.
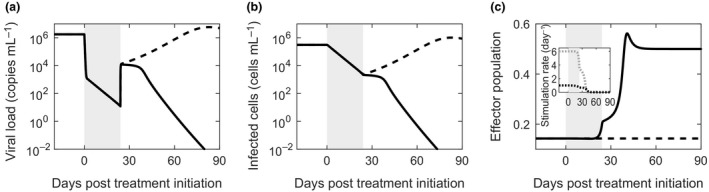
Model prediction of EOT +/SVR. Changes in (a) the viral load, (b) the infected cell population and (c) the effector population in a chronically infected individual as a function of time from the start of treatment with DAAs predicted by our model with (solid) and without (dashed) the immunologic hypothesis. The rates of activation (black dotted) and exhaustion (gray dotted) of effector cells, defined by the second and third terms on the right‐hand side of Equation (4), respectively, corresponding to the case with the immunologic hypothesis are shown in the inset in c. The treatment duration is shaded. The parameter values employed are in Table 1 and correspond to those in Figure 3b.
Following the EOT, drug action ceased and viral production from infected cells was restored to its pre‐treatment rate. The pseudo steady balance between viral production and clearance was again lost, but now in the opposite sense, leading to a surge in viremia. An “inverse” of the first phase decline thus resulted. A new pseudo steady state of virion and infected cell populations was established at a much higher viremia corresponding to the increased viral production rate from infected cells (pI ≈ cV).
The subsequent dynamics was determined by the CTL response. During treatment, in accordance with the immunologic hypothesis, the reduction in viremia resulted in an increase in the CTL population (Figure 2c). Note that in our model, as in previous formalisms,35, 36 the variable E is a scaled variable, allowing a compact representation of the net effect of CTLs subsuming the CTL population size and the level of CTL exhaustion. For simplicity, we refer to E as the CTL population. The product mE represents the rate of killing of infected cells by CTLs, where m links E to absolute rates of infected cell death. As we show below, the value of mE we estimate is consistent with independent estimates of CTL killing of infected hepatocytes. The increase in the CTL population above was due to a reduction in the rate of CTL exhaustion (Figure 2c, inset). The increased CTL population during treatment turned out to be sufficient not to let the increase in viremia past the EOT be long‐lasting. CTL action steadily controlled viremia past the EOT (Figure 2a), further reducing the level of exhaustion (Figure 2c, inset). Eventually, the competition between CTL activation and exhaustion by infected cells was resolved in favor of activation, resulting in a significant rise in the CTL pool (Figure 2c). This larger CTL pool destroyed the infected cell population (Figure 2b), causing a sharp decline in viremia and eventually leading to SVR (Figure 2a). As the infection was cleared, the CTL population declined and reached a new steady state corresponding to the level in the absence of infection and exhaustion (Figure 2c). (Note that immunological memory is not explicitly considered in this model, in keeping with extant models of CTL exhaustion.34, 36)
To confirm the influence of the immunologic hypothesis in our predictions of EOT+/SVR, we solved the model equations also in the absence of the immunologic hypothesis. Here, the CTL population was held fixed at the pre‐treatment level (E = E 0) and no reversal of exhaustion was allowed. The model effectively reduced to the basic model of viral kinetics.21 The viral level rose after the EOT and eventually reached pre‐treatment levels, marking the failure of treatment (Figure 2a–c, dashed lines).
Comparisons of model predictions with patient data
We next compared model predictions to data of viral load changes in two patients who achieved EOT+/SVR following DAA‐based therapy of ultra‐short durations10, 11 (see Methods). We assumed that the restoration of exhausted CTLs was negligible in the short period during therapy (~3 weeks) and fit the resulting reduced, basic model of viral kinetics to the data during therapy. The best‐fit predictions described patient data well (Figure 3). (Sensitivity analysis indicated that parameter estimation could be done robustly; see Supplementary figure 3). The best‐fit parameter values (Table 1) are consistent with previous estimates. For instance, the viral clearance rate, c = 6.3 day−1, is close to the reported38 average of 6.2 ± 1.8 day−1; the drug efficacy, ε = 0.9991, is consistent with the mean of 0.997 estimated for sofosbuvir‐based treatments14, 18; and the death rate of infected cells, δ = 0.06 day−1 and 0.2 day−1 for the two patients, is in the range of values, 0.01–0.4 day−1, reported earlier.20
Figure 3.
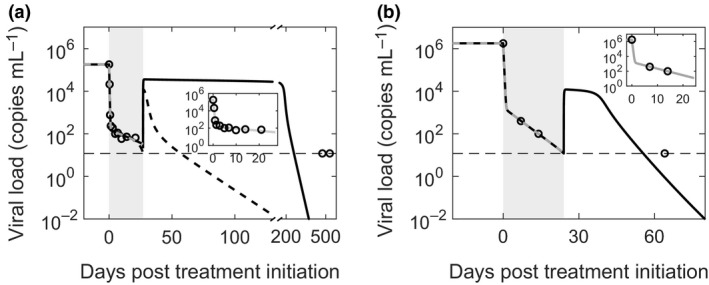
Comparisons with patient data. Model predictions (solid lines) compared with data (symbols) from two patients, shown separately in a and b, who achieved EOT +/SVR (see text for details of the patients). The best‐fits to the data during therapy are shown superimposed (gray dashed lines) and in expanded view (insets). The best‐fit parameter estimates and their 95% CIs are as follows: (a) δ = 0.059 (0.026–0.091) day−1, ε = 0.9991 (0.9988–0.9994), and c = 6.3 (5.8–6.8) day−1. These yielded p = 4.4 virions cell−1 day−1 and m = 0.24 mL cells−1 day−1. The minimal values of dE = 4 per day and kD = 2.67 × 104 cells mL −1 (see Methods) yielded SVR just before the last measured time point (solid line). The low second phase slope (δ = 0.059 day−1), implying weak effector killing of infected cells, and the long gap between the EOT and the last measurement yielded best‐fit parameters that predicted high viremia over extended durations past the EOT, which may be unrealistic. A low second phase slope may also arise due to infected cell proliferation despite strong effector killing. A model that included cell proliferation (Supplementary text 1; Supplementary figure 1) captured the data well and resulted in rapid viral load reduction past the EOT leading to SVR within a few weeks (dashed line). During the period under treatment, predictions of the two models are indistinguishable. (b) δ = 0.204 (0.200–0.208) day−1. ε = 0.9991 and c = 6.3 day−1 were the same as in a. These yielded p = 35.7 virions cell−1 day−1 and m = 1.36 mL cells−1 day−1. Furthermore, dE = 6 day−1 and kD = 1.95 × 103 cells mL −1 were the minimal estimates. The limit of detection is shown as a thin dashed line. The other parameter values employed are in Table 1.
We then estimated parameters defining CTL exhaustion as those that yielded EOT+/SVR for the treatment duration employed but not any shorter, ensuring that viremia became undetectable in the predictions within the timeframe reported clinically. With these limiting estimates of the parameters, our model predictions were consistent with the patient data (Figure 3). The predictions during therapy were indistinguishable from those of the basic model, justifying our assumption above. Furthermore, from the estimates of m (Table 1) and the evolution of E, the rate of loss of infected cells due to CTL killing, mE, we estimated was in the range 0.04–0.16 day−1 and 0.2–0.8 day−1 for the two patients, respectively, which was similar to the rate, 0.14 ± 0.21 day−1, estimated independently from an analysis of acute infection in chimpanzees.40 Model predictions thus described viral load changes during treatment and the observed EOT+/SVR quantitatively. The immunologic hypothesis was thus consistent with patient data.
Bistability and the origin of EOT+/SVR
The EOT+/SVR phenomenon was sensitive to model parameters. For instance, reducing m, the strength of the CTL response, while keeping all other parameters fixed, resulted in viral rebound and treatment failure (Figure 4a). Similarly, reducing k D resulted in viral rebound (Figure 4b). For parameter values that led to viral rebound, increasing the treatment duration restored EOT+/SVR (Figure 4c). The divergent outcomes, viral rebound or SVR, realized with subtle variations in model parameter values or treatment duration implied the existence of bistability in the system.
Figure 4.
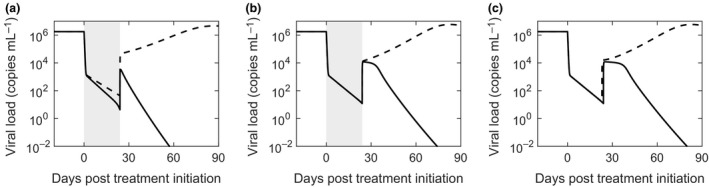
Dependence of EOT +/SVR on parameter values. Model predictions of viral load changes under conditions leading to EOT +/SVR (solid lines) and treatment failure (dashed lines). (a) m = 1.5 mL cells−1 day−1 (solid) and m = 1 mL cells−1 day−1 (dashed); (b) kD = 2 × 103 cells mL−1 (solid) and 1 × 103 cells mL−1 (dashed); (c) m = 1.36 mL cells−1 day−1; τ d = 24 days (solid) and 23 days (dashed). The treatment period is shaded in a and b. The other parameter values employed are in Table 1 corresponding to Figure 3b.
To elucidate the bistability, we solved our model equations at steady state in the absence of treatment (ε = 0). We explored the resulting states as functions of m, with all the other parameters constant. We found that when m was low, less than ~0.07 mL cells−1 day−1, a single stable steady state with high viremia, ~106 copies mL−1, marking chronic infection, existed (Figure 5a). The corresponding effector population was low, marking significant exhaustion (Figure 5b). (Linear stability analysis is presented in Supplementary text 3 and Supplementary figure 4.) When m was between ~0.07 and ~0.27 mL cells−1 day−1, the system exhibited two stable steady states, chronic infection with high viremia and viral clearance. The effector population was low in the first and high in the second. The stable states were separated by an unstable steady state with intermediate viremia of ~104 copies mL−1 and an intermediate effector population. For very high values of m, greater than ~0.27 mL cells−1 day−1, the system was again monostable with viral clearance the only admissible steady state. The corresponding effector population reflected the steady state CTL level in the absence of infection.
Figure 5.
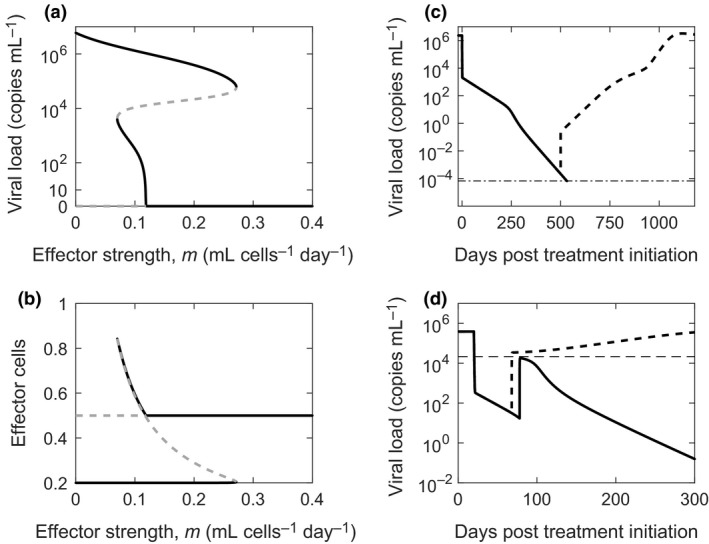
Bistability and treatment outcomes. Bifurcation diagrams indicating stable (black) and unstable (gray) steady state viral loads (a) and effector cell populations (b) as functions of the strength of the effector response, m. Viral load changes during and after therapy when m = 0.055 mL cells−1 day−1 (c) and m = 0.2 mL cells−1 day−1 (d). In c, τ d = 500 days (dashed line) and 552 days (solid line). The thin dot‐dashed black line marks the cure boundary. In d, τ d = 48 days (dashed line) and 58 days (solid line). The thin dashed line marks the unstable steady state viral load when m = 0.2.
We note that over a narrow range of values m, ~0.07 to ~0.12 mL cells−1 day−1, a low viremic stable state arose instead of complete viral clearance. Whether this is akin to the low viremia seen in some patients following SVR with PR treatment41 or a consequence of not incorporating other arms of the immune response, such as NK cells, in our model, remains to be established. Parameter values can be identified that preclude the low viremic state in our model (Supplementary figure 5). Note that viremia became undetectable after ~8 years in all the patients with low viremia after SVR barring one who had a reinfection with a different strain of HCV.41 Here, we therefore assumed that the low viremic state also represented viral clearance.
Treatment could drive the system from the chronic infection state to clearance. When m was small and the system monostable, treatment had to last till the virus was completely cleared, i.e., viremia crossed the cure boundary. Any residual viremia at the EOT would lead to viral rebound and treatment failure. For instance, with m = 0.055 mL cells−1 day−1, ending treatment even after the viremia was reduced to ~10−4 copies mL−1 led to viral rebound and treatment failure (Figure 5c). Here, EOT+/SVR was not possible. In contrast, when the system was bistable, treatment had to last long enough to drive viremia past the intermediate unstable state to a point where upon cessation of therapy the surge in the viremia due to the inverse first phase did not allow the viremia to cross the unstable boundary again. The system would then spontaneously clear the virus without the need for any treatment. This behavior marked EOT+/SVR. For instance, with m = 0.2 mL cells−1day−1, treatment of 48 days led to the inverse first phase allowing viremia to increase above the unstable boundary of 2.15 × 104 copies mL−1, leading to viral rebound and treatment failure, whereas treatment of 58 days kept viremia below the unstable boundary and led to EOT+/SVR (Figure 5d). The observed EOT+/SVR thus originated from the bistability intrinsic to the system. At the highest values of m, chronic infection was not admissible, potentially representing individuals who mount strong CTL responses and spontaneously clear HCV.42
The minimum required treatment duration
The calculations above indicated that the minimum treatment duration to achieve EOT+/SVR was that required to drive viremia past the intermediate steady state and contain it below the boundary soon after treatment cessation. We solved our model equations to estimate this requisite treatment duration as a function of m and k D. Note that although we varied m above to illustrate bistability, variations in other model parameters could also yield bistability. Here, we considered k D additionally, as it was one of the parameters that modulated the level of CTL exhaustion. We varied m and k D over ranges that encompassed values that described the patient data in Figure 3. All the other parameters, including the treatment efficacy, were kept at the values corresponding to the patients. Recall that the patients achieved SVR following 27 days and 24 days of therapy, respectively. With the first patient (Figure 3a), as m was lowered, the required treatment duration increased (Figure 6a). Higher values of m, marking higher CTL killing rates, required shorter durations. Similarly, decreasing k D, which worsened CTL exhaustion, required longer treatment durations, and vice versa (Figure 6a). We repeated the calculations with parameter values corresponding to the second patient above (Figure 3b), and found the same qualitative behavior (Figure 6b). The treatment durations were different, however, for the two cases, even with the same values m and k D, reflecting differences in the other parameters between the two patients.
Figure 6.
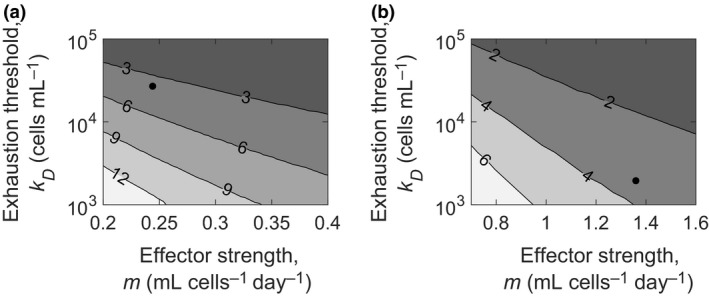
Minimum required treatment duration. Contour plots of model predictions of the minimum treatment duration required in weeks to achieve SVR as functions of the parameters m and kD with the other parameters representative of the patient data in (a) Figure 3a and (b) Figure 3b. The parameter values defining the patients are shown as black dots.
Thus, given a set of parameter values representing an individual, our model can be applied to estimate the minimum duration of treatment required to achieve EOT+/SVR.
Discussion
An understanding of the intriguing EOT+/SVR phenomenon holds promise not only of unraveling new insights into our immune response to HCV, and to pathogens in general, but also of defining new limits on the required durations of DAA treatments. In this study, we constructed a mathematical model of viral kinetics based on the proposed immunologic hypothesis underlying EOT+/SVR and found that it recapitulated the EOT+/SVR phenomenon and data of viral load changes in patients treated with DAAs who experienced EOT+/SVR. Importantly, the model predicted that EOT+/SVR originated from the bistability intrinsic to the dynamical system governing the interactions between the virus, target cells, infected cells and effector cells in an infected individual. Furthermore, it showed how, exploiting this bistability, the minimum treatment duration required to realize EOT+/SVR can be estimated, presenting an avenue for systematically reducing DAA treatment durations from the current guidelines.
The bistability of the system arose at intermediate strengths of the effector cell response to the infection. When the response was very strong, chronic infection was not established, with the sole steady state marking the clearance of infection. This behavior may be reminiscent of those individuals who clear the infection spontaneously. Strong CTL responses have been implicated in spontaneous clearance,43 which happens in an average of ~26% of infected individuals.42 When the response was very weak, chronic infection with high viremia was the only steady state possible. Individuals with this behavior may represent those who experience viral rebound after the EOT, whether viremia was detectable at the EOT or not. Cure is possible in such individuals when treatment lasts until viremia drops below the cure boundary. With intermediate strengths of the effector response, both chronic infection and viral clearance became stable steady states separated by an unstable steady state with intermediate viral load. EOT+/SVR would result in such patients when treatment drives viremia from the chronic state to below the unstable intermediate state to a point that does not allow resurgence past the unstable boundary following the EOT. The system then spontaneously reaches the stable state of viral clearance. The time it takes for treatment of a given efficacy to achieve the desired reduction in viremia defines the minimum duration for which the treatment must be administered.
The extent of the rise in viremia soon after the EOT can be estimated. The pseudo steady states of viral production and clearance just before and after the EOT imply that the fold‐increase in viremia soon after the EOT would be 1/(1‐ε), where the treatment efficacy ε is readily estimated from early viral kinetics following the start of therapy. The rise in viremia post‐treatment by the factor 1/(1‐ε) has been recognized earlier using the basic model of viral kinetics in the context of PR treatment assuming a constant target cell population.44 Whether the resulting viremia would lie above or below the intermediate unstable boundary is more difficult to predict because the boundary is less well estimated. The boundary depends on parameters defining CTL activation and exhaustion dynamics as well as the strength of the CTL response, which remain difficult to measure or estimate. In our model, these would be the parameters m in Equation (2) and b E, k B, d E, k D and n in Equation (4). Measurements that allow estimation of these latter parameters would enable the application of our model to specify the unstable boundary and hence define personalized treatment durations. A confounding factor is that measurements of HCV‐specific CTL levels in the blood may not be representative of the effector response in the liver.45 CTL‐induced infected cell death rates have been estimated previously by analyzing measurements of serum alanine aminotransferase levels during acute infection in chimpanzees.40 Future studies may reveal whether such measurements during the treatment of chronic infection in humans bear signatures of the reversal of exhaustion and hence can be analyzed to estimate the unknown parameters above. The fraction of patients treated who achieve EOT+/SVR appears to vary widely across treatments and patient populations.3, 5, 6, 7, 8, 9, 10, 11, 12 Weak effector responses and/or inadequate treatment durations may underlie the inability of patients to achieve EOT+/SVR compared to those who do in the latter reports. Again, future studies that may quantify the inter‐patient variations in CTL dynamics and response may help explain the wide variations in the fraction of patients achieving EOT+/SVR in the reports above.
By showing that the immunologic hypothesis is consistent with patient data of viral load changes, our study adds an important missing piece to the evidence gathered so far in support of the hypothesis.23, 24, 25, 31, 32, 33 Our study, however, does not negate the alternative, virologic hypothesis. Indeed, the two hypotheses are not mutually exclusive. To evaluate the consistency of the immunologic hypothesis with patient data, we constructed a model that considered the latter hypothesis alone and showed that it was able to capture the same patient data that was captured by a model based on the virologic hypothesis.18 While a model can be constructed readily that incorporates both the hypotheses, patient data in addition to viral load changes during therapy, such as viral infectivity or the strength of the effector cell response, may be required to distinguish between the hypotheses. The relative extents to which the two hypotheses contribute to EOT+/SVR remains unknown. Delineating the contributions of the two hypotheses in patients undergoing different DAA‐based treatments would lead to a more comprehensive description of EOT+/SVR as well as more accurate estimates of the minimum required treatment duration for specific DAA combinations.
EOT+/SVR has been achieved recently in a patient treated with DAAs during the acute phase of infection,46 where CTL exhaustion may not have set in to the same extent as in the chronic phase of infection. Whether this adds to the evidence in support of the virologic hypothesis or whether sufficient CTL exhaustion had set in by the start of treatment, which was 9 weeks after infection, for the immunologic hypothesis to hold in the patient remains unknown. Similarly, EOT+/SVR has also been reported in some individuals treated with PR.27, 28, 29, 30 Interferon is argued to have a pleiotropic influence on CTLs, enhancing their proliferation and activation in the early stages of infection and rendering them more exhausted during the late stages of infection.47 Indeed, early initiation of PR treatment has been suggested to improve treatment outcomes.48 Furthermore, blockade of interferon signaling during chronic LCMV infection of mice has been shown recently to clear the infection.49, 50 Whether a critical time following infection exists within which the start of PR therapy does not exacerbate CTL exhaustion remains to be ascertained. Low level viremia has been shown to persist for several years in patients successfully treated with PR, arguing further for a role of the immune system in effecting a complete cure of HCV infection.41
Our model employed several simplifying assumptions. First, following the basic model of viral kinetics,21 DAA efficacy was assumed to be constant during therapy. Pharmacokinetic effects and the accumulation of resistance‐associated mutations,51 which would result in a time‐varying drug efficacy, were not considered. Furthermore, DAAs may have multiple modes of antiviral action,52 which we ignored. Second, we considered the simplest model of CTL dynamics that includes antigen‐driven activation and exhaustion. The description has been employed successfully to explain the post‐treatment control of HIV‐1 infection.36 More sophisticated models that incorporate the dependence of exhaustion on sustained antigenic stimulation have been proposed,35, 37 but have been argued to have similar qualitative features as the simpler model employed here.36 Third, studies have argued that in addition to CTL function, NK cell function is restored during IFN‐free DAA therapy,53 which we did not consider. Finally, we did not consider viral evolution leading to immune escape, which may underlie cases such as with the one patient who showed detectable viremia at the EOT, achieved undetectable viremia at week 4 past the EOT, but relapsed at week 12 past the EOT.9 Our aim was to construct a model that captured the essential features leading to EOT+/SVR according to the immunologic hypothesis and compare its predictions with patient data, which the above simplifications did not compromise.
In summary, our study elucidates the origin of EOT+/SVR based on the immunologic hypothesis, describes patient data of viral load changes, and presents an avenue to define minimum DAA treatment durations. Quantifying the extent to which the immunologic hypothesis contributes to EOT+/SVR with different DAA combinations, a promising avenue for future studies, would facilitate the identification of optimal durations of DAA‐based treatments.
Methods
Parameter estimates and solution of model equations
We employed the following parameter estimates (Table 1). Following previous studies, we set the target cell production and loss rates to s = 105 cells mL−1 day−1 and d T = 0.01 day−1, corresponding to a target cell population in an uninfected individual of 107 cells mL−1,14, 18, 39 and the infection rate of target cells, β = 10−8 mL cell−1 day−1.14, 18, 51 We let the death rate of infected cells other than by CTL killing be the same as the natural death rate of target cells, neglecting any HCV‐induced cytopathicity; thus, ω = d T. We let the CTL production, death and activation rates be λ = 1 cell mL−1day−1, μ = 2 day−1, b E = 1 day−1 and k B = 103 cells mL−1.35, 36 The viral production and clearance rates, p and c, the drug efficacy, ε, the strength of CTL killing, m, and the parameters governing CTL exhaustion, d E, k D and n, are expected to vary across individuals. We estimated them by comparisons of model predictions with patient data (see below). We ensured that k D > k B to let CTL exhaustion occur at higher antigen levels than CTL activation. We solved model equations in MATLAB with initial conditions marking the pre‐treatment steady state, obtained by setting the left‐hand sides of all the equations to zero. We examined the sensitivity of our model predictions to parameter variations by computing partial rank correlation coefficients54 (Supplementary figure 3).
Patient data
We considered published data of viral load changes in two patients who experienced EOT+/SVR with ultra‐short DAA‐based treatments.10, 11 The same data have been employed in a recent modeling study based on the virologic hypothesis.18 One patient received treatment with sofosbuvir and ribavirin for 27 days.10 The last reported viral load measurement during therapy was at day 21 from the start of therapy, when viremia was detectable. The patient was then lost to follow up until day 475, when viremia was reported undetectable. The second patient was treated with a combination of peritaprevir, ombitasvir, dasabuvir plus ritonavir and ribavirin for 24 days.11 The last reported viral load measurement during therapy was at day 14 from the start of therapy, when viremia was detectable. At the first measurement past the EOT, at day 64 from the start of therapy, viremia was undetectable and remained so for over 7 months past the EOT. Data was digitized using the Engauge digitizer.
Comparisons of model predictions with patient data
The number of unknown parameters was too large to fit our model directly to the data. We therefore employed the following procedure. The treatments of the two patients were ultra‐short, lasting < 4 weeks. We assumed that during this period, the effector population, E, remained approximately equal to its pre‐treatment value, E 0. Equation (4) above could then be ignored, reducing the model to the basic model of HCV kinetics. Fitting the reduced model to patient data from one patient10 during treatment then allowed estimation of ε, c, and the composite parameter δ = ω + mE 0. With the other patient,11 because of infrequent sampling, we set ε and c to the values obtained above, which were similar to the values estimated elsewhere,18 and fit the data using δ as an adjustable parameter. We performed data fitting using the function NLINFIT in MATLAB.
We estimated the remaining parameters as follows. The pre‐treatment steady state implied that T 0 = s/(d T+βV 0), I 0 = βV 0 T 0/δ, p = cV 0/I 0 and from Equations (1), (2), (3), (4). Knowledge of the pre‐treatment viral load, V 0, thus allowed estimation of T 0, I 0 and p from the first three relationships above. The fourth relationship allowed defining E 0 as a function of the unknown exhaustion parameters, d E, k D and n. Note that because δ = ω + mE 0, this implied that m was also defined as a function of the latter three parameters. Many combinations of these latter parameters were likely to yield admissible solutions of our equations. Data of viral load changes past the EOT were not available to define these parameters uniquely. To restrict choices, we let n = 3, a value used previously.36 (Using n = 1, also used previously,36 did not alter the stability properties; see Supplementary figure 5.) We then identified minimal estimates of d E and k D such that EOT+/SVR was achieved with the administered treatment duration and no shorter and the viremia became undetectable within the timeframe reported. For this, we first fixed d E = 2 day−1, also employed previously,36 and solved model equations (Equations (1), (2), (3), (4)) for different values of k D and identified the smallest value of k D for which the administered treatment duration yielded SVR within 3000 days. We picked 3000 days as an upper bound for SVR based on previous studies where low level viremia was detected with sensitive assays up to 8 years after having received successful PR treatment.41 If this was not possible for any value of k D, we increased d E and repeated the above procedure until the latter criterion was satisfied. We then assumed higher values of d E and repeated the above exercise until we found parameters where viremia became undetectable on the same timescale but before the first reported time point past the EOT for the two patients. We examined how model predictions of viral load changes during treatment compared with patient data to ensure consistency with the best‐fit parameters identified above. Note that parameters defining CTL exhaustion during HCV infection remain unknown. Our goal was not to estimate the latter parameters precisely, but instead to examine whether the immunologic hypothesis was consistent with data of viral load changes in patients experiencing EOT+/SVR.
Bistability and the estimation of the minimum required treatment duration
We found roots of the nonlinear algebraic equations corresponding to the steady states of the model equations when ε = 0 for a range of values of the parameters quantifying CTL effector function and exhaustion. Root finding was done using Mathematica. In particular, we explored the influence of m and constructed a bifurcation diagram to illustrate the steady states of the system. We performed linear stability analysis to assess the stability of the steady states. We identified parameter regimes where two stable states, chronic infection and viral clearance, were separated by an unstable intermediate steady state. Treatment that allowed crossing the unstable boundary from the chronic infection state and ensured that viremia stayed across the boundary following the cessation of treatment would yield EOT+/SVR. Next, using parameter values spanning the above regimes, we solved model equations (Equations (1), (2), (3), (4)) with ε > 0 for different treatment durations τ d. For each parameter combination, we identified the minimum τ d required to yield EOT+/SVR within 3000 days of the start of treatment. SVR was defined as achieved when the viral load dropped below the cure boundary of 1 virion in 15 L.
Conflict of Interest
The authors declare that they have no conflicts of interest.
Supporting information
Acknowledgments
This work was supported by the Wellcome Trust/DBT India Alliance Senior Fellowship IA/S/14/1/501307 (NMD) and the Wellcome Trust/DBT India Alliance Intermediate Fellowship IA/I/13/1/500901 (RR). We thank Pranesh Padmanabhan, Rajat Desikan and Rubesh Raja for comments.
References
- 1. World Health Organization . Guidelines for the screening care and treatment of persons with chronic hepatitis C infection. Geneva. 2016. [PubMed]
- 2. Horner SM, Naggie S. Successes and challenges on the road to cure hepatitis C. PLoS Pathog 2015; 11: e1004854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Kohli A, Osinusi A, Sims Z, et al Virological response after 6 week triple‐drug regimens for hepatitis C: a proof‐of‐concept phase 2A cohort study. Lancet 2015; 385: 1107–1113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Lau G, Benhamou Y, Chen G, et al Efficacy and safety of 3‐week response‐guided triple direct‐acting antiviral therapy for chronic hepatitis C infection: a phase 2, open‐label, proof‐of‐concept study. Lancet Gastroenterol Hepatol 2016; 1: 97–104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Sarrazin C, Wedemeyer H, Cloherty G, et al Importance of very early HCV RNA kinetics for prediction of treatment outcome of highly effective all oral direct acting antiviral combination therapy. J Virol Methods 2015; 214: 29–32. [DOI] [PubMed] [Google Scholar]
- 6. Sidharthan S, Kohli A, Sims Z, et al Utility of hepatitis C viral load monitoring on direct‐acting antiviral therapy. Clin Infect Dis 2015; 60: 1743–1751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Harrington PR, Deming DJ, Komatsu TE, et al Hepatitis C virus RNA levels during interferon‐free combination direct‐acting antiviral treatment in registrational trials. Clin Infect Dis 2015; 61: 666–667. [DOI] [PubMed] [Google Scholar]
- 8. Maasoumy B, Vermehren J, Welker MW, et al Clinical value of on‐treatment HCV RNA levels during different sofosbuvir‐based antiviral regimens. J Hepatol 2016; 65: 473–482. [DOI] [PubMed] [Google Scholar]
- 9. Malespin M, Benyashvili T, Uprichard SL, et al Prevalence of end of treatment RNA‐positive/sustained viral response in HCV patients treated with sofosbuvir combination therapies. Therap Adv Gastroenterol 2017; 10: 68–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Meissner EG, Nelson A, Marti M, et al Sustained virologic response for chronic hepatitis C infection after 27 days of treatment with sofosbuvir and ribavirin. Open Forum Infect Dis 2014; 1: 013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Hasin Y, Shteingart S, Dahari H, et al Hepatitis C virus cures after direct acting antiviral‐related drug‐induced liver injury: case report. World J Hepatol 2016; 8: 858–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Hezode C, Chevaliez S, Scoazec G, et al P0843: on‐treatment viral kinetics do not predict SVR in patients with advanced liver disease receiving sofosbuvir in combination with daclatasvir or simeprevir for 12 weeks. J Hepatol 2015; 62: S654–S655. [Google Scholar]
- 13. Ferenci P, Laferl H, Scherzer TM, et al Peginterferon alfa‐2a and ribavirin for 24 weeks in hepatitis C type 1 and 4 patients with rapid virological response. Gastroenterology 2008; 135: 451–458. [DOI] [PubMed] [Google Scholar]
- 14. Dahari H, Canini L, Graw F, et al HCV kinetic and modeling analyses indicate similar time to cure among sofosbuvir combination regimens with daclatasvir, simeprevir or ledipasvir. J Hepatol 2016; 64: 1232–1239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Sansone N, Dahari H, Subramanya G, et al Modeling HCVcc infection reveals new insights into the dynamics that maintain the in vitro HCV steady state and the mechanisms of action of the NS5A inhibitor daclatasvir. Hepatology 2014; 60: 1165A. [Google Scholar]
- 16. McGivern DR, Masaki T, Williford S, et al Kinetic analyses reveal potent and early blockade of hepatitis C virus assembly by NS5A inhibitors. Gastroenterology 2014; 147: 453–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Liu D, Ji J, Ndongwe TP, et al Fast hepatitis C virus RNA elimination and NS5A redistribution by NS5A inhibitors studied by a multiplex assay approach. Antimicrob Ag Chemother 2015; 59: 3482–3492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Goyal A, Lurie Y, Meissner EG, et al Modeling HCV cure after an ultra‐short duration of therapy with direct acting agents. Antivir Res 2017; 144: 281–285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Nguyen THT, Guedj J, Uprichard SL, et al The paradox of highly effective sofosbuvir‐based combination therapy despite slow viral decline: can we still rely on viral kinetics? Sci Rep 2017; 7: 10233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Dixit NM, Layden‐Almer JE, Layden TJ, et al Modelling how ribavirin improves interferon response rates in hepatitis C virus infection. Nature 2004; 432: 922–924. [DOI] [PubMed] [Google Scholar]
- 21. Perelson AS, Guedj J. Modelling hepatitis C therapy–predicting effects of treatment. Nat Rev Gastroenterol Hepatol 2015; 12: 437–445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. German P, Mathias A, Brainard D, et al Clinical pharmacokinetics and pharmacodynamics of ledipasvir/sofosbuvir, a fixed‐dose combination tablet for the treatment of hepatitis C. Clin Pharmacokinet 2016; 55: 1337–1351. [DOI] [PubMed] [Google Scholar]
- 23. Martin B, Hennecke N, Lohmann V, et al Restoration of HCV‐specific CD8 + T cell function by interferon‐free therapy. J Hepatol 2014; 61: 538–543. [DOI] [PubMed] [Google Scholar]
- 24. Barrett L, Shivasabesan G, Wang C, et al Altered HCV specific T cell immunity very early in interferon free HCV DAA therapy. J Hepatol 2013; 58: S1. [Google Scholar]
- 25. Shrivastava S, Wilson E, Poonia B, et al Augmentation of hepatitis C virus‐specific immunity and sustained virologic response. J Viral Hepat 2017; 24: 742–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Maini MK, Schurich A. Direct‐acting antivirals trump interferon‐alpha in their capacity to rescue exhausted T cells upon HCV clearance. J Hepatol 2014; 61: 459–461. [DOI] [PubMed] [Google Scholar]
- 27. Denis J, Rautou PE, Lambare B, et al Chronic hepatitis C: viral clearance several months after discontinuation of therapy in two non‐responders. Infection 2007; 35: 197. [DOI] [PubMed] [Google Scholar]
- 28. Annicchiarico BE, Siciliano M, Avolio AW, et al A 5‐year prospective study of the late resolution of chronic hepatitis C after antiviral therapy. Aliment Pharmacol Ther 2007; 25: 1039–1046. [DOI] [PubMed] [Google Scholar]
- 29. Cho SH, Lee SW, Choi SR, et al Delayed viral clearance of chronic hepatitis C in patients after treatment failure. Gut Liv 2011; 5: 110–114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Sato A, Ishii T, Adachi K, et al Delayed viral clearance after 6‐week treatment with peginterferon plus ribavirin in a patient with chronic hepatitis C virus genotype 1b. Case Rep Gastroenterol 2016; 10: 417–422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Tay SS, Wong YC, McDonald DM, et al Antigen expression level threshold tunes the fate of CD8 T cells during primary hepatic immune responses. Proc Natl Acad Sci USA 2014; 111: E2540–E2549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Fuller MJ, Callendret B, Zhu B, et al Immunotherapy of chronic hepatitis C virus infection with antibodies against programmed cell death‐1 (PD‐1). Proc Natl Acad Sci USA 2013; 110: 15001–15006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Gardiner D, Lalezari J, Lawitz E, et al A randomized, double‐blind, placebo‐controlled assessment of BMS‐936558, a fully human monoclonal antibody to programmed death‐1 (PD‐1), in patients with chronic hepatitis C virus infection. PLoS ONE 2013; 8: e63818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Bonhoeffer S, Rembiszewski M, Ortiz GM, et al Risks and benefits of structured antiretroviral drug therapy interruptions in HIV‐1 infection. AIDS 2000; 14: 2313–2322. [DOI] [PubMed] [Google Scholar]
- 35. Johnson PLF, Kochin BF, McAfee MS, et al Vaccination alters the balance between protective immunity, exhaustion, escape, and death in chronic infections. J Virol 2011; 85: 5565–5570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Conway JM, Perelson AS. Post‐treatment control of HIV infection. Proc Natl Acad Sci USA 2015; 112: 5467–5472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Bocharov GA. Modelling the dynamics of LCMV infection in mice: conventional and exhaustive CTL responses. J Theor Biol 1998; 192: 283–308. [DOI] [PubMed] [Google Scholar]
- 38. Neumann AU, Lam NP, Dahari H, et al Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon‐α therapy. Science 1998; 282: 103–107. [DOI] [PubMed] [Google Scholar]
- 39. Padmanabhan P, Garaigorta U, Dixit NM. Emergent properties of the interferon‐signalling network may underlie the success of hepatitis C treatment. Nat Commun 2014; 5: 3872. [DOI] [PubMed] [Google Scholar]
- 40. Dahari H, Major M, Zhang X, et al Mathematical modeling of primary hepatitis C infection: noncytolytic clearance and early blockage of virion production. Gastroenterology 2005; 128: 1056–1066. [DOI] [PubMed] [Google Scholar]
- 41. Veerapu NS, Raghuraman S, Liang TJ, et al Sporadic reappearance of minute amounts of hepatitis C virus RNA after successful therapy stimulates cellular immune responses. Gastroenterology 2011; 140: 676–685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Micallef JM, Kaldor JM, Dore GJ. Spontaneous viral clearance following acute hepatitis C infection: a systematic review of longitudinal studies. J Viral Hepat 2006; 13: 34–41. [DOI] [PubMed] [Google Scholar]
- 43. Abdelwahab SF. Cellular immune response to hepatitis‐C‐virus in subjects without viremia or seroconversion: is it important? Infect Ag Cancer 2016; 11: 23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Dahari H, Lo A, Ribeiro RM, et al Modeling hepatitis C virus dynamics: liver regeneration and critical drug efficacy. J Theor Biol 2007; 247: 371–381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Steinert EM, Schenkel JM, Fraser KA, et al Quantifying memory CD8 T cells reveals regionalization of immunosurveillance. Cell 2015; 161: 737–749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Shteyer E, Dahari H, Gafanovich I, et al End of treatment RNA‐positive/sustained viral response in an individual with acute hepatitis C virus infection treated with direct‐acting antivirals. Therap Adv Gastroenterol 2017; 10: 429–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Odorizzi PM, Wherry EJ. An interferon paradox. Science 2013; 340: 155–156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48. Kamal SM, Fouly AE, Kamel RR, et al Peginterferon alfa‐2b therapy in acute hepatitis C: impact of onset of therapy on sustained virologic response. Gastroenterology 2006; 130: 632–638. [DOI] [PubMed] [Google Scholar]
- 49. Teijaro JR, Ng C, Lee AM, et al Persistent LCMV infection is controlled by blockade of type I interferon signaling. Science 2013; 340: 207–211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50. Wilson EB, Yamada DH, Elsaesser H, et al Blockade of chronic type I interferon signaling to control persistent LCMV infection. Science 2013; 340: 202–207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51. Rong L, Dahari H, Ribeiro RM, et al Rapid emergence of protease inhibitor resistance in hepatitis C virus. Sci Transl Med 2010; 2: 30ra2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. Guedj J, Dahari H, Rong L, et al Modeling shows that the NS5A inhibitor daclatasvir has two modes of action and yields a shorter estimate of the hepatitis C virus half‐life. Proc Natl Acad Sci USA 2013; 110: 3991–3996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53. Serti E, Chepa‐Lotrea X, Kim YJ, et al Successful interferon‐free therapy of chronic hepatitis C virus infection normalizes natural killer cell function. Gastroenterology 2015; 149: 190–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54. Marino S, Hogue IB, Ray CJ, et al A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol 2008; 254: 178–196. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


