Abstract
Substitution by generic drugs is allowed when bioequivalence to the originator drug has been established. However, it is known that similarity in exposure may not be achieved at every occasion for all individual patients when switching between formulations. The ultimate aim of our research is to investigate if pharmacokinetic subpopulations exist when subjects are exposed to bioequivalent formulations. For that purpose, we developed a pharmacokinetic model for gabapentin, based on data from a previously conducted bioavailability study comparing gabapentin exposure following administration of the gabapentin originator and three generic gabapentin formulations in healthy subjects. Both internal and external validation confirmed that the optimal model for description of the gabapentin pharmacokinetics in this comparative bioavailability study was a two‐compartment model with absorption constant, an absorption lag time, and clearance adjusted for renal function, in which each model parameter was separately estimated per administered formulation.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Interchange of bioequivalent formulations can for an individual still result in high ratios for AUC and/or Cmax, outside the 80.00–125.00% margin.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ We are investigating those individual deviations by pharmacokinetic modeling and simulation, to challenge the appropriateness of the current bioequivalence requirements in regulatory approval of drugs.
WHAT THIS STUDY ADDS TO OUR KNOWLEDGE
☑ A pharmacokinetic model of four different gabapentin formulations was developed and validated, which could aid in the research into the interchangeability of generics.
HOW THIS MIGHT CHANGE CLINICAL PHARMACOLOGY OR TRANSLATIONAL SCIENCE
☑ Ultimately, our research could lead to increased trust in the use of generic medicines, either by confirming the appropriateness of the bioequivalence assessment, or by identifying issues for potential process improvement.
Generic medicines are drugs comparable to their originator counterparts, containing similar amounts of active substance(s). Generic drugs can only be marketed when pharmaceutical comparability to the originator has been demonstrated and the patent of the originator has expired. Financial investment for the development of generic drugs is markedly lower as compared to that for development of a new active substance medicinal product (i.e., originator drug), as there is no need to repeat the studies on safety and efficacy of the active substance. Therefore, generic drugs are usually sold for lower prices, generally resulting in healthcare cost savings.
About 80% of all pharmacy‐filled prescriptions in the United States are filled with generic drugs.1 In Europe, market shares of generic drugs may differ between countries.2 In the Netherlands, 72.4% of all drug prescriptions in 2015 were for generic drugs, while these accounted only for 16.5% of total drug‐associated costs.3 If available in the Netherlands, 97.1% of the prescriptions are filled with generic drugs. This high percentage in the Netherlands is presumably partly a result of the way health insurance companies execute national law and in the case of drug shortages, pharmacists are often forced to substitute with other equivalent (generic) drugs.4, 5
Registration of generic drugs requires proof of bioequivalence to the originator. If generic drugs contain an equal amount of active substance(s), proof of bioequivalence can be provided by statistically confirmed comparable bioavailability. Bioequivalent formulations are subsequently expected to demonstrate essentially similar efficacy and safety under identical circumstances.
Even though evidence for clinical inequivalence could not be identified for cardiovascular and antiepileptic drugs,6, 7, 8 a large portion of patients and healthcare professionals have doubts regarding quality, safety, and efficacy of generic drugs and hold a negative opinion towards generic drug substitution.9 For instance, in the field of epilepsy many issues regarding seizure control are reported and various clinical guidelines recommend to avoid generic drug substitution.10
To demonstrate bioequivalence, usually a randomized crossover study with pharmacokinetic endpoints is conducted, comparing two formulations, of which one is the originator. Bioequivalence is confirmed when 90% confidence intervals (CIs) of the geometric mean ratios for area under the curve (AUC) and peak concentration (Cmax) are within prespecified limits, which are normally 80.00 to 125.00%, as for instance described in the “guideline on the investigation of bioequivalence” by the European Medicines Agency (EMA)11 and the draft guidance “bioequivalence studies with pharmacokinetic endpoints for drugs submitted under an ANDA” by the US Food and Drug Administration (FDA).12 The bioequivalence approach, however, is based on average values and only accounts partially for the variation observed for an individual's pharmacokinetic parameters. In theory, high ratios for AUC and/or Cmax outside the 80.00–125.00% margin could be observed upon administration of different formulations in a single individual, even though these formulations were proven to be bioequivalent. Ultimately, we want to investigate those individual deviations and to challenge the appropriateness of the current bioequivalence requirements in regulatory approval of drugs, by investigating whether pharmacokinetic subpopulations exist, demonstrating low or high ratios for AUC and/or Cmax when exposed to bioequivalent formulations of gabapentin, using a nonparametric pharmacokinetic modeling approach. The study described in this article represents the first step in which we build and validate a pharmacokinetic model for gabapentin based on pharmacokinetic data from a previously conducted comparative bioavailability study comparing gabapentin exposure following administration of the gabapentin branded formulation and three generic gabapentin formulations currently marketed in the Netherlands.
RESULTS
In the first step of the modeling, four different structural models were considered. By addition of a Tlag (lag time) in the one‐compartment with absorption constant model, the Akaike Information Criterion (AIC) decreased (–219) (Table 1). Likelihood of the model with a second compartment was higher compared to the one‐compartment model; the AIC was reduced (AIC from 3802 to 3669). Model fit further improved with the Tlag introduced in the two‐compartment model, with no significant changes in bias and precision. Overall, a reduction of the AIC of 233 was observed by introduction of the second compartment and Tlag parameters. Based on AIC, bias and precision, as well as the visual predictive checks (VPCs), it was concluded that a two‐compartment model with addition of Tlag best explained the observed data. The regression equation of the observed vs. the predicted concentration is y = 0.997x + 0.0295 with an R2 of 0.887 (bias: –0.0194 and imprecision: 0.851).
Table 1.
Model selection statistics
| Model | Parameters | AIC | ΔAIC | Bias | Imprecision |
|---|---|---|---|---|---|
| Structural models | |||||
| 1 comp + Ka | Ka, V, Ke | 3802 | 0.0018 | 0.8543 | |
| 1 comp + Ka + Tlag | Ka, Tlag, V, Ke | 3583 | −219 | −0.0114 | 0.8467 |
| 2 comp + Ka | Ka, V, Ke, KCP, KPC | 3669 | −133 | 0.0103 | 0.8638 |
| 2 comp + Ka + Tlag | Ka, Tlag, V, Ke, KCP, KPC | 3569 | −233 | 0.0194 | 0.8514 |
| Level of separation | |||||
| Separation of Ka | Ka1, Ka2, Ka3, Ka4, Tlag, V, Ke, KCP, KPC | 2546 | −1023 | −0.0052 | 0.8284 |
| Separation of Tlag | Ka, Tlag1, Tlag2, Tlag3, Tlag4, V, Ke, KCP, KPC | 3576 | +7 | −0.0362 | 0.8540 |
| All parameters separated ('96 pseudo subjects') | Ka, Tlag, V, Ke, KCP, KPC | 1588 | −1981 | −0.0214 | 0.7888 |
| Covariate selection | |||||
| Weight | Ka, Tlag, V, Ke, KCP, KPC | 1613 | +25 | −0.0884 | 0.8063 |
| Renal | Ka, Tlag, V, Ke, KCP, KPC | 1585 | −3 | −0.0280 | 0.7795 |
| Weight + Renal | Ka, Tlag, V, Ke, KCP, KPC | 1600 | +12 | −0.0653 | 0.8262 |
Akaike Information Criterion (AIC), bias (mean error), and imprecision (mean squared error) are shown.
The second step in this modeling exercise was refinement to include structure with regard to the four different formulations. Based on the chosen base model (two‐compartment, Ka, Tlag) a comparison to three additional models was made. These models were 1) separation of Ka per formulation, 2) separation of Tlag per formulation, and 3) separation of all parameters (Ka, Tlag, V, KCP, KPC, and Ke) per formulation. Numerical results of this comparison are depicted in Table 1 and show that model fit was improved by allowing separate estimates for Ka per formulation but not when allowed for separation on Tlag. The likelihood of the model was strongly improved for the “pseudo subject” model, in which each parameter was independently estimated per treatment period, the AIC was reduced by 1981 (from 3569 to 1588), compared to no separation at all. Therefore, this model was chosen as the final structural model for further refinement. The regression equation of the observed vs. the predicted concentration for this model is y = 0.995x + 0.022 with an R2 of 0.98 (bias: −0.0214 and imprecision: 0.7888).
The third step in the model‐building process was covariate selection. Based on stepwise linear regressions, weight and renal function were selected as the covariates with the potential to improve model fit. Weight (mean 71.0, range 52.7–97.0 kg) was tested as a multiplicative term on V (Equation 1).
Equation 1: Weight as a multiplicative term on V.
Renal function was estimated by creatinine clearance (mean 120, range 71.2–183 ml/min), which was estimated from the serum creatinine concentration, by using the Cockcroft–Gault equation. There is no indication that gabapentin undergoes metabolism in humans. Instead, it is eliminated unchanged solely by renal excretion.13 A multiplicative term of renal function (CrCl) on the renal clearance (Kr) is therefore expected to adequately represent clearance (Ke) (Equation 2).
Equation 2: Clearance (Ke) as a multiplicative term of renal function (CrCl) on renal clearance (Kr).
From Table 1; the covariate weight as a multiplicative term on V did not significantly improve the likelihood of the model (AIC +25), indicating no significant dependency of volume of distribution on weight. However, the model fit improved with renal function correlated with gabapentin clearance by a multiplicative function of renal function on the elimination constant. An AIC reduction of 3 was computed, when renal function on elimination was included in the model. A combination of both weight on volume and renal function on clearance did not further improve model fit (AIC+ 12) relative to the model with renal function only.
Thus, the final model for description of the gabapentin pharmacokinetics in the bioequivalence study was a two‐compartment model with absorption constant, an absorption lag time, and elimination adjusted for renal function in which each model parameter was separately estimated per administered formulation (Equation 3).
Equation 3: Final model equations.
The observed vs. the predicted concentration plots are shown in Figure 1, both for the population prediction and the individual prediction. The regression equation is y = 0.995x + 0.0256 with an R2 of 0.98 (bias: –0.0280 and imprecision: 0.7795).
Figure 1.
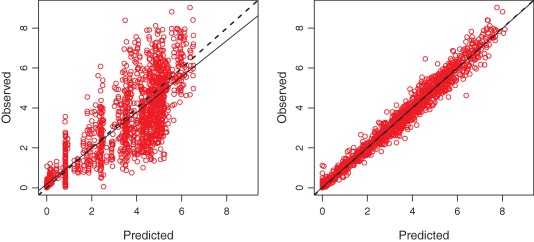
Population (left) and individual (right) predicted vs. observed values for the final two‐compartment model with absorption constant, an absorption lag time, elimination adjusted for renal function, and all parameters separately estimated per formulation, line of identity (dashed line), and linear regression (solid line). [Color figure can be viewed at http://www.cpt-journal.com]
Residual plots for the final model are shown in Figure 2. Weighted residuals demonstrate an even spread over the concentration range as well as over the time span. A slight tendency can be observed, with some underpredictions in the lower concentration range. However, as can be seen from the histogram of residuals, the majority of residuals are centered around zero. The D'Agostino–Pearson test for nonnormality tests was not significant (P = 0.587); thus, the assumption is made that the residual error follows a normal distribution.
Figure 2.
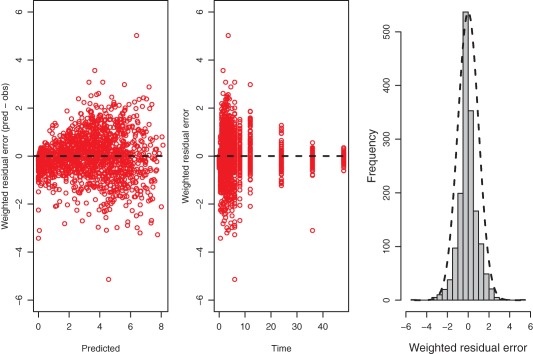
Residual plots; weighted residuals (predicted – observed) vs. predictions (left), weighted residuals (predicted – observed) vs. time (middle) and a histogram of residuals with an overlay of a normal curve (right). [Color figure can be viewed at http://www.cpt-journal.com]
A VPC was performed for the final model, as depicted in Figure 3. The scatterplot VPC with prediction intervals shows a good correlation but some added variability on the distribution and elimination phase. An overview of estimated pharmacokinetic parameters from both the observed concentrations and from predicted time‐observation profiles is provided in Table 2. Despite a small underprediction of the model concentrations (mean deviation from Cmax: 7.95%, AUC0‐t: 5.08%, AUC0‐inf: 6.23%) and some added variability on half‐life (mean ± SD, observed: 8.24h ± 2.82, predicted: 8.84 ± 10.67), no obvious deviation is observed for the parameters.
Figure 3.
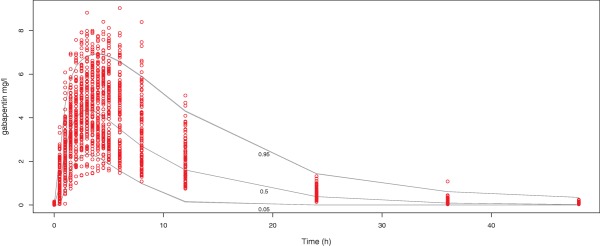
Scatterplot VPC, observed data from the study is represented in circles, prediction intervals (quantiles 0.05, 0.5, and 0.95) determined from 1,000 simulations as solid lines. [Color figure can be viewed at http://www.cpt-journal.com]
Table 2.
Noncompartmental analysis derived pharmacokinetic parameters Cmax AUC0‐t, AUC0‐inf, Tmax and T1/2 from observed concentrations and individual Bayesian posterior final model predicted time‐observation profiles, per treatment
| Formulation 1 | Formulation 2 | Formulation 3 | Formulation 4 | |
|---|---|---|---|---|
| Cmax (mg/l) observed | 5.33 ± 1.79 | 5.43 ± 1.86 | 5.48 ± 1.44 | 5.62 ± 1.65 |
| Cmax (mg/l) predicted | 4.99 ± 1.71 | 4.87 ± 1.65 | 5.11 ± 1.36 | 5.16 ± 1.52 |
| AUC0‐t (h.mg/l) observed | 63.42 ± 25.72 | 61.55 ± 24.70 | 61.16 ± 20.80 | 62.08 ± 22.91 |
| AUC0‐t (h.mg/l) predicted | 59.92 ± 24.71 | 58.87 ± 24.01 | 58.88 ± 19.83 | 57.92 ± 22.04 |
| AUC0‐inf (h.mg/l) observed | 64.49 ± 25.68 | 62.39 ± 24.68 | 62.45 ± 20.88 | 63.03 ± 23.13 |
| AUC0‐inf (h.mg/l) predicted | 60.18 ± 24.62 | 59.12 ± 23.92 | 59.02 ± 19.87 | 58.29 ± 22.01 |
| Tmax (h) observed | 4.0 (2.50‐8.0) | 4.25 (2.0‐8.0) | 3.50 (1.5‐6.0) | 3.75 (1.5‐8.0) |
| Tmax (h) predicted | 3.5 (1.8‐8.8) | 3.7 (2.2‐6.4) | 3.0 (1.6‐6.2) | 3.7 (1.6‐6.0) |
| T1/2 (h) observed | 8.12 ± 2.70 | 8.08 ± 2.08 | 9.08 ± 3.63 | 7.66 ± 2.63 |
| T1/2 (h) predicted | 7.66 ± 5.94 | 7.92 ± 6.85 | 7.53 ± 4.25 | 12.24 ± 18.81 |
All parameters are mean ± SD, but Tmax median and range.
Estimated pharmacokinetic parameter values obtained with the final model are tabulated in Table 3.
Table 3.
Estimated parameter values for the final model, weighted median, 95% confidence interval around the median (CI) and between occasion variability, % (BOV)
| Parameter | wMedian and 95% CI | BOV |
|---|---|---|
| Ka (h−1) | 0.26 (0.23–0.31) | 35% |
| Tlag (h) | 0.30 (0.21–0.35) | 75% |
| V (l) | 90.0 (83.5–106) | 34% |
| KCP (h−1) | 0.16 (0.12–0.36) | 110% |
| KPC (h−1) | 0.82 (0.30–1.69) | 68% |
| Ke (h−1) | 0.32 (0.29–0.36) | 34% |
Ke recalculated from rate per ml/min creatinine clearance.
Parameter values are summarized as median and the 95% CI around the median, as calculated by a probability‐weighted Monte Carlo simulation (n = 1,000) from the support point distribution. The between occasion variability (BOV) is calculated as the population mean from the estimates of each subjects' four pseudo subjects coefficient of variation.
External validation of the model was performed with data obtained from a separate pharmacokinetic (bioequivalence) study with an oral 800 mg gabapentin formulation which was submitted to the Medicines Evaluation Board (MEB) in support of a generic application. The nonparametric adaptive grid algorithm (NPAG) distribution from the final model was used as input (“prior”) for the external data, to construct an observed vs. predicted concentration plot, as shown in Figure 4. A high correlation can be observed, with a regression equation y = 0.925x ‐ 0.0294 with an R2 of 0.952.
Figure 4.
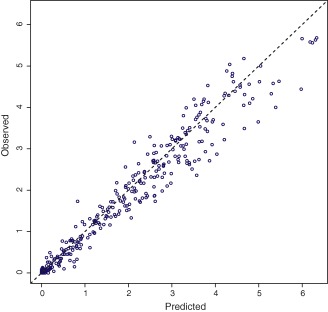
Individual predicted vs. observed values from separately obtained gabapentin validation data (800 mg bioequivalence study). [Color figure can be viewed at http://www.cpt-journal.com]
DISCUSSION
Both internal and external validation confirmed that the optimal model for description of the gabapentin pharmacokinetics in this comparative bioavailability study was a two‐compartment model with absorption constant, an absorption lag time, and clearance adjusted for renal function, in which each model parameter was separately estimated per administered formulation.
The ultimate goal of our model is to perform simulations for the identification of pharmacokinetic subpopulations or outliers with an aberrant exposure to gabapentin outside the 80.00–125.00% margin when switching between bioequivalent formulations. Since the aim of our research is to investigate the influence of formulation on bioequivalence, one could argue that our model selection was biased towards a model with parameters separately estimated per formulation. However, we used a structured method of model selection and objective assessment of the selection parameters and thereby avoid such bias. Further, by separation of all model parameters per administered formulation we chose the most naïve approach to the data. Therefore, we were able to construct the best possible model for the explanation of these data.
The rationale for the models with separation only of Ka and Tlag is based on the general assumption regarding generic drugs that only the absorption phase and not the distribution or elimination phase is influenced by possible formulation differences. However, a limitation of those models is that the parameters for the distribution and elimination phase are fixed to the same value, for each subject. This is not an adequate representative for the true values of these parameters, as natural variability between occasions is expected to be present in any study, even where subjects serve as their own controls. By allowing separation of all parameters of the absorption, distribution, and elimination phase, we allow for this interoccasion variability. An additional randomized 5th period in the gabapentin study, with a repeated administration of one of the four formulations, solely dissimilar by occasion, would have allowed computing an estimation of the true interoccasion variability directly derived from the pharmacokinetic data. With the current study design, which is the usual for regulatory establishment of bioequivalence, it is not possible to separate variability due to occasion vs. variability from formulation. However, the absence of a “true” estimation of the interoccasion variability is not necessarily a weakness of the data and the model. Within the current “pseudo subject” model, the interoccasion variability is not fixed to the amount we would have computed based on repeated administration of one formulation between two occasions. This model is without any assumptions on the interoccasion variability.
Population pharmacokinetic models can be statistically classified as parametric or nonparametric. We choose to perform nonparametric population pharmacokinetic modeling, even though it is common practice to use parametric modeling in drug development and evaluation. In drug application dossiers submitted to regulatory authorities, the parametric program NONMEM is the most frequently used. However, an advantage of the nonparametric approach is that no assumptions are made with regard to the distribution of described parameter values. Entire joint distributions with probabilities are estimated based on the data, instead of estimating a parameter mean or median (population standard value “Theta”) and deviation (individual random effect “Eta”).14 The absence of those assumptions in the nonparametric approach allows discovery of non‐prespecified subpopulations. This theoretical characteristic of nonparametric modeling was confirmed by Neely et al., by accurately detecting a bimodal elimination and one pharmacokinetic outlier.19 Considering the aim of our study, it is justified that nonparametric modeling is the most appropriate method, optimizing our chances of identifying pharmacokinetic subpopulations.
Model uncertainties
The polynomial coefficients for the error model should ideally be determined by the bioanalytical lab based on observed variation at standard concentrations. However, in the absence of detailed information about the accuracy and precision of this bioanalytical method, we estimated the error polynomial coefficients based on data from other bioanalytical gabapentin methods seen in registration files of the MEB. The chosen polynomial coefficients represent a coefficient of variation between 2.75–0.95%. The Lambda term was fitted by NPAG in the final model to be 0.2990, indicating a low amount of process noise and a well‐executed pharmacokinetic characterization.
Gabapentin has been modeled before, using a combined approach of parametric (NONMEM) and nonparametric modeling.15 The final model from this study was a one‐compartment model with a fixed absorption constant (0.44 h−1) and a nonlinear bioavailability parameter. Our final model deviates from the previously described model by the absence of a function for the absorption, an additional distribution compartment, and renal function correlated clearance. An explanation for reaching another optimal model could be the richer data input (i.e., 96 occasions of 17 blood samples each in our case vs. 25 occasions of 10 blood samples each in the previous study). In our research, nonlinearity of the bioavailability was not explored, as only one dose strength was administered. The estimated Ka in our study (median 0.26, range 0.11–1.09 h−1) was within the same extent. Another parametric model found a one‐compartment model with absorption constant (0.053–0.461 h−1) and lag time (0.48–2.29 h−1), with covariates creatinine clearance and race (Black vs. other) on gabapentin clearance and weight and population (healthy subjects vs. patients) on volume of distribution.16 Again, an explanation of the observed differences could be a richer data input compared to this study (average 1.6 samples per patient).
In addition to Ka and Tlag, a relative bioavailability term (F, proportion) was explored to be included in the model. Due to the high correlation of F with Ka and the inability to accurately estimate F in the absence of intravenous data, it was concluded to estimate Ka and treat F as a fixed (but random) population parameter, to avoid unnecessary complication of the estimated absorption. As an alternative, it was planned to estimate F as a relative term. The F could then be estimated relative to one of the formulations, but this became irrelevant with the introduction of the “pseudo subject” model.
Creatinine clearance was used to estimate renal function using the Cockcroft–Gault equation. Although validity of the estimation by Cockcroft–Gault is questioned in certain patient populations such as elderly and overweight subjects,17 we believe this is an accurate estimator for our data, which was obtained in young healthy adult volunteers with normal weight (included subject were in the age range of 21–55 years and their mean BMI was in the range of 19.9–30.0 kg/m2).
The external validation was performed using a gabapentin dataset obtained from the registration files of the MEB. In this study, no serum creatinine values were presented. To allow for a Cockcroft–Gault estimation of the creatinine clearance, average serum creatinine values (male and female) from the four‐way study were used. This was believed to be the best available estimate of renal function. With the external data, a high correlation was observed and external validation of our model could be inferred.
To conclude, gabapentin pharmacokinetic data was shown to be best described by a two‐compartment model with an absorption constant and absorption lag time, with clearance adjusted for renal function and each model parameter separately estimated per administered formulation. The final model adequately describes the observed data, does not show deviating trends in the goodness of fit diagnostics, and is in line with current pharmacokinetic gabapentin knowledge. The model as described is considered fit for further analyses and simulations. Such future simulations using the model will be aimed to identify a potential subpopulation of individual patients with increased risk for altered pharmacokinetics as a result of switching between bioequivalent formulations.
METHODS
Gabapentin pharmacokinetic data
Gabapentin pharmacokinetic data were previously gathered in a four‐way crossover comparative bioavailability study, comparing four different oral immediate release formulations of 800 mg gabapentin that were previously accepted to be bioequivalent and therefore registered by the Dutch MEB.18 In that study, 24 healthy volunteers (14 females and 10 males) were enrolled and completed the study. The mean age was 35 years (range: 21–55), mean body mass index was 23.6 kg/m2 (range: 19.9–30.0), and mean creatinine clearance 120 mL/min (range: 71.2–183.3). Gabapentin levels were measured in plasma samples, drawn predose and at 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 6, 8, 12, 24, 36, and 48 h postdosing, during each period. Adverse events and vital signs were monitored and standard laboratory evaluations were performed. Pharmacokinetic parameters Cmax AUC0‐t, AUC0‐inf, Tmax, T1/2, Kel, and AUC0‐t /AUC0‐inf were computed and an analysis of variance (ANOVA) was performed using ln‐transformed Cmax, AUC0‐t, and AUC0‐inf. The 90% CIs were calculated for Cmax, AUC0‐t, and AUC0‐inf. Bioequivalence was confirmed between all different formulations.
Model building in Pmetrics
A total of 1,610 concentration timepoints was included in the model‐building process. Nonparametric population pharmacokinetic modeling was performed using the Pmetrics package (v. 1.5; Laboratory of Applied Pharmacokinetics and Bioinformatics, Los Angeles, CA) using R (v. 3.2.2, Vienna, Austria) that uses the algebraic model solver and NPAG.19 In NPAG, four different structural base models were compared, i.e., a one‐ and a two‐compartment model with an absorption constant, both with or without an absorption lag time. For these comparisons, parameters to be estimated were absorption constant (Ka, rate, unit per hour), absorption lag time (Tlag, hours), volume of distribution (V, liter), elimination constant (Ke, rate, unit per hour), transfer rate from central to peripheral compartment (KCP, rate, unit per hour), and peripheral to central (KPC, rate, unit per hour). Boundaries for the parameter estimates were determined based on gabapentin knowledge, estimated values and for KCP/KPC on expected intercompartmental clearance and volume of central and peripheral compartments. Upper parameter boundaries were 1.25 h−1 (Ka), 200 L (V), 0.008 h.ml−1 (Ke), 1.5 h (Tlag), 2.0 h−1 (KCP), and 2.0 h−1 for KPC.
Information with regard to the formulation was incorporated in the structural model by constructing models able to separately estimate four different parameter values for each subject, based on the administered formulation. A model was constructed to estimate four Ka values per subject, four Tlag values per subject, or four different values for all estimated parameters. The latter was achieved by dividing subjects' separate sampling visits into “pseudo” subjects for this analysis, four per true subject, thus 96 in total.
The applied error model per observation (1/erroR2) is a polynomial equation for the SD = 0.02 + 0.0075*(concentration), and error = (SD2 + Lambda2)0.5. The Lambda value is a fitted term to capture extra process noise on the observed values.
Selection of the optimal structural model was based on minimization of bias (mean predication error) and imprecision (mean square prediction error) and assessed using VPC and the reduction of the AIC.20 The AIC is defined as (2 × k) – 2 × ln(L), with k for the number of parameters and L the likelihood. Scatterplot VPCs are with prediction intervals (quantiles 0.05, 0.5, and 0.95) from simulation (n = 1,000). Selection of covariates (available covariates in the dataset were serum creatinine (both at predose screening and at follow‐up), age, sex, race, weight, and height) to be included in the model was based on linear regression of each subject's covariates vs. the Bayesian posterior parameter values. Inclusion of these covariates in the final model was based on the same selection criteria as the structural model selection.
Model evaluation
Internal validation was tested by residual error plots and the D'Agostino–Pearson test21 for normality in distribution of the residuals, as implemented in Pmetrics. Noncompartmental analysis derived pharmacokinetic parameters Cmax AUC0‐t, AUC0‐inf, Tmax, and T1/2 (computed by the “makeNCA” function in Pmetrics) from both the observed concentrations and from individual Bayesian posterior predicted time–observation profile were compared.
External validation of the model was performed using a dataset from an independent pharmacokinetic study as filed during registration at the MEB for another generic formulation of gabapentin. In this study, subjects received a single oral formulation of 800 mg and plasma gabapentin concentrations were determined predose and at 0.5, 1, 1.5, 2, 3, 4, 5, 6, 8, 12, 16, 24, 26, 48, and 60 h postdosing. This external validation was performed using 352 concentration timepoints. A total of 22 subjects were included in the analysis, of which there were 14 males and 8 females. The mean age was 35 years (range: 23–47 years), and their mean body mass index was 23.3 kg/m2 (range: 19.2–26.9 kg/m2).
CONFLICT OF INTEREST/DISCLOSURE
P.G., Y.Y., and M.M. are appointed at the Medicines Evaluation Board in The Netherlands. No further conflicts of interest.
AUTHOR CONTRIBUTIONS
P.G. wrote the article Y.Y., W.Y., M.N., M.M., D.B., and C.N. designed the research; P.G. and W.Y. performed the research.
ACKNOWLEDGMENT
The authors thank Dr. Jelliffe for all inspiring discussions.
FUNDING
No funding was received for this work.
References
- 1. Fact about Generic drugs. FDA, 30 May 2012. Available: <https://www.fda.gov/downloads/Drugs/ResourcesForYou/Consumers/BuyingUsingMedicineSafely/UnderstandingGenericDrugs/UCM305908.pdf> Accessed: 18 Apr 2017.
- 2. Dylst, P. & Simoens, S. Does the market share of generic medicines influence the price level?: A European analysis. Pharmacoeconomics 29, 875–882 (2011). [DOI] [PubMed] [Google Scholar]
- 3. Stichting Farmaceutische Kengetallen . Opnieuw meer generieke medicijnen verstrekt. Pharm Weekbl 151–120 (2016). [Google Scholar]
- 4. Besluit Zorgverzekering. Artikel 2.8.3. <http://wetten.overheid.nl/BWBR0018492/geldigheidsdatum_01-01-2017> Accessed 3 Apr 2017.
- 5. Pauwels, K. , Simoens, S. , Casteels, M. & Huys, I. Insight into European drug shortages: a survey of hospital pharamacists. PLoS One 10, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Kesselheim, A.S. et al Clinical equivalence of generic and brand‐name drugs used in cardiovascular disease: a systematic review and meta‐analysis. JAMA 300, 2514–2526 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Kesselheim, A.S. et al Seizure outcomes following the use of generic vs. brand‐name antiepileptic drugs: a systematic review and meta‐analysis. Drugs 70, 605–621 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Manzoli, L. et al Generic vs. brand‐name drugs used in cardiovascular diseases. Eur. J. Epidemiol. 31, 351–368 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Colgan, S. et al Perceptions of generic medication in the general population, doctors and pharmacists: a systematic review. BMJ Open 15, e008915 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Atif, M. , Azeem, M. & Sarwar, M.R. Potential problems and recommendations regarding substitution of generic antiepileptic drugs: a systematic review of literature. Springerplus 5, 182 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Guideline on the investigation of bioequivalence. Committee for Medicinal Products for Human Use (CHMP), European Medicines Agency (EMA), 2010. Doc. Ref.: CPMP/EWP/QWP/1401/98 Rev. 1/ Corr** <http://www.ema.europa.eu/docs/en_GB/document_library/Scientific_guideline/2010/01/WC500070039.pdf> Accessed 3 Apr 2017.
- 12. Guidance for Industry: Bioequivalence Studies with Pharmacokinetic Endpoints for Drugs Submitted Under an ANDA, U.S. Department of Health and Human Services Food and Drug Administration Center for Drug Evaluation and Research (CDER), 2013. <https://www.fda.gov/ucm/groups/fdagov-public/@fdagov-drugs-gen/documents/document/ucm377465.pdf> Accessed 3 Apr 2017.
- 13. Neurontin product information, SmPC, December 2016.
- 14. Mould, D.R. & Upton, R.N. Basic concepts in population modeling, simulation, and model‐based drug development. CPT Pharmacometrics Syst. Pharmacol. 1, e6 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Carlsson, K.C. et al A population pharmacokinetic model of gabapentin developed in nonparametric adaptive grid and nonlinear mixed effects modeling. Ther. Drug Monit. 31, 86–94 (2009). [DOI] [PubMed] [Google Scholar]
- 16. Ouellet, D. , Bockbrader, H.N. , Wesche, D.L. , Shapiro, D.Y. & Garofalo, E. Population pharmacokinetics of gabapentin in infants and children. Epilepsy Res. 47, 229–241 (2001). [DOI] [PubMed] [Google Scholar]
- 17. Scappaticci, G.B. & Regal, R.E. Cockcroft‐Gault revisited: New deliverance on recommendations for use in cirrhosis. World J. Hepatol. 9, 131–138 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Yu, Y. et al Interchangeability of gabapentin generic formulations in the Netherlands: a comparative bioavailability study. Clin. Pharmacol. Ther. 94, 519–524 (2013). [DOI] [PubMed] [Google Scholar]
- 19. Neely, M.N. , van Guilder, M.G. , Yamada, W.M. , Schumitzky, A. & Jelliffe, R.W. Accurate detection of outliers and subpopulations with Pmetrics, a nonparametric and parametric pharmacometric modeling and simulation package for R. Ther. Drug Monit. 34, 467–476 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 19, 716–723 (1974). [Google Scholar]
- 21. D'Agostino, R. Transformation to normality of the null distribution of G1. Biometrika 57, 679–681 (1970). [Google Scholar]


