Environmental Determinants of Hemorrhagic Fever with Renal Syndrome in High-Risk Counties in China: A Time Series Analysis (2002–2012)

Abstract.

The transmission pattern of hemorrhagic fever with renal syndrome (HFRS) is associated with environmental conditions, including meteorological factors and land-cover. In the present study, the association between HFRS and environmental factors (including maximum temperature, relative humidity, rainfall, and normalized difference vegetation index) were explored in two typical counties in Northeast and two counties in Northwest China with severe HFRS outbreaks by using seasonal autoregressive integrated moving average model with exogenous variables (SARIMAX). The results showed that rainfall with 3- to 4-month lag was closely associated with HFRS in the two counties in Northeast China, whereas relative humidity with 1- or 5-month lag significantly impacts HFRS transmission in the two counties in Northwest China. Moreover, the SARIMAX models exhibit accurate forecasting ability of HFRS cases. Our findings provide scientific support for local HFRS monitoring and control, and the development of a HFRS early warning system.

INTRODUCTION

Hemorrhagic fever with renal syndrome (HFRS) is a rodent-borne disease caused by hantavirus (belongs to the Hantaviridae family). The predominant hosts of the agents, that is, Hantaan virus and Seoul virus are Apodemus agrarius and Rattus norvegicus, respectively. Once infected, patients experience five clinical stages, including febrile, hypotensive shock, oliguric, polyuric, and convalescent, along with typical symptoms, such as fever, headache, encephalopathy, and hemorrhages.^1,2 China reports the largest number of hantavirus infections in the world; specifically during 2005–2012, there were approximately 99,000 reported HFRS cases. Currently, HFRS remains of considerable public health concern in China.

Previous studies focused on large scale evaluations of HFRS epidemiology, especially country and city level,^3–8 and these studies gave a global description of HFRS transmission in China. Given that small-scale studies will yield more precise and a better quantification of the local characteristics of HFRS transmission, the present study chose four high-risk HFRS-affected counties from Heilongjiang and Shaanxi provinces, where the largest number of HFRS cases are documented in China.^9–12 It was found that HFRS variation exhibits multi-annual cycles (especially around 1 year cycle) in various locations, for example, macroscopically, HFRS cases in China shows bimodal seasonal peaks, that is, May–June and November^8,11,13; microscopically, two main cycles (1 and 3–4 years) were detected by wavelet analysis in Changsha⁴; similarly, HFRS cases in Xi’an also have a period of 0.8–1.2 years.¹⁰ Moreover, it is reported that HFRS transmission is closely associated with the environmental factors, such as climatic variability and land-cover characteristics because the activity and population of virus hosts, which play an important role in HFRS transmission, are sensitive to these local environmental factors.^3,5,14,15 For example, atmospheric moisture has a significant effect on HFRS transmission⁴; Lin et al.¹⁶ found that temperature shows positive and negative effects on HFRS for it is lower or higher than 17°C, respectively, whereas relative humidity and rainfall are negatively associated with HFRS. Monthly variation in HFRS and its association with environmental factors can help public health managers to make policy decisions on HFRS control and prevention through the development of forecasting models.

Seasonal autoregressive integrated moving average models with exogenous variables (SARIMAX) can account for the information from both the seasonal variation of the disease itself and the relationship between the considered disease and impact factors, showing great power in time series forecasting. In other words, SARIMAX model not only captures periodic characteristics of considered disease series but also depicts a cross-correlation of considered disease and noise series. It has been widely used in various diseases forecasting in recent decades, such as influenza, syphilis, bacillary dysentery, scarlet fever, and pulmonary tuberculosis.^17–21 Generally, SARIMAX model shows better performance in disease prediction than single SARIMA model by including exogenous variables.¹⁸ Currently, many regression models have been applied in HFRS forecasting, which also took into consideration of the variation of HFRS and environmental factors with different time lags. For instance, Zhang et al.⁹ built Poisson regression models to explore the relationship between HFRS and climatic factors and found that rainfall, temperature, relative humidity, and multivariate El Niño Southern Oscillation index with 3-to 5-month lag were associated with HFRS; similarly, Xiao et al.⁵ also used Poisson regression model and the results showed that rodent hosts’ density and El Niño Southern Oscillation index were associated with HFRS by 2- to 6-month lag. However, they ignored the noise series part embedded in the original HFRS series, which may also contribute to spatiotemporal variation in HFRS incidence. Furthermore, the comparison of environmental factors associated with HFRS transmission among various locations in HFRS forecasting by using SARIMAX is still lacking.

The main objectives of the present study were to model the variability of HFRS cases in four high-risk HFRS counties and quantify the relationship between HFRS incidence and environmental factors (including temperature, relative humidity, rainfall, and normalized difference vegetation index [NDVI]). Meanwhile, the present study proposed a rigorous framework of SARIMAX model to characterize the HFRS transmission in each county, which will benefit the local HFRS monitoring, controlling, and policy-making.

MATERIALS AND METHODS

Data collection.

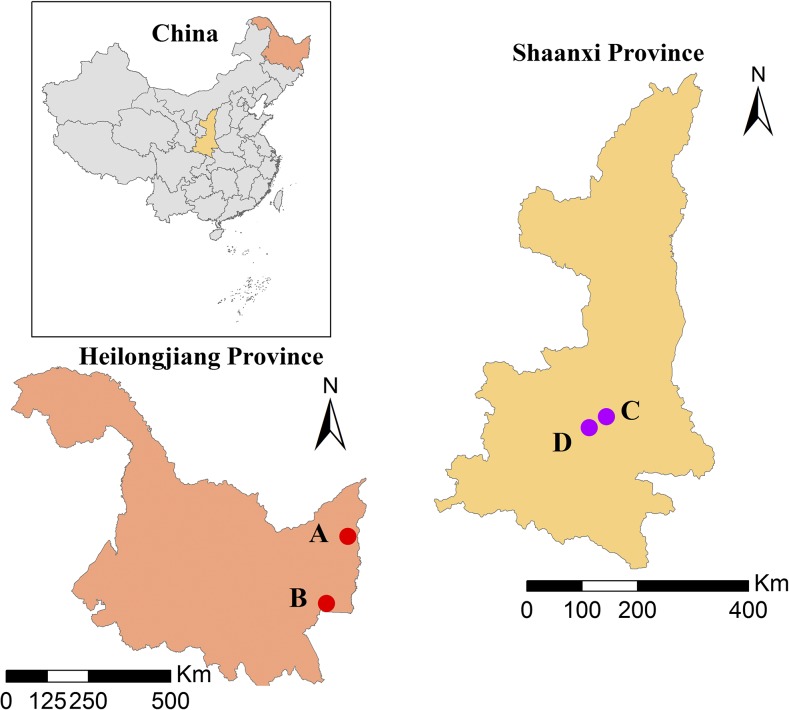
Monthly HFRS cases in four severe HFRS outbreak counties (i.e., Raohe, Mishan, Chang’an, and Hu counties) during the period of 2002–2012 were collected from China Information System for Disease Control and Prevention. Raohe and Mishan counties are located in Northeast China, whereas Chang’an and Hu counties locate in Northwest China (Figure 1). The total documented HFRS cases in these four counties are 675, 1,013, 3,638, and 1,588 cases, respectively. Corresponding monthly maximum temperature, relative humidity, precipitation, and NDVI were collected from China Meteorological Data Sharing Service System (http://data.cma.cn/) and Free Vegetation Products (http://www.vgt.vito.be/). The reasons why we chose these four counties were that these four counties suffered high HFRS infections and such reported HFRS case data were of high quality and easy to get, which will benefit the modeling process.

Figure 1.

Geographical locations of four counties (A, B, C, and D represent Raohe, Mishan, Chang’an, and Hu counties, respectively). This figure appears in color at www.ajtmh.org.

Seasonal autoregressive integrated moving average model with exogenous variables.

In this study, the time series approach, SARIMAX model, was used to simultaneously describe the seasonal variation of HFRS outbreaks and explore its environmental associations (including meteorological and land-cover factors) as follows:

$$Y_t={\displaystyle \sum {\text{β}}_{i,t}{X}_{i,t}}+Z_t,$$ (1)

where $Y_t$ represents the log-transformed HFRS cases with “t” as the time variable with scale unit of month, that is, the HFRS cases were assumed to follow Poisson distribution, $X_{i,t}$ represents exogenous variables (i.e., environmental regressors) and ${\text{β}}_i$ represent the corresponding coefficients, $Z_t$ satisfies the SARIMA equation with model structure $\left(p,\hspace{0.17em}d,\hspace{0.17em}q\right)\times {\left(P,\hspace{0.17em}D,\hspace{0.17em}Q\right)}_S$ as follows:

$${\Phi }_P\left(B^S\right){\mathrm{\varphi }}_p\left(B\right){\nabla }_S^D{\nabla }^d{Z}_t={\Theta }_Q\left(B^S\right){\text{θ}}_q\left(B\right){\text{ε}}_t,$$ (2)

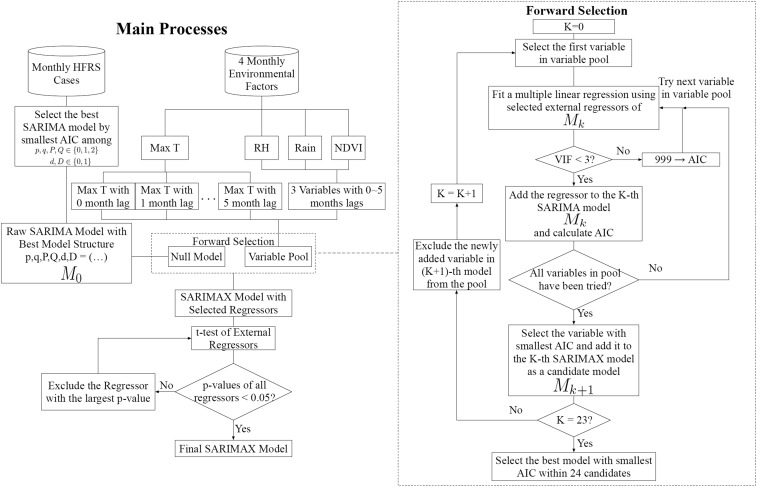
where p, d, and q are the nonseasonal parameters of SARIMA model, representing the orders of general autoregressive, differencing, and moving average processes, respectively. P, D, and Q are the seasonal parameters of SARIMA model, representing the orders of seasonal autoregressive, differencing, and moving average processes, respectively. S represents the periodicity and ${\text{ε}}_t$ is white noise series (the mean value of ${\text{ε}}_t$ is zero). B represents a backshift operator, for example, $B^i{Z}_t=Z_{t-i}$; $\nabla$ represents differencing processes, for example, ${\nabla }^d={\left(1-B\right)}^d$, ${\nabla }_S^D={\left(1-B^S\right)}^D$; and ${\mathrm{\varphi }}_p\left(B\right)=1-{\mathrm{\varphi }}_{1}B-\cdots -{\mathrm{\varphi }}_p{B}^p$ and ${\Phi }_P\left(B^S\right)=1-{\Phi }_1{B}^S-\cdots {\Phi }_P{B}^{PS}$ are the operators of general and seasonal autoregressive processes with coefficients $\left\{{\mathrm{\varphi }}_1,\dots {\mathrm{\varphi }}_p\right\}$ and $\left\{{\Phi }_1,\dots {\Phi }_P\right\}$, whereas ${\text{θ}}_q\left(B\right)=1-{\text{θ}}_{1}B-\cdots {\text{θ}}_q{B}^q$ and ${\Theta }_Q\left(B^S\right)=1-{\Theta }_1{B}^S-\cdots {\Theta }_Q{B}^{QS}$ are the operators of general and seasonal moving average processes with coefficients $\left\{{\text{θ}}_1,\dots {\text{θ}}_q\right\}$ and $\left\{{\Theta }_1,\dots {\Theta }_Q\right\}$. Given that 1-year period was detected in HFRS outbreaks as mentioned earlier, the periodicity parameter (S) in SARIMAX model was set to 12 months. For illustration purpose, a simple example of SARIMA model can be found in the Supplemental Text 1. An outline of SARIMAX modeling process is given in Figure 2 and more detailed explanations of the various part of Figure 2 follows next.

• 1.Through varying the values of (p, d, q) (P, D, Q)₁₂ (i.e., the values of p, P and q, Q are chosen from 0, 1, 2, whereas the values of d, D are chosen from 0, 1), different SARIMA models (totally 324 models) with various structure were applied to the time series of log-transformed HFRS cases in each county. Akaike information criterion (AIC) value can be used to evaluate the goodness of fit. Therefore, the model with the lowest AIC value was regarded as the best raw SARIMA model.
• 2.Based on the raw SARIMA model, a forward regressor selection approach was applied to build a SARIMAX model by selecting the exogenous variables from the variable pool (including four environmental variables with 0- to 5-month lag, 20 regressors in total). Two criteria were adopted in the SARIMAX modeling, composing two main processes of the forward regressor selection, that is, making sure the selected variables were not collinear and selecting the variable with the best fitting performance. Totally, 20 loops were implemented for selecting regressors in the forward selection process. In each loop, every variable in the variable pool will be separately tried and added into the SARIMAX model. 1) Multicollinearity in various regressors represent that the regressors contain similar information and using such regressors will result in unprecise modeling. Therefore, the first criterion is that the only regressors without multicollinearity should be kept in each loop of the forward selection process. Before every trial step for adding a new regressor into the SARIMA model, a multiple linear regression between selected regressors as independent variables and log-transformed HFRS cases as dependent variables was fitted and then variance inflation factors (VIFs) of each regressor were calculated to check the presence of multicollinearity of the considered regressors. Only when the VIF values of all considered regressors were less than three, that is, showing non-multicollinearity, the new regressor would be used to fit SARIMAX model and the corresponding AIC will be calculated for further comparison with the AICs of other regressors in the same loop; otherwise, the new regressor would be abandoned by assigning a large value of AIC (i.e., 999), so that it will not be considered in the following model performance comparison in forward selection. 2) The second criteria is that only one regressor with the lowest AIC in each loop would be finally selected and added into the SARIMAX model by comparing the AIC values of all given regressors in the variable pool. After one loop selection, the selected regressor will be removed from the variable pool; meanwhile, the rest of the regressors were still kept in the variable pool for consideration in the next loop of forward selection.
• 3.Because of the high dimensionality of the considered regressors, the selected regressors by step (2) should pass the t-test to avoid over-fitting. On the other hand, a threshold (0.05) for P value of t-test was set to distinguish the regressors significantly associated with HFRS outbreaks with the other regressors. In this step, the regressor with the largest P value (> 0.05) among all regressors is excluded from the SARIMAX model until all remaining regressors pass the t-test. The previously described analysis was conducted in R 3.3.0.

Figure 2.

An outline of the SARIMAX modeling.

SARIMAX model evaluation.

The HFRS forecasting contained two phases: 1) the first 10 years data (2002–2011) were used to fit the SARIMAX model; 2) the remaining 1 year data (2012) were used to test the performance of fitted SARIMAX model. The accuracy of SARIMAX was evaluated by mean absolute error and root mean squared error (RMSE).

RESULTS

SARIMA model.

SARIMA models with various structures were established in the four counties based on the HFRS data from 2002 to 2011, and the results of all considered models are shown in Supplemental Table 1. Through selecting the smallest AIC value within these SARIMA models, the best raw SARIMA models were achieved and listed in Supplemental Table 2. The structures of the selected SARIMA models were (1,0,1) × (0,1,1)₁₂, (2,0,0) × (0,1,1)₁₂, (1,0,0) × (0,1,1)₁₂, and (1,1,1) × (0,1,1)₁₂ for Raohe, Mishan, Chang’an, and Hu counties, respectively. Interestingly, the seasonal structures of the SARIMA models in the four counties are the same and only the HFRS series in Hu County is not stationary. Using these models to forecast the HFRS cases in 2012, the performance of the four fitted SARIMA models are 0.6490, 0.6390, 0.7780, and 0.7029 in terms of R².

SARIMAX model.

The best SARIMA model structures were used to build the SARIMAX models with exogenous environmental variables as covariates (i.e., monthly maximum temperature, relative humidity, rainfall, and NDVI) during the period of 2002–2011 in the four counties, respectively, by forward variable selection, multicollinearity analysis, and t-test criteria. The results showed that relative humidity with 4-month lag (β = 0.0248, P = 0.0186), rainfall with 1-month lag (β = 0.0042, P = 0.0301), and NDVI with 1-month lag (β = 0.0094, P = 0.0424) are significantly associated with HFRS cases in Raohe County. Similarly, rainfalls with 3-month lag (β = 0.0053, P = 0.0301) and 4-month lag (β = 0.0053, P = 0.0332) are associated with HFRS cases in Mishan County. Hemorrhagic fever with renal syndrome transmission was related to relative humidity with 1-month lag (β = −0.0227, P = 0.0028) and 5-month lag (β = 0.0164, P = 0.0320) and NDVI with 2-month lag (β = 0.0132, P = 0.0008) in Chang’an County. Finally, HFRS was related to relative humidity with 5-month lag (β = 0.0163, P = 0.0201) in Hu County. The corresponding coefficients of various parameters and the performance of the SARIMAX models are shown in Table 1. Moreover, no significant autocorrelation was found at various lags in the ACF of residuals for the four SARIMAX models (Supplemental Figure 1). The four models for Raohe, Mishan, Chang’an, and Hu counties, respectively, were given as the follows:

$$\begin{array}{l}\ln (\text{cases}+1)=\text{SARIMA}\left(\mathrm{1,0,1}\right)\times {\left(\mathrm{0,1,1}\right)}_{12}+0.0248{\text{RH}}_{t-4}+0.0042{\text{RAIN}}_{t-1}+0.0094{\text{NDVI}}_{t-1}\text{,}\\ \ln (\text{cases}+1)=\text{SARIMA}\left(\mathrm{2,0,0}\right)\times {\left(\mathrm{0,1,1}\right)}_{12}+0.0053{\text{RAIN}}_{t-3}+0.0053{\text{RAIN}}_{t-4},\\ \ln (\text{cases}+1)=\text{SARIMA}\left(\mathrm{1,0,0}\right)\times {\left(\mathrm{0,1,1}\right)}_{12}-0.0227{\text{RH}}_{t-1}+0.0164{\text{RH}}_{t-5}+0.0132{\text{NDVI}}_{t-2}\text{,}\\ \ln (\text{cases}+1)=\text{SARIMA}\left(\mathrm{1,1,1}\right)\times {\left(\mathrm{0,1,1}\right)}_{12}+0.0163{\text{RH}}_{t-5}.\end{array}$$ (3a–3d)

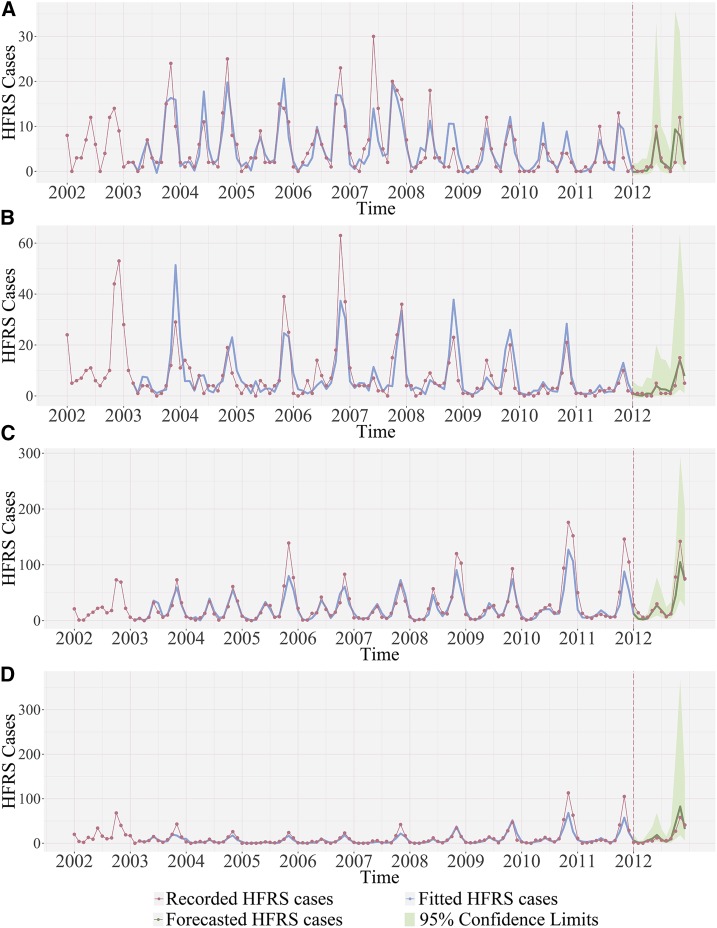
The equations were used to forecast the HFRS cases in 2012. More detailed information of Eq. (3) can be found in Supplemental Text 2. Figure 3 showed the fitting and forecasting of HFRS cases during the period of 2002–2011 and 2012, respectively; the fitting part and forecasting part were separated by the vertical dash lines in the figure. According to the SARIMAX models shown in Eq. (3), to predict the HFRS cases in the current month, previous 12–14 months HFRS data were required for the input of SARIMAX model; that is why the fitted value of HFRS cases (blue lines) in Figure 3 started at January 2003–March 2003. The SARIMAX models showed good fitness by comparing the model outputs to the recorded HFRS cases. In addition, the statistics results (Table 1) of the forecasted HFRS cases gave the RMSE of the four counties as 2.5014, 1.5688, 15.6855, 9.6626, respectively.

Table 1.

SARIMAX model of hemorrhagic fever with renal syndrome cases in four counties from China during 2002–2012

County	Model fitting								Model forecasting
	Model structure	Model components	Estimate	Standard error	t value	P value	R2	AIC	R2	RMSE	MAE
Raohe	(1,0,1) × (0,1,1)12	AR1	0.8779	0.1281	6.8508	0.0000	0.7147	198.3775	0.5691	2.5014	1.4694
		MA1	−0.6183	0.2249	−2.7489	0.0070
		SMA1	−0.6343	0.1195	−5.3070	0.0000
		RH_lag4	0.0248	0.0104	2.3882	0.0186
		RAIN_lag1	0.0042	0.0019	2.1962	0.0301
		NDVI_lag1	0.0094	0.0046	2.0531	0.0424
Mishan	(2,0,0) × (0,1,1)12	AR1	0.2764	0.0998	2.7687	0.0066	0.6475	228.3015	0.8485	1.5688	1.2864
		AR2	0.2364	0.0962	2.4583	0.0154
		SMA1	−0.6179	0.1108	−5.5751	0.0000
		RAIN_lag3	0.0053	0.0024	2.1959	0.0301
		RAIN_lag4	0.0053	0.0024	2.1553	0.0332
Chang’an	(1,0,0) × (0,1,1)12	AR1	0.4185	0.0915	4.5719	0.0000	0.8114	166.5807	0.8450	15.6855	9.6851
		SMA1	−1.0000	0.2232	−4.4795	0.0000
		RH_lag1	−0.0227	0.0074	−3.0570	0.0028
		RH_lag5	0.0164	0.0076	2.1712	0.0320
		NDVI_lag2	0.0132	0.0038	3.4593	0.0008
Hu	(1,1,1) × (0,1,1)12	AR1	−0.2864	0.1491	−1.9206	0.0572	0.7796	173.3146	0.6941	9.6626	6.3573
		MA1	−0.5550	0.1443	−3.8451	0.0002
		SMA1	−0.7351	0.1222	−6.0149	0.0000
		RH_lag5	0.0163	0.0069	2.3568	0.0201

AIC = Akaike information criterion; MAE = mean absolute error; RMSE = root mean squared error.

Figure 3.

Hemorrhagic fever with renal syndrome cases fitting and forecasting performance by SARIMAX models for (A) Raohe County, (B) Mishan County, (C) Chang’an County, and (D) Hu County. This figure appears in color at www.ajtmh.org.

Moreover, to test the consistence of the associated environmental variables, another SARIMAX^# model in each of the four counties was constructed during the period 2002–2012 (the symbol # was used to distinguish it from the previous SARIMAX model), and similar results were obtained (Supplemental Table 3), that is, rainfall with 1- and 4-month lag and NDVI with 1-month lag effects were found in Raohe County; in Mishan, Chang’an, and Hu counties, the same environmental variables with the same month’s lag were associated with HFRS compared with SARIMAX models, which proved that the variables remained in the SARIMAX models shows considerable and consistent contributions on HFRS transmission.

DISCUSSION

Using the SARIMAX models, the present study explored the association between HFRS cases and environmental factors in four severe HFRS outbreak counties in China and forecasted the HFRS transmission in these four counties. Findings indicated that using the environmental factors can improve the accuracy of the SARIMA model fitting; meanwhile, in the final SARIMAX model, the environmental factors can be regarded as related factors or indicators for HFRS forecasting.

The superiority of SARIMAX model is that it can not only capture the variability of the infectious disease across time but also quantify associated factors. Specifically, the SARIMAX models in the four counties have the same autoregressive part (i.e., AR1 in Table 1), which directly represents the infectious pattern of HFRS across time. In other words, the current HFRS cases are closely related to the HFRS cases at previous time instant. Meanwhile, the nonstationary seasonal characteristics of the recorded HFRS cases were also depicted by the four SARIMAX models, including differencing and seasonal moving average part (SMA1, Table 1). On the other hand, previous evidence indicates that HFRS is associated both directly and indirectly with environmental factors.^14–16 Compared with the low correlation coefficients of HFRS cases and the considered four environmental variables with various time lags (Supplemental Table 4), some environmental factors showed a significant association with HFRS incidence, which is likely to be due to seasonal and infectious characteristics dominating HFRS transmission locally.

In the present study, HFRS cases were assumed to follow a Poisson distribution; hence, HFRS data were log-transformed for SARIMAX modeling. During the modeling process, a zero mean Gaussian independent and identically distributed noise was fitted and the residual plots (Supplemental Figure 1) showed reasonable shapes. However, when the fitted or forecasted values were log-transformed back to the original cases, the positive residual will be exaggerated and the negative residual will be compressed, resulting in positive residual mean and asymmetric prediction limits. For this reason, Figure 3 shows the mean of the residuals (i.e., the recorded HFRS cases minus the fitted or forecasted values) are larger than zero.

Comparing the environmental factors in the final SARIMAX model between the two counties in Northeast China and two counties in Northwest China, we found that rainfall showed great effects on HFRS transmission in Northeast China, whereas relative humidity showed significant effects on HFRS transmission in Northwest China. In other words, the HFRS transmission is nonstationary and exhibits local characteristics. In Northeast China, the monthly mean rainfall of the Raohe and Mishan counties are 45.42 and 45.54 mm, respectively, which is smaller than the monthly mean rainfall of Chang’an and Hu counties in Northwest China, that is, 58.46 and 59.35 mm, respectively. Therefore, rainfall is indeed a limiting factor and shows significant impacts on HFRS transmission in Raohe and Mishan counties. Sufficient rainfall can help accelerate the primary food production, which would benefit the population growth of rodent hosts.¹⁴ Primary food of rodents can be coarsely denoted by NDVI.³ The present study also found that NDVI closely related to HFRS transmission in Raohe County, providing further support to the hypothesis that the availability of food to rodents may be a significant factor influencing HFRS transmission. Moreover, the data during 2002–2012 were used to build another SARIMAX^# model, and the results also showed that rainfall is an important factor in Raohe and Mishan counties. In summary, the survival of rodents and its reproduction may dominate HFRS transmission in Northeast China. On the other hand, HFRS in Chang’an and Hu counties from Northwest China exhibited significant association with relative humidity. In SARIMAX^# model, the same environmental factors were detected. Because of the fact that the relative humidity can also influence hantavirus infectivity,⁴ our findings suggest that relative humidity can be an indicator variable for forecasting HFRS transmission locally.

Our results also demonstrate that the influence of environmental factors on HFRS is lagged over time. The present study showed that rainfall has a 3- to 4-month lag effect on HFRS in the Mishan County in Northeast China, which is similar to the results of the HFRS study of Elunchun and Molidawahancer counties⁹; similarly, 3-month lag effects of rainfall on HFRS have also been found in Junan County and Huludao city.^22,23 In addition, HFRS incidence showed a close association with 1-month lag with rainfall, which is also suggested by the study of Xiao et al.³ The present study also found 1-month and 5-month lag effects of relative humidity on HFRS in Chang'an and Hu counties, which confirms the previous evidence obtained by Xiao et al.⁴ and Li et al.²⁴ In summary, our model including corresponding detected environmental factors in various counties can form a sound early warning system for local departments of public health to monitor the risk of HFRS. Moreover, given the lag effects of environmental factors, local managers of public health can use the built SARIMAX model to forecast in almost real-time HFRS cases; simultaneously, such lag effects provide sufficient time for the local managers to prepare in advance to allocate available interventions (e.g., vaccine, rodent control, and the dissemination or effective preventive measures to at-risk populations).

Yet, some shortcomings of the present study should be acknowledged. The maximum likelihood method was used to fit the SARIMA model at the stage of the model structure selection, which required optimizing the negative log-likelihood of the SARIMA model over the parameters; when this constraint cannot be satisfied, the negative log-likelihood became infinity, resulting in lack of fit of the SARIMA model. For this reason, the total number of trial SARIMA models was not the same for different counties (see Supplemental Table 1). In addition, rodent density is directly associated with HFRS transmission, which is not considered in the present study because of the lack of such data. Future work should focus on combining rodent density and meteorological factors and land-cover to study HFRS transmission in the entire eastern part of China.

Note: Supplemental information, figure, and tables appear at www.ajtmh.org.