Interim evaluation of efficacy or futility in group-sequential trials with multiple co-primary endpoints

Abstract

We discuss group-sequential designs in superiority clinical trials with multiple co-primary endpoints, i.e., when trials are designed to evaluate if the test intervention is superior to the control on all primary endpoints. We consider several decision-making frameworks for evaluating efficacy or futility, based on boundaries using group-sequential methodology. We incorporate the correlations among the endpoints into the calculations for futility boundaries and sample sizes as a function of other design parameters including mean differences, the number of analyses, and efficacy boundaries. We investigate the operating characteristics of the proposed decision-making frameworks in terms of efficacy/futility boundaries, power, the Type I error rate and sample sizes, while varying the number of analyses, the correlations among the endpoints, and the mean differences. We provide an example to illustrate the methods and discuss practical considerations when designing efficient group-sequential designs in clinical trials with co-primary endpoints.

1. Introduction

Superiority clinical trials with “co-primary” endpoints are designed to evaluate if the test intervention is superior to the control on all primary endpoints. Failure to demonstrate superiority on any single endpoint implies that superiority to the control intervention cannot be concluded. For K co-primary endpoints (K ≥ 2), the hypotheses are formulated as follows: the hypothesis for each endpoint is tested at significance level of α with the null hypothesis H_0k : δ_k ≤ 0 versus H_1k : δ_k > 0, and the hypotheses for co-primary endpoints are the null hypothesis ${\text{H}}_0:{\cup }_{k=1}^K{\text{H}}_{0k}$ versus the alnternative hypothesis ${\text{H}}_1:{\cap }_{k=1}^K{\text{H}}_{1k}$ (The union H₀ of K individual nulls is tested against the intersection alternative H₁), where δ_k is the mean difference in the test and control interventions and positive values of δ_k represent the test intervention’s benefit.

Use of co-primary endpoints in clinical trials is increasingly common, especially in medical product development, where indications include Alzheimer disease, irritable bowel syndrome, acute heart failure, Duchenne and Becker muscular dystrophy, diabetes mellitus and so on. In many such trials, the sample size is often unnecessarily large and impractical. For example, Green et al. (2009) reported the results of a multicenter, randomized, double-blind, placebo-controlled trial in patients with mild Alzheimer disease (Tarenflurbil study), where co-primary endpoints were cognition as assessed by the Alzheimer Disease Assessment Scale Cognitive Subscale (ADAS-Cog) and functional ability as assessed by the Alzheimer Disease Cooperative Study activities of daily living (ADCS-ADL) as Committee for Medicinal Products for Human Use (CHMP) (2008) and Food and Drug Administration (FDA) (2013) recommended the two co-primary endpoints in the development of drugs for the treatment of Alzheimer disease. The study was sized for 1600 participants in total (equally-sized groups) based on a power of 96% to detect the between-group joint difference in the two primary endpoints (using a one-sided test at 2.5% significance level, with the standardized mean differences between the two groups of 0.2 for both endpoints, assuming zero correlation between the two endpoints). To overcome the issue, recently many authors have discussed the approach to the design and analysis of co-primary endpoints trials in fixed-sample (size) design (please see extensive references in Offen et al. (2007) and Sozu et al. (2015)).

Group-sequential designs for multiple co-primary endpoints are a more attractive design feature rather than the fixed-sample designs because they offer the possibility of stopping a trial when evidence is overwhelming, thus providing efficiency (Hung and Wang, 2009). Recently Asakura et al. (2014, 2015) discussed two decision-making frameworks associated with interim evaluation of efficacy in clinical trials with two co-primary endpoints in a group-sequential setting. One framework is to reject the null hypothesis if and only if statistical significance is achieved for the two endpoints simultaneously at the same interim timepoint of the trial. The other is a generalization of this, i.e., to reject the null hypothesis if superiority is demonstrated for the two endpoints at any interim timepoint (i.e., not necessarily simultaneously at the same interims). The former framework is independently discussed by Cheng et al. (2014) and evaluated in clinical trials with two co-primary endpoints. Hamasaki et al. (2015) discussed more flexible decision-making frameworks, allowing the different timepoints of analyses among the endpoints. Jennison and Turnbull (1993), and Cook and Farewell (1994) discussed the decision-making frameworks associated with interim evaluation of efficacy and futility to monitor the efficacy and safety responses. For group-sequential designs with other inferential goal settings, Pocock et al. (1987) and Tang et al. (1989) discussed a method based on a generalized least squares procedure by O’Brien (1984), and Jennison and Turnbull (1991) discuss a method based on chi-square and F test statistics, where a trial is designed if the test intervention has an overall effect across the endpoints compared with the control intervention, but does not necessarily evaluate the effect on any specific endpoint. When the aim is to evaluate an effect on at least one endpoint (multiple primary endpoints), Tang and Geller (1999), Glimm et al. (2010) and Tamhane et al. (2010, 2012) considered methods based on the closed testing principle, and Kosorok et al. (2004) discussed a global alpha-spending function to control the Type I error and a multiple decision rule to control error rates for concluding wrong alternative hypotheses.

The Tarenflurbil trial mentioned above, failed to demonstrate a beneficial effect of tarenflurbil. In fact, the observed ADCS-ADL scores in the tarenflurbil group were smaller (smaller scores being worse) than for the placebo group. If the design had included an interim futility assessment, the trial may have been stopped earlier, saving valuable resources and time, and preventing patients from being exposed to an ineffective intervention unnecessarily. In many trials, in addition to efficacy assessments, it is desirable to conduct interim assessments for futility (Gould and Pecore, 1982; Ware et al., 1985; Snapinn et al., 2006). There are two fundamental approaches for the interim futility assessment, i.e., based on: (1) the conditional power (Lan and Halperin, 1982; Lachin, 2005) and (2) futility boundaries using group-sequential methodology (DeMets and Ware, 1980, 1982; Whitehead et al., 2003).

In this paper, we consider group-sequential designs in superiority clinical trials with multiple co-primary endpoints with the decision-making frameworks evaluating efficacy (rejecting the null hypothesis) or futility (accepting the null hypothesis), where efficacy and futility boundaries are prespecified and determined using any group-sequential method. Jennison and Turnbull (1993) provided the fundamentals for this design. When planning interim efficacy and futility assessments in clinical trials with multiple co-primary endpoints, the approach determines efficacy and futility boundaries to preserve the desired Type I and II errors, analogously to the single endpoint case. The method by Jennison and Turnbull (1993) (JT method) determines the efficacy and futility boundaries based on methods in Emerson and Fleming (1989). Both of the efficacy and futility boundaries are fixed for any values of correlation among the endpoints but the JT method incorporates the correlations into the power assessment. The efficacy boundary for each endpoint is usually determined independently using group-sequential methods (e.g., Lan-DeMets (LD) error-spending method (Lan and DeMets, 1983)) to control the Type I error, analogously to the single primary endpoint case (Asakura et al., 2014). However the efficacy boundary could be adjusted by incorporating the correlations among the endpoints (Chuang-Stein et al. (2007) and Kordzakhia et al. (2010) discussed this for fixed-sample designs). This strategy may provide smaller sample sizes but also introduces challenges. The sample size calculated to detect the joint effect may be smaller than the sample size calculated for each individual endpoint. Furthermore the correlation is usually unknown and estimates from prior studies may be incorrect. This calls into question whether or not the significance level should be adjusted based on the unknown nuisance parameter. On the other hand, when planning for interim futility assessment in trials with multiple co-primary endpoints, the futility boundary could be adjusted by the correlations. Although a use of non-adjusted futility boundary discussed in the JT method is simple, it is unclear how adjusting the futility boundary by incorporating the correlations, may affect the decision-making for accepting the null hypothesis. In this paper, to investigate this issue, we use the futility boundary adjusted by the correlations and investigate how the adjusting affects the decision-making for rejecting or accepting the null hypothesis in terms of power and Type I error rate. Please see extensive references in Jennison and Turnbull (1999) and Hamasaki et al. (2016).

In addition, the JT method simply assumed that both of efficacy and futility assessments are performed at the same interims and described a simple decision-making framework for rejecting or accepting the null hypothesis associated with multiple co-primary endpoints. In addition to this simple framework, we consider two other, more flexible decision-making frameworks which allow selecting different interim evaluation timing and the number of interim analyses for efficacy and futility assessments. The decision-making frameworks allow for a delay of the efficacy assessments for outcomes with a smaller (standardized) mean effect size which require a larger sample size, and allow for earlier futility assessments for outcomes with a larger mean effect size which require a smaller sample size. These could save costs in error spending (Type I and II errors) and improve the efficiency (increase power and reduce required sample sizes).

This paper is structured as follows: in Section 2, we describe the decision-making frameworks for implementing the efficacy and futility assessments in group-sequential clinical trials with multiple co-primary endpoints. In Section 3, we describe the methods for calculating efficacy and futility boundaries based on the decision-making frameworks, and illustrate the behavior of the efficacy and futility boundaries as the size of mean difference and the number of analyses, vary. In Section 4, we investigate the operating characteristics of the decision-making frameworks in terms of power, the Type I error and sample sizes as a function of the size of mean differences and the correlations. In Section 5, we provide an example to illustrate the decision-making framework. In Section 6, we discuss two practical considerations in the application of the methods to clinical trials. In Section 7, we summarize the findings.

2. Group-sequential designs for efficacy and futility assessments

2.1. Statistical settings

Consider a randomized, group-sequential, superiority clinical trial comparing the test intervention (T) with the control intervention (C) based on K continuous outcomes to be evaluated as co-primary endpoints. Suppose that a maximum of L analyses are planned, where the same number of analyses with a common information space are selected for all of the endpoints. Let n_l and rn_l be the cumulative number of participants on the T and the C groups at the lth analysis (l = 1,…, L), respectively, where r is the sampling ratio. Hence, up to n_L and rn_L participants are recruited and randomly assigned to the T and the C groups, respectively. Let responses to the T be denoted by Y_Tki and responses to the C by Y_Ckj (k = 1,…, K; i = 1,…, n_L; j = 1,…, rn_L). Assume that (Y_T1i,…, Y_TKi) and (Y_C1j,…, Y_CKj) are independently K– variate normally distributed as (Y_T1i,…, Y_TKi) ~ N_K(μ_T; Σ) and (Y_C1j,…, Y_CKj) ~ N_K(μ_C; Σ), where μ_T and μ_C are mean vectors given by μ_T= (μ_T1,…, μ_TK)^T and μ_C= (μ_C1,…, μ_CK)^T, re-spectively. For simplicity, Σ is known covariance matrix given by Σ = {ρ_kk′σ_kσ_k′} with $\text{var}\left[Y_{Tki}\right]=\text{var}\left[Y_{\text{C}kj}\right]={\sigma }_k^2$ and corr [Y_Tki, Y_Tk′i] = corr[Y_Ckj, Y_Ck′j] = ρ_kk′ (1 ≤ k < k′ ≤ K; K ≥ 2).

Let δ_k and Δ_k denote the mean differences and the standardized mean differences between the T and the C respectively, where δ_k = μ_Tk − μ_Ck and Δ_k = δ_k/σ_k (k = 1,…, K). Suppose that positive values of δ_k indicate favorability of the T. As mentioned in Section 1, to evaluate the superiority of the T relative to the C, we are interested in testing the null hypothesis H₀ : δ_k ≤ 0 for at least one k versus the alternative hypothesis H₁ : δ_k > 0 for all k. Let (Z_1l,…, Z_Kl) be the statistics for testing the hypotheses at the lth analysis, given by $Z_{kl}=\left({\overline{Y}}_{\text{T}kl}-{\overline{Y}}_{\text{C}kl}\right)/\left({\sigma }_k\sqrt{(1+r)/\left(r{n}_l\right)}\right)$, where ${\overline{Y}}_{\text{T}kl}$and ${\overline{Y}}_{\text{C}kl}$ are the sample means given by ${\overline{Y}}_{\text{ Tk}l}=n_l^{-1}{\sum }_{i=1}^{n_l}{Y}_{\text{T}ki}$ and ${\overline{Y}}_{\text{C}kl}={\left(r{n}_l\right)}^{-1}{\sum }_{j=1}^{r{n}_l}{Y}_{\text{C}kj}$. Thus, each Z_kl is normally distributed as $\text{N}\left(\sqrt{r{n}_l/(1+r)}{\delta }_k/{\sigma }_k,1^2\right)$ under H₁. As the joint distribution of (Z_1l,…, Z_Kl) is K-variate normal with the correlation ρ_kk′ and the joint distribution of (Z_k1,…, Z_kL) is L-variate normal with the correlation ${\rho }_{k{k}^{\prime }}$, the joint distribution of (Z₁₁,…, Z_K1,…, Z_1L,…, Z_KL) is K × L multivariate normal with their correlation given by ${\rho }_{k{k}^{\prime }}\sqrt{n_l/n_{l^{\prime }}}\left(k\ne k^{\prime };l\ne l^{\prime }\right)$.

2.2. Decision-making frameworks, corresponding power functions and sample sizes

We now describe the decision-making frameworks with the rules for rejecting or accepting H₀ when implementing both of efficacy and futility assessments.

When assessing the futility on K co-primary endpoints in a group-sequential setting, the decision-making rule is to accept H₀ if the test statistic for at least one endpoint crosses a prespecified group-sequential-based futility boundary at any interim analysis. If the trial is planned with binding futility boundary and not stopped when at least one test statistic has crossed the futility boundary, then the Type I error will be inflated, analogously to trials with a single primary endpoint. In this situation the non-binding futility boundary could be used. To investigate the fundamental properties of the group-sequential designs, in this paper, we only discuss the non-binding futility boundary, assuming that the trial may not be stopped when at least one test statistic has crossed the futility boundary. On the other hand, when assessing efficacy, there are two options for testing H₀. One is to reject H₀ if each test statistic crosses the prespecified group-sequential-based efficacy boundary at any interim analysis (i.e., not necessarily simultaneously). If some but not all of the test statistics cross the boundary at an interim analysis, then the trial continues but subsequent hypothesis testing is repeatedly conducted only for the previously non-significant endpoint(s). As discussed in Asakura et al. (2014) and Hamasaki et al. (2015), this could offer the opportunity of stopping measurement of an endpoint for which superiority has already been demonstrated. Stopping measurement may be desirable if the endpoint is very invasive or expensive (e.g., data from a liver biopsy or gastro-fiberscope, or data from expensive imaging). The other option is a special case of the first one: reject H₀ if all of the test statistics cross the boundary at the same interim analysis. If any of the test statistics do not cross the boundary, then the trial continues until all of the test statistics cross the boundary at the same interim analysis.

In combining the two decision-making rules for efficacy assessment with the decision-making rule for futility assessment, we consider an option that allows selecting different timings and number for interim analyses for efficacy and futility assessments. For example, two interim analyses for efficacy assessment (with information times of 0:50 and 0:75) and one interim analysis for futility assessment (with information times of 0:25) could be conducted. This provides an opportunity for detecting an early negative sign for either of endpoints, but also has flexibility for delaying efficacy analyses to improve the power. This will be shown in Section 4.

Based on these concepts, we describe three decision-making frameworks with corresponding stopping rules and power definitions.

DF-1: The first decision-making framework is: (i) to accept H₀ if the test statistic for at least one endpoint crosses a prespecified group-sequential-based futility boundary at any interim analysis, and (ii) to reject H₀ if each test statistic crosses the prespecified group-sequential-based efficacy boundary at any interim analysis (i.e., not necessarily simultaneously), where the efficacy and futility assessments are repeatedly only conducted on the endpoint which statistic has not yet crossed both of the efficacy and futility boundaries. Thus DF-1 offers the opportunity of stopping measurement of an endpoint for which superiority has already been demonstrated. Here suppose that L_k analyses are planned for efficacy or futility assessments for endpoint k, and a total number of analyses L is the sum of the number of analyses over all endpoints, excluding the duplications of the same information time $n_{l_k}/n_L\left(={\mathcal{I}}_{l_k}\right)=n_{l_{k^{\prime }}}/n_L\left(={\mathcal{I}}_{l_{k^{\prime }}}\right)$ (l_k = 1,…, L_k; l_k′ = 1,…, L_k′; 1 ≤ L_k, L_k′ ≤ L). The stopping rule for DF-1 is formally given follows:

Until the lth analysis (l = 1,…, L – 1),

if $Z_{k{l}_k}\le c_{\text{F}k{l}_k}$ for at least one endpoint, for some 1 ≤ l_k ≤l, then accept H₀ and stop the trial,

if $Z_{k{l}_k}>c_{\text{E}k{l}_k}$ for each endpoint k, for some 1 ≤ l_k ≤ l, then reject H₀ and stop the trial,

otherwise, continue to the (l + 1)th analysis,

at the Lth analysis, for the endpoints which statistics have not yet crossed both of the efficacy and futility boundaries until the (L – 1)th analysis

if $Z_{k{L}_k}\le c_{\text{F}k{L}_k}$ for at least one endpoint, then do not reject H₀,

if $Z_{k{L}_k}>c_{\text{E}k{L}_k}$ for non-significant endpoint(s) until the (L – 1)th analysis, then reject H₀,

where $c_{\text{E}kl}{}_{{}_k}$ and $c_{\text{F}kl}{}_{{}_k}$ are the efficacy and futility boundaries. The efficacy boundaries $c_{\text{E}k{l}_k}$ are prespecified and determined separately, using any group-sequential method to control the Type I error rate, analogously to the single primary endpoint case. The futility boundaries $c_{\text{F}k{l}_k}$ are also prespecified and determined for achieving the desired power 1 – β and controlling the marginal Type I error rate to the pre-specified level α with c_FkL = c_EkL at the final analysis, using any group-sequential method. The method for calculating the efficacy and futility boundaries is discussed in Section 3. Defining ${\delta }^{*}=\left({\delta }_1^{*},\dots ,{\delta }_K^{*}\right)$ to be the clinically meaningful differences in means between the two interventions to be detected with high probability, the power corresponding to the DF-1 at δ = δ^* is

$$1-\beta ={\text{Pr}}_{\mathit{\text{δ}}=\mathit{\text{δ}}*}\left[\underset{k=1}{\overset{K}{\cap }}\left\{A_{k1}\cup \underset{l_k=2}{\overset{L_k}{\cup }}\left\{\underset{{l^{\prime }}_k=1}{\overset{l_{k-1}}{\cap }}{B}_{k{l^{\prime }}_k}\cap A_{k{l}_k}\right\}\right\}\right],$$ (1)

where $A_{k{l}_k}=\left\{Z_{k{l}_k}>c_{\text{E}k{l}_k}\right\}$, $B_{k{l}_k}=\left\{c_{\text{F}k{l}_k}<Z_{k{l}_k}\le c_{\text{E}k{l}_k}\right\}$ and δ = (δ₁,…, δ_K).

DF-2: The second framework is a special case of the DF-1. A major difference in the decision-making rule is to reject H₀ if all of the test statistics cross the boundary at the same interim analysis. The stopping rule is formally given as follows:

Until the lth analysis (l = 1,…, L – 1),

if $Z_{k{l}_k}\le c_{\text{F}k{l}_k}$ for at least one endpoint, for some 1 ≤ l_k ≤ l, then accept H₀ and stop the trial,

if $Z_{k{l}_k}>c_{\text{E}k{l}_k}$ for all endpoints, at the same l_kth interim analysis, then reject H₀ and stop the trial,

otherwise, continue to the (l + 1)th analysis,

at the Lth analysis,

if $Z_{k{L}_k}\le c_{\text{F}k{L}_k}$ for at least one endpoint, then do not reject H₀,

if $Z_{k{L}_k}>c_{\text{E}k{L}_k}$ for all endpoints, then reject H₀.

Therefore, the power corresponding to the DF-2 at δ = δ^* is

$$1-\beta ={\text{ Pr}}_{\mathit{\text{δ}}=\mathit{\text{δ}}*}\left[\underset{k=1,{\mathcal{I}}_l{}_{{}_1}=\dots ={\mathcal{I}}_{l_K}}{\overset{K}{\cap }}\left\{A_{k1}\cup \underset{l_k=2}{\overset{L_k}{\cup }}\left\{\underset{{l^{\prime }}_k=1}{\overset{l_{k-1}}{\cap }}{C}_{k{l^{\prime }}_k}\cap A_{k{l}_k}\right\}\right\}\right],$$ (2)

where $C_{k{l}_k}=\left\{Z_{k{l}_k}>c_{\text{F}k{l}_k}\right\}$.

DF-3: The above two decision-making frameworks are flexible, but different timings of the interim analyses between the efficacy and futility assessments may also introduce operational challenges. To avoid the operational difficulties, one may opt for restricting when H₀ is rejected or accepted. Both of efficacy and futility assessments are performed at the same interim analysis, and if the test statistic for at least one endpoint does not cross the prespecified futility boundary and if the test statistic for any endpoint does not cross the prespecified efficacy boundary, then the trial continues until a joint significance for all endpoints is established at the same interim analysis. The third framework is same as discussed in Jennison and Turnbull (1993). The stopping rule for the most simplified decision-making framework is formally given as follows:

Until the lth analysis (l = 1,…, L – 1),

if Z_kl ≤ c_Fkl for at least one endpoint, then accept H₀ and stop the trial,

if Z_kl > c_Ekl for all endpoints, then reject H₀ and stop the trial,

otherwise, continue to the (l + 1)th analysis,

at the Lth analysis,

if Z_kL ≤ c_FkL for at least one endpoint, then do not reject H₀,

if Z_kL > c_EkL for all endpoints, then reject H₀.

Based on this decision-making framework, the corresponding power at δ = δ^* is

$$1-\beta ={\text{ Pr}}_{\delta =\delta *}\left[\underset{k=1}{\overset{K}{\cap }}{A}_{k1}\cup \underset{l=2}{\overset{L}{\cup }}\left\{\underset{l^{\prime }=1}{\overset{l-1}{\cap }}\left\{C_{1l^{\prime }}\cap \cdots \cap C_{K{l}^{\prime }}\right\}\cap \left\{A_{1l}\cap \cdots \cap A_{Kl}\right\}\right\}\right],$$ (3)

where C_kl = {Z_kl > c_Fkl} and 1 ≤ l′ ≤ l ≤ L.

The powers (1), (2) and (3) defined above can be evaluated using the numerical integration method in Genz (1992) or other simulation-based method. The power calculation requires considerable computing time and memory especially with a large number of endpoints or number of analyses. The accuracy of the computation should be carefully controlled as it is sensitive to the number of endpoints and the number of analyses.

Based on these powers (1), (2) and (3), we discuss two sample size concepts, i.e., the maximum sample size (MSS) and the average sample number (ASN). The MSS is the sample size required for the final analysis to achieve the desired power 1 – β. The ASN is the expected sample size under a specific parameter reference. The MSS is given by the smallest integer not less than n_L satisfying the power for a group-sequential strategy at the prespecified values for δ_k, σ_k, and ρ_kk′, with Fisher’s information time for the interim analyses. The ASN is the expected sample size under hypothetical reference values and provides information regarding the number of participants anticipated in a group-sequential design to reach a decision point. Detailed calculation for the ASN is given in Appendix.

2.3. The probability of rejecting the null hypothesis

We now consider a simple situation where a clinical trial is designed to evaluate a joint effect on two co-primary endpoints (K = 2) with two planned analyses (L = 2). With an assumption of σ₁ = σ₂ = 1, based on the DF-1 including both of efficacy and futility assessments at the interim analysis, the probability of rejecting the H₀ is

$$\begin{array}{l}\text{Pr}\left[Z_{11}>c_{\text{E}11},Z_{12}>c_{\text{E}21}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[Z_{11}>c_{\text{E}11},c_{\text{F21}}<Z_{21}\le c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[c_{\text{F}11}<Z_{11}\le c_{\text{E}11},Z_{12}>c_{\text{E}12},Z_{21}>c_{\text{E}21}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}[c_{\text{F}11}<Z_{11}\le c_{\text{E}11},Z_{12}>c_{\text{E}12},c_{\text{F}21}<Z_{21}\le c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\Delta }_1,{\Delta }_2,{\rho }_{12}]\hfill \end{array}$$ (4)

Similarly the probability of rejecting H₀ based on DF-2 including both of efficacy and futility assessments at the interim analysis is

$$\begin{array}{l}\text{Pr}\left[Z_{11}>c_{\text{E}11},Z_{12}>c_{\text{E}21}|{\text{Δ}}_1,{\text{Δ}}_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[Z_{11}>c_{\text{E}11},Z_{12}>c_{\text{E}12},c_{\text{F}21}<Z_{21}\le c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\text{Δ}}_1,{\text{Δ}}_2,{\text{Δ}}_{12}\right]\hfill \\ +\text{Pr}\left[c_{\text{F}11}<{\text{Z}}_{11}\le c_{\text{E}11},Z_{12}>c_{\text{E}12},Z_{21}>c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\text{Δ}}_1,{\text{Δ}}_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[c_{\text{F}11}<Z_{11}\le c_{\text{E}11},Z_{12}>c_{\text{E}12},c_{\text{F}21}<Z_{21}\le c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\text{Δ}}_1,{\Delta }_2,{\rho }_{12}\right]\hfill \end{array}$$ (5)

Comparing the probability (4) with the probability (5), it is clear that DF-1 is more powerful than DF-2 under H₁ (less conservative under H₀) as the second and third probabilities in (4) are larger than the corresponding probabilities in (5). The probability of rejecting H₀ based on DF-1 including only an efficacy assessment at the interim analysis is

$$\begin{array}{l}\text{Pr}\left[Z_{11}>c_{\text{E}11},Z_{12}>c_{\text{E}21}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[Z_{11}>c_{\text{E}11},Z_{21}\le c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[Z_{11}\le c_{\text{E}11},Z_{12}>c_{\text{E}12},Z_{21}>c_{\text{E}21}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \\ +\text{Pr}\left[Z_{11}\le c_{\text{E}11},Z_{12}>c_{\text{E}12},Z_{21}\le c_{\text{E}21},Z_{22}>c_{\text{E}22}|{\Delta }_1,{\Delta }_2,{\rho }_{12}\right]\hfill \end{array}$$ (6)

Comparing the probability (4) with the probability (6), it is clear that DF-1 which includes only an efficacy assessment is more powerful than DF-1 with both efficacy and futility assessments under H₁ (less conservative under H₀). This is because the second, third and fourth probabilities in (4) are smaller than the corresponding probabilities in (6). This result may help illustrating the operating characteristics of the decision-making frameworks. However, it is unclear how the power under each decision-making framework may behave as design parameters vary (including mean differences, correlations, and the number of analyses). It is also important to determine how much the power changes with the allocation of futility assessments. In Section 4, we investigate the operating characteristics of the decision-making frameworks.

3. Critical boundaries for efficacy and futility assessments

3.1. Critical boundary and sample size calculations

The efficacy and futility boundaries $c_{\text{E}k{l}_k}$ and $c_{\text{F}k{l}_k}$ are determined using the error-spending functions to spend both of the Type I and II error rates. $c_{\text{E}k{l}_k}$ is determined independent of $c_{\text{F}k{l}_k}$ and separately calculated for each endpoint and treated as if the endpoints are not correlated. But $c_{\text{F}k{l}_k}$ is iteratively determined as a function of the standardized mean differences, the MSS and $c_{\text{E}k{l}_k}$ with the restriction c_FkL = c_EkL, by incorporating the correlations among the endpoints into the calculation. Then the marginal Type II error rate β_k, the probability of crossing $c_{\text{F}k{l}_k}$ at any analysis for each endpoint under H₁, is spent depending on the error-spending function. For simplicity, here we consider a situation where both of the efficacy and futility assessments are performed at the same interim analysis, i.e., l_k = l. First, for δ_k = 0, the efficacy boundary $c_{\text{E}{k}_l}$ is determined such that:

$$\text{Pr}\left[Z_{k1}\le c_{\text{E}k1},\dots ,Z_{kl-1}\le c_{\text{E}kl-1},Z_{kl}>c_{\text{E}kl}\right]=f_k\left({\mathcal{I}}_l\right)-f_k\left({\mathcal{I}}_{l-1}\right),$$

where Pr [Z_k1 > c_Ek1] = f_k$\left({\mathcal{I}}_1\right)$, and f_k$\left({\mathcal{I}}_l\right)$ is an error-spending function for endpoint k, which describes the Type I error rate spent until the lth analysis with the information time ${\mathcal{I}}_l$, and f_k(0) = 0 and f_k(1) = α. Once $c_{\text{E}{k}_1}$ has been determined, for ${\delta }_k={\delta }_k^{*}$, the futility boundary $c_{\text{F}{k}_l}$ is determined such that:

$$\text{Pr}\left[c_{\text{F}k1}<Z_{k1}\le c_{\text{E}k1},\dots ,c_{\text{F}kl-1}<Z_{kl-1}\le c_{\text{E}kl-1},Z_{kl}\le c_{\text{F}kl}\right]=g_k\left({\mathcal{I}}_l\right)-g_k\left({\mathcal{I}}_{l-1}\right)$$

where Pr [Z_k1 ≤ c_Fk1] = g_k$\left({\mathcal{I}}_1\right)$ and g_k$\left({\mathcal{I}}_l\right)$ is an error-spending function for endpoint k, which describes the Type II error rate spent until the lth analysis with the information time ${\mathcal{I}}_l$, and g_k(0) = 0 and g_k(1) = β_k. In Appendix, we describe the iterative procedure to identify the efficacy and futility boundaries $c_{\text{E}k{l}_k}$ and $c_{\text{F}k{l}_k}$ including the calculation for n_L. The R codes to reproduce the results presented in this paper is available as Supporting Information on the journal’s web page (http://onlinelibrary.wiley.com/doi/10.1002/bimj.200800143/suppinfo).

If all of the correlations among the endpoints are assumed to be zero, i.e., ρ₁₂ = ⋯ = ρ_{K –1,K} =0, and the standardized mean differences are equal, then the futility boundary can be simply determined, using a group-sequential method with the adjusted Type II error rate of 1 – (1 – β)^1/K, analogously to the single primary endpoint case. However if the endpoints are assumed to be correlated perfectly, i.e., ρ₁₂ = ⋯ = ρ_{K –1,K} =1, and the standardized mean differences are equal, then the futility boundary can be given by using a group-sequential method with the unadjusted Type II error rate of β, analogously to the single primary endpoint case. Further numerical evaluation of the behavior of the futility boundary will be discussed in Section 3.2.

3.2. Behavior of efficacy and futility boundaries

We investigate how the efficacy and futility boundaries behave when varying design parameters, i.e., mean differences, the number of analyses and correlation. For illustration, consider a simple clinical trial where the superiority of a T relative to C is evaluated based on two co-primary endpoints (EP1 and EP2). The trial is designed to evaluate both of efficacy and futility at the same interim analysis with the number of analyses (L =2, 3 and 4). The sample size per intervention group (equally-sized groups: r =1) is calculated to detect a joint effect with the power of 80% by using a one-sided test with a significance level of α=2.5%, where the standardized mean differences (Δ₁, Δ₂) are (0.1,0.1), (0.1,0.2), (0.2,0.2), (0.2,0.3) and (0.3,0.3), and the correlations between EP1 and EP2 are ρ₁₂ = 0.0, 0.3, 0.5, 0.8 and 1.0.

Table 1 displays the efficacy and futility boundaries for the DF-1, determined based on the O’Brien-Fleming(OF)-type boundary (O’Brien and Fleming, 1979) by using LD error-spending function, for spending the Type I and II errors, with equally-spaced increments of information. Table 1 illustrates that the regions based on the efficacy and futility boundaries for the two endpoints is narrower when the mean differences are larger and when the correlation is higher. When Δ₁ = Δ₂, the futility boundaries for both endpoints vary with the correlation. If ρ₁₂ = 0.0, then the futility boundaries for both endpoints are equal to the ones individually calculated for each endpoint with the power of $\sqrt{1-\beta }=89.4\%$ and ones with the power of 1 – β =80% if ρ₁₂ = 1.0. When Δ₁ > Δ₂, then the futility boundaries do not vary with the correlation. For example, when (Δ₁, Δ₂) = (0.1,0.2), the futility boundaries for EP1 are −0.822, 0.609, 1.401 and 2.014 for each analysis and are equal to those calculated for EP1 to detect Δ₁ = 0.1 with the power of 1 – β=80%. On the other hand, for EP2, the futility boundaries are −5.140, −1.504, 0.542 and 2.014 for each analysis. In this situation, the calculated sample size per intervention group is 1782 which is equal to the one calculated for EP1 with Δ₁ = 0.1 and 1 – β=80%. The futility boundaries for EP2 are equal to those calculated to detect Δ₂ with the marginal power for EP2 under this sample size (the marginal power for EP2 is close to one under the sample size).

Table 1.

OF-type efficacy and futility boundaries with standardized mean differences, the number of analyses, and correlation. The efficacy and futility assessments are conducted for the two endpoints at the same interim analysis based on DF-1 (β =20% and α =2.5%, and equally-spaced increments of information time).

			Futility(Correlation)
			ρ12=0.0		ρ12=0.3		ρ12=0.5		ρ12=0.8		ρ12=1.0
No. of analyses/Information time		Efficacy	EP1	EP2	EP1	EP2	EP1	EP2	EP1	EP2	EP1	EP2
(Δ1, Δ2) = (0.1,0.1)
2	1/2	2.963	0.287	0.287	0.313	0.313	0.340	0.340	0.407	0.407	0.559	0.559
	1	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969
3	1/3	3.710	−0.662	−0.662	−0.621	−0.621	−0.579	−0.579	−0.473	−0.473	−0.237	−0.237
	2/3	2.511	1.014	1.014	1.030	1.030	1.045	1.045	1.084	1.084	1.170	1.170
	1	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993
4	1/4	4.333	−1.362	−1.362	−1.309	−1.309	−1.255	−1.255	−1.122	−1.122	−0.821	−0.821
	1/2	2.963	0.345	0.345	0.371	0.371	0.398	0.398	0.463	0.463	0.609	0.609
	3/4	2.359	1.299	1.299	1.309	1.309	1.320	1.320	1.345	1.345	1.402	1.402
	1	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014
(Δ1, Δ2) = (0.1,0.2)
2	1/2	2.963	0.559	−1.049	0.559	−1.409	0.559	−1.409	0.559	−1.409	0.559	−1.409
	1	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969
3	1/3	3.710	−0.238	−3.552	−0.238	−3.552	−0.238	−3.552	−0.238	−3.552	−0.238	−3.552
	2/3	2.511	1.170	−0.039	1.170	−0.039	1.170	−0.039	1.170	−0.039	1.170	−0.039
	1	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993
4	1/4	4.333	−0.822	−5.140	−0.822	−5.140	−0.821	−5.141	−0.821	−5.141	−0.821	−5.141
	1/2	2.963	0.609	−1.504	0.609	−1.504	0.609	−1.503	0.609	−1.503	0.609	−1.503
	3/4	2.359	1.401	0.542	1.401	0.542	1.402	0.542	1.402	0.542	1.402	0.542
	1	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014
(Δ1, Δ2) = (0.2,0.2)
2	1/2	2.963	0.285	0.285	0.312	0.312	0.338	0.338	0.405	0.405	0.558	0.558
	1	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969
3	1/3	3.710	−0.665	−0.665	−0.623	−0.623	−0.580	−0.580	−0.474	−0.474	−0.239	−0.239
	2/3	2.511	1.014	1.014	1.029	1.029	1.045	1.045	1.084	1.084	1.170	1.170
	1	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993
4	1/4	4.333	−1.363	−1.363	−1.314	−1.314	−1.260	−1.260	−1.126	−1.126	−0.823	−0.823
	1/2	2.963	0.345	0.345	0.369	0.369	0.395	0.395	0.461	0.461	0.608	0.608
	3/4	2.359	1.299	1.299	1.308	1.308	1.319	1.319	1.344	1.344	1.401	1.401
	1	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014
(Δ1, Δ2) = (0.2,0.3)
2	1/2	2.963	0.540	−0.464	0.545	−0.457	0.550	−0.450	0.555	−0.443	0.558	−0.440
	1	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969
3	1/3	3.710	−0.263	−1.949	−0.255	−1.938	−0.247	−1.926	−0.239	−1.915	−0.239	−1.915
	2/3	2.511	1.161	0.536	1.164	0.540	1.167	0.544	1.170	0.548	1.170	0.548
	1	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993
4	1/4	4.333	−0.849	−3.062	−0.844	−3.055	−0.834	−3.040	−0.823	−3.026	−0.823	−3.026
	1/2	2.963	0.596	−0.488	0.599	−0.484	0.603	−0.477	0.608	−0.470	0.608	−0.470
	3/4	2.359	1.396	0.962	1.397	0.964	1.399	0.967	1.401	0.970	1.401	0.970
	1	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014
(Δ1, Δ2) = (0.3,0.3)
2	1/2	2.963	0.283	0.283	0.308	0.308	0.338	0.338	0.405	0.405	0.555	0.555
	1	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969	1.969
3	1/3	3.710	−0.668	−0.668	−0.629	−0.629	−0.581	−0.581	−0.483	−0.483	−0.240	−0.240
	2/3	2.511	1.012	1.012	1.027	1.027	1.045	1.045	1.081	1.081	1.169	1.169
	1	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993	1.993
4	1/4	4.333	−1.364	−1.364	−1.314	−1.314	−1.263	−1.263	−1.128	−1.128	−0.821	−0.821
	1/2	2.963	0.344	0.344	0.369	0.369	0.394	0.394	0.460	0.460	0.609	0.609
	3/4	2.359	1.299	1.299	1.308	1.308	1.318	1.318	1.344	1.344	1.402	1.402
	1	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014	2.014

4. Operating characteristics: behavior of power, ASN and the Type I error

In this section, we investigate the operating characteristics of the decision-making frameworks described in Section 2.2. We discuss the power and Type I error rate under a given sample size for a one-sided test. For illustration, we consider a randomized clinical trial designed to compare a T to a C based on the two co-primary endpoints (EP1 and EP2). We discuss the nine group-sequential designs shown in Table 2: the first five designs include efficacy and futility assessments for both endpoints at the same interim analyses (the same interim assessment). The last four include a futility assessment for both endpoints only at the first interim analysis and then only efficacy assessments for both endpoints at later interim analyses (the different interim assessment), where the maximum number of analyses is 2, 3 or 4. The efficacy and futility boundaries for the two endpoints are determined based on the OF-type boundary using the LD error-spending function for the Type I and II errors, with equally or unequally-spaced increments of information time, where the significance level for a one-sided test is α = 2.5%.

Table 2.

Group-sequential designs for efficacy or futility assessments in clinical trials with two co-primary endpoints (EP1 and EP2).

			Information time
Situation	Design No.	Assessment	1/4	1/2	3/4	1
1.  Futility and efficacy assessments for both endpoints at the same interim analysis: the same interim assessment	#1–1	Efficacy	Both	Both	Both	Both
		Futility	Both	Both	Both	Both
	#1–2	Efficacy		Both	Both	Both
		Futility		Both	Both	Both
	#1–3	Efficacy	Both		Both	Both
		Futility	Both		Both	Both
	#1–4	Efficacy	Both	Both		Both
		Futility	Both	Both		Both
	#1–5	Efficacy		Both		Both
		Futility		Both		Both
2.  Futility assessment only conducted at the first interim analysis and then efficacy assessment at later interim analyses: the different interim assessment	#2–1	Efficacy		Both	Both	Both
		Futility	Both			Both
	#2–2	Efficacy			Both	Both
		Futility		Both		Both
	#2–3	Efficacy			Both	Both
		Futility	Both			Both
	#2–4	Efficacy		Both		Both
		Futility	Both			Both

4.1. Power behavior

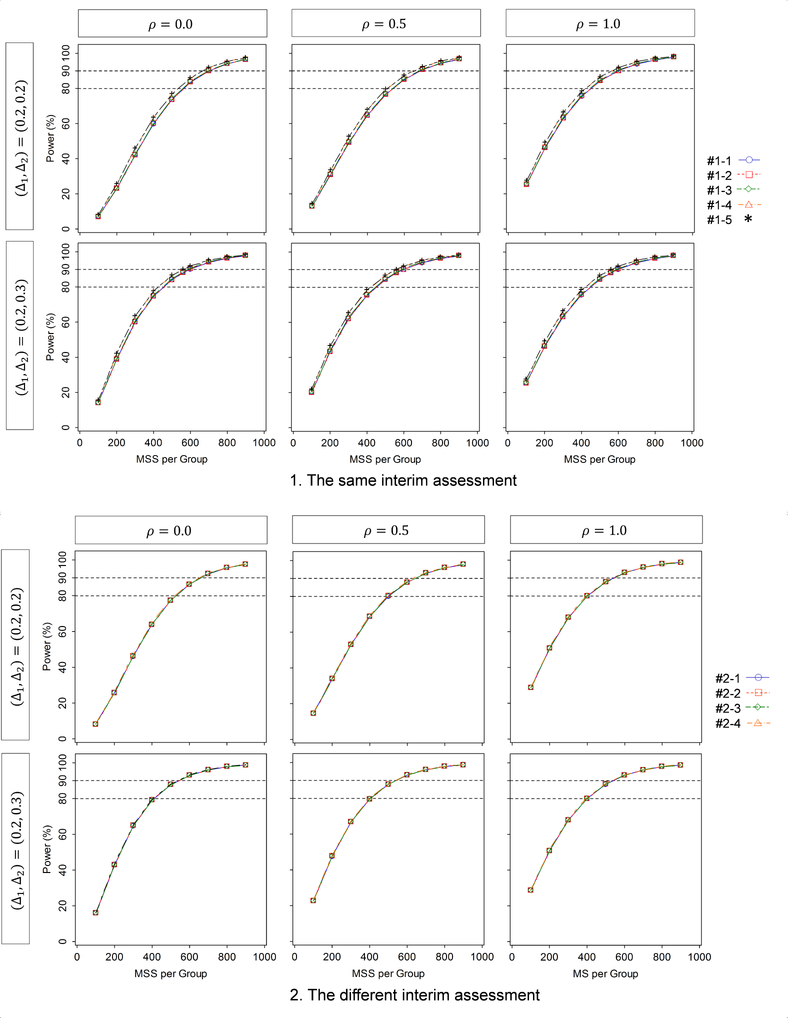
First we evaluate how the power behaves with the given MSS per intervention group, the correlation between the two endpoints, and the standardized mean differences for the two endpoints, where the MSS (equally-sized group: r =1) is varied from n_L =100 to 900 by 100; the correlation varies from ρ₁₂ = 0.0, 0.5 and 1.0; the standardized mean differences are (Δ₁, Δ₂) = (0.2,0.2) and (0.2,0.3) for the same and different interim assessments. The results are displayed in Figure 1. When conducting the assessment for both of efficacy and futility at the same interims (upper figures), if the two standardized mean differences are equal, i.e., (Δ₁, Δ₂) = (0.2,0.2), then the power is increased with a larger sample size and a higher correlation. On the other hand, if one standardized mean difference is larger than the other, i.e., (Δ₁, Δ₂) = (0.2,0.3), then the power is increased with a larger sample size but is not greatly affected by the correlation. For both equal and unequal mean differences, although there is no meaningful difference in the power among the five designs (the maximum difference is 1.6%), the smallest power is given by Design #1–1 and the largest is given by Design #1–5. Among Designs #1–2, #1–3 and #1–4 (L =3), the smallest power is given by Design #1–2 and the largest is given by Design #1–4.

Figure 1.

Behavior of the power as a function of the standardized mean difference and correlation, for the group-sequential designs shown in Table 2 (DF-1).

When conducting the different interim assessment for efficacy and futility (bottom figures), similarly as in the same interim assessment, if (Δ₁, Δ₂) = (0.2,0.2), then the power is increased with a larger sample size and a larger correlation. On the other hand, if (Δ₁, Δ₂) = (0.2,0.3) and (0.3,0.2), then the power is increased with a larger sample size but is not greatly affected by the correlation. For both equal and unequal standardized mean differences, although there is no appreciable difference in the power among the five designs (the maximum difference is 0.4%), the lowest power is given by Design #2–2 and the highest is given by Design #2–4. The different interim assessment provides higher power than the same interim assessment although the differences are small (the maximum difference is 1.1%).

In summary, higher correlation increases the power if the standardized mean differences are equal, but does not otherwise affect power. A larger number of analyses decreases the power. Allocation of the efficacy and/or futility assessment to interim analyses with earlier information time increases the power.

4.2. ASN behavior

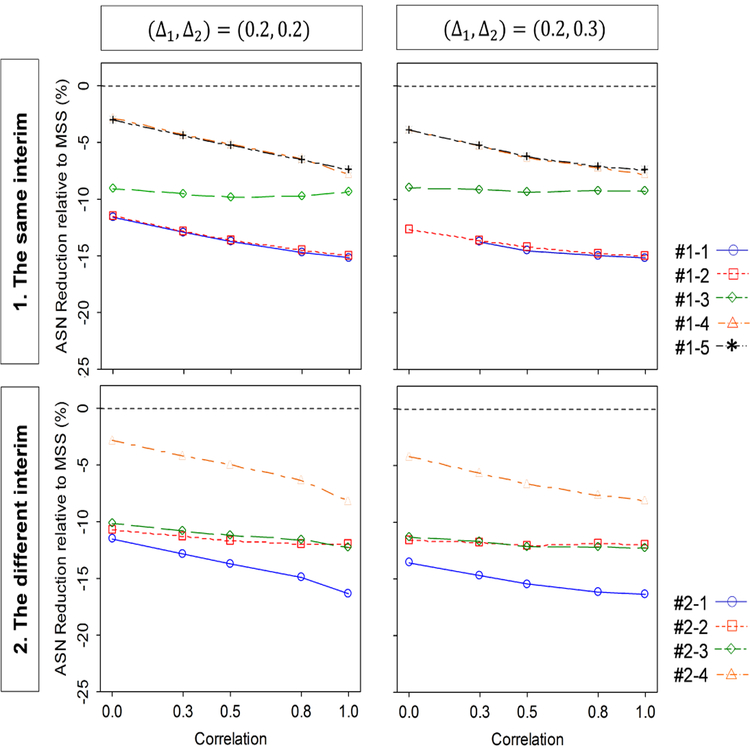
Next, we evaluate how the ASN under a given MSS per intervention group behaves as a function of the correlation between the two endpoints and the standardized mean differences for the two endpoints. The correlation is selected as ρ₁₂ = 0.0, 0.3, 0.5, 0.8 and 1.0. The standardized mean differences (Δ₁, Δ₂) =(0.2,0.2) and (0.2,0.3) for same and different interim assessments. Under these parameter configurations, the given MSS per intervention group are calculated to detect the joint effect of (Δ₁, Δ₂) with the power of 80% at the significance level of 2.5% for a one-sided test, assuming zero correlation between the two endpoints, in a fixed-sample size design; they are 516 for (Δ₁, Δ₂) = (0.2,0.2), and 402 for (Δ₁, Δ₂) = (0.2,0.3). The result is displayed as a reduction in ASN relative to the given MSS ((ASN–MSS)/MSS) × 100) in Figure 2. When conducting the assessment for both of efficacy and futility at the same interims, the ASN reduction is larger with higher correlation if (Δ₁, Δ₂) = (0.2,0.2), but is not much changed by correlation if (Δ₁, Δ₂) = (0.2,0.3). For both equal and unequal standardized mean differences, the largest ASN reduction is given by Design #1–1 and smallest by Design #1–5. Among Designs #1–2, #1–3 and #1–4 (L =3), the largest reduction is given by Design #1–2 and the smallest is by Design #1–4.

Figure 2.

Behavior of the ASN (sample size reduction relative to MSS) as a function of the standardized mean difference and correlation, for the group-sequential designs shown in Table 2 (DF-1).

When conducting the different interim assessment for efficacy and futility, similarly as in the same interim assessment, the power is increased with a higher correlation if (Δ₁, Δ₂) =(0.2,0.2), but it is not much changed by correlation if (Δ₁, Δ₂) = (0.2,0.3). For both equal and unequal mean differences, the largest ASN reduction is given by Design #2–1 and smallest by Design #2–4. Designs #2–2 provides a larger reduction than Design #2–3 if (Δ₁, Δ₂) = (0.2,0.2) and (0.2,0.3). The different interim assessment provides a larger ASN reduction than the same interim assessment.

In summary, higher correlation increases the ASN reduction if the standardized mean differences are equal, but does not otherwise affect the ASN. A larger number of analyses increases the ASN reduction. Allocation of the efficacy and/or futility assessments to interim analysis with earlier information time decreases the ASN reduction.

4.3. Type I error behavior

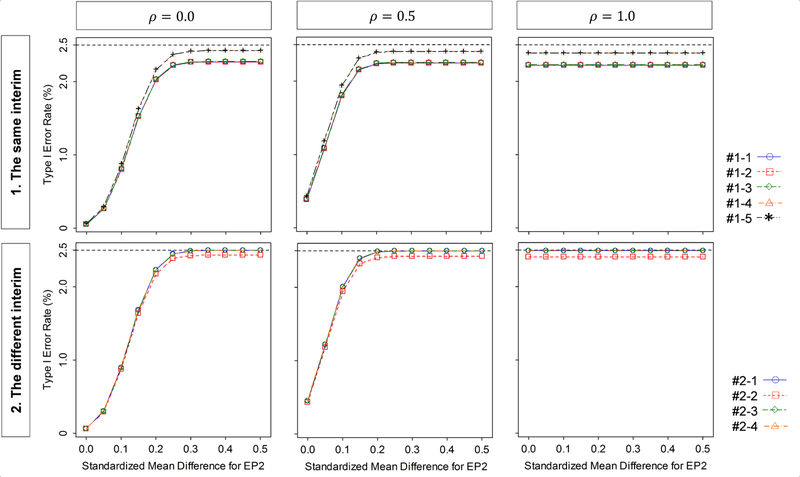
Finally, we evaluate how the Type I error behaves with the standardized mean differences for the two endpoints and the correlation between the two endpoints. The standardized mean differences is selected as (Δ₁, Δ₂) = (0.0, ${\Delta }_2^{*}$) with ${\Delta }_2^{*}$ = 0.0 to 0.5 by 0.05, and the correlation is ρ₁₂ = 0.0, 0.5 and 1.0, and the significance level for the one sided test is α = 2.5%. The MSS per intervention group is 516 which has 80% power to detect the joint effect on the two endpoints with the standardized mean differences of (Δ₁, Δ₂) = (0.2,0.2) at the significance level of α = 2.5% for a one-sided test. The results are displayed in Figure 3. When conducting the assessment for both of efficacy and futility at the same interims, the Type I error rate is increased as ${\Delta }_2^{*}$ increases and as the correlation increases, but is never larger than the targeted significance level of 2.5%. The smallest Type I error rate is given by Design #1–4 and the largest is by Design #1–5. Among Designs #1–2, #1–3 and #1–4 (L =3), the smallest Type I error rate is given by Design #1–2 and the largest is by Design #1–4.

Figure 3.

Behavior of the Type I error rate as a function of the standardized mean difference ${\Delta }_2^{*}$ and correlation ρ₁₂, for the group-sequential designs shown in Table 2 (DF-1).

When conducting the assessment for efficacy and futility at the different interims, similarly as in the same interim assessment, the Type I error rate is increased as ${\Delta }_2^{*}$ increases and as ρ₁₂ increases. However it is never larger than the targeted significance level of 2.5%. The Type I error rates for Designs #2–1, #2–3, and #2–4 are at most achieved at the targeted level, but not for Design #2–2. The smallest Type I error rate is given by Design #2–2 and the largest is by Design #2–3 although there is no meaningful difference in Type I error rate among Designs #2–1, #2–3 and #2–4. The same interim assessment provides a smaller Type I error rate than the different interim assessment but differences are negligible (the maximum difference is 0.2%).

In summary, higher correlation increases the Type I error rate but not above the targeted significance level. A larger number of futility assessments decreases the Type I error rate. Allocation of the futility assessments to interim analyses with later information time decreases the Type I error rate.

5. An illustration: Tarenflurbil study

We illustrate the concepts with an example from the Tarenflurbil study (Green et al., 2009) described in the Introduction. Recall that the study was designed to evaluate if tarenflurbil was superior to placebo on two co-primary endpoints, (i) change score from baseline on the ADAS-cog, and (ii) change score on the ADCS-ADL. The original design called for 800 participants per intervention group to provide a power of 96% to detect the joint between-group difference in the two primary endpoints using a one-sided test at the 2.5% significance level, with an alternative hypothesis of a standardized effect mean difference of 0.2 for both endpoints. The correlation between the two endpoints was assumed to be zero.

Table 3 displays the efficacy and futility boundaries, MSS and ASN per intervention group (equally-sized groups: r =1) in the DF-1 for the group-sequential designs shown in Table 2 (the different interim assessment). The MSS was calculated with an alternative hypothesis of a standardized mean difference for both ADAS-Cog (Δ₁ =0.2) and ADCS-ADL (Δ₂ =0.2), with the power of 96% at the one-sided significance level of 2.5%, where ρ₁₂ = 0.0, 0.3, 0.5, 0.8 and 1.0, and σ₁ = σ₂ =1.0. The ASN is calculated under (Δ₁, Δ₂) =(0.2,0.2), (0.0,0.2) and (0.0,0.0). The efficacy and futility boundaries are determined commonly based on the OF-type boundary by using LD error-spending function for the Type I and II errors, with equally or unequally-spaced increments of information.

Table 3.

Efficacy and futility boundaries, MSS and ASN (per intervention group) in group-sequential designs for Tarenflurbil study, including efficacy and futility assessments for the two endpoints based on DF-1 for the group-sequential designs shown in Table 2.

			Information time				ASN(Δ1,Δ2)
Design No.	ρ12	Assessment	1/4	1/2	3/4	1	MSS	(0.2,0.2)	(0.2,0.0)	(0.0,0.0)
#1–1		Efficacy	4.333	2.963	2.359	2.014
	0.0	Futility	−2.459	−0.195	1.083	2.014	836	623	564	489
	0.3		−2.441	−0.186	1.086	2.014	831	608	559	498
	0.5		−2.412	−0.172	1.092	2.014	824	594	553	502
	0.8		−2.322	−0.128	1.110	2.014	798	563	532	500
	1.0		−2.044	0.009	1.165	2.014	725	498	468	468
#1–2		Efficacy	→	2.963	2.359	2.014
	().()	Futility	→	−0.194	1.083	2.014	836	623	565	492
	0.3		→	−0.186	1.086	2.014	831	608	561	501
	0.5		→	−0.172	1.092	2.014	824	595	555	505
	0.8		→	−0.127	1.110	2.014	798	564	533	503
	1.0		→	0.010	1.165	2.014	725	500	472	472
#1–3		Efficacy	4.333	→	2.340	2.012
	0.0	Futility	−2.460	→	1.096	2.012	835	669	650	624
	0.3		−2.442	→	1.100	2.012	829	661	645	623
	0.5		−2.413	→	1.106	2.012	822	654	639	620
	0.8		−2.323	→	1.126	2.012	796	629	617	606
	1.0		−2.048	→	1.187	2.012	722	566	554	554
#1–4		Efficacy	4.333	2.963	→	1.969
	0.0	Futility	−2.492	−0.242	→	1.969	809	725	644	546
	0.3		−2.471	−0.232	→	1.969	804	703	638	559
	0.5		−2.446	−0.220	→	1.969	796	684	630	564
	0.8		−2.355	−0.176	→	1.969	111	644	602	562
	1.0		−2.080	−0.044	→	1.969	696	564	524	524
#1–5		Efficacy	→	2.963	→	1.969
	0.0	Futility	→	−0.241	→	1.969	809	725	645	548
	0.3		→	−0.231	→	1.969	804	703	639	561
	0.5		→	−0.219	→	1.969	796	684	631	567
	0.8		→	−0.175	→	1.969	771	644	604	565
	1.0		→	−0.043	→	1.969	696	565	527	527
#2–1		Efficacy	→	2.963	2.359	2.014
	0.0	Futility	−2.482	→	→	2.014	817	618	811	809
	0.3		−2.462	→	→	2.014	812	603	806	804
	0.5		−2.435	→	→	2.014	804	589	797	795
	0.8		−2.343	→	→	2.014	111	558	769	767
	1.0		−2.076	→	→	2.014	701	493	689	689
#2–2		Efficacy	→	—>	2.340	2.012
	0.0	Futility	→	−0.224	→	2.012	819	661	649	552
	0.3		→	−0.214	→	2.012	814	654	643	565
	0.5		→	−0.201	→	2.012	806	646	635	571
	0.8		→	−0.158	→	2.012	780	622	608	569
	1.0		→	−0.027	→	2.012	705	560	531	531
#2–3		Efficacy	→	→	2.340	2.012
	0.0	Futility	−2.483	→	→	2.012	817	660	811	809
	0.3		−2.463	→	→	2.012	811	653	805	803
	0.5		−2.436	→	→	2.012	803	645	797	794
	0.8		−2.347	→	→	2.012	776	620	770	767
	1.0		−2.076	→	→	2.012	700	557	688	688
#2–4		Efficacy	→	2.963	→	1.969
	0.0	Futility	−2.495	→	→	1.969	807	725	803	799
	0.3		−2.478	→	→	1.969	801	702	796	793
	0.5		−2.450	→	→	1.969	793	683	788	785
	0.8		−2.357	→	→	1.969	767	643	761	758
	1.0		−2.087	→	→	1.969	691	563	681	681

When only a futility assessment is conducted at the first interim analysis and then only efficacy assessments at later interim analyses are conducted for both endpoints, the smallest MSS is given by Design #2–4. The largest ASN reduction under (Δ₁, Δ₂) =(0.2,0.2) is given by Design #2–1, but the largest ASN reduction under (Δ₁, Δ₂) = (0.0,0.2) and (0.0,0.0) by #2–2. On the other hand, when both efficacy and futility assessments are conducted at the same analysis for both endpoints, the smallest MSS is given by Design #1–4 or #1–5, but the largest ASN reductions under all of the standardized mean difference combinations by Design #1–1 or #1–2.

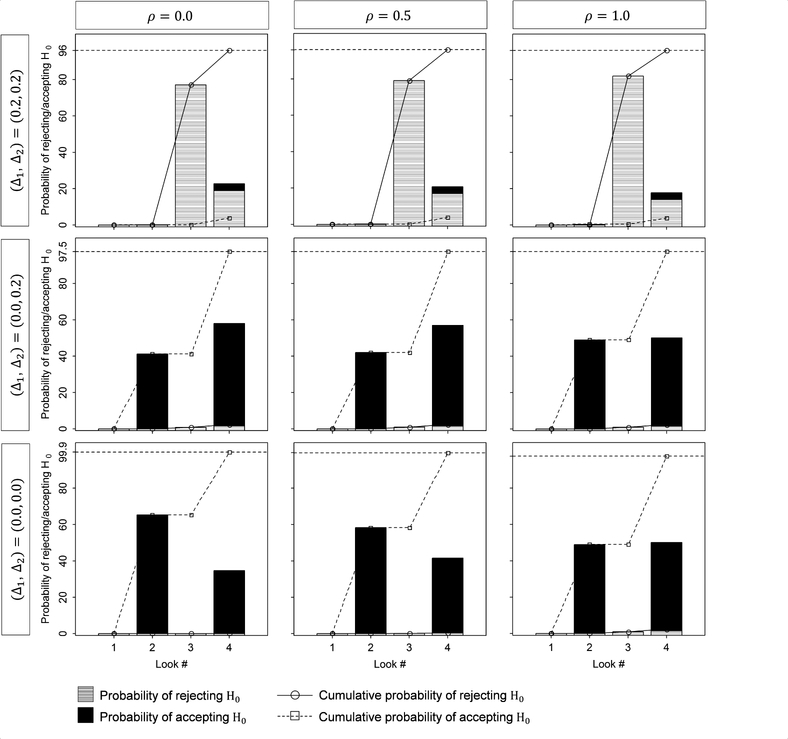
Figure 4 summarizes the probability of rejecting or accepting H₀ when using Design #2–2 shown in Table 2, with ρ₁₂ = 0.0, 0.5, and 1.0, and (Δ₁, Δ₂) = (0.2, 0.2), (0.0, 0.2) and (0.0, 0.0). For (Δ₁, Δ₂) = (0.2, 0.2) or (0.0, 0.2), when ρ₁₂ =0.0, it is difficult to reject or accept H₀ at the earlier analyses, but easier later on. On the other hand, as ρ₁₂ goes toward one, it is easier to reject or accept H₀ at the earlier analyses. For (Δ₁, Δ₂) = (0.0, 0.0), it is easier to reject H₀ at the earlier analyses, but difficult later on.

Figure 4.

Tarenflurbil study: The probability of rejecting or accepting the null hypothesis H₀ under hypothetical reference values for the group-sequential design #2–2 shown in Table 2 (DF-1).

6. Two practical considerations

When constructing efficient group-sequential strategies in clinical trials with multiple co-primary endpoints, there are two practical considerations. One is whether the correlation should be incorporated into futility boundary and sample size calculations or whether correlation should be assumed to be zero. Correlation estimates may be available from pilot or other studies. A conservative approach is to assume that the correlations are zero even if non-zero correlations are expected.

Table 4 summarizes the power and ASN under a given MSS and true correlation between the endpoints. The given MSS per intervention group (equally-sized groups: r =1) is calculated to detect a joint effect on the two endpoints with a power of 80% using one-sided test with a significance level of α = 2.5%, with DF-1 based on the OF-type boundaries for efficacy and futility using the LD error-spending function, where both of efficacy and futility assessments are conducted with equally-spaced increment in information.

Table 4.

Power and ASN under a given MSS and true correlation between the endpoints ${\rho }_{12}^{*}$. The given MSS per intervention group (equally-sized groups: r =1) is calculated to detect a joint effect on the two endpoints with a power of 80% using one-sided test with a significance level of α = 2.5%, with (Δ₁, Δ₂) =(0.2,0.2) and hypothetical correlation ρ₁₂ during planning, where both of efficacy and futility assessments are conducted based on DF-1 and critical boundaries are determined by OF-type boundary using the LD error-spending function with equally-spaced increment in information.

Hypo, correlation	No. of analyses		True correlation	ASN(Δ1,Δ2)
ρ12	L	MSS	${\rho }_{12}^{*}$	Power(%)	(0.2,0.2)	(0.2,0.0)	(0.0,0.0)
0.0	1	516
	2	529	0.0	80.0	500	365	305
			0.3	81.2	492	366	317
			0.5	82.4	486	367	325
			0.8	84.8	474	367	341
			1.0	89.5	456	367	367
	3	548	0.0	80.1	468	345	289
			0.3	81.3	460	345	298
			0.5	82.4	454	346	306
			0.8	84.9	443	346	321
			1.0	89.5	427	346	346
	4	560	0.0	80.0	456	329	277
			0.3	81.3	447	330	285
			0.5	82.4	440	330	292
			0.8	84.9	428	330	306
			1.0	89.5	410	330	330
0.5	1	490
	2	505	0.0	77.3	477	343	287
			0.3	78.7	469	344	298
			0.5	80.0	464	345	306
			0.8	82.8	454	345	321
			1.0	87.9	438	345	345
	3	524	0.0	77.3	448	323	269
			0.3	78.8	441	324	278
			0.5	80.0	435	324	286
			0.8	82.8	425	325	300
			1.0	87.9	410	325	325
	4	536	0.0	77.3	437	308	258
			0.3	78.7	429	309	266
			0.5	80.0	423	310	273
			0.8	82.8	412	310	287
			1.0	87.9	395	310	310
1.0	1	393
	2	415	0.0	64.1	380	263	225
			0.3	66.6	377	265	233
			0.5	68.7	375	266	238
			0.8	72.8	370	267	249
			1.0	80.1	363	267	267
	3	434	0.0	64.1	364	243	198
			0.3	66.6	359	245	206
			0.5	68.6	356	246	213
			0.8	72.8	351	247	226
			1.0	80.0	344	247	247
	4	446	0.0	64.1	357	233	190
			0.3	66.6	351	235	198
			0.5	68.6	348	236	204
			0.8	72.8	342	237	216
			1.0	80.1	333	237	237

The standardized mean differences are (Δ₁, Δ₂) = (0.2,0.2), the numbers of analyses are L =2, 3, and 4, and the hypothetical correlations during planning are ρ₁₂ =0.0, 0.5 and 1.0. The power is calculated under the true correlation ${\rho }_{12}^{*}$ = 0.0, 0.3, 0.5, 0.8 and 1.0 with (Δ₁, Δ₂) = (0.2,0.2). The ASN is calculated under the true correlation ${\rho }_{12}^{*}$ = 0.0, 0.3, 0.5, 0.8 and 1.0 with (Δ₁, Δ₂) = (0.2,0.2), (0.0,0.2) and (0.0,0.0). When the true correlation is ${\rho }_{12}^{*}$ = 0.5, the boundary and sample size are calculated with the hypothetical correlation ρ₁₂ = 0.0 during planning, the MSSs are 529, 548 and 560 for L =2, 3, and 4 respectively. This is approximately 5% larger than the MSSs of 505, 524 and 536 calculated with ρ₁₂ = 0.5. The power under the MSS with the true correlation is 2.4% higher than the target power of 80%. When the true correlation is ${\rho }_{12}^{*}$ = 1.0, the boundary and sample sizes are calculated with the hypothetical correlation of ρ₁₂ = 0.0 during planning, and the MSS is 26% larger than MSS of 415, 434 and 446 calculated with ρ₁₂ =1.0. However, the power under the MSS with the true correlation is 9.5% higher than the target power. Conversely, when the true correlation is ${\rho }_{12}^{*}$ = 0.0, the boundary and sample size are calculated with the hypothetical correlation ρ₁₂ = 0.5 or 1.0 during planning, the power under the calculated sample size under the MSS with the true correlation ${\rho }_{12}^{*}$ = 0.0 is 2.6% or 16.0% lower than the target power of 80%. However, assuming zero correlations is conservative when there is concrete evidence of higher correlations. In this situation, one approach is to use the confidence limit method discussed in Tamhane, Wu, and Mehta (2012) which takes sampling error associated with the correlations into account by use of the upper confidence limit of the correlation. The advantage of incorporating the correlation into the calculation of the futility boundary, power, and sample sizes is minimal when the standardized mean differences among the endpoints are unequal. In cases where the effects are expected to be different across the endpoints, trials can be sized based on the endpoint with the smaller standardized effect as if it was a trial with a single primary endpoint without Type II error adjustment.

A second consideration is the choice of boundary-type for the efficacy and futility assessments based on the error-spending function for each endpoint. We have discussed the common boundary-type for the efficacy and futility assessments among the endpoints. For example, when considering a clinical trial with the two co-primary endpoints, one option is to select the OF-type for calculating the efficacy boundary and the Pocock (PC)-type boundary (Pocock, 1977) for the futility boundary, for both endpoints. Another option is to select the OF-type for efficacy and futility boundaries for one endpoint and the PC-type boundaries for the other endpoint. If the trial is designed to detect effects on at least one endpoint with a prespecified ordering of endpoints, then the selection of different boundaries for each endpoint can provide a higher power than using the same boundary for both of the endpoints (Glimm et al., 2010; Tamhane et al., 2012). However, as shown in Asakura et al. (2014) and Hamasaki et al. (2015), the selection of a different boundary-type has a minimal effect on the power and ASN in clinical trials with co-primary endpoints including those with only efficacy assessments. Table 5 illustrates the MSS and ASN with a combination of OF- and PC-type boundaries for two endpoints (EP1 and EP2) (a common combination between the efficacy and futility assessments). The MSS per intervention group (equally-sized groups: r =1) is calculated to detect a joint effect on the two endpoints with a power of 80% using one-sided test with a significance level of α = 2.5%, where ρ₁₂ =0. Both of efficacy and futility assessments are conducted based on DF-1 and critical boundaries are determined using the LD error-spending function with equally-spaced increment in information. The ASN is calculated under H₁. When the standardized mean differences between the endpoints are unequal, i.e., (Δ₁, Δ₂) = (0.1,0.2), the combination of the OF-type boundary for both endpoints provides the smallest MSS. But, the combination of the OF-type boundary for EP1 and the PC-type boundary for EP2 provides a larger MSS only by one patient and a slightly smaller ASN than the combination of the OF-type boundary for both endpoints. On the other hand, when the standardized mean differences between the endpoints are equal, i.e., (Δ₁, Δ₂) = (0.2,0.2), the combination of the OF-type boundary for both endpoints provides the smallest MSS. The combination of the OF-type boundary for EP1 and the PC-type boundary for EP2 provides a larger MSS and larger ASN than the combination of the OF-type boundary for both endpoints. For the combination of boundary type for efficacy and futility assessments (a common combination between the endpoints) which is not shown in the paper, the findings from the single endpoint suggest that the OF-type for both assessments provides the highest power and the smallest MSS. These results suggest that the selection of a different boundary-type has a minimal effect on the power and ASN in clinical trials with co-primary endpoints including trials with both efficacy and futility assessments. In terms of the power and ASN, a practical option is to select the OF-type boundary for efficacy and futility assessments. If the standardized mean differences are not equal, then a different type of boundary may be considered: OF-type boundary for endpoint(s) with a smaller standardized mean difference and a PC-type boundary for endpoint(s) with a larger standardized mean difference. A more complex option is to have a different boundary-type selection for all of the efficacy and futility assessments and endpoints but this is less practical.

Table 5.

MSS and ASN with a combination of OF-type and PC-type boundaries for two endpoints (EP1 and EP2). The MSS per intervention group (equally-sized groups: r =1) is calculated to detect a joint effect on the two endpoints with a power of 80% using one-sided test with a significance level of α = 2.5%, where ρ₁₂ = 0. Both of efficacy and futility assessments are conducted based on DF-1 and critical boundaries are determined using the LD error-spending function with equally-spaced increment in information. The ASN is calculated under H₁.

Standardized mean difference (Δ1,Δ2)	The number of analyses
	Boundary-type		L = 2		L = 3		L = 4
	EP1	EP2	MSS	ASN	MSS	ASN	MSS	ASN
(0.1,0.2)	OF	OF	1658	1473	1734	1385	1782	1343
	OF	PC	1659	1458	1735	1378	1783	1336
	PC	OF	2005	1381	2174	1376	2264	1338
	PC	PC	2005	1352	2174	1273	2264	1236
(0.2,0.2)	OF	OF	529	500	548	468	560	456
	OF	PC	592	510	628	482	648	468
	PC	PC	649	470	700	450	728	438

7. Summary

Increasingly clinical trials are being designed with more than one co-primary endpoint to more comprehensively evaluate intervention’s multidimensional effects. As with trials involving a single primary endpoint, designing co-primary endpoint trials to include interim analyses (i.e., with repeated testing) may provide resource efficiency and minimize the number of trial participants exposed to an ineffective intervention. However, this creates challenges in the evaluation of power and the calculation of sample size during trial design. We discuss group-sequential designs in clinical trials with multiple co-primary endpoints, and evaluate decision-making frameworks for stopping for efficacy or futility, based on boundaries using group-sequential methodology. The basic idea in the paper is similar to that introduced by the JT method, but the proposed methodology includes the two advances compared with JT method: (1) methodology for determining the efficacy and futility boundaries, and (2) decision-making frameworks for rejecting or accepting the null hypothesis associated with multiple co-primary endpoints. We summarize the main differences between our methods (AHE methods) and the JT methods shown in Table 6.

Table 6.

The main differences between the AHE methods and the JT methods

	The JT methods	The AHE methods
Efficacy and futility boundary determination	Power family by Emerson and Fleming (1989)	Error-speeding method by Lan and De-Mets (1983)
Incorporation of correlation in power and futility boundary	Power assessment only	Power assessment and futility boundary calculations- allows evaluation of how adjusting the futility boundary by incorporating the correlations, may affect the decision-making for accepting the null hypothesis
Decision-making framework for rejecting the null hypothesis	Simple- conducts both of the efficacy and futility assessments at the same interim analyses	Flexible- allows for different timings for efficacy and futility assessments and provides savings for error spending (Type I and II errors), thus improving the efficiency (increasing power and reducing required sample sizes)
Calculation of power and sample sizes	Requires a simple iterative procedure	Requires a complex iterative procedure

We incorporate correlations among the endpoints into the boundary and sample size calculations and illustrate the behavior of the futility boundary with varying mean differences and number of analyses. We investigate the operating characteristics of the proposed decision-making frameworks in terms of the power, the Type I error and sample size with varying number of analyses, the correlations among the endpoints, and the standardized mean differences. We provide an example illustrating the methods and discuss two practical considerations when designing the efficient group-sequential designs in clinical trials with co-primary endpoints. These results are useful for designing an efficient clinical trial with multiple co-primary endpoints. When conducting group-sequential efficacy and futility assessments in these trials, there is an advantage of incorporating correlations among the endpoints into the futility boundary and sample size calculations particularly when the correlations are large and the effects on the endpoints are similar. A larger number of analyses decreases the power, but increases the reduction in ASN. Efficacy and futility assessments at earlier information time increase the power but decrease the reduction in ASN. The power for assessing efficacy and futility at different interim analyses is larger than one for assessing both of efficacy and futility at the same interim analyses. Careful consideration is needed regarding the frequency and timing of the efficacy and futility assessments. When there is a high confidence that all of the endpoints could be statistically significant, then assessing efficacy and futility at different interim analysis timepoints could save costs in Type I and II errors spending and increase power and reduce the required sample sizes. However, when there is uncertainty in demonstrating a joint effect on all of the endpoints, the decision-making framework that includes both efficacy and futility assessments at the same interim analysis timepoint is a better strategy because the number of trial participants exposed to an ineffective intervention can be minimized.

Our discussion has been restricted to continuous outcomes being evaluated in a superiority clinical trial with two interventions when the aim is to evaluate effects on all endpoints. However, the methods provide a foundation for designing randomized trials with other outcome scales. Cook and Farewell (1994) provided some guide on designing clinical trials with two time-to-event outcomes in a group-sequential setting. However, time-to-event outcomes are more complex and require careful consideration when designing clinical trials in a group-sequential setting. As discussed in Hamasaki et al. (2013) and Sugimoto et al. (2013) in the fixed-sample designs, the strength of the association among the time-to-event outcomes may depend on time. The censoring mechanism further complicates the design of these trials. In addition, as Hung et al. (2016) point out, the allocation of the Type I error to each interim analysis is more complicated as the amount of information for the endpoints may be different at any particular interim timepoint of the trial.

The methods also provide the foundation for designing randomized trials with other inferential goal, i.e., when the aim is to evaluate an effect on at least one endpoint (multiple primary endpoints). For example, in many oncology settings, the most commonly used primary endpoint is overall survival (OS) defined as the time from randomization until death from any cause. OS in general requires long follow-up periods after disease progression, which leads to quite long and also expensive studies. Therefore, many clinical trials include a short-term primary endpoint such as time to progression (TTP) or progression-free survival (PFS), defined as the time from randomization until tumor progression or death. One strategy is to assess futility only for TTP (or PFS) at earlier interim analyses and to assess the efficacy for either TTP and OS at later interim analyses if negative signs are not detected for TTP at the earlier interim analyses. If a negative sign is detected for TTP at the earlier interim analysis, the trial is terminated. The methods could be also applicable to select the most promising endpoint(s) among the candidate endpoints in explanatory clinical trials. One may consider stopping measurement for an endpoint which statistic has already crossed the futility boundary. If all statistics for the endpoints cross the futility boundary, the trial is terminated. As mentioned above, note that careful consideration is required to deal with censoring scheme and time-dependent association in designing clinical trials with multiple time-to-event outcomes.

Our research motivation comes from Tarenflurbil study which included two co-primary endpoints in the treatment of early stage Alzheimer Disease. In addition to Alzheimer Disease, the two co-primary endpoint situation is the common in other disease areas, e.g., asthma, benign prostatic hyperplasia, irritable bowel syndrome, oncology, and vaccines. Therefore, we focused the two co-primary endpoint situation as a fundamental and common occurrence although the methods were generalized to a situation with more than two co-primary endpoints. Three co-primary endpoints are also common in some disease areas, e.g., acute pain, fibromyalgia, low back pain, osteoarthritis, and election dysfunction. An extension to more than two endpoints is straightforward, but the computational cost will be very expensive in the power evaluations using a numerical integration method as shown in Appendix. In this situation, a Monte-Carlo simulation-based method provides a good alternative but the number of replications for simulations should be carefully chosen to control simulation error in calculating the empirical power.

Appendix

A.1. ASN calculation

As defined in Section 2, the ASN is the expected sample size under hypothetical reference values which is given by

$$\text{ASN}=\sum _{l=1}^{L-1}{n}_l{P}_l\left({\delta }_1,\dots ,{\delta }_K\right)+n_L\left(1-\sum _{l=1}^{L-1}{P}_l\left({\delta }_1,\dots ,{\delta }_K\right)\right),$$

where P_l(δ₁,…, δ_K) = P_El + P_Fl, and P_El and P_Fl are the stopping probabilities for efficacy or futility at the lth analysis, assuming that the true values of the mean difference are (δ₁,…, δ_K). The ASN provides information regarding of the number of participants anticipated in a group-sequential design in order to reach a decision point. We briefly describe the several definitions of the ASN corresponding to the decision-making frameworks. For DF-1, the stopping probabilities at the first analysis are

$$P_{\text{E}1}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cap }}{A}_{k1}|{\mathcal{I}}_{k1}={\mathcal{I}}_1\right]\text{ and }{P}_{\text{F}1}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cup }}{E}_{k1}|{\mathcal{I}}_{k1}={\mathcal{I}}_1\right],$$

and at the lth analysis (l ≥ 2),

$$P_{\text{E}l}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cap }}\left\{A_{k1}\cup \left\{\underset{l_k^{\prime }=2}{\overset{l_k}{\cup }}\left\{\underset{l_k^{″}=1}{\overset{l_k^{\prime }-1}{\cap }}{B}_{k{l}_k^{″}}\cap A_{k{l}_k^{\prime }}\right\}\right\}\right\}\right]-\sum _{l^{\prime }=1}^{l-1}{P}_{\text{E}{l}^{\prime }}$$

and

$$P_{\text{F}l}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cup }}{E}_{k1}\cup \underset{l_k^{\prime }=2}{\overset{l_k}{\cup }}\left\{\underset{k=1}{\overset{K}{\cup }}\left\{\underset{l_k^{″}=1}{\overset{l^{\prime }-1}{\cap }}{D}_{k{l}_k^{″}}\right\}\cap \underset{k=1}{\overset{K}{\cup }}{E}_{k{l}_k^{\prime }}\right\}\right]-\sum _{l^{\prime }=1}^{l-1}{P}_{\text{F}{l}^{\prime }},$$

where $A_{k{l}_k}=\left\{Z_{k{l}_k}>c_{\text{E}k{l}_k}\right\}$, $B_{k{l}_k}=\left\{c_{\text{F}k{l}_k}<Z_{k{l}_k}\le c_{\text{E}k{l}_k}\right\}$, $C_{k{l}_k}=\left\{Z_{k{l}_k}>c_{\text{F}k{l}_k}\right\}$, $D_{k{l}_k}=\left\{Z_{k{l}_k}\le c_{\text{E}k{l}_k}\right\}$ and $E_{k{l}_k}=\left\{Z_{k{l}_k}\le c_{\text{F}k{l}_k}\right\}$, and l_k is the latest analysis for endpoint k on or before the information time at the lth analysis (i.e., ${\mathcal{I}}_{l_k}\le {\mathcal{I}}_l$).

Similarly for the DF-2, stopping probabilities at the first analysis are at

$$P_{\text{E}1}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cap }}{A}_{k1}|{\mathcal{I}}_{k1}={\mathcal{I}}_1\right]\text{ and }{P}_{\text{F}1}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cup }}{E}_{k1}|{\mathcal{I}}_{k1}={\mathcal{I}}_1\right],$$

at the lth analysis (l ≥ 2),

$$P_{\text{E}l}=\text{Pr}\left[\underset{k=1,{\mathcal{I}}_{l_1^{\prime }}=\dots ={\mathcal{I}}_{l_K^{\prime }}}{\overset{K}{\cap }}\left\{A_{k1}\cup \underset{l_k^{\prime }=2}{\overset{l_k}{\cup }}\left\{\underset{l_k^{″}=1}{\overset{l_k^{\prime }-1}{\cap }}{C}_{k{l}_k^{″}}\cap A_{k{l}_k^{\prime }}\right\}\right\}\right]-\sum _{l^{\prime }=1}^{l-1}{P}_{{\text{El}}^{\prime }},$$

and

$$P_{\text{F}l}=\text{Pr}\left[\underset{l_k^{\prime }=1}{\overset{l_k}{\cup }}\left\{\underset{l_k^{″}=1}{\overset{l_K^{\prime }}{\cap }}\left\{\underset{k=1,{\mathcal{I}}_{l_1^{″}}=\dots ={\mathcal{I}}_{l_K^{″}}}{\overset{K}{\cup }}{D}_{k{l}_k^{″}}\right\}\cap \underset{k=1}{\overset{K}{\cup }}{E}_{k{l}_k^{\prime }}\right\}\right]-\sum _{l^{\prime }=1}^{l-1}{P}_{\text{F}{l}^{\prime }}.$$

Furthermore, for DF-3, the sopping probabilities the 1st analysis are

$$P_{\text{E}1}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cap }}{A}_{k1}\right]\text{ and }{P}_{\text{F}1}=\text{Pr}\left[\underset{k=1}{\overset{K}{\cup }}{E}_{k1}\right],$$

and at the lth analysis (l ≥ 2),

$$P_{\text{E}l}=\text{ Pr }\left[\underset{l^{\prime }=1}{\overset{l-1}{\cap }}\left\{\underset{k=1}{\overset{K}{\cap }}{C}_{k{l}^{\prime }}\cap \underset{k=1}{\overset{K}{\cup }}{D}_{k{l}^{\prime }}\right\}\cap \underset{k=1}{\overset{K}{\cap }}{A}_{kl}\right]$$

and

$$P_{\text{F}l}=\text{Pr}\left[\underset{l^{\prime }=1}{\overset{l-1}{\cap }}\left\{\underset{k=1}{\overset{K}{\cap }}{C}_{k{l}^{\prime }}\cap \underset{k=1}{\overset{K}{\cup }}{D}_{k{l}^{\prime }}\right\}\cap \underset{k=1}{\overset{K}{\cup }}{E}_{kl}\right],$$

where A_kl = {Z_kl > c_Ekl}, C_kl = {Z_kl > c_Fkl}, D_kl = {Z_kl ≤ c_Ekl} and E_kl = {Z_kl ≤ c_Fkl}.

A.2. An iterative procedure for identifying the efficacy and futility boundaries, including the calculation for MSS

As a general case, we only describe the procedure for DF-1. The following is an iterative procedure for identifying the efficacy and futility boundaries $c_{\text{E}k{l}_k}$ and $c_{\text{F}k{l}_k}$ including the calculation for MSS n_L.

Step 1: Determine c_Ek1,…, $c_{\text{E}k{L}_k}$ using any group-sequential method.

Step 2: Select the two initial values $n_L^{(m-1)}$ and $n_L^{(m)}$ (m = 1, 2,…,).

Step 3: Select the initial values ${\beta }_k^{(j-1,m)}$ and ${\beta }_k^{(j,m)}$, where ${\beta }_k^{(j,m)}$ is the marginal Type II error rate for Endpoint k (j = 1; 2,…,).

Step 4: Calculate $n_L\left({\beta }_k^{(j,m)}\right)$ and c_Fk1,…, $C_{\text{F}k{L}_k}$, satisfying ${\beta }_{k1}^{(j,m)}=\text{Pr}\left[Z_{k1}\le c_{\text{F}k1}\right]$ and

$${\beta }_{kl}^{(j)}=\text{ Pr }\left[\underset{l^{\prime }=1}{\overset{l-1}{\cap }}\left\{c_{\text{F}k{l}^{\prime }}<Z_{k{l}^{\prime }}\le c_{\text{E}k{l}^{\prime }}\right\}\cap \left\{Z_{kl}\le c_{\text{E}kl}\right\}\right]$$

With ${\sum }_{l=1}^{L_k}{\beta }_{kl}^{(j,m)}={\beta }_k^{(j,m)}$ and $c_{\text{F}k{L}_k}=c_{\text{E}k{L}_k}$, using any group-sequential method (k = 1,…, K; l = 2,…, L_k).

Step 5: Update the value of β_k using the equation based on basic linear interpolation

$${\beta }_k^{(j+1,m)}=\frac{{\beta }_k^{(j-1,m)}\left\{n_L\left({\beta }_k^{(j,m)}\right)-n_L^{(m)}\right\}-{\beta }_k^{(j,m)}\left\{n_L\left({\beta }_k^{(j-1,m)}\right)-n_L^{(m)}\right\}}{n_L\left({\beta }_k^{(j,m)}\right)-n_L\left({\beta }_k^{(j-1,m)}\right)}.$$

Step 6: Calculate $n_L\left({\beta }_k^{(j+1,m)}\right)$ and c_Fk1,…,$c_{\text{F}k{L}_k}$ under current ${\beta }_k^{(j+1,m)}$ as with Step 4.

Step 7: If $\left|{\beta }_k^{(j+1,m)}-{\beta }_k^{(j,m)}\right|$ is within a prespecified error tolerance, then stop iterative procedures with ${\beta }_k^{(m)}$. Otherwise, go back to Step 5. Note: Calculate ${\beta }_k^{(m)}$, satisfying $n_L\left({\beta }_k^{(m)}\right)=n_L^{(m)}$, for all k.

Step 8: Calculate $f\left(n_L^{(m)}\right)$ which is the power (1) (DF-1) under the current $n_L^{(m)}$, using the c_Fk1,…, $C_{\text{F}k{L}_k}$ calculated at Step 6.

Step 9: Update the value of n_L, using the equation based on basic linear interpolation

$$n_L=\frac{n_L^{(m-1)}\left\{f\left(n_L^{(m)}\right)-(1-\beta )\right\}-n_L^{(m)}\left\{f\left(n_L^{(m-1)}\right)-(1-\beta )\right\}}{f\left(n_L^{(m)}\right)-f\left(n_L^{(m-1)}\right)}.$$

Step 10: If n_L is an integer, $n_L^{(m+1)}=n_L$; otherwise, $n_L^{(m+1)}=\left[n_L\right]+1$, where [n_L] is the greatest integer less than n_L. If $n_L^{(m+1)}=n_L^{(m)}$, stop the iterative procedures with $n_L^{(m+1)}$ as the final value. Otherwise, repeat Steps 3 to 9.

Options for the two initial values $n_L^{(0)}$ and $n_L^{(1)}$ include the sample sizes calculated for detecting the smallest standardized mean differences min[Δ₁,…, Δ_K] with the marginal power 1 – β with a one-sided test at the significance level of α. Another option is calculated by the same method but with the marginal power (1 – β)^1/K. This is because n_L lies between these options.

A.3. Computing time for evaluating the power

The following table illustrates the CPU time (in seconds) taken for calculating the power under a given sample size on a DELL Precision T7300 (Intel(R) Xeon(R) CPU E5–2630/2.60GHz/RAM 8.00GB/32bit operating system) for DF-3 with varying the number of endpoints (K), the number of analyses (L) and correlation ρ_kk′, where K =2 and 3; L =2, 3, 4 and 5; and a common correlation ρ = ρ_kk′ = 0.0, 0.5 and 0.8. The given sample sizes of 516 for K =2 and 586 for K =3 are enough to detect a joint effect on all endpoints (assuming a common effect size Δ = Δ_k = 0.2, and zero correlations among the endpoints) with the power of 80% at the significance level of 2.5% for a one-sided test in the fixed sample design. The O’Brian-Fleming-type boundary is commonly selected for efficacy and futility on all of the endpoints, with equally spaced increments of information. The program for calculating the power is coded in FORTAN 77/90, including the subroutine for computing the multivariate normal distribution function values, MVNDST developed by Professor Alan Genz of Washington State University (the subroutine MVNDST is available on at his website http://www.math.wsu.edu/faculty/genz/software/fort77/). In our study, computing the multivariate normal distribution function values using the subroutine MVNDST began with a maximum number of function values (MAXPTS) of 5000, an absolute error tolerance (ABSEPS) of0.00001, and a relative error tolerance (RELEPS) of zero. If the estimated absolute error (ERROR) is larger than required tolerance (ABSEPS), i.e., ERROR > ABSEPS, then MAXPTS is increased by 1000 to decrease the estimated absolute error.

Based on the result, except for the case of K =3 and L =4 and 5, the CPU time taken for calculating the power under a given sample size is within 10 seconds. As our algorithm generally requires 4 to 6 iterations for finding the final maximum sample size, depending on the initial values, the maximum CPU time is supposed to be one minutes. However, in the case of K =3 and L =5, the CPU time taken for calculating the power under a given sample size is over 300 seconds and the CPU time taken for finding the final maximum sample size is supposed to be over half hour. In this situation, a Monte-Carlo simulation-based method provides a good alternative but the number of replications for simulations should be carefully chosen to control simulation error in calculating the empirical power. For the case of K =3 and L =5, the Monte-Carlo simulation-based method can shorten the CPU time in less than one-quarter, where the number of replications is 100,000.

Appendix Table 1.

CPU time (in seconds) taken for calculating the power under a given sample size for DF-3 with varying the number of endpoints (K), the number of analyses (L) and common correlation ρ. The given sample sizes of 516 for K =2 and 586 for K =3 are enough to detect a joint effect on all endpoints (assuming a common effect size Δ = Δ_k = 0.2 and zero correlations among the endpoints) with the power of 80 % at the significance level of 2.5% for a one-sided test in the fixed sample design. The O’Brian-Fleming-type boundary is commonly selected for efficacy and futility on all of the endpoints, with equally spaced increments of information. The number of replications for power evaluation by Monte-Carlo simulation is 100,000.

		K =2		K =3
# of analyses L	Correlation ρ	Numerical integration	Monte-Carlo simulation	Numerical integration	Monte-Carlo simulation
2	0.0	0.14	44.59	0.78	75.69
	0.3	0.28	43.82	0.97	74.35
	0.5	0.39	42.73	2.36	73.02
	0.8	0.44	41.64	11.54	70.65
3	0.0	0.67	49.14	2.56	85.72
	0.3	0.87	48.06	3.81	82.96
	0.5	1.12	47.11	5.74	80.96
	0.8	1.37	45.72	11.39	77.42
4	0.0	1.01	55.27	40.06	97.31
	0.3	1.47	54.13	41.54	93.73
	0.5	1.23	52.96	43.23	91.34
	0.8	2.31	50.95	51.53	85.97
5	0.0	5.66	61.67	381.78	108.78
	0.3	6.29	60.06	383.92	104.40
	0.5	6.75	58.70	388.93	101.24
	0.8	8.89	56.53	411.05	101.24