Abstract
Stereoscopic endoscopes have been used increasingly in minimally invasive surgery to visualise the organ surface and manipulate various surgical tools. However, insufficient and irregular light sources become major challenges for endoscopic surgery. Not only do these conditions hinder image processing algorithms, sometimes surgical tools are barely visible when operating within low-light regions. In addition, low-light regions have low signal-to-noise ratio and metrication artefacts due to quantisation errors. As a result, present image enhancement methods usually suffer from heavy noise amplification in low-light regions. In this Letter, the authors propose an effective method for endoscopic image enhancement by identifying different illumination regions and designing the enhancement design criteria for desired image quality. Compared with existing image enhancement methods, the proposed method is able to enhance the low-light region while preventing noise amplification during image enhancement process. The proposed method is tested with 200 images acquired by endoscopic surgeries. Computed results show that the proposed algorithm can outperform state-of-the-art algorithms for image enhancement, in terms of naturalness image quality evaluator and illumination index.
Keywords: endoscopes, image processing, biomedical optical imaging, medical image processing, medical robotics, image enhancement, surgery
Keywords: low-light region, low signal-to-noise ratio, heavy noise amplification, endoscopic image enhancement, different illumination regions, enhancement design criteria, desired image quality, existing image enhancement methods, image enhancement process, endoscopic surgery, naturalness image quality evaluator, illumination index, noise suppression, stereoscopic endoscopes, minimally invasive surgery, surgical tools, insufficient light sources, irregular light sources, image processing algorithms
1. Introduction
Endoscopic surgery is increasingly performed for minimally invasive procedures. During the operation, the surgeon uses stereoscopic endoscopes to visualise organ surfaces in the body and manipulate various surgical tools. In principle, the data acquired are high-quality HD stereoscopic images, with the potential to provide secondary information to the surgeons, such as 3D reconstructed scenes, tool tracking, and object recognition. Nevertheless, all these applications assume that the images are acquired under an ideal environment that is free of artefacts, noise, and illumination non-uniformities. In practice, the endoscopic images suffer from some serious problems, such as insufficient illumination and a relatively narrow field of view [1]. Since the illumination distribution is extremely non-linear, such problems cannot be easily resolved by adjusting the light source intensity. As a result, algorithms such as 3D scene reconstruction and object recognition can suffer greatly in terms of robustness and produce erroneous results. Moreover, when surgeons are operating within low-light regions, the visibility of tools is often poor, severely increasing the risk of damaging and even puncturing important organs, such as liver and spleen. Therefore, there is a clinical need for endoscopic image enhancement to reduce surgical risks.
1.1. Related work
Image enhancement is an active technique and widely used in the field of the computer vision community. Many image enhancement methods were presented to address different issues for natural images. Most of them focus on contrast enhancement and dynamic range compression instead of illumination enhancement. Thus, these methods are not suitable for endoscopic image enhancements.
Classical approaches including the gamma correction-based method [2] and Retinex theory-based method [3] provide the fundamentals of the image enhancement algorithms. In gamma correction, the pixels with low-intensity values are mapped to higher intensity values following a non-linear projection operator. This method can effectively improve the visibility of low-light regions but suffer from contrast degradation and visual inconsistency. In retinex theory, the perceived image is often modelled with the illumination and reflectance components, where the illumination is assumed to be piece-wise linear. Earlier algorithms such as single-scale Retinex [4] and multi-scale Retinex algorithms [5, 6] use a centre-surround function to mimic the illumination gain of human visual system. These methods improve the lightness as well as the image contrast but they also suffer from over-enhancement, which degrades the naturalness of the image, as well as heavy colour distortions, which requires additional post-processing techniques such as colour restoration and histogram equalisation. To reduce over-enhancement and colour degradation, Wang et al. [7] proposed a image enhancement method by enhancing contrast and preserving the naturalness of the illumination. Recently, Guo et al. [8] proposed an effective low-light image enhancement algorithm, where an improved illumination map is estimated by imposing a structure prior on the maximum values in R, G, and B channels.
Although the existing methods are able to improve the illumination of dark images while preserving details, there is still a major challenge to be overcome. In low-light regions, the image pixels tend to suffer from low signal-to-noise ratio. Since image enhancement is a scaling operation by nature, the enhancement algorithm often amplify image noise in the process. Recently, Su and Jung [9] tried to address this problem by introducing a two-step perceptual enhancement algorithm to suppress camera noise in low-light images, but the algorithm seems to be less effective for endoscopic images.
1.2. Contribution
This Letter proposes a new image enhancement method based on identification in three illumination regions. The proposed method can enhance the visibility of the low light region of endoscopic images, preserve the naturalness of the image, and reduce noise/artifact amplification. The proposed method thus improves the image quality of endoscopic images, and can be used as an important pre-processing step for other image processing algorithms.
2. Method
We consider the Retinex model defined as
| (1) |
where R represents the natural reflectance of the true scene, T the illumination map, and denotes the element-wise productor operator. Given the observed endoscopic image L, there are generally two ways. One way is to estimate an approximate illumination such that the reflectance R can be well recovered by using , where denotes the element-wise division operator. Alternatively, (1) can be rewritten as
| (2) |
where represents the enhancement factor. Instead of estimating T, another way is to design the enhancement factor E for an enhanced image so that it can achieve a visual quality that is expected for R. This Letter focuses on the second way.
Our enhancement factor E is designed to achieve the following goals: (i) For image region with good illumination, it aims to preserve its visual appearance and local contrast. (ii) For image region with low illumination but intact details, it aims to improve its luminance, as well as enhancing local contrast. (iii) For regions with extremely low illumination and lossy details, it aims to improve its luminance, but suppress amplification of local changes that are mainly contributed by noise and quantisation errors. The workflow of the proposed method is displayed in Fig. 1.
Fig. 1.
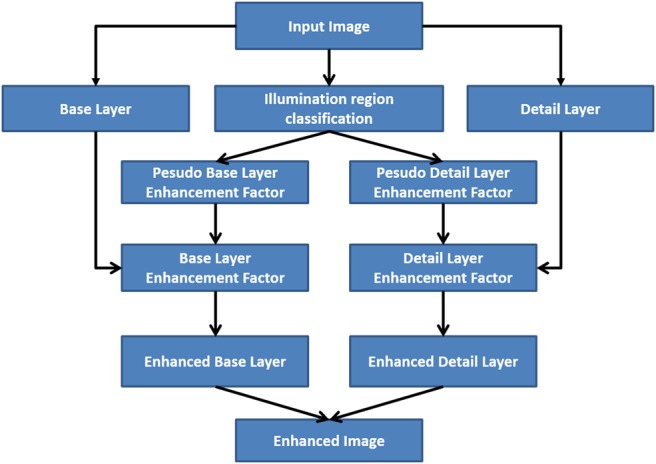
Proposed algorithm workflow for endoscopic image enhancement
To implement our method, we first partition the input endoscopic image into three regions: well-lit, low-light, and lossy. Let and let be the V-space element through converting from RGB space to HSV space by HSV transformation. The illumination region sets are defined as
| (3) |
where denotes the well-lit region, denotes the low-light region, denotes the lossy region, represents the V-space obtained, and mI(x) represents the well-known dark channel image, defined as: . Three threshold parameters , , and satisfy .
After the three illumination regions are identified, the captured image is decomposed into a base layer and a detail layer, where the base layer would represent the smooth varying luminance of the image, and the detailed layer would capture local details and contrasts. The two layers are processed and enhanced differently in order to achieve the expected image quality. Similar techniques have been employed with great success in other tone-mapping algorithms such as [10] for user interactive detail enhancement for artistic purposes. To extract the base and detail layers, we use the edge preserving smooth filter as below:
| (4) |
where is a edge-preserving filter. In this Letter, we employ the tree filter [11] to extract detail and base layers since the tree filter has linear time computational speed and strong edge-preserving smoothing power.
For the base layer, a pseudo enhancement factor can be constructed directly to ensure , the overall luminance of enhanced image , will be close to . Since the base layer represents the smoothly varying luminance, and it is generally free of noise and artifacts, we can directly apply strong scaling factors to enhance its low-light region without worrying about noise amplification. In this case, we construct our enhancement factor analogue to the classic gamma correction formulation, where pixels with an intensity value less than will be non-linearly mapped to a higher intensity value close to . is given as follows:
| (5) |
where is the V-space of the base layer and is a positive parameter <1, which is also known as the gamma compression coefficient. The lower the gamma, the higher the compression, and as a result, the image appears brighter. In general, this process would also compress the local contrast and reduce local detail. However, since the base layer is smooth and is expected to have a uniform distribution, the gamma compression does not cause any problem.
Similarly, we can also construct a pseudo enhancement factor for the detail layer. Due to the extremely low-signal-to-noise ratio and high degree of quantisation error present in , the local changes we observe in this region are mostly contributed by noise and artefacts. As a result, unlike in gamma correction, where there is a high gain for low-intensity pixels, we would like to have a linear gain for low-intensity pixels in order to suppress noise amplification while maintaining the natural appearance of enhanced image. The construction of is given as follows:
| (6) |
where is a constant parameter, representing the linear enhancement factor.
To enforce the piece-wise linear assumption of the illumination T, we smooth the pseudo enhancement factors and by using a Gaussian function to yield and , respectively:
| (7) |
where and are Gaussian kernels where has a smaller size than , and denotes the discrete linear convolution operation. Finally, each enhancement factor will be applied to both the base and detail layers, respectively. The enhanced image is obtained by
| (8) |
3. Results
3.1. Experiment setup
In the experiments, we compare our methods with three state-of-the-art image enhancement algorithms: NPEA [7], LIME [8], and TwoStep [9]. All algorithms are implemented and compared in MATLAB R2018a on a Windows 10 64-bit desktop with an Intel i7-4770 CPU. We evaluate our algorithm on 200 images acquired by real endoscopic surgeries, where the design parameters are , , , , . We chose to separate well-lit region and low-light region. We chose and as two reasonably small parameters to identify lossy region according to (3). and are enhancement parameters, where is chosen for the non-linear enhancement of the low-light region and is chosen for the linear enhancement of lossy region. The values of and are determined empirically, as they seem to provide consistent and effective enhancements without visible detail compression and noise amplification. As decreases, the enhancement power at low-light region would increase and as increases, the enhancement power at lossy region would increase.
3.2. Quantitative validation
We use the naturalness image quality evaluator (NIQE) to quantitatively measure the enhanced image quality [12], which by default measures any deviations from statistical regularities observed in natural images. In this study, instead of using the default nature image model, we trained our statistical model based on 50 hand-picked pristine endoscopic images that are free of visible image noise/artefacts and have relatively bright illumination. In a similar study, Luo et al. [13] also used this approach to measure the image quality of endoscopic images, which was shown to be effective. A smaller score of NIQE would indicate better perceptual image quality.
As shown in Table 1, we listed the mean NIQE and standard deviations for all enhanced images given by four different enhancement algorithms. From the proposed method, we obtained a superior NIQE of 2.46 ± 0.12, indicating that our results have consistently higher image quality, compared with the other methods. The higher naturalness index values, yielded by the other methods, indicate increases in noise and blur during the enhancement process.
Table 1.
Mean naturalness index computed based on the 200 enhanced endoscopy images, represented as mean ± standard deviation, using four different algorithms
Aside from the naturalness of the image, we also evaluate the enhanced images based on illumination uniformity. Following the framework from [14–16], the illumination of the enhanced image can be described by , where is a region centred at pixel x, and y is the location index within the region . When the illumination is uniform, the intensity distribution of should be close to uniform, which means the standard deviation of should be small. Thus, we let denote the standard deviation of the intensity of and use it as an index to measure the illumination uniformity of enhanced image. In Table 2, we have the average illumination uniformity index of the original input images and the enhanced images given by four different algorithms. From this comparison, we can see that the proposed method and NPEA yield the lowest and thus provide better illumination uniformity for the enhanced images.
Table 2.
Mean illumination uniformity index computed based on the 200 original endoscopy images and the enhanced images using different algorithms
3.3. Qualitative validation
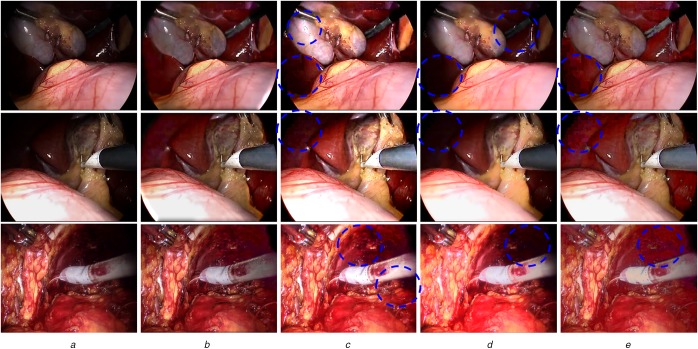
To further illustrate the performance of our algorithm, we also provide visual comparisons. Fig. 2 displays the enhancement results of three endoscopic images obtained by the proposed algorithm and three other state-of-the-art enhancement algorithms. We observe that the proposed method effectively enhances the visibility of the low-light region and reveals hidden surgical tools and organ surface information, while preventing noise amplification and providing a more natural surgical scene. In comparison, LIME is also able to enhance the visibility and contrast of the input images, however it causes over-enhancement, under-enhancement, and noise amplification, as indicated in Fig. 2c. From Fig. 2d, we can see that the TwoStep method demonstrates good noise suppression ability. However, its illumination enhancement ability is relatively weak and it may over smooth image details as shown in the circled regions. Finally, the NPEA method is able to improve the visibility of low-light image but it also suffers from severe noise amplification and contrast degradation, shown in Fig. 2e.
Fig. 2.
Visual comparisons of enhanced images using four algorithms
a Original input
b Results by our algorithm, showing enhanced images with natural appearance
c Results by LIME, showing good contrast but also amplified noise and over-enhancement
d Results by TwoStep, showing smooth image but also blur and weak enhancement
e Results by NPEA, showing good enhancement but also amplified noise
4. Conclusions
In this Letter, an image enhancement algorithm with effective noise suppression ability is proposed for endoscopic images. The algorithm first identifies different illumination regions and then processed the illumination and detail layers separately to meet the enhancement design criteria for desired image quality. From our experiments using 200 test endoscopic images, the proposed algorithm yielded an average NIQE of 2.46 and an average illumination index of 0.22, quantitatively demonstrating superior performance than other state-of-the-art algorithms. By visual inspection, the proposed method is able to maintain the contrasts and colours in the well-lit image regions, while significantly improving the visibility of the low-light regions. By comparison, we can see visible image artefacts amplified by other algorithms, while our approach yields enhanced images with more natural appearances and higher image quality. All the results confirm that our method has superior performance than the other state-of-the-art algorithms, and can effectively enhance the endoscopic image without amplifying underlying noise/artefact in the low-light regions.
On average, the computational time for our algorithm to process an endoscopic image with 480 × 854 resolution is 1.02 s. The computational time will be greatly reduced through parallel implementation in C++ using a GPU and enabling it to run in real time. Although naturalness index is a good quantitative measurement, surgeons’ preferences are also important. In the future, a psychophysical study will be carried out by recruiting surgeons to qualitatively evaluate endoscopic images enhanced by different algorithms.
5. Acknowledgments
The authors thank Dr. John S.H. Baxter and Dr. Xiongbiao Luo for their valuable suggestions and assistance in this research.
6. Funding and declaration of interests
None declared.
7 References
- 1.Vogt F., Krĝer S., Niemann H., et al. : ‘A system for real-time endoscopic image enhancement’. Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Berlin, Germany, November 2003, pp. 356–363 [Google Scholar]
- 2.Farid H.: ‘Blind inverse gamma correction’, IEEE Trans. Image Process., 2001, 10, (10), pp. 1428–1433 (doi: 10.1109/83.951529) [DOI] [PubMed] [Google Scholar]
- 3.Land E.H.: ‘The retinex theory of color vision’, Sci. Am., 1977, 237, (6), pp. 108–129 (doi: 10.1038/scientificamerican1277-108) [DOI] [PubMed] [Google Scholar]
- 4.Jobson D.J., Rahman Z.U., Woodell G.A.: ‘Properties and performance of a center/surround retinex’, IEEE Trans. Image Process., 1997, 6, (3), pp. 451–462 (doi: 10.1109/83.557356) [DOI] [PubMed] [Google Scholar]
- 5.Rahman Z.U., Jobson D.J., Woodell G.A.: ‘Multi-scale retinex for color image enhancement’. IEEE Int. Conf. on Image Processing, Lausanne, Switzerland, September 1996, vol. 3, pp. 1003–1006 [Google Scholar]
- 6.Jobson D.J., Rahman Z.U., Woodell G.A.: ‘A multiscale retinex for bridging the gap between color images and the human observation of scenes’, IEEE Trans. Image Process., 1997, 6, (7), pp. 965–976 (doi: 10.1109/83.597272) [DOI] [PubMed] [Google Scholar]
- 7.Wang S., Zheng J., Hu H.M., et al. : ‘Naturalness preserved enhancement algorithm for non-uniform illumination images’, IEEE Trans. Image Process., 2013, 22, (9), pp. 3538–3548 (doi: 10.1109/TIP.2013.2261309) [DOI] [PubMed] [Google Scholar]
- 8.Guo X., Li Y., Ling H.: ‘LIME: Low-light image enhancement via illumination map estimation’, IEEE Trans. Image Process., 2017, 26, (2), pp. 982–993 (doi: 10.1109/TIP.2016.2639450) [DOI] [PubMed] [Google Scholar]
- 9.Su H., Jung C.: ‘Perceptual enhancement of low light images based on two-step noise suppression’, IEEE. Access., 2018, 6, pp. 7005–7018 (doi: 10.1109/ACCESS.2018.2790433) [Google Scholar]
- 10.Eilertsen G., Mantiuk R.K., Unger J.: ‘Real-time noise-aware tone mapping’, ACM Trans. Graph., 2015, 34, (6), p. 198 (doi: 10.1145/2816795.2818092) [Google Scholar]
- 11.Bao L., Song Y., Yang Q., et al. : ‘Tree filtering: efficient structure-preserving smoothing with a minimum spanning tree’, IEEE Trans. Image Process., 2014, 23, (2), pp. 555–569 (doi: 10.1109/TIP.2013.2291328) [DOI] [PubMed] [Google Scholar]
- 12.Mittal A., Soundararajan R., Bovik A.C.: ‘Making a completely blind image quality analyzer’, IEEE Signal Process. Lett., 2013, 20, (3), pp. 209–212 (doi: 10.1109/LSP.2012.2227726) [Google Scholar]
- 13.Luo X., McLeod A.J., Pautler S.E., et al. : ‘Vision-based surgical field defogging’, IEEE Trans. Med. Imaging, 2017, 36, (10), pp. 2021–2030 (doi: 10.1109/TMI.2017.2701861) [DOI] [PubMed] [Google Scholar]
- 14.Forsyth D.A.: ‘A novel approach to colour constancy’. Second Int. Conf. on Computer Vision, Tampa, FL, USA, December 1988, pp. 9–18 [Google Scholar]
- 15.Funt B., Shi L.: ‘The rehabilitation of MaxRGB’. Color and Imaging Conf., San Antonio, TX, USA, January 2010, pp. 256–259 [Google Scholar]
- 16.Joze H.R.V., Drew M.S., Finlayson G.D., et al. : ‘The role of bright pixels in illumination estimation’. Color and Imaging Conf., Los Angeles, CA, USA, January 2012, pp. 41–46 [Google Scholar]