Ongoing Alpha Activity in V1 Regulates Visually Driven Spiking Responses

Abstract

The interlaminar connections in the primate primary visual cortex (V1) are well described, as is the presence of ongoing alpha-range (7–14 Hz) fluctuations in this area. Less well understood is how these interlaminar connections and ongoing fluctuations contribute to the regulation of visual spiking responses. Here, we investigate the relationship between alpha fluctuations and spiking responses to visual stimuli across cortical layers. Using laminar probes in macaque V1, we show that neural firing couples with the phase of alpha fluctuations, and that magnitude of this coupling is particularly pronounced during visual stimulation. The strongest modulation of spiking activity was observed in layers 2/3. Alpha-spike coupling and current source density analysis pointed to an infragranular origin of the alpha fluctuations. Taken together, these results indicate that ongoing infragranular alpha-range fluctuations in V1 play a role in regulating columnar visual activity.

Introduction

Anatomical studies describe an intricate pattern of anatomical connectivity between the layers that collectively make up the cortical columnar microcircuitry of primary visual cortex (V1; Douglas et al. 1989; Callaway 1998; Douglas and Martin 2004; Bannister 2005). However, the functional interactions that arise from the dense connections between neurons in different laminar compartments are still largely unknown. Optogenetics has provided a novel means to disentangle the impact of neural activity in one layer on activity in layers above and below. In particular, photoactivation of neurons in deep cortical layers (layers 5 and 6), but not in superficial layers (1–3), modulates the magnitude of columnar spiking activity in rodent visual cortex (Olsen et al. 2012; Beltramo et al. 2013; Bortone et al. 2014). Taken together, these studies suggest that neurons in the deep layers of the cortex are in a privileged position to regulate spiking output in other cortical layers. Infragranular control over neural excitability across the cortical column is a particularly intriguing hypothesis, given that these layers are a major target of cortical feedback projections (Maunsell and Van Essen 1983; Douglas and Martin 2004; Nascimento-Silva et al. 2014). Through their modulation of infragranular neurons, such feedback projections could exercise gain control over spiking responses in other layers, including cortically projecting neurons in superficial layers. One possibility is that this modulation occurs through projections from layer 5 to layer 2/3, which constitutes one of the most extensive interlaminar projections within the cortical microcircuit (Binzegger et al. 2004).

Layer 5 neurons have also been implicated in the generation of alpha-range activity (∼7–15 Hz, with the exact frequency range depending on the study). The study of alpha-range activity in investigations of vision and cognition has a long history, driven by the prominence (power) of alpha measured over occipital cortex in humans (Berger 1929). While it is currently unknown how alpha recorded from the human scalp relates to neural activity recorded intracranially, several hypotheses have been proposed. In particular, a subpopulation of layer 5 pyramidal cells that fire rhythmically in the alpha frequency range (Silva et al. 1991; Sun and Dan 2009) has been suggested to serve as a neuronal pacemaker for the columnar microcircuit (da Silva 1991; Connors and Amitai 1997; Jones et al. 2000, 2009; Jensen and Mazaheri 2010). One theory about the functional role of cortical alpha activity, referred to as the “pulsed inhibition” hypothesis, purports that alpha cycles reflect periodic inhibition of local neurons (Jensen and Mazaheri 2010). A predicted outcome of this hypothesis is that the magnitude of spiking varies with the phase of concomitant alpha fluctuations. Indeed, this kind of relationship between spiking and alpha phase has been demonstrated in motor regions and somatosensory cortex (Bollimunta et al. 2008, 2011; Haegens et al. 2011; van Kerkoerle et al. 2014) under a variety of conditions. In visual cortex, others have identified a relationship between alpha and multiunit spiking activity (Bollimunta et al. 2008, 2011; van Kerkoerle et al. 2014). However, the role of alpha-spike coupling and its laminar specificity during sustained sensory processing remains to be elucidated.

Here, we tested for layer-specific interactions between the alpha cycle and fluctuations in spiking activity within a cortical column and the dependence of this relationship on sensory stimulation. More specifically, we used laminar probes to record locally referenced alpha local field potentials (LFP) and population spiking in macaque V1 during periods of sustained sensory stimulation and periods without explicit visual stimulation. We found that spiking activity throughout the column, especially in the supragranular layers, was phase-locked to ongoing alpha-range fluctuations. Current source density (CSD) analysis paired with coupling analysis suggested that the origin of these alpha-range fluctuations was in layer 5. Alpha-spike coupling was present across sensory conditions and was particularly pronounced during periods of visual stimulation. Taken together, these results are congruent with the notion that V1 activity, particularly in cortico-cortically projecting supragranular layers, is regulated by alpha fluctuations.

Materials and Methods

Subjects

Two healthy adult male macaques (Macaca mulatta), B and E, were used in 56 recording sessions (23 from E). All procedures were approved by the Animal Care and Use Committee of the National Institute of Mental Health and were in compliance with regulations set by AAALAC.

Surgical Preparations

Two separate surgical procedures were performed on each animal. For all surgeries, general anesthesia was induced with an intramuscular injection of ketamine hydrochloride (10 mg/kg) and maintained with isoflurane anesthesia (1.5–2.0%) throughout the procedure. Vital signs, including blood pressure, heart rate, SpO₂, CO₂, respiratory rate, and body temperature, were monitored continuously. During the first surgery, a custom-made fiberglass head holder was attached to the animal's skull using self-curing dental acrylic (Lang, Inc., Wheeling, IL, USA) and ceramic screws (Thomas Recording GmbH, Giessen, Germany). In a subsequent procedure, a craniotomy was performed over the caudal aspect of area V1 where the representation of perifoveal visual field is located. A plastic recording chamber was implanted around this location using the same ceramic screws and self-curing acrylic as used for the head holder. Animals received prophylactic antibiotics and analgesics (buprenorphine, acetaminophen, and ketoprofen) for at least 3 days following all surgical procedures.

Experimental Conditions

During all experimental sessions, animals were placed in a darkened recording booth and sat in a custom-designed primate chair (Precision Plastic, Gibson City, IL, USA) with their heads restrained. For the visual stimulation condition, animals were given liquid reward for successfully acquiring and maintaining fixation on a small (0.01–0.1 degrees of visual angle, dva) white spot displayed on the center of the monitor. At the beginning of each session, we manually mapped receptive fields by passing a rectangular bar of cardinal orientations across the visual field while animals fixated. We used the audible multiunit response on each electrode contact to determine the extent of visual space that reliably evoked spiking responses at the electrode location. This aggregate receptive field then was used to determine the placement of the main stimulus set. Typically, stimuli were 2 dva in diameter (Table 1), with one stimulus completely covering the mapped receptive field (Table 2). Following receptive field mapping, we initiated the main task which proceeded as follows: after 1000 ms (monkey B) or 1500 ms (monkey E) of sustained fixation on a central cue, an array of 4 identical, static circular gratings appeared on the screen (Fig. 1a). For reasons beyond the current study, more than one grating was shown, and these gratings were presented randomly to either the right or left eye and were displayed in either a red or green hue. Within a session, these gratings were presented at the same eccentricity, equidistant to each other such that one grating was shown in each quadrant of the visual field.

Table 1.

Stimulus size

	Diameter (dva)					N
	Mean	SD	Minimum	Maximum	N < 2
Monkey B	2.1	0.2	1.8	3	1	32
Monkey E	2.1	0.2	2	2.5	0	23

Table 2.

Receptive field eccentricity and size

	Eccentricity (dva)		Horizontal diameter (dva)		Vertical diameter (dva)		Area (dva2)		N
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Monkey B	4.0	0.7	1.6	0.9	1.8	0.9	3.4	3.2	32
Monkey E	3.4	0.7	1.6	0.7	1.3	0.4	2.3	2.0	23

Figure 1.

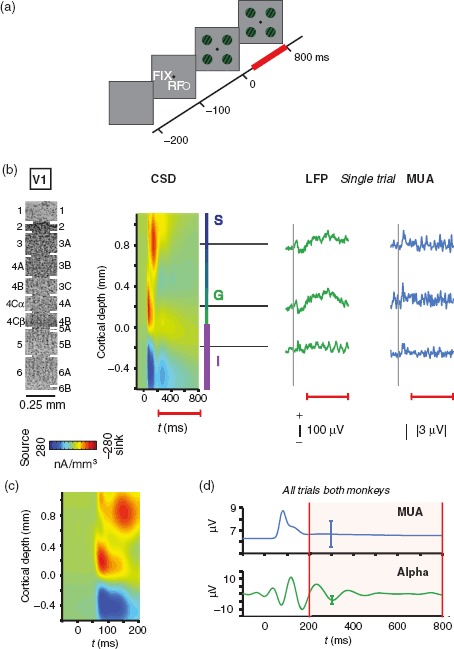
Experimental paradigm. (a) Animals maintained steady fixation on a central fixation spot (FIX) while 4 equieccentric gratings appeared on the screen (t = 0 ms). One of these gratings covered the previously mapped V1 receptive field (RF). (b) A laminar probe with 16 or 24 electrode contacts spaced 100 μm apart was used to measure LFP and MUA simultaneously across all laminae of V1. Visually evoked CSD, shown here aligned and averaged across 56 sessions in 2 monkeys, was used to determine the laminar position of each electrode contact. Per convention, the bottom boundary of the initial current sink served as the zero point, with positive values indicating more superficial cortical locations. S, G, and I mark the CSD-derived locations of supragranular, granular, and infragranular compartments, respectively. The Nissl-stained section shown for scale on the left is from V1 of monkey E. The image is aligned to the electrophysiological data and labeled following Brodmann's (left) and Hässler's (right) schemes. LFP and MUA traces on the right show the visually evoked response from a single experimental trial (monkey E). Note the distinct low-frequency oscillation in the infragranular LFP. Dashed vertical lines indicate the onset of the visual grating stimulus. Red lines below indicate the extent of the analysis window. (c) CSD shows the initial CSD response with higher temporal resolution. (d) Stimulus-evoked responses following the onset of the grating stimuli are shown for V1 spiking activity (MUA) and alpha LFP (7–14 Hz) averaged across all contacts, both animals and all sessions (N = 56). Error bars indicate standard deviation (SD). All subsequent analyses were focused on the period 200 ms through 800 ms following stimulus onset (shaded region between red vertical lines).

Analyses were averaged over all visual gratings since stimulus-specific response modulation was beyond the scope of this study. Unless stated otherwise, analyses for the visual stimulation condition were restricted to the time window starting 200 ms after the onset of the visual gratings through 800 ms following this onset. If the monkeys' gaze left the fixation window of 1.0–1.5 dva around the central fixation cue, the trial was aborted and the next trial began after a 1- to 5-s delay. The average number of trials per session was 682 (median 681). To compare laminar neural coupling during visual stimulation with coupling in the absence of visually driven activity, we used the prestimulation period in each trial (100–700 ms following fixation).

Visual Display

Stimuli were presented on 27-inch thin-film transistor monitors (X2Gen MV2701, 1024 × 768 resolution) positioned at a viewing distance of 80 cm using a mirror stereoscope. A PC (Kontron, Poway, CA, USA) using NVIDIA Quadro FX 3000 graphics boards was used to run custom-written software (ESS/STIM; copyright Dr D. Sheinberg, Brown University, Providence, RI, USA) to produce the visual stimuli used in this study. The animals' eye movements were continually recorded at 200 Hz using an infrared light sensitive camera and the commercially available eye-tracking software (Eye Link II, RS Research, Osgoode, Canada). Animals performed a brief perimetric calibration procedure for the eye-tracking software at the beginning of each session. All eye movements and behavioral events were synced to the neurophysiological data using a separate PC running a real-time operating system (QNX Software Systems, Kanata, ON, Canada).

Neurophysiological Recordings

Broadband (0.5 Hz–12.207 kHz) extracellular voltage fluctuations were recorded with an acute laminar probe inside an electromagnetic radio frequency-shielded booth. For each session, a custom-made chamber-mounted microdrive was used to lower the laminar probe into dorsal V1, caudal to the lunate sulcus. The laminar probe consisted of 16 or 24 microelectrode contacts, linearly spaced 0.1 mm apart with impedances ranging 0.2–0.8 MΩ at 1 kHz (Plexon UProbe, Plexon, Inc., Dallas, TX, USA). Extracellular voltages were measured in reference to the shaft of the probe and were collected simultaneously from all microelectrode contacts. Voltage-fluctuating signals were amplified, filtered, and digitized using a 64-channel RZ2 recording system (Tucker Davis Technologies, Alachua, FL, USA). During data collection, the LFP was extracted by filtering between 0.5 and 500 Hz and digitizing at 1.0173 kHz. Multiunit activity (MUA) was extracted by high-pass filtering at 300 Hz and digitizing at 24.4141 kHz (see the section “Multiunit Analysis”). Both signals were stored for subsequent offline analysis.

Data Analysis

All offline analysis was performed using the custom-written code in MATLAB (MathWorks, Natick, MA, USA).

Multiunit Analysis

Although single neurons can be isolated with laminar probes in a way that is comparable to that of standard microelectrodes, isolating cells on all electrode contacts of the array simultaneously proved difficult in practice. For this reason, we opted to use MUA as a proxy for the activity of local neurons. Specifically, we full-wave rectified the recorded high-pass filtered (at 300 Hz) data, and then decimated the signal by a factor of 20 to obtain the time-varying power in the spiking range. We low-pass filtered the resulting signal at 50 Hz using a Butterworth filter with an order of 4.

CSD Analysis

CSD analysis of visual responses to brief flashes of light has been shown to reliably indicate the location of the primary geniculate input in V1 (granular layer 4C) by a distinct current sink that is thought to reflect combined excitatory postsynaptic potentials of the initial retino-geniculate volley of activation (Mitzdorf 1985). To compute the visually evoked CSD, we applied an estimate of the second spatial derivative appropriate for multiple contact points (Nicholson and Freeman 1975). Specifically, we used the three-point formula:

$$\text{CSD}(t,c)=-\frac{x(t,c-z)+x(t,c+z)-2x(t,c)}{z^2},$$

where x is the extracellular voltage recorded in μV at time t from an electrode contact at position c, and z is the electrode intercontact distance (0.1 mm). To yield CSD in units of current per unit volume, we multiplied the resulting CSD from the formula above by 0.35 S/mm, an estimate of the conductivity of cortex (Ranck 1963). We applied this transformation to data collected during the fixation paradigm, with each trial aligned to the onset of the visual gratings described in the section “Experimental Conditions.” Using this approach, we were able to locate the bottom of a prominent initial current sink in all sessions. After excluding superficial and deep electrode contacts that did not record a visual response (due to their placement outside of the cortical gray matter), we aligned all subsequent intersession averages to this reference point (Fig. 1b; Maier et al. 2011, 2014). Representations of CSD as a function of time and space were computed by interpolating CSD between adjacent electrode contacts and smoothing the result with a 2D-Gaussian filter (σ = 0.1; Pettersen et al. 2006; Godlove et al. 2014; Ninomiya et al. 2015). While the theoretical foundations of CSD analysis are based on several assumptions regarding recording parameters and cortical geometry that are difficult to control for (Tenke et al. 1993), the technique has proved remarkably robust against many of these potential reasons for concern in practice (Kajikawa and Schroeder 2015).

Alpha-Locked Spiking

To determine the degree of coupling between alpha phase and columnar spiking, we band-limited the LFP from a select electrode contact (−0.2 mm) into the 7- to 14-Hz band using a bidirectional Chebyshev type I filter with an order of 2. We then detected amplitude troughs in this band-limited alpha LFP by calculating the second temporal derivative. We triggered the time-varying analog MUA from all recording contacts of the laminar probe to the time of alpha troughs, t_x. More specifically, we averaged the analog MUA between t_x− 100 ms and t_x+ 100 ms, approximating the duration of more than one full 7-Hz cycle. Alpha amplitude troughs within the first 100 ms or last 100 ms of the analysis window were excluded. This procedure resulted in multiple alpha-locked MUA epochs for each trial and electrode contact. We averaged the trough-locked analog MUA within each electrode contact and each trial. Previous work has shown that there are frequency-specific LFP power differences among the layers of V1 (Steriade et al. 1990; Kramer et al. 2008; Sun and Dan 2009; Maier et al. 2011; Xing et al. 2012; Smith et al. 2013). To account for baseline differences in the MUA voltage between layers, we calculated the difference between the mean alpha-locked MUA and the mean MUA amplitude across the epoch for each depth in each session. We assessed the significance of this coupling by computing a t-score for each time point in the epoch at each depth. To calculate this t-score, we compared our results against a randomly shuffled control, obtained by pairing the alpha signal from one trial with the MUA from a different, randomly selected trial, and did so for all trials and sessions in the data set. All statistics were Bonferroni-corrected for multiple comparisons.

Phase-Dependency of Spiking

We verified results obtained by the alpha-locking of spiking activity using a second procedure. We chose 3 representative laminar recording sites (0.8, 0.2, and −0.2 mm), corresponding to supragranular (layer 2/3), granular (layer 4C), and infragranular (layer 5) locations, respectively. We band-limited bipolar (re-referenced to signal recorded 200 µm superficial to the site) LFP into the alpha band using the same filter as above for each representative depth. We extracted the phase of the band-limited alpha from the output of the Hilbert transform at each cortical depth. We then computed the mean MUA as a function of the alpha cycle. Specifically, we divided the 360° wide phase cycle into 20° wide bins. Then, we assigned all MUA samples to their respective alpha-phase bin, and averaged the MUA amplitude within each bin. We calculated the amount that each MUA bin deviated from the mean MUA amplitude by converting all values into percent difference by first subtracting and then dividing by the mean MUA across all phase bins, and multiplying the result by 100. To visualize the data in polar coordinates, we half-wave rectified the result, which revealed positive deviations from the mean (units referred to as percent coupling). Significant differences in coupling magnitude were assessed using a paired t-test at each depth and were corrected for multiple comparisons.

Evoked Versus Induced Response

We repeated the percent coupling procedure described above to make several other comparisons. First, we confirmed that any coupling effect we observed was not a consequence of filtering method (Supplementary Fig. 1). To confirm this, we filtered the LFP from an infragranular site (−0.2 mm) into 1-Hz wide bands centered on 8, 10, 12, and 14 Hz using a finite-impulse response filter (FIRLS) with a frequency-dependent order [2 cycles of each frequency, or an order of 1000 Hz/frequency (Hz) * 2; Spaak et al. 2012]. Then, we computed the deviation of MUA around the phase cycle for these signals as described above. Second, we repeated the percent coupling procedure to compare coupling during the early (200–500 ms) and late (500–800 ms) halves of the analysis window (Supplementary Fig. 2). We tested for differences in coupling between early and late halves of the analysis window using multiple Wilcoxon signed-rank tests and accounted for multiple comparisons using Bonferroni correction. As a second control to determine if coupling resulted from the initial transient visual response, we performed the alpha-locked spiking procedure again after subtracting the average evoked response. Specifically, for each session, we subtracted the trial-averaged evoked response from each trial for LFP and MUA, filtered LFP into the alpha band, and averaged epochs of MUA aligned to alpha troughs (Supplementary Fig. 3). Finally, we repeated the percent coupling procedure to compare coupling using alpha filtered from the LFP and alpha filtered from LFP re-referenced to a site 200 µm superficial to each contact (bipolar alpha LFP). We compared coupling of MUA across the 3 alpha-phase sites (0.8, 0.2, and −0.2 mm) for all MUA depths using 3 × 1 ANOVAs and post hoc multiple comparison tests (Supplementary Fig. 4).

Modulation Index

We used the modulation index (MI) proposed by Tort et al. (2010) to assess coupling between MUA and the phase of LFP across a range of narrow frequency bands. Specifically, we filtered the LFP at one laminar recording location (−0.2 mm) into 2-Hz wide bands in 1 Hz increments between 3 and 40 Hz. We used a finite-impulse response filter with a frequency-dependent order [2 cycles of each frequency, or an order of 1000 Hz/frequency (Hz) * 2; Spaak et al. 2012]. Then, for each frequency, we calculated the MI between the LFP and MUA at all cortical depths. Specifically, for each of these pairs, we binned MUA amplitude as a function of alpha phase (N = 30 bins), and computed a single MI value (Tort et al. 2010). The mean MUA amplitude within each phase bin was normalized by dividing by the sum of all phase bin means, resulting in distribution P. Tort et al.'s (2010) MI measures the Kullback–Leibler distance between this phase-amplitude distribution and a uniform distribution using the following formula:

$$\text{MI}=\frac{\log (N)-\left(-{\sum }_{j=1}^{N}P(j)\log [P(j)]\right)}{\text{log(}N)},$$

where j represents a single bin among N total bins. To determine which aspects of the resulting MI matrix are specific to the infragranular layers, we repeated this procedure using LFP from a granular recording location (0.2 mm) and subtracted this reference granular MI map from the infragranular MI map.

Alpha-Locked CSD

To evaluate the laminar profile of CSD associated with alpha activity, we first extracted an infragranular alpha signal using the same approach as outlined under “Alpha-Locked Spiking.” We then determined the time of alpha troughs, t_x, which we used to trigger and average the LFP across all electrode contacts. We next used a Butterworth filter to high-pass filter the alpha-locked LFP at 4 Hz to account for low-frequency drift, and computed an estimate of the second spatial derivative using the procedures detailed in “CSD Analysis.” To align the alpha-locked CSD with concomitant spiking activity, we averaged MUA for each electrode contact within the same window. To investigate the temporal evolution of the laminar CSD profile throughout the alpha-phase cycle, we repeated this procedure, replacing alpha troughs with alpha peaks.

Numerical Simulation

To assess the robustness of MI to varying levels of signal, we performed a numerical simulation. We first produced a test signal by multiplying the amplitude of a high-frequency periodic signal (1000 Hz) with a 10-Hz sinusoid to which we added varying levels of random (Gaussian) noise. We used 3 different levels of noise, each set to approximate the average root mean square of the alpha-range LFP recorded during visual stimulation in the supragranular, granular, and infragranular layers, respectively. The amplitude of the high-frequency signal was set to approximate the mean magnitude of MUA. The amplitude of the low-frequency signal was set to approximate the mean alpha power on low or high alpha power trials. To find these means, for each recording session, we calculated the mean band-limited alpha power for all trials. We split trials into the top 30% of the alpha power distribution and the bottom 30% of trials in the distribution, and then averaged their respective means to create a high and low alpha category of trials, respectively. Using the test signal, the MI was then computed between filtered low-frequency and high-frequency signals. One thousand simulations were run for each low and high alpha power level. We averaged the MI across all simulations and used two-sample t-tests to test for differences in MI between low-amplitude and high-amplitude low-frequency simulations.

Secondary to the simulation, we used the analysis from stratifying the data into low alpha power and high alpha power trials to confirm that differences in MI could result from equal magnitude MUA. Specifically, we averaged the MUA from low infragranular alpha power and high infragranular alpha power trials across the cortical depth. We used a two-sample t-test to compare the mean magnitude of MUA for low alpha power and high alpha power trials. Then, we computed the MI for these trials and averaged the result across the cortical depth. We performed a two-sample t-test to test for differences in MI for these 2 categories of trials.

Power Spectral Density and Time–Frequency Representations

We computed the power spectral density (PSD) of the bipolar LFP from 3 representative depths (0.8, 0.2, and −0.2 mm) for visual stimulation and prestimulation conditions. To calculate the PSDs, we used Welch's method with a window size of 512 and an overlap of 256. The time–frequency analysis was performed using the multitaper approach provided by the Chronux Toolbox for Matlab (http://chronux.org/, last accessed November 20, 2014; Bokil et al. 2010). Specifically, we calculated the power in different frequency bands over time using a moving window of 150 ms, stepping every 1 ms. We converted the output into units of dB, averaged across sessions, and z-score transformed the resulting matrix. Then, at each frequency, we baseline-corrected the estimation of power over time by subtracting the mean z-score for time points occurring approximately 300–160 ms before stimulus onset.

Eye Movement Analysis

Previous work shows that the frequency of saccades occurs at a low frequency (<5 Hz; Ito et al. 2013). Furthermore, saccades are accompanied by an increase in power across a range of low frequencies, including the alpha–beta band, in V1 (Bosman et al. 2009). To determine if small saccades made during fixation drove the coupling effect described in this study, we related microsaccades to the alpha LFP. We used the MATLAB implementation of the microsaccade detection method published by Otero-Millan et al. (2014) to determine the onset of microsaccades. We excluded microsaccades with amplitude of <0.3°. Within the visual stimulation analysis window, we determined the alpha phase recorded at the time of a detected eye movement. Then, we binned the alpha phase at the time of microsaccades across 20° wide bins. We calculated the relative frequency of this distribution for each session by dividing the number of counts in each alpha-phase bin by the total number of detected microsaccades. A Rayleigh z-test for nonuniformity was calculated on the set of phases across sessions, prior to binning, for each monkey E and monkey B. The distribution was considered statistically significantly different from uniform if ln(P) > ln(−ln(α)), with α = 0.05 (Siapas et al. 2005; Liebe et al. 2012).

Results

The primary goal of this study was to determine whether coupling of spiking activity with the alpha-phase cycle in V1 is of specific relevance to visual stimulation. Towards this aim, we recorded both spiking and LFP across all layers of macaque V1 simultaneously while the animals performed a visual task that was interspersed with periods without stimulation. We examined the covariation of spiking with the endogenous alpha LFP cycle when the animal was presented with visual stimuli, comparing the phase coupling with the preceding period that was devoid of visual stimulation in each trial. The results are described in the following sections.

Phase-Locking of Spiking Responses to Alpha Fluctuations

We asked whether spiking activity in V1 shows significant coupling with the alpha LFP phase during periods of prolonged (>500 ms) visual stimulation. During each session, grating stimuli were presented inside the aggregate receptive field of the cortical column from which we recorded (Fig. 1a and Tables 1 and 2). The visual response following the onset of the gratings initiated in the middle layers (Fig. 1b,c). The right portion of Figure 1b plots data from a single trial, showing typical oscillatory cycles. We restricted analysis to the period in which there was a sustained visual response that was long enough to evaluate the slow-varying alpha signal, which corresponded to the time between 200 and 800 ms following stimulus onset (Fig. 1d). Importantly, owing to this time window, the initial transient response was not included in the analysis. On average, low-frequency (<20 Hz) LFP decreased following visual stimulation in both monkeys (Supplementary Fig. 5b). However, the spectral pattern differed among layers, with lower layers showing a trend of higher alpha power during visual stimulation (Supplementary Fig. 5a).

We confirmed that alpha and spiking coupled as others have described (Bollimunta et al. 2008, 2011; Buffalo et al. 2011; Haegens et al. 2011; van Kerkoerle et al. 2014) using an alpha-phase reference from the deep layers. With this signal, we tested for coupling of spiking activity (MUA) along the entire cortical depth, exploiting the 100-μm sampling afforded by our laminar probes. The laminar distribution of alpha-MUA coupling is shown for both animals as mean alpha-locked MUA in Figure 2a. On average, visual spiking responses in all cortical layers varied with infragranular alpha LFP. This alpha coupling of spiking activity did not derive from the stimulus presentation itself, as it was comparable between the initial and later part of the response (Wilcoxon signed-rank tests, P > 0.05, Bonferroni-corrected; Supplementary Fig. 2). Furthermore, our results were qualitatively the same as in Figure 2 when we subtracted the mean evoked response for each session from every trial, and repeated our analysis (Supplementary Fig. 3).

Figure 2.

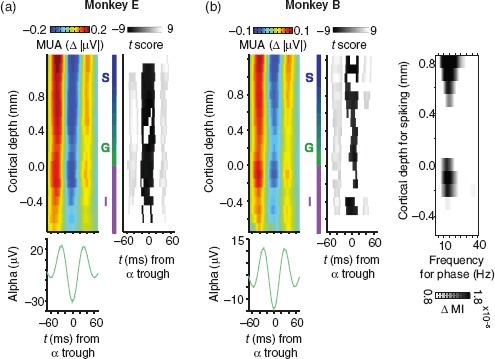
Coupling of alpha and columnar V1 spiking responses. (a) Colored plots represent the laminar profile of population spiking (MUA) aligned to infragranular alpha troughs. Grayscale plots to the right indicate the corresponding t-score values for statistical comparison. The t-score maps are thresholded to indicate significance at the 0.05 alpha level (Bonferroni-corrected). Left column: monkey E (N = 23 sessions). Right column: monkey B (N = 33 sessions). Alpha-band LFP was chosen from the electrode contact positioned 0.2 mm below the layer 4C current sink. The average alpha waveform (green) for the same set of sessions is shown below the alpha-aligned MUA (error bars are standard error of the mean, SEM). (b) Laminar profile of phase-coupled spiking as a function of LFP frequency. Each data point represents the magnitude of coupling expressed as Tort's MI. MI values were calculated for 3-Hz wide frequency bands incremented in steps of 1 Hz. LFP was taken from an infragranular electrode contact (−0.2 mm). To emphasize laminar specificity, MI values are contrasted to a similarly computed map that used LFP from the granular layer (0.2 mm). Data are averaged across both monkeys (N = 56 sessions).

We asked whether this coupling between spikes and LFP was specific to the alpha range. We quantified phase-to-amplitude coupling between the LFP and MUA using Tort's MI (see Materials and Methods; Tort et al. 2010), and show the result as a function of cortical depth and frequency (Fig. 2b). We observed that columnar spiking coupled with infragranular LFP across a broad range of low frequencies, with the strongest coupling centered on the high alpha/low beta range. This frequency-dependency of the coupling was more restricted for MUA in deep layers compared with superficial layers.

Coupling Is Enhanced with Stimulation and Strongest for Supragranular Spiking

We further tested whether the observed alpha-spike coupling was dependent on visual stimulation. We compared conditions with a grating in the receptive field with the task period just prior to the onset of gratings. For the majority of sites, there was a clear and consistent phase selectivity of MUA before and after visual stimulation (Fig. 3). However, the magnitude of coupling was significantly different between prestimulation and visual stimulation for all but two of the comparisons (paired t-tests, Bonferroni-corrected, P < 0.05).

Figure 3.

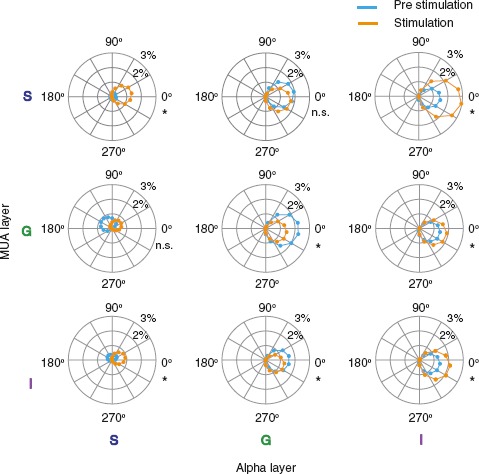
Phase coupling of V1 spiking across the infragranular alpha cycle before and after visual stimulation. Spiking magnitude is plotted relative to the alpha phase as a function of laminar position and condition. Columns correspond to alpha LFP from supragranular to infragranular layers (left to right). Rows correspond to MUA from supragranular to infragranular layers (top to bottom). Each data point depicts deviation of MUA from the mean at a given phase angle after half-wave rectifying. Data are averaged across monkeys (N = 56 sessions). Asterisks indicate statistically significant differences in peak coupling amplitude between prestimulation and visual stimulation (paired t-tests, P < 0.05, Bonferroni-corrected).

Spiking in the superficial layers coupled most strongly with bipolar alpha LFP in the infragranular layers (Fig. 3 and Supplementary Fig. 4). For spiking in every laminar compartment, the infragranular bipolar (re-referenced) alpha LFP provided the strongest phase reference for alpha-MUA coupling (Supplementary Fig. 4). For the infragranular alpha phase, coupling of spiking in supragranular layers was stronger than spiking for other compartments (3 × 1 ANOVA, P < 0.01). The robust laminar specificity of alpha coupling of columnar spiking suggests a unique role for alpha activity in infragranular layers. Since additional analytic steps are needed to disambiguate the cellular origins of LFP (Kajikawa and Schroeder 2011, 2015), we will return to this point below. While the laminar profile of coupling was largely conserved between conditions, the magnitude of coupling was consistently enhanced with stimulation.

Laminar differences in alpha-spike coupling could be caused by higher signal-to-noise ratios (SNR) of alpha in some layers relative to others. To rule out this potential confound, we performed a numerical simulation. We used the mean alpha power across trials with the highest alpha power (top one-third) for high alpha simulations and mean alpha power across trials with the lowest alpha power (bottom one-third) for low alpha simulations. Unlike previous work (van Kerkoerle et al. 2014), we observed no significant difference in mean MUA across the cortical depth for low and high alpha power trials from a single depth (two-sample t-test, P = 0.662; Supplementary Fig. 6a). It is possible that the relationship between MUA and alpha power is laminar-specific. The simulated results revealed no significant differences in mean MI between high and low alpha levels, suggesting that SNR differences are unlikely to account for the laminar specificity in neural coupling we observed (Supplementary Fig. 6c; two-sample t-tests; P = 0.928, P = 0.343, P = 0.471, respectively). Thus, the laminar profile of the alpha coupling of columnar spiking must be explained by other factors, such as the intrinsic connectivity of the columnar microcircuit (see “Discussion”).

Laminar Origin of Alpha Fluctuations

Finally, we investigated sites of putative synaptic activity giving rise to the alpha fluctuations during visual stimulation. We used CSD analysis, which is a well-established analytic technique for estimating microscopic current sinks and sources in the extracellular medium from laminar recording data (Nicholson and Freeman 1975; Mitzdorf and Singer 1979; Mitzdorf 1985; Tenke et al. 1993). We were interested in the location and temporal evolution of current sinks and sources associated with the alpha cycle that underlies intracolumnar coupling. Following an approach similar to previous studies, we analyzed the distribution of laminar current sinks and sources in V1 around the alpha-phase cycle (Bollimunta et al. 2011; Spaak et al. 2012; van Kerkoerle et al. 2014). Specifically, we computed the CSD on epochs of LFP aligned to peaks and troughs from alpha LFP from infragranular layers (Fig. 4). This analysis revealed a columnar pattern of multiple time-varying current sinks and sources that was highly reliable in both animals. A prominent feature of this alpha-locked CSD profile was that spiking activity was lowest when prominent current sinks emerged below the layer 4C/5 boundary. These current sinks are believed to be indicative of excitatory synaptic activity (Mitzdorf 1985); however, they could represent any voltage changes in the extracellular medium—including those from spikes and intrinsic membrane oscillations (Buzsáki et al. 2012). This pattern of sinks and sources around the alpha cycle during visual stimulation aligns with the spatial location and timing of sinks and sources from previous work during the resting state (Bollimunta et al. 2011; Spaak et al. 2012; Ninomiya et al. 2015), suggesting common generators of alpha activity across conditions. Thus, the CSD analysis points to layer 5 as the most likely origin of the observed alpha fluctuations, consistent with previous experimental and theoretical work (da Silva 1991; Silva et al. 1991; Connors and Amitai 1997; Jones et al. 2000, 2009; Sun and Dan 2009; Jensen and Mazaheri 2010).

Figure 4.

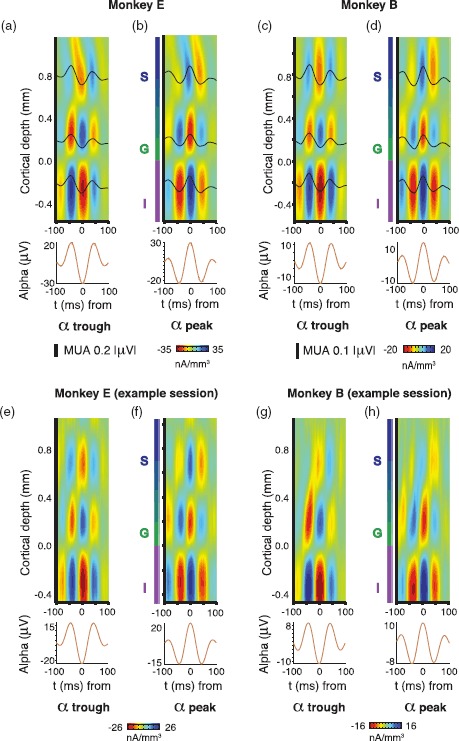
Laminar distribution of alpha-locked extracellular current sinks and sources during visual stimulation. (a) Mean CSD around infragranular (−0.2 mm) alpha troughs for monkey E (N = 23). At 3 laminar locations, mean MUA for the same time period is superimposed (black lines). (b) Mean CSD around infragranular alpha peaks for monkey B. (c and d) Same as (a), but for monkey B (N = 33 sessions). (e–h) Same as a–d, but for example sessions in each monkey.

No Consistent Relationship Between Microsaccades and Alpha Phase

Microsaccades can cause transient activation that might manifest as spurious coupling. We tested for this possibility by determining the instantaneous alpha phase at the time of a microsaccade. We found that there was no systematic relationship between alpha-phase angle and microsaccade frequency. The distribution of alpha phase at the time of microsaccades was not significantly different from uniform for both animals (Rayleigh z-test for nonuniformity, P > 0.05; Supplementary Fig. 7).

Discussion

The results presented in this paper show that spiking responses across all layers of primate striate cortex are coupled with alpha-range extracellular field potentials in infragranular layers. This coupling between spiking and the alpha-phase cycle was strongest for spiking in upper cortical layers and strongest during periods of visual stimulation. Importantly, alpha-spike coupling persisted during the sustained visual response, after the initial transient response had tapered. This result cannot be explained by small microsaccades made during fixation. In the sections below, we discuss our findings in greater detail and provide speculative explanations that could account for our results.

Laminar Specificity of Alpha-Spike Coupling During Visual Stimulation

Our data show that alpha-range field potentials are strongly coupled with spiking throughout the column but especially in supragranular layers during visual stimulation. We assessed current sinks and sources related to alpha activity in V1 using an analytic approach similar to previous work (Bollimunta et al. 2008; 2011; van Kerkoerle et al. 2014). In agreement with previous alpha CSD analyses, we found the strongest alpha-locked sink in deep layers below the layer 4C/5 border at the time of alpha troughs. At counter-phase (coincident with deep layer alpha peaks), the sign of the sinks and sources reversed so that a sink was present in the granular layer. These alpha-locked CSD patterns suggest endogenous activation of granular and infragranular compartments that alternates at a low frequency (∼7–14 Hz). We observed an alternation in spiking across the entire cortical column that coincided with this rhythmic modulation. Even after attenuating the effects of volume conduction inherent in LFP signals by using bipolar LFP (Kajikawa and Schroeder 2011, 2015), this effect was strongest for spiking in supragranular layers around the infragranular alpha cycle.

Interlaminar Control Over the Cortical Column

Taken together, our findings support the hypothesis that synaptic modulation of neurons at specific locations within V1's laminar microcircuit modulates spiking throughout the entire column. The anatomical layout of the V1 microcircuit suggests that layer 5 neurons, in particular, exert strong control over neurons within the same cortical column (Dantzker and Callaway 2000; Binzegger et al. 2004). Layer 5 neurons also have a tendency to produce activity in the theta/alpha range (5–12 Hz) in in vitro slice preparations from mouse sensorimotor cortex (Silva et al. 1991) as well as rat visual cortex (Sun and Dan 2009). These rhythmic firing patterns are believed to be carried out by a morphologically distinct class of cells in layer 5 that elicit rhythmic bursts 5–15 times a second, with each train consisting of 2–5 spikes occurring at 150–300 Hz (Connors and Amitai 1997). This finding also agrees with early in vivo recordings in dogs, which suggest that infragranular neurons operating in the alpha range may act as “pacemakers” (Lopes da Silva and Storm Van Leeuwen 1977).

One possible mechanistic model that could describe our results is that projections from layer 5 neurons to more superficial layers exert a net inhibitory effect through interneurons (Connors 1984; Chagnac-Amitai et al. 1990). Activation of these superficially projecting neurons could be reflected in the infragranular sink, coincident with the alpha LFP trough, and the net inhibitory effect could be reflected in the concomitant relative decrease in spiking (Fig. 4a,c). This interpretation is congruent with the general observation that alpha activity in visual cortex is associated with periodic inhibition of neural activity (Klimesch et al. 2007; Jensen and Mazaheri 2010; Händel et al. 2011; Jensen et al. 2012; Bareither et al. 2014; Chaumon and Busch 2014). Whether this rhythmic modulation of spiking is best conceived as gating or pulsed inhibition, the periodic fluctuation of columnar activity might be an important synchronizing element in the integration of feedforward visual inputs with feedback from higher cortical areas.

Role of Feedback and Other Nonlocal Signals

As stated above, it is possible that the rhythmic fluctuation we observed does not emerge within V1, but is inherited from other regions. One proposition is that feedback from other cortical areas regulates excitability across the column. In line with this explanation, neurons in the infragranular layers of cortex are the origin (Markov et al. 2013) and target (Maunsell and Van Essen 1983; Nascimento-Silva et al. 2014) of cortical feedback. Alpha activity within these layers thus might constitute the spectral signature of communication between cortical areas (Donner and Siegel 2011; Self et al. 2013; van Kerkoerle et al. 2014; Bastos et al. 2015). Indeed, intra-areal LFP coherence in the low-frequency range is highest between the infragranular layers of V1 and V2 (von Stein et al. 2000).

An alternative, but not mutually exclusive, explanation is that the thalamus is involved in rhythmically modulating neurons in V1, and ultimately intracolumnar coupling. For example, the lateral geniculate nucleus (LGN) may control neurons in primary target layers 4C and 6 in V1 in a unidirectional manner, or through a thalamocortical loop (Fitzpatrick et al. 1994; Bollimunta et al. 2011). In line with the notion of geniculate involvement, LGN interneurons modulate thalamocortical relay neurons in the alpha range (Lőrincz et al. 2009). Indeed, alpha activity in the LGN couples with infragranular activity in V1 (Bastos et al. 2014), supporting the idea that the alpha-range fluctuations in the LGN, perhaps in concert with infragranular neural activity, could control excitability across the column in V1.

A third possibility is that second-order thalamic nuclei, such as the pulvinar, are involved in regulating alpha activity in V1 (Lopes da Silva et al. 1980; Palva and Palva 2007; Saalmann et al. 2012). Pulvinar neurons engage in low-frequency oscillatory bursting (Lopes da Silva and Storm Van Leeuwen 1977), and supragranular V1 spiking activity has been shown to critically depend on pulvinar input (Purushothaman et al. 2012). The alpha-spike coupling observed in our study could be congruent with pulvinar-based modulation of spiking activity. However, this hypothetical scenario necessitates further explanation given the relatively weak alpha-locked current sinks and sources in the supragranular layers, which constitute the primary projection target of pulvinar neurons (Jones 2001).

Future work will need to determine the specific cell types within V1 involved in the rhythmic control of population spiking activity during sensory processing, if this alpha coupling of spiking activity generalizes to other visual areas, and whether this rhythmic modulation of spiking is intrinsic to V1 or if other structures are involved in its regulation.

Supplementary Material

Supplementary material can be found here.

Funding

This work was supported by the Intramural Research Program of the NIMH and grants by the Whitehall Foundation, the Knights Templar Eye Foundation, and the Alfred P. Sloan Foundation to A.M.