Know Your Limitations: Assumptions in the Single-Beat Method for Estimating Right Ventricular–Pulmonary Vascular Coupling

Nearly 45 years ago, Suga and colleagues (1) proposed a new approach for quantifying heart pump function based on the concept of elastance or elasticity. Elasticity is a material property that describes how much stress is required to cause material deformation. To illustrate, if the ventricle is a balloon, its elasticity can be measured by how much air (or blood) pressure is required to cause an increase in volume. Unlike a balloon that has constant material properties, a ventricle has time-changing material properties. During filling, the ventricle has a low elasticity, which enables a large increase in volume for a small increase in pressure; during isovolumic contraction, the elasticity increases such that ventricular pressure increases, even though there is no change in volume. Then, during ejection and isovolumic relaxation, elasticity increases and decreases to its diastolic value. One benefit of the time-varying elasticity, or elastance, is that it can be measured from pressure–volume loops. A second is that it is load independent for the left ventricle (1), as well as the right ventricle (2).

Building on the concept of ventricular time-varying elastance, but turning attention toward the problem of the “interaction between the right heart ventricle and its arterial load” (3), Hroar Piene proposed that ventricular elastance should match or couple to the opposition to pulsatile flow in the pulmonary vasculature when “a linkage exists between their two structures”; that is, during systole. Unfortunately, he could not arrive at an analytical solution because the time-varying opposition to flow, or impedance, was computed from a graphical analysis of pressure and flow waves at the time. A year later, Sunagawa and others showed that matching end-systolic elastance (Ees), measured from the ratio of end-systolic pressure to end-systolic volume over multiple heart beats with varying preload, to arterial elastance at end systole (Ea), calculated as end-systolic pressure divided by stroke volume, was a simple and robust approach for assessing ventricular–vascular or ventriculoarterial interactions (or ventricular–vascular coupling) (4).

This new concept found broader use with the development of estimates of Ees based on a single heartbeat instead of multiple beats with varying preload. This “single-beat” method was first developed by Sunagawa and colleagues and validated for the left ventricle, using data from healthy dogs and humans (5, 6), and then validated for the right ventricle using data from healthy dogs (7).

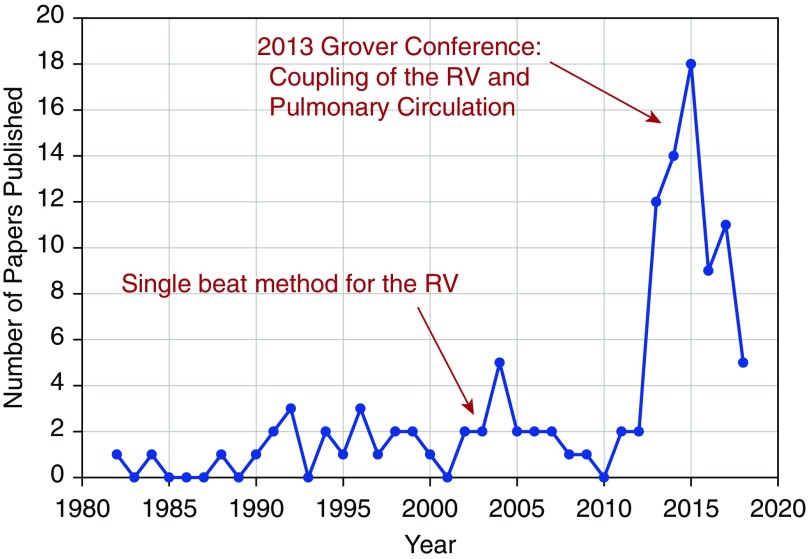
Fast forward to today, and an informal survey of PubMed using search terms such as (“right ventricle” AND “pulmonary arterial” AND “coupling” NOT “conduit”) or (“right” AND “ventriculoarterial”) or (“right ventricular elastance” AND “pulmonary elastance”) led to the histogram of publications in English-language journals seen in Figure 1. Although use of both the original multibeat method and the newer single-beat method is obviously increasing, it requires a deeper analysis beyond the scope of this commentary to understand which approaches were used in which publications, and more important, what assumptions were used.

Figure 1.

Histogram of papers published in English-language journals indexed by PubMed, based on a collection of search terms and some curation. Note that a large number of papers published between 2013 and 2015 were part of the Grover Conference Series on Coupling of the RV and Pulmonary Circulation. Results for 2018 are those indexed by May 29. RV = right ventricle.

In this issue of the Journal, Tello and colleagues (pp. 816–818) question the assumption that mean pulmonary artery pressure (mPAP) is an accurate approximation of the right ventricular (RV) end-systolic pressure (ESP), which is often used to calculate RV Ees and Ea, using the single-beat method (8). This is an important study because, as the authors point out, the assumption that mPAP is equal to ESP was validated only in small cohort of healthy, male subjects (9). Although challenges in identifying the end-systolic point on the triangular-shaped RV pressure–volume loop were considered in the first description of the single-beat method for the RV (8), pressure–volume loops are known to change shape in the setting of RV pressure overload (10), which may further increase differences between mPAP and RV ESP. Therefore, Tello and colleagues set out to evaluate the mPAP–ESP relationship in RV overload resulting from pulmonary arterial hypertension (PAH) (8).

In their small cohort of patients with PAH, the authors demonstrate that mPAP underestimates ESP in PAH, with the degree of underestimation proportional to the degree of PAH severity. The consequence of this error is that substitution of mPAP for ESP leads to overestimation of Ees and underestimation of Ea. These discrepancies are compounded when computing ventricular–vascular coupling by Ees/Ea, such that the mPAP-based coupling ratio is significantly higher than the RV ESP-based coupling ratio. Thus, this study highlights the importance of knowing your limits (or the limits of your assumptions) and the consequences of computing metrics derived from healthy subjects in diseased populations.

Although the article has many strengths and important implications for the field, as highlighted earlier, it has its own limitations that affect interpretation of the findings. First, similar to many studies in patients with PAH, because of the rarity of the disease, the sample size is small (20 subjects). Second, similar to many studies that require invasive hemodynamics, no comparison data are provided for healthy control patients. With such a small sample size and no healthy control group, it is premature for the authors to propose a general equation to estimate ESP from mPAP; it may not apply to either healthy subjects, those with more severe PAH, older or younger cohorts, and so on. In addition, as RV–pulmonary vascular coupling is increasingly being estimated at exercise or with dobutamine stimulation, it is important to know how mPAP relates to ESP under these conditions. Finally, the major limitation of this work is the lack of comparison to the gold standard calculation of Ees from a family of pressure–volume loops at varying preload (11); that is, the multibeat method. Although challenging, it is possible to collect RV pressure–volume loops clinically, using the Valsalva maneuver to vary preload (12, 13). Only by incorporating preload-altering maneuvers into protocols for RV pressure–volume loop acquisition using conductance catheters (as was done in the present study) in large clinical cohorts can the limits of important assumptions in the calculation of Ees, Ea, and Ees/Ea be truly understood.

Tello and colleagues make another important point in their study related to assumptions: Ees/Ea has not been shown to correlate with outcomes in PAH (8). A “volume-only” approximation of Ees/Ea (stroke volume divided by end-systolic volume), which has its own limiting assumptions, independently predicted outcomes in a relatively large PH population (n = 50) (14), but the only studies that used the multibeat method did not include long-term follow-up (12, 13), and studies using the single-beat method failed to show any prognostic value of Ees/Ea (14, 15). Given the potential underestimation of Ees/Ea with worsening PAH, use of mPAP for RV ESP in the single-beat method may have blunted the sensitivity of this metric to detect clinically relevant changes. Whether the single-beat estimate of Ees/Ea with an accurate ESP value or even the multibeat calculation of Ees/Ea has strong prognostic value in PAH remains an open question.

Quantifying ventricular–vascular coupling remains promising as a tool for assessing cardiopulmonary status in the context of RV pressure overload. To improve our understanding of the implications and clinical relevance of this metric, future work should include validation of methods for calculating Ees/Ea, either in clinical studies applying the gold standard of varying preload or in large animal studies that recapitulate PAH phenotypes. As assumptions are validated, longer-term studies that include assessment of how Ees, Ea, and Ees/Ea change over time and in response to therapy should be pursued to determine the prognostic and clinical relevance of these metrics. The study by Tello and colleagues in this issue is a positive step in this direction (8).