Functional feature construction for individualized treatment regimes

Abstract

Evidence-based personalized medicine formalizes treatment selection as an individualized treatment regime that maps up-to-date patient information into the space of possible treatments. Available patient information may include static features such race, gender, family history, genetic and genomic information, as well as longitudinal information including the emergence of comorbidities, waxing and waning of symptoms, side-effect burden, and adherence. Dynamic information measured at multiple time points before treatment assignment should be included as input to the treatment regime. However, subject longitudinal measurements are typically sparse, irregularly spaced, noisy, and vary in number across subjects. Existing estimators for treatment regimes require equal information be measured on each subject and thus standard practice is to summarize longitudinal subject information into a scalar, ad hoc summary during data pre-processing. This reduction of the longitudinal information to a scalar feature precedes estimation of a treatment regime and is therefore not informed by subject outcomes, treatments, or covariates. Furthermore, we show that this reduction requires more stringent causal assumptions for consistent estimation than are necessary. We propose a data-driven method for constructing maximally prescriptive yet interpretable features that can be used with standard methods for estimating optimal treatment regimes. In our proposed framework, we treat the subject longitudinal information as a realization of a stochastic process observed with error at discrete time points. Functionals of this latent process are then combined with outcome models to estimate an optimal treatment regime. The proposed methodology requires weaker causal assumptions than Q-learning with an ad hoc scalar summary and is consistent for the optimal treatment regime.

1 Introduction

It is widely recognized by clinical and intervention scientists that the best possible care requires personalized treatment based on individual patient characteristics (Piquette-Miller et al., 2007; Insel, 2009; Hamburg and Collins, 2010; Lauer and Collins, 2010; Topol, 2012). Individualized treatment regimes (ITRs) formalize personalized treatment selection as a function from current patient information to a recommended treatment. An optimal ITR maximizes the expectation of a desirable outcome when applied to an entire population of interest. There has been a recent surge of research on developing estimators for optimal ITRs including regression-based estimators (Lu et al., 2011; Qian and Murphy, 2011a; McKeague and Qian, 2011), and direct-search estimators (Zhao et al., 2012; Zhang et al., 2012a,b; Orellana et al., 2010). ITRs are the atoms of dynamic treatment regimes (Murphy, 2003; Robins, 1986, 1989, 1997, 2004) which are currently a subject of intense research including both estimation (Henderson et al., 2010a; Zhao et al., 2011; Goldberg and Kosorok, 2012; Zhang et al., 2013; Moodie et al., 2013; Laber et al., 2014) and inference (Chakraborty et al., 2010; Moodie and Richardson, 2010; Chakraborty et al., 2013; Laber et al., 2013b); recent surveys include Schulte et al. (2014); Chakraborty and Moodie (2013); Chakraborty and Murphy (2014).

Despite this influx of research, most existing methods for estimating optimal ITRs from observational or randomized study data assume that each patient is measured at the same, fixed time points and that patient measurements are made without error. This is unrealistic in many clinical settings where noisy patient measurements are taken at clinic visits which are sparsely observed and irregularly spaced. Thus, to apply existing estimation methods, a standard approach is to reduce patient longitudinal information into an ad hoc scalar summary which is assumed to be measured perfectly. However, this potentially obfuscates important scientific information contained the patient longitudinal process, ignores measurement error, requires strong causal assumptions, and may lead to an ITR of poor quality.

We model the pre-treatment patient longitudinal information as a noisy proxy of a smooth latent process and employ methods from functional data analysis to form a regression-based estimator of the optimal ITR. We assume that the effect of the true latent process is represented either as: (i) an inner product of the latent process and an unknown, nonparametrically modeled, coefficient function; or (ii) a non-linear parametric functional of the latent process. Under mild regularity conditions, we prove that the proposed estimator is consistent if the true optimal decision rule is linear in the static patient information and depends on the true latent process as described above. The proposed estimator applies to both randomized and observational studies with sparsely observed, irregularly spaced, and noisy longitudinal measurements. While we focus on a single binary treatment decision, the proposed work provides a foundation for several extensions including multiple treatments and treatment decision points.

There are several recently proposed methods that use functional data to inform construction of optimal ITRs. McKeague and Qian (2014), Ciarleglio et al. (2015), and Ciarleglio et al. (2016) developed estimators for optimal ITRs that allow for pre-treatment functional predictors that are densely sampled without noise. In contrast, as mentioned previously, our focus is on sparse, noisy, and irregularly spaced data.

Our approach uses non-parametric estimators of the mean and covariance functions of the latent process. An alternative approach would be to posit parametric models for the mean and/or covariance functions using, e.g., mixed-effects models (Laird and Ware, 1982; Diggle et al., 2002; Fitzmaurice et al., 2012); this approach is especially appealing in contexts where scientific theory can be used to inform the choice of parametric model. Our proposed approach can also be used with such models, however, in our motivating biomedical applications there is not sufficient theory to inform the choice of these models so we will not discuss this approach further.

In Section 2, we review regression-based estimators of the optimal ITR and conditions needed to identify the optimal ITR using randomized or observational data. In Section 3, we describe our proposed estimator and state conditions under which it consistently estimates the optimal ITR. The finite sample performance of the proposed estimator is illustrated using simulation experiments in Section 4 and application to a study of major depressive disorder in Section 5. Extensions and open problems are discussed in Section 6.

2 Regression-based methods for estimating optimal ITRs

Assume that data available to estimate an ITR are of the form ${\mathcal{D}}_n={\{({\mathbf{X}}_i,W_i({\mathbf{T}}_i),A_i,Y_i)\}}_{i=1}^n$ which comprise n i.i.d. copies of a trajectory {X, W(T), A, Y} where: $\mathbf{X}\in {\text{ℝ}}^p$ denotes pre-treatment subject covariate information; W(T) = {W(T₁), …, W(T_M)} denotes M pretreatment proxy measurements taken at times T = (T₁, …, T_M); A ∈ {−1, 1} denotes treatment assigned; and $Y\in \text{ℝ}$ denotes an outcome coded so that higher values are better. Capital letters, like X, denote random variables and lowercase letters, like x, denote instances of these random variables. Both M and T are treated as random variables as the number and timing of observations varies across subjects. Observation times T are allowed to vary in number, be sparse, and irregularly spaced. For example, in the STAR*D study of major depressive disorder, W(T) might denote patient-reported Quick Inventory of Depressive Symptomatology (QIDS-SR, Rush et al., 2003), recorded at each clinic visit.

An ITR π maps available patient information to a recommended treatment so that π : dom X × dom W(T) → dom A. Under π, a patient presenting with X = x and W(T) = w(t) would be recommended treatment π{x, w(t)}. To define an optimal ITR, we use potential outcomes (Rubin, 1978; Splawa-Neyman et al., 1990). Let Y^∗(a) denote the potential outcome under treatment a ∈ {−1, 1} and define Y^∗(π) = Σ_{a∈{−1, 1}} Y*(a)1_π{X,_W(T)}=a to be the potential outcome under ITR π. The optimal ITR, say π^opt, satisfies $\mathbb{E}{Y}^{\ast }({\pi }^{\mathrm{opt}})\ge \mathbb{E}{Y}^{\ast }(\pi )$ for all π. To define the optimal ITR in terms of the data-generating model we use assume: (C1) consistency, Y = Y*(A); (C2) positivity, there exists ε > 0 so that ε < P {A = a|X, W(T)} for each a ∈ {−1, 1} with probability one; and (C3) ignorability, {Y*(−1), Y*(1)} ⫫ A|X W(T). Assumption (C3) is true by construction in a randomized study, but unverifiable with data from an observational study (Robins et al., 2000). A common justification for (C3) in the analysis of an observational study is that patient covariates, i.e., {X, W(T)}, are sufficiently rich so as to capture all information used in the treatment decision process. However, current analysis methods implicitly require the stronger causal assumption (C3’) {Y*(−1), Y*(1)} ⫫ A|X, s {W(T)}, where s{w(t)} is a pre-specified, ad hoc, summary of w(t). The proposed method incorporates w(t) directly into the model and is thereby more consistent with (C3).

Define $Q\{\mathbf{x},w(\mathbf{t}),a\}=\mathbb{E}\left\{Y\right|\mathbf{X}=x,W(\mathbf{T})=w(\mathbf{t}),A=a\}$. Under (C1)–(C3), it can be shown that π^opt{x, w(t)} = arg max_{a∈{−1, 1}} Q{x, w(t), a}. Regression-based estimators postulate a working model for Q{x, w(t), a} which is fit using the data, say $\widehat{Q}\{\mathbf{x},w(\mathbf{t}),a\}$, and then used to infer the optimal ITR through ${\widehat{\pi }}^Q\{\mathbf{x},w(\mathbf{t})\}=\text{arg}{\text{max}}_a\widehat{Q}\{\mathbf{x},w(\mathbf{t}),a\}$. Postulating a working model for Q{x, w(t), a} that fully incorporates w(t) is difficult because this information is often sparsely observed and irregularly spaced. Thus, a common strategy is to assume Q{x, w(t), a} = Q[x, s {w(t)}, a] for some scalar summary s{w(t)}. In this case, one can use standard regression methods, e.g., linear regression, to estimate Q{x, w(t), a}, by regressing Y on X, s{W(T)}, and A. For example, Chakraborty et al. (2013), Chakraborty and Moodie (2013), Laber et al. (2013a), and Schulte et al. (2014), use the slope of QIDS-SR, s{w(t)} = {w(t_m) − w(t₁)}/(t_m − t₁) in their analyses of STAR*D; while this quantity is informed by clinical expertise, it is not informed by the response Y, the treatment A, nor does it account for potential measurement error in QIDS-SR as a proxy for depression severity. Another common ad hoc summary is the most recent pre-treatment measured score s{w(t)} = t_m (e.g., Shortreed et al., 2011; Nahum-Shani et al., 2012; Laber et al., 2014, 2013b); again, this summary may be informed by expert judgment but is not data-driven. In the context of an observational study, allowing w(t) to enter regression model only through s{w(T)} is implicitly assuming that the stronger causal assumption (C3’) holds.

For clarity, we describe a simple version of regression-based estimation of the optimal ITR using a linear working model for Q{x, w(t), a} of the form Q{x, w(t), a; θ} = x^⊺α + βs{w(t)} + a[x^⊺δ + γs{w(t)}], where θ = (α^⊺, β, δ^⊺, γ)^⊺ and s{w(t)} is a fixed and known scalar summary of w(t). Let P_n denote the empirical measure and define ${\widehat{\theta }}_n=\text{arg}{\text{min}}_{\theta }{\mathbb{P}}_n{[Y-Q\{X,W(\mathbf{T}),A;\theta \}]}^2$. A regression-based estimator of the optimal ITR is ${\widehat{\pi }}^Q\{\mathbf{x},w(\mathbf{t})\}=\text{arg}{\text{max}}_{a}Q\left\{\mathbf{x},w(\mathbf{t}),a;{\widehat{\theta }}_n\right\}$. Regression-based estimators are convenient, intuitive, and benefit from standard regression o diagnostics and model-building techniques. For these reasons, we use the foregoing regression-based estimator as the basis for the estimators described in Section 3. However, in some settings, direct-search estimators (Zhao et al., 2012; Zhang et al., 2012a,b, 2013) may be more appropriate; see Remark 3.4 in Section 3 for a description of direct-search estimation.

3 Functional Q-learning for estimating optimal ITRs

Treating patient longitudinal information as sparse functional data we derive estimators of the optimal ITR, π^opt {x, w(t)}, that do not require ad hoc summary of w(t). Without loss of generality suppose that 0 ≤ T₁ < … < T_M ≤ 1. We assume that W(t) = Z(t) + (t) for all t ∈ [0, 1], where Z(·) is a square integrable latent process with smooth mean and covariance functions, and ε(·) is mean-zero white noise process. Thus, we assume that the subject longitudinal measurements W(T) are noisy realizations of the true latent process Z(·) at time points T. We introduce two general models for $\mathbb{E}\left\{Y\right|\mathbf{X},Z(\cdot ),A\}$: (i) a linear model in X, A, and Z(T); and (ii) a hybrid model that combines linear effects for X and A and a linear effect of f{Z(·); η} for a parametric functional f(·; η) indexed by unknown parameters η. These two classes of models serve as building blocks for more complex classes of models which could be obtained by adding polynomial terms or other nonlinear basis functions.

3.1 Linear working model for $\mathbb{E}\left\{Y\right|\mathbf{X},Z(\cdot ),A\}$

We assume a linear model of the form

• (A1) $\mathbb{E}\{Y|\mathbf{X}=\mathbf{x},Z(\cdot )=z(\cdot ),A=a\}={\mathbf{x}}^{⊺}{\alpha }^{\ast }+{\displaystyle {\int }_0^{1}z(t){\beta }^{\ast }(t)dt+a}\left\{{\mathbf{x}}^{⊺}{\delta }^{\ast }+{\displaystyle {\int }_0^{1}z(t){\gamma }^{\ast }(t)dt}\right\},$

where α* and β*(·) are the main effects associated with X and Z(·) and δ* and γ*(·) are interaction effects. If the coefficient functions β*(·) and γ*(·) were known and the latent process Z(·) were observed, then (A1) would correspond to a linear model. However, the coefficient functions are unknown and Z(·) is not observed. Model (A1) was studied by McKeague and Qian (2014) and Ciarleglio et al. (2015) in the setting where Z(·) is observed on a fine grid of points for each subject.

The idea behind our estimation procedure is to use orthogonal basis function expansions for both the latent process and the unknown coefficient functions, and then reduce the infinite summation by an appropriate finite truncation. Let the spectral decomposition of the covariance function, G(t, t′) = Cov{Z(t), Z(t′)}, be G(t, t′) = Σ_k≥1 λ_kϕ_k(t)ϕ_k(t′), where {λ_k, ϕ_k(·)}_k≥1 are the pairs of eigenvalues/eigenfunctions with λ₁ > λ₂ > … ≥ 0, and {ϕ_k(·)}_k≥1 form and orthonormal basis in L²[0, 1]. Then Z(·) can be represented using the Karhunen–Loéve expansion as Z(t) = μ(t) + Σ_k≥1 ξ_kϕ_k(t), where ${\xi }_k\triangleq {\displaystyle {\int }_0^1\{Z(t)-\mu (t)\}{\varphi }_k(t)dt}$ are functional principal component scores, which have mean zero, variance λ_k, and are mutually uncorrelated. Using the eigenfunctions {ϕ_k(·)}_k≥1, the coefficient functions β*(·) and γ*(·) can be represented as ${\beta }^{\ast }(t)={\sum }_{k\ge 1}{\beta }_k^{\ast }{\varphi }_k(t)$ and ${\gamma }^{\ast }(t)={\sum }_{k\ge 1}{\gamma }_k^{\ast }{\varphi }_k(t)$, where ${\beta }_k^{\ast }\triangleq {\displaystyle {\int }_0^1\beta (t){\varphi }_k(t)dt}$ and ${\gamma }_k^{\ast }\triangleq {\displaystyle {\int }_0^1\gamma (t){\varphi }_k(t)dt}$ are unknown basis coefficients. We assume that X has an intercept term. Thus, the model (A1) can be equivalently written as $\mathbb{E}\{Y|\mathbf{X}=\mathbf{x},Z(\cdot )=z(\cdot ),A=a\}={\mathbf{x}}^{⊺}{\alpha }^{\ast }+{\displaystyle {\sum }_{k\ge 1}{\xi }_k{\beta }_k^{\ast }+a}\left({\mathbf{x}}^{⊺}{\delta }^{\ast }+{\displaystyle {\sum }_{k\ge 1}{\xi }_k{\gamma }_k^{\ast }}\right)$, where we have absorbed ∫ μ(t)β*(t)dt and ∫ μ(t)γ*(t)dt into the intercept and main effect of treatment.

To obtain an expression for Q{x, w(t), a} we assume:

• (A2) Y is conditionally independent of W(·) given Z(·);

• (A3) A is independent of Z(·) given X and W(T), and 0 < c₁ ≤ P(A = 1|X, W(T)) ≤ c₂ < 1 with probability one for fixed constants c₁ and c₂;

• (A4) Z(·) is independent of X given W(T);

• (A5) Z(·), W(·), β(·), and γ(·), belong to L²[0, 1].

The foregoing assumptions are relatively mild: (A2) states that the noise–corrupted process W(·) provides no additional information about Y given the true signal Z(·); (A3) is satisfied if treatment is assigned according to observables X and W(T) and all subjects have a positive probability of receiving each treatment; (A4) allows us to estimate Z(·) using W(T) without reference to X, this simplifies notation and calculations but is not necessary (Jiang and Wang, 2010).

Under assumptions (A1)–(A5)

$$Q\{\mathbf{x},w(\mathbf{t}),a\}={\mathbf{x}}^{⊺}{\alpha }^{\ast }+{\displaystyle \sum _{k\ge 1}{\beta }_k^{\ast }\mathbb{E}}\{{\xi }_k|W(\mathbf{T})=w(\mathbf{t})\}+a\left[{\mathbf{x}}^{⊺}{\delta }^{\ast }+{\displaystyle \sum _{k\ge 1}{\gamma }_k^{\ast }\mathbb{E}}\{{\xi }_k|W(\mathbf{T})=w(\mathbf{t})\}\right].$$ (1)

Let ${\text{ℓ}}_k\{w(\mathbf{t})\}\triangleq \mathbb{E}\{{\xi }_k|W(\mathbf{T})=w(\mathbf{t})\}$ and let K be the number of terms in a finite truncation of the infinite summations in the foregoing display. Under the assumption of joint normality of the functional principle components and measurement error, ℓ_k{w(t)} = λ_kϕ_k(t) {Φ(t)ΛΦ(t)^⊺ + σ²I_m}⁻¹ Φ(t)w(t), where ϕ_k(t) = {ϕ_k(t₁), …, ϕ_k(t_m)}^⊺, Φ(t) is the m × K matrix {ϕ₁(t) ⋯ ϕ_K(t)}, Λ = diag{λ₁, …, λ_K} is K × K diagonal matrix, I_m is the m × m identity matrix, and Var {ε(t)} ≡ σ² is the error variance.

From (1), if the functions ℓ_k{w(t)} k ≥ 1 were known, then the parameters α*, δ*, β*, γ* could be estimated by the regression of Y on X, ℓ_k{W(T)} k ≥ 1, A. However, these functions are not known because the process Z(·) is not directly observable, the basis functions {ϕ_k(·)}_k≥1 are not known, or both. We use functional principal component analysis (Silverman and Ramsay, 2005; Yao et al., 2005; Di et al., 2009) to construct estimators ${\widehat{\text{ℓ}}}_{n,k}\{w(\mathbf{t})\}$ of ℓ_k{w(t)} for k = 1, …, K. Subsequently, we regress Y on X, A, and ${\widehat{\text{ℓ}}}_{n,k}\{W(\mathbf{T})\}1\le k\le K$. The complete algorithm, which we term linear functional Q-learning, is as follows.

• (FQ1) Use functional principal components to construct estimators ${\widehat{\varphi }}_{n,k}(\cdot )$ of and of ℓ_k{w(t)}.

• (FQ2) Let θ ≜ (α^⊺, δ^⊺, β₁, …, β_K, γ₁, …, γ_K)^⊺, define

  $${\widehat{Q}}_n^K\{\mathbf{x},w(\mathbf{t}),a;\theta \}\triangleq {\mathbf{x}}^{⊺}\alpha +{\displaystyle \sum _{k=1}^K{\beta }_k{\widehat{\text{ℓ}}}_k(w(\mathbf{t}))+a\left\{{\mathbf{x}}^{⊺}\delta +{\displaystyle \sum _{k=1}^K{\gamma }_k{\widehat{\text{ℓ}}}_k(w(\mathbf{t}))}\right\}},$$

  and compute ${\widehat{\theta }}_n=\text{arg}{\text{min}}_{\theta }{\mathbb{P}}_n{\left[Y-{\widehat{Q}}_n^K\{\mathbf{X},W(\mathbf{T}),A;\theta \}\right]}^2$.

• (FQ3) The estimated optimal decision rule is ${\widehat{\pi }}_n^{FQ}(\mathbf{x},w(\mathbf{t}))=\text{arg}{\text{max}}_a{\widehat{Q}}_n^K\left\{\mathbf{x},w(\mathbf{t}),a;{\widehat{\theta }}_n\right\}$.

The finite truncation K corresponds to the number of leading functional principal components and can be selected using the percentage variance explained, cross-validation, or information criteria (see Yao et al., 2005). In our simulation experiments and illustrative application we chose K using the percentage variance explained.

The following results provide convergence rates for the functional Q-learning estimator. Subsequently, we establish that ${\widehat{\pi }}_n^{\text{FQ}}$ is consistent for the optimal regime π^opt and derive rates of convergence for the difference $\mathbb{E}{Y}^{\ast }({\pi }^{\text{opt}})-\mathbb{E}{Y}^{\ast }({\widehat{\pi }}^{\text{FQ}})$, commonly known as the regret of applying the estimated regime ${\widehat{\pi }}^{\text{FQ}}$ (Lai and Robbins, 1985; Henderson et al., 2010b). Recall that ${\mathcal{D}}_n$ denotes the observed data. Proofs are given in the Supplemental Material. We use the following assumptions:

• (A6) ${\text{lim}}_{n\to \text{∞}}{\displaystyle {\cup }_{i=1}^n{\mathbf{T}}_i}$ forms a dense set in [0, 1] with probability one;

• (A7) ε(·) is a Gaussian white-noise process;

• (A8) ${\text{sup}}_t{ }_{\in \tau }|\widehat{\mu }(t)-\mu (t)|=O_p(n^{-\mathrm{\Delta }})$ for some positive Δ, where $\widehat{\mu }(t)$ is an estimator of $\mu (t)\triangleq \mathbb{E}\{Z(t)\}$;

• (A9) ${\text{sup}}_{t,t^{\prime }}{ }_{\in \tau }|\widehat{G}(t,t\prime )-G\left(t,t\prime \right)|=O_p(n^{-\mathrm{\Delta }})$ for some positive Δ, where $\widehat{G}(t,t\prime )$ is an estimator of G(t, t′) ≜ Cov{Z(t), Z(t′)};

• (A10) $|{\widehat{\sigma }}^2-{\sigma }^2|=O_p(n^{-\mathrm{\Delta }})$ for some positive Δ, where ${\widehat{\sigma }}^2$ is an estimator of ${\sigma }^2\triangleq \text{Var}\{\epsilon (t)\}$;

• (A11) $\mathbb{E}{\Vert \mathbf{X}\Vert }^4<\text{∞}$ and E[XX^⊺] is non-singular;

• (A12) ${\displaystyle {\sum }_{k\ge 1}{\lambda }_k^2<\text{∞}}$;

• (A13) $|{\beta }_k^{\ast }|\le C{k}^{-\varsigma }$ and $|{\gamma }_k^{\ast }|\le C{k}^{-\varsigma }$ for all k ≥ 1, some ς > 1, and some C > 0.

Assumptions (A5)–(A10) are standard in sparse functional data analysis (Yao et al., 2005; Hall and Hosseini-Nasab, 2006; Li and Hsing, 2010; Staicu et al., 2014); (A11) is a standard assumption in regression; and (A12)–(A13) are common in scalar-on-function regression models (Hall et al., 2007; Lian, 2011; Shin and Lee, 2012).

Theorem 3.1

Assume (A1)–(A13). Let K_n be an increasing sequence of integers such that K_n → ∞ and K_n/n^2Δ → 0 as n → ∞, then

$$\mathbb{E}\left\{|{\widehat{Q}}_n^{K_n}\left\{\mathbf{X},W(\mathbf{T}),A;{\widehat{\theta }}_n\right\}-Q\{\mathbf{X},W(\mathbf{T}),A\}||{\mathcal{D}}_n\right\}=O_p(K_n{n}^{-1/2}+K_n^{1/2}{n}^{-\mathrm{\Delta }})$$

The sequence K_n is dictated by the rate of decay of the tail sum ${\displaystyle {\sum }_{k\ge m}{\lambda }_k^2}$ as m → ∞; in the extreme case in which λ_k = 0 for all sufficiently large k then one can set K_n to be a constant (i.e., it need not diverge to infinity, see the Supplemental Materials for additional details). As indicated by (A8)–(A10), the constant Δ is dictated by the slowest rate of convergence among the estimators $\widehat{\mu }$, $\widehat{G}$, and $\widehat{\sigma }$; this rate depends on the sampling design as well as the smoothness of the mean and covariance functions of the latent process (Yao et al., 2005; Hall and Hosseini-Nasab, 2006; Li and Hsing, 2010). For example, with kernel-based estimators of the mean and covariance functions under a sparse sampling design it can be shown that Δ = 1/4 is sufficient under mild regularity conditions (see Yao et al., 2005). If the functional predictor is observed on a dense grid without error, then it is possible to obtain Δ = 1/2 (Zhang and Wang, 2016). It can be seen that if Δ = 1/2 and λ_k = 0 for all but finitely many values, so that K_n can be chosen to be a constant, then the rate in the preceding theorem is parametric; however, in the sparse and noisy design we consider here we expect Δ < 1/2 (see Zhang and Wang, 2016) in which case the resulting rates are sub-parametric.

Corollary 3.2

Assume that the conditions for Theorem 3.1 hold and furthermore that $P[Q\{\mathbf{X},W(\mathbf{T}),1\}-Q\{\mathbf{X},W(\mathbf{t}),-1\}=0]=0$, then $\mathbb{E}\left\{|{\widehat{\pi }}_n^{FQ}\{\mathbf{X},W(\mathbf{T})\}-{\pi }^{\text{opt}}\{\mathbf{X},W(\mathbf{T})\}||{\mathcal{D}}_n\right\}$ converges to zero in probability.

Corollary 3.3 (Qian and Murphy, 2011)

Assume that the conditions for Theorem 3.1 hold, then

$$\mathbb{E}{Y}^{\ast }\left({\pi }^{\text{opt}}\right)-\mathbb{E}\left\{Y^{\ast }\left({\widehat{\pi }}_n^{\text{FQ}}\right)\right\}=O_P\left\{\left(K_n{n}^{-1/2}+K_n^{1/2}{n}^{-\mathrm{\Delta }}\right)\right\}$$

The estimated coefficients ${\widehat{\beta }}_{n,k}$, ${\widehat{\gamma }}_{n,k}$, k = 1, …, K and the estimated basis functions ${\widehat{\varphi }}_{n,k}(\cdot )$ can be used to form estimates of the coefficient functions β(t) and γ(t) indexing the Q-function Q{x, w(t), a} via ${\widehat{\beta }}_n(t)={\displaystyle {\sum }_{k=1}^K{\widehat{\beta }}_{nk}{\widehat{\varphi }}_{nk}(t)}$ and ${\widehat{\gamma }}_n(t)={\displaystyle {\sum }_{k=1}^K{\widehat{\gamma }}_{nk}{\widehat{\varphi }}_{nk}(t)}$. Plotting the estimated coefficient functions shows how the latent process is being weighted over [0, 1] in the Q-function and thus may be scientifically informative. For example, a coefficient function that is large in magnitude and of opposite in sign at the endpoints of [0, 1] but small in magnitude in the middle of [0, 1] suggests that the change in Z(t) from the beginning to the end of the observation period is important. In this way, the linear functional Q-learning algorithm can uncover important relationships between the outcome and evolving patient characteristics including how these characteristics should be used to dictate treatment. However, in some cases, existing scientific theory may suggest a particular form for $\mathbb{E}\{Y|\mathbf{X},Z(\cdot ),A\}$ which may be nonlinear. We consider this case next.

3.2 Nonlinear working models for $\mathbb{E}\{Y|\mathbf{X},Z(\cdot ),A\}$

In some settings, nonlinear features of a patient’s latent longitudinal process may be highly clinically informative. For example, in the context of depression and anxiety, an important feature of a patient’s evolving health status is the degree of waxing and waning of patient symptomatology (Wittchen et al., 2000). In this section, we develop functional Q-learning nonlinear summaries of the latent process that are known and suggested by domain experts or are unknown but assumed to belong to a parametric class of nonlinear models; the extension to non-parametric classes of functionals is discussed in Remark 3.5. In the context of major depressive disorder an important feature might be the variation in an individuals depression level as captured by $f\{Z(\cdot );\eta \}=\eta {\displaystyle {\int }_0^1|Z^{\prime }(t)|dt}$, where $\eta \in \text{ℝ}$ and Z′(t) denotes the derivative of Z(t). In this section, we construct estimators of π^opt under the assumption

$$\mathbb{E}\left\{Y|\mathbf{X}=\mathbf{x},Z(\cdot )=z(\cdot ),A=a\right\}={\mathbf{x}}^{⊺}{\alpha }^{\ast }+f\left\{z(\cdot );\eta \right\}+a\left[{\mathbf{x}}^{⊺}{\delta }^{\ast }+g\left\{z(\cdot );\rho \right\}\right]$$, (A1’)

where f and g are functionals from L²[0, 1] in to $\text{ℝ}$ indexed by unknown parameters $\eta \in {\text{ℝ}}^k$ and $\rho \in {\text{ℝ}}^q$. If Z(·) was observed, then (A1’) reduces to a parametric nonlinear regression model. Under (A1’) and (A2)–(A5)

$$Q\{\mathbf{x},w(\mathbf{t}),a\}={\mathbf{x}}^{⊺}{\alpha }^{\ast }+\mathbb{E}[f\{Z(\cdot );\eta \}|W(\mathbf{T})=w(\mathbf{t})]+a({\mathbf{x}}^{⊺}{\delta }^{\ast }+\mathbb{E}[g\{Z(\cdot );\rho \}|W(\mathbf{T})=w(\mathbf{t})]).$$

Let G{·|w(t)} denote the conditional distribution of Z(·) given W(T) = w(t), then

$$Q(\mathbf{x},w(\mathbf{t}),a)={\mathbf{x}}^{⊺}{\alpha }^{\ast }+{\displaystyle \int f\{u(\cdot );\eta \}dG\{u(\cdot )|w(\mathbf{t})\}+a}\left[{\mathbf{x}}^{⊺}{\delta }^{\ast }+{\displaystyle \int g\{u(\cdot );\rho \}dG\{u(\cdot )|w(\mathbf{t})\}}\right].$$ (2)

We construct an estimator of Q{x, w(t), a} by first estimating G{·|w(T)} and then applying nonlinear least squares to estimate the remaining parameters in (2). To estimate G{·|w(t)} we assume that the loadings {ξ_k}_k≥1 are a discrete-time, mean-zero Gaussian process with independent components and Var(ξ_k) = λ_k for all k ≥ 1. Under this assumption it can be seen that Z(·) given W(T) = w(t) follows a Gaussian process with mean function $m\left\{w\left(\mathbf{t}\right)\right\}\left(t\right)=\mathbb{E}\left\{Z\left(t\right)|W\left(\mathbf{t}\right)=w\left(\mathbf{t}\right)\right\}$ and covariance kernel

$$\mathcal{K}\{w(\mathbf{t})\}(t,v)=\mathbb{E}\left([Z(t)-m\{w(\mathbf{t})\}(t)]Z(v)-m\{w(\mathbf{t})\}(v)]|W(\mathbf{t})=w(\mathbf{t})\right).$$

Expressions for the maximum likelihood estimators of m{w(t)}(t) and $\mathcal{K}\{w(\mathbf{t})\}(t,v)$ are obtained using the joint normality of {Z(t), Z(v), W(T)}, however, these estimators depend on the unknown basis functions {ϕ_k(·)}_k≥1 and loading variances {λ_k}_k≥1. Let ${\widehat{m}}_n^K${w(t)}(t) and ${\widehat{\mathcal{K}}}_n^K\{w(\mathbf{t})\}(t,v)$ denote the estimators obtained by replacing {ϕ_k(·)}_k≥1 and {λ_k}_k≥1 with the functional principal components estimators ${\left\{{\widehat{\varphi }}_k(\cdot )\right\}}_{k=1}^K$ and ${\left\{{\widehat{\lambda }}_k\right\}}_{k=1}^K$, where K is a finite truncation. Let ${\widehat{G}}_n^K\{\cdot |w(\mathbf{t})\}$ denote the distribution of Gaussian process with mean ${\widehat{m}}_n^K\{w(\mathbf{t})\}(t)$ and covariance kernel ${\widehat{\mathcal{K}}}_n^K\{w(\mathbf{t})\}(t,v)$. The nonlinear functional Q-learning algorithm is:

• (NFQ1) Apply (FQ1) to construct estimators ${\widehat{\varphi }}_{nk}(\cdot )$ of ϕk(·), and ${\widehat{\text{ℓ}}}_{nk}\{w(\mathbf{t})\}$ for k = 1, …, K where K is a finite truncation.

• (NFQ2) Let ζ, ≜ (α⊺, δ⊺, η⊺, ρ⊺)⊺, define

  $${\widehat{Q}}_n^K\{\mathbf{x},w(\mathbf{t}),a;\zeta \}\triangleq {\mathbf{x}}^{⊺}\alpha +{\displaystyle \int f\{u(\cdot );\eta \}d{\widehat{G}}_n^K\{u(\cdot )|w(\mathbf{t})\}}+a\left[{\mathbf{x}}^{⊺}\delta +{\displaystyle \int g\{u(\cdot );\rho \}d{\widehat{G}}_n^K\{u(\cdot )|w(\mathbf{t})\}}\right],$$

  and use nonlinear least squares to compute ${\widehat{\zeta }}_n=\text{arg}{\text{min}}_{\zeta }{\mathrm{P}}_n{\left[Y-{\widehat{Q}}_n^K{\{\mathbf{X},W(\mathbf{T}),A;\zeta \}}^{\prime }\right]}^2$.

• (NFQ3) The estimated optimal decision rule is ${\widehat{\pi }}_n^{\mathit{NFQ}}\{\mathbf{x},w(\mathbf{t})\}=\text{arg}{\text{max}}_a{\widehat{Q}}_n^K\left\{\mathbf{x},w(\mathbf{t}),a;{\widehat{\zeta }}_n\right\}$.

  The above algorithm, can be implemented using existing statistical software with the requisite integrals being evaluated using Monte Carlo methods. Implementations of the algorithms using the R programming language (http://cran.r-project.org/) are available in the Supplemental Material. Under conditions on the smoothness of f and g, consistency of the non-linear functional Q-learning estimator follows from an argument similar to proof of Theorem 3.1.

Remark 3.4

One criticism of regression-based methods is that the form of the estimated optimal ITR is dictated by the form of the estimated Q-function. Thus, a parsimonious ITR requires a parsimonious Q-function, which may be prone to misspecification. On the other hand, a complex and expressive Q-function may lead to a complex ITR that is difficult to communicate to domain experts. This has led increased interest in direct–search, also known as policy–search, algorithms that model the marginal mean outcome as a function on the space of ITRs and then to use the maximizer of this fitted model to estimate the optimal ITR; the appeal of these methods is that the maximizer can be restricted to belong to a pre-specified class of ITRs that are interpretable or satisfy cost or logistical constraints. It is possible to use functional Q-learning to construct direct–search estimators with sparse longitudinal data. Let Π denote a class of ITRs of interest. It can be shown (Qian and Murphy, 2011b) that $\mathbb{E}{Y}^{\ast }(\pi )=\mathbb{E}\left[Q\{\mathbf{X},W(\mathbf{T}),A\}{1}_{A=\pi \left\{\mathbf{X},W(\mathbf{T})\right\}}/P\{A|\mathbf{X},W(\mathbf{T})\}\right]$, where P{a|x, w(t)} denotes the propensity score P{A = a|X = x, W(T) = w(t)}. In a randomized clinical trial the propensity score is known, in observational studies this must be estimated from data. Let $\widehat{P}\{a|\mathbf{x},\mathbf{w}(\mathbf{t})\}$ denote an estimator of the propensity score and $\widehat{Q}\{\mathbf{x},w(\mathbf{t}),a\}$ an estimator of the Q-function constructed using functional Q-learning. An estimator of $\mathbb{E}{Y}^{\ast }(\pi )$ is $\widehat{V}(\pi )={\mathbb{P}}_n\left[\widehat{Q}\{\mathbf{X},W(\mathbf{T}),A\}{1}_{A=\pi \left\{\mathbf{X},W(\mathbf{T})\right\}}/\widehat{P}\{A|\mathbf{X},W(\mathbf{T})\}\right]$. A policy–search estimator of the optimal ITR is ${\widehat{\pi }}_{\text{PS}}=\text{arg}{\text{max}}_{\pi }{ }_{\in \mathrm{\Pi }}\widehat{V}(\pi )$. In this formulation, it is possible to increase the complexity of the Q-function without bincreasing the complexity of the estimated optimal ITR. For this reason, with policy–search estimators it is typical to use a non-parametric estimator of the Q-function. We discuss non-parametric estimators in the next remark.

Remark 3.5

The preceding estimation algorithm can be extended to handle more general classes of models for the conditional mean of the outcome given covariates and the latent functional process. For example, one might postulate an additive model of the form

$$\mathbb{E}\{Y|\mathbf{X}=\mathbf{x},Z(\cdot )=z(\cdot ),A=a\}=b(\mathbf{x})+f\{z(\cdot )\}+a[c(\mathbf{x})+g\{z(\cdot )\}],$$

where c, $b\in \mathcal{C}$ are unknown functions, f, $g\in \text{ℱ}$, and $\mathcal{C}\subseteq {\text{ℝ}}^{{\text{ℝ}}^p}$ and $\text{ℱ}\subseteq {\text{ℝ}}^{L^2[0,1]}$ are (possibly infinitely dimensional) unknown classes of functions. Assuming this model, let $\mathcal{U}=\left(b,c,f,g\right)$ and define ${\widehat{G}}_n^K$ as in the nonlinear functional Q-learning algorithm. The Q-function is

$${\stackrel{\sim }{Q}}_n^K\{\mathbf{x},w(\mathbf{t}),a;\mathfrak{U}\}=b(\mathbf{x})+{\displaystyle \int f\{u(\cdot )\}d{\widehat{G}}_n^K\{u(\cdot )|w(\mathbf{t})\}}+a\left[c(\mathbf{x})+{\displaystyle \int g\{u(\cdot )\}d{\widehat{G}}_n^K\{u(\cdot )|w(\mathbf{t})\}}\right].$$

Hence, $\mathcal{U}$ can be estimated using penalized least squares

$${\stackrel{\sim }{\mathfrak{U}}}_n^{\tau }=\text{arg}\underset{\mathfrak{U}}{\text{min}}{\mathbb{P}}_n{\left[Y-{\stackrel{\sim }{Q}}_n^K\{\mathbf{X},W(\mathbf{T}),A;\mathfrak{U}\}\right]}^2+{\mathrm{P}}_{\tau }(\mathfrak{U}),$$

where ${\mathcal{P}}_r$ is a penalty function indexed by a vector of tuning parameters $\mathrm{\lambda }\in {\text{ℝ}}^q$. The estimated optimal ITR ${\stackrel{\sim }{\pi }}_n^{\text{NFQ}}\{\mathbf{x},w(\mathbf{t})\}=\text{arg}{\text{max}}_a{\stackrel{\sim }{Q}}_n^K\left\{\mathbf{x},w(\mathbf{t}),a;{\stackrel{\sim }{\mathfrak{U}}}_n^{\tau }\right\}.$

As discussed previously, nonparametric functional Q-learning can be used in the context of policy-search algorithms. In addition, one can compare the estimated policy using parametric functional Q-learning with the estimated policy using nonparametric functional Q-learning as a means of diagnosing model misspecification. However, developing a formal test of the parametric functional Q-learning model against a nonparametric alternative would require extending the asymptotic theory presented in the preceding section to handle nonparametric estimators; we leave this to future work.

4 Empirical study

In this section we examine the finite sample performance of functional Q-learning. Performance of an estimated ITR, $\widehat{\pi }$, is measured in terms of the average marginal mean outcome $\mathbb{E}\{Y^{\ast }(\widehat{\pi })\}$. To form a baseline for comparison, we implemented standard Q-learning with linear models working models in X and a fixed summary function s{W(T)}. We consider two potential summary functions, the last observed value in the longitudinal trajectory s_L{W(T)} = W(T_M), and the mean $s_M\{W(\mathbf{T})\}=\overline{W}\text{(}\mathbf{T}\text{)}=M^{-1}{\displaystyle {\sum }_{j=1}^{M}W(T_j)}$. Let ${\widehat{\pi }}_n^{Q_{\text{last}}}$ and ${\widehat{\pi }}_n^{Q_{\text{mean}}}$ denote the estimated optimal ITRs using Q-learning with s_L{W(T)} and s_μ{W(T)}. Reported simulation results are based on 1000 Monte Carlo replications.

4.1 Linear generative models

To evaluate functional Q-learning with a linear model for $\mathbb{E}\{Y|\mathbf{X},Z(\cdot ),A\}$ we use the following class of generative models: X ∼ Normal {0, Ω_p(r)}, {Ω_p(r)}_i,j = r^|i−j|, ς ~ Normal(0, I_K), $Z(t)={\displaystyle {\sum }_{k=1}^K{\zeta }_k{b}_k(t)}$, t ∈ [0, 1], τ ∼ Normal(0, 1), $Y={\mathbf{X}}^{⊺}{\alpha }^{\ast }+{\displaystyle {\int }_0^{1}Z(t){\beta }^{\ast }(t)dt+A\left\{{\mathbf{X}}^{⊺}{\delta }^{\ast }+{\displaystyle {\int }_0^{1}Z(t){\gamma }^{\ast }(t)dt}\right\}+\tau }$, M ∼ Uniform{c, c + 1, …, c + d}, and T|M = m ~ Uniform[0, 1]^m, where ${\{b_k(t)\}}_{k=1}^K$ is a cubic B-spline basis with six equally spaced knots. Thus, this class of generative models is indexed by: the dimension p, coefficient vectors α* and δ*, number of basis functions K, autocorrelation r, sparsity parameters c and d, and the coefficient functions β*(t) and γ*(t). Throughout, we fix p = 5, α* ≡ −1, δ* = (−0.1, 0, …, 0), r = 1/2, and K = 10. We consider two sparsity settings: c = 5, d = 15 which we term sparse, and c = 15, d = 10 which we term moderate. We consider three settings for the coefficient functions: (S1) γ*(t) = β*(t) ∝ 1; (S2) γ*(t) = β*(t) ∝ 1_t>0.90; and (S3) γ*(t) = β*(t) ∝ t − 1/2. Setting (S1) corresponds to a simple average of Z(t) and thus Q-learning using the summary s_M{W(T)} may be expected to perform well, whereas Q-learning with the summary s_L{W(T)} may be expected to perform poorly; setting (S2) corresponds to the average of Z(t) only over the last 10% of the time domain and therefore Q-learning using the summary s_L{W(T)} may be expected to perform well, whereas Q-learning with the summary s_M{W(T)} may be expected to perform poorly; and setting (S3) corresponds to a contrast between early and late values of Z(t) and thus neither summary s_M{W(T)} nor s_L{W(T)} captures salient features of the functional predictor and therefore Q-learning with either of these features may be expected to perform poorly.

In each setting, to control the effect size, we scale the coefficient functions so that $\mathbb{E}|{\displaystyle {\int }_0^{1}Z(t){\beta }^{\ast }(t)dt|=2}$. We assume that W(t) = Z(t)+ε(t) where ε(t) is a standard Gaussian white-noise process. We use training sets of size n = 250, results with larger sample sizes were qualitatively similar and are omitted.

Table 1 shows the marginal mean outcomes for functional Q-learning, Q-learning, and a random regime that assigns treatment by random guessing with P(A = 1) = P (A = −1) = 1/2. Functional Q-learning performs favorably compared with Q-learning in all examples considered. The performance of Q-learning appears to depend critically on the choice of summary; e.g., as anticipated, Q-learning with the summary s_M{W(T)} performs well in (S1) but poorly in (S2) and (S3), whereas Q-learning with the summary s_L{W(T)} performs well in (S3) but poorly in (S1) and (S2).

Table 1.

Estimated mean outcome under linear generative models for functional Q-learning, Q-learning with ad hoc features, and random guessing. Results are computed from 1000 datasets of size n = 250. Monte Carlo standard errors are in the second decimal place.

Example	Sparsity	$\mathbb{E}{Y}^{\ast }\left({\pi }^{\text{opt}}\right)$	$\mathbb{E}{Y}^{\ast }\left({\widehat{\pi }}^{FQ}\right)$	$\mathbb{E}{Y}^{\ast }\left({\widehat{\pi }}^{Q_{\text{last}}}\right)$	$\mathbb{E}{Y}^{\ast }\left({\widehat{\pi }}^{Q_{\text{mean}}}\right)$	$\mathbb{E}{Y}^{\ast }\left({\pi }^{\text{Rand}}\right)$
(S1)	Sparse	3.0	2.81	1.83	2.74	0.90
(S1)	Moderate	3.0	2.86	1.79	2.86	0.90
(S2)	Sparse	3.0	2.61	1.88	1.75	0.92
(S2)	Moderate	3.0	2.81	1.88	1.80	0.92
(S3)	Sparse	3.0	2.43	2.29	1.86	0.94
(S3)	Moderate	3.0	2.58	2.40	1.87	0.94

4.2 Nonlinear generative models

To evaluate functional Q-learning with a nonlinear model for $\mathbb{E}\{Y|\mathbf{X},Z(\cdot ),A\}$ we use the same class of generative models as in Section 4.1 except that Y = X^⊺α* + f{Z(·); η} + A[X^⊺δ* + g{Z(·); ρ}] + τ, where f{z(·); η} and g{z(·); ρ} are functionals of z(·) indexed by unknown parameters η and ρ, and all other parameters are as in Section 4.1. In the settings we consider here f ≡ g and f{z(·); η} = ηf₀{z(·)} where $\eta \in \text{ℝ}$, and f₀{z(·)} is a known functional of z(·) We consider three settings for f₀: (S4) $f_0\{z(\cdot )\}={\displaystyle {\int }_0^{1}tz(t)dt}$; (S5) $f_0\{z(\cdot )\}={\displaystyle {\int }_0^1{\{z^{\prime }(t)\}}^{2}dt}$, where z′(t) denotes the derivative of z(·) at t; and (S6) f₀{z(·)} = sup_t∈[0,1] z(t) − inf_t∈[0,1] z(t). To control the treatment effect size, the constant η is chosen so that $\eta \mathbb{E}|f_0\{z(\cdot )\}|=1$.

Table 2 shows the marginal mean outcomes under functional Q-learning, Q-learning, and random guessing. Functional Q-learning consistently obtains a higher marginal mean outcome than competing methods in all settings. This suggests that if there is strong scientific theory to guide the form of the Q-function, then functional Q-learning may perform well. However, the poor performance of Q-learning with the last observation illustrates that misspecification of the form of f{z(·); η} could lead to poor performance of functional Q-learning, e.g., by incorrectly choosing f{z(·); η} to approximate z(t_m).

Table 2.

Estimated mean outcome under nonlinear generative models for functional Q-learning, Q-learning with ad hoc features, and random guessing. Results are computed from 1000 datasets of n = 250. Monte Carlo standard errors are in the second decimal place.

Example	Sparsity	$\mathbb{E}{Y}^{\ast }\left({\pi }^{\text{opt}}\right)$	$\mathbb{E}{Y}^{\ast }\left({\widehat{\pi }}^{FQ}\right)$	$\mathbb{E}{Y}^{\ast }\left({\widehat{\pi }}^{Q_{\text{last}}}\right)$	$\mathbb{E}{Y}^{\ast }\left({\widehat{\pi }}^{Q_{\text{mean}}}\right)$	$\mathbb{E}{Y}^{\ast }\left({\pi }^{\text{Rand}}\right)$
(S4)	Sparse	3.0	2.98	2.73	2.58	2.53
(S4)	Moderate	3.0	2.99	2.73	2.61	2.53
(S5)	Sparse	3.0	2.55	1.99	1.99	2.05
(S5)	Moderate	3.0	2.60	2.05	2.06	2.05
(S6)	Sparse	3.0	2.86	2.60	2.59	2.55
(S6)	Moderate	3.0	2.91	2.55	2.54	2.55

5 Application to STAR*D

Sequenced Treatment Alternatives to Relieve Depression (STAR*D, www.star-d.org; Fava et al. 2003; Rush et al. 2004) is a multi-stage, randomized trial of patients with major depressive disorder. We use data from the first stage of the trial to illustrate functional Q-learning (data can be obtained through www.nimh.nih.gov). For simplicity and to match the development of our methodology, we restrict attention to the first randomized stage of the trial and compare the two most prevalent treatments with complete outcome and covariate data: Citalopram augmented with Bupropion (A = 1) and Citalopram augmented with Buspirone (A = −1). Complete data is available on n = 192 subjects. Subjects were observed for up to 14 weeks before the initial treatment, visit times are recorded in days from baseline; almost all (92%) of subjects in the complete data visited the clinic six times during this period. We use the pre-randomization self-rated Quick Inventory of Depressive Symptomatology (QIDS) as our longitudinal predictor. The left panel of Figure 1 shows the raw QIDS score for 50 randomly sampled subjects, we have highlighted two subjects to emphasize heterogeneity in the observed patterns. Based on a survey of clinical papers and previous analyses on STAR*D (see Pineau et al., 2007; Fava et al., 2008; Young et al., 2009; Chakraborty et al., 2013; Schulte et al., 2014; Novick et al., 2015, and references therein) we include as covariates: mean Clinical Global Impression (CGI) score taken over pre-randomization visits, sex, number of comorbidities at baseline, education level (indicator of some college or above), and the log number of major depressive episodes per year between diagnoses and enrollment. To be consistent with our paradigm of maximizing a desirable outcome we use 27 minus the average QIDS score over the course of post-randomization follow-up in the first stage as our outcome. Fitting a linear working model, e.g., equation (1), to the observed data and using fifty-fold cross-validation yields an estimated value of 19.35. The center panel of Figure 1 shows the smoothed longitudinal trajectories recovered from the functional principal components analysis and Table 3 shows the estimated coefficients for non-functional predictors. In contrast, using Q-learning and using the QIDS at the time of randomization in place of the QIDS longitudinal trajectory yields a cross-validated value of 16.69. Because the marginal mean outcome of an estimated optimal treatment regime is a non-smooth functional of the underlying generative distribution standard methods for inference do not apply (van der Vaart, 1991; Laber and Murphy, 2011; Hirano and Porter, 2012). To provide a rough sense of the uncertainty in the difference in value between functional and standard Q-learning, we calculated a Z-statistic using fifty differences in value computed across each fold of the cross-validation; the resultant Z-value was 1.88, so that functional Q-learning is nearly two (crudely estimated) standard errors above the mean using standard Q-learning. Thus, incorporating longitudinal information shows promising results in this limited example. Furthermore, the analysis also produces an estimate of $\widehat{\gamma }(\cdot )$which is shown in the right panel of Figure (1); the estimated coefficient function weights recent observations most heavily and contrasts them with data in the first half of the study.

Figure 1.

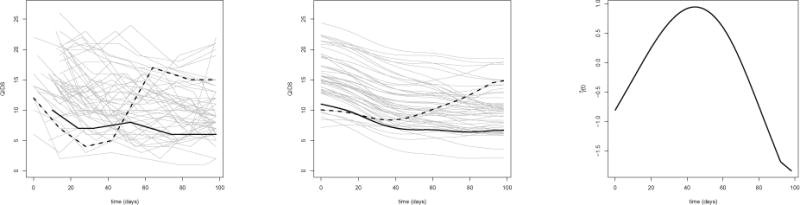
Left: Observed self-rated QIDS scores for 50 randomly selected subjects. Center: Estimated trajectories using functional principal components. Right: Estimated coefficient function $\widehat{\gamma }(\cdot )$.

Table 3.

Estimated coefficients and 95% nonparametric bootstrap confidence intervals for non-functional predictors.

Term	Estimate	95% Bootstrap CI
Intercept	19.46	(17.24, 21.95)
CGI	−0.50	(−1.25, 0.26)
Sex	−0.52	(−1.17, 0.18)
Number Comorbidities	0.18	(−0.39, 0.80)
Depressive Episodes (Log)	−0.21	(−0.47, 0.11)
Education	0.45	(−0.22, 1.11)
Treatment	0.48	(−2.22, 2.50)
Treatment × CGI	−0.20	(−0.79, 0.64)
Treatment × Sex	0.23	(−0.47, 0.94)
Treatment × Number Comorbidities	−0.073	(−0.65, 0.53)
Treatment × Depressive Episodes (Log)	−0.031	(−0.31, 0.26)
Treatment × Education	−0.050	(−0.62, 0.72)

6 Discussion

We proposed functional Q-learning as means of incorporating sparse, irregularly spaced, noisy longitudinal data into the estimation of optimal ITRs. We proved that under regularity conditions, including correct specification of the outcome regression models, the estimated optimal ITR is consistent for the true optimal ITR. Furthermore, the proposed method requires less stringent causal assumptions than standard Q-learning used with an ad hoc summary of longitudinal information. The proposed methodology performed favorably compared with standard methods in simulation experiments.

The proposed methodology lays the groundwork for a number of important extensions. One such extension is to incorporate the proposed estimator into each step of multiple stage Q-learning (Schulte et al., 2014) to analyze data from sequential multiple assignment randomized studies or observational longitudinal data with multiple treatments. The proposed estimators could also be extended to incorporate multivariate longitudinal processes, e.g., through additive regression models, and to discrete longitudinal processes, e.g., through latent threshold models. Finally, as noted in Remark 3.4, the proposed methodology can be used to build direct–search algorithms to estimated the optimal ITR within a pre-specified class of ITRs. We are currently pursuing a number of these extensions.