Bayesian integrative model for multi-omics data with missingness

Abstract

Motivation

Integrative analysis of multi-omics data from different high-throughput experimental platforms provides valuable insight into regulatory mechanisms associated with complex diseases, and gains statistical power to detect markers that are otherwise overlooked by single-platform omics analysis. In practice, a significant portion of samples may not be measured completely due to insufficient tissues or restricted budget (e.g. gene expression profile are measured but not methylation). Current multi-omics integrative methods require complete data. A common practice is to ignore samples with any missing platform and perform complete case analysis, which leads to substantial loss of statistical power.

Methods

In this article, inspired by the popular Integrative Bayesian Analysis of Genomics data (iBAG), we propose a full Bayesian model that allows incorporation of samples with missing omics data.

Results

Simulation results show improvement of the new full Bayesian approach in terms of outcome prediction accuracy and feature selection performance when sample size is limited and proportion of missingness is large. When sample size is large or the proportion of missingness is low, incorporating samples with missingness may introduce extra inference uncertainty and generate worse prediction and feature selection performance. To determine whether and how to incorporate samples with missingness, we propose a self-learning cross-validation (CV) decision scheme. Simulations and a real application on child asthma dataset demonstrate superior performance of the CV decision scheme when various types of missing mechanisms are evaluated.

Availability and implementation

Freely available on the GitHub at https://github.com/CHPGenetics/FBM

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Multi-level omics data refer to the combined molecular data in various types, for example, genome, transcriptome, methylome and proteome data, measured on a common cohort of patients. The availability of multi-level omics data in both magnitude and varieties poses challenges as well as opportunities to understand fundamental mechanisms of diseases and pathologies. Compared with separately discovering the association patterns between each omics data and phenotypes, an integrative framework that simultaneously integrates multiple omics data types will uncover more insightful regulatory machineries between different omics data and will hence deepen our understanding to hereditary and environmental causes in pathology (Richardson et al., 2016; Tseng et al., 2012, 2015).

In the literature, many strategies have emerged for integration of multi-omics data. To cluster samples for identifying unknown disease subtypes, integrative clustering (iCluster; Shen et al., 2009), Bayesian consensus clustering (Lock and Dunson, 2013), group structured integrative clustering (GS-iCluster; Kim et al., 2017) and integrative sparse K-means (IS-Kmeans; Huo et al., 2017) have been developed for integrative clustering of multi-omics data. For association and prediction modelling, Integrative Bayesian Analysis of Genomics (iBAG) (Wang et al., 2013) investigates association patterns of mRNA expressions and methylation with clinical outcome via a mechanistic model for associating methylation with gene expression and then a clinical model for direct association between expression and clinical outcome or via methylation. A Bayesian hierarchical model is then established for the inference. Such Bayesian hierarchical modelling has gained popularity in multi-omics integrative analysis due to its flexibility in model construction for complex regulatory structure, convenience to incorporate prior biological knowledge and advances in modern computing. In the association and prediction modelling, we usually focus on two key goals in the inference: firstly, to select predictive biomarkers for the phenotype and secondly, to predict clinical outcome from the selected biomarkers. As tens of thousands of features are available in omics data, the first goal of feature selection is essential in interrogating the biological and pathological mechanism of a targeted disease. The second goal could be of immediate clinical use, for example, assisting diagnosis of a disease, directing the best treatment decision and predicting drug response.

One obstacle for applying multi-omics integrative methods in real applications is missing data. Due to various reasons (e.g. limited budget, bad tissue quality or insufficient tissue amount), it is common that only partial samples have all omics data types (Voillet et al., 2016). For example, TCGA breast cancer study had 922 samples measured in methylation array, yet only 781 were measured in miRNA expression and 587 were measured for gene expression. Almost 40% of the samples are missing at least one type of omics data. To circumvent this pitfall, a naïve and convenient solution is by complete case (CC) analysis, where samples with any missing measurement are ignored. This approach results in dramatic decrease of sample size and thus decreases of statistical power, especially when more omics data types are combined. The shortcoming of CC in omics studies is recently noticed by statisticians, for example, Voillet et al. (2016) who developed a multiple imputation approach focusing on multiple factor analysis for multiple omics data. However, a unified framework serving the aforementioned purpose of feature selection, prediction as well as missingness handling is still lacking. In Bayesian methods for analysis of data with some predictors that are missing at random, marginal distribution of those predictors are usually modelled (Ibrahim et al., 2002; Little and Rubin, 2002). The data augmentation method is used to obtain the posterior distribution of parameters of interest (Tanner and Wong, 1987). In each iteration of the data augmentation procedure, missing values are imputed from the conditional distribution of those covariates given observed data under current parameters and model parameters are subsequently drawn from their posterior distribution calculated from the imputed dataset. In this article, we are motivated by the iBAG model combining mRNA expression methylation, clinical variables to predict a targeted continuous outcome. We propose a full Bayesian model with missingness (FBM) that allows iBAG to handle situations when partial samples are missing with mRNA expression or methylation. Extensive simulations and real applications demonstrated superior performance in feature selection and prediction accuracy of the new approach compared with naïve CC approach. The model can be extended to other omics data types or other targeted outcomes (e.g. binary or survival).

The article is structured as the following. In Section 2.1, we introduce the motivation, the original iBAG model and the proposed FBM. Section 2.2 discusses the inference of prediction and feature selection of FBM (Section 2.2.1) and evaluation benchmarks (Section 2.2.2). Section 3 contains extensive simulations to evaluate performance of FBM and Section 4 proposes a cross-validation (CV) decision scheme to determine whether and how to incorporate samples with missingness in FBM. Section 5 includes an application to a childhood asthma dataset with 460 individuals. Final conclusion and discussion are presented in Section 6.

2 Materials and methods

2.1 Motivation and the full Bayesian model with missingness

2.1.1 Motivation

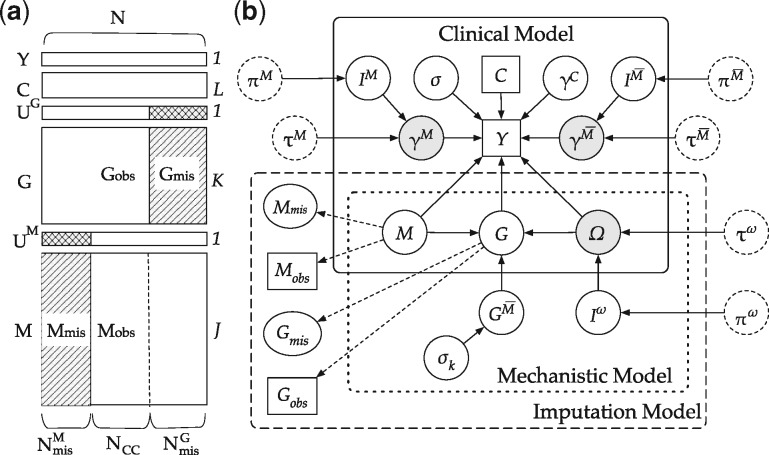
IBAG is a two-layer Bayesian hierarchical model for vertical integrative analysis of multi-level omics data, assuming data are complete. However, in reality, a large proportion of missing data is commonly seen due to budget or limitation in tissue collection. Figure 1a gives an example of data structure with missingness. Suppose there are a total of N samples, $\mathbf{Y}$ indicates the clinical outcome of interest; C indicates clinical factors; ${\mathbf{G}}_{N\times K}=\left({\mathbf{G}\prime }_{obs,N_{obs}^G\times K},{\mathbf{G}\prime }_{mis,N_{mis}^G\times K}\right)\prime$ indicates the gene expression with missingness, where ${\mathbf{U}}^G=\left(U_1^G,\dots U_N^G\right)$ is the missing indicator; likewise, ${\mathbf{M}}_{N\times J}=\left(\mathbf{M}{\prime }_{obs,N_{obs}^M\times J},\mathbf{M}{\prime }_{mis,N_{mis}^M\times J}\right)\prime$ indicates methylation data with missingness, where ${\mathbf{U}}^M=\left(U_1^M,\dots U_N^M\right)$ is the missing indicator. U = 1 indicates missing and U = 0 indicates observed. For example, number of samples with methylation level missing is $N_{obs}^G=N-{\sum }_{k=1}^K{U}_k^G$. We assume $U_i^M\times U_i^G\ne 1$ for $\forall \hspace{0.17em}1\le i\le N$. The original iBag model takes only the complete data and is subject to loss of statistical power. To handle missingness, we propose a full Bayesian model with missingness inspired by iBAG model, to achieve three goals simultaneously: feature selection, prediction and missing data imputation. In Section 2.1.2, we briefly introduce the iBAG model. In Section 2.1.3, we propose our full Bayesian model for multi-omics integration with missingness imputation.

Fig. 1.

(a) Illustration of missing pattern adopted in this article. Slash-shaded area represents missing data, cross-shaded area represents value 1 for missing indicator vectors U^G and U^M. (b) DAG of the model and parameters. The square in the DAG denotes observed data, solid circle denotes variable to be updated, circle in grey colour is the variable of interests, dashed circle denotes prior. Solid arrows indicate stochastic dependencies, and dashed arrows indicate deterministic dependencies

2.1.2 iBAG

In iBAG, the mechanistic model in the first layer assesses gene-methylation effect and divides gene expressions into two parts, the part regulated by methylation (${\mathbf{G}}^M$) and the part regulated by other mechanisms (${\mathbf{G}}^{\overline{M}}$).

$$\mathbf{G}={\mathbf{G}}^M+{\mathbf{G}}^{\overline{M}},{\mathbf{G}}^M=M\Omega ,$$

where ${\mathbf{G}}^M={\left(g_{nk}^M\right)}_{N\times K}=\left({\mathbf{g}}_1^M,\dots ,{\mathbf{g}}_K^M\right),\hspace{0.17em}{\mathbf{G}}^{\overline{M}}={\left(g_{nk}^{\overline{M}}\right)}_{N\times K}=\left({\mathbf{g}}_1^{\overline{M}},\dots ,{\mathbf{g}}_K^{\overline{M}}\right),\hspace{0.17em}\mathbf{\Omega }={\left({\omega }_{jk}\right)}_{J\times K}:{\omega }_{jk}$ denotes the ‘gene-methylation’ effect that estimates the (conditional) effect of jth methylation feature on the kth gene.

The second layer called clinical model assesses the association between gene expression (${\mathbf{G}}^M$ and ${\mathbf{G}}^{\overline{M}}$) and the phenotype:

$$\mathbf{Y}=\mathbf{C}{\mathbf{\gamma }}^C+{\mathbf{G}}^M{\mathbf{\gamma }}^M+{\mathbf{G}}^{\overline{M}}{\mathbf{\gamma }}^{\overline{M}}+ϵ,$$

where ${\mathbf{\gamma }}^C=\left({\gamma }_1^C,\dots {\gamma }_L^C\right):{\gamma }_l^C$ denotes the effect of the lth clinical factor on the clinical outcome Y. ${\mathbf{\gamma }}^M=\left({\gamma }_1^M,\dots {\gamma }_K^M\right):{\gamma }_k^M$ denotes the gene expression effect of ${\mathbf{g}}_k^M$on clinical outcome Y, called a type M effect. ${\mathbf{\gamma }}^{\overline{M}}=\left({\gamma }_1^{\overline{M}},\dots {\gamma }_K^{\overline{M}}\right):{\gamma }_k^{\overline{M}}$ denotes the gene expression effect of ${\mathbf{g}}_k^{\overline{M}}$on clinical outcome Y, called a type $\overline{M}$ effect.

2.1.3 Full Bayesian model with missingness

Figure 1b gives a full representation of our model. Our model contains three parts: mechanistic model, clinical model and an imputation model derived from the previous two models. The mechanistic model and clinical model stem from the iBAG model introduced in Section 2.1.2. Here, we will focus on two novel parts added to the original iBAG model: the sparsity-induced spike-and-slab priors (Ishwaran and Rao, 2005) for feature selection in both mechanistic and clinical models, and an imputation model to deal with missing omics data.

There are a total of eight groups of parameters that need to be estimated: γ^M, ${\gamma }^{\overline{M}}$, γ^C, Ω, ${\sigma }_k^2$’s, ${\mathbf{G}}^{mis},\hspace{0.17em}{\mathbf{M}}^{mis},\hspace{0.17em}{\sigma }^2$, γ^M and ${\gamma }^{\overline{M}}$ are our parameters of interests. Investigators may also find Ωs important if they are interested in further inference on methylation-gene regulation. The corresponding Monte Carlo Markov Chain (MCMC) Gibbs sampler will be further discussed in Supplementary Appendix Section 2.

The original iBAG model placed a Laplace prior on γ^M and ${\gamma }^{\overline{M}}$ for shrinkage purpose, however, it does not set the effects to exact zeros. To conduct natural variable selection, we instead use a spike-and-slab prior to induce sparsity. In addition, we also perform feature selection in ω using the same spike-and-slab prior, considering that not all the methylation sites are regulating the gene expression. So we will have:

$$\left[{\gamma }_k^M|I_k^M,{\left({\tau }^M\right)}^2\right]\sim \left(1-I_k^M\right)N(0,{10}^{-6})+I_k^{M}N(0,{\left({\tau }^M\right)}^2);$$

$$\left[I_k^M|{\pi }^M\right]\sim Bern\left({\pi }^M\right),\hspace{0.17em}\left[{\pi }^M\right]\sim Unif(0,1);$$

$$\left[{\gamma }_k^{\overline{M}}|I_k^{\overline{M}},{\left({\tau }^{\overline{M}}\right)}^2\right]\sim \left(1-I_k^{\overline{M}}\right)N(0,{10}^{-6})+I_k^{\overline{M}}N(0,{\left({\tau }^{\overline{M}}\right)}^2);$$

$$\left[I_k^{\overline{M}}|{\pi }^{\overline{M}}\right]\sim Bern\left({\pi }^{\overline{M}}\right),\hspace{0.17em}\left[{\pi }^{\overline{M}}\right]\sim Unif(0,1);$$

$$\left[{\omega }_j|I_j^{\omega },{\left({\tau }^{\omega }\right)}^2\right]\sim \left(1-I_j^{\omega }\right)N(0,{10}^{-6})+I_j^{\omega }N(0,{\left({\tau }^{\omega }\right)}^2);$$

$$\left[I_j^{\omega }|{\pi }^{\omega }\right]\sim Bern\left({\pi }^{\omega }\right),\hspace{0.17em}\left[{\pi }^{\omega }\right]\sim Unif(0,1);$$

where $I_k^M,\hspace{0.17em}{I}_k^{\overline{M}}$ and $I_j^{\omega }$ are binary indicators and $N(0,{10}^{-6})$ represents a narrow spike and ${\tau }^2$ represents the wide slab. A Jeffery’s prior is put on ${\left({\tau }^M\right)}^2,\hspace{0.17em}{\left({\tau }^{\overline{M}}\right)}^2,\hspace{0.17em}{\left({\tau }^{\omega }\right)}^2$, i.e.:

$$p{\left({\tau }^M\right)}^2\propto {\left({\tau }^M\right)}^{-2},p{\left({\tau }^{\overline{M}}\right)}^2\propto {\left({\tau }^{\overline{M}}\right)}^{-2},p{\left({\tau }^{\omega }\right)}^2\propto {\left({\tau }^{\omega }\right)}^{-2}.$$

For ${\mathbf{G}}_{mis}$ and ${\mathbf{M}}_{mis}$ (Fig. 1b), we impose the following imputation model:

$${\mathbf{g}}_{mis,k}\sim MV{N}_{N_{mis}^G\times N_{mis}^G}\left({\mathbf{M}}_{{\mathcal{J}}_k}{\omega }_k,{\sigma }_k^2{\mathbf{I}}_{N_{mis}^G\times N_{mis}^G}\right);$$

$${\mathbf{m}}_{mis,j}\sim MV{N}_{N_{mis}^M\times N_{mis}^M}\left(0,{\left({\sigma }^m\right)}^2{\mathbf{I}}_{N_{mis}^M\times N_{mis}^M}\right),$$

where MVN denotes the multivariate normal distribution and ${({\sigma }^m)}^2=1$ if the methylation value is already standardized with mean 0 and standard deviation 1. Note that here we assume the methylation data are in $M\hspace{0.17em}value$ according to Du et al. (2010). If $\beta \hspace{0.17em}value$ is to be used, we may need to replace the above prior with a truncated normal distribution bounded between 0 and 1. All other variables are given non-informative priors. Details can be found in the Supplementary Appendix Section 2.

Remarks:

• Following Wang et al. (2013), we assume gene-gene independence and methylation-methylation independence. However, we are aware that this assumption deviates from real data, so we also propose a model with gene-gene and methylation-methylation correlations considered (see Supplementary Appendix Section 3). Albeit having the options, we will mainly discuss our model with independence assumptions in this article, for two reasons: first, the computational burden for estimating covariance matrices are high. Second, with moderate correlations in simulated data, considering dependency has limited gain in performance compared with model with independence assumption.

• We assume that the methylations are many-to-one mapped to genes, i.e. only the methylation within the promoter region of the gene is mapped to the gene, and each methylation will only be mapped to one gene. The mapping is also assumed to be known from biology background knowledge in our model. The methylation level is centred around 0 if we are using m-value.

• It is reasonable and necessary to assume that if for all the ω_j where j are within the promoter region of gene k, we let $I_j^{\omega }=0$, then we automatically have $I_k^M=0$. That is, $I_k^M\ne 0$ only when at least one methylation is selected.

• Two strategy could be adopted to deal with collinearity issue between methylation sites. First, we proposed a random selection strategy based on pairwise Pearson correlation (see Supplementary Appendix Section 4). Second, one may conduct principal component analysis (PCA) on methylation sites, and use the first few PCs explaining large proportion of variation.

2.2 Inference and evaluation

The full Bayesian hierarchical model in the last section allows fast Gibbs sampler. Full conditional formula for iterative sampling are shown in Supplementary Appendix Section 2. The final parameter estimates are calculated by averaging stabilized MCMC iterations (i.e. removing the first B_r burn-in period in MCMC iterations). The burn-in period B_r is determined using Geweke’s convergence diagnostics (Geweke, 1992). Geweke diagnostics aims to test whether the first $a\%$ and last $b\%$ of the MCMC iterations have equal mean, and thus decide whether the samples are drawn from a stationary distribution. As suggested by Geweke, the first 10% of MCMC total iterations are taken as burn-ins once the MCMC chain pass the diagnosis.

2.2.1 Prediction and feature selection

The Bayesian integrative model generates two major inference outcomes: prediction and feature selection. For prediction, denote ${\widehat{\gamma }}_{(b)}^C,\hspace{0.17em}{\widehat{\gamma }}_{(b)}^M,\hspace{0.17em}{\widehat{\gamma }}_{(b)}^{\overline{M}}$, and ${\widehat{\Omega }}_{(b)}$ as the simulated parameter estimates from the b-th iteration. For a new sample with omics data (${\mathbf{C}}_{new},\hspace{0.17em}{\mathbf{G}}_{new},\hspace{0.17em}{\mathbf{M}}_{new}$), we average prediction of y from the ($B-B_r$) stable MCMCs by ${\widehat{y}}_{new}=({\sum }_{b=B_r+1}^B{\widehat{y}}_{new}^{(b)})/(B-B_r)$, where ${\widehat{y}}_{new}^{(b)}={\mathbf{C}}_{new}·{\widehat{\gamma }}_{(b)}^C+{\mathbf{M}}_{new}·{\widehat{\Omega }}_{(b)}·{\widehat{\gamma }}_{(b)}^M+({\mathbf{G}}_{new}-{\mathbf{M}}_{new}·{\widehat{\Omega }}_{(b)})·{\widehat{\gamma }}_{(b)}^{\overline{M}}$. And RMSE will be calculated from those estimates:

$$RMSE=\sqrt{\sum _{i=1}^N{(y_i-{\widehat{y}}_{new,i})}^2/N}$$ (1)

where the choice of N is discussed in Section 2.2.2.

Next, we summarize feature selection indicators $I_{k,(b)}^M$ and $I_{k,(b)}^{\overline{M}}$ for gene k and the b-th MCMC to determine the set of genes predictive to outcome y. Given the b-th iteration, we define the selection indicator for gene k as $I_{k,(b)}$ so that gene k is selected if either the impact on outcome is through methylation ($I_{k,(b)}^M$) or not ($I_{k,(b)}^{\overline{M}}$). In other words, $I_{k,(b)}=(I_{k,(b)}^M)\hspace{0.17em}OR\hspace{0.17em}(I_{k,(b)}^{\overline{M}})=1-(1-I_{k,(b)}^M)(1-I_{k,(b)}^{\overline{M}})$ for $B_r+1\le b\le B$ and $1\le k\le K$. To control FDR at gene level, we apply Bayesian false discovery rate (BFDR) proposed by Newton (2004):

$$BFDR(t)=\frac{\sum _{k=1}^K{\widehat{P}}_k(H_0|D)d_k(t)}{\sum _{k=1}^K{d}_k(t)}$$

where ${\widehat{P}}_k(H_0|D)=1-({\sum }_{b=B_r+1}^B{I}_{k,(b)})/\left(B-B_r\right)$ is the posterior probability of gene k belonging to null hypothesis H₀ (i.e. gene k is not selected given observed data $\mathcal{D}$), $d_k(t)=I({\widehat{P}}_k(H_0|D)<t)$, and t is a tuning threshold. Given the definition of BFDR, the q-value of gene k can be defined as $q_k=mi{n}_{t\ge {\widehat{P}}_k(H_0|D)}BFDR(t)$. This q-value will later be used for feature selection decision, which is comparable to frequentist approaches. Among selected genes, one may perform post hoc analysis to further investigate $c_k^M=({\sum }_{b=B_r+1}^B{I}_{k,(b)}^M)/\left(B-B_r\right)$ and $c_k^{\overline{M}}=({\sum }_{b=B_r+1}^B{I}_{k,(b)}^{\overline{M}})/\left(B-B_r\right)$ and determine whether the impact of gene k to outcome is through methylation, non-methylation or both.

2.2.2 Benchmarks for evaluation

To evaluate the performance, the basic approach we compare with is the CC analysis. For full Bayesian model with missingness, we will also choose to impute gene expression only (FBM_G), methylation only (FBM_M) or both (FBM_GM) when applicable. In simulation studies, we also perform analysis of the complete data (full) to examine the reduction of accuracy caused by missingness.

To benchmark performance of outcome prediction, we consider RMSE (Equation 1). In simulation studies, after parameter estimates are obtained we generate a new testing dataset with large sample size (N = 2000) and compute RMSE. In real data analysis, we perform 50-fold cross-validation (CV) on complete cases for RMSE evaluation. In each iteration, $N^{CC}=2\%$ of complete-case samples are set aside as test dataset, all remaining data are used to perform CC and FBMs analyses. The parameter estimates are then applied to the test data for outcome prediction. After ten iterations, cross-validated RMSE can be evaluated on all complete-case samples with $N=N^{CC}$ in Equation 1.

To evaluate feature selection performance, we order genes by q-value, plot receiver operating characteristic (ROC) curves and calculate area under curve (AUC) in simulations since the underlying true predictive genes are known. For real data, since we do not know the true features, we treat the gene selection result from full data analysis (full) as a surrogate of gold standard and compare gene selection from CC (or FBMs) to the full data analysis by tracing the top number of selected genes on the x-axis (e.g x = 100 top selected genes by CC and full) and the overlapped number from CC and full on the y-axis (Fig. 4b). Comparing the curves of CC and FBMs, a higher curve closer to the diagonal line shows more similar gene selection to ‘full’ and thus an indication of better performance.

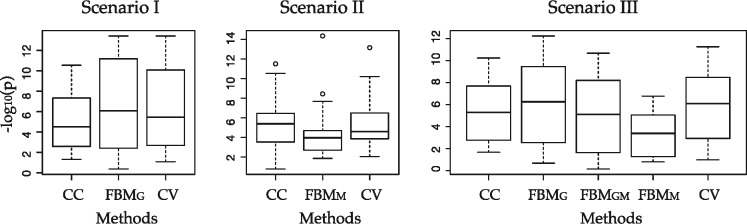
Fig. 4.

(a and b) In missing Scenario I ($\alpha =50\%, \beta =0$) and Scenario II ($\alpha =0, \beta =50\%$), scatter plot of RMSEs between two methods are shown, where circle means cross-validation scheme generates correct decision, and cross means mistakes. Sample size N varies from $50, 100, 200, 500$. (c) Box plot of RMSE of different methods and CV selection scheme in Scenario III ($\alpha =\beta =25\%$)

3 Simulation studies

3.1 Simulation schemes

To evaluate performance of our full Bayesian model with missingness, we perform simulation based on data structure described in Section 2. Specifically, the clinical and methylation data matrices are simulated from N(0, 10) and N(0, 1) with $N=\left(50, 100, 200, 500\right)$, L = 2 and J = 2000. Each methylation site is randomly assigned to a gene, with the constraint that each gene contains at least one methylation site. In the mechanistic model, $I_j^{\omega }=1,\hspace{0.17em}{\omega }_{jk}=5$ and ${\sigma }_k^2=4$ for $1\le j\le J$ and $1\le k\le K$, where the total number of genes K = 1000. We then simulate gene expression matrices from $N(\mathbf{M}\Omega ,diag({\sigma }_1^{\mathrm{2}},\dots {\sigma }_K^2))$. In the clinical model, 10 genes are randomly selected to impact clinical outcome through methylation and 10 randomly impact not through methylation (i.e. The I^M vector has 10 out of K genes equal one and the remaining are zero, and similarly for $I^{\overline{M}}$. The selected genes in I^M and $I^{\overline{M}}$ can possibly overlap). For selected genes in I^M and $I^{\overline{M}}$, the corresponding ${\mathbf{\gamma }}_k^M$ and ${\mathbf{\gamma }}_k^{\overline{M}}$ are set to 10. The coefficients for clinical data ${\mathbf{\gamma }}_l^C$ ($1\le l\le L$) are also set at 10 and ${\sigma }^2=9$ to simulate clinical outcome Y.

After full multi-omics datasets are simulated, data with missingness are generated with $\alpha \%$ of samples with missing gene expression data and another non-overlapping $\beta \%$ of samples with missing methylation data. We simulate three scenarios of missingness: (I) Missing only gene expression data with (α, β)=(0.1, 0), (0.2, 0) and (0.5, 0); (II) Missing only methylation data with (α, β)=(0, 0.1), (0, 0.2), (0, 0.5); (III) Non-overlapping samples missing either gene expression or methylation data with (α, β)=(0.1, 0.1), (0.2, 0.2), (0.3, 0.3). For Scenario I, we evaluate CC and FBM_G approaches and compare with full. Similarly for Scenario II, we compare CC, FBM_M and full. Finally for Scenario III, we compare CC, FBM_G, FBM_M, FBM_GM and full. In this case, FBM_G imputes gene expression but ignores samples with missing methylation and similarly, FBM_M imputes methylation but ignores samples with missing gene expression. FBM_GM utilizes all samples and imputes both gene expression and methylation.

3.2 Results

Figure 2 shows the outcome prediction performance by RMSE for all three scenarios. We first focus on small sample size situations $N=50-200$. In Scenario I, CC, FBM_G and full have similar performance when $\alpha =10\%$ missing but FBM_G clearly outperforms CC when missingness increases to 20% and 50%, showing the benefit of imputation as expected. In contrast, FBM_M performs much worse than CC in Scenario II with $\beta =10\%$ methylation missingness and FBM_M only slightly outperform CC when missingness increases to 50%. Results of Scenario III are consistent with results of Scenarios I and II. FBM_M and FBM_GM perform worse than CC at $\alpha =\beta =10\%$. FBM_M, FBM_G and FBM_GM outperform CC at $\alpha =\beta =50\%$. It is worth noting that when sample size increases to N = 500, the data information is strong enough such that CC has performance similar to full. Imputation almost always create more data uncertainty and have worse performance than CC, especially since the majority of the imputed data are irrelevant to the clinical outcome.

Fig. 2.

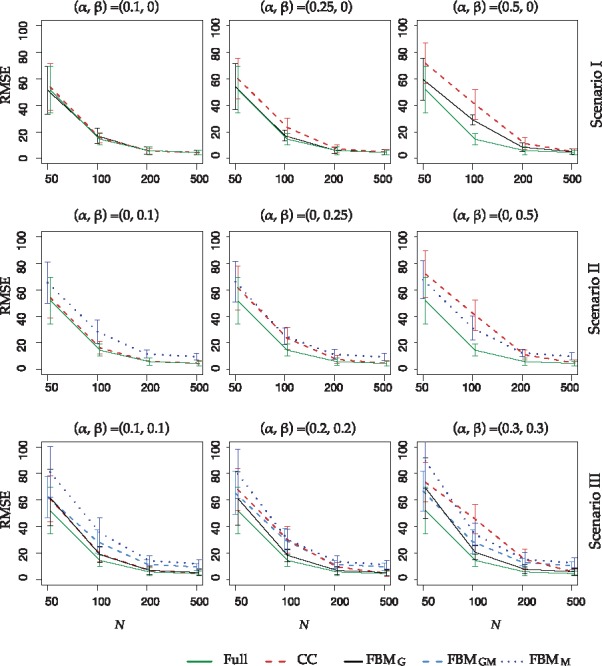
Model prediction by RMSE$(\widehat{y})$ comparing different methods and full data

We next examine feature selection performance by AUC values in Table 1 (ROC curves shown in Figure 3 and Supplementary Figure S1a–c). In Scenario I, FBM_G always has higher AUC values than CC especially when missingness α increases to 25% or 30%. On the contrary, FBM_M has lower AUC than CC except for N = 50, 100 in $\beta =50\%$. The message becomes mixed in Scenario III as expected.

Table 1.

AUC of different methods in simulation studies

			Scenario I		Scenario II		Scenario III
Missing	N	Full	CC	FBMG	CC	FBMM	CC	FBMG	FBMGM	FBMM
Lowa	50	0.676	0.649	0.672	0.631	0.613	0.616	0.628	0.652	0.583
	100	0.899	0.867	0.878	0.883	0.777	0.826	0.753	0.826	0.703
	200	0.967	0.976	0.983	0.961	0.863	0.946	0.859	0.913	0.789
Meda	50	0.676	0.619	0.665	0.626	0.597	0.574	0.61	0.646	0.528
	100	0.899	0.813	0.862	0.807	0.774	0.762	0.745	0.826	0.699
	200	0.967	0.941	0.961	0.939	0.861	0.903	0.858	0.917	0.795
Higha	50	0.676	0.53	0.637	0.557	0.588	0.534	0.583	0.636	0.512
	100	0.899	0.699	0.835	0.681	0.742	0.638	0.75	0.833	0.7
	200	0.967	0.892	0.964	0.88	0.814	0.828	0.782	0.883	0.765

^aLow, medium and high missing proportion for Scenario I and II are 10%, 25% and 50% for either α or β, respectively; and for Scenario III is 10%, 20% and 30% for both α and β.

Fig. 3.

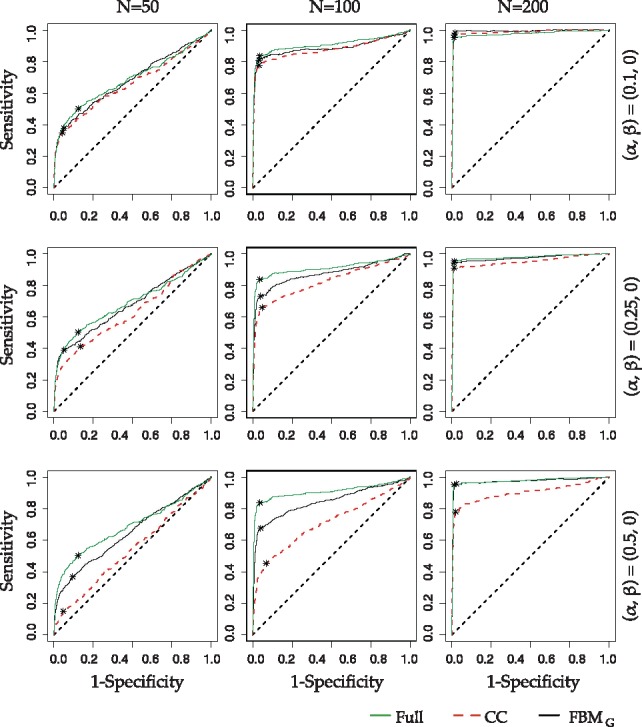
The ROC curves for feature selection comparison on Scenario I: $\alpha \ne 0, \beta =0$. Asterisk on each ROC curve is the point with maximum Youden index

We noticed that since methylation is the up-regulator of gene expression and indirectly impact the clinical outcome, imputing methylation is generally less effective than imputing gene expression. With increasing missing proportion, the benefit of imputation escalates. But when the missing proportion is small or sample size large, the uncertainty brought by imputation will overshadow the contribution from partially observed data (see Supplementary Appendix Section 5).

4 Impute or not: a decision scheme by cross-validation

From the mechanistic model in Figure 1b, gene expression and methylation data are not symmetric. Methylation data can be predictive to gene expression data and further predictive to outcomes. On the other hand, gene expression data are less predictive to methylation to help outcome prediction. As we have shown in simulations, imputations do not always improve prediction performance compared with CC analysis. Whether imputation would improve outcome prediction depends on the types of missingness (missing the upstream methylation data or missing the downstream gene expression data or both), the proportion of missingness and sample size. To guide the decision, we propose a self-learning CV scheme. Specifically, we apply 10-fold CV by leaving 10% of CC samples as the test set (for Scenario III N = 500, we apply 50-fold CV). We apply CC, FBM_G, FBM_M and FBM_GM to the remaining training data, calculate parameter estimates and apply to test set. The procedure is repeated across all 10-folds and RMSE can be calculated on all test sets. The method with the smallest RMSE is selected to determine whether and how to impute. We conducted sensitivity analysis for this CV scheme (see Supplementary Appendix Section 1.2). We note that to evaluate performance of CV scheme in RMSE evaluation of outcome prediction in the Section 5, nested CV will be used (i.e. An outer loop of CV is used to evaluate RMSE and an inner loop of CV scheme for method selection is performed in each training set of the outer loop).

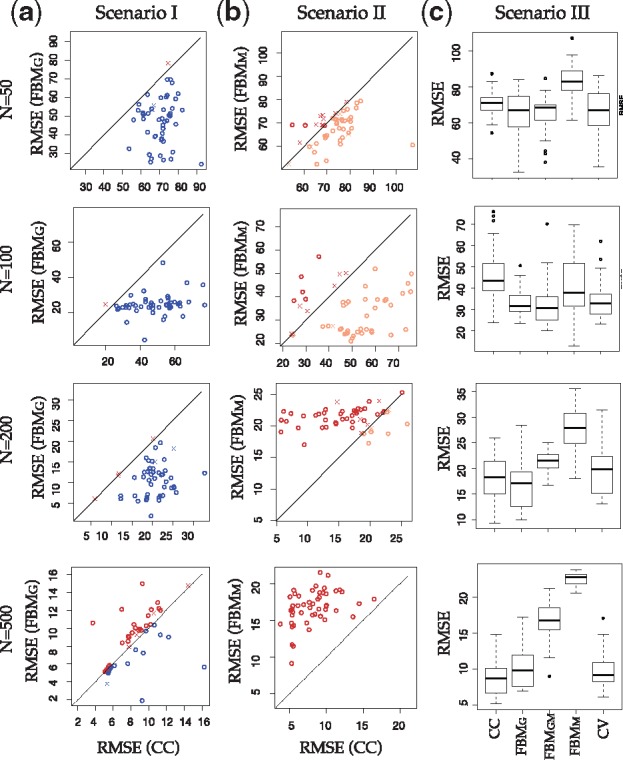
Figure 4 shows scatter plot of RMSE performance comparing FBM_G and CC in Scenario I (Fig. 4a;$\alpha =50\%$ missing gene expression) and FBM_M and CC in Scenario II (Fig. 4b;$\beta =50\%$ missing methylation) in 50 independent simulations. In Scenario I, FBM_G generally has smaller RMSE than CC in small sample sizes (N = 50, 100, 200). But for N = 500, RMSE of FBM_G becomes slightly larger than CC on average. For missing methylation in Scenario II, FBM_M performs better than CC at N = 50 but gradually becomes worse than CC at N = 100, 200 and 500. We applied the CV scheme in each simulation to determine whether imputation should be performed or not. Simulations shown by circles represent correct decisions (i.e. CV scheme decides to impute and the RMSE of imputation is indeed smaller than RMSE of CC or vice versa) and cross represents incorrect decision. The result shows universally high accuracy of CV scheme decision. When the decision is wrong, imputation and CC RMSEs are close to each other (near the diagonal line) and the incorrect decision only minimally impacts the outcome prediction. Figure 4c shows box plots of RMSE generated from different approaches (CC, FBM_G, FBM_M, FBM_GM, CV) for Scenario III ($\alpha =\beta =25\%$). At N = 50, FBM_G and FBM_GM both perform well and CV generates similar small RMSE. When N increases to 500, FBM_GM becomes much worse and CC performs slightly better than FBM_G. Again, the CV scheme makes mostly correct decision and thus generates small RMSE close to the lowest. In conclusion, the simulation results indicate effectiveness of the CV scheme in determining the best strategy of whether and how to impute when encountering missingness in multi-omics data.

5 Real application

5.1 Data and approach

We apply the proposed full Bayesian model with missingness to 460 children asthma nasal epithelium samples obtained from asthma study at Children’s Hospital of Pittsburgh, with complete DNA methylation data from Illumina 450k chips and RNA-Seq gene expression data. All data were preprocessed with standard procedures and bioinformatics tools. We used M-value for methylation level for better model fitting. The RNA-seq gene expression counts were transformed to TPM (transcripts per million), a continuous value also more valid for the model assumptions. We filter out genes with small mean expression level (<130.41) or small standard deviation (<23.83) to obtain K = 1000 genes for the analysis. We then select methylation sites matched to these 1000 genes. Since some genes have many corresponding methylation sites, we perform PCA to identify the top eigen-methylation sites as input to the model. We take no more than three PCs per gene or less than three PCs that explain at least 75% variation. This generates J = 2619 eigen-methylation features for the analysis. The PCA analysis reduces redundant (highly correlated) information in methylation sites and independence of eigen-methylation features fits the model assumptions well. Similar to simulation, we generate three scenarios of missingness: (I) $\alpha =50\%$, (II) $\beta =50\%$, (III) $\alpha =\beta =20\%$. For each scenario, we repeat 50 times.

Serum Immunoglobulin E (IgE) level is a primary clinical outcome in children asthma studies. We take log-transformed IgE level as our clinical outcome, and age and gender as clinical variables. Together with the gene expression and methylation PCs, we run our model with full data and three scenarios of missingness to compare CC approach and full Bayesian model with missingness (FBM_G, FBM_M and FBM_GM).

5.2 Outcome prediction and feature selection

Table 2 shows the RMSE of outcome prediction from complete case analysis and FBMs. When 50% samples have missing gene expression (Scenario I), FBM_G had reduced RMSE compared with CC (dropped from 43.34.19 to 36.04). In contrast, FBM_M had inflated RMSE compared with CC when 50% of missing methylation (51.59 compared with 39.54 in Scenario II). When gene expression and methylation both missed 20% of samples (i.e. 40% of samples had missing values in Scenario III), FBM_G had the smallest RMSE (38.71) compared with FBM_GM (46.15), FBM_M (54.23) and CC (39.09). Our CV scheme performed the automatic selection of whether and how to impute, and the RMSE was always close to the best (I: 36.61, II: 41.09 and III: 40.02). Figure 5a shows scatter plot or box plot of RMSEs of different methods in all three Scenarios. Similar to the simulation result, CV scheme mostly selected the best method and the mistakes were near the diagonal line with little predictive impact.

Table 2.

RMSE (S.E.) of different methods

Methods	Scenario I	Scenario II	Scenario III
CC	43.34 (5.33)	39.54 (6.85)	39.09 (5.43)
FBMG	36.04 (4.73)		38.71 (5.73)
FBMGM			46.15 (4.74)
FBMM		51.59 (6.71)	54.23 (4.50)
CV	36.61 (3.78)	41.09 (6.17)	40.62 (7.36)

Fig. 5.

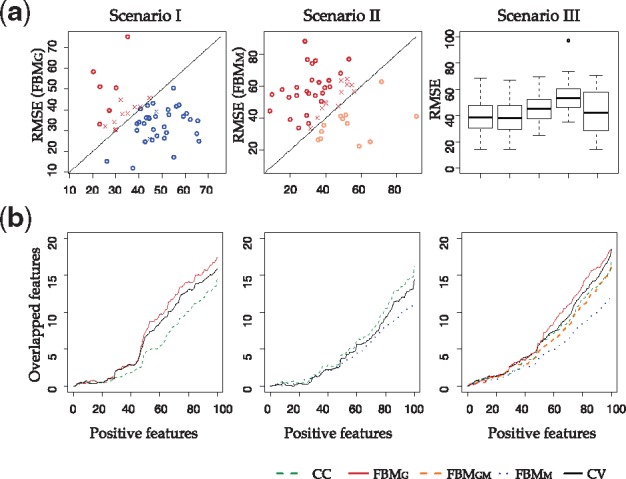
(a) Scatter plot of RMSEs between two methods are shown, where circle means cross-validation scheme generates correct decision, and cross means mistakes. (b) The number of overlapped genes (features) selected by each methods compared with full asthma data. On x axis is the top number of genes selected by each method

Unlike in simulation, no underlying truth is available for real data and thus calculation of AUC is not possible. Figure 5b treats the predicted outcome from full data as the surrogate of underlying truth and compare feature selection from each method with the surrogate (i.e. x-axis shows the same number of features selected by the designated method and full and y-axis demonstrates the overlap between the two). A curve with higher overlap shows better similarity of feature selection with the surrogate, an indication of better performance. Similar to the RMSE result, FBM_G performed better than CC in Scenario I, CC better than FBM_M in Scenario II, and FBM_G and CC performed better than FBM_M and FBM_GM in Scenario III. CV scheme performs close to the best. All results from this real application are largely aligned with our observations in simulation studies.

We next investigate whether feature selection from the imputation methods or method selected by CV scheme represent better functional annotation in a biological sense. We obtained the top 200 genes from feature selection of each method by posterior probability order and then performed pathway enrichment analysis by one-sided Fisher’s exact test. We collected 2467 pathways from four pathway databases (KEGG, Reactome, Biocarta and GO) with the restriction of pathway size between 10 and 500. The enrichment p-values were then adjusted for multiple comparisons by Benjamini–Hochberg procedure. We found 27 enriched pathways from the full data analysis under FDR = 1%. We used these 27 pathways as a surrogate of gold standard to benchmark functional annotation performance of each method. Figure 6 shows box-plots of the minus log-transformed p-values from pathway enrichment of the 27 pathways in each method. As expected, FBM_G had better p-value significance distribution than CC in Scenario I. In Scenario II, CC performed better than FBM_M. FBM_GM and FBM_G outperformed CC in Scenario III. The CV scheme automatically determined whether and how to impute, and it always perform close to the best in each scenario.

Fig. 6.

Compare different methods for the $-lo{g}_{10}(p)$ value of the top 27 pathways taken from full data with q-value <0.01

6 Discussion

Integrative analysis of multi-level omics data brings unique insights to the modulating relationship between different types of omics data. Feature selection and model prediction are two important goals in multi-omics integration, which empowers discovery of disease-associated biomarkers, survival prediction and risk assessment. Several methods have been developed to fulfil these goals, including iBAG using a two-layer Bayesian hierarchical model to discover both association between genes and clinical outcome, and that between gene and upstream regulators. However, none of these methods are able to handle the potential large proportion of missing data in the data integration. In this article, we propose a full Bayesian model with missingness (FBM) inspired by iBAG model, to jointly perform feature selection, model prediction and missing data incorporation. In addition to the mechanistic model and clinical model originally proposed by iBAG, FBM includes a third layer of missingness model to incorporate samples with missingness. The flexibility of Bayesian hierarchical modelling and Gibbs sampler technique enables us to jointly model association among data and infer parameters in all three layers of models together. The Laplace (double exponential) prior initially used in iBAG could not realize exact feature selection. FBM applied spike-and-slab prior for more effective feature selection and allows Bayesian FDR control. We demonstrated outcome prediction and feature selection performance of FBM using extensive simulations.

From the extensive simulations, we then further realized that imputation is not always favoured over complete case analysis. For example, in high dimensional genomic data analysis, when missingness exists in upstream regulators (i.e. methylation), uncertainty will be increased to impair final inference. When the missing proportion is relatively small and the sample size is large (i.e. signal is strong), CC analysis also often outperforms FBM. To decide the best handling of data with missingness, we proposed a self-learning cross-validation decision scheme. Previously, we have developed a similar self-training selection scheme to select the best microarray missing value imputation method and its downstream biological impact (Brock et al., 2008; Oh et al., 2011). In both simulation and the childhood asthma application, we showed superior performance of the CV scheme in prediction outcome and feature selection.

While Bayesian hierarchical model allows complex parameter structures, it also comes with a computational cost when using conventional inference approaches such as Metropolis–Hastings or its special case, Gibbs sampling. In FBM, fast Gibbs sampling was applicable using conjugate priors and the convergence was generally fast (B = 2000). We have optimized the R code using C++ with Rcpp package. The computing takes 90 min for a reasonably large dataset with N = 500 samples, K = 1000 genes, J = 2000 methylations and B = 2000 MCMC iterations using a regular computer with 1 Intel Xeon CPU (2.40 GHz). Since the computation burden grows linearly with sample size, feature size and number of iterations, applying FBM with parallel computing could be a solution to substantially speed up computing and allow routine omics applications. An R package, data and source code to replicate all results in this article are available on GitHub (https://github.com/CHPGenetics/FBM).

Funding

This work was supported by the National Institutes of Health [RO1 CA190766 to Z.F., T.M., L.Z., and G.C.T.’s, RO1 MD011764 and RO1 HL117191 to W.C. and J.C.C.’s].

Conflict of Interest: none declared.