First Acid Ionization Constant of the Drinking Water Relevant Chemical Cyanuric Acid from 5 to 35 °C

Abstract

Cyanuric acid is present in drinking water when chemicals commonly referred to as dichlor (anhydrous sodium dichloroisocyanurate or sodium dichloroisocyanurate dihydrate) or trichlor (trichloroisocyanuric acid) are used as alternative free chlorine sources. Cyanuric acid and its ionization products combine with hypochlorous acid, forming various chlorinated cyanurates through a series of equilibrium reactions. Methods to measure the free chlorine (hypochlorous acid plus hypochlorite ion) concentration in systems adding cyanuric acid exhibit measurement bias. To overcome this limitation, one option is use of the established water chemistry of the free chlorine and cyanuric acid system to estimate free chlorine concentrations. Unfortunately, the equilibrium water chemistry has only been determined for 25 °C, limiting the usefulness of the water chemistry estimate in actual drinking water systems where temperatures may vary over a wide range (e.g., 5 to 35 °C). As a first step in extending the water chemistry model to relevant drinking water temperatures, the first acid ionization constant (K₆) for cyanuric acid (H₃Cy) and its first ionization product (H₂Cy^–) was determined using spectrophotometric techniques from 5 to 35 °C where $\ln {\mathrm{K}}_6=-\frac{\mathrm{4,013}}{{\mathrm{T}}_{\mathrm{K}}}-2.58$ or ${\mathrm{p}\mathrm{K}}_6=\frac{\mathrm{1,743}}{{\mathrm{T}}_{\mathrm{K}}}+1.12$ and ΔH° = 33.4 ± 1.7 kJ mol^–1. As an example of temperature’s impact (pH 7), the H₂Cy^– fraction of total cyanurate (sum of H₃Cy and H₂Cy^–) effectively doubles from 5 to 35 °C. With K₆’s temperature dependence established, studies can be conducted to update the existing water chemistry model with temperature dependence, allowing free chlorine concentration simulation in drinking water systems with cyanuric acid present.

INTRODUCTION

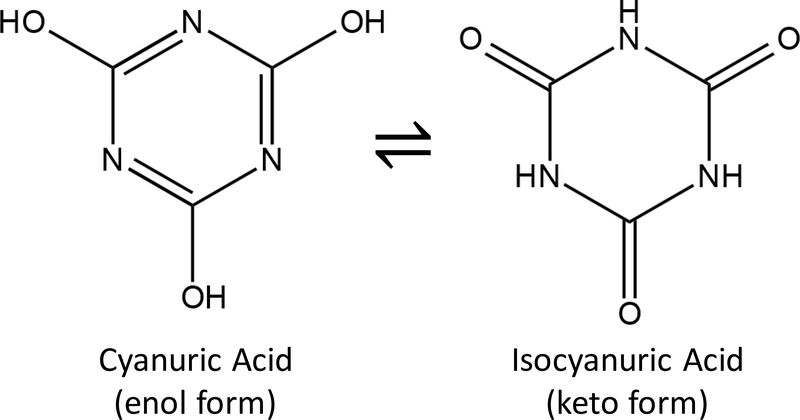
Cyanuric acid (Figure 1) and its dissociation products are present in drinking water when chemicals commonly referred to as dichlor (anhydrous sodium dichloroisocyanurate or sodium dichloroisocyanurate dihydrate) or trichlor (trichloroisocyanuric acid) are used as alternative free chlorine (hypochlorous acid, HOCl, plus hypochlorite ion, OCl^–) sources.¹ The C₃N₃O₃ moiety (Figure 1) is typically denoted as Cy; therefore, cyanuric acid is represented as H₃Cy, H₂Cy^– is the first ionization product, Cl₃Cy is trichlor, and Cl₂Cy is dichlor. Although the focus of the current research is a drinking water application, cyanuric acid, dichlor, and trichlor have been added to outdoor swimming pools since 1958 to stabilize chlorine residual by minimizing sunlight related degradation² and are used as disinfectants and algicides in cooling towers.³ Furthermore, industrial uses of cyanuric acid include its use as a flame retardant additive in various plastics and resins and reducing nitrogen oxides in coal, oil, or gas fired boilers.⁴

Figure 1.

– Cyanuric acid chemical structures.

The World Health Organization (WHO) provides guidelines for the addition of dichlor and cyanuric acid to drinking water where the WHO specifies maximum concentrations of 50 and 40 mg L^–1, respectively.^{5, 6} In the United States (US) and under the Federal Insecticide, Fungicide, and Rodenticide Registration Act (FIFRA), dichlor or trichlor use for the routine treatment of drinking water was first approved in July 2001.¹ Furthermore and as of January 2018, NSF/ANSI 60 certification has been obtained by six manufacturers for dichlor and seven manufacturers for trichlor addition to drinking water.⁷ For greater detail on dichlor and trichlor’s use in drinking water, including disinfectant effectiveness compared to using free chlorine alone, reasons for use, and existing practical questions (e.g., potential unregulated disinfection byproducts), the reader is directed to a recent review by Wahman⁸.

When cyanuric acid is present in water with free chlorine, a rapid equilibrium is obtained between H₃Cy and its three dissociation products, HOCl, and chlorinated cyanurates that has been established at 25 °C by O’Brien, et al.⁹. One complicating factor with the use of dichlor or trichlor in drinking water systems is that the free chlorine concentration (i.e., the effective disinfectant when using dichlor or trichlor) cannot be measured accurately by typically used methods in these systems. Because of the fast equilibrium between H₃Cy and its three dissociation products, HOCl, and chlorinated cyanurates; free chlorine N,N–diethyl–p–phenylenediamine (DPD) and amperometric titration based methods measure the total chlorine (free chlorine plus the chlorine bound in chlorinated cyanurates, TOTCl) in the water and overestimate the true free chlorine residual present.^{10, 11} Consequently, free chlorine concentrations cannot be accurately determined to verify disinfectant efficacy. For example, compliance with US primary disinfection requirements or numeric disinfectant residual requirements (i.e., greater than detectable) in the distribution system required by several states¹² is currently not possible. In fact, the Utah Division of Drinking Water has recently issued a plan review policy for dichlor or trichlor installations that notes the free chlorine measurement issue.¹³

To overcome the limitation of directly measuring free chlorine in systems with free chlorine and cyanuric acid present, one option is to use the established water chemistry of the free chlorine and cyanuric acid system to estimate the free chlorine concentration. For instance, a web–based application has been recently developed to assist in free chlorine’s estimation when cyanuric acid is present (https://usepaord.shinyapps.io/cyanuric/).14 Unfortunately, the water chemistry has only been determined for 25 °C, limiting the usefulness of the water chemistry estimate in actual drinking water systems where temperature may vary over a wide range (e.g., 5 to 35 °C). Therefore, there exists an immediate need to expand the water chemistry model to include temperatures from 5 to 35 °C. It is also desirable that future research focus on new methods for directly measuring free chlorine in systems with cyanuric acid present such as the possible quencher trimethoxybenzene.¹⁵

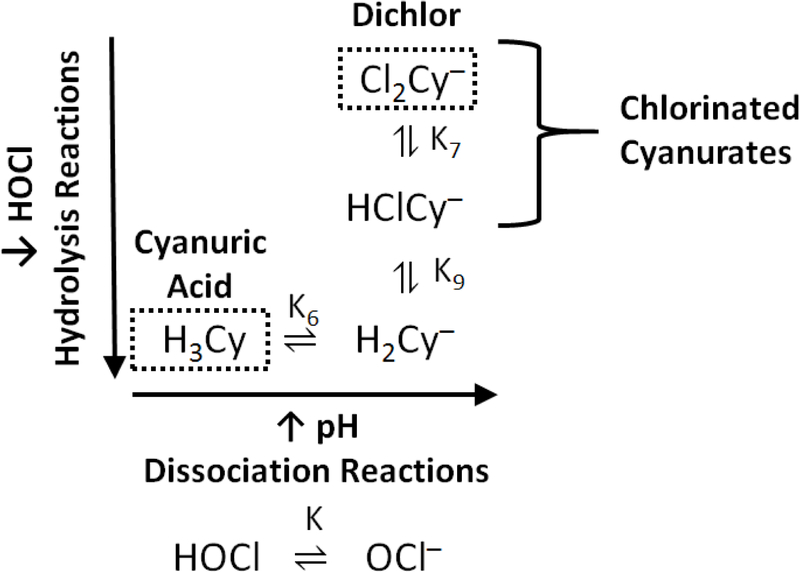
The complete water chemistry model for the free chlorine and cyanuric acid system consists of ten independent temperature dependent equilibrium reactions (Supplementary Information (SI) Figure S1),⁹ but under relevant drinking water conditions (i.e., 6.5 ≤ pH ≤ 9.5, TOTCl ≤ 10 mg Cl₂ L^–1, and total cyanurate ≤ 10 mg Cy L^–1), the system can be simplified to four (K, K₆, K₇, and K₉) temperature dependent equilibrium reactions (Figure 2 and Figure 3). As an example and for simulations using an implementation of the complete water chemistry model (SI Figure S1)¹⁴ and the previously stated relevant drinking water conditions, the chlorine containing species in the simplified system (HOCl, OCl^–, HClCy^–, and Cl₂Cy^–) represent greater than 98% of the TOTCl between pHs 7.0 and 8.5 and still represent greater than 95% of the TOTCl for the extreme pHs of 6.5 and 9.5 where H₂ClCy and ClCy^2– represent the other 5% of TOTCl.

Figure 2.

– Relevant hypochlorous acid, cyanuric acid, cyanuric acid ionization products, and chlorinated cyanurate equilibria under drinking water conditions and chemical dosages. Hydrogen ion for dissociation reactions and water and hypochlorous acid for hydrolysis reactions are not shown for clarity. Adapted with permission from Brady, et al.³². Copyright 1963 American Chemical Society.

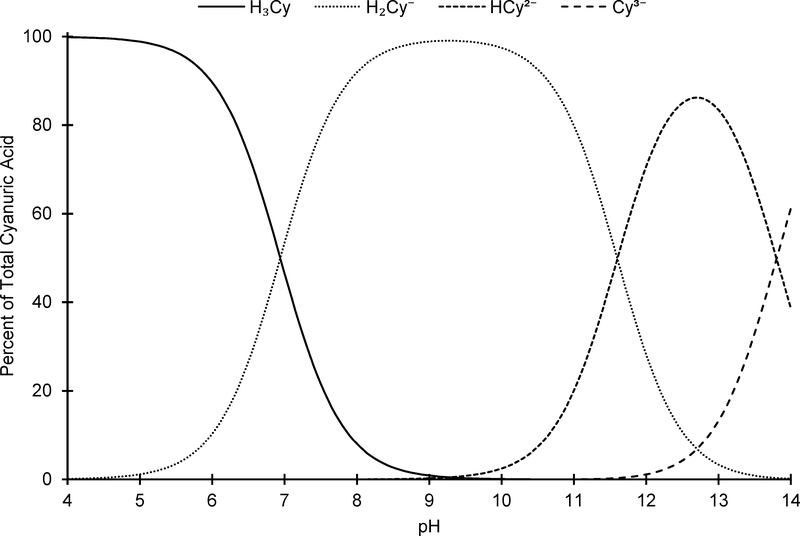
Figure 3.

– Cyanuric acid dissociation at 25 °C, using pK values from O’Brien, et al.⁹ adjusted to 0 M ionic strength.

Two of the reactions in the simplified model (Figure 2) represent the acid–base chemistry of free chlorine (K) and cyanuric acid (K₆) that can be readily isolated with each chemical for determination. Using the determined K and K₆ relationships, the remaining two reactions (K₇ and K₉) involving chlorinated cyanurates, which are expected to be temperature dependent,^16–18 could then be studied in parallel.

The temperature dependence for the ionization constant of HOCl (K) is established.¹⁹ Preliminary studies on the temperature dependence of the remaining three equilibrium constants (K₆, K₇, and K₉) have been reported by Solastiouk¹⁸, but the experiments provided few details on the experimental procedure to verify assumptions made in the analysis and were limited in scope, leaving the temperature dependence of these three equilibrium constants in question and requiring a rigorous evaluation.

Thus, to expand the existing water chemistry model to a range of relevant drinking water temperatures, determination of the temperature dependence of K₆, K₇, and K₉ is required. The current research represents the first step in extending the water chemistry model by determining the first acid ionization constant (K₆) for cyanuric acid using spectrophotometric techniques from 5 to 35 °C. With K₆’s temperature dependence established, further studies can be conducted to resolve K₇ and K₉’s temperature dependence, providing the necessary information to update the existing water chemistry model (e.g., the aforementioned web–based application) to simulate free chlorine concentrations in drinking water systems with cyanuric acid present. Even though the focus on the current research is drinking water conditions, the results presented herein also may have applications to chlorinated cyanurate use in outdoor swimming pools and industry as previously mentioned.

EXPERIMENTAL

Reagent Preparation

Solutions were prepared in ultra–pure water (18.2 MΩ–cm, Barnstead NANOpure Diamond). Stock cyanuric acid solutions (1,000 mg Cy L^–1 total cyanurate) were prepared from reagent grade cyanuric acid (Acros Organics), accounting for reagent purity of 98%. Under the experimental conditions, total cyanurate (TOTCy) is the sum of H₃Cy and H₂Cy^– as Cy. Phosphate buffers were made from sodium phosphate dibasic anhydrous (Fisher Chemical) and adjusted to the target pH with 0.05 and 0.5 N hydrochloric acid (HCl, Fisher Chemical) or sodium hydroxide (NaOH, Fisher Chemical) as required.

Spectrophotometric Measurements

All spectrophotometric measurements were conducted with a 1–cm quartz cuvette using a spectrophotometer (Hach DR/4000U Spectrophotometer) set to read a single wavelength of 214 nm, corresponding to the peak absorbance of H₂Cy^–.^{9, 20} The spectrophotometer was blanked with ultra–pure water prior to use. Triplicate absorbance measurements were taken and averaged for any measured sample. The sample pH and temperature were measured immediately prior to each spectrophotometric measurement with a pH electrode with automatic temperature compensation connected to a pH meter (Orion pH electrode and Orion Star A211 pH meter) that had been calibrated with nominal pH standards of 4, 7, and 10 per manufacturer’s instructions.

General Experimental Conditions

All experiments and associated measurements were conducted in a temperature controlled chamber maintained nominally at either 5, 10, 15, 20, 25, 30, or 35 °C. For each temperature, three experiments were conducted where a complete experiment set consisted of molar absorptivity experiments for (1) H₃Cy and (2) H₂Cy^– and an (3) ionization constant determination experiment for K₆.

Molar Absorptivity Experiments

H₃Cy molar absorptivity estimation.

For each H₃Cy molar absorptivity experiment, duplicate standards were prepared at concentrations of 0, 74, 100, 126, 150, and 200 mg Cy L^–1 TOTCy and adjusted to a nominal pH of 1.8 with 6 N HCl (Fisher Scientific). At a pH of 1.8, the absorbance contribution of H₂Cy^– is negligible (i.e., < 0.1%).^{9, 20} The slope from the linear regression of the absorbance at 214 nm versus the H₃Cy molar concentration is the molar absorptivity (ε) of H₃Cy at 214 nm (ε_0,214nm).

H₂Cy^– molar absorptivity estimation.

For each H₂Cy^– molar absorptivity experiment, duplicate standards were made at concentrations of 0, 6, 9, 12, 15, and 18 mg Cy L^–1 TOTCy in a 2 mM phosphate buffer adjusted to a nominal pH of 9.0. At a pH of 9.0, greater than 98% of TOTCy is present as H₂Cy^–. Use of greater pHs is limited because interferences from the second ionization product (HCy^2–) may occur.^{9, 20} The slope from the linear regression of the absorbance at 214 nm versus the H₂Cy^– molar concentration is the molar absorptivity of H₂Cy^– at 214 nm (ε_1,214nm). Because pK₆ was found to shift to greater values with decreasing temperature, two molar absorptivity experiments were conducted at pH 9.5 for the two lowest temperatures (5 and 10 °C) to evaluate impacts on ε_1,214nm.

Estimated molar absorptivity multiple comparison analysis.

To evaluate the molar absorptivity values determined at the various temperatures used in the current research for H₃Cy and H₂Cy^–, Tukey’s method of multiple comparisons was used to determine whether statistically significant differences existed between molar absorptivity estimates.^{21, 22} A multiple comparison analysis was conducted separately for the H₃Cy and H₂Cy^– molar absorptivity estimates.

For the H₃Cy and H₂Cy^– molar absorptivity experiments, Equation 1 defines the magnitude of a significant difference between two molar absorptivities (y_i and y_j) where differences greater than that determined by Equation 1 are considered significant. In Equation 1, q_k,v,α is the significance level (α = 0.95) of the studentized range for k means (7 for H₃Cy or 9 for H₂Cy^–) and v degrees of freedom (77 for H₃Cy or 99 for H₂Cy^–) where v = N – k and N is the total sample number (84 for H₃Cy or 108 H₂Cy^–), n_i and n_j are the two compared sample sizes (n_i = n_j = n = 12), and S_pool is the pooled standard deviation of the H₃Cy and H₂Cy^– molar absorptivity estimates. Calculations for Equation 1 were performed manually using q_k,v,α values from Harter²².

$${\mathrm{y}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{j}}\pm \frac{{\mathrm{q}}_{\mathrm{k},\mathrm{v},\mathrm{\alpha }}}{\sqrt{2}}{\mathrm{S}}_{\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}}\sqrt{\frac{1}{{\mathrm{n}}_{\mathrm{i}}}+\frac{1}{{\mathrm{n}}_{\mathrm{j}}}}={\mathrm{y}}_{\mathrm{i}}-{\mathrm{y}}_{\mathrm{j}}\pm {\mathrm{q}}_{\mathrm{k},\mathrm{v},\mathrm{\alpha }}\frac{{\mathrm{S}}_{\mathrm{p}\mathrm{o}\mathrm{o}\mathrm{l}}}{\sqrt{\mathrm{n}}}$$ (1)

Ionization Constant Determination Experiments

Absorption Model Derivation.

For the first ionization constant of cyanuric acid (H₃Cy ⇌ H₂Cy^– + H⁺), Equations 2 and 3 represent relationships for the equilibrium constant and TOTCy concentration, respectively. In Equations 2 and 3, K_6,TK is the first ionization constant of cyanuric acid at the given temperature in Kelvin (T_K), γ₁ is the activity coefficient for singly charged ions, square brackets indicate concentrations, braces indicate activities, and the activity coefficient of the uncharged H₃Cy was assumed to be one.

$${\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}=\frac{\left\{{{\mathrm{H}}_2\mathrm{C}\mathrm{y}}^{-}\right\}\left\{{\mathrm{H}}^{+}\right\}}{\left\{{\mathrm{H}}_3\mathrm{C}\mathrm{y}\right\}}=\frac{{\mathrm{\gamma }}_1\left[{{\mathrm{H}}_2\mathrm{C}\mathrm{y}}^{-}\right]\left\{{\mathrm{H}}^{+}\right\}}{\left[{\mathrm{H}}_3\mathrm{C}\mathrm{y}\right]}$$ (2)

$$\left[\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{C}\mathrm{y}\right]=\left[{\mathrm{H}}_3\mathrm{C}\mathrm{y}\right]+\left[{{\mathrm{H}}_2\mathrm{C}\mathrm{y}}^{-}\right]$$ (3)

From Equations 2 and 3, Equations 4 and 5 represent the concentration fraction of TOTCy that is H₃Cy (α₀) or H₂Cy^– (α₁), respectively. Refer to the SI for a derivation of Equations 4 and 5.

$${\mathrm{\alpha }}_0=\frac{\left[{\mathrm{H}}_3\mathrm{C}\mathrm{y}\right]}{\left[\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{C}\mathrm{y}\right]}=\frac{{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}}{{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}+{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}}$$ (4)

$${\mathrm{\alpha }}_1=\frac{\left[{{\mathrm{H}}_2\mathrm{C}\mathrm{y}}^{-}\right]}{\left[\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{C}\mathrm{y}\right]}=\frac{{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}}{{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}+{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}}$$ (5)

The total absorbance (Abs_λ) at any given wavelength (λ) is the sum of the individual contributions from H₃Cy and H₂Cy^– based on their respective concentrations, molar absorptivities at λ (ε_0,λ and ε_1,λ), and absorbance cell pathlength (l). Using Equations 4 and 5 and a 1–cm pathlength (l = 1 cm), Equation 6 represents the relationship between Abs_λ and K_6,TK.

$${\mathrm{A}\mathrm{b}\mathrm{s}}_{\mathrm{\lambda }}={\mathrm{\epsilon }}_{0,\mathrm{\lambda }}\left[{\mathrm{H}}_3\mathrm{C}\mathrm{y}\right]+{\mathrm{\epsilon }}_{1,\mathrm{\lambda }}\left[{{\mathrm{H}}_2\mathrm{C}\mathrm{y}}^{-}\right]=\frac{\left[\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{C}\mathrm{y}\right]}{{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}+{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}}\left({\mathrm{\epsilon }}_{0,\mathrm{\lambda }}{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}+{\mathrm{\epsilon }}_{1,\mathrm{\lambda }}{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}\right)$$ (6)

Both H₃Cy and H₂Cy^– absorb in the ultraviolet wavelength region. Specifically, H₂Cy^– has a maximum absorbance at 214 nm whereas H₃Cy’s molar absorptivity is approximately 1% of H₂Cy^– at 214 nm.⁹ If the molar absorptivities at 214 nm for H₃Cy (ε_0,214nm) and H₂Cy^– (ε_1,214nm) are known and using Equation 6, the first ionization constant at a given temperature (K_6,TK), pH, ionic strength (μ), and TOTCy is related to the total absorbance at 214 nm (Abs_214nm) by Equation 7.

$${\mathrm{A}\mathrm{b}\mathrm{s}}_{214\mathrm{n}\mathrm{m}}=\frac{\left[\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{C}\mathrm{y}\right]}{{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}+{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}}\left({\mathrm{\epsilon }}_{\mathrm{0,214}\mathrm{n}\mathrm{m}}{\mathrm{\gamma }}_1\left\{{\mathrm{H}}^{+}\right\}+{\mathrm{\epsilon }}_{\mathrm{1,214}\mathrm{n}\mathrm{m}}{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}\right)$$ (7)

In Equation 7, the hydrogen ion activity, {H⁺}, is calculated from pH measurements where pH = –log₁₀{H⁺}. The single charge ion (z = 1) activity coefficient (γ₁) is determined from the Davies equation using Equation 8.²³ In Equation 8, the term A_DH is the Debye–Hückel constant that is determined from Equation 9 at the specified temperature in Kelvin (T_K),²³ and in Equation 9, the dielectric constant for water (ε_water) is determined at the specified temperature in °C (T_c) from Equation 10.²⁴

$$\log {\mathrm{\gamma }}_{\mathrm{z}}=-{\mathrm{A}}_{\mathrm{D}\mathrm{H}}{\mathrm{z}}^2(\frac{\sqrt{\mathrm{\mu }}}{1+\sqrt{\mathrm{\mu }}}-0.2\mathrm{\mu })$$ (8)

$${\mathrm{A}}_{\mathrm{D}\mathrm{H}}=1.82\mathrm{x}{10}^6{\left({\mathrm{\epsilon }}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{\mathrm{T}}_{\mathrm{K}}\right)}^{-3/2}$$ (9)

$${\mathrm{\epsilon }}_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=87.740-0.40008{\mathrm{T}}_{\mathrm{c}}+9.398\mathrm{x}{10}^{-4}{{\mathrm{T}}_{\mathrm{c}}}^2-1.410\mathrm{x}{10}^{-6}{{\mathrm{T}}_{\mathrm{c}}}^3$$ (10)

Ionization constant experiments.

To acquire the required data to allow estimation of K₆ from Equation 7 for various temperatures, triplicate 15 mg Cy L^–1 TOTCy standards were created in 2 mM phosphate buffer adjusted to nominal pHs of 6.0, 6.5, 7.0, 7.5, 8.0, and 8.5 at each experimental temperature. Abs_214nm readings were taken as previously described.

Ionic strength calculation.

To account for slight variations in μ between samples, μ was calculated for each sample using Equation 11 based on known chemical additions, the measured pH and temperature, and a charge balance to account for the acid or base addition required to obtain the measured pH. In Equation 11, c_i and z_i are the concentration and charge of the i^th ionic species, respectively. For the μ calculations, relationships for phosphate and water ionization constants with temperature were taken from Goldberg, et al.²⁵ and Stumm and Morgan²⁶, respectively.

$$\mathrm{\mu }=\frac{1}{2}{\sum }_{\mathrm{a}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{o}\mathrm{n}\mathrm{s}}{\mathrm{c}}_{\mathrm{i}}{{\mathrm{z}}_{\mathrm{i}}}^2$$ (11)

Ionization constant temperature dependence.

The basic relationship of K₆ with T_K is shown by Equation 12.²⁶ In Equation 12, ΔH⁰ is the standard enthalpy change of the reaction while R is the universal gas constant (8.314 × 10^–3 kJ mol^–1 K^–1). If ΔH⁰ is assumed to be independent of T_K (i.e., constant), Equation 13 results which can be further simplified to Equation 14. Combining Equations 7 and 14 gives Equation 15, in which A and B are adjustable parameters and $\mathrm{A}=\frac{\Delta {\mathrm{H}}^0}{\mathrm{R}}$.

$$\frac{\mathrm{d}\ln {\mathrm{K}}_6}{\mathrm{d}{\mathrm{T}}_{\mathrm{K}}}=\frac{\Delta {\mathrm{H}}^0}{\mathrm{R}{{\mathrm{T}}_{\mathrm{K}}}^2}$$ (12)

$$\ln \frac{{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}2}}}{{\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}1}}}={\int }_{{\mathrm{T}}_{\mathrm{K}1}}^{{\mathrm{T}}_{\mathrm{K}2}}\frac{\Delta {\mathrm{H}}^0}{\mathrm{R}{{\mathrm{T}}_{\mathrm{K}}}^2}\mathrm{d}{\mathrm{T}}_{\mathrm{K}}=\frac{\Delta {\mathrm{H}}^0}{\mathrm{R}}(\frac{1}{{\mathrm{T}}_{\mathrm{K}1}}-\frac{1}{{\mathrm{T}}_{\mathrm{K}2}})$$ (13)

$$\ln {\mathrm{K}}_{6,{\mathrm{T}}_{\mathrm{K}}}=-\frac{\Delta {\mathrm{H}}^0}{\mathrm{R}{\mathrm{T}}_{\mathrm{K}}}+\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}=-\frac{\mathrm{A}}{{\mathrm{T}}_{\mathrm{K}}}+\mathrm{B}$$ (14)

$${\mathrm{A}\mathrm{b}\mathrm{s}}_{214\mathrm{n}\mathrm{m}}=\frac{\left[\mathrm{T}\mathrm{O}\mathrm{T}\mathrm{C}\mathrm{y}\right]}{{\mathrm{\gamma }}_1\{{\mathrm{H}}^{+}\}+\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{\mathrm{A}}{{\mathrm{T}}_{\mathrm{K}}}+\mathrm{B}\right)}({\mathrm{\epsilon }}_{\mathrm{0,214}\mathrm{n}\mathrm{m}}{\mathrm{\gamma }}_1\{{\mathrm{H}}^{+}\}+{\mathrm{\epsilon }}_{\mathrm{1,214}\mathrm{n}\mathrm{m}}\mathrm{e}\mathrm{x}\mathrm{p}(-\frac{\mathrm{A}}{{\mathrm{T}}_{\mathrm{K}}}+\mathrm{B}\left)\right)$$ (15)

Parameter estimation.

Estimation of parameters A and B in Equation 15 and subsequent determination of K₆ by Equation 14 at various temperatures were accomplished in R, a freeware language and environment for statistical computing and graphics available for download at http://www.r-project.org/.²⁷ R’s capabilities were extended through the use of the nlstools package Version 1.0–2,²⁸ a free user–contributed package downloaded through the R software. In the R software, the function nls() was used to conduct a nonlinear least–squares estimate of parameters A and B by minimizing the residual sum of squares between all (n = 126) the experimentally measured and Equation 15 predicted Abs_214nm values.

RESULTS AND DISCUSSION

Molar Absorptivity Experiments

Molar absorptivity estimates.

Molar absorptivity experiments were conducted at each temperature for both H₃Cy and H₂Cy^– at 214 nm. A summary of the molar absorptivity estimates is presented in Table 1. Molar absorptivity estimates at a given temperature resulted in extremely good linear regressions for both H₃Cy (0.997 ≤ R² ≤ 0.999) and H₂Cy^– (0.998 ≤ R² ≤ 1.000). For the temperatures studied, the molar absorptivity estimates ranged from 83.8 to 103 and 9,107 to 10,715 M^–1 cm^–1 for H₃Cy and H₂Cy^–, respectively. O’Brien²⁰ reported a molar absorptivity for H₃Cy at 214 nm of 100 M^–1 cm^–1 while various values for H₂Cy^– have been reported, including 8,800;²⁰ 10,170;²⁹ and 11,700 M^–1 cm^–1.³⁰ Overall, the molar absorptivity estimates from the current research encompass a relatively tight range and are comparable to values previously reported for H₃Cy and H₂Cy^–.

Table 1 –

Molar absorptivity estimate summary (number of samples (n) = 12 for each estimate).

Cyanuric Acid (H3Cy), pH = 1.82 ± 0.057
Temperature ± Standard Deviation – °C	Molar Absorptivity Estimate ± 95% Individual Confidence Interval – M −1 cm−1	R2
5.2 ± 0.22	83.8 ± 1.43	0.997
10.2 ± 0.11	89.8 ± 0.90	0.999
15.7 ± 0.73	89.9 ± 1.12	0.999
19.2 ± 0.087	87.3 ± 1.39	0.998
24.5 ± 0.17	90.1 ± 1.29	0.998
30.0 ± 0.18	103 ± 1.24	0.999
34.0 ± 0.30	91.8 ± 1.55	0.998
Cyanuric Acid First Ionization Product (H2Cy−), pH = 9.00 ± 0.010
Temperature ± Standard Deviation – °C	Molar Absorptivity Estimate ± 95% Individual Confidence Interval – M−1cm−1	R2
5.0 ± 0.083	10,211 ± 56	1.000
10.2 ± 0.12	10,528 ± 174	0.998
16.0 ± 0.22	10,715 ± 59	0.998
19.4 ± 0.11	9,324 ± 59	1.000
24.2 ± 0.13	9,591 ± 42	1.000
30.5 ± 0.10	10,218 ± 80	1.000
34.7 ± 0.15	9,107 ± 88	1.000
Cyanuric Acid First Ionization Product (H2Cy−), pH = 9.51 ± 0.0092
Temperature ± Standard Deviation – °C	Molar Absorptivity Estimate ± 95% Individual Confidence Interval – M−1cm−1	R2
5.2 ± 0.11	10,376 ± 59	1.000
10.4 ± 0.12	10,650 ± 179	0.998

Multiple comparisons.

SI Figure S2 provides a comparison of the various molar absorptivity estimates where the bars represent 95% confidence intervals (CIs) determined from Tukey’s multiple comparison test previously described. When comparing two molar absorptivity estimates in SI Figure S2, the molar absorptivity estimates are considered statistically different if the bars from one molar absorptivity estimate do not overlap the other molar absorptivity estimate. A summary of the multiple comparisons is provided in SI Table S1, detailing each individual comparison that can be made. Even though similar, SI Table S1 shows that most of the molar absorptivity estimates were statistically different from one another at the various temperatures with no apparent pattern, indicating some random variability in the estimate possibly occurring from variability in absorbance measurements or solution preparation. Therefore, during the subsequent analysis for the first ionization constant experiments, the temperature specific molar absorptivity estimates were used as they were conducted at the same time that the ionization constant experiment was conducted, providing the best estimate of the relationship between absorbance and concentration when the ionization constant experiment was conducted.

Finally, for the two H₂Cy^– experiments conducted at the two lowest temperatures, there was no significant difference whether or not the experiment was conducted at pH 9.0 or 9.5; therefore, the assumption from previous research²⁰ that pH 9.0 was sufficient to use for H₂Cy^– molar absorptivity estimation was validated for these extreme temperatures where an increase in pK₆ might have required a higher pH to be used to be certain that H₂Cy^– is the only meaningful species present.

Ionization Constant Experiments

Source data.

Experimental data obtained from the ionization constant experiments is summarized in SI Table S2, consisting of 126 data points (18 at each experimental temperature). The calculated μ of the samples consisted of a relatively narrow range (4.1–6.1 mM), resulting in similar γ₁ values for all samples (0.92–0.93).

Estimated parameters and comparison with previous research.

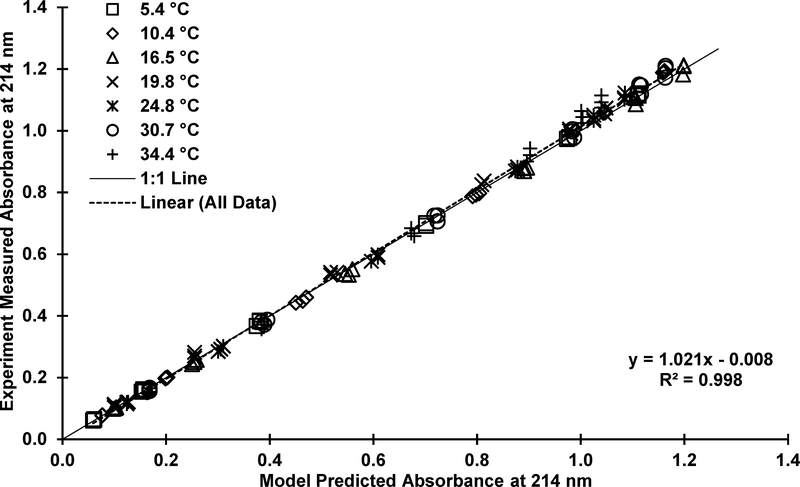
Using the data presented in SI Table S2 and molar absorptivity values from Table 1, A and B were estimating using Equation 15 and subsequently used to estimate K₆ at various temperatures with Equation 14. A summary of the model fit to the experimental data is provided in Figure 4 where the model predicted absorbance is compared to the experimentally measured absorbance at 214 nm. Ideally, these points would form a line with a slope of one passing through the origin. The linear regression results in a line with a slope of nearly one (1.02 ± 0.0056, 95% CI), a minimal intercept (0.0083 ± 0.0074, 95% CI), and excellent R² (0.998), indicating that the model represents the experimental data very well and that the assumption of constant ΔH⁰ (Equation 13) is justified.

Figure 4.

– Comparison of model predicted (Equation 15) absorbance versus experimentally measured absorbance at 214 nm.

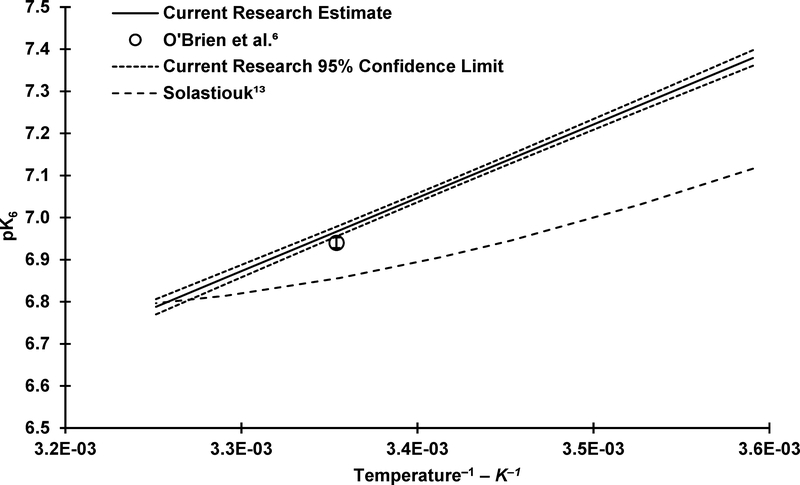
A summary of the estimates of A and B along with pK₆ values ranging from 5 to 35 °C is provided in Table 2 along with comparisons with the 25 °C O’Brien, et al.⁹ estimate. The O’Brien, et al.⁹ estimate was adjusted to μ = 0 M (pK₆ = 6.94 ± 0.013, 95% CI) from their experimental conditions of μ = 20 mM (pK₆ = 6.88 ± 0.013, 95% CI) as described in the SI. Although significantly different, the current 25 °C estimate (pK₆ = 6.97 ± 0.012, 95% CI) compares well with that of O’Brien, et al.⁹ where the two estimates of K₆ are within 5% of each other. From the estimated value of A, ΔH° is estimated to be 33.4 ± 1.7 kJ mol^–1 (95% CI).

Table 2 –

Cyanuric acid first acid ionization constant estimates (K₆) and associated parameters (5 to 35 °C). Values determined in the current research unless otherwise noted.

Temperature – °C	pK6 ± 95% Confidence Interval (μ = 0 M)
5	7.39 ± 0.019
10	7.28 ± 0.014
15	7.17 ± 0.011
20	7.07 ± 0.010
25	6.97 ± 0.012
25a	6.94 ± 0.013a
30	6.87 ± 0.015
35	6.78 ± 0.019
Parameter (Units)	Value ± 95% Confidence Interval
A (K)	4,013 ± 207
B	–2.58 ± 0.71
ΔH0 (kJ mol−1)	33.4 ± 1.7

^aO’Brien, et al.⁹

Prior to O’Brien, et al.⁹, previous researchers estimated pK₆ with reported values ranging from 6.5 to 7.0.^{29, 31, 32} More recently, Jang, et al.³³ estimated a similar pK₆ to that of O’Brien, et al.⁹ and the current research (6.9) using both experimental (spectrophotometric) and computational (density functional theory quantum mechanical model) methods, supporting the reasonableness of the O’Brien, et al.⁹ and current pK₆ estimate.

As mentioned previously, Solastiouk¹⁸ conducted preliminary experiments to determine the temperature dependence of K₆, and the result of these experiments was Equation 16 (μ ≈ 0 mM).

$${\mathrm{p}\mathrm{K}}_6=31.08-0.154{\mathrm{T}}_{\mathrm{K}}+2.44\mathrm{x}{10}^{-4}{{\mathrm{T}}_{\mathrm{K}}}^2$$ (16)

Figure 5 displays a comparison of the current temperature dependent estimates of pK₆ with those of Solastiouk¹⁸ along with the 25 °C value from O’Brien, et al.⁹ for reference. The results from the current research are markedly different from those presented by Solastiouk¹⁸, and after accounting for differences in ionic strength, the 25 °C K₆ value from O’Brien, et al.⁹ is also substantially different (22%) than that determined by Solastiouk¹⁸. Insufficient detail is provided by Solastiouk¹⁸ to ascertain a definitive reason for these discrepancies, but one possible reason for the difference is an assumption made by Solastiouk¹⁸ during data analysis. Solastiouk¹⁸ assumed that the concentration fraction of TOTCy that is H₂Cy^– (α₁) varied little with temperature from the value at 25 °C which is clearly not the case if pK₆ is changing with temperature. For instance, Table 3 provides a summary of how α₁ varies with temperature at a series of pH values, using the pK₆ values determined in the current research. Although not specifically stated, it can be inferred that Solastiouk¹⁸ conducted the experiment at or near a pH of 4.8; therefore, Table 3 provides pH values ranging around a pH of 4.8.

Figure 5.

– Comparison of current research estimated pK₆ and literature reported values. pK₆ values adjusted to 0 M ionic strength as necessary.

Table 3 –

Temperature impact on fraction (α₁) of total cyanuric acid, [H₃Cy] + [H₂Cy⁻], present as the first ionization product (H₂Cy⁻) at various pHs.

Temperature – °C	Calculated α1 for Given pH as %
	4.50	4.80	5.50	6.50
5	0.13	0.26	1.28	11.5
10	0.17	0.33	1.65	14.3
15	0.21	0.43	2.10	17.6
20	0.27	0.54	2.64	21.3
25	0.34	0.68	3.30	25.5
30	0.42	0.84	4.09	29.9
35	0.53	1.04	5.02	34.6

CONCLUSIONS

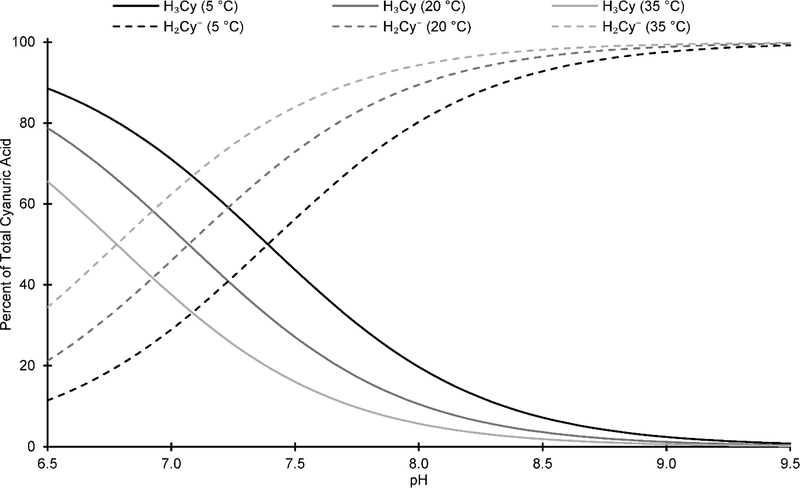
The results presented herein provide the first rigorous estimation of the first ionization constant of cyanuric acid (K₆) from 5 to 35 °C where $\ln {\mathrm{K}}_6=-\frac{\mathrm{4,013}}{{\mathrm{T}}_{\mathrm{K}}}-2.58$ or ${\mathrm{p}\mathrm{K}}_6=\frac{\mathrm{1,743}}{{\mathrm{T}}_{\mathrm{K}}}+1.12$ and ΔH° = 33.4 ± 1.7 kJ mol^–1. Figure 6 summarizes the temperature impact on the speciation of cyanuric acid at 5, 20, and 35 °C. Over the pH range of approximately 6.5 to 8, the speciation of cyanuric acid changes substantially with temperature. For example, at pH 7.0, H₂Cy^– represents 29 and 62% of TOTCy at 5 and 35 °C, respectively, meaning that the H₂Cy^– fraction effectively doubles from 5 to 35 °C.

Figure 6.

– Cyanuric acid speciation with temperature under drinking water relevant pHs (ionic strength = 0 M).

With the addition of K₆’s temperature dependence to the known temperature dependence of K, only two temperature dependent equilibrium constants (K₇ and K₉) remain to be determined to allow extension of the free chlorine and cyanuric acid system water chemistry model to a range of relevant drinking water temperatures. These experiments and resulting extension of the web–based application to simulate the water chemistry are the focus of ongoing research.