Multi-Layer Multi-View Classification for Alzheimer’s Disease Diagnosis

Abstract

In this paper, we propose a novel multi-view learning method for Alzheimer’s Disease (AD) diagnosis, using neuroimaging and genetics data. Generally, there are several major challenges associated with traditional classification methods on multi-source imaging and genetics data. First, the correlation between the extracted imaging features and class labels is generally complex, which often makes the traditional linear models ineffective. Second, medical data may be collected from different sources (i.e., multiple modalities of neuroimaging data, clinical scores or genetics measurements), therefore, how to effectively exploit the complementarity among multiple views is of great importance. In this paper, we propose a Multi-Layer Multi-View Classification (ML-MVC) approach, which regards the multi-view input as the first layer, and constructs a latent representation to explore the complex correlation between the features and class labels. This captures the high-order complementarity among different views, as we exploit the underlying information with a low-rank tensor regularization. Intrinsically, our formulation elegantly explores the nonlinear correlation together with complementarity among different views, and thus improves the accuracy of classification. Finally, the minimization problem is solved by the Alternating Direction Method of Multipliers (ADMM). Experimental results on Alzheimers Disease Neuroimaging Initiative (ADNI) data sets validate the effectiveness of our proposed method.

Introduction

Alzheimer’s Disease (AD) is a severe irreversible neurodegenerative disease, devastating lives of millions in the world (Cuingnet et al. 2011). Its early diagnosis, and treatment can improve the quality of life dramatically for both patients and their caregivers. There have been several studies (Weiner et al. 2017) in the recent years exploiting different aspects of the disease, and hence there are multiple modalities of data (e.g., Magnetic Resonance Imaging (MRI) and Positron Emission Tomography (PET)) or multiple types of features available for this task (May et al. 1999). Generally, an important aspect of such works is that these features are often complementary, since they are from different measurements representing the same subject(s). On the other hand, it is evident that each individual modality alone cannot characterize the categories comprehensively, as each of them encodes different but interrelated properties of the data (Chaudhuri et al. 2009; Xu et al. 2013; Gong et al. 2016; Luo et al. 2013a; 2013b). Considering each modality (or type of features) as one view of the data, we propose to model the problem as a multi-view learning framework. Specifically, in this paper, we introduce a novel model for multi-view learning applied to the vital task of AD diagnosis.

Owing to the usefulness of exploiting the complementarity among multiple modalities or multiple types of features, multi-view learning has been the focus of intense investigation. Earlier methods usually tried to minimize the disagreement between two views based on co-training (Kumar and Daumé 2011). There are various theoretical analyses (Blum and Mitchell 1998; Chaudhuri et al. 2009; Wang and Zhou 2007) supporting the success and appropriateness of such approaches. Besides, multiple kernel learning (MKL) (Zien and Ong 2007; Liu et al. 2017) is another way of handling multiple views, which uses a predefined set of kernels for multiple views and learns an optimal combination of kernels to integrate these views. Recently, some methods are proposed to advocate for the learning of a latent common subspace across different views, typically, based on canonical correlation analysis (CCA) (Chaudhuri et al. 2009; Kakade and Foster 2007). For AD diagnosis, the recent works (Zhu et al. 2014, 2016) propose to transform the original features from different modalities to a common space by canonical correlation analysis. Although great progress has been achieved, some main limitations still exist: (1) Most existing methods usually explore linear correlation between multi-view input data and class labels, thus, they are not applicable to uncover complex correlations, compared to nonlinear methods; (2) MKL based methods map the features into a kernel space to explore the nonlinearity among the features and labels, however, simply weighting different views will not be enough for exploiting the complex correlation within each view and among different views, e.g., high-order correlations.

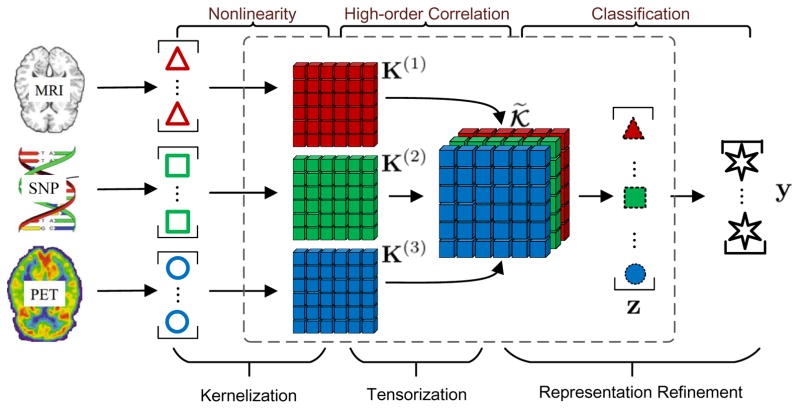
In this paper, we propose a novel multi-view learning approach termed as Multi-Layer Multi-View Classification (ML-MVC), which focuses on addressing the above limitations in a unified framework. As shown in Fig. 1, given the data with multiple views (taking multiple modalities as example), our method aims to simultaneously explore the complex correlation between input and output, as well as the complementarity among multiple views. Based on the multiple modalities or multiple types of features of data, referred to as multi-view input, we introduce a middle layer for feature extraction with kernel technique to account for nonlinearity. Accordingly, the classification model is learned based on the mapped and refined middle-layer features (or latent representation) instead of the original ones. Furthermore, to exploit the correlation among multiple views, the kernel matrices are jointly stacked and regarded as a tensor, which is low-rank constrained to capture the complementary information from multiple views. As shown in Fig. 1, the dashed box indicates the middle layer for the latent representation corresponding to the nonlinear feature mapping and high-order correlation of multiple views. Empirical results on real data demonstrate the effectiveness of the proposed method. The optimization of our model is conducted by the Alternating Direction Method of Multipliers (ADMM) (Boyd et al. 2011).

Figure 1.

Illustration of the multi-layer multi-view learning framework for AD prediction. Our model jointly exploits the nonlinear feature mapping, explores high-order correlation of multiple views and learns classification model.

The highlights of the proposed ML-MVC method and this paper are summarized as follows: (1) We simultaneously explore the complex correlation between features and classes, while exploiting the high-order correlation among multiple kernel matrices of different views. (2) The method can be regarded as a multi-layer model, where the middle layer is equipped with kernel trick to account for nonlinearity, corresponding to the latent representation. (3) Instead of performing prediction based on the kernel mapping features, our method learns the prediction model based on the refined kernel mapping features, which thoroughly explores the correlation of multiple views. (4) Based on the Alternating Direction Method of Multipliers (ADMM) (Boyd et al. 2011), our method is optimized efficiently and the convergence can be practically reached. (5) The experiments on multi-modalilty and multi-feature Alzheimers Disease Neuroimaging Initiative (ADNI) dataset validate the effectiveness of our method for classification on multi-view data.

Problem Formulation

Notations

Let x₁, ···, x_N ∈ ℝ^D denote N feature vectors of N samples in the D-dimensional space, and X = [x₁, ···, x_N] is the D × N feature matrix whose columns are the samples. For the v^th view, we use ${\mathbf{x}}_i^{(v)}$ and X^(v) to denote one sample and the feature matrix, respectively.Y = [y₁, ···, y_N] is the corresponding label matrix with y_i = [y_i1, ···, y_iC]^⊤ being the label vector of the i^th sample, and y_ij = 1 if sample x_i belong to the j^th class, and y_ij = 0 otherwise, where C is the number of classes. We use the bold calligraphic font to denote a high-order tensor, e.g., 𝓚. For clarity, the main notations used in this paper are listed in Table 1.

Table 1.

Table of main notations used in the paper.

Model Specification
Notation	Meaning
X(v) ∈ ℝDv×N	feature matrix of the vth view
Y ∈ℝC×N	label matrix
Z(v) ∈ ℝK×N	latent representation for the vth view
P(v) ∈ ℝK×N	projection corresponding to the vth view
S ∈ ℝC×VK	classification model
𝓚 ∈ ℝK×N×V	tensor of kernel matrices
𝓖 ∈ ℝK×N×V	auxiliary variables in tensor form
𝓦 ∈ ℝK×N×V	Lagrange multiplier in tensor form
K(m)/G(m)	unfolded matrix of tensor 𝓚/𝓖
μ > 0	penalty hyperparameter for constraints

Background

Given the multi-view training data as {X⁽¹⁾, …, X^(V); Y}, where X^(v) ∈ ℝ^D_v×N is the feature matrix for the v^th view and Y ∈ ℝ^C×N is the class label matrix. Accordingly, a straightforward formulation for the multi-view learning is as follows:

$$\underset{\mathbf{W},\mathbf{B}}{min}{\Vert \mathbf{Y}-\mathbf{WX}-\mathbf{B}\Vert }_F^2+\lambda {\Vert \mathbf{W}\Vert }_F^2,$$ (1)

where $\mathbf{X}=[{\mathbf{X}}^{(1)};\cdots ;{\mathbf{X}}^{(V)}]\in {ℝ}^{{\sum }_{v=1}^V{D}_v\times N}$ concatenates different views directly, with D_v being the dimensionality of the v^th view. ||·||_F is the Frobenius norm. W = [w₁, ···, w_C]^⊤ ∈ ℝ^C×D are learned models for C classes, where $D={\sum }_{v=1}^V{D}_v$. B ∈ ℝ^C×N corresponds to bias. This objective function directly extends the conventional ridge regression for multi-view data. Although simple in form and easy for optimization, there are two main issues: (1) The simple concatenation of multiple views may suffer from the curse of dimensionality and could not well explore the complementarity among different views. (2) This model focuses on linear correlation between multi-view input and class labels, which makes it improper for more complex problems. In this work, we focus on addressing these issues in a seamless framework.

Multi-Layer Multi-View Classification

To address the nonlinearity issues, we aim to design a multilayer objective function with the following general form

$$\underset{\mathbf{S},{\mathbf{W}}^{(v)}}{min}\mathcal{L}(\mathbf{SZ},\mathbf{Y})+\underset{\text{Feature-mapping}\text{Regularization}}{\underbrace{{\lambda }_1{\mathcal{R}}_1({\{{\mathbf{W}}^{(v)}\}}_{v=1}^V)}}+\underset{\text{Model}\text{Regularization}}{\underbrace{{\lambda }_2{\mathcal{R}}_2(\mathbf{S})}},$$ (2)

where ℒ(·) is the loss function and λ₁ > 0, λ₂ > 0 are tradeoff factors for two regularization terms ℛ₁(·) and ℛ₂(·). Z = [Z⁽¹⁾; ···; Z^(V)] concatenates the latent representation of multiple views. Compared with the straightforward formulation in Eq. 1, rather than directly learning classification model based on the original features, we introduce a middle layer to learn the latent representation, i.e., ${\mathbf{Z}}^{(v)}=[{\mathbf{z}}_1^{(v)},\dots ,{\mathbf{z}}_N^{(v)}]$, where ${\mathbf{z}}_i^{(v)}={\mathbf{W}}^{(v)}{\mathbf{x}}_i^{(v)}+{\mathbf{b}}^{(v)}$ and the bias b^(v) can be omitted since it can be absorbed into the projection matrixW^(v) (Nie et al. 2010). Then, based on the latent representation, the classification model S is learned, forming our multi-layer model. For nonlinearity, according to the Representer Theorem (Dinuzzo and Schölkopf 2012), we have:

Theorem 1

Given any fixed matrix S, the objective function in (2) w.r.t. W^(v) is defined over a Hilbert space ℋ. If (2) has a minimizer w.r.t. W^(v), it admits a linear representer theorem of the form W^(v) = P^(v)X^(v)⊤, where P^(v) ∈ ℝ^K×N is the coefficient matrix.

According to (Dinuzzo and Schölkopf 2012), the proof of Theorem 1 is straightforward due to the decoupled property for each model ${\mathbf{w}}_c^{(v)}$. By introducing kernel mapping with Representer Theorem, we have $\mathrm{\Phi }({\mathbf{X}}^{(v)})=[\varphi ({\mathbf{x}}_1^{(v)}),\cdots ,\varphi ({\mathbf{x}}_N^{(v)})]$ with ϕ(·) mapping the original feature x^(v) to ϕ(x^(v)), and accordingly, we have W^(v) = P^(v)Φ(X^(v))^⊤. For simplicity, we use the same ϕ(·) for different views. Therefore, based on (2) the objective function turns out to be

$$\underset{\mathbf{S},{\mathbf{P}}^{(v)},\stackrel{\sim }{{\mathbf{K}}^{(v)}}}{min}\frac{1}{2}{\Vert \mathbf{SZ}-\mathbf{Y}\Vert }_F^2+\underset{{\mathcal{R}}_1:\text{Feature-mapping}\text{Regularization}}{\underbrace{\frac{\gamma }{2}\sum _{v=1}^V{\Vert {\mathbf{P}}^{(v)}\mathrm{\Phi }{({\mathbf{X}}^{(v)})}^{\top }\Vert }_F^2}}+\underset{{\mathcal{R}}_2:\text{Model}\text{Regularization}}{\underbrace{\frac{\eta }{2}{\Vert \mathbf{S}\Vert }_F^2}}.$$ (3)

Since we aim to explore the correlations among different views using a tensor structure instead of directly concatenating each type of features, there is one important issue that we need to take care of. Specifically, we should note that the data from different views (e.g., different modalities of medical imaging data) often have different dimensionalities, while we have to arrange them into a single tensor with fixed dimensionality for all of them. Thanks to the advantages of the kernel technique, our objective function could naturally resolve the mentioned issues and explore the high-order correlations among multiple views as follows:

$$\begin{gathered} \underset{\mathbf{S},{\mathbf{P}}^{(v)},\stackrel{\sim }{{\mathbf{K}}^{(v)}}}{min}\frac{1}{2}{\Vert {\mathcal{P}}_O(\mathbf{SZ}-\mathbf{Y})\Vert }_F^2 \\ +\underset{{\mathcal{R}}_3:\text{High-order}\text{correlation}}{\underbrace{\alpha {\Vert \stackrel{\sim }{\mathcal{K}}\Vert }_{\ast }+\frac{\beta }{2}{\Vert \mathcal{K}-\stackrel{\sim }{\mathcal{K}}\Vert }_F^2}} \\ +\underset{{\mathcal{R}}_1:\text{Feature-mapping}\text{Regularization}}{\underbrace{\frac{\gamma }{2}\sum _{v=1}^V{\Vert {\mathbf{P}}^{(v)}\stackrel{\sim }{\mathrm{\Phi }{({\mathbf{X}}^{(v)})}^{\top }}\Vert }_F^2}}+\underset{{\mathcal{R}}_2:\text{Model}\text{Regularization}}{\underbrace{\frac{\eta }{2}{\Vert \mathbf{S}\Vert }_F^2}} \\ s.t.\mathcal{K}=\mathcal{T}({\mathbf{K}}^{(1)},\dots ,{\mathbf{K}}^{(V)}),\stackrel{\sim }{\mathcal{K}}=\mathcal{T}(\stackrel{\sim }{{\mathbf{K}}^{(1)}},\dots ,\stackrel{\sim }{{\mathbf{K}}^{(V)}}), \\ \mathbf{Z}=[{\mathbf{Z}}^{(1)};\cdots ;{\mathbf{Z}}^{(V)}]\text{and}{\mathbf{Z}}^{(v)}={\mathbf{P}}^{(v)}\stackrel{\sim }{{\mathbf{K}}^{(v)}}, \end{gathered}$$ (4)

where the operator 𝒯(·) constructs a tensor by combining multiple kernel matrices (naturally with equal dimensionality) as shown in Fig. 1. We have the kernel matrix corresponding to the v^th view K^(v) = Φ(X^(v))^⊤Φ(X^(v)) and try to seek the more reasonable $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$ to exploit the high-order correlation, i.e., ${\mathbf{K}}^{(v)}=\stackrel{\sim }{{\mathbf{K}}^{(v)}}+{\mathbf{E}}^{(v)}$. ℘_O acts as a filter function, which forces the loss to only account for the labeled samples. Specifically, let o_i be an indicator variable showing the existence of label for sample i, i.e., o_i = 1 if we have the label, and a very small scalar ε > 0 otherwise. o will then be defined as the indicator vector from all indicator variables of training samples. Accordingly, we can define a diagonal matrix O = diag(o), denoted as the filter matrix, and hence ℘_O(A) = AO. Note that ε > 0 is a small value to strictly guarantee the unique solution of the optimization problem (see P^(v) and $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$-subproblems in the next section).

We introduce a low-rank tensor constraint to jointly explore the intrinsic correlations across multiple kernel matrices of these multiple views. Note that tensor can be seen as a generalization of the matrix concept, and hence we define the tensor nuclear norm similar to (Liu et al. 2013b; Tomioka et al. 2011), which generalizes the matrix (i.e., 2- mode or 2-order tensor) case (e.g., (Liu et al. 2013a)) to higher-order tensor as

$${\Vert \mathcal{K}\Vert }_{\ast }=\sum _{m=1}^M{\xi }_m{\Vert {\mathbf{K}}_{(m)}\Vert }_{\ast },$$ (5)

where ξ_m’s are constants satisfying ξ_m > 0 and ${\sum }_{m=1}^M{\xi }_m=1$. Without prior, we set ξ₁ = … = ξ_M = 1/M. 𝓚 ∈ ℝ^{I₁×I₂×…×I_M} is a M-order tensor, and K_(m) is the matrix by unfolding the tensor 𝓚 along the m^th mode defined as unfold_m(𝓚) = K_(m) ∈ ℝ^{I_m×(I₁×…×I_m−1×I_m+1…×I_M)} (De Lathauwer et al. 2000; Zhang et al. 2015). The nuclear norm ||·||_* controls the tensor under a low-rank constraint. In essence, the nuclear norm of a tensor is a convex combination of the nuclear norms of all matrices unfolded along each mode.

Remarks

1) The model regularizer ℛ₂(·) for S can be customized for different tasks. For example, we employ Frobenius norm for AD/PD diagnosis which belongs to multiclass classification, while for multi-label classification, we can use other techniques (e.g., low-rank) to explore the correlation among different labels. 2) The matrices $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$s are approximations of the kernel matrices K^(v)s, and it is difficult to ensure $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$s to be strict kernel matrices. 3) For our model, the kernels themselves can be regarded as the entries of feature vectors within a generalized linear model (Roth 2004), i.e., $\varphi ({\mathbf{x}}^{(v)})={[k({\mathbf{x}}^{(v)},{\mathbf{x}}_1^{(v)}),\dots ,k({\mathbf{x}}^{(v)},{\mathbf{x}}_N^{(v)}),1]}^{\top }$.

To summarize, our model has the following merits: (1) Our model focuses on exploring complex correlations among the features and the class labels by introducing a middle layer equipped with kernel technique; (2) Benefiting from the kernel technique, the high-order correlation of different views is thoroughly exploited by learning the latent representation approximate to the kernel matrices of different views equipped with a low-rank tensor; (3) Both the complex input-output correlation and the high-order multi-view correlation are addressed seamlessly in a unified framework.

Optimization

Our objective function in Eq. (4) simultaneously seeks to optimize multiple projections P^(v)s, matrices $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$s and model S. Since it is not jointly convex with respect to all the variables P^(v)s, $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$s and S, we employ Alternating Direction Method of Multipliers (ADMM) (Boyd et al. 2011). To adopt the alternating direction minimization strategy to our problem, we need to make our objective function separable. Therefore, we introduce auxiliary variables 𝓖, and induce the following equivalent problem to be minimized

$$\begin{gathered} \mathcal{L}({\mathbf{P}}^{(1)},\dots ,{\mathbf{P}}^{(V)};\stackrel{\sim }{{\mathbf{K}}^{(1)}},\dots ,\stackrel{\sim }{{\mathbf{K}}^{(V)}};\mathbf{S};\mathcal{G};\mathcal{W}) \\ =\frac{1}{2}{\Vert {\mathcal{P}}_O(\mathbf{SZ}-\mathbf{Y})\Vert }_F^2 \\ +\frac{\gamma }{2}\sum _{v=1}^V{\Vert {\mathbf{P}}^{(v)}\stackrel{\sim }{\mathrm{\Phi }{({\mathbf{X}}^{(v)})}^{\top }}\Vert }_F^2 \\ +\frac{\beta }{2}{\Vert \mathcal{K}-\stackrel{\sim }{\mathcal{K}}\Vert }_F^2+\langle \mathcal{W},\stackrel{\sim }{\mathcal{K}}-\mathcal{G}\rangle +\frac{\mu }{2}{\Vert \stackrel{\sim }{\mathcal{K}}-\mathcal{G}\Vert }_F^2 \\ +\frac{\eta }{2}{\Vert \mathbf{S}\Vert }_F^2+\alpha {\Vert \mathcal{G}\Vert }_{\ast }, \end{gathered}$$ (6)

where 𝓦 is the Lagrange multiplier in tensor form. The operator 〈·, ·〉 defines the tensor inner product and μ is a positive penalty scalar. For the above objective function, the sub-problems can be solved as follows:

• Update P^(v). The objective function with respect to updating P^(v) is

  $$\underset{{\mathbf{P}}^{(v)}}{min}\frac{1}{2}{\Vert (\sum _{u\ne v}{\mathbf{S}}^{(u)}{\mathbf{Z}}^{(u)}+{\mathbf{S}}^{(v)}{\mathbf{P}}^{(V)}\stackrel{\sim }{{\mathbf{K}}^{(v)}}-\mathbf{Y})\mathbf{O}\Vert }_F^2+\frac{\gamma }{2}{\Vert {\mathbf{P}}^{(v)}\stackrel{\sim }{\mathrm{\Phi }{({\mathbf{X}}^{(v)})}^{\top }}\Vert }_F^2.$$

Taking the derivative with respect to P^(v) and setting it to zero, we get

$$\begin{gathered} \mathbf{A}{\mathbf{P}}^{(v)}+{\mathbf{P}}^{(v)}\mathbf{B}=\mathbf{C} \\ \text{with}\mathbf{A}=\gamma {({\mathbf{S}}^{\top }\mathbf{S})}^{-1},\mathbf{B}=\stackrel{\sim }{{\mathbf{K}}^{(v)}}{\mathbf{O}}^{\top }\mathbf{O}\text{and} \\ \mathbf{C}={({\mathbf{S}}^{\top }\mathbf{S})}^{-1}({\mathbf{S}}^{{(v)}^{\top }}(\mathbf{Y}-\sum _{u\ne v}{\mathbf{S}}^{(u)}{\mathbf{Z}}^{(u)})){\mathbf{O}}^{\top }\mathbf{O}. \end{gathered}$$ (7)

The above equation is a Sylvester equation (Bartels and Stewart 1972), and we have the follow proposition:

Proposition 1

The Sylvester equation (7) has a unique solution.

Proof

The Sylvester equation AP^(v) + P^(v)B = C has a unique solution for P^(v) exactly when there are no common eigenvalues of A and -B (Bartels and Stewart 1972). Since B is a positive definite matrix, all of its eigenvalues are positive: b_i > 0. While since A is a positive semi-definite matrix, all of its eigenvalues are nonnegative: a_i ≥ 0. Hence, for any eigenvalues of A and B, a_i + b_j > 0. Accordingly, the Sylvester equation (7) has a unique solution.

• Update $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$. To update $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$, we should optimize the following objective function

  $$\begin{gathered} \underset{\stackrel{\sim }{{\mathbf{K}}^{(v)}}}{min}\frac{1}{2}{\Vert (\sum _{u\ne v}{\mathbf{S}}^{(u)}{\mathbf{Z}}^{(u)}+{\mathbf{S}}^{(v)}{\mathbf{P}}^{(v)}\stackrel{\sim }{{\mathbf{K}}^{(v)}}-\mathbf{Y})\mathbf{O}\Vert }_F^2 \\ +\frac{\gamma }{2}{\Vert \mid {\mathbf{P}}^{(v)}\stackrel{\sim }{\mathrm{\Phi }({\mathbf{X}}^{(v)})}\Vert }_F^2+\frac{\beta }{2}\sum _{v=1}^V{\Vert {\mathbf{K}}^{(v)}-\stackrel{\sim }{{\mathbf{K}}^{(v)}}\Vert }_F^2 \\ +\langle {\mathbf{W}}^{(v)},\stackrel{\sim }{{\mathbf{K}}^{(v)}}-{\mathbf{G}}^{(v)}\rangle +\frac{\mu }{2}{\Vert \stackrel{\sim }{{\mathbf{K}}^{(v)}}-{\mathbf{G}}^{(v)}\Vert }_F^2, \end{gathered}$$
  where 𝓖 = 𝒯(G⁽¹⁾, …, G^(V)), 𝓦 = 𝒯(W⁽¹⁾, …, W^(V)) with G^(v) andW^(v) corresponding to the v^th view. Taking the derivative with respect to $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$ and setting it to zero, we get the following equation

  $$\mathbf{A}\stackrel{\sim }{{\mathbf{K}}^{(v)}}+\stackrel{\sim }{{\mathbf{K}}^{(v)}}\mathbf{B}=\mathbf{C}\text{with}\mathbf{A}=(\beta +\mu ){({\mathbf{P}}^{\top }{\mathbf{S}}^{\top }\mathbf{SP})}^{-1},\mathbf{B}={\mathbf{O}}^{\top }\mathbf{O},\mathbf{C}={({\mathbf{P}}^{\top }{\mathbf{S}}^{\top }\mathbf{SP})}^{-1}({\mathbf{P}}^{\top }{\mathbf{S}}^T\mathbf{Y}{\mathbf{O}}^{\top }\mathbf{O}+\beta \mathbf{K}+\mu \mathbf{G}-{\mathbf{P}}^{\top }{\mathbf{S}}^{\top }\sum _{u\ne v}{\mathbf{S}}^{(u)}{\mathbf{Z}}^{(u)}{\mathbf{O}}^{\top }\mathbf{O}-\gamma {\mathbf{P}}^{\top }\mathbf{P}-\mathbf{W}).$$ (8)

  Similar to (7), the above equation is also a Sylvester equation (Bartels and Stewart 1972) and has a unique equation.

• Update S. To update the model S, we should optimize the following objective function

  $$\underset{\mathbf{S}}{min}\frac{1}{2}{\Vert (\mathbf{SZ}-\mathbf{Y})\mathbf{O}\Vert }_F^2+\frac{\eta }{2}{\Vert \mathbf{S}\Vert }_F^2.$$
  Taking the derivative with respect to S and setting it to zero, we get the updating rule as

  $$\mathbf{S}=(\mathbf{YO}{\mathbf{O}}^{\top }{\mathbf{Z}}^{\top }){(\mathbf{ZO}{\mathbf{O}}^{\top }{\mathbf{Z}}^{\top }+\eta \mathbf{I})}^{-1}.$$ (9)
• Update 𝒢. To update the tensor auxiliary variable 𝓖, we should optimize the following objective function

  $$\underset{\mathcal{G}}{min}\alpha {\Vert \mathcal{G}\Vert }_{\ast }+\frac{\mu }{2}{\Vert \mathcal{G}-(\stackrel{\sim }{\mathcal{K}}+\frac{1}{\mu }\mathcal{W})\Vert }_F^2.$$

According to the tensor rank definition in Eq. (5), we have the equivalent formulation as

$$\underset{{\mathbf{G}}_{(m)}}{min}\alpha \sum _{m=1}^M{\Vert {\mathbf{G}}_{(m)}\Vert }_{\ast }+\frac{\mu }{2}\sum _{m=1}^M{\Vert {\mathbf{G}}_{(m)}-(\stackrel{\sim }{{\mathbf{K}}_{(m)}}+\frac{1}{\mu }{\mathbf{W}}_{(m)})\Vert }_F^2.$$ (10)

Accordingly,G_(m) could be efficiently updated with ${\mathbf{G}}_{(m)}^{\ast }={\text{prox}}_{{\lambda }_m}^{tr}(\stackrel{\sim }{{\mathbf{K}}_{(m)}}+\frac{1}{\mu }{\mathbf{W}}_{(m)})$. λ_m = α/μ denotes the thresholds of the spectral soft-threshold operation ${\text{prox}}_{{\lambda }_m}^{tr}(\mathbf{L})=\mathbf{U}max(\mathbf{S}-{\lambda }_m,0){\mathbf{V}}^T$ with L = USV^T being the Singular Value Decomposition (SVD) of the matrix L, and the max operation being taken element-wise. Intuitively, the solution is truncated according to the matrix $\stackrel{\sim }{{\mathbf{K}}_{(m)}}$. We update all G_(m)s and thus the tensor 𝓖 is updated accordingly.

Additionally, the Lagrange multipliers can be updated as follows:

$$\mathcal{W}\leftarrow \mathcal{W}+\mu (\stackrel{\sim }{\mathcal{K}}-\mathcal{G}).$$ (11)

For clarification, the optimization procedure is summarized in Algorithm ??.

Remarks

Note that, simply initializing all the block variables with zero will mislead the optimizations to trivial solutions. Based on this, we randomly initialize S and can obtain rather stable performance in practice.

Algorithm 1.

Optimization for our ML-MVC model.

Complexity and Convergence

Our method is composed of four main sub-problems. For updating P^(v) and $\stackrel{\sim }{{\mathbf{K}}^{(v)}}$, the classical algorithm for the Sylvester equation is the Bartels Stewart algorithm (Bartels and Stewart 1972), whose complexity is O(N³). The complexity of updating S is O(N²C + CNK + K³), where C, K and N are the size of label set, the dimension of latent representation, and the number of samples, respectively. For updating 𝓖 (the nuclear norm proximal operator), the complexity is O(N³). Overall, the total complexity is O(N²C + CNK + K³ + N³) for each iteration. Under the condition C ≪ K and C ≪ N, the total complexity is basically O(K³ + N³). It is difficult to generally prove the convergence for our algorithm. Fortunately, empirical evidence on the real data presented suggests that the proposed algorithm has very strong and stable convergence behavior even with randomly initialized S.

Experiments

Experiment setup

In all experiments, the data are split into 10 non-overlapping folds with 9/10 and 1/10 as training and testing data, and reporting the average results and standard deviation. We conduct standard 10-fold cross-validation for each split with the hyperparameters selected from {0.01, 0.1, 1, 10, 100} for α, and {0.1, 1, 10, 100} for the other hyperparameters. Gaussian kernel is employed for each type of features, i.e., $k({\mathbf{x}}_i,{\mathbf{x}}_j)=\langle \varphi ({\mathbf{x}}_i),\varphi ({\mathbf{x}}_j)\rangle =exp(\frac{{\Vert x_i-x_j\Vert }^2}{2{\sigma }^2})$ where σ = median({||x_i − x_j||}_i≠j). For hyperparameters of other methods, they are tuned for the best performance according to their respective published papers. We conducted experiments on two different sets of data with multiple modalities and multiple types of features. We evaluate the performance of all methods in terms of accuracy.

Compared methods

To comprehensively evaluate the proposed method, we divide the compared methods into 3 groups, i.e., methods using one, two and all three types of modalities/features. We employ a support vector classification model as the basic classifier which is from the LIBSVM toolbox ¹ publicly available for the compared methods. The comparison methods include: • Single view and two-view concatenation using SVM (with Gaussian kernel); • Multiview CCA (Rupnik and Shawe-Taylor 2010) which can obtain one common space for multiple views. • Matrix Completion (Cabral et al. 2011) which predicts the class label with matrix completion based on a Rank Minimization criterion, with all views concatenated. • Multiclass Multiple Kernel Learning (Zien and Ong 2007) which provides a convenient and principled way based on MKL for multiclass problems. • Vector-valued Manifold Regularization based Multi-View Learning (VMR-MVL) (Minh et al. 2013), which is a semi-supervised multi-view classification method.

The intuitions for comparing with these methods are: (1) Single-view methods operate on each view independently using SVM, thus, they provide the evaluation of the quality for each view. Moreover, it can clarify if the multi-view treatment is essential for the overall performance or not. (2) Multiple-view methods can integrate multiple views, and here several of them are employed as comparisons to evaluate the effectiveness of our method in integrating multiple views. (3) Since nonlinearity (using kernel technique) is involved in our method, we employed kernel SVM as the basic classifier. (4) VMR-MVL is a very related method to ours, which also uses both training and testing multi-view data in the formulation.

Results on data with multiple modalities

First, we test our method on the multi-modality data set with 3 modalities, i.e., MRI, PET and Single Nucleotide Polymorphisms (SNP) genetics data. There are 360 subjects in this study, including 85 AD, 185 mild cognitive impairment (MCI), and 90 normal controls (NC) subjects, where MCI is the early stage of AD and these subjects have their MRIs scanned at first screening time.

For this study, we download ADNI 1.5T MR and PET images from the ADNI website ². The MR images are collected by using a variety of scanners with protocols individualized for each scanner. To ensure the quality, these MR images are corrected for spatial distortion caused by B1 field inhomogeneity and gradient nonlinearity. The PET images are collected by 30–60 min post Fluoro-Deoxy Glucose (FDG) injection. The operations, i.e., averaging, spatially alignment, interpolation to standard voxel size, intensity normalization, and common resolution smoothing are performed for these images. In our experiments, we extract 93 ROI-based neuroimaging features for each neuroimage (i.e., MRI or PET). In addition, for SNP data, according to the AlzGene database ³, only SNPs that belong to the top AD gene candidates are selected. Accordingly, there are 3123 SNP features used.

Results and Analysis

The performance of our method along with the compared methods are reported in Table 2, where View1, View2 and View3 correspond to MRI, SNP and PET data, respectively. The values in red, green and blue indicate the top three performers, and several observations are drawn as follows: (1) The methods using multiple views are generally superior to the methods with one single view. For example, compared with SVM using View1, SVM with both View1 and View3 achieves an improvement of about 6%, and the performance of SVM with two views are usually much better than those of SVM with single view. This confirms the necessity and effectiveness of integrating multiple views. (2) Compared with other multi-view methods, ours outperforms all, which demonstrates the effectiveness of our method for classification with multi-view data. (3) Though competitive result is achieved, with low-rank tensor constraint, the performance improvement of 4.6% is further obtained. This validates the effectiveness of exploring multiple views with low-rank high-order tensor. It is very important to note that we are classifying the the data into three classes simultaneously, as opposed to binary methods that are widely and conventionally used in neuroimaging fields. Hence, it is not fair to directly compare our results with theirs, as our method exploits a more realistic and practical case.

Table 2.

Accuracy on multi-modality data.

No.	Configuration	Accuracy
1	View1	0.517 ± 0.064
2	View2	0.508 ± 0.107
3	View3	0.542 ± 0.101
4	View1+View2	0.531 ± 0.061
5	View1+View3	0.575 ± 0.073
6	View2+View3	0.556 ± 0.109
7	AllViewConcatenate	0.608 ± 0.075
8	Multiview CCA	0.581 ± 0.072
9	Matrix Completion	0.514 ± 0.092
10	MultiClass MKL	0.582 ± 0.091
11	VMR-MVL	0.579 ± 0.081
12	Ours (α = 0)	0.579 ± 0.050
13	Ours + Tensor (α = 10)	0.625 ± 0.069

Results on data with multiple types of features

Here, we also conduct experiments on the resting-state functional MRI (RS-fMRI) data set with multiple types of features. In this study, there are 195 subjects, including 32 AD, 95 MCI, and 68 NC subjects. The RS-fMRI data are acquired from ADNI and parcellated into 116 regions according to the Automated Anatomical Labeling (AAL) template. The mean RS-fMRI time series of each brain region is band-pass filtered (0.015–0.15 Hz). Head motion parameters (Friston24), mean BOLD signal of white matter, and mean BOLD signal of cerebrospinal fluid are all regressed out from the RS-fMRI data to further reduce artifacts. Similar to fMRI analysis methods, we construct the functional connectivity network for each subjects, by calculating the Pearson’s correlation of the mean signals from each pair of the ROIs. This constructs a full graph with correlation values and weights on the edges.

Three types of features are extracted from these graphs, and each is considered as a view in our multi-view method: (1) Nodal betweenness: The betweenness centrality is a measure of centrality in a graph, based on shortest paths. For each pair of nodes in a graph, there exists at least one shortest path between the nodes. The nodal betweenness centrality is the number of these shortest paths that pass through node i. (2) Nodal clustering coefficients: The coefficients are computed for each node to quantify the probability that the neighbors of node i are also connected to each other. (3) Nodal local efficiency: The efficiency of a network measures how efficiently information is exchanged within a network, which gives a precise quantitative analysis of the networks’ information flow. The local efficiency represents the efficiency of a subgraph, which consists of all node i’s neighbors.

Results and Analysis

The performance of all compared methods are listed in Table 3, where View 1, View 2 and View 3 denote nodal betweenness, nodal clustering coefficients and nodal local efficiency, respectively. According to the performance, several observations are drawn as follows: (1) Generally, SVM with multiple views is slightly superior to SVM for each single view. We note that these multiple types of features for this dataset are extracted from different aspects of one single modality, which generally leads to less complementarity among different views than that of multiple modalities. (2) Similar to the results reported in Table 2, our method outperforms all the other competitors, while much better performance is achieved when using the low-rank tensor constraint. (3) The kernelized methods are generally superior than linear ones, which demonstrates that exploring nonlinear correlation between features and class label is powerful. Overall, the results validate the effectiveness of simultaneously exploring nonlinear correlation between features and labels, and exploiting the complimentary information among multiple views as well.

Table 3.

Accuracy on multi-feature data.

No.	Configuration	Accuracy
1	View1	0.461 ± 0.128
2	View2	0.466 ± 0.125
3	View3	0.471 ± 0.115
4	View1+View2	0.477 ± 0.117
5	View1+View3	0.462 ± 0.096
6	View2+View3	0.477 ± 0.122
7	AllViewConcatenate	0.467 ± 0.119
8	Multiview CCA	0.482 ± 0.106
9	Matrix Completion	0.410 ± 0.115
10	MultiClass MKL	0.451± 0.113
11	VMR-MVL	0.481 ± 0.131
12	Ours (α = 0)	0.481 ± 0.108
13	Ours + Tensor (α = 100)	0.502 ± 0.122

Model Analysis

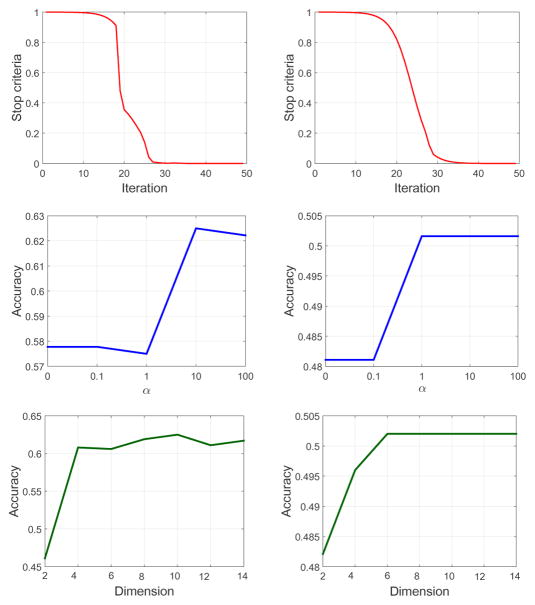
To well characterize our model, we provide several analytical curves for our method. Firstly, as shown in the top row of Fig. 2, in practice the convergence of our algorithm can be achieved within less than 50 iterations for both multi-modality and multi-feature cases. Secondly, according to the middle row of Fig. 2, it is observed that our low-rank tensor constraint is relatively effective and the performance is robust with respect to different tradeoff hyperparameter α in our objective function (4). Finally, the dimensionality of the latent representation is explored in the bottom row of Fig. 2, which demonstrates that our method can achieve promising results with a relatively low dimensionality.

Figure 2.

Model analysis on multi-modality (left column) and multi-feature (right column) data. The rows from top to bottom correspond to convergence curves, performance with respect to α and K, respectively.

Conclusion

We have proposed a novel multi-view learning method to take advantage of multiple views of data. By introducing kernel technique, our model well explores the complex correlations among features and class labels. Furthermore, by constraining the kernel matrices of different views to be low-rank tensor, the high-order correlation among different views is thoroughly exploited. Experiments on both multi-modality and multi-feature data clearly validated the superiority of our method over the state-of-the-arts. Although effective, there are also several directions to improve our method in the future, including incorporating weights for different views and more efficient optimization algorithm for large-scale data.