Soft Tissues Store and Return Mechanical Energy in Human Running

Abstract

During human running, softer parts of the body may deform under load and dissipate mechanical energy. Although tissues such as the heel pad have been characterized individually, the aggregate work performed by all soft tissues during running is unknown. We therefore estimated the work performed by soft tissues (N = 8 healthy adults) at running speeds ranging 2 – 5 m· s⁻¹, computed as the difference between joint work performed on rigid segments, and whole-body estimates of work performed on the (non-rigid) body center of mass (COM) and peripheral to the COM. Soft tissues performed aggregate negative work, with magnitude increasing linearly with speed. The amount was about −19 J per stance phase at a nominal 3 m· s⁻¹, accounting for more than 25% of stance phase negative work performed by the entire body. Fluctuations in soft tissue mechanical power over time resembled a damped oscillation starting at ground contact, with peak negative power comparable to that for the knee joint (about −500 W). Even the positive work from soft tissue rebound was significant, about 13 J per stance phase (about 17% of the positive work of the entire body). Assuming that the net dissipative work is offset by an equal amount of active, positive muscle work performed at 25% efficiency, soft tissue dissipation could account for about 29% of the net metabolic expenditure for running at 5 m· s⁻¹. During running, soft tissue deformations dissipate mechanical energy that must be offset by active muscle work at non-negligible metabolic cost.

Introduction

During steady-state running, the body performs active and passive work summing to zero over each stride. As characterized previously (Farris and Sawicki, 2011; Novacheck, 1998; Schache et al., 2011; Winter, 1983), the leg joints perform positive and negative work within each stride, with active muscles accounting for nearly all of the metabolic energy expenditure (Margaria et al., 1963). Passive “soft tissues” such as the heel pad (Chi and Schmitt, 2005), cartilage, and intervertebral discs (among others, see Fig. 1) help cushion the body. That cushioning functions in part to dissipate mechanical energy. Although their mechanical properties are well understood, it is unknown how much energy soft tissues dissipate in aggregate and in comparison to muscles. An estimate of soft tissue work might provide insight on the active work of muscles and the attendant metabolic cost of running.

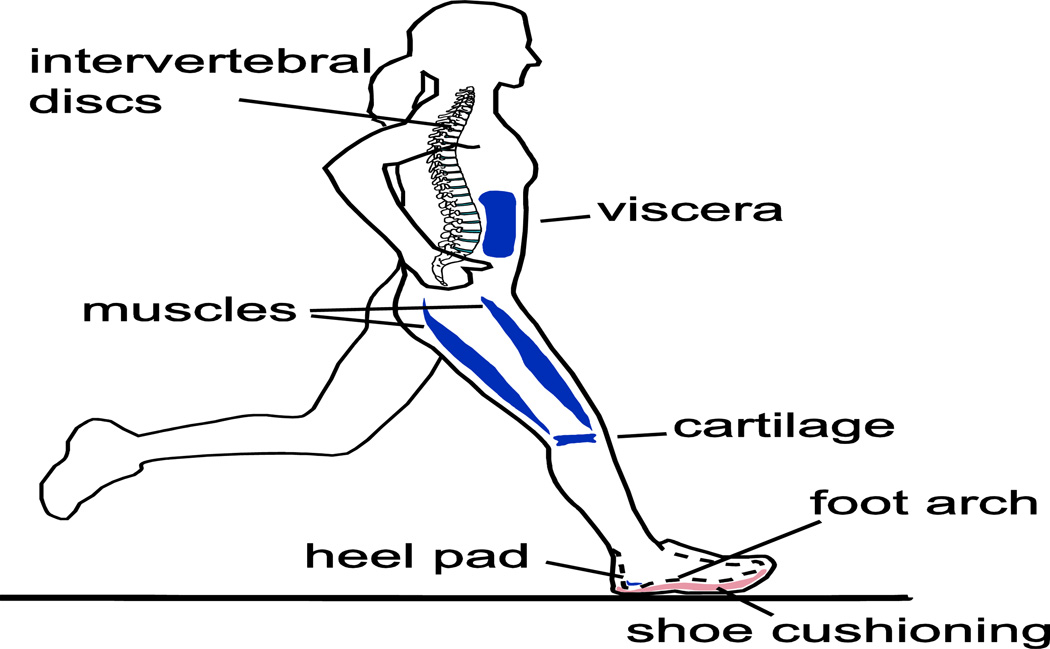
Figure 1.

Soft tissues whose deformations may store and return mechanical energy during running. The passive deformation of heel pads, plantar fascia, cartilage at joints, intervertebral discs, muscles (deformations separate from muscle contraction), skin, and even shoes may contribute.

The leg joints account for most of the mechanical power produced during running. Although the joint power trajectories are rather complex, their effect on the whole body is fairly simple: Following a brief small burst of positive work (about 0 – 2.5 % of a stride starting at ground contact), most of the stance phase resembles a mass-spring system (McMahon and Cheng, 1990), with one main large burst of negative work (2.5 – 15% stride, termed Collision here), and then one large burst of positive work (15 – 34% stride, termed Rebound) prior to the Aerial (34 – 50%) and Swing (50 – 100%) phases. Much of the work observed at the joints might actually be performed by elastic tendon. The amount is measured to be more than half in turkeys (Roberts et al., 1997), and indirectly projected to be similar in humans (Cavagna and Kaneko, 1977). If there were no other dissipation in the body, then the work fluctuations would be due only to elastic tendon and to equal magnitudes of active negative and positive work by muscle, all summing to zero over a stride.

There is, however additional dissipation by soft tissues. The heel pad, plantar fascia, and other elements of the foot both cushion the body and provide elastic energy return (Ker et al., 1988). Soft tissues in the lower leg explain how impact forces are transmitted and damped during running and jumping (Pain and Challis, 2006) and how they can modulate peak joint forces (Liu and Nigg, 2000; Nigg and Liu, 1999; Wakeling and Nigg, 2001). From measurements of skin motion, the thigh and shank also absorb considerable mechanical energy during each stance phase (Schmitt and Günther, 2011). But soft tissue deformations can be challenging to measure, for example through embedded force recordings in cadaveric specimens (Ker et al., 1987; Pai and Ledoux, 2010), or extensive motion capture of the skin (Günther et al., 2003) and potentially for the entire body. As a result, there are no estimates for the overall work performed by soft tissue deformations during in situ running, nor of the active work needed to offset the dissipation.

The aggregate work of soft tissues can be estimated, albeit indirectly. This relies on the discrepancy of total mechanical work performed according to two different measures: (1) joint powers as estimated by rigid-body inverse dynamics, and (2) rate of work performed on the (non-rigid) body center of mass (COM) as measured by ground reaction forces, and on the periphery as measured by inverse dynamics (Zelik and Kuo, 2012). Their difference indicates work performed by soft tissues, showing substantial dissipation during human walking (Zelik and Kuo, 2010) and particularly in the obese (Fu et al., 2014). The dissipation is also highly dependent on impacts, as demonstrated in jumping (Zelik and Kuo, 2012), suggesting possible contributions to running as well.

Because the muscles must actively offset any net dissipation in the body, soft tissue deformations may affect the metabolic cost of both walking and running. The purpose of the present study was to estimate these contributions during human running. We expect that (1) soft tissues perform both negative and positive work within each stance phase, (2) yielding substantial net negative work, and (3) in increasing amount at faster running speeds, due to the greater impacts.

Materials and Methods

We estimated the work of soft-tissue deformations for 8 young healthy adults (7 males, 1 female; aged 20–34 yrs.; body mass M 74.9 ± 13.0 kg, and leg length L 0.94 ± 0.044 m, mean ± s.d.) running at a range of speeds. The subjects ran on an instrumented treadmill at a comfortable range of speeds determined by their level of fitness (a total range of 2.2 to 5 m· s⁻¹) in 7 randomized experimental trials lasting 1 minute each. Of the 8 subjects, 6 landed on their rear-foot, while two tended to land on their mid-foot or forefoot, as determined by observing the subjects’ gait. All subjects gave informed consent according to approved Institutional Review Board procedures.

We recorded ground reaction forces and motion capture. Forces were recorded on a split-belt instrumented treadmill (Bertec, Columbus, OH, USA) at 960 Hz. Kinematic data were collected at 480 Hz with an eight-camera motion capture system (PhaseSpace Inc., San Leandro, CA, USA), with markers placed bilaterally on the ankle (lateral mallelous), knee (lateral epicondyle), hip (greater trochanter), shoulder (acromion of scapula), elbow (lateral epicondyle of humerus), and wrist (trapezium). Additional tracking markers were placed on the shanks, thighs, trunk, upper and lower arm, pelvis (sacrum, left/right anterior superior iliac spine) and each foot (calcaneous, fifth metatarsal). Inverse dynamics calculations (Fig.2) were performed using standard commercial software (Visual3D, C-Motion, Germantown, MD, USA) and its associated anthropometric model with 6-DOF joints. Analog force data were filtered at 25 Hz and marker motion was filtered at 10 Hz (low-pass Butterworth) before computing inverse dynamics.

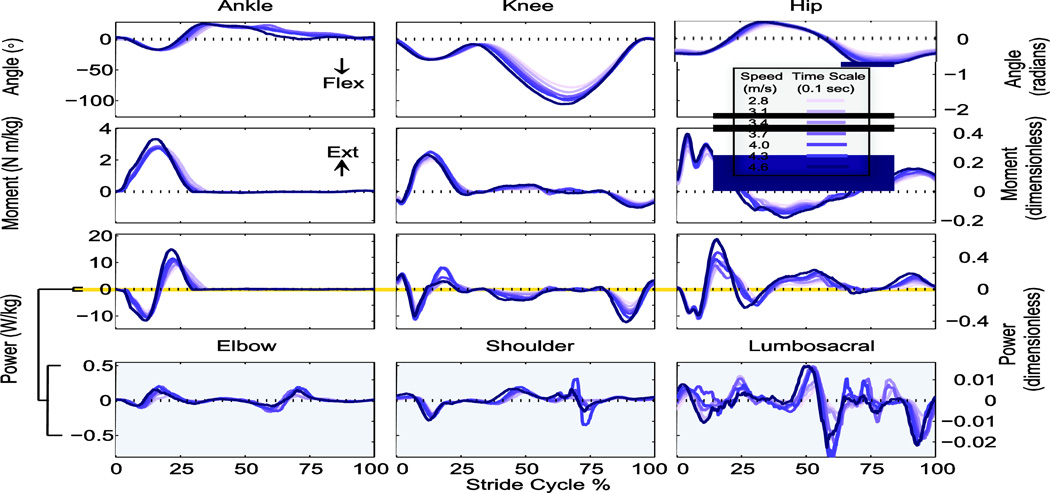
Figure 2.

Mean joint angle, moment, and power trajectories over a stride at seven running speeds. Angles and moments shown are sagittal plane values, and powers shown include three-dimensional rotation and translation, averaged across subjects (N = 8) at each point in the stride cycle (beginning and ending with same-side ground contact). Elbow, shoulder, and lumbosacral joints are shown on an expanded scale due to smaller power contributions. Angles (°) and moments (N·m·kg⁻¹) are defined as positive in extension. Dimensionless units (right-hand axes) are defined using body mass, leg length, and gravitational acceleration as base units.

These data were used to estimate soft tissue work using a previously developed method (e.g., (Fu et al., 2014; Zelik and Kuo, 2012)). At each point in time during a stride, the joint powers derived from rigid body inverse dynamics, and the unknown soft tissue power, must sum to equal the whole body fluctuations in mechanical power (“total mechanical power”). For the former, we use the term Joint Power for the aggregate power from all measured joints (and originating from positive and negative work of muscles and tendons) using inverse dynamics, summed at each sample in time (Fig. 3A). Joint Power cannot differentiate between possible sources of the power, which could include muscle, tendon, friction, and other deformations. Individual joint powers were computed from relative three-dimensional rotation and translation of each connected pair of body segments (also called “6-DOF powers”), which helps account for inaccurate joint center locations (Buczek et al., 1994; Fu et al., 2014).

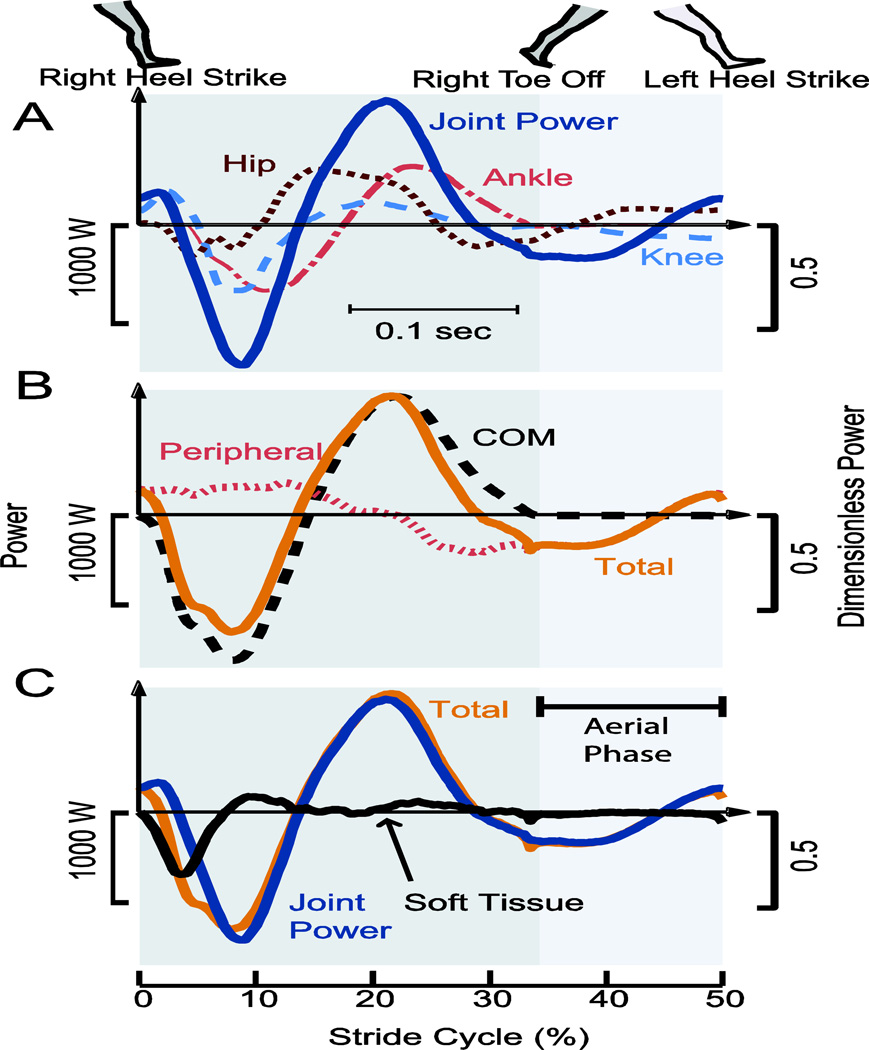
Figure 3.

Power trajectories over a step (half a stride) for a representative subject running at 3.4 m·s^-1. (A.) Joint Power, referring to the summed power of all measured joints, shown here along with stance leg’s ankle, knee, and hip. (B.) Center of mass (COM) work rate plus Peripheral power equals Total power for the body. (C.) Soft Tissue power is the estimated as the difference between Total power and Joint Power. Power is shown in W (left-hand axes) and in dimensionless units (right-hand axes). Representative subject has body mass 71.2 kg, leg length 0.94 m.

For total mechanical power, we computed the sum of work rates on the COM (Donelan et al., 2002) and for moving body segments relative to the COM (termed COM work rate and peripheral work rate or power, respectively). The COM work rate was calculated (Fig. 3B) from the three-dimensional dot product of ground reaction force and the COM velocity, the latter estimated by integrating forces assuming periodic strides. Peripheral power (Fig. 3B) to move segments relative to the COM was calculated as the time derivative of translational and rotational energy of segments relative to the COM (Cavagna and Kaneko, 1977; Zelik and Kuo, 2012). While COM work includes soft tissue motions, peripheral power relies on rigid body kinematics, and therefore neglects soft tissue deformations.

We used the difference between Total mechanical power and Joint Power as an indicator of soft-tissue work (Figs. 3C & 4). We expected considerable soft tissue negative work during Collision, with some fraction returned elastically as positive work, but with net negative work over a stride. This also implies that Joint Power might yield net positive work over a stride, as is the case for walking (Kuo et al., 2005; Zelik and Kuo, 2012). To summarize the work over a stride, we computed the positive, negative, and net work for each power quantity, for example by integrating only the positive intervals within a stride to yield positive work per stride. Corresponding average work rates or powers were computed by multiplying work per stride by stride frequency.

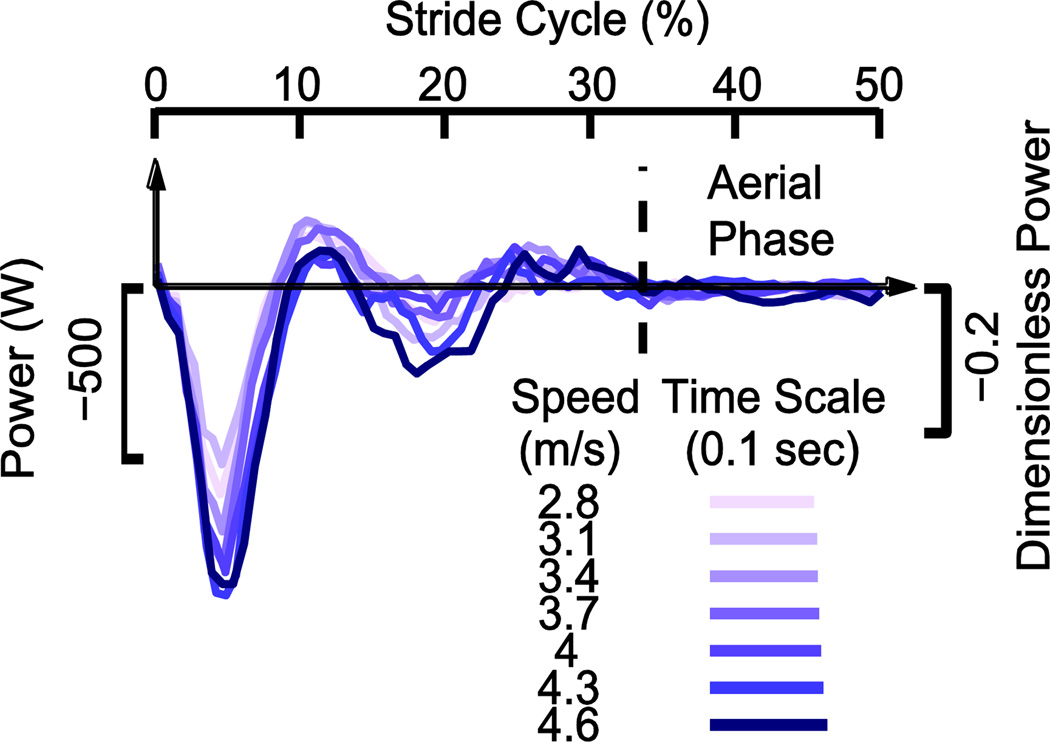
Figure 4.

Soft-tissue power over a step (half a stride) for a representative subject. Soft tissue performs net negative work during a step, a majority of which occurs as the foot impacts the ground during the stance phase. The profile resembles a spring-mass-damper system, with a damped elastic rebound (about 10 – 15% of stride).

Analyses were normalized as follows. Joint moments, angular velocities, and powers were averaged across multiple strides as a function of stride time (0 – 100%) for each subject and condition. To account for differences in subject size, we used body mass M, leg length L, and gravitational acceleration g as base units for non-dimensionalization. Mean power and work normalization constants were Mg^3/2L^1/2 = 2184 W and MgL = 678 J respectively; mean running speed normalization constant was g^1/2L^1/2 = 3.04 m· s⁻¹.

To summarize how work varied with running speed, we used linear regression fits (Cavagna et al., 1977, 1964). Regressions were performed using a subject-specific random effects model with constant slope, so that each subject was given a best-fit offset and a slope between the two regression variables that was constant across all subjects. Analysis of covariance (ANCOVA) was used to test for differences between regression coefficients across different measures of mechanical power, with specific comparisons made with post-hoc t-tests. Significance of all statistical tests was tested based on α = 0.05. To facilitate comparisons, work measures were also reported from regressions at a nominal speed of 3 m· s⁻¹.

Results

The ankle, knee, and hip were generally observed to produce more power with increasing speed (Fig. 2). Each of these joints had distinct phasing, but with a sum (Joint Power) that resembled a simple sinusoid during stance phase (Fig. 3A). Peripheral work rate was generally found to be out of phase with the work performed on the COM (Fig. 3B). Joint Power qualitatively displayed similar trends of negative and positive work compared to Total work rate during stance phase, with the largest discrepancy occurring at the beginning of collision (Fig. 3C).

Soft tissue power exhibited a trajectory over time resembling the damped oscillation of mass-spring-damper system. It began with a large peak of negative power (about −500 W at 3 m· s⁻¹), comparable to the peak for the knee (about −470 W; Fig. 3), followed shortly thereafter by a smaller positive peak of power (Fig. 4). The first peak increased with running speed, whereas the rest of the oscillation amplitude was less clearly dependent on running speed. Both peaks occurred within the Collision phase for the COM, so that the soft tissue oscillation was about twice the frequency of the COM’s oscillation.

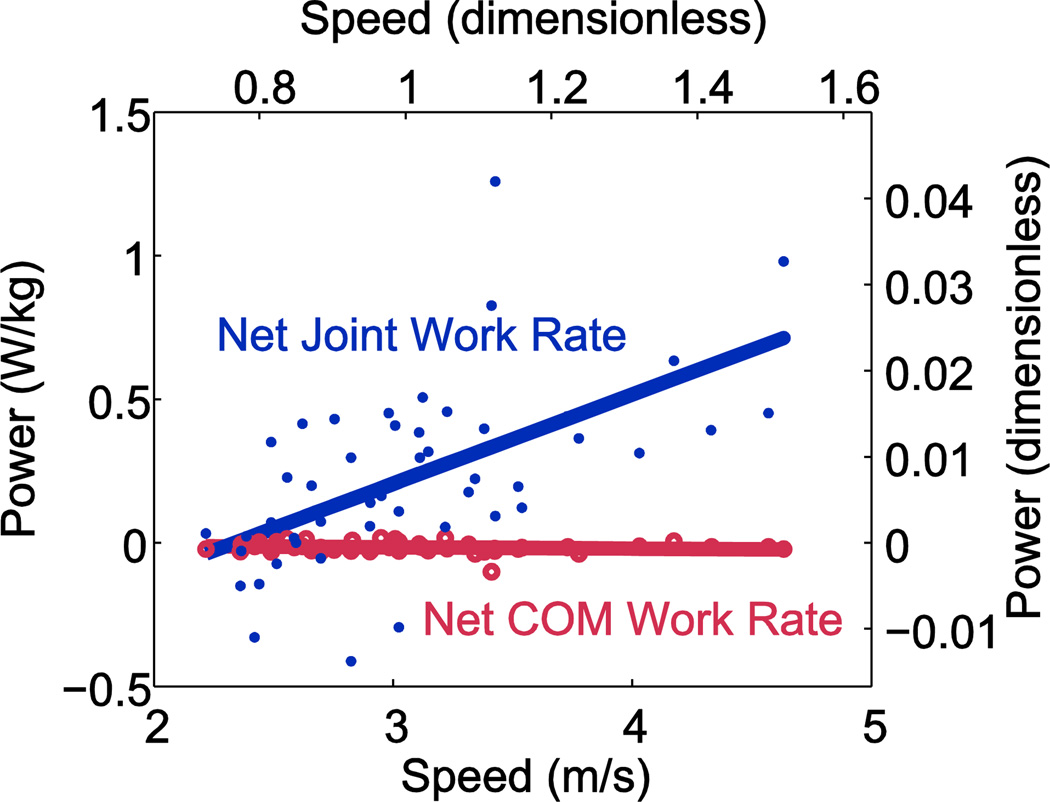
There was an increasing discrepancy between positive and negative joint work with speed. The net summed Joint Work rate was positive and approximately linear with running speed (Fig. 5). In contrast, net Total work rate was close to zero at all running speeds, as expected.

Figure 5.

Average net work rates for center of mass (COM) work and Joint Work across running speeds. Average work rate, defined as net work per stride multiplied by stride frequency. Net COM work rate is close to zero at all running speeds, as expected during steady gait, while Joint Work rate is net positive at most speeds. Data shown were linearly fit with running speed (N=8).

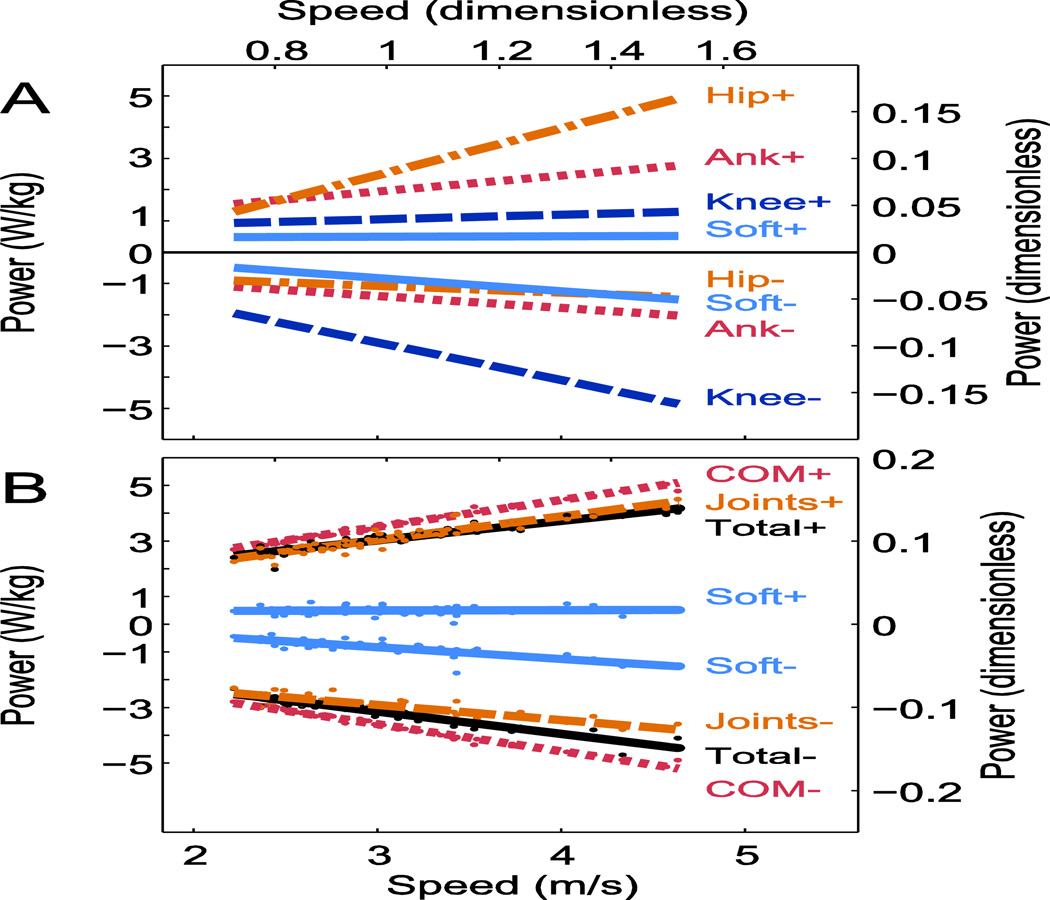
Much of the joint work discrepancy was explained by soft tissue work, which was net negative. Net soft tissue power was quite small at low speeds, but became more negative in proportion to speed, accounting for over 20% of the total negative work of the body at 5 m· s⁻¹ (Fig. 6; see Table 1 for details). The net power was composed of negative power by soft tissues (about −58 W at 3 m· s⁻¹; see Table 1), also changing approximately linearly with speed (-28.5 W per 1 m· s⁻¹), as well as a smaller amount of positive work (at about 40 W rate) not significantly changing with speed (Table 1). The negative power from soft tissues was on the same order of magnitude as the negative work of the joints (Fig. 6A; Table 1), particularly the hip (about −78 W at 3 m· s⁻¹ speed).

Figure 6.

Trends in average positive and negative power vs. running speed (N=8). (A.) Average positive and negative work rates for ankle, knee, hip, and soft-tissue, the latter performing work comparable to the leg joints. (B.) Positive and negative work rates for four measures: center of mass (COM) work, Joint Power, Total work (sum of COM and Peripheral work), and Soft Tissue Work (Total minus Joint Power).

Table 1.

Quantitative results for stride parameters and powers, from linear regressions against running speed. Slope and offset refer to regression coefficients (±95% confidence interval, c.i.), reported with , R², significance (S) denoted by asterisk with criterion P < 0.05. Dimensionless (d’less) quantities are computed using body mass, leg length, and gravitational acceleration as base units.

Measure	Normal (SI)	Normal (d'less)	Slope ± c.i.	Offset ± s.d.	R2	S	P
Speed	3.07 ± 0.59 m • S−1	1.01 ± 0.59	NA	NA	NA	NA	NA
Step Frequency	2.81 ± 0.17 s−1	0.87 ± 0.053	0.15 ± 0.02	0.72 ± 0.045	0.85	*	8.90E-19
Step Length	1.09 ± 0.174 m	1.1 ± 0.18	0.92 ± 0.036	0.22 ± 0.056	0.98	*	6.20E-39
Stance Time	0.284 ± 0.04 s	0.91 ± 0.13	−0.42 ± 0.042	1.3 ± 0.07	0.91	*	1.00E-22
Aerial Time	0.0727 ± 0.0319 s	0.23 ± 0.1	0.22 ± 0.043	0.00087 ± 0.08	0.73	*	2.60E-13
Pos Total Power	234 ± 47.2 W	0.1 ± 0.021	0.071 ± 0.011	0.033 ± 0.0096	0.8	*	7.80E-16
Pos Joint Power	235 ± 55.4 W	0.11 ± 0.025	0.087 ± 0.014	0.018 ± 0.013	0.79	*	2.50E-15
Pos COM Power	271 ± 49.4 W	0.12 ± 0.022	0.099 ± 0.0052	0.022 ± 0.0074	0.97	*	1.20E-33
Pos Soft Power	40.3 ± 23.5 W	0.018 ± 0.011	0.0011 ± 0.011	0.017 ± 0.0097	0		0.85
Pos Ankle Power	150 ± 34.5 W	0.067 ± 0.015	0.052 ± 0.017	0.015 ± 0.014	0.47	*	3.70E-07
Pos Knee Power	83.6 ± 36.5 W	0.037 ± 0.016	0.015 ± 0.012	0.022 ± 0.015	0.13	*	0.019
Pos Hip Power	197 ± 95.4 W	0.088 ± 0.043	0.15 ± 0.017	−0.066 ± 0.021	0.89	*	5.60E-21
Neg Total Power	−236 ± 53 W	−0.11 ± 0.024	−0.082 ± 0.011	−0.023 ± 0.014	0.84	*	3.90E-18
Neg Joint Power	−219 ± 49.2 W	−0.098 ± 0.022	−0.055 ± 0.012	−0.041 ± 0.015	0.66	*	2.80E-11
Neg COM Power	−271 ± 49.4 W	−0.12 ± 0.022	−0.099 ± 0.0054	−0.021 ± 0.0072	0.97	*	3.80E-33
Neg Soft Power	−59.2 ± 27 W	−0.027 ± 0.012	−0.043 ± 0.012	0.016 ± 0.011	0.57	*	6.10E-09
Neg Ankle Power	−104 ± 29.3 W	−0.047 ± 0.013	−0.039 ± 0.0077	−0.0072 ± 0.011	0.72	*	7.90E-13
Neg Knee Power	−218 ± 64.3 W	−0.098 ± 0.029	−0.12 ± 0.012	0.025 ± 0.019	0.92	*	6.00E-24
Neg Hip Power	−81.1 ± 46.7 W	−0.036 ± 0.021	−0.022 ± 0.0082	−0.013 ± 0.019	0.41	*	3.20E-06
Net COM Power	−0.461 ± 1.65 W	−0.00021 ± 0.00074	−0.00046 ± 0.0014	0.00019 ± 0.00048	0.01		5.10E-01
Net Joint Power	16.9 ± 43.4 W	0.0076 ± 0.019	0.032 ± 0.018	−0.024 ± 0.018	0.23	*	0.00099
Net Soft Power	−18.9 ± 45.5 W	−0.0085 ± 0.02	−0.042 ± 0.02	0.033 ± 0.02	0.31	*	0.00011

The magnitudes of negative Total work rate and negative Joint Power increased roughly linearly with running speed (Fig. 6B). There was a significant difference between the measures in both the slope and the offset (ANCOVA, P=1E-5 and P=4E-12, respectively), with total negative work rate larger in magnitude than Summed Joint negative work (−231 W and −214 W, respectively, at 3 m· s⁻¹; paired t-tests, P<0.001). There was a significant difference (ANCOVA P=2E-5) between the slopes for positive Total work rate and positive Joint power, but an insignificant difference in offsets (ANCOVA P=0.65). Total positive work rate was not significantly different from Joint Power (228 W vs. 229 W, respectively, at 3 m· s⁻¹; paired t-tests, p=0.58).

Soft tissue work was most prominent during the stance phase. At nominal 3 m· s⁻¹, soft tissues accounted for −18.8 J of negative work and 12.6 J of positive work during stance, and practically no work during the aerial phase. Negative soft-tissue work during stance phase accounted for about 27% of negative Total Work during stance phase (about −69.0 J), and 24 % of negative Total Work during the entire step (about −77.6 J).

Discussion

We tested if soft tissues contribute significant mechanical work during locomotion and how its magnitude changes with running speeds. Our results show that soft tissues performed significant negative work and positive work during stance phase, with more negative work at faster running speed. We interpret these findings to suggest that soft tissues may behave in aggregate in a damped elastic manner. While the negative work may be helpful for cushioning, the net work has implications for the energetics of running. Moreover, the substantial amount of soft tissue work means that traditional inverse dynamics methods may underestimate the work performed by the body during running, particularly at higher speeds.

One of the simplest indicators of soft tissue work is the discrepancy in overall joint work as measured by inverse dynamics. Net Joint Work Rate was positive at about 7% of the negative Total Work Rate magnitude at 3 m· s⁻¹, and nearly 18% at 5 m· s⁻¹. This discrepancy suggests that joint work fails to capture a portion of the body’s negative work that increases with running speed. An additional indicator is the soft tissue estimate, with a net rate of about −18 W at 3 m· s⁻¹ speed. Similar types of discrepancies have previously revealed differences, with rigid-body inverse dynamics failing to explain more of the work required to run downhill rather than uphill (DeVita et al., 2008), to land from a jump compared to taking off (Zelik and Kuo, 2012), or to walk at higher speeds (Zelik and Kuo, 2010) or with obesity (Fu et al., 2014). Our present finding for level running is consistent with the expectation that greater impacts cause more soft-tissue dissipation.

The main effect of soft tissues during running was to perform negative work shortly after ground contact, at about 5% of a stride (Fig. 3). Its negative power peak was somewhat in advance of the negative work of the joints and COM. This suggests distal contributions, because upper body deformations would be expected to be in phase with the slower oscillation of the COM. In particular, the plantar fascia, heel pads, and tendons in the leg may dominate the negative power peak. The foot and leg appear well-suited to absorb ground impact peaks (Ker et al., 1988), whereas proximal tissues experience smaller impacts (Pain and Challis, 2006; Riemer et al., 2008). For running at 4.8 m· s⁻¹, Schmitt and Günther (2011), estimated 30–60 J dissipated in the thigh and shank, somewhat exceeding our estimates, perhaps because individual soft tissues can potentially oscillate out of phase with each other, and we examine only aggregate effects. Both localized and aggregate measures may help explain soft tissue work and its effect on locomotion.

Soft tissue deformations likely also occur elsewhere in the body. In fact, all tissues are technically deformable, although the dissipation should be dominated by the softest tissues in series with the ground. We previously speculated that the intervertebral discs, articular cartilage, and viscera contribute most substantially in walking (Zelik and Kuo, 2010). Here, the earlier timing of soft tissue work relative to COM, suggests that viscera and proximal tissues might perform less mechanical work than an equivalent amount of soft tissue in the leg. In fact, soft tissue appeared to rebound and perform positive work at about the same time that the COM (and therefore viscera and intervertebral discs) was approaching peak negative work. This is consistent with a damped elastic rebound with faster natural oscillation frequency than the overall body. We expect that the point and path of foot-ground contact may influence characteristics of the soft-tissue power such as frequency and magnitude, but have insufficient data to draw conclusions here.

Our findings may have implications for the energetics of running. Humans expend about 900 W of net metabolic power to run at 3 m· s⁻¹, and about 1100 W at 5 m· s⁻¹ (Margaria et al., 1963). Because steady running requires an average of zero net work, the net negative work of soft tissues must be offset by an equal amount of active positive work by muscle. Assuming an efficiency of 25% (Margaria et al., 1963), the work to offset soft tissues would account for about 72 W of metabolic power at 3 m· s⁻¹ and 319 W at 5 m· s⁻¹, or about 8% and 29%, respectively, of the net metabolic power at those speeds. Thus, soft tissue dissipation may come at a substantial metabolic cost. But it could also be beneficial for running economy, because without the cushioning of soft tissues, humans might actively cushion themselves more with additional work from muscles (Skinner et al., 2015), with an attendant metabolic cost (Tung et al., 2014).

One limitation of our soft tissue measure is that it actually captures work not performed at the rigid bodies normally measured during locomotion. Some of our “soft tissues” could therefore actually be considered joints in other methodologies. For example, the longitudinal arch of the foot performs negative and positive work, mediated in part by active muscle (Kelly et al., 2015). The metatarsophalangeal (MTP) joint also performs significant work late in stance during running (over −20 J at 4 m· s⁻¹; Stefanyshyn and Nigg, 1997). We did not record from such joints, whose work would either appear as soft tissue work or be attributed to other measured joints. We also did not measure deformation of bone, which has higher natural frequencies (Reilly and Burstein, 1975) than we could observe and which would be expected to be negligible compared to softer tissues. With higher sampling rates, our methods could theoretically capture aggregate effects of bone deformation. Or with enough motion capture markers, even very small or very rigid deformations could theoretically be measured directly, and treated as virtual joints between smaller and more numerous rigid bodies (Schmitt and Günther, 2011). Many structures in the body could perform significant work not measured by conventional methods of inverse dynamics, but perhaps capturable by more and faster sampling.

Our study was confined to slow to medium running speeds. In that range, soft tissues dissipated an amount of energy proportional to the running speed and returned a constant amount of energy. These linear relationships do not necessarily hold for higher running speeds and sprinting, for which the soft tissue contributions remain unknown. Another limitation was that our estimates use rigid-body models for the work performed peripheral to the COM, therefore not capturing some deformations. Peripheral soft tissue work refers to deformations about the COM that are anti-phase with each other. We expect it to be small, but such motion could therefore potentially add to our own central estimates, although we did not measure it. Finally, by assuming that the net work of steady state running is equal to zero on level ground, we have implicitly assumed that the work of overcoming friction in the air and ground is negligible, an assumption argued for by others (Margaria, 1968; Willems et. Al., 1995).

When soft tissues are of interest and expected to play a significant role, standard inverse dynamics may not accurately reflect the energetics of the body. During running, ignoring the energetics of soft tissue is nearly tantamount to ignoring the knee, which had comparable power trajectories (Fig. 3). An understanding of such limitation may be crucial when relying on experimental data to give insight into how humans move or to guide design of locomotive technology.

Soft tissues contribute significantly to the dynamics of running in terms of energy dissipation, storage, and return. Their deformations can help cushion the body, performing some of the negative work required of each stance phase and potentially offloading active dissipation by muscle. It can also return some positive work, but most of the negative work must be offset by active positive work by muscle. Besides being important for understanding normal human gait, analysis of soft tissue dynamics may be important for the production of prostheses and robots, which are often built using mostly rigid components. Most biological tissues, and many non-biological materials, deform under heavy loads, with potential consequences for the dynamics of running.