Abstract
Forces generated by the growth cone are vital for the proper development of the axon and thus brain function. Although recent experiments show that forces are generated along the axon, it is unknown whether the axon plays a direct role in controlling growth cone advance. Here, we use analytic and finite element modeling of microtubule dynamics and the activity of the molecular motors myosin and dynein to investigate mechanical force balance along the length of the axon and its effects on axonal outgrowth. Our modeling indicates that the paradoxical effects of stabilizing microtubules and the consequences of microtubule disassembly on axonal outgrowth can be explained by changes in the passive and active mechanical properties of axons. Our findings suggest that a full understanding of growth cone motility requires a consideration of the mechanical contributions of the axon. Our study not only has potential applications during neurodevelopment but might also help identify strategies to manipulate and promote axonal regrowth to treat neurodegeneration.
Introduction
The human brain is densely packed with billions of axons that provide pathways for neuronal signaling. Axons are long, slender protrusions that emerge from neuronal cell bodies and are interconnected through synaptic connections. A proper development of the axon is of vital importance for brain function (1). Mechanical forces play an important role in axonal outgrowth and development (2, 3). Most research on the role of mechanics has focused on the pulling force generated at the growth cone through retrograde actin flow (4). Recent experiments and theory, however, reveal that forces are generated along the axon (5, 6, 7, 8, 9). Here, we build on that work to better understand how forces control axonal outgrowth.
The axon is developed as an intricate structure of a wide range of components. The main structure is formed by an array of longitudinally aligned microtubules that are interconnected by proteins, such as dynein (10), kinesin (11), and tau (12, 13, 14). During the initial stages of neurite formation, microtubules are short with a length of around 1 μm. As axons grow longer, the average microtubule length increases to greater than 100 μm long in cultured neurons (15). In parallel, actin rings start to assemble around the microtubules after 2 days in culture and mature over the course of about 2 weeks (16, 17).
Microtubules are highly dynamic structures that polymerize and depolymerize continuously. Experimental evidence shows that microtubule polymerization is necessary for axonal elongation (1, 18). As an underlying mechanism, it has been hypothesized that microtubule assembly generates a pushing force at the growth cone that promotes axonal elongation (19). Somewhat paradoxically, however, high doses of taxol, which promote microtubule assembly and stabilize microtubule dynamics, have been shown to slow down axonal elongation (20, 21). In contrast, very low concentrations of taxol and epothilone (EPO) have been reported to increase outgrowth (22, 23, 24, 25, 26, 27).
In turn, microtubule disassembly, or loss in microtubule mass, leads to a decrease in axonal outgrowth and to an increase in neuronal tension within minutes (28, 29). The rapid onset of effect and increase in tension suggests the resulting inhibition of growth is an acute effect as opposed to the long-term reduction of nutrient delivery due to a reduction in transport. Although the increase in tension is predominantly attributed to a decrease in pushing forces associated with microtubule assembly (30, 31), there could be other effects. For example, it is reasonable that microtubule disassembly reduces the number of functional dynein motors and, thereby, it reduces the extensile force generation by dynein (32). Alternatively, microtubule depolymerization may lead to an increase in actin tension through activation of myosin downstream of the release of guanine nucleotide exchange factor H1 (GEF-H1), also known as Lbc’s first cousin (Lfc) or Rho guanine nucleotide exchange factor 2 (ARHGEF2). Indeed, the release of GEF-H1 is known to promote myosin activity (33) through the pathway GEF-H1 Rho Rho kinase myosin light chain myosin (34, 35) and has recently been shown to regulate axonal elongation (36). Although the importance of microtubules in axonal elongation is undoubted, why outgrowth is sensitive to changes in microtubule assembly and disassembly remains puzzling.
Axons are complex materials, and interest in analytic and computational modeling has grown dramatically in the past few years to understand their elongation during development (5, 6, 9, 37, 38) and failure after injury (12, 14, 39, 40). Analytic approaches have the strength of abstractly modeling the complex process of growth over long timescales of hours to days (6, 9, 38) but may not be well suited for understanding the internal geometry of axons and the roles of specific proteins. Finite element approaches, which conventionally treat neurons as elastic solids, are excellent for the study of traumatic injury over short timescales of <10 s (12, 14). They offer the advantage that elements in the model directly represent the configuration of individual proteins such as tau and microtubules. Nonetheless, the treatment of axons as solids does not capture the fluid-like permanent deformation that occurs during growth and retraction (7, 9, 41, 42). Our group has recently extended the standard finite element method to allow elastic finite elements to make and break connections (5). This framework enables us to model dynamic protein interactions in which noncovalent bonds, such as those between tau and microtubule, form and break continuously (43). Thereby, we are able to simulate the developmental process of neurite outgrowth and the failure of axons to high forces in a single model (39, 40).
Here, we use our framework to investigate the mechanical force balance along the length of the axon and its effects on axonal outgrowth. With this in mind, we extend our previous model of the microtubule cytoskeleton (5) to include the actin cortex and develop an analytical model for the mechanical response of the axon. We show that by consideration of the axon as an active partner with the growth cone, plausible answers to standing questions about axonal elongation emerge. Our results demonstrate that high doses of taxol may slow down axonal elongation by increasing axon viscosity. Low doses of taxol destabilize microtubules, which lowers axon viscosity and, thereby, increases axonal outgrowth. Finally, microtubule disassembly may slow down elongation by a reducing the number of dynein and activating myosin in the cortex.
Methods
Computational model
In our computational model, we consider the intricate structure of the axon as a composition of microtubules, actin, and the growth cone that are all interconnected by cross-linking proteins. We assign dynamic behavior to each of these components based on biological observations. The dynamic behavior of a particular protein or microtubule is referred to as its mechanism. We use the finite element method, which we extended to facilitate modeling of molecular mechanisms, to solve the computational model of the axon (5, 39, 40).
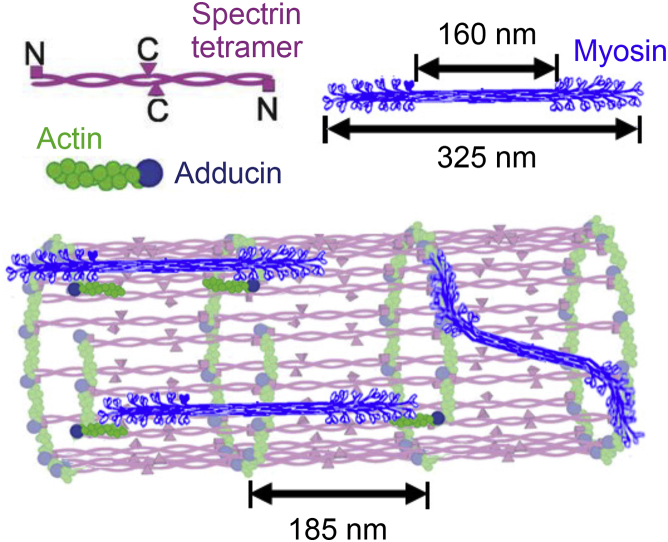
The actin cortex is the first major component of the axon structure. Its core consists of an assembly of spectrin, actin, and adducin, with adducin-capping short actin filaments and the calponin homology domain of spectrin binding to actin rings (16, 17, 44). Although cartoons of actin rings typically show short filaments that run perpendicular to the longitudinal axis, current experimental data simply reveal punctate clusters of actin staining and do not address the precise filament orientation. Bipolar myosin filaments may generate forces that cause actin to run in the longitudinal direction (see Fig. 1). Given the spacing of actin rings and myosin distribution (∼185 nm) and the dimensions of myosin filaments (a head-free core of ∼160 nm and a total length of ∼325 nm), a single filament may span one or two rings and may run at an angle (45, 46).
Figure 1.
A model of spectrin/actin cortex illustrating three ways myosin may generate longitudinal forces. Although short actin filaments are typically represented as oriented perpendicular to the longitudinal axis, myosin filaments may pull them so they run parallel. Given the geometries of myosin filaments and actin rings, a single bipolar filament may span one or two rings. Additionally, myosin filaments may be orientated at an angle, generating circumferential and longitudinal forces. The figure was adapted from (17, 86) with permissions. To view this figure in color, go online.
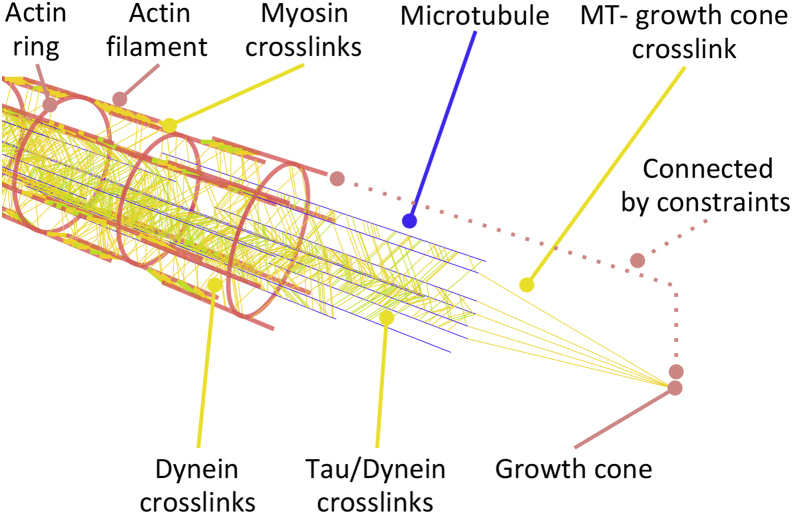
Here, we develop a finite element model of the actin cytoskeleton focused on capturing the active fluid behavior of axons. In the early stages of this work, we explored the use of cross-linked actin meshworks in which filaments could rotate in all three dimensions, but we found them to be computationally expensive. As a compromise, we settled on the idea of an actin ring that surrounds the microtubule cytoskeleton with longitudinal filaments connected with myosin motors (see Fig. 2). The actin rings in our model are rigid but serve as a place holder for a dynamic meshwork of actin filaments. We assume six longitudinal filaments per cross section arranged in a circular array that defines a cylindrical shell around the axon. Experimental evidence shows that myosin generates contractile forces along the axon (8), which we implement by assigning the myosin mechanism to each myosin protein cross-link (see Dynein and Myosin). We randomly insert these myosin proteins in our model based on a protein density input parameter and such that myosin is evenly distributed along the axon.
Figure 2.
A sketch of our computational model of the axon. We model the axon as a system of longitudinally aligned microtubules that are cross-linked by tau and dynein proteins. The microtubules are surrounded by an actin cortex that is cross-linked by myosin proteins. Dynein protein cross-links connect actin filaments to microtubules. The growth cone is simplified by a single point that is firmly connected to the actin cortex using displacement constraints. The most distal set of microtubules can push the growth cone forward through cross-links that only carry compression. To view this figure in color, go online.
Without any other structures, such as the microtubules or the growth cone, the actin cortex would collapse into a point because of the contractile forces that are generated by myosin cross-links. This collapse is in part counteracted by the second major component of the axon structure: the growth cone. Indeed, retrograde actin flow in the growth cone provides a pulling force on the actin cortex (4, 47). We represent the growth cone as a single point that is firmly attached to the most distal set of actin filaments (see Fig. 2). We apply an external force of 1 nN to the growth cone node to represent its pulling force on the actin.
The actin cortex surrounds the third major component of the axon structure: the microtubule system (5, 48, 49). The microtubule system consists of longitudinally aligned microtubules along the length of the axon that can polymerize and depolymerize at their plus ends. Experiments show that microtubule assembly may generate pushing forces when the microtubule is stalled (30, 50). We do not include these forces in the axon because analysis of Eb1 comets in axons suggests stalling events are rare and transient (51). Within an axon cross section, the microtubules are arranged in a triangular grid of 19 potential microtubule sites. On average, only half of the potential sites are occupied by a microtubule in each cross section. Neighboring microtubules are interconnected by cross-link proteins, either tau or dynein. These proteins are randomly added to the model based on a protein density input parameter. We model the dynamic behavior, or mechanism, of tau protein as a repeated detachment and reattachment of the protein (5, 39, 40). Dynein protein generates an active force that is associated with an extensile pushing force to the axon (see Dynein and Myosin). Note that we use the term protein cross-link to allude to the mechanical role of the protein (52), even though the physiological interaction is generally more complex. For example, tau protein forms a noncovalent bond with microtubules and is believed to interact with tau protein from neighboring microtubules through an electrostatic zipper (53).
In addition to other microtubules, a microtubule may also interact with the actin cortex or the growth cone depending on its location within the axon. Along the axon, microtubules that are close to actin filaments interact with these actin filaments through dynein protein cross-links. These proteins push the microtubules forward and pull the actin filaments backward (54, 55). Microtubules can also interact with the growth cone by pushing it forward (31). This interplay between microtubules and the growth cone is implemented by a set of finite elements that connect each plus end of the distal microtubules to the growth cone node. Each of these elements will be attached if the distal end of the microtubule is within a threshold distance from the growth cone. The elements detach immediately upon tensile loading. In the attached state, the microtubules are firmly connected to the growth cone and can, thereby, exert pushing forces to the growth cone. Once detached, the microtubules do not directly interact with the growth cone; instead, they interact only directly through the cross-links with actin along the axon. At the proximal end of the axon, the first node of each microtubule and actin filament is clamped, which represents the boundary condition imposed by the cell body. Further, all nodes in the model are constrained to have no movement in the lateral direction. We provide an overview of all parameters that we use in our axon model in Table 1.
Table 1.
Parameters of the Axon Model
| Parameter | Value | Unit | Reference |
|---|---|---|---|
| Axon length | 40 | μm | (78) |
| Axon diameter | 540 | nm | (49) |
| Microtubules per cross section | 9.5 | – | (48) |
| Microtubule length | 10 | μm | (15, 79) |
| Microtubule stiffness | 1200 | MPa | (80) |
| Microtubule area | 400 | nm2 | (81) |
| (De-)polymerization time | 50 | s | (82) |
| Dynein/tau angle | 30 | deg | (49) |
| Myosin angle | 75 | deg | (49) |
| Dynein/tau stiffness | 70 | MPa | (65) |
| Myosin stiffness | 40 | MPa | (65) |
| Cross-link area | 1 | nm2 | – |
| Max. cross-link stretch | 1.5 | – | – |
| External load | 1000 | pN | (69, 83, 84) |
| Cytosol viscosity | 5 | mPa⋅s | (85) |
deg, degree; Max, maximal.
We emphasize that here we choose to focus on actin and myosin in the cortex because they are critical in the process of axonal elongation and guidance (56). In addition, from a biophysical standpoint, actin and myosin generate the majority of contractile forces in neurons. In particular, disruption of actin and myosin reduces the rest tension in neurons by 90 and 70%, respectively (57, 58). Although we acknowledge that spectrin and membrane tension are important for a full model of the axon, we do not implement these here for the following reasons. First, the in-plane membrane tension in chick sensory neurons has been measured as 3 pN/μm (59). As the average diameter and circumference of chick sensory neurons is 1.5 and 4.7 μm, respectively, the force contribution due to membrane tension is 10 pN. More recently, when spectrin in Caenorhabditis elegans neurons was disrupted, the membrane tension decreased by 10 pN/μm, which amounts to a total reduction of ∼20 pN in membrane tension (60). Both contributions are small in comparison to the total neuronal tension of ∼1–2 nN (7). Second, although spectrin is essential to maintain the integrity of axons when they experience large rapid stresses and strains, it does not play a central role in the process of wiring the nervous system (61). In particular, animals null for α-spectrin or expressing mutated versions of α-spectrin, which inhibit tetramer formation, have very mild defects in the organization of the nervous system (62, 63).
The strength of our approach is that it allows us to model the interconnected nature of the cortical actin and microtubule cytoskeleton in a computationally inexpensive manner. Because this is a single structure that only moves in the longitudinal axon direction, simulations of axonal elongation representing 5 min of elongation can be run in ∼8 h on 12 CPUs, which is ∼10 times faster than when rotations are included. The advantage of this approach is that mechanical properties of the actin cortex and microtubules in the computational model can be investigated over a reasonable time frame. The obvious compromise is that the detailed structure of actin and the proteins which cross-link it are simplified. In these terms, the model can be viewed as a stepping stone to molecular dynamic simulations, which fully describe the length, orientation, and cross-linking of axonal actin.
Analytical model
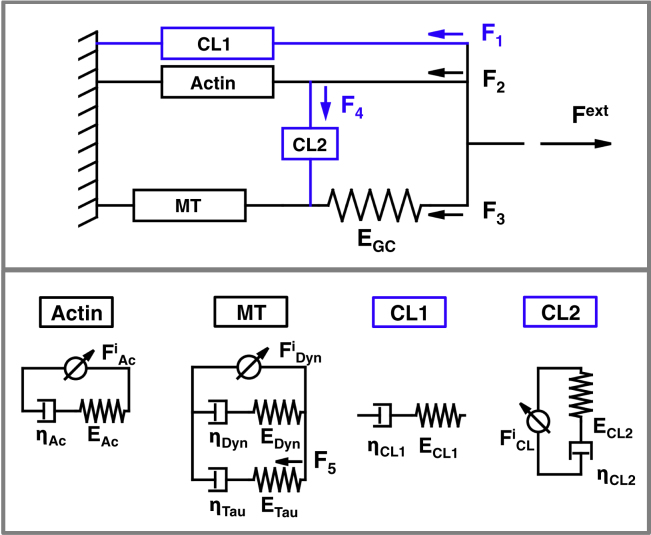
Here, we present an analytical model that captures the full behavior of the computational model in a homogenized sense with a small collection of spring and dashpot components (see Fig. 3; middle). Similar to our computational model, the simple analytical model contains the actin cortex in parallel to the microtubule system (see Fig. 3; top). In previous work, we demonstrated that the dynamics of detachment and reattachment of proteins within the microtubule system can be represented by a simple viscoelastic Maxwell component of a spring and dashpot connected in series (5). The spring represents the collective elastic properties of the proteins, and the dashpot captures the dynamic detachment and reattachment properties that lead to viscous effects. We therefore propose that the actin cortex and microtubule system are Maxwell components in parallel to a motor component that represents the internal force generated by the proteins (see Fig. 3; bottom left).
Figure 3.
A sketch of our analytical model of the axon. The simplest analytical model consists of an actin and microtubule system that act in parallel. The actin and microtubules systems can be represented by one or two viscoelastic Maxwell components in parallel to an internally generated force (bottom) (5). Each Maxwell component represents the elastic and viscous response of one protein, either dynein, tau, or myosin. Our full analytical model (top) accounts for the cross-links between microtubules and actin through additional viscoelastic Maxwell components. The interaction of between the microtubules and the growth cone is included by a growth cone spring with stiffness that alternates between and . The parameters represent the flow of forces in the analytical model and , , and are material parameters that represent stiffness, viscosity, and internal force generation, respectively. To view this figure in color, go online.
The actin cortex and microtubule system in our analytical model are not sufficient to fully represent the overall response of our computational model. In addition, we need to capture the interaction between the microtubules and the growth cone in the analytical model and, furthermore, we need to include the effects of dynein protein cross-links between microtubules and actin. The interaction between the growth cone and the microtubules system is represented by a growth cone spring between the microtubule system and the axon tip (see Fig. 3). The stiffness of the growth cone spring is an output parameter of our model, but it is either zero or infinite. Zero stiffness versus infinite stiffness indicates that the microtubules are either disconnected or connected to the growth cone:
| (1) |
The dynein protein cross-links between microtubules and actin are represented by two boxes, CL1 and CL2. The necessity for two boxes arises from the two distinct mechanical roles these cross-links play. The CL2 box acts on the relative displacement between actin and microtubules, . It only influences the behavior of the model when the motion differs. The CL1 box in contrast represents the additional stiffness and viscosity that is provided by the dynein proteins, even when . The CL1 box is needed because in the computational model (and in real axons) stiffness and viscosity are measured by applying a force to the end of the axon and measuring total strain or strain rate. Nonetheless, along the axon, there is variation in number of cross-links, which leads to regions that are weak. Because springs and dashpots in series sum by the rule , will drop as the variation in increases. An important effect of adding dynein cross-links is that it couples the actin and microtubules. Because this decreases the local variation along the axon, it increases the measured viscosity and stiffness for the system as a whole.
To obtain the governing equations for the analytical model, we need the relation between force and displacement for an individual Maxwell component:
| (2) |
Using classical force equilibrium, we identify the forces in the actin cortex, , the microtubule system, , the growth cone spring, , and the cross-links between microtubules and actin, and , from Fig. 3 as follows:
| (3) |
By combining Eqs. 2 and 3 and splitting into a dynein and tau contribution using , we obtain the following:
| (4) |
With the additional compatibility equation, , and force equilibrium , the system of Eqs. 1 and 4 can be solved for the unknowns , , , , , , , , and .
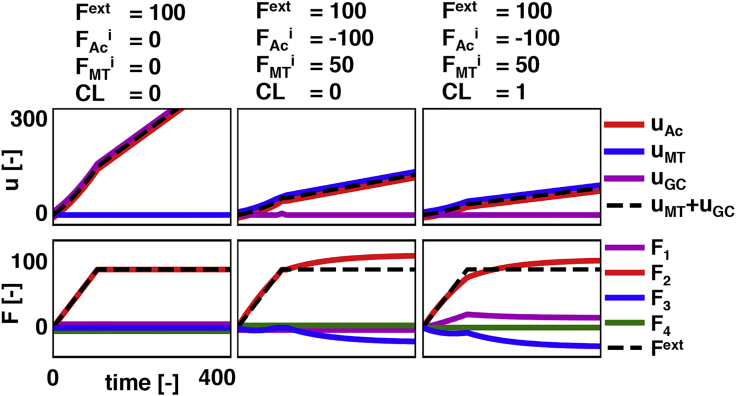
Fig. 4 shows three different model problems that visualize the different components of the analytical model. In the first model problem, we only apply an external force to the system and do not include protein cross-links between the actin and microtubules or internal force generation. As expected, the external force on the growth cone pulls the actin forward but leaves the microtubules behind. In the second example, the actin and microtubule system are generating internal forces. For this analysis, we select the contracting internal force in the actin to exactly balance the applied external force. The extensile internal force by the microtubules, therefore, push the growth cone forward. Fig. 4 (middle) indeed shows that the axon is elongating and both the actin and microtubules system are loaded. After adding cross-links between microtubules and actin (see Fig. 4; right), the axon displacements are similar but slightly reduced because of the additional stiffness and viscosity of the axon. The nonzero force indicates the additional cross-links indeed carry some of the external applied force. Collectively, the analytical model behaves as intuitively expected.
Figure 4.
Forces and displacements in our analytical model for three simple load cases. In all cases, we use , , . In the case of no internal force generation and the absence of microtubule-actin cross-links, the actin cortex stretches because of the applied load, and the microtubule system does not deform (left). When the contractile force in the actin is equal to the external force and the microtubule system generates extensile force, the microtubule system pushes into the growth cone and moves together with the actin system (middle). The addition of cross-links between microtubules and actin reduces the total elongation rate and affects the force distributions in actin and microtubules (right). The reduction in total elongation rate is due to the CL1 box in our analytical model (see Fig. 3) that represents the heterogeneity in the displacements of actin and microtubules along the length of the axon. Note, all gradual changes in the force curves are due to the viscoelastic components in the analytical model. To view this figure in color, go online.
Results
Dynein and Myosin
Experiments show that axonal outgrowth is affected by the competing forces of dynein and myosin proteins (10, 55). Dynein proteins generate extensile forces in the microtubule system (32), whereas myosin protein contract the axon (8). In this section, we investigate the effects of these competing forces in our model of the axon. We first systematically vary the dynein and myosin protein densities in our computational model and probe the effects on axon stretch rate and viscosity. We then calibrate our analytical model to reproduce the homogenized response of the computational simulation.
Computational model problem
To investigate the competing forces between dynein and myosin in our computational model, we create mechanisms to represent the dynamic behavior of dynein and myosin proteins. The power stroke of dynein has been well characterized experimentally (64, 65). Each dynein protein contains a binding domain at one end and a walking domain at the other. The binding domain of the protein is firmly attached to a microtubule, whereas the walking domain moves toward the minus end of the microtubule. The myosin power stroke is conceptually similar to dynein (66). The major differences are that myosin proteins are bipolar, meaning that both ends are walking domains, and myosin walks to the plus end of actin filaments. We implement this molecular walking by a repeating process of attachment, active contraction, and detachment of the protein (5).
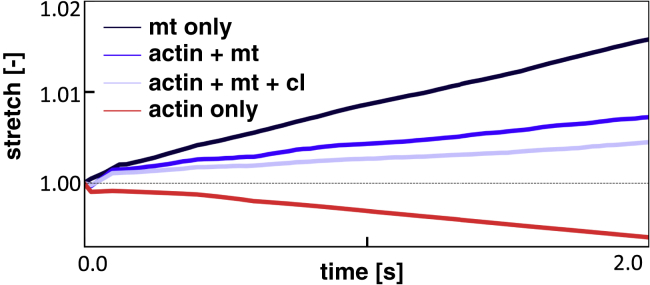
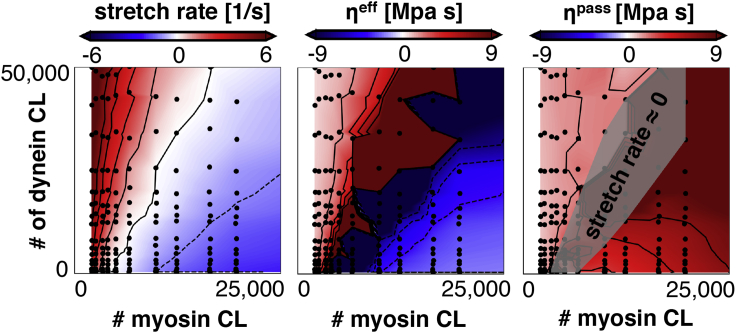
We assign the dynein mechanism to each cross-link in the microtubule system and the myosin mechanism to each cross-link in the actin cortex. To simplify, we do not include tau proteins and microtubule dynamics in this section. We apply an external force of pN to model the growth cone. Fig. 5 shows the output of four characteristic simulations in which we vary the number of myosin and dynein protein cross-links. The competing effect of dynein and myosin is clearly visible as an increased dynein density leads to axon elongation, and an increased myosin density results in axon contraction. For each simulation, we obtain an average stretch rate during the simulation and compute the effective axon viscosity as and the passive viscosity as (5). The effective viscosity can be interpreted as the measured viscosity of the axon, whereas the passive viscosity is calculated when the internal forces are factored out. We systemically vary dynein and myosin densities and record axonal stretch rates and viscosities. Fig. 6 shows contour plots of all three quantities as functions of the number of dynein and myosin proteins. Every black dot in the plots represents the average of 10 simulations with the same input parameters. Note that we use protein density as an input parameter and, therefore, the exact number of dynein or myosin proteins is not directly controlled. Therefore, the black dots in Fig. 6 are not arranged in a perfectly rectangular array. The contour plot of axon stretch rate (see Fig. 6; left) demonstrates the competing effects of dynein and myosin. The highest stretch rates are obtained for a high number of dynein proteins and a low number of myosin proteins. Conversely, axonal contraction is promoted by a low number of dynein and high number of myosin proteins. The effective viscosity of the axon, , changes from positive to negative when the axon switches from elongating to contracting, and it approaches when the stretch rate approaches . These trends are consistent with the effective viscosity measurements in active fluids (5). The passive viscosity (see Fig. 6; right) increases with the total number of myosin and dynein, which is consistent with our previous findings (5). We note that dynein proteins between actin and microtubules push microtubules forward and pull actin back. Because these forces are equal and opposite, they cancel one another and do not affect axon elongation.
Figure 5.
Axon stretch versus time for different configurations of the computational model. Located in the key, “mt only” consists only of microtubules with dynein proteins and, similarly, “actin only” includes only actin filaments with myosin proteins. These two systems are combined in actin + mt. Finally, the two systems are connected by dynein cross-links between actin filaments and microtubules in actin + mt + cl. The applied external load, , is equal for all for simulations. The results demonstrate the competition between extensile dynein forces and contractile myosin forces. The addition of cross-links between microtubules and actin leads to an increase in passive viscosity of the axon that reduces the axon stretch. To view this figure in color, go online.
Figure 6.
Contour plots of stretch rate , effective viscosity , and passive viscosity as a function of the total number of myosin and dynein proteins in our computational model. The competition between dynein and myosin is apparent as the axon stretch rate increases with the number of dynein proteins and decreases with the number of myosin proteins. The effective viscosity, , approaches when the axon stretch rate approaches zero, characteristic for active solids and fluids (5). Note that this phenomenon arises when internal forces balance external forces such that the axon does not extend or contract. This lack of motion results in an effective viscosity that approaches infinity. The passive viscosity, , increases with the total number of dynein and myosin, consistent with previous findings (5). We added a gray patch over the contour for passive viscosity where the stretch rate is approximately zero. In this region, the effective viscosity approaches and, therefore, the computation for passive viscosity will be inaccurate. Each black dot in the contour plots represents one set of input parameters for the computational model. To account for the randomness in our computational model, we computed the average of n = 10 simulations to obtain each computational data point. To view this figure in color, go online.
Analytical model problem
To reproduce the computational results in our analytical model, we assume the stiffness, viscosity, and internal force generation in the microtubule system and actin system all depend linearly on the number of dynein or myosin proteins (5):
| (5) |
In addition, we set parameters that are not included in the computational model for this section to zero: and . We substitute the relations in Eq. 5 into the analytical model in Analytical Model to obtain the governing equations as a function of the coefficients , , , , , and . We then obtain the values for these coefficients such that the analytical model best reproduces the overall response of the discrete axon model simulation. To that end, we perform a numerical optimization to minimize the difference between the analytical prediction and the computational results in Fig. 6.
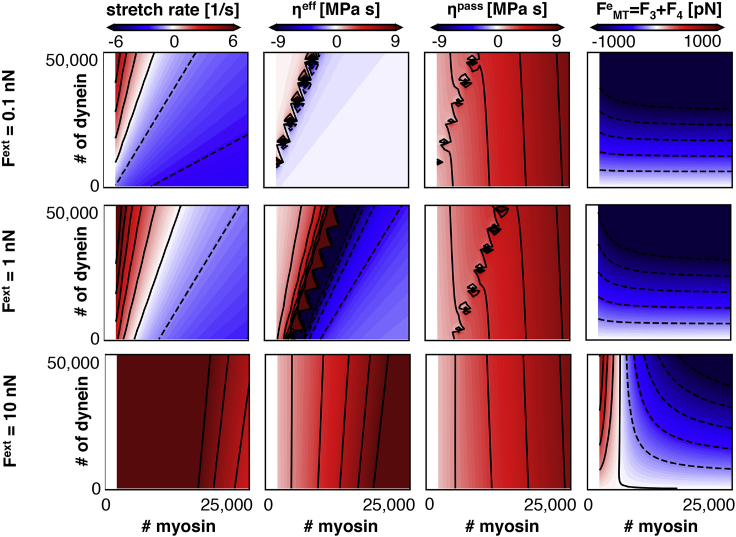
Fig. 7 (middle row) shows the stretch rate and viscosity contours that result from the optimization. First, the contour plots are qualitatively and quantitatively similar to the computational results in Fig. 6, showing that the analytical model in Analytical Model plus the relations in Eq. 5 accurately represent the computational model. The outputs of the analytical model allow us to obtain additional model quantities, such as the forces across the axonal cytoskeleton (see Fig. 7; right). The microtubule system is under compression as the dynein proteins are pushing the microtubules into the growth cone. The compressive force is maximal for high numbers of both myosin and dynein proteins, which is consistent with their respective contractile and extensile power strokes. We have added the top and bottom row to Fig. 7 to demonstrate the effects of . As expected, observed trends are independent of the precise value of , and the passive viscosity is unaffected by changes in .
Figure 7.
Contour plots of stretch rate , effective viscosity , passive viscosity , and force through the microtubule system , as a function of the total number of myosin and dynein proteins and for different values of in our analytical model. The stretch rate and viscosity contour plots show good agreement with the computational results in Fig. 6, which confirms that the analytical model captures the physics of the computational model. The forces through the microtubules system, , become more compressive for high numbers of dynein proteins because of the additional extensile force generation that pushes the growth cone forward. Increasing the number of myosin proteins reduces the stretch rate of the axon because of the contractile forces generated by myosin. To view this figure in color, go online.
Microtubule dynamics and tau cross-linking
Experimental evidence shows that applying high doses of taxol to the axon stabilizes microtubules dynamics and, in parallel, slows down axonal elongation, whereas low doses increase elongation. In this section, we seek to identify potential mechanisms that explain these observations. We probe the effects of microtubule dynamics on axon viscosity and, thereby, on axon outgrowth. In contrast to the previous section, we now assume that all cross-links between microtubules represent tau protein. We also probe the effects of the characteristic time constant for attachment and detachment on axon viscosity. To isolate these effects, we simplify the actin cortex as a viscous damper. Thus, our computational model only consists of microtubules with tau protein cross-links.
Computational model problem
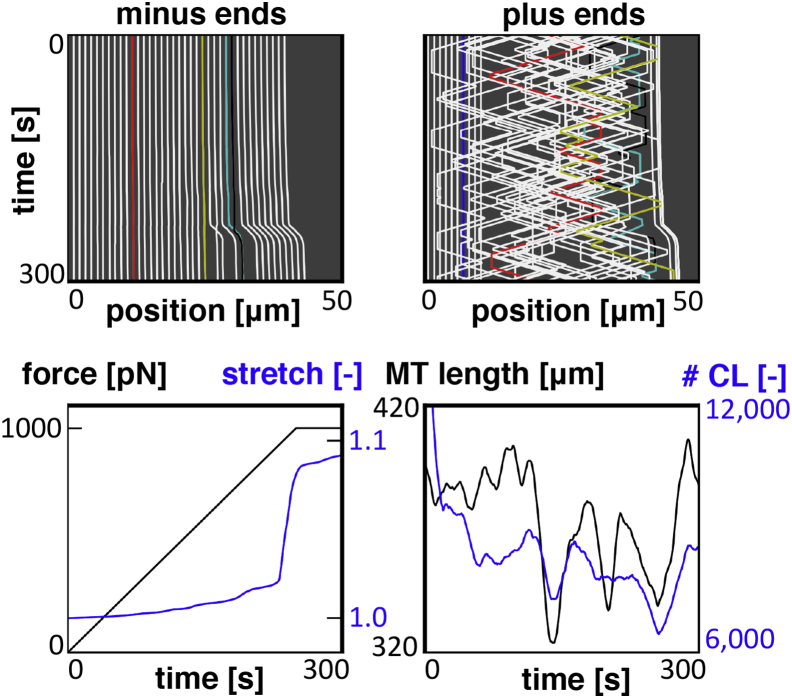
In previous work, we have provided the implementation details of microtubule dynamics in our computational framework (39). Here, we characterize microtubule dynamics solely by the polymerization and depolymerization rates of microtubules, which we abbreviate as the (de-)polymerization rate. We anticipate that increasing the (de-)polymerization rate will reduce axon viscosity as depolymerization of a microtubule leads to an immediate detachment of all protein cross-links on the depolymerizing portion of the microtubule, whereas microtubule polymerization only leads to a delayed attachment of cross-links based on their characteristic attachment rate. The net effect of microtubule dynamics is then a reduction of the total number of attached cross-links that manifests itself in a reduced axonal viscosity (5). Note, we expect this effect even when the total microtubule mass is, on average, preserved throughout the entire simulation (see Fig. 8; bottom right). Fig. 8 shows the output of a characteristic simulation of the axon and illustrates the dynamic behavior of the microtubules using the kymographs of their minus and plus ends. The minus ends move forward during the simulation, but they do not (de-)polymerize, whereas the plus ends (de-)polymerize continuously. Fig. 8 (bottom left) shows the external force and axon stretch versus time. After computing the average stretch rate of the axon during the simulation, these curves translate into the effective axon viscosity, . We do not include sharp jumps in axon stretch to compute the average stretch rate, because these jumps are analogous to breaking of the axon. We repeat the axon simulations for different (de-)polymerization rates and compute the average axon stretch rate and viscosity for each simulation (see Fig. 9).
Figure 8.
Characteristic output of a single simulation with microtubule dynamics. The kymographs track the position of the minus and plus ends of each microtubule throughout the simulation (top). The minus ends do not polymerize and, therefore, they follow the axon deformation. In contrast, the plus ends of the microtubules are highly dynamic through continuous (de-)polymerization. The total microtubule length will therefore vary throughout the simulation (bottom right). The total number of cross-links in the model follows the same trends as the total microtubule length, because the total microtubule length determines the available positions for cross-links to attach. The applied external force and the axon stretch are shown versus time (bottom left). Sudden increases in axon stretch are caused by the development of weak spots along the axon where many microtubules have depolymerized. To view this figure in color, go online.
Figure 9.
Axon stretch versus time for n = 150 simulation with characteristic time constant of the cross-links, s, and varying microtubule (de-)polymerization rates. The colored regions of each curve represent the regions that are used to compute average stretch rate and viscosity for that particular simulation. We only use time after s to make sure the simulations have reached a steady state. In addition, we do not include sharp jumps in the axon stretch that are due to weak spots in the axon as a result of excessive microtubule depolymerization in a cross section of the axon. To view this figure in color, go online.
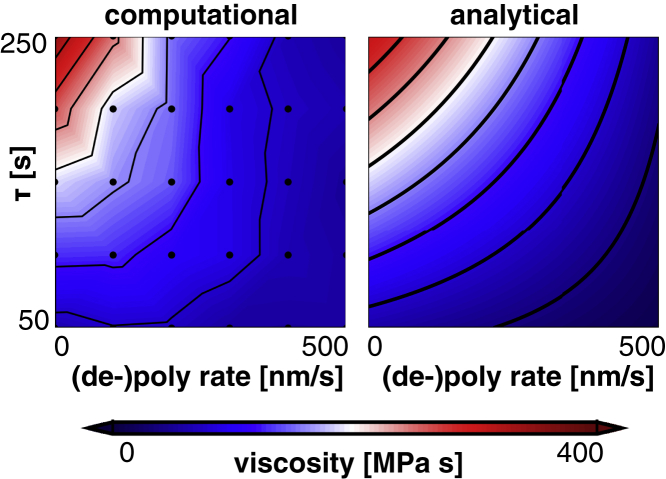
In addition to probing the effects of microtubule dynamics, in this section, we also vary the characteristic time constant of attachment and detachment of the cross-links, τ, and we investigate the effects on axon viscosity (see Fig. 10; left). As reported before (5), axon viscosity increases with increasing values of τ. More notably, Fig. 10 demonstrates that axon viscosity decreases for higher microtubule (de-)polymerization rates as expected. This result is especially interesting because it provides a mechanistic explanation for the reduction in axonal outgrowth after exposure to high doses of taxol and the increase in elongation in response to low doses of taxol and EPO that have recently been shown to destabilize microtubules (23, 24).
Figure 10.
Contours of effective axon viscosity as a function of (de-)polymerization rate and characteristic time constant of the cross-links for the computational (left) and analytical (right) models. Axon viscosity increases with increase in the characteristic time constant and with decrease in microtubule (de-)polymerization rate. These results suggest that stabilizing microtubule dynamics increases axon viscosity. To view this figure in color, go online.
Analytical model problem
To reproduce the computational results in our analytical model, we relate stiffness, ETau, and viscosity, ηTau, to the characteristic time constant of the cross-links and to the (de-)polymerization rate of microtubules. We propose these relations as follows:
| (6) |
where , , and are material parameters that we fit to the computational results. We choose the linear dependence of the number of cross-links on microtubule rate, , for its simplicity and good fit with computational data. Fig. 10 (right) shows the axon viscosity that best fit the computational data. Again, the analytical model accurately represents the computational results in Fig. 10 (left). Collectively, Fig. 10 demonstrates that inhibiting microtubule dynamics increases the viscosity of the axon and, thereby, it reduces axonal outgrowth.
GEF-H1 pathway
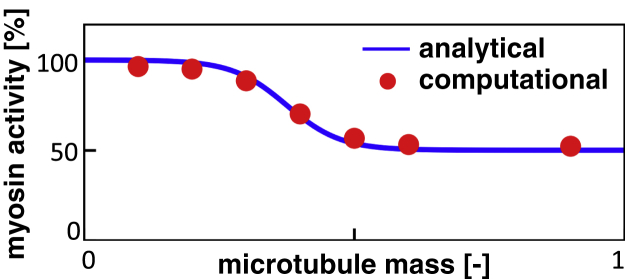
In this section, we proceed from microtubule dynamics to study the effects of microtubule disassembly, or loss in microtubule mass, on axonal outgrowth. Experimental evidence shows that the induction of microtubule disassembly blocks axonal elongation (28). We expect this is partly due to a reduction in the number of dynein protein cross-links that reduces the extensile force generation in the axon. In addition, based on nonneuronal cells, a decrease in microtubule mass upregulates myosin activity through the release of GEF-H1 (33, 36). In this section, we investigate the potential effects of this pathway on axonal elongation. We assume myosin activity, that is the number of myosin proteins, is at a maximum when no microtubules are present and at a minimum when all microtubule sites within a cross section are occupied. We expect this decrease is nonlinear as is common for signaling pathways. As a simplification, we propose an S-curve relation between myosin activity and microtubule mass, illustrated in Fig. 11:
| (7) |
where represents the fraction of potential microtubules (MT) sites that are occupied and denotes a -smooth generalization of the discontinuous Heaviside function. We further assume that half of the cross-links between the microtubules are tau proteins and the other half are dynein proteins.
Figure 11.
Myosin activity versus microtubule mass. The blue line represents our model for myosin activity in Eq. 9. The red dots are results from simulations that verify the correct implementation of our microtubule mass myosin activity pathway. To view this figure in color, go online.
Computational model problem
We implement the relation in Eq. 7 in our computational model by varying the characteristic detachment time of the myosin proteins as follows:
| (8) |
is computed for each cross-link individually by counting the number of microtubule sites that are occupied in the axon cross section at the location of the myosin protein cross-link. Fig. 11 demonstrates that this implementation indeed yields the relation between microtubule mass and the number of myosin cross-links as determined analytically in Eq. 7.
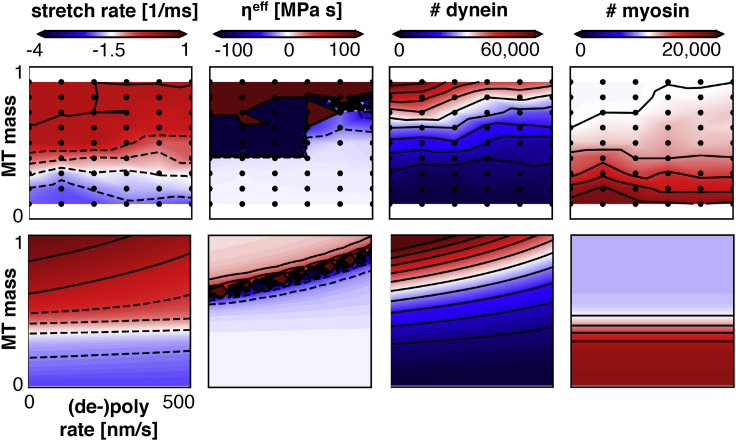
Fig. 12 shows the contour plots of axon stretch rate, effective viscosity, and number of dynein and myosin proteins as a function of microtubule rate of (de-)polymerization, , and microtubule mass . First, the number of myosin cross-links is independent of microtubule rate but depends on microtubule mass consistent with Eq. 7. The number of dynein cross-links decreases with the square of the microtubule mass, , which is consistent with the combinatorial scaling of the number of cross-links in a set of microtubules. The number of dynein proteins also decreases with increasing microtubule dynamics as an emergent effect (see previous section). The axon stretch rate and viscosity depend on microtubule rate and mass consistently with these number of dynein and myosin proteins.
Figure 12.
Contour plots of several axon properties versus microtubule (de-)polymerization rate and microtubule mass from the computational model (top) and analytical model (bottom). Consistent with Microtubule Dynamics and Tau Cross-Linking, axon viscosity decreases for increasing (de-)polymerization rates. More pronounced, the stretch rate in the axon increases when microtubule mass increases. This trend follows as an increase in microtubule mass will reduce myosin activity and, thereby, reduce the contractile force generation in the actin cortex. The trends in viscosity are consistent with the contours of numbers of dynein and myosin proteins and their effects as demonstrated in Dynein and Myosin. To view this figure in color, go online.
Analytical model problem
To relate microtubule mass to axon outgrowth, we analytically model the number of myosin, dynein, and tau proteins:
| (9) |
was obtained in the previous section, and and are fitted to the computational results. The stiffness, viscosity, and internal force generation in the microtubule system and actin cortex are then obtained as follows:
| (10) |
in which , , , , , and were obtained in previous sections, and and are fitted to the computational simulations with our discrete axonal model. Fig. 12 shows that the analytical model accurately captures the overall computational results. As microtubule mass decreases, myosin activity increases, dynein activity decreases, and axons retract. Reducing microtubule dynamics increases dynein, increases viscosity, and reduces axonal outgrowth.
Discussion
The abundant presence and relevance of mechanical forces during axonal outgrowth has been well acknowledged over several decades (2, 3, 67). For example, mechanical forces are generated by anterograde actin flow in the growth cone (47) by dynein and myosin proteins along the axon (8, 32) and by microtubule assembly (30, 31). Together with relevant mechanical properties, such as stiffness and viscosity, these forces contribute to the rate of axonal outgrowth (42). However, the precise role of each individual aspect in determining axonal outgrowth is not fully understood.
Most research in the literature has focused on the role of the growth cone in axonal elongation. Indeed, the growth cone exerts a pulling force on the axon that facilitates axonal elongation (68). However, recent experiments have shown that mechanical forces are regulated along the length of the axon (7, 69). Here, our focus in on understanding the role of the axon as an active partner with the growth cone. Because it is extremely difficult to isolate individual effects in an experimental setting, we use computational modeling as a powerful alternative to probe and isolate the different contributions to the mechanics and outgrowth of the axon. We propose a computational and an analytical model of the axon that accurately capture its physiology and mechanical behavior. Our axon model consists of a microtubule system of longitudinally aligned microtubules that are interconnected by tau and dynein proteins. The dynein cross-links generate extensile forces along the length of the axon. The microtubule system is surrounded by an actin cortex that consists of actin filaments and myosin cross-links that generate contractile forces. Microtubules and actin filaments that are close together can be connected by protein cross-links. We focus on dynein proteins that push the microtubules forward and the actin backward. Finally, we model the growth cone as a simple point that exerts a pulling force on the actin cortex. The microtubules may push the growth cone forward but are unable to apply pulling forces on the growth cone in our model.
In Dynein and Myosin, we perform a systematic study to explore the role of dynein and myosin concentrations within the force balance in the axon. Figs. 5, 6, and 7 demonstrate that the contractile forces by myosin and extensile forces by dynein decrease and increase axonal outgrowth, respectively. These competing mechanisms may lead to axon contraction or extension, depending on the ratio of active myosin and dynein proteins. This raises the possibility that the effects of altering the activities of these proteins may in part be due to changes in their activity along the axon (36).
An interesting phenomenon from the field of active fluids is that the effective or measured viscosity is dramatically affected by the ratio between internally generated force and externally applied forces (5, 70). In particular, when the internal and external forces are equal and opposite, there will be no deformation of the axon. Consequently, the effective viscosity, , will approach infinity. In the axon, this happens when the contractile forces by myosin balance the pulling force of the growth cone plus the extensile forces generated by dynein. Figs. 6 and 7 show that our modeling captures this large variation in effective viscosity as well. These large variations provide a partial explanation as to why reported values of mechanical properties of cells and tissues are notable in having extremely large variations (71).
In Microtubule Dynamics and Tau Cross-Linking, we investigate the effects of microtubule dynamics on axonal outgrowth, which is motivated by experimental evidence that shows that high doses of taxol slow down axonal elongation (20, 72). Here, we show that cross-link density along the length of the axon increases when microtubule dynamics are stabilized (see Fig. 8). In previous work (5), we have shown that axon viscosity increases linearly with cross-link density and, therefore, axonal outgrowth is reduced. Therefore, we propose that taxol may lead to an increase in the number of cross-links, which then increases viscosity and reduces axon outgrowth. Fig. 10 shows that our axon model confirms this hypothesis. Interestingly, recent work demonstrated that very low concentrations of EPO and taxol increase the probability of microtubule disassembly in the presence of Eb1 (24). In parallel, these low concentrations can increase neuronal outgrowth. Our work provides a plausible hypothesis that this may occur through lowering the viscosity of the axon.
We proceed from the stabilization of microtubule dynamics in Microtubule Dynamics and Tau Cross-Linking to microtubule depolymerization and, therefore, loss in microtubule mass in GEF-H1 Pathway. It is well accepted that induction of microtubule disassembly blocks axonal elongation. Most of the work on explaining this observation has focused on the growth cone. Here, we consider the effects of microtubule disassembly on the neuronal force balance along the length of the axon. Our previous modeling indicates that dynein only generates a net pushing force on microtubules when its cargo-binding domain is associated with the plus ends of microtubules (5). Because microtubule disassembly disrupts the plus ends of microtubules (73), we expect a large effect on dynein force generation along the length of the axon. Fig. 12 supports this prediction as our model indeed shows that reduction in microtubule mass reduces the number of dynein and, thereby, also reduces extensile force generation and axonal outgrowth.
Myosin may also play a role in the effects of microtubule disassembly on axonal outgrowth. It has been well recognized that myosin is important for axonal elongation (8, 10, 74, 75) (see also Dynein and Myosin). Once again, most research on myosin has focused on growth cone, but here we consider the potential contributions along the length of the axon. In particular, upregulation of myosin activity in the cortex upon microtubule disassembly may contribute to the reduction in axonal outgrowth. Studies in nonneuronal cells have shown an increase in myosin activity as a result of GEF-H1 release caused by microtubule disassembly (33, 36). In addition, GEF-H1 plays an important role in the regulation of axon outgrowth (18, 36). Therefore, we explore the effects microtubule disassembly might have on neuronal force balance. We adopt a relation between microtubule mass and myosin activity that resembles a typical signaling pathway (see Fig. 11). Fig. 12 then shows that reduction in microtubule mass increases the number of myosin proteins, reduces the axon stretch rate, and increases the effective axon viscosity.
We believe our work provides a powerful foundation for investigating more complex physical phenomena that contribute to axonal outgrowth. For example, the initiation, outgrowth and structural development of an axon is affected by a wide range of extracellular cues (76). In addition, adhesion between the axon and its substrate and within the actin membrane is an important mechanical cue that influences and guides the development of the axon (77). In future work, spectrin should be included to better understand how axons respond to large stresses and strain (61). We believe that our extension of the finite element framework to allow the explicit assignment of molecular mechanisms to individual elements provides many opportunities of using the finite element method to model active or living materials.
In summary, we propose a mechanistic model of the axon to understand the role of the axon as an active partner of the growth cone in axonal outgrowth. Our results demonstrate mechanisms by which dynein and myosin motors, microtubule dynamics, and microtubule disassembly affect axon viscosity and, thereby, axonal outgrowth. These results provide mechanistic explanations for observed and unexplained effects of high and low doses of taxol and microtubule disassembly on axon development. Our study not only has potential applications during neurodevelopment but might also help identify strategies to manipulate and promote axonal regrowth to treat neurodegeneration. In particular, the modeling suggests the most effective strategy to promote axonal regeneration is to maximize MT dynamic instability and dynein force generation while minimizing myosin II activity. This comes with the caveat that dramatically increasing or decreasing MT mass may slow elongation through effects on motors and passive mechanical properties.
Author Contributions
R.d.R. designed the research, performed the research, developed the computational tools, analyzed the data, and wrote the article. E.K. designed the research, performed the research, and wrote the article. K.E.M. designed the research, performed the research, and wrote the article.
Acknowledgments
This study was supported by the Stanford Graduate Fellowship to R.d.R. and by the Bio-X Interdisciplinary Initiatives Seed Grants Program seed grant “Molecular Mechanisms of Chronic Traumatic Encephalopathy” and the National Science Foundation grant “Understanding Neurodegeneration across the Scales” CMMI 1727268 to E.K.
Editor: Jochen Guck.
References
- 1.Coles C.H., Bradke F. Coordinating neuronal actin-microtubule dynamics. Curr. Biol. 2015;25:R677–R691. doi: 10.1016/j.cub.2015.06.020. [DOI] [PubMed] [Google Scholar]
- 2.Goriely A., Budday S., Kuhl E. Advances in Applied Mechanics. Elsevier; 2015. Neuromechanics: from neurons to brain; pp. 79–139. [Google Scholar]
- 3.Suter D.M., Miller K.E. The emerging role of forces in axonal elongation. Prog. Neurobiol. 2011;94:91–101. doi: 10.1016/j.pneurobio.2011.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Athamneh A.I., Suter D.M. Quantifying mechanical force in axonal growth and guidance. Front. Cell. Neurosci. 2015;9:359. doi: 10.3389/fncel.2015.00359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.de Rooij R., Miller K.E., Kuhl E. Modeling molecular mechanisms in the axon. Comput. Mech. 2017;59:523–537. doi: 10.1007/s00466-016-1359-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jakobs M., Franze K., Zemel A. Force generation by molecular-motor-powered microtubule bundles; implications for neuronal polarization and growth. Front. Cell. Neurosci. 2015;9:441. doi: 10.3389/fncel.2015.00441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.O’Toole M., Lamoureux P., Miller K.E. Measurement of subcellular force generation in neurons. Biophys. J. 2015;108:1027–1037. doi: 10.1016/j.bpj.2015.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Tofangchi A., Fan A., Saif M.T.A. Mechanism of axonal contractility in embryonic Drosophila motor neurons in vivo. Biophys. J. 2016;111:1519–1527. doi: 10.1016/j.bpj.2016.08.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Recho P., Jerusalem A., Goriely A. Growth, collapse, and stalling in a mechanical model for neurite motility. Phys. Rev. E. 2016;93:032410. doi: 10.1103/PhysRevE.93.032410. [DOI] [PubMed] [Google Scholar]
- 10.Ahmad F.J., Hughey J., Baas P.W. Motor proteins regulate force interactions between microtubules and microfilaments in the axon. Nat. Cell Biol. 2000;2:276–280. doi: 10.1038/35010544. [DOI] [PubMed] [Google Scholar]
- 11.del Castillo U., Winding M., Gelfand V.I. Interplay between kinesin-1 and cortical dynein during axonal outgrowth and microtubule organization in Drosophila neurons. eLife. 2015;4:e10140. doi: 10.7554/eLife.10140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ahmadzadeh H., Smith D.H., Shenoy V.B. Mechanical effects of dynamic binding between tau proteins on microtubules during axonal injury. Biophys. J. 2015;109:2328–2337. doi: 10.1016/j.bpj.2015.09.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Krieg M., Stühmer J., Goodman M.B. Genetic defects in β-spectrin and tau sensitize C. elegans axons to movement-induced damage via torque-tension coupling. eLife. 2017;6:1–35. doi: 10.7554/eLife.20172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Soheilypour M., Peyro M., Mofrad M.R.K. Buckling behavior of individual and bundled microtubules. Biophys. J. 2015;108:1718–1726. doi: 10.1016/j.bpj.2015.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Yu W., Baas P.W. Changes in microtubule number and length during axon differentiation. J. Neurosci. 1994;14:2818–2829. doi: 10.1523/JNEUROSCI.14-05-02818.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leterrier C., Dubey P., Roy S. The nano-architecture of the axonal cytoskeleton. Nat. Rev. Neurosci. 2017;18:713–726. doi: 10.1038/nrn.2017.129. [DOI] [PubMed] [Google Scholar]
- 17.Xu K., Zhong G., Zhuang X. Actin, spectrin, and associated proteins form a periodic cytoskeletal structure in axons. Science. 2013;339:452–456. doi: 10.1126/science.1232251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Conde C., Cáceres A. Microtubule assembly, organization and dynamics in axons and dendrites. Nat. Rev. Neurosci. 2009;10:319–332. doi: 10.1038/nrn2631. [DOI] [PubMed] [Google Scholar]
- 19.Buxbaum R.E., Heidemann S.R. An absolute rate theory model for tension control of axonal elongation. J. Theor. Biol. 1992;155:409–426. doi: 10.1016/s0022-5193(05)80626-5. [DOI] [PubMed] [Google Scholar]
- 20.Letourneau P.C., Ressler A.H. Inhibition of neurite initiation and growth by taxol. J. Cell Biol. 1984;98:1355–1362. doi: 10.1083/jcb.98.4.1355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Voelzmann A., Hahn I., Prokop A. A conceptual view at microtubule plus end dynamics in neuronal axons. Brain Res. Bull. 2016;126:226–237. doi: 10.1016/j.brainresbull.2016.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Brizuela M., Blizzard C.A., Dickson T.C. The microtubule-stabilizing drug Epothilone D increases axonal sprouting following transection injury in vitro. Mol. Cell. Neurosci. 2015;66:129–140. doi: 10.1016/j.mcn.2015.02.006. [DOI] [PubMed] [Google Scholar]
- 23.Hellal F., Hurtado A., Bradke F. Microtubule stabilization reduces scarring and causes axon regeneration after spinal cord injury. Science. 2011;331:928–931. doi: 10.1126/science.1201148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mohan R., Katrukha E.A., Akhmanova A. End-binding proteins sensitize microtubules to the action of microtubule-targeting agents. Proc. Natl. Acad. Sci. USA. 2013;110:8900–8905. doi: 10.1073/pnas.1300395110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Popovich P.G., Tovar C.A., Jakeman L.B. Independent evaluation of the anatomical and behavioral effects of Taxol in rat models of spinal cord injury. Exp. Neurol. 2014;261:97–108. doi: 10.1016/j.expneurol.2014.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ruschel J., Hellal F., Bradke F. Axonal regeneration. Systemic administration of epothilone B promotes axon regeneration after spinal cord injury. Science. 2015;348:347–352. doi: 10.1126/science.aaa2958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sengottuvel V., Leibinger M., Fischer D. Taxol facilitates axon regeneration in the mature CNS. J. Neurosci. 2011;31:2688–2699. doi: 10.1523/JNEUROSCI.4885-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Athamneh A.I.M., He Y., Miller K.E. Neurite elongation is highly correlated with bulk forward translocation of microtubules. Sci. Rep. 2017;7:7292. doi: 10.1038/s41598-017-07402-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Joshi H.C., Chu D., Heidemann S.R. Tension and compression in the cytoskeleton of PC 12 neurites. J. Cell Biol. 1985;101:697–705. doi: 10.1083/jcb.101.3.697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Dogterom M., Kerssemakers J.W., Janson M.E. Force generation by dynamic microtubules. Curr. Opin. Cell Biol. 2005;17:67–74. doi: 10.1016/j.ceb.2004.12.011. [DOI] [PubMed] [Google Scholar]
- 31.Rauch P., Heine P., Käs J.A. Forces from the rear: deformed microtubules in neuronal growth cones influence retrograde flow and advancement. New J. Phys. 2013;15:1–15. [Google Scholar]
- 32.Roossien D.H., Lamoureux P., Miller K.E. Cytoplasmic dynein pushes the cytoskeletal meshwork forward during axonal elongation. J. Cell Sci. 2014;127:3593–3602. doi: 10.1242/jcs.152611. [DOI] [PubMed] [Google Scholar]
- 33.Chang Y.C., Nalbant P., Bokoch G.M. GEF-H1 couples nocodazole-induced microtubule disassembly to cell contractility via RhoA. Mol. Biol. Cell. 2008;19:2147–2153. doi: 10.1091/mbc.E07-12-1269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kakiashvili E., Speight P., Szászi K. GEF-H1 mediates tumor necrosis factor-α-induced Rho activation and myosin phosphorylation: role in the regulation of tubular paracellular permeability. J. Biol. Chem. 2009;284:11454–11466. doi: 10.1074/jbc.M805933200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Salhia B., Hwang J.H., Rutka J.T. Role of myosin II activity and the regulation of myosin light chain phosphorylation in astrocytomas. Cell Motil. Cytoskeleton. 2008;65:12–24. doi: 10.1002/cm.20240. [DOI] [PubMed] [Google Scholar]
- 36.Takano T., Wu M., Kaibuchi K. Discovery of long-range inhibitory signaling to ensure single axon formation. Nat. Commun. 2017;8:33. doi: 10.1038/s41467-017-00044-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.García-Grajales J.A., Jérusalem A., Goriely A. Continuum mechanical modeling of axonal growth. Comput. Methods Appl. Mech. Eng. 2017;314:147–163. [Google Scholar]
- 38.Purohit P.K. Tension dependent growth and retraction of neurites. Procedia IUTAM. 2015;12:185–192. [Google Scholar]
- 39.de Rooij R., Kuhl E. Microtubule polymerization and cross-link dynamics explain axonal stiffness and damage. Biophys. J. 2018;114:201–212. doi: 10.1016/j.bpj.2017.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.de Rooij R., Kuhl E. Physical biology of axonal damage. Front. Cell. Neurosci. 2018;12:144. doi: 10.3389/fncel.2018.00144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Dennerll T.J., Lamoureux P., Heidemann S.R. The cytomechanics of axonal elongation and retraction. J. Cell Biol. 1989;109:3073–3083. doi: 10.1083/jcb.109.6.3073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.O’Toole M., Lamoureux P., Miller K.E. A physical model of axonal elongation: force, viscosity, and adhesions govern the mode of outgrowth. Biophys. J. 2008;94:2610–2620. doi: 10.1529/biophysj.107.117424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wegmann S., Schöler J., Muller D.J. Competing interactions stabilize pro- and anti-aggregant conformations of human Tau. J. Biol. Chem. 2011;286:20512–20524. doi: 10.1074/jbc.M111.237875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Bañuelos S., Saraste M., Djinović Carugo K. Structural comparisons of calponin homology domains: implications for actin binding. Structure. 1998;6:1419–1431. doi: 10.1016/s0969-2126(98)00141-5. [DOI] [PubMed] [Google Scholar]
- 45.Berger S.L., Leo-Macias A., Salzer J.L. Localized myosin II activity regulates assembly and plasticity of the axon initial segment. Neuron. 2018;97:555–570.e6. doi: 10.1016/j.neuron.2017.12.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Billington N., Wang A., Sellers J.R. Characterization of three full-length human nonmuscle myosin II paralogs. J. Biol. Chem. 2013;288:33398–33410. doi: 10.1074/jbc.M113.499848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gomez T.M., Letourneau P.C. Actin dynamics in growth cone motility and navigation. J. Neurochem. 2014;129:221–234. doi: 10.1111/jnc.12506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bray D., Bunge M.B. Serial analysis of microtubules in cultured rat sensory axons. J. Neurocytol. 1981;10:589–605. doi: 10.1007/BF01262592. [DOI] [PubMed] [Google Scholar]
- 49.Hirokawa N. Cross-linker system between neurofilaments, microtubules, and membranous organelles in frog axons revealed by the quick-freeze, deep-etching method. J. Cell Biol. 1982;94:129–142. doi: 10.1083/jcb.94.1.129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dogterom M., Yurke B. Measurement of the force-velocity relation for growing microtubules. Science. 1997;278:856–860. doi: 10.1126/science.278.5339.856. [DOI] [PubMed] [Google Scholar]
- 51.Stepanova T., Smal I., Galjart N. History-dependent catastrophes regulate axonal microtubule behavior. Curr. Biol. 2010;20:1023–1028. doi: 10.1016/j.cub.2010.04.024. [DOI] [PubMed] [Google Scholar]
- 52.van den Bedem H., Kuhl E. Tau-ism: the Yin and Yang of microtubule sliding, detachment, and rupture. Biophys. J. 2015;109:2215–2217. doi: 10.1016/j.bpj.2015.10.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fitzpatrick A.W.P., Falcon B., Scheres S.H.W. Cryo-EM structures of tau filaments from Alzheimer’s disease. Nature. 2017;547:185–190. doi: 10.1038/nature23002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.He Y., Francis F., Baas P.W. Role of cytoplasmic dynein in the axonal transport of microtubules and neurofilaments. J. Cell Biol. 2005;168:697–703. doi: 10.1083/jcb.200407191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Myers K.A., Tint I., Baas P.W. Antagonistic forces generated by cytoplasmic dynein and myosin-II during growth cone turning and axonal retraction. Traffic. 2006;7:1333–1351. doi: 10.1111/j.1600-0854.2006.00476.x. [DOI] [PubMed] [Google Scholar]
- 56.Letourneau P.C. Volume 109. American Cancer Society; Chichester, UK: 2016. Cytoskeleton in Axon Growth. [Google Scholar]
- 57.Dennerll T.J., Joshi H.C., Heidemann S.R. Tension and compression in the cytoskeleton of PC-12 neurites. II: quantitative measurements. J. Cell Biol. 1988;107:665–674. doi: 10.1083/jcb.107.2.665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Koch D., Rosoff W.J., Urbach J.S. Strength in the periphery: growth cone biomechanics and substrate rigidity response in peripheral and central nervous system neurons. Biophys. J. 2012;102:452–460. doi: 10.1016/j.bpj.2011.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hochmuth F.M., Shao J.Y., Sheetz M.P. Deformation and flow of membrane into tethers extracted from neuronal growth cones. Biophys. J. 1996;70:358–369. doi: 10.1016/S0006-3495(96)79577-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Krieg M., Dunn A.R., Goodman M.B. Mechanical control of the sense of touch by β-spectrin. Nat. Cell Biol. 2014;16:224–233. doi: 10.1038/ncb2915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hammarlund M., Jorgensen E.M., Bastiani M.J. Axons break in animals lacking β-spectrin. J. Cell Biol. 2007;176:269–275. doi: 10.1083/jcb.200611117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Hülsmeier J., Pielage J., Stork T. Distinct functions of α-spectrin and β-spectrin during axonal pathfinding. Development. 2007;134:713–722. doi: 10.1242/dev.02758. [DOI] [PubMed] [Google Scholar]
- 63.Khanna M.R., Mattie F.J., Thomas G.H. Spectrin tetramer formation is not required for viable development in Drosophila. J. Biol. Chem. 2015;290:706–715. doi: 10.1074/jbc.M114.615427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.King S.M. First edition. Academic Press; Cambridge, MA: 2011. Dyneins: Structure, Biology and Disease. [Google Scholar]
- 65.Mallik R., Carter B.C., Gross S.P. Cytoplasmic dynein functions as a gear in response to load. Nature. 2004;427:649–652. doi: 10.1038/nature02293. [DOI] [PubMed] [Google Scholar]
- 66.Tyska M.J., Warshaw D.M. The myosin power stroke. Cell Motil. Cytoskeleton. 2002;51:1–15. doi: 10.1002/cm.10014. [DOI] [PubMed] [Google Scholar]
- 67.Bray D. Mechanical tension produced by nerve cells in tissue culture. J. Cell Sci. 1979;37:391–410. doi: 10.1242/jcs.37.1.391. [DOI] [PubMed] [Google Scholar]
- 68.Lamoureux P., Buxbaum R.E., Heidemann S.R. Direct evidence that growth cones pull. Nature. 1989;340:159–162. doi: 10.1038/340159a0. [DOI] [PubMed] [Google Scholar]
- 69.Rajagopalan J., Tofangchi A., A Saif M.T. Drosophila neurons actively regulate axonal tension in vivo. Biophys. J. 2010;99:3208–3215. doi: 10.1016/j.bpj.2010.09.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Saintillan D. Rheology of active fluids. Annu. Rev. Fluid Mech. 2018;50:563–592. [Google Scholar]
- 71.Chatelin S., Constantinesco A., Willinger R. Fifty years of brain tissue mechanical testing: from in vitro to in vivo investigations. Biorheology. 2010;47:255–276. doi: 10.3233/BIR-2010-0576. [DOI] [PubMed] [Google Scholar]
- 72.Gornstein E.L., Schwarz T.L. Neurotoxic mechanisms of paclitaxel are local to the distal axon and independent of transport defects. Exp. Neurol. 2017;288:153–166. doi: 10.1016/j.expneurol.2016.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Prahl L.S., Castle B.T., Odde D.J. Quantitative analysis of microtubule self-assembly kinetics and tip structure. Methods Enzymol. 2014;540:35–52. doi: 10.1016/B978-0-12-397924-7.00003-0. [DOI] [PubMed] [Google Scholar]
- 74.Hur E.M., Yang I.H., Zhou F.Q. Engineering neuronal growth cones to promote axon regeneration over inhibitory molecules. Proc. Natl. Acad. Sci. USA. 2011;108:5057–5062. doi: 10.1073/pnas.1011258108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Ketschek A.R., Jones S.L., Gallo G. Axon extension in the fast and slow lanes: substratum-dependent engagement of myosin II functions. Dev. Neurobiol. 2007;67:1305–1320. doi: 10.1002/dneu.20455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Barnes A.P., Polleux F. Establishment of axon-dendrite polarity in developing neurons. Annu. Rev. Neurosci. 2009;32:347–381. doi: 10.1146/annurev.neuro.31.060407.125536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Koser D.E., Thompson A.J., Franze K. Mechanosensing is critical for axon growth in the developing brain. Nat. Neurosci. 2016;19:1592–1598. doi: 10.1038/nn.4394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Caminiti R., Carducci F., Innocenti G.M. Diameter, length, speed, and conduction delay of callosal axons in macaque monkeys and humans: comparing data from histology and magnetic resonance imaging diffusion tractography. J. Neurosci. 2013;33:14501–14511. doi: 10.1523/JNEUROSCI.0761-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Yogev S., Cooper R., Shen K. Microtubule organization determines axonal transport dynamics. Neuron. 2016;92:449–460. doi: 10.1016/j.neuron.2016.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Gittes F., Mickey B., Howard J. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 1993;120:923–934. doi: 10.1083/jcb.120.4.923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Suresh S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007;3:413–438. doi: 10.1016/j.actbio.2007.04.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Bunker J.M., Wilson L., Feinstein S.C. Modulation of microtubule dynamics by tau in living cells: implications for development and neurodegeneration. Mol. Biol. Cell. 2004;15:2720–2728. doi: 10.1091/mbc.E04-01-0062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Hällström W., Lexholm M., Prinz C.N. Fifteen-piconewton force detection from neural growth cones using nanowire arrays. Nano Lett. 2010;10:782–787. doi: 10.1021/nl902675h. [DOI] [PubMed] [Google Scholar]
- 84.Siechen S., Yang S., Saif T. Mechanical tension contributes to clustering of neurotransmitter vesicles at presynaptic terminals. Proc. Natl. Acad. Sci. USA. 2009;106:12611–12616. doi: 10.1073/pnas.0901867106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Haak R.A., Kleinhans F.W., Ochs S. The viscosity of mammalian nerve axoplasm measured by electron spin resonance. J. Physiol. 1976;263:115–137. doi: 10.1113/jphysiol.1976.sp011624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Niederman R., Pollard T.D. Human platelet myosin. II. In vitro assembly and structure of myosin filaments. J. Cell Biol. 1975;67:72–92. doi: 10.1083/jcb.67.1.72. [DOI] [PMC free article] [PubMed] [Google Scholar]