Mapping the Ligand Binding Landscape

Abstract

The interaction between a ligand and a protein involves a multitude of conformational states. To achieve a particular deeply bound pose, the ligand must search across a rough free-energy landscape with many metastable minima. Creating maps of the ligand binding landscape is a great challenge, as binding and release events typically occur on timescales that are beyond the reach of molecular simulation. The WExplore enhanced sampling method is well suited to build these maps because it is designed to broadly explore free-energy landscapes and is capable of simulating ligand release pathways that occur on timescales as long as minutes. WExplore also uses only unbiased trajectory segments, allowing for the construction of Markov state models (MSMs) and conformation space networks that combine the results of multiple simulations. Here, we use WExplore to study two bromodomain-inhibitor systems using multiple docked starting poses (Brd4-MS436 and Baz2B-ICR7) and synthesize our results using a series of MSMs using time-lagged independent component analysis. Ranking the starting poses by exit rate agrees with the crystal structure pose in both cases. We also predict the most stable pose using the equilibrium populations from the MSM but find that the prediction is not robust as a function of MSM parameters. The simulated trajectories are synthesized into network models that visualize the entire binding landscape for each system, and we examine transition paths between deeply bound stable states. We find that, on average, transitions between deeply bound states convert through the unbound state 81% of the time, implying a trial-and-error approach to ligand binding. We conclude with a discussion of the implications of this result for both kinetics-based drug discovery and virtual screening pipelines that incorporate molecular dynamics.

Introduction

Much effort in computational medicinal chemistry is devoted to finding the correct pose for a given ligand. Docking algorithms examine a large set of possible binding modes and use empirical scoring functions to determine which of these has the lowest free energy. The accuracy of a given docking algorithm is typically tested by measuring the root mean-square distance (RMSD) between the lowest free-energy pose to a single crystal structure pose for a large ensemble of protein-ligand systems (1, 2, 3). Such pose predictions can be very important for the development of lead molecules in the drug discovery process because they provide an intuition for structure-activity relationships. However, in general, multiple binding poses can exist with similar probabilities—especially in nonoptimized protein-ligand systems during screening—and a single-pose paradigm can neglect valuable information that can aid the drug discovery process. For instance, alternative poses with slightly higher free energies can be stabilized during ligand design (4). Also, the connectivity between states can be taken into account to design inhibitors with long residence times (5, 6), increasingly seen as a desirable objective in drug design (7, 8).

It can thus be beneficial to examine multiple ligand binding poses during the design process. The set of all binding poses can be viewed as points on a multidimensional ligand-binding free-energy landscape that each occur with some finite probability (9). A map of this landscape that shows a large ensemble of possible poses and how they are connected with both each other and the unbound state would be a valuable tool in ligand design. A complete, accurate map would allow for the prediction of binding mechanism, free energy, and kinetics and could be used to predict how the stability of these states would change as chemical modifications are made to the ligand. Unfortunately, construction of these maps is challenging because structural data from experiment is limited to only the most stable states and molecular simulation is easily trapped by deep metastable free-energy minima.

Recent progress in both hardware and software for molecular simulation is providing our first glimpses to the paths of ligand (un)binding and their kinetics (10). Ligand release kinetics can be efficiently predicted in some cases using random acceleration molecular dynamics (11); however, this method cannot produce absolute binding kinetics, and the external force can affect the ensemble of pathways in ways that are hard to predict. Ligand release paths have been determined using the metadynamics method, in which a biasing potential is introduced along an order parameter that describes the binding or release process (12). This has allowed for the characterization of extremely rare ligand release events, such as the unbinding of dasatinib from Src kinase with a mean first passage time (MFPT) of ∼20 s (13) and the unbinding of a type II inhibitor from p38 MAP kinase with an MFPT of ∼7 s (14). Although techniques have been developed to subtract the effect of biasing forces on estimates of free energy and kinetics (15), there is no clear way to subtract the impact of the biasing force on the transitions between different microstates.

A number of enhanced sampling methods for ligand-protein interactions employ only unbiased dynamics, which are suitable for building maps of the binding landscape. The adaptive multilevel splitting method uses a series of loops that begin and end in the bound state, progressing farther and farther toward the unbound state as the simulation progresses (16). This has been used to study the release of benzamidine from trypsin, which has an MFPT of 1.6 ms (17). Adaptive Markov state modeling, in which on-the-fly Markov state models (MSMs) are used to direct the seeding of new simulations, has also been used on the trypsin-benzamidine system (18). Another method, weighted ensemble (WE) (19), uses a set of parallel trajectories that are balanced between regions of space using cloning and merging operations. This has been used in conjunction with the Northrup-Allison-McCammon method (20) to estimate binding rates using Brownian dynamics (21) and coarse-grained models (22).

The WExplore enhanced sampling method (23) is a variant of WE that has been used to study long-timescale ligand release processes. WExplore is particularly suited to study high-dimensional systems because it builds a set of hierarchical Voronoi polyhedra on the fly to divide the space into regions and to guide the cloning and merging operations in the WE framework. WExplore has characterized unbinding paths of a series of molecular fragments from the FK-506 binding protein (24) and has extensively sampled the trypsin-benzamidine system, discovering three distinct ligand release pathways (25). This method was also used to sample both binding and release pathways of a series of host-guest systems for the SAMPL6 challenge (26), with release pathway timescales as long as 830 s. Finally, WExplore studied release pathways of the N-(1-[1-oxopropyl]-4-piperidinyl)-N′-(4-[trifluoromethoxy]phenyl)-urea ligand from the enzyme-soluble epoxide hydrolase, experimentally determined to have an MFPT of 660 s (27). WExplore is well suited to map ligand binding landscapes in that it is both 1) built on unbiased dynamics and 2) capable of sampling ligand release events occurring on timescales of seconds to minutes.

Here, we use WExplore to sample the ligand binding landscapes for two protein-ligand complexes and test its ability to predict global free-energy minima when starting from inaccurate starting points. We focus on two bromodomains: small epigenetic reader domains composed of four left-handed α-helices, which recognize ϵ-N-acetylated lysine residues. There are currently 61 known distinct human bromodomains that are contained in 46 different proteins (28). Bromodomains have been of intense therapeutic interest in recent years (29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40) because bromodomain inhibitors have been proposed as treatments for cancer, diabetes, and inflammation. Much attention has been given to the bromodomain and extraterminal (BET) family, including Brd4, for which the first inhibitor was discovered in 2010 (41).

The first complex studied here involves Baz2B (bromodomain adjacent to zinc finger domain protein 2B), which has a relatively small lysine binding pocket and is considered one of the least-druggable bromodomain targets (29). Drouin et al. (34) developed a chemical probe, “ICR,” that is selective for bromodomains Baz2A and Baz2B. We study here the interaction between Baz2B and an intermediate compound “ICR7” (Protein Data Bank (PDB): 4XUB), which has slight differences from ICR and is ∼10-fold less potent for Baz2B binding (half maximal inhibitory concentration, IC50 ≈ 1.1 μM). We also examine the well-studied Brd4 protein, which has two distinct bromodomain subunits. Zhang et al. (30) developed an inhibitor “MS436” that preferentially binds to the first bromodomain (Brd4(1)) over the second (K_i ≈ 40 nM). The interaction of MS436 with Brd4(1) (PDB: 4NUD) is the second complex studied here.

Starting from two very different docked poses for each system, we use WExplore molecular dynamics sampling to generate unbinding pathways. We obtain pathways that connect the docked bound states to alternative binding poses, as well as quasibound and unbound states. The simulation results are then synthesized into MSMs that are visualized as networks and used to predict the globally stable bound poses, which can differ from both starting points. Transition paths that connect the two ligand orientations are analyzed, and we quantify the fraction of transition paths that interconvert on the protein surface versus interconverting in the bulk. We conclude with a discussion of the implication of these results for the screening of future bromodomain inhibitors.

Methods

Docking

Docking is performed using Autodock Vina (3) and AutoDockTools from MGLTools package 1.5.6. Coordinates of the protein are taken from PDB: 4XUB (34) and PDB: 4NUD (30) for Baz2B and Brd4, respectively. We use a cubic grid with 80³ points, 0.375 Å spacing, and a center taken from the center of geometry of the ligand in the crystal structure. Crystallographic waters are not included in the docking procedure. We retain the top nine models and use these to choose two starting structures for each protein-ligand system that we label poses A and B. More on how these poses are chosen is given in Starting Poses.

Molecular dynamics sampling

The CHARMM36 force field is used for all minimization and molecular dynamics simulation, and dynamics are run using the CHARMM program (42) with an OpenMM interface for GPU dynamics. Ligands are parameterized with CGenFF (43, 44), and four systems total are built for proteins Baz2B and Brd4, each with poses A and B. Each system is solvated using TIP3 waters and a cubic box with a cutoff of 12 Å, and ions are added to neutralize the system: for Brd4, three chlorine atoms are added, and for Baz2B, no ions are required. The systems are then energy minimized using harmonic restraints on the protein and ligand atoms: 500 steps of steepest descent followed by 500 steps of the adopted basis Newton-Raphson method. The minimization is then repeated with the restraints removed. Each system is heated gradually from 50 to 300 K by increments of 25 K, with 5000 dynamics steps at each temperature. The systems are then equilibrated with 500 ps of simulation, and the resulting conformation is used to initialize our WExplore simulations.

During dynamics, covalent bonds to hydrogen atoms are constrained with the SHAKE algorithm with a tolerance of 10⁻⁸. Nonbonded interactions are computed with the particle mesh Ewald method using a Gaussian width (κ) of 0.32 and 96 grid points along the x, y, and z directions. Lennard-Jones interactions are calculated up to an 8.5 Å cutoff. A constant temperature is maintained using a Langevin heatbath with a reference of 300 K and a friction coefficient of 1.0 ps⁻¹. A constant pressure is maintained with a Monte Carlo barostat coupled to a reference pressure of 1.0 atm. The MC barostat uses volume moves attempted every 50 time steps. A 2 fs time step is used for all simulations performed here.

WExplore

WExplore (23) is an enhanced sampling technique built on the WE method (19). In this technique, an ensemble of trajectories is run forward in time and is periodically managed by a central process that can clone or merge trajectories to sample over a set of regions as evenly as possible. A set of regions is defined in conformation space, and trajectories are cloned in under-represented regions (e.g., saddle points) and merged in over-represented regions (e.g., high-probability basins of attraction). The WE method has largely been implemented by defining these regions along one or two order parameters (22, 45, 46, 47), and the key advance of the WExplore method was to define regions in a high-dimensional-order parameter space using hierarchical Voronoi polyhedra (for more information, see (23)). We have found WExplore to be useful for discovering new regions of conformational space (48), and it works best for low-entropy to high-entropy transitions, such as ligand unbinding pathways (10, 24, 25, 27).

In WExplore, trajectories are assigned to regions using distance measurements to a set of characteristic conformations of the system (called “images”), which are dynamically defined over the course of the simulation. To measure distances between conformations, we first align the two conformations using a set of residues in the binding pocket that are within 8 Å of the ligand in its initial pose; the distance between the conformations is then the RMSD between the sets of ligand atoms without any further alignment. This captures ligand rotation, translation, and reorganization and is suitable for building diverse ensembles of ligand-bound poses. As in previous work, we use a four-level region hierarchy with critical distances of 2.5, 3.5, 5.0, and 10 Å (25, 27); we also use 10,000 dynamics steps (Δt = 20 ps) between cloning and merging operations.

This method bears some similarity to Markov state modeling approaches because both are run using entirely unbiased dynamics. However, an advantage of the WE family of methods is that observables can—in principle—be calculated without invoking a Markovian assumption by assigning a statistical weight to each trajectory that governs how strongly it contributes to statistical averages. For instance, in this work, the unbinding trajectory flux that determines the unbinding rate constant, k_off, is directly calculated using the sum of the weights of unbinding trajectories. In practice, some observables are slow to equilibrate and are more efficiently calculated using a Markov model. In this work, Markov models are used to calculate the equilibrium probabilities of each state to make predictions for the most probable binding poses.

The weights of trajectories are initialized to be equal and are modified only during cloning and merging events, as follows. When a trajectory is cloned, its weight is divided among the clones, thus conserving probability. When two trajectories A and B are merged, the resulting trajectory C has weight w_C = w_A + w_B, and it takes on conformation A with probability w_A/w_C and conformation B with probability w_B/w_C. Here, following previous work (25), to improve sampling efficiency, we impose maximal and minimal weights that walkers can achieve: w_max = 0.1 and w_min = 1e⁻¹². This is enforced by disallowing cloning or merging operations that would violate these rules.

For each of the four systems, we perform three WExplore simulations with 48 trajectories each. These are run for 730 cycles, which are comprised of 20 ps of sampling for each trajectory followed by merging and cloning operations. In aggregate, we report on 701 ns per WExplore simulation or 8.4 μs total. The simulations were performed using nodes equipped with four NVIDIA K80 graphics processing units, which complete the dynamics for a single cycle in an average of 7.9 min. The combined set of simulations reported here required ∼6.9 node weeks or 27 graphics processing unit weeks.

Exit rates and ensemble definitions

To calculate the exit rates, we employ an ensemble-splitting strategy (49), in which two basins (bound and unbound) are used to define binding and unbinding ensembles. Here, we define a system to be in the unbound basin if the closest distance between the ligand and the protein is greater than 10 Å. The bound basin (although no definition is required in this work) could be defined as the set of structures in which the ligand RMSD is less than 2.0 Å from the starting pose after alignment to the binding site. Our simulations are run in the “unbinding ensemble,” in which trajectories are initialized in the bound basin and are terminated in the unbound basin. The trajectory flux from the unbinding ensemble into the unbound basin is equal to the unbinding rate constant (k_off) and can be calculated as the sum of the weights of the exiting trajectories divided by the elapsed time. Similarly, the binding rate could be determined by running simulations in the “binding ensemble,” in which trajectories are initialized in the unbound basin and terminated in the bound basin, although this is not done here. We have found previously that, although rate measurements from trajectory flux can vary significantly between WExplore simulations, the average over an ensemble of simulations can compare well to experimentally determined off rates (25, 27).

MSM and network modeling

Because our simulation results broadly sample the ensemble of ligand bound poses, including complete exit trajectories, there is considerable overlap between those that start in pose A and those that start in pose B. We use coclustering to synthesize the two data sets and use these models to visualize our pose network, predict globally stable states, and determine properties of A ↔ B transition ensembles.

For the pose networks, we cluster using a set of ligand-protein distances. This allows all poses to be distinguished on a structural basis, creating a detailed view of the free-energy landscape. For both Baz2B and Brd4, the set of distances was constructed using two sets of atoms (a set of selected ligand atoms and the set of protein Cα atoms that are within 20 Å of the center of mass of the ligand) and choosing every possible combination of atoms between the two sets. The selected atoms for each ligand was a set of heavy atoms—13 for MS435 and 15 for ICR7, selected manually—that cover all functional groups of the ligand (Fig. S1). The set of ligand-protein distances (962 for Brd4-MS435 and 1035 for Baz2B-ICR7) is used as a base set of features to describe our data set.

We then use time-lagged independent component analysis (tICA) (50, 51) to identify coordinates that change slowly as a function of time. As WExplore uses a set of trajectories that are cloned and merged at each time step, knowledge of the trajectory history is required for the tICA analysis. This was accomplished by construction of a branching tree of trajectories using the wepy package (52), allowing each point to be traced backward in time in a unique fashion. Many tICA clustering parameters were used in this work to examine the robustness of our cluster predictions. We varied the number of dimensions used in tICA analysis (n_tICA = 3, 5, 10), the tICA lag-time (τ_tICA = 0.2, 1 ns), the Markov model lag-time (Δt ≤ τ ≤ 50Δt), and the number of clusters (n_c = 500, 800, 1200). Because the initial sampling is heavily concentrated around the initial points chosen from docking, we also discard a fraction of the initial data (0 ≤ f_d ≤ 0.7). Parameters used in specific tICA cluster sets are given in Table S1, and for each set, we construct 48 Markov models (six τ values and eight discard fractions). We construct another 48 Markov models without tICA clustering for each of n_c = 500, 800, and 1200. These use k-means clustering directly on the set of ligand-protein distances. In total, we compute predictions of the globally stable state using 720 different Markov models for each of the Brd4 and Baz2B systems.

For the network models, each cluster is represented as a node, and nonzero off-diagonal elements of the transition matrix (denoted here as t_ij for transitions from i to j) are represented as edges. As in previous work (25, 27, 53), the weight of an edge between nodes i and j (e_ij) is as follows:

$$e_{ij}=100\frac{1}{2}\left(\frac{t_{ij}}{{\sum }_k{t}_{ik}}+\frac{t_{ji}}{{\sum }_k{t}_{jk}}\right),$$ (1)

that is, the average of the conditional transition probabilities in either direction between i and j multiplied by 100. Determination of transition matrices, weight calculations, and graph construction were performed with the CSNAnalysis package v0.5 (54). Network layouts are created in Gephi using the Force Atlas algorithm with repulsion strength 200, attraction strength 10, and maximal displacement 10. The layout is minimized first while allowing for node overlap, followed by a brief minimization while preventing overlap, with the maximal displacement reduced to 1.0.

Results

The Results describes the construction of the initial bound poses (Starting Poses) and the analysis of the WExplore sampling runs. The runs are first analyzed by determining the exit rate separately for each starting pose (Ranking Poses by Exit Rates), which does not involve a Markovian assumption but provides only coarse detail on which binding mode is preferred for each ligand-protein complex. A series of MSMs are constructed (MSMs for Pose Prediction), from which we estimate binding affinities and stable poses. A single Markov model is then chosen for further analysis: visualization of pose networks (Bound Pose Networks) and analysis of pose interconversion pathways (Pose Interconversion Pathways).

Starting poses

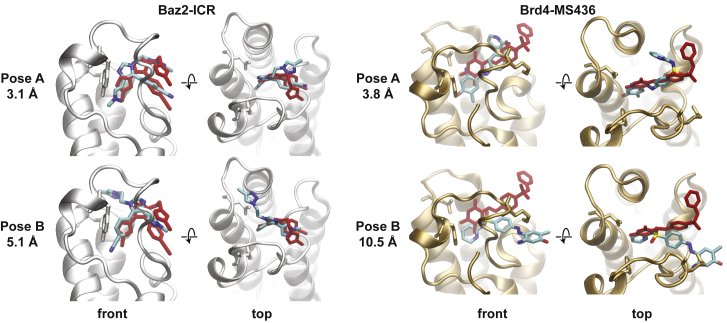
We use Autodock Vina (3) to generate a set of nine possible bound poses for both Baz2B and Brd4 (Figs. S2 and S3). From this set, we select two poses that show large differences in their global orientation while maintaining high predicted affinities. We also take care not to choose poses with very low RMSD to the crystal structure because we aimed to test whether we could predict the crystal structure when using an inaccurate starting point. Two such starting points are used for each complex as initial structures for WExplore MD sampling (Fig. 1). RMSD to the crystal structure for all four starting structures ranges from 3.1 to 10.5 Å. Pose A for Baz2B has roughly the same orientation as the crystal structure but is shifted further into the binding pocket. The N6 atom of the methyl-pyrazole group, which in the crystal structure forms a hydrogen bond with Asn1944, is roughly 3 Å deeper, forming a hydrogen bond with the Tyr1901 side chain. The N5 atom on the central imidazole ring moves down to form a similar interaction with Asn1944. Pose A for Brd4 is also shifted ∼3 Å deeper into the pocket. Pose B in both cases is bound in a completely different orientation. In Baz2B, the nitrile group is bound to the recognition pocket, with the triazole and imidazole rings spreading in different directions. In Brd4, the ligand is rotated ∼180°, with the 2-aminopyridine ring deeply bound in the pocket.

Figure 1.

Initial poses from docking. (left) Front and top views of starting poses A and B of the Baz2B-ICR7 system. Residues Tyr1901 and Asn1944 are shown in licorice representation. (right) Front and top views of starting poses A and B of the Brd-MS436 system. Protein residues Tyr97 and Asn140, which are homologous to those shown in Baz2B, are shown in licorice. In both cases, the crystal structure pose is shown in red, and poses A and B are shown with colors according to atom type. To see this figure in color, go online.

Ranking poses by exit rates

Exit points (where the system enters the unbound basin) are obtained in each of the 12 WExplore simulations. We obtain a total of 371 exit points for Baz2B and 124 for Brd4, which reflects the higher affinity of the MS436 ligand (Table 1). These exit points all represent structures that have at least 10 Å of clearance between the ligand and the protein. As seen in Fig. S4, they are heterogeneous and are widely distributed in space surrounding the protein.

Table 1.

Pose-Specific Dissociation Kinetics Determined by Exit Point Weights

		Number of exits			Total Exits	wtotala	koff (s−1)a	MFPToffb
		Run 1	Run 2	Run 3
Baz2B	Pose A	38	78	53	169	0.035 ± 0.016	2.4 ± 1.1 × 106	420 ± 190 ns
	Pose B	68	58	76	202	0.10 ± 0.04	6.6 ± 2.7 × 106	150 ± 60 ns
Brd4	Pose A	25	28	24	77	5.4 ± 4.2 × 10−8	3.6 ± 2.9	280 ± 220 ms
	Pose B	24	9	14	47	3.2 ± 2.6 × 10−5	2.2 ± 1.8 × 103	0.46 ± 0.37 ms

^aErrors shown are the standard error of the mean.

^bError in MFPT is calculated as δ_MFPT = δ_koff(MFPT)².

Using the sum of the weights of these exit points, we determine off-rates for each protein and starting pose. A small, threefold difference was observed in k_off between ligand poses in the Baz2B system, with pose A predicted to be slower. For Brd4, we predict pose A to have a slower off rate than pose B by a factor of ∼600. Thus, as a pose-ranking technique, the exit flux would predict pose A to be more stable than pose B in both cases. However, as in previous work, the exit fluxes have high run-to-run variability, as seen by the large error estimates in both w_total and k_off in Table 1.

It is important to keep in mind that the link between a pose-specific k_off and the thermodynamic probability of a binding pose is not straightforward. In other words, long exit times do not imply that a particular pose is stable or that it is a relevant template to use for drug design. The most probable ligand pose will form a basin of attraction in the free-energy landscape, and a set of nearby poses—although they themselves may be unstable—will commit to that basin with high probability and thus have a similarly low k_off value. Thus, to understand the link between pose-specific k_off and pose probability, we must understand how poses are connected with both each other and with the unbound state.

MSMs for pose prediction

Special considerations for WE data sets

As all of the WExplore simulations are run with the natural energy function (e.g., no biasing forces), we can employ MSM analysis to divide our conformation space into a set of states and estimate their equilibrium probabilities. Although this is possible with WE data sets, the directed cloning and merging operations introduce some special considerations into how the transition count matrices should be constructed. To illustrate this, consider a WE simulation as a branching “trajectory tree,” with each trajectory growing upward in time (Fig. 2). Cloning events can be viewed as branchpoints of this tree, and merging events result in the termination of a branch, with its weight transferred to another point in the tree. For a given transition matrix lag time (τ = nΔt), a count matrix can be constructed by the set of all possible tree paths P = {(a₀ → b₀), (a₁ → b₁), ...}, where a and b are connected by a path of length n. So, once all of the structural data is clustered, the cluster assignments are used to label the tree, and the transition count matrix could be constructed as

$$t_{ij}=\sum _{a,b\in P}\delta \left(c_a-i\right)\delta \left(c_b-j\right),$$ (2)

where c_x is the cluster assignment of conformation x in the trajectory tree and δ(x) is a δ function. However, this transition matrix construction is problematic because it gives all paths equal weight, regardless of the statistical weight of the trajectory determined by the WE algorithm. To appreciate this, consider the set of trajectories that begin in the bottom state in Fig. 2. The rightmost trajectories have been cloned and would thus be over-represented compared to the others if the transition matrix was constructed according to Eq. 2. In fact, because low-probability unbinding trajectories are systematically amplified in the simulations here, the transition count matrix would be systematically biased toward the unbound states. For this reason, it is proper to follow the standard approach of WE simulations, in which trajectories contribute to observables according to their statistical weight. These weights account for the cloning and merging steps in the WExplore algorithm and are shown for the final states in Fig. 2:

$$t_{ij}^w=\sum _{a,b\in P}{w}_b\delta \left(c_a-i\right)\delta \left(c_b-j\right),$$ (3)

where w_b is the weight of the trajectory at point b in the tree. In the next section, we compare both of these approaches.

Figure 2.

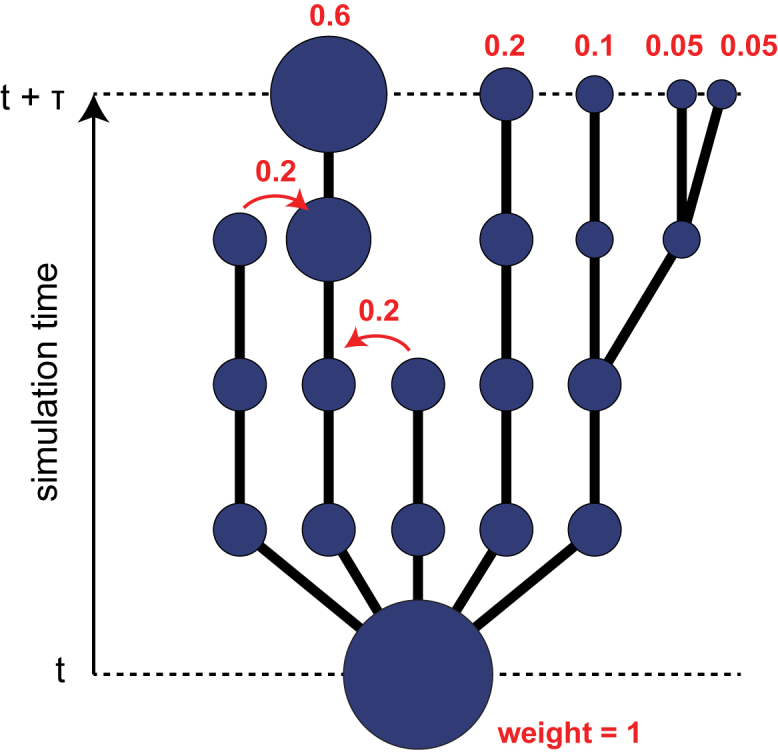
Trajectory tree schematic. Merging and cloning events in WE simulations can be represented as a branching tree. Cloning events are branching points, and merging events result in the termination of one branch and the transfer of its weight to another branch (curved arrows). To construct a transition count matrix with a lag time of τ, all possible complete paths between t = nτ and t = (n + 1)τ should be considered. There are five such paths in this schematic. To see this figure in color, go online.

Estimates of binding affinity

We construct a series of Markov models for the unweighted (Eq. 2) and weighted (Eq. 3) transition count matrices. For each model, we calculate the equilibrium probabilities (p_i) for each state i and estimate the binding affinity (K_D) using the sum of the probabilities of the unbound states:

$$K_D=C\frac{{\sum }_{i\in U}{p}_i}{1-{\sum }_{i\in U}{p}_i},$$ (4)

where a state i is in U if the minimal distance between the ligand and the protein is greater than 5 Å and C is the concentration of ligand, which here is equal to 4.3 mM, calculated as $1/N_{A}V$, where N_A is Avagadro’s number and V is the box volume in liters. The minimal ligand-protein distance for each cluster is determined using an average of 10 randomly chosen structures from each cluster. It is important to note that our simulations are strictly in the unbinding ensemble, that is, trajectories are initialized in the bound state and are terminated once they achieve a minimal ligand-protein distance greater than 10 Å (i.e., enter the unbound basin). Our simulations neglect trajectories that begin and end in the unbound basin; for this reason, we expect unbound states to be undersampled, and we view the K_D calculated by Eq. 4 as a lower bound.

As expected, we observe significant differences between K_D values calculated using the weighted and unweighted transition count matrices. The K_D values for all parameter sets are shown as heat maps in Figs. S5–S8, although they do not vary significantly between the parameter sets. The most significant variation between parameter sets is for the weighted transition count matrices of Brd4-MS436, which have K_D values ranging from 1.3 nM (for n_tICA = 5, τ_tICA = 0.2 ns, n_c = 500) to 820 nM (for n_tICA = 5, τ_tICA = 1 ns, n_c = 500). The average (on a logarithmic scale) minimal and maximal K_D values for the two systems and two count matrices are summarized in Table S2. The weighted count matrix shows excellent agreement with the K_i for Brd4-MS436. For Baz2B-ICR7, only the IC50 was measured, although the IC50 and K_i values were almost equal for a closely related compound (34). All of the Markov models that we construct predict a binding constant that is higher by at least a factor of 20, which is discussed further in the Discussion. In both cases, the weighted count matrices (Eq. 3) achieve a much better agreement with experimental binding constants than the unweighted matrices (Eq. 2), and these are used for all subsequent analyses.

Prediction of lowest free-energy poses

For each set of Markov model parameters, we determine the lowest free-energy pose in each network and calculate the RMSD of this state to the crystal structure. The RMSDs shown are averages over 10 randomly chosen structures for the lowest free-energy cluster. These low free-energy pose RMSDs are shown as heat maps for all of the tICA parameter sets examined in Figs. S9–S12. RMSD heat maps for two sets of clustering parameters are shown for both systems in Fig. 3. Fig. 3 A shows the results for n_tICA = 5, τ_tICA = 0.2 ns, and n_c = 1200. For this set of parameters, structures similar to pose A are not always predicted to be more stable than those similar to pose B, but we find large regions of stability where the lowest free-energy pose has a low RMSD (<2.5 Å) to the crystal structure. In Fig. 3 B, the number of tICA dimensions is increased from 5 to 10, and the predictions for the most stable pose are changed considerably. In general, we find that predictions for the lowest free-energy pose are sensitive to tICA clustering parameters (see Figs. S9–S12).

Figure 3.

RMSD of lowest free-energy poses. The lowest free-energy node is determined for several values of two parameters: the Markov model lag time and the percentage of initial data that is excluded. (A and B) Heat maps show the RMSD of the lowest free-energy pose determined by the Markov model to the crystal structure. These maps are constructed using τ_tICA = 0.2 ns and n_c = 1200, with n_tICA = 5 for (A) and 10 for (B). The complete set of maps is shown in Figs. S9–S12. The average lowest free-energy pose RMSD is shown as a function of the percentage of initial data discarded (p_excl, C) and the Markov model lag time (τ, D). Points are calculated as the average of all data shown in Figs. S9–S12. Error bars show the standard error of the mean. In both panels, Brd4-MS436 data is shown as a thick black line, and Baz2B-ICR7 is shown as a thin line. To see this figure in color, go online.

To generally examine whether our pose prediction improves as a function of lag time (τ) or the percentage of initial data excluded from analysis (p_excl), we averaged the low free-energy pose RMSDs along these axes. We find a clear trend for Baz2B that increasing predictions improve with increasing p_excl (Fig. 3 C). For Brd4, we find that the predicted RMSD initially deteriorates and then improves with increasing p_excl. Interestingly, we find that the average quality of predictions for both Baz2B and Brd4 does not improve with longer Markov model lag times (Fig. 3 D). We also find that we consistently achieve better results for the Baz2B-ICR7 system compared to the Brd4-MS436 system.

To investigate whether the tICA vectors are reporting on long-timescale interactions, we use the tICA vectors to color the pose networks described in the next section (Figs. S13 and S14). In both cases, the first tICA vector (which reports on the longest timescale process) corresponds to transitions between the pose A region and the rest of the network. The second tICA vector corresponded to transitions between the unbound/quasibound states and the deeply bound states. Vectors 3–5 described transitions between disparate communities within the quasibound ensemble, the only exception being Baz2B-tICA4, which also describes transitions between two adjacent deeply bound communities (see Pose Interconversion Pathways for more details). We conclude that the tICA analysis is working as intended, as the vectors capture the longest-timescale motions in our system. To compare, we also generate a separate set of Markov models without using tICA in which the set of ligand-protein distances was directly clustered. This is helpful because it eliminates the need to define τ_tICA and n_tICA. However, we obtain similar mixed results for the RMSD predictions, in which only small domains of robustness are found and different results can be obtained with different numbers of clusters (Fig. S15).

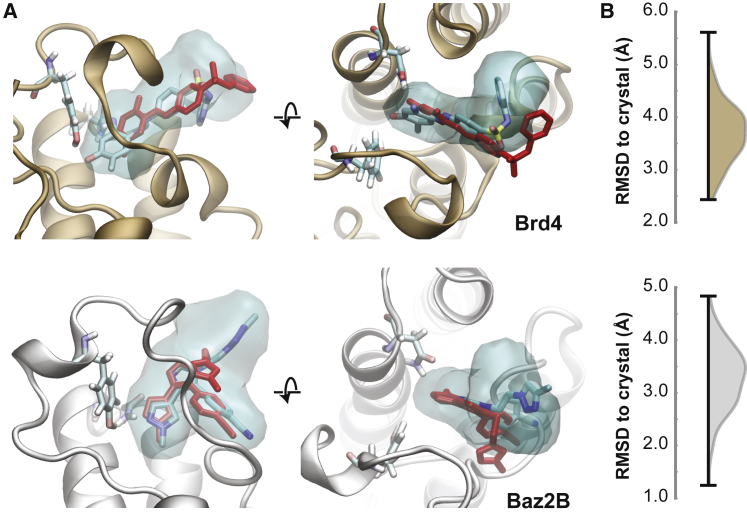
To investigate these poses in more detail, we randomly pick a set of 100 structures from the clusters from n_tICA = 5, τ_tICA = 0.2 ns, and n_c = 1200 that are predicted to be the most stable for higher p_excl. The median structure from this set (with the lowest ligand RMSD to the other members) is shown, along with density maps that are calculated from all set members, in Fig. 4. We see a significant amount of variation within the set of structures for both systems. For Brd4, we see that the median structure is bound significantly lower than the crystal structure pose, in line with starting pose A. We do not reproduce the orientation of the solvent-exposed pyridine ring observed in the crystal structure, although this could be due to interactions between other copies of Brd4 in the crystal lattice (Fig. S16). Poses sampled from the lowest free-energy cluster have RMSD values to crystal ranging from 2.4 to 5.5 Å. We find better agreement for the Baz2B-ICR7 system, with RMSD values ranging from 1.2 to 4.9 Å. The median structure reproduces the crystal structure interactions in the binding pocket, and this is consistent across the majority of structures examined. The density becomes more spread out for the solvent-facing triazole ring, which is observed partly in an unstacked orientation relative to the benzonitrile group. This is in line with NMR measurements of the ICR7 compound, which indicate that the triazole and benzonitrile groups do not exhibit a stacked conformation in solution (34). However, the lack of stability of the bound, stacked conformation could still indicate that ring-stacking interactions are not sufficiently strong in our parameterization of the force field for ICR7.

Figure 4.

Structures from the lowest free-energy clusters. Ligand densities are shown for a set of 100 randomly chosen structures from the nodes identified in Fig. 3A. (A) The crystallographic pose is shown in red, and the median ligand pose is shown colored by atom type. Two residues are shown that are important for binding: Tyr97 and Asn140 for Brd4 and Tyr1901 and Asn1944 for Baz2B. The ligand density is determined using the VolMap tool of VMD and is shown at an isovalue of 0.1. (B) The RMSD distribution of the 100 selected poses to the crystal pose is shown for Brd4 (top) and Baz2B (bottom). To see this figure in color, go online.

Bound pose networks

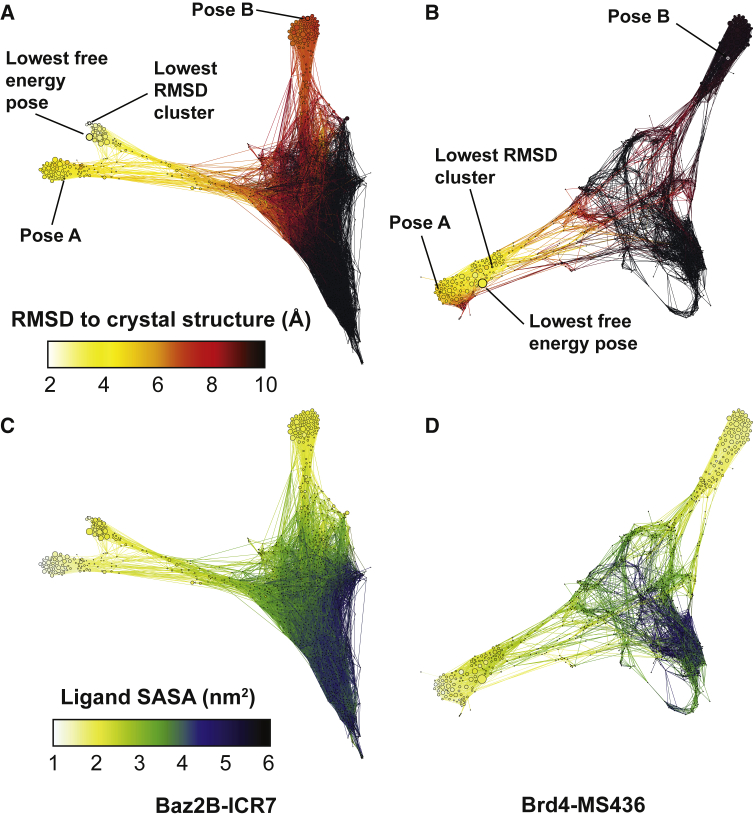
We use conformation space networks to visualize the landscape of bound poses for both systems (Fig. 5). We again focus on a single set of MSM parameters (n_tICA = 5, τ_tICA = 0.2 ns, n_c = 1200, p_excl = 70, and τ = 0.2 ns), and although the parameters affect the weights of specific states in the network, the overall topology of the network is robust. Edges are given a weight according to Eq. 1 using the weighted transition matrix elements from Eq. 3. For visualization, only edges with a weight greater than 0.4 are shown, and nodes that are not connected to the giant component of the network are discarded. After filtering, the Baz2B network shows 1195 nodes $\left(99\text{\%}\right)$ and 15,848 edges $\left(66\text{\%}\right)$, and the Brd4 network shows 1157 nodes $\left(96\text{\%}\right)$ and 7442 edges $\left(49\text{\%}\right)$. These numbers illustrate that the Baz2B system is much more interconnected than Brd4, which is also clear from visual inspection of the networks.

Figure 5.

Networks of bound poses. The simulations starting from poses A and B are synthesized into networks in which each node is a bound pose and the connections show the poses that are observed to interconvert in the molecular dynamics simulations. In all networks, nodes are given a size according to their weight, as determined by the MSM with n_tICA = 5, τ_tICA = 0.2 ns, n_c = 1200, p_excl = 70, and τ = 0.2 ns. (A and B) Nodes are colored according to their RMSD to the crystal structure, determined using the average over 10 randomly chosen structures from each node. The clusters corresponding to starting poses A and B are labeled for each network, as well as the predicted lowest free-energy pose for this set of MSM parameters. (C and D) Nodes are colored according to their ligand SASA. In both networks, quasibound (green) and unbound (blue/black) nodes form a dense cluster, with deeply bound states (white/yellow) radiating outward from this cluster. To see this figure in color, go online.

The nodes in Fig. 5, A and B are colored according to the RMSD of the ligand to the crystal structure after aligning to the Cα atoms in the binding site. In both cases, starting pose A has a much lower RMSD to the crystal than pose B, as shown in Fig. 1. The lowest free-energy pose for this set of MSM parameters is indicated in both cases, as described above. Because of the nature of the network layout minimization algorithm, nodes that are far apart tend to interconvert more slowly than nodes that are close together. Tight groups of nodes can thus be considered to be in the same basin of attraction and to interconvert relatively quickly. For both systems, we find the lowest free-energy pose to be in the same basin of attraction as the lowest RMSD pose to the crystal structure.

The nodes in Fig. 5, C and D are colored according to the ligand solvent-accessible surface area (SASA). From these, we can clearly identify three deeply bound basins of attraction for Baz2B-ICR7 (yellow and white nodes) and two deeply bound basins for Brd4-MS436. The “pose A basin” for Baz2B-ICR7 corresponded to a deeper insertion of the ICR7 ligand, with roughly the same orientation as the crystal structure. The network shows that the crystal structure basin is “off pathway” with respect to “pose A” binding and unbinding transitions. The Brd4-MS436 “pose A basin” is also more deeply bound than the crystal structure and the lowest free-energy pose. However, the crystal structure in this case is “on pathway” with respect to “pose A” binding and unbinding transitions.

From the SASA network plots, it is also apparent how many distinct local minima exist with relatively similar predicted probabilities. The lowest free-energy poses have probabilities of 0.015 and 0.027 for Baz2B and Brd4, respectively. For Baz2B, there are 25 other states with at least half of this probability, with RMSDs to crystal ranging from 2.9 to 9.8 Å. For Brd4, there are seven other states that are at least half as probable, with RMSDs to crystal ranging from 3.0 to 9.9 Å. This abundance of states with similar stabilities underscores the challenge of conclusively predicting a single stable pose.

Pose interconversion pathways

The pose networks provide a detailed description not only of binding and unbinding pathways but the interconversion of different states. When a ligand interconverts between different bound poses, will this occur while the ligand remains loosely associated with the protein? Or will the ligand first unbind and then rebind in a different orientation? To answer this question, we label a set of nodes as “unbound” if the minimal distance between the ligand and the protein is greater than 5 Å. Note that this must be smaller than the cutoff we use for terminating unbinding trajectories (10 Å). We then divide the remainder of each network into communities using a modularity optimization algorithm implemented in Gephi (55). An extended transition matrix (T_α) is constructed (size 2N × 2N, where N = 1200 is the number of states) using an auxiliary variable α, where α = 0 if a trajectory has not yet visited the unbound state and α = 1 indicates a trajectory has visited the unbound state. To examine transition paths between communities A and B, we add probability sinks to T_α by replacing columns that correspond to A and B with identity vectors (i.e., probability can get in but cannot get out). By iteratively multiplying this matrix against itself, we can examine its steady state behavior and, for each state i, measure the committor probabilities $p_A^{U-}$, $p_B^{U-}$, $p_A^{U+}$, and $p_B^{U+}$, where the subscript indicates the destination basin and the superscript indicates if the transition path did (U+) or did not (U−) go through the unbound state. The probability of an A to B transition path being mediated by the unbound state is then equal to

$$p_{A\to U\to B}=\sum _{j\notin A}{\xi }_A\left(j\right)\frac{p_B^{U+}\left(j\right)}{p_B^{U+}\left(j\right)+p_B^{U-}\left(j\right)},$$ (5)

where ξ_A(i) is the probability that a trajectory, initialized in basin A, will exit into state i. The exit probabilities (ξ_A(i)) are calculated again using a sink matrix, this time using a sink for each state that is not in basin A. This analysis (referred to as “hub score analysis”) was previously used to study interconversion paths in protein-folding conformation space networks (53, 56) and is implemented in the CSNAnalysis package (54).

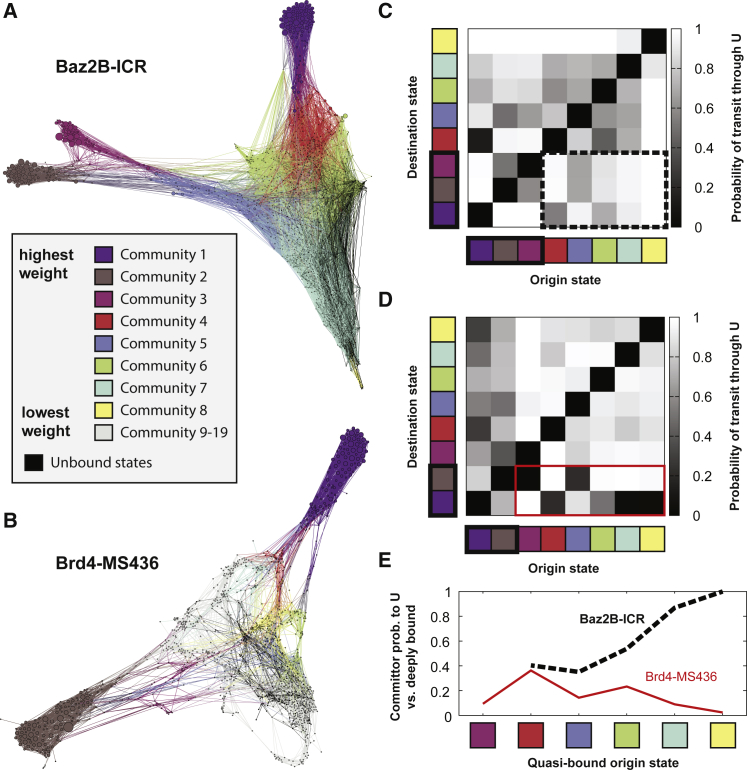
Fig. 6 shows the communities in each network (Fig. 6, A and B) and the probabilities that transition paths between these communities are mediated by the unbound state (Fig. 6, C and D). In both networks, the unbound states are shown as black nodes. It is important to note that the unbound states are not expected to form a cohesive interconverting community because the ligand can unbind from anywhere on the protein and a wide variety of unbound states are observed (as shown in Fig. S4). For Baz2B, there are three “deeply bound” communities: one for each of “pose A” (C2) and “pose B” (C1) and an additional community that includes the lowest free-energy state (C3). Brd4 has two deeply bound communities, corresponding to poses A and B. The community indices are ordered according to their total weight, with community 1 having the highest total weight.

Figure 6.

Bound-to-bound transition paths using the unbound state as a mediator. (A and B) Conformation space networks for Baz2B-ICR7 and Brd4-MS436, colored to show communities identified by modularity optimization. In both networks, communities are ordered according to their total weight, with community 1 (purple) having the highest weight. The unbound states are shown in black. In (B), communities 9–19 are shown in gray and are not considered in further analysis. (C and D) Matrices of mediation probabilities are shown for both systems. Each element in the matrix shows the probability that a transition path from the origin state to the destination state uses the unbound state as a mediator. For Baz2B-ICR7 (C), the first three communities are labeled “deeply bound” and are highlighted with a black rectangle. The dotted line surrounds the mediation probabilities for “quasibound” to “deeply bound” transitions. For Brd4-MS436 (D), the first two communities are labeled “deeply bound,” and “quasibound” to “deeply bound” transitions are marked with a solid red line. (E) compares the committor probability between unbound states and the set of deeply bound states for each quasibound starting state. To see this figure in color, go online.

In the bottom left of the matrices in Fig. 6, C and D, we see the probabilities that interconversion paths between the highest-weighted communities go through the unbound state. For Baz2B interconversion between the “pose B” community (C1, purple), with the “pose A” community (C2, gray) almost always goes through the unbound state (p = 0.99). Similarly, paths from “pose B” to C3 (magenta), which contains the crystal structure pose, go through the unbound state with p = 0.98. In the dashed rectangle, we see that paths from “quasibound” communities (C4–C8) to deeply bound communities go through the unbound state with high probability. Remarkably, even paths from C2 to C3 go through the unbound state with p = 0.504 and from C3 to C2 with p = 0.579. The lowest unbound mediation probability is for paths from C1 to C4 (p = 0.130), where C4 is directly between C1 and the unbound states. With this exception, we conclude that in the Baz2B network, interconversion between poses mostly proceeds through unbinding and rebinding. Significant differences are observed for the Brd4 mediation probabilities. Each quasibound state has a deeply bound state that it can transition to directly without passing through the unbound states (Fig. 6 D: dark gray and black squares in the red rectangle). However, transitions between the two deeply bound states are still mediated through unbound states more often than not (p = 0.820 for C1–C2 and p = 0.728 for C2–C1).

To further investigate the binding landscape, we determine the probability that quasibound trajectories will commit to either one of the deeply bound states or to the unbound states. A committor probability is determined for each quasibound state, and a weighted average (using the equilibrium weights of each state) is shown in Fig. 6 E for each community. We see significant differences between the two bromodomain-inhibitor systems, with most of the Baz2 quasibound communities committing to the unbound state and all of the Brd4 quasibound communities committing to deeply bound states. The Brd4-MS436 system can thus be thought of as a “dual-funnel”-shaped landscape, with two minima near poses A and B. The quasibound states exist halfway down this funnel and help guide the ligand to one of the two deeply bound orientations. In the Baz2B-ICR7 system, the quasibound states have still not crossed the rate-limiting step of binding, and the ligand is still free to reorient or not to bind at all. Although we only have examined two protein ligand systems, it is tempting to speculate that “funneling” is a hallmark of higher-affinity ligands, for which low free-energy, deeply bound states influence the committor probability of binding intermediates.

Discussion

Mapping the ligand binding landscape can teach us how ligands bind, how poses are connected, and which poses are the most stable. Here, we have shown that WExplore is able to efficiently build a model of the binding landscape and sample events with waiting times up to 280 ms (the release of MS436 from pose A). However, it is limited by the accuracy of the force field used for both the ligand and the protein. In particular, we suspect that the parameterization of ICR underpredicted the stability of the ring-stacked conformation. This could have led to the overprediction of the K_D in Table S2 and the extremely short MFPTs of ligand release (420 and 150 ns for poses A and B, respectively). In contrast, a Baz2B probe with 60 nM affinity, GSK2801, was measured using biolayer interferometry to have a k_off of 6.95 × 10⁻³ s⁻¹, which would have an MFPT of 144 s (36).

Pose prediction by integrating unbinding simulations into a network model presents a novel approach to a difficult problem. Previously, it was shown that long, straightforward simulations can discover binding poses. Shan et al. directly simulated binding of two inhibitors to Src kinase, obtaining four binding events in 150 μs of total simulation (57). Generally, ligand binding occurs more quickly than unbinding and is thus more amenable to direct simulation. However, the residence time of each pose, which can be obtained only through simulating ligand release, is also necessary to rank pose stability. Clark et al. used induced fit docking in combination with metadynamics to determine pose stability (58). Ten trajectories were run for each pose, each 10 ns in length. The authors showed an improvement over induced fit docking alone, and the cost of this approach (100 ns per ligand per pose) is much cheaper than the approach presented here (2.1 μs per pose). However, the metadynamics approach can only rank poses and cannot discover new poses that were not in the induced docking set. It also requires the definition of an order parameter that is appropriate to use for each pose and each system, which is not straightforward. It is worth noting also that our combined network model approach becomes more accurate as more starting poses are added to the system. One could imagine, for example, adding short simulations from a large number of additional starting poses to the networks constructed here.

The finding that most poses interconvert through the unbound state has direct implications for the discovery of new bromodomain inhibitors. A common approach in virtual screening is to combine docking with molecular dynamics simulations to evaluate binding pose stability (59, 60, 61). This is typically done as a filter late in a screening pipeline, for instance, to select the top 24 compounds in a set of 55 (62). To assess the stability of binding poses, it is common to use trajectories that are tens to hundreds of nanoseconds in length. (For comparison, the longest trajectories run here are 14.6 ns in length). In the regime in which poses interconvert directly without unbinding, a single stability measurement could report on multiple poses. However, as we find that different poses are typically connected through the unbound state, we would recommend testing multiple putative bound poses for each compound during screening and discarding only compounds that show no stable poses.

This finding has similar implications for kinetics-based drug design. In the regime in which poses interconvert directly, all poses will have similar off rates. Interconverting through the unbound state implies that a weighted average of pose-specific unbinding rate constants $\left(k_{\text{off}}^i\right)$ should be used to determine an apparent rate constant $\left(k_{\text{off}}^{\text{app}}\right)$:

$$k_{\text{off}}^{\text{app}}=\frac{{\sum }_{i\in \mathit{\Omega }}{\mathit{\pi }}_i{k}_{\text{off}}^i}{{\sum }_{i\in \mathit{\Omega }}{\pi }_i},$$ (6)

where the sum is over the set of all bound states (Ω) and π_i is the probability of state i. If one bound state is much more populated than the others (e.g., ${\pi }_i\gg {\pi }_j$ $\mathit{\forall }$ $j\ne i$), then $k_{\text{off}}^{\text{app}}\approx k_{\text{off}}^i$.

Mapping the binding landscape could also aid in our understanding of biological processes. By studying the landscape of natural protein-ligand association processes such as enzyme substrates, we can observe whether proteins have evolved to maximize the fraction of successful binding encounters. Nature-inspired strategies to maximize binding rates could be useful to help improve binding affinities, as well as improve the selectivity profiles of covalent inhibitors.

Author Contributions

A.D. designed the project, performed the computation and analysis, and wrote the manuscript.

Editor: Alan Grossfield.