Dynamics of Chromatin Fibers: Comparison of Monte Carlo Simulations with Force Spectroscopy

Abstract

To elucidate conformational dynamics of chromatin fibers, we compared available force-spectroscopy measurements with extensive Monte Carlo simulations of nucleosome arrays under external force. Our coarse-grained model of chromatin includes phenomenological energy terms for the DNA-histone adhesion and the internucleosome stacking interactions. We found that the Monte Carlo fiber ensembles simulated with increasing degrees of DNA unwrapping and the stacking energy 8 kT can account for the intricate force-extension response observed experimentally. Our analysis shows that at low external forces (F < 3.0 picoNewtons), the DNA ends in nucleosomes breathe by ∼10 bp. Importantly, under these conditions, the fiber is highly dynamic, exhibiting continuous unstacking-restacking transitions, allowing accessibility of transcription factors to DNA, while maintaining a relatively compact conformation. Of note, changing the stacking interaction by a few kT, an in silico way to mimic histone modifications, is sufficient to transform an open chromatin state into a compact fiber. The fibers are mostly two-start zigzag folds with rare occurrences of three- to five-start morphologies. The internucleosome stacking is lost during the linear response regime. At the higher forces exceeding 4 picoNewtons, the nucleosome unwrapping becomes stochastic and asymmetric, with one DNA arm opened by ∼55 bp and the other arm only by ∼10 bp. Importantly, this asymmetric unwrapping occurs for any kind of sequence, including the symmetric ones. Our analysis brings new, to our knowledge, insights in dynamics of chromatin modulated by histone epigenetic modifications and molecular motors such as RNA polymerase.

Introduction

The hierarchical organization of eukaryotic DNA into nucleosomes and higher-order structures has profound implications for DNA accessibility by regulatory factors. Nucleosome arrays present a barrier to DNA-binding proteins in two ways. First, the DNA fragments wrapped in nucleosomes are 145–147 bp (1, 2), whereas the linkers are 15–80 bp long depending on the organism and cell type (3), indicating that more than two-thirds of the eukaryotic genome is sterically blocked by histones. The second obstacle is the chromatin compaction induced by internucleosome stacking interactions (4). It is widely accepted that posttranslational modifications of histone tails can alter these interactions and thereby change the level of compaction of chromatin and the DNA accessibility (5, 6, 7, 8, 9). Therefore, elucidating the structural details of conformational transitions in chromatin is one of the central problems in molecular cell biology.

One of the promising approaches to this problem is force spectroscopy, which allows for picoNewton (pN) manipulation and nanometer-precision measurements of single chromatin fibers under external force (10, 11, 12, 13, 14, 15, 16, 17). However, the structural interpretation of the data at the subnucleosomal level remains elusive. For example, there are ongoing debates about the existence of regular stacked fiber arrays at low forces versus open unstacked conformations and solenoid versus zigzag geometries and whether the internucleosomal stacking plays a role or the unwrapping of DNA from histones can account for all the force-spectroscopy observations (10, 11, 12, 13, 14, 15, 16, 17, 18, 19). To obtain structural information at the mononucleosomal level, an appropriate stereochemical model that adequately describes the known structural and dynamic characteristics of chromatin fibers is necessary.

Cui and Bustamante (10) were the first to analyze chromatin fiber stretching under external force, using optical tweezers. They interpreted the nonlinear force-extension curves as a transition between condensed and decondensed states of the fiber. Fitting their data by the worm-like chain polymer model, they estimated the internucleosome interaction energy, E, to be ∼3 kT (in solution containing 40–150 mM NaCl). Unwrapping of nucleosomal DNA was not considered in their model. Kruithof et al. (13) used magnetic tweezers and the 601 nucleosome positioning sequence to probe the unfolding of chromatin at a higher resolution, particularly at small forces. They found that at forces up to F ≈ 3 pN, the fiber stretches reversibly similar to a Hookean spring, whereas at force F ≈ 4 pN, there is a plateau, hypothetically related to the unstacking of nucleosomes. Based on a two-state statistical-mechanical model of the fiber, a higher estimate for the stacking energy was suggested, E ≈ 14 kT (in the presence of Mg²⁺ ions). It was proposed that a fiber with the nucleosome repeat length (NRL) 167 bp has the two-start “stiff” configuration, whereas NRL = 197 bp corresponds to a more flexible solenoid conformation. Later on, van Noort and co-workers (15) presented a more elaborate theoretical analysis of the force-extension curves. They estimated the stacking energy to be E ≈ 10 kT, with ∼30 bp DNA being unwrapped even at small forces.

However, the same experimental data were interpreted differently by other authors. For example, Victor et al. (18) explained both the linear and the plateau force regimes observed by Kruithof et al. (13) by gradual unwrapping of DNA, solely within the zigzag model of fiber morphology. Chien and van der Heijden (19) also suggested that the force plateau regime represents the unwrapping of DNA rather than the unstacking of nucleosomes. They put the upper limit E ≈ 1 kT on the stacking interaction. This short overview demonstrates that the interpretation of force-extension data based on “simple” polymer models is quite ambiguous. In particular, the stacking energy estimates vary from E ≈ 1 to 15 kT based on the same data. Clearly, a more sophisticated model of chromatin is required that is in accord with experimental observations and resolves more structural details.

Potentially, Monte Carlo (MC) simulations can shed light on the conformational dynamics of chromatin fibers, including force-induced chromatin unraveling. To span efficiently a structurally rich conformational space of oligonucleosomal arrays, various coarse-grained MC approaches have been employed (20, 21, 22, 23, 24, 25, 26, 27, 28, 29). In particular, Collepardo-Guevara and Schlick (24) used an integrated chromatin coarse-grained model to analyze the role of dynamic-linker histone in chromatin fiber softening. However, because the ability of the nucleosomal DNA to peel off the histone was not included in this model, the simulated fiber extensions were noticeably less than those observed experimentally. Recently, Dobrovolskaia et al. (25) and Lequieu et al. (26) independently introduced coarse-grained models to investigate the dynamics of force-induced unwrapping of DNA in single nucleosomes. Kepper et al. (27) considered DNA unwrapping, and although their model adequately describes the inner-turn unwrapping of DNA at high forces, at small forces (F < 6 pN) their calculations overestimate the stretching response of the fiber measured experimentally.

Overall, the MC simulation studies published so far correctly reproduce certain parts of experimentally observed fiber unraveling but fail to describe the whole process precisely. Therefore, we found it necessary to perform a new round of systematic MC simulations of chromatin fibers under external force, especially in light of the recent high-resolution force-spectroscopy measurements revealing the dynamic unwrapping-rewrapping transitions in nucleosomes in great detail (11, 12, 13, 14, 15, 16). These data indicate that the low-force extension brings about a gradual symmetric unwrapping of DNA, whereas at high forces, the unwrapping becomes stochastic and asymmetric, with one DNA arm opened much stronger than the other arm (16).

Here, we used the available data on the DNA unzipping dwell times (12) to elucidate a free-energy profile for unwrapping and from that analyze, in silico, the dynamic response of nucleosomal arrays to external force. We employed our coarse-grained model of chromatin fiber that has proven to be effective in predicting conformational and topological aspects of nucleosomal arrays with variable NRL (30). This approach allowed us to distinguish between unwrapping and unstacking of nucleosomes in different force regimes in agreement with experiments.

Materials and Methods

We simulated nucleosome arrays consisting of 12 sequential nucleosome-linker units. The variable parameters of the system were the NRL and the DNA unwrapping, U, in bp, stacking energy E in kT, and external force F in pN. We used the template crystal structure of a nucleosome core particle with the Widom 601 DNA sequence resolved by x-ray crystallography (PDB: 3MVD (31)). This part was assumed to be fixed during simulations and only goes through rigid body motions except for the unwrapped DNA, which is treated as a part of the “dynamic” linker DNA. The linker DNA was modeled at the level of dimeric steps, and its trajectory was described by six base-pair step parameters (30, 32). The geometry of the linker DNA fluctuates around the regular B-DNA. Note that a system of linker size L (NRL = 145 + L) and average unwrapping U has 6 × (L + 2U + 1) degrees of freedom per nucleosome.

We used the following energy terms: elastic, electrostatic, histone H4 tail-acidic patch interactions, and the steric hindrance as we employed in a previous study (30). Moreover, the work done by the external force and changes in the adhesion energy of unwrapped DNA were added to the total energy (Fig. S1). Here are some details regarding the energy terms:

• 1)The elastic energy of the linker DNA deformations was calculated using a knowledge-based quadratic potential function (32).
• 2)The electrostatic energy was calculated using the Coulomb potential with a 30-Å cutoff. Positive charges on arginines and lysines, as well as negative charges on aspartates, glutamates, and DNA phosphates were considered. All charges were partially neutralized to mimic the salt screening effects.
• 3)Stacking or the H4 tail – acidic patch interactions were modeled phenomenologically, with the variable internucleosome interaction energy E and a 35-Å range of action (30).
• 4)Steric clashes were modeled by a van-der-Waals-like repulsion potential.
• 5)Work done by the external force F was calculated as –F × Z_ext, where the last term is the fiber extension measured along the external force.
• 6)The DNA-histones adhesion energy was obtained by translating the DNA unzipping dwell times measured by Hall et al. (12) into the energy profile G_adh(U) (Fig. S2).

For starting conformations, the DNA linkers were constructed randomly using the Gaussian sampling method (33). Afterward, the following MC steps were performed:

• 1)randomly selecting a DNA base-pair step in one of the “dynamic” linkers and alteration of its six parameters by adding a random perturbation,
• 2)updating positions of all nucleosomes in the nucleosome array, and
• 3)computing the energy difference and performance of the Metropolis acceptance test (34).

Every construct was simulated for 150 million MC steps for a given E and force F. The final 100 million MC steps were used for statistical averaging of various parameters of the system (e.g., average Z_ext and fraction of stacked nucleosomes). Two rounds of simulations were performed, first with constant unwrapping U and then with the dynamic unwrapping. The first round gave us a general idea on the level of the fiber extension that would match the experiment at each force regime. However, this approach does not reflect the asynchronous and stochastic nature of the nucleosome unwrapping. Therefore, in the second round, the DNA unwrapping was described by the independent parameters U^L_i and U^R_i representing the numbers of unwrapped basepairs at the left and right ends of nucleosome i. A snapshot of such a nucleosomal array is depicted in Fig. 1. Details of the fiber geometry, energy terms, and MC moves are given (Figs. S1–S3).

Figure 1.

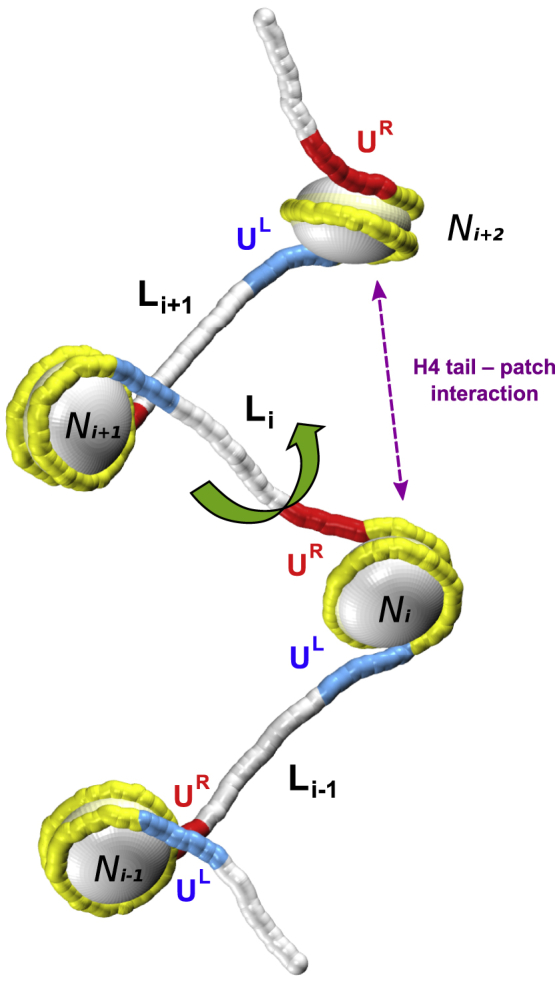
Schematic presentation of a nucleosome array and the variable parameters of the system. The DNA unwrapping is described by parameters U^L and U^R representing the numbers of unwrapped basepairs at the left and right ends of nucleosomes. (The U^L and U^R values are changing independently in each nucleosome.) The static histone cores are shown by the white beads and the static wrapped DNA is shown in yellow, whereas the dynamic linkers are shown as white, blue, and red tubes. In a single MC step, a dynamic linker L_i (connecting nucleosomes N_i and N_i+1) is chosen. Then, in this linker, a dimeric step is selected for modification (green arrow). Details of the fiber geometry, energy terms, and MC moves are given in Figs. S1–S3. To see this figure in color, go online.

In the first round of simulations, fibers with unwrapping U = 0, 5, …, 60, and 72 bp (free DNA) and stacking energy E = 0, 6, 8, 10, and 12 kT were analyzed. In all cases, the force was varied from 0 to 8 pN with steps of 0.5 pN. We found that the best fit of the force-extension data was obtained for E = 8 kT. This stacking energy was used in the second round of simulations with stochastic unwrapping of nucleosomes. Overall, ∼3000 simulations (3000 × 150 million MC steps) were performed on the National Institutes of Health supercomputer cluster, Biowulf.

Compactness of the chromatin and distribution of internucleosomal distances are important characteristics describing the geometry of a fiber. We measured the level of compaction by the average stacked fraction (SF) of nucleosomes in a fiber. The SF was calculated by dividing the total stacking energy to the maximal possible stacking energy for each MC snapshot. We also calculated the frequency of internucleosome interactions (FINI) in our MC ensembles. This value represents nearest-neighbor interactions along the chromatin fiber. To calculate the FINI, two nucleosomes i and i+n are considered to be in contact if the center-to-center distance is less than 120 Å. Total contacts are normalized to all possible neighbors with distance n along the fiber. These contact map profiles provide important information regarding the fiber morphology.

Results

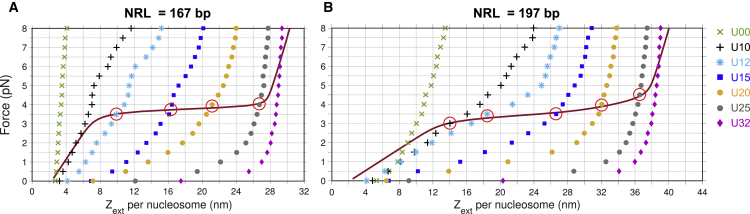
In this study, we compared extensive MC simulations with the force-spectroscopy measurements reported by Meng et al. (15), who employed DNA vectors with inserts containing 30 × 167 and 15 × 197 bp repeats of the Widom 601 nucleosome positioning sequence. Extracting the force-extension response of the nucleosome arrays from raw experimental data is explained in Fig. S4. The adjusted experimental data are presented in Fig. 2 as thick solid lines. For the MC simulations, first we analyzed the role of the uniform DNA unwrapping in the fiber stretching in the absence of stacking interactions (E = 0). Then, we investigated how changes in the internucleosome stacking energy, E, influence the force-extension maps of the fibers. Comparison of the Meng et al. (15) data with MC simulations revealed a consistent picture of unstacking and unwrapping of nucleosomes as a function of external force. Furthermore, our simulations are in agreement with the stochastic asymmetric unwrapping of nucleosomes observed by Ngo et al. (16).

Figure 2.

Force-extension profiles for fibers with NRL = 167 bp (A) and 197 bp (B) for various degrees of unwrapping of nucleosomes, U, varying from 0 to 32 bp, with stacking energy E = 0. The symbols represent the average extension per nucleosome obtained from MC simulations. The solid curves represent experimental data (15). The circles indicate the points of intersection of the MC curves with the experimental (F, Z_ext) curves in the central plateau region. Simulations were performed for forces from 0 to 8 pN in steps of 0.5 pN. The standard deviation (SD) of the extension, Z_ext, is ∼1 nm at low forces; it shrinks below 0.2 nm at high forces. Curves for U = 5, 60 bp, and free DNA are presented in Fig. S5. To see this figure in color, go online.

Role of nucleosome unwrapping in the fiber stretching

The experimental and MC-simulated force-extension (F, Z_ext) responses are presented in Figs. 2 and S5. The experimental curves are naturally divided into the following three regions:

The left shoulder, with forces less than 3 pN

The MC-simulated curves demonstrate a linear force-extension dependence for small uniform unwrapping U ≤ 12 bp in this regime. Importantly, the inclination of the MC curves for U ∼10 bp are close to that of the experimental curves (for both NRL = 167 and 197 bp). Of note, the slope of the (F, Z_ext) curve (or stretching stiffness of the fiber) strongly depends on the nucleosome spacing: the stiffness is 0.65 pN/nm for NRL = 167 bp and 0.3 pN/nm for NRL = 197 bp, in close agreement with experimental data. Therefore, the experimentally observed linear response is not necessarily an indication of a fully stacked fiber as proposed earlier (15, 17).

The plateau region, with intermediate forces F = 3–4 pN

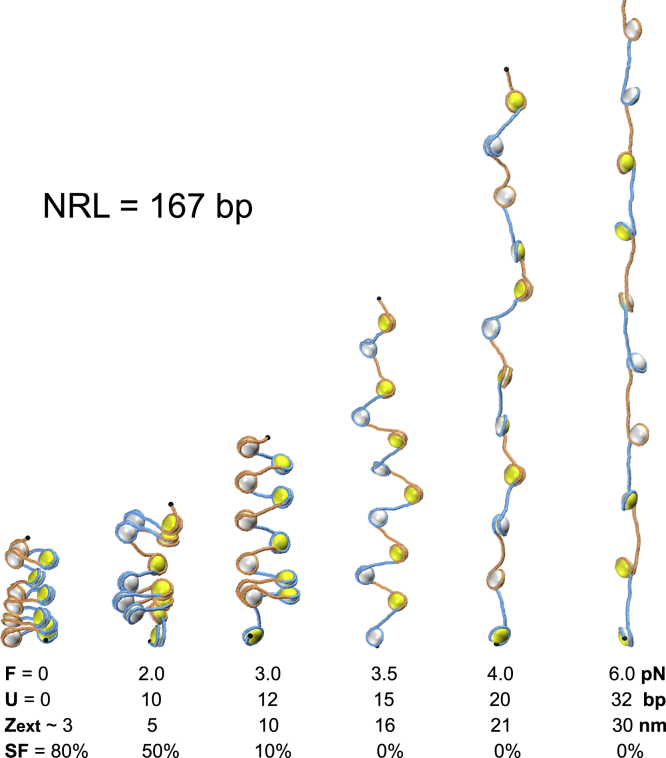
The left and right boundaries of the plateau approximately correspond to U = 10 and 25 bp. Here, inclinations of the experimental force-extension curves are close to zero, indicating significant fiber stretching under the constant load. The MC curves intersect the experimental (F, Z_ext) curves in the central plateau region (see the circles in Fig. 2). Remarkably, the increase in fiber extension in the plateau region is nearly the same, ΔZ_ext = 20 ± 2 nm, for NRL = 167 and 197 bp, which is in accord with equal unwrapping of nucleosomal DNA in these two cases. This requires that at this level of fiber extension (Z_ext > 10–15 nm for NRL = 167–197 bp, respectively) the internucleosome stacking is lost. Figs. 3 and S6 represent the stretched conformations simulated at E = 8 kT. They show that before the plateau force (F ≈ 3.5 pN) all internucleosomal stacks disappear.

Figure 3.

Typical conformations of chromatin fiber with NRL = 167 bp simulated for external forces increasing from 0 to 8 pN. Our comparative analysis reveals that at small forces, F ≤ 3.0 pN, the DNA unwrapping is insignificant, U ≤ 12 bp, and the fiber remains relatively compact despite numerous stacking-unstacking events. With an increase in applied force, the unwrapping of nucleosomal DNA becomes more pronounced and increases to U = 20 bp at F = 4 pN and up to U = 32 bp at F = 8 pN. These MC simulations were performed for stacking energy E = 8 kT. Note, however, that for F = 3.5 pN and higher, the internucleosome stacking is lost completely, and therefore, the results do not depend on the E value. The force-unwrapping, force-extension, and force-unstacking dependencies are presented at the bottom. Fiber conformations for NRL = 197 bp are presented in Fig. S6 (see also the Video S1 and S2). To see this figure in color, go online.

The right shoulder, with forces higher than 4 pN

The experimental curves display a “steep” inclination at F > 4.0 pN. The severely extended conformations of the fiber at these forces indicate a significant unwrapping of nucleosomal DNA by U = 25–32 bp, which corresponds to a complete unfolding of the outer-turn DNA (Fig. 4 A). Notably, for U ≥ 25 bp, the force-extension curves behave similar to a semiflexible polymer. The MC curves for U = 25–72 bp can be fitted by the worm-like chain model with the persistence length ranging from 20 to 70 nm (Fig. S5).

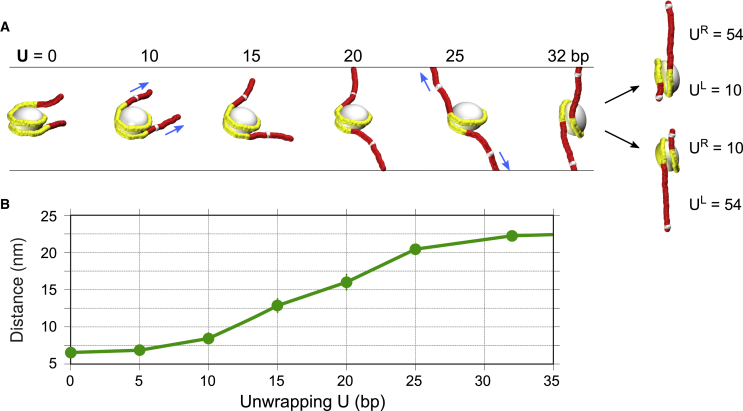
Figure 4.

Gradual unwrapping of nucleosomes facilitates fiber stretching. (A) Typical conformations of nucleosomes in extended fibers. For unwrapping U = 0, all nucleosomal DNA is attached to histones (shown in yellow). For U > 0, the unwrapped DNA is represented by the red fragments located between the ends of the yellow fragments and the white markers (NCP positions 1 and 145). An increase in U brings about an increase in the angle between the DNA end vectors (arrows starting at the white markers) so that for U = 25–32 bp, this angle is ∼180°, with the end vectors perfectly aligned along the external force. The alternative asymmetric conformations on the right, with U^L and U^R equal to 10 or 54 bp, have the same average degree of unwrapping as the U = 32 bp case and generate the same level of extension (Z_ext). However, the form of the adhesion energy profile and the stochastic dynamic of unwrapping-rewrapping dictates that these asymmetric conformations are preferable (Figs. 5 and S8). (B) The nucleosome end-to-end distance (between the white markers in (A)) as a function of unwrapping, U. The largest increase in this distance occurs between U = 10 and 25 bp, which roughly corresponds to the plateau limits (Fig. 2). To see this figure in color, go online.

The structural details of the fiber extension become clear from analysis of the nucleosome end-to-end distance as a function of unwrapping U, or end-to-end distance Dist(U) (Fig. 4 B). Indeed, the slope of the Dist(U) curve is the highest in the interval U = 10–25 bp. Here, unwrapping of the nucleosome by 10 bp brings about an increase in the end-to-end distance of ∼8 nm, whereas at the left and right ends of the Dist(U) plot, the same unwrapping produces an increase of only ∼2 nm. The Dist(U) dependence can be explained qualitatively by comparing trajectories of the partially unfolded nucleosomal DNA (Fig. 4 A). When unwrapping increases from U = 10 to 25–32 bp, the angle between the DNA linkers (or the end vectors) increases from zero to ∼180°; accordingly, the nucleosome end-to-end distance (and the total length of the fiber) also significantly increases. Earlier, similar unfolding geometries were reported for single nucleosomes under external tension (25, 26, 35). Overall, these geometric considerations provide a simple structural explanation of the nonlinear relationship between fiber stretching, Z_ext, and unwrapping of DNA in nucleosomes, U (Fig. 2).

Internucleosome stacking and fiber stretching

As shown in the previous section, the increasing unwrapping accompanying an increase in external force appears to explain most of the experimental observations. However, there is a discrepancy between our MC simulations and experimental results for NRL = 197 bp at the small force regime; MC simulations predict a more extended fiber than the experiments demonstrate. For example, at F = 1 pN, MC predicts an average extension Z_ext ≈ 8.0 nm, whereas the experiment shows a ∼6.0 nm extension (Fig. 2 B). This difference might be an indication of the attractive stacking interactions that force the fiber to shrink.

Therefore, we systematically changed the stacking energy E from 0 to 12 kT and unwrapping U up to 15 bp (for both NRL = 167 and 197 bp); see Fig. S7. (The values U > 15 bp are excluded from consideration, because they do not show a stable linear behavior at small forces.) Overall, the stretching behavior of the fibers is characterized by two “natural” trends: unwrapping makes a fiber more flexible and leads to more extended conformations, whereas an increase in stacking interaction makes a fiber stiffer and reduces the length of the fiber. As follows from the force-extension curves presented in Fig. S7, the stacking energy E ≈ 8 kT can reproduce the experimentally observed extension of the chromatin fiber.

Dynamic unwrapping of nucleosomes

Until now, we assumed that the DNA unwrapping (described by the model parameter U) is the same in all nucleosomes. However, the DNA unwrapping is a stochastic process (16, 36, 37). To take this into account, we considered a more sophisticated model with independent unwrapping of DNA at the left and right ends of each nucleosome and the DNA-histones adhesion energy, G_adh(U), calculated as described in the Supporting Materials and Methods.

Before proceeding to the results of these simulations, note that according to the unzipping experiments by Hall et al. (12), the DNA-histone interactions are the strongest at positions 15–25 bp from the nucleosome ends and at positions 55–73 bp (that is, close to the nucleosome dyad), with relatively weak interactions in other regions of nucleosomal DNA. Accordingly, the adhesion energy function (modeling these interactions) has a nonlinear profile (Fig. S2). As shown below, this is important for understanding the dynamic unwrapping of nucleosomal DNA.

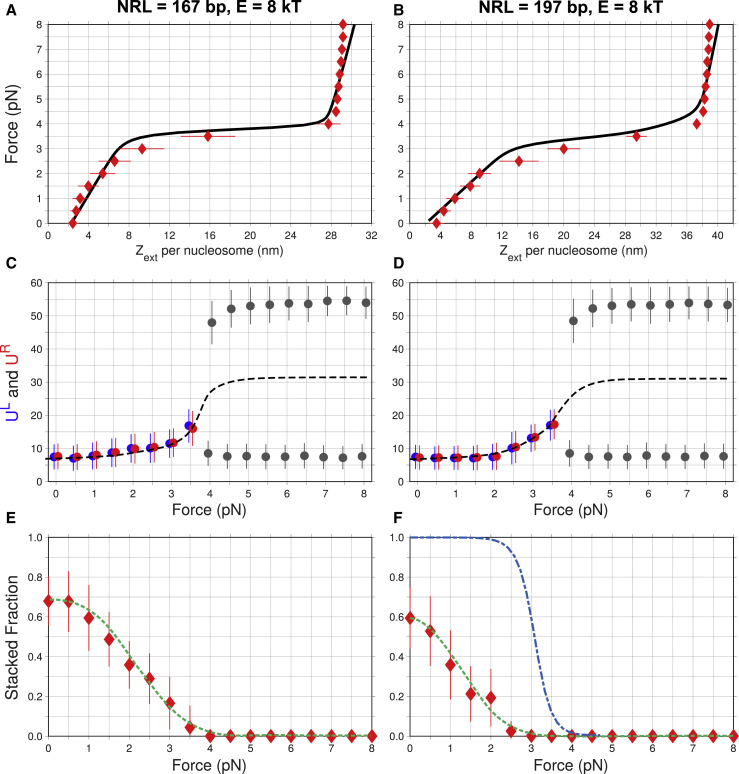
The force-extension dependencies obtained in these simulations are generally consistent with the experimental data, for both NRL = 167 and 197 bp (Fig. 5, A and B). Note, in particular, that the largest increase in Z_ext is observed in the plateau region, where changes in the fiber extension are the strongest according to the Meng et al. (15) measurements. At small forces, F ≤ 3.0 pN, the average unwrapping (U^L and U^R) changes from 8 to 12 bp (Fig. 5, C and D). These values are very close to our estimates based on the uniform unwrapping simulations (Figs. 2 and S7, C and D).

Figure 5.

Response of the nucleosomal arrays (extension, unwrapping, and stacked fraction (SF)) to the external force. (A and B) The MC force-extension profiles (red diamonds) were calculated using the adhesion potential, G_adh(U), for DNA unwrapping (Fig. S2) and E = 8 kT for stacking interactions. Note that the linear response persists up to F = 2.0–2.5 pN in both cases. The solid curves represent the adjusted experimental data (15). (C and D) DNA unwrapping at the left and right ends of nucleosomes (U^L in blue and U^R in red) is shown as a function of force. The average values are shown as circles, and SDs are shown as bars. As the external force increases from 0 to 3 pN, the DNA unwrapping (U^L and U^R) gradually changes from 8 to 12 bp, with an SD ∼4 bp. These values are the averages over all 12 nucleosomes in the array and are in accord with our findings for the uniform U values (Figs. 2 and S7). At F ≥ 4.0 pN, the DNA unwrapping undergoes bifurcation into two branches with U ≈ 8 and 54 bp. Here, the circles and bars are shown in gray (i.e., not in red or blue), because asymmetric unwrapping occurs stochastically, that is, on average the chances of each nucleosome end (U^L or U^R) to be strongly unwrapped are equal (see Figs. S2 and S8 for details). The dashed curves represent the average unwrapping for both nucleosomal ends and exhibit a sigmoidal trend. (E and F) Average SFs of nucleosomes in fibers are shown as a function of force. Stacking energy is E = 8 kT. The sigmoidal blue curve is a result of statistical-mechanical modeling by Meng et al. (Fig. 3 D in (15)). The dashed green curves are sigmoidal fits over the MC results. Note that we do not observe a fully stacked fiber (SF = 1) at any force. To see this figure in color, go online.

At force F = 4.0 pN, we observed an abrupt change in DNA unwrapping. As shown in Fig. 5, C and D, the values U^L and U^R split into two branches, with U ≈ 8 and 54 bp. Both U^L and U^R values are equally likely to be in the top and bottom branches; therefore, for F = 4.0 pN and higher, we used gray symbols (instead of red or blue). Additional details of this bifurcation are presented in Figs. S2 and S8. The main result is that at forces F ≥ 4.0 pN, the distribution of DNA unwrapping becomes bimodal, with one peak corresponding to the U^L and U^R values ∼10 bp and the second peak corresponding to a significant unwrapping of 55 (±10) bp. The bimodal distribution of DNA unwrapping (U^L ≠ U^R) helps decrease the total adhesion energy under strong tension. (For example, it is more favorable to have a strong unwrapping U ≈ 55 bp at one end, rather than to have intermediate unwrapping U ≈ 30 bp at the both ends of a nucleosome). Also, note that the asymmetrically unwrapped nucleosomes have Z_ext values comparable to the symmetric structure (Fig. 4 A). Therefore, the amount of work done by the external force is similar for the symmetric and asymmetric unwrapping. In turn, the observed bimodality is a consequence of the specific shape of the adhesion energy profile, namely, its downward curvature at U ≈ 25 bp (Fig. S2). Importantly, there is no cooperativity in asymmetric unwrapping of neighboring nucleosomes, that is, the left and right arms of adjacent nucleosomes unwrap independently.

Probably, the most unexpected observation is that at high forces, the nucleosomes’ spontaneous unwrapping occurs asymmetrically despite their intrinsically symmetric structure (we did not consider sequence asymmetries in our computations). These results are consistent with the fluorescence force-spectroscopy measurements by Ngo et al. (16) for the quasisymmetric sequence 601RTA. Using single-molecule fluorescence resonance energy transfer spectroscopy at force F = 5–15 pN, they observe considerable unwrapping at one end of nucleosome, whereas the other end remains (almost) fully wrapped. The probability of opening is equal for both sides of nucleosome 601RTA when averaged over many experimental traces, but in each individual trace, only one end is open. These observations may have profound consequences for the regulation of transcription.

Dynamic stacking of nucleosomes in the linear force regime

We found that the nucleosome arrays are not fully stacked in MC-simulated fibers. Because of thermal fluctuations, a significant number of nucleosome stacks are broken at E = 8 kT, even in the absence of external force (Fig. 5, E and F). An increase in the external force leads to a rapid, sigmoidal decrease in the SF of nucleosomes. A similar sigmoidal type of behavior was predicted by Meng et al. (15) based on a multistate statistical mechanical modeling of chromatin stretching (see blue curve in Fig. 5 F). However, it is assumed in the cited model that the fiber remains in a regular, fully stacked configuration during the linear phase of extension. The transition from a fully stacked to a fully unstacked fiber occurs at the plateau force F ≈ 3.5 pN according to their model (13, 15). Our MC simulations, without any assumption on the fiber regularity, indicate that sigmoidal transition occurs at smaller forces (F ≈ 3.0 pN), and all nucleosome stacks are disrupted before the plateau force regime begins. Thus, according to our computations, the plateau region represents unwrapping and not unstacking of nucleosomes (for E = 8 kT, faithfully reproducing the experimental data (15)). If, however, the stacking energy is increased to E = 12 kT, the fibers remain fully stacked up to forces ∼2.0 pN (Fig. S9), and the plateau level can exceed 4 pN (Fig. S7, E and G).

In summary, our results strongly suggest that the linear response (observed for the left shoulder of the force-extension curve) does not necessarily mean that nucleosomes are fully stacked in this regime (15). The more recent data on the fibers with the histone H4 tails cross-linked to the H2A acidic patches (17) are also compatible with the dynamic stacking model described here. It is highly likely that upon cross-linking, certain amounts of stacking interactions become permanent, whereas the fiber as a whole remains partially unstacked.

Simulation trajectories

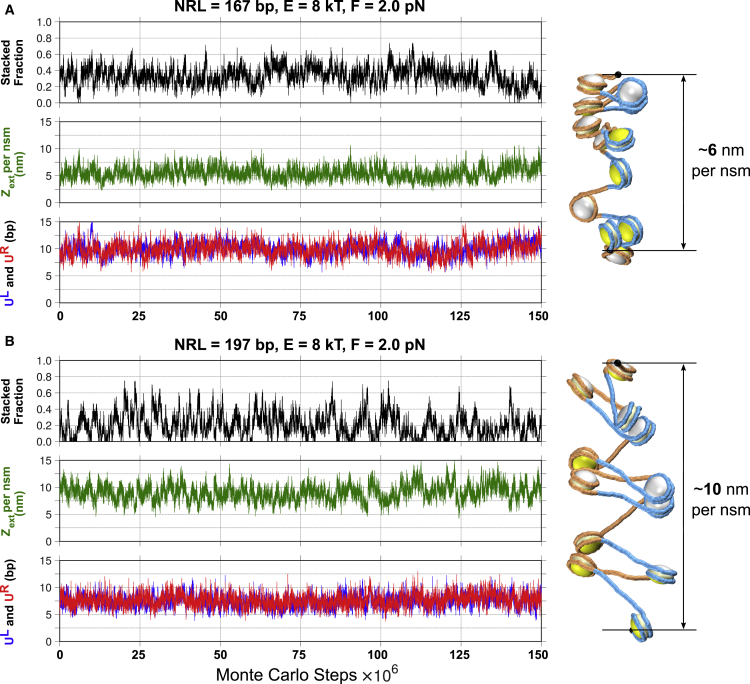
The highly dynamic nature of nucleosome arrays, in simulations with E = 8 kT, is shown in the MC trajectories presented in Fig. 6. Whereas the total energy equilibrates quickly, variations in structural parameters such as the SF of nucleosomes and extension per nucleosome, Z_ext, remain significant. This means the equilibrium comprises multiple stacking-unstacking transitions at small forces. In other words, fiber is neither completely stacked nor completely open at all times. Examples of such half-open structures are given in Fig. 6. Note that the averages of U^L, U^R, and Z_ext demonstrate a remarkable stability in equilibrium, despite wide variations in the SF of nucleosomes, from SF = 0 to 0.7 (Fig. 6). The SD of extension per nucleosome, Z_ext, is ∼1.0 nm, or ∼20% of the average value at small forces, comparable to fluctuations observed in experiment (Fig. S4). It is notable that stacking-unstacking fluctuations do not produce any detectable stepwise extensions (Fig. 6). In addition, the U^L and U^R variations, averaged over 12 nucleosomes in the array, are presented in this figure. Similar traces for higher forces, the average unwrapping as a function of force, as well as statistics of U^L and U^R values for individual nucleosomes in the 12-mer arrays are shown in Fig. S8. In particular, we found that on average, unwrapping of the terminal nucleosomes is similar to that of the internal ones (Fig. S8).

Figure 6.

Changes in the fiber parameters during MC simulations show dynamic unwrapping and stacking of fibers. 150 × 10⁶ MC equilibrated steps are shown for NRL = 167 bp (A) and 197 bp (B) at F = 2 pN. (Top) The fraction of stacked nucleosomes is shown. Equilibrium involves multiple stacking-unstacking transitions. (Middle) The extension per nucleosome is presented. The SD of extension is ∼1.1 nm for NRL = 167 bp construct and ∼1.4 nm for 197 bp. (Bottom) U^L and U^R are shown as a function of MC steps. Note that these U^L and U^R values are the averages over 12 nucleosomes in the array. Examples of the equilibrated conformations are shown on the right. Note that the structures became half open during simulations. They show the ∼6-nm vs. ∼10-nm extensions consistent with the experimental data (15); see Fig. 5, A and B. To see this figure in color, go online.

Internucleosome contacts

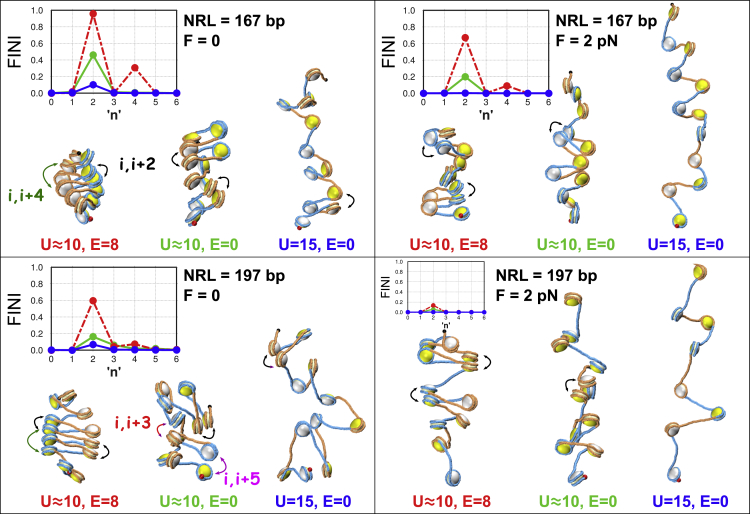
In addition to the SF of nucleosomes, we calculated the FINI in our MC ensembles (Fig. 7). This approach is similar to the electron-microscopy-assisted nucleosome interaction capture analysis of the cross-linked nucleosome arrays made by Grigoryev et al. (38). These contact-map profiles provide important information about the relative compactness of the fiber and its morphology. For example, we observe a decrease in the FINI values if the nucleosome spacing is increased (NRL = 167 vs. 197 bp) or if an external force is applied (F = 0 vs. 2 pN). Naturally, an increase in the stacking energy places the distal nucleosomes in close proximity (cf. E = 0 with E = 8 kT). A decrease in unwrapping from U = 15 to 10 bp also results in additional interactions between the nucleosome beads.

Figure 7.

Geometry and frequency of internucleosome contacts are shown for F = 0 and 2 pN. The insets show the frequency of internucleosome interactions (FINI) between nucleosomes (i, i + n). Red indicates the interaction patterns for E = 8 kT and U ≈ 10 bp, green indicates E = 0 and U ≈ 10 bp, and blue indicates E = 0 and U = 15 bp. The two-start arrangement, n = 2, is the most frequent configuration of the fiber. Contacts between nucleosomes i and i + 2 are highlighted by black double-sided arrows. Rare events with n = 3, 4, and 5 are shown by red, green, and pink arrows, respectively. Two nucleosomes are considered to be in contact if the center-to-center distance is less than 120 Å. Details of FINI calculation are described in the Materials and Methods. To see this figure in color, go online.

The FINI contact maps show that the canonical zigzag fibers (n = 2) are dominant, whereas rare events of n = 3–5 corresponding to the three-start and five-start morphologies are also possible, albeit with much lower frequencies (Fig. 7; NRL = 197 bp, F = 0). In addition, the FINI profiles have peaks at n = 4 for E = 8 kT (Fig. 7). This implies that clusters of at least five stacked nucleosomes arranged in two-start zigzag conformations are relatively frequent in our MC ensembles. Of note is that recently, using single-molecule force spectroscopy, Li et al. (39) found that tetranucleosome intermediates frequently appear in nucleosomal arrays. Thus, it is tempting to speculate that our results support such transient two-start clusters of stacked nucleosomes.

Discussion

We performed intensive MC simulations of unfolding of 30-nm chromatin fibers and compared the results with force spectroscopy measurements. This analysis provides detailed information about the level of compaction, range of internucleosome interactions, and dynamics of nucleosome unwrapping. Our coarse-grained model was proven successful at predicting optimal conformations and topological variability of chromatin fibers. We found a remarkable similarity between the computed optimal fiber conformations and the existing x-ray and electron cryomicroscopy structures (30). Topological variability as a function of NRL was predicted using our coarse-grained model and successfully tested experimentally (40). Recently, we found a close similarity between sedimentation velocity measured experimentally and MC simulations (41) demonstrating that our predicted conformations are likely to represent adequately the ensemble of fiber structures in vitro. Here, by adding dynamic unwrapping to that force field, we simulated oligonucleosome arrays under an external stretching force, F. Comparing the force-extension curves generated by simulations with the experimental data allowed us to elucidate the effect of different regimes of force on fiber unfolding.

Recently, Hall et al. (12) generated a detailed map of histone-DNA interactions along the DNA sequence by mechanically unzipping the DNA of single nucleosomes. By measuring the dwell times of the unzipping fork, they concluded that the terminal ∼5–15 basepairs from the nucleosomal ends do not show any significant interaction with histones and thus, can unwrap easily. We translated their data into an adhesion energy profile, G_adh(U). MC simulations utilizing this adhesion potential demonstrate that as the external force increases, the degree of unwrapping also increases. At small forces (F = 0–3 pN) the nucleosomes breathe by U ≈ 10 bp at the ends. The breathing might be slightly more pronounced for short NRLs because of the stronger distortions of the linker DNA caused by the tighter packing. The breathing of the 601 nucleosomal DNA at the ends is also consistent with the accessibility of terminal 10–20 bp of nucleosomal DNA for cleavage by micrococcal nuclease (42). One can expect the end DNA breathing to be even more pronounced for natural DNA sequences because their affinity to histones is lower than in the 601 sequence (43, 44).

In both constructs, with NRL = 167 and 197 bp, a plateau occurs at intermediate force F ≈ 3.5 pN. The width of this plateau could only be explained by considerable unwrapping (U ≈ 25–32 bp) of the nucleosomes after complete loss of stacking. Therefore, the plateau region can be interpreted as the unpeeling of the outer-turn DNA by an external force approximately equal to the adhesive force between DNA and the histone core. In other words, the height of the plateau is mostly determined by the intranucleosomal interactions in contrast to the earlier models, suggesting that the height of the plateau is defined by the strength of the internucleosome stacking (13, 15, 27). As follows from our MC simulations, the linear regime in the force-extension curve is entirely consistent with the dynamic stacking-unstacking of nucleosomes. This is another important difference from the existing model (15) assuming that nucleosomes are fully stacked in the linear regime.

We were also able to uncover the molecular-mechanical origin of the stochastic asymmetric unwrapping of nucleosomes observed experimentally by Ngo et al. (16). We found that it is the shape of the adhesion potential that dictates the “lopsided” opening of the nucleosome ends even if the DNA sequence is symmetric (Fig. S2). (A similar asymmetric unwrapping was observed for an asymmetric adhesion potential; data not shown). This inherent dynamic asymmetry of nucleosome revealed under external force may play a role in the nucleosome maintenance during transcription and remodeling because it has been shown that a high fraction of nucleosomes survives after being transcribed (45, 46) or remodeled (47). The coordinated unwrapping-rewrapping between the two nucleosome ends may help stabilize one H2A/H2B dimer during the exchange or modification of the other dimer (48).

There is strong evidence that such mechanical asymmetry of nucleosomes may influence gene expression. The in vitro transcription studies demonstrated that nucleosomes form a polar barrier to transcriptional elongation (49, 50). The molecular motors such as RNA-polymerase exert forces between 5 and 15 pN (51, 52). Under these forces, the nucleosomes would unravel asymmetrically, as observed by Ngo et al. (16), thus modulating processivity of RNA-polymerase along the nucleosomal array. In addition, the stochastic and asymmetric unwrapping of nucleosomes would significantly increase the accessibility of nucleosomal DNA to transcription factors, such as p53 (53).

Regarding the internucleosomal interactions, it is generally accepted that posttranslational (epigenetic) modifications of the histone tails can significantly change the stacking and therefore alter condensation of chromatin (4, 5). However, the strength of the stacking energy, E, remains a subject of debate (10, 11, 12, 13, 14, 15, 16, 17, 18, 19). To the best of our knowledge, only two direct measurements of internucleosome interaction were published. Mangenot et al. (54) used osmometry and electrophoretic mobility to study the interaction between isolated nucleosome core particles (NCPs). They report a range of values between 3 and 10 kT under 100–150 mM NaCl. More recently, Funke et al. (55) integrated two nucleosomes in a DNA origami-based force spectrometer and found the free energy of stacking to be −1.6 kcal/mol. Their measurements were made at 10 mM MgCl₂ and cryogenic temperatures. Note, however, that the fiber stretching experiments are typically performed in the presence of no more than 1–2 mM of Mg²⁺ ions to avoid aggregation (56). Our computations suggest that the range of energies for unstacked chromatin is E ≈ 0–3 kT, whereas E ≥ 12 kT condenses the fiber (see representative fiber conformations for E = 3 (open), 8 (half-open), and 12 kT (compact) shown in Fig. S9). Intermediate energy values represent chromatin randomly opening and closing under thermal fluctuations. For the given force-spectroscopy settings (15), our estimate of stacking energy is E ≈ 8 kT. The MC-simulated conformations largely resembled two-start packing, with rare events of three- to five-start morphologies. We did not observe one-start stacking folds.

Further details of the chromatin dynamics could be revealed using our current coarse-grained model with appropriate modifications. A more sophisticated DNA-histone interaction force field is essential to simulate the sequence-dependent aspects of the nucleosome dynamics in the context of long chromatin fibers. After implementing these modifications of the force field, the nucleosome breathing and sliding can be analyzed for naturally occurring DNA sequences. At the higher levels, the dynamic unfolding of fibers under fixed topology can be simulated to mimic accommodation of the DNA supercoiling during transcriptional elongation (40, 57, 58).

In summary, we developed a novel, to our knowledge, coarse-grained model of chromatin fiber that is consistent with the force-extension data by Meng et al. (15) and observations of stochastic and asymmetric unwrapping of nucleosomes made by Ngo et al. (16). The force-induced gradual unwrapping accompanied by dynamic stacking-unstacking transitions account for the experimental observations (15). Our approach brings new, to our knowledge, insights into the dynamics of nucleosomal arrays, which is critical for various DNA-related cellular processes.

Author Contributions

D.N. and V.B.Z. designed the research. D.N. developed the MC software and performed the research, then D.N. and V.B.Z. analyzed the data and wrote the article.

Editor: Jason Kahn.