Tunneling Probability Increases with Distance in Junctions Comprising Self-Assembled Monolayers of Oligothiophenes

Abstract

Molecular tunneling junctions should enable the tailoring of charge-transport at the quantum level through synthetic chemistry but are hindered by the dominance of the electrodes. We show that the frontier orbitals of molecules can be decoupled from the electrodes, preserving their relative energies in self-assembled monolayers even when a top-contact is applied. This decoupling leads to the remarkable observation of tunneling probabilities that increase with distance in a series of oligothiophenes, which we explain using a two-barrier tunneling model. This model is generalizable to any conjugated oligomers for which the frontier orbital gap can be determined and predicts that the molecular orbitals that dominate tunneling charge-transport can be positioned via molecular design rather than by domination of Fermi-level pinning arising from strong hybridization. The ability to preserve the electronic structure of molecules in tunneling junctions facilitates the application of well-established synthetic design rules to tailor the properties of molecular-electronic devices.

Introduction

The exponential decay of the tunneling probability of an electron (observed as electric current) with increasing distance is ubiquitous. When tunneling occurs through molecules, their electronic structure can significantly decrease¹ or increase² the rate of tunneling compared to vacuum, but it is always observed to decrease exponentially with distance.³ Molecular structures provide unrestricted design opportunities to modulate charge-transport at the quantum level from the bottom up.⁴ Theoretical predictions even suggest that tunneling probabilities can be made to increase with increasing molecular length.⁵ That is why understanding and controlling tunneling charge-transport at the molecule-level is the central challenge of molecular-electronics (ME). Realizing nanoscale devices requires a fundamental understanding of the alignment of energy levels and how they respond to topological and electronic modifications of molecular structures in single-molecule and molecular-ensemble tunneling junctions.⁶ These relationships are understood well in bulk organic/molecular semiconductors, where electronic properties can largely be predicted using density functional theory (DFT) and implemented synthetically; however, in ME, the electronic structure of molecules is strongly perturbed by the electrodes. The key to possible future applications of ME is deterministic control over the positions of resonances in the transmission probability with the Fermi-level (E_f) of the electrodes.

The energies of the molecular orbitals (i.e., electron affinities and ionization potentials) that determine the transmission probability can be controlled through the inclusion of heteroatoms and functional groups, just as the work function of an electrode depends on its composition. When a molecule binds to an electrode, however, the offset between E_f and the frontier orbitals narrows, becoming relatively insensitive to their gas-phase values.⁷ For clarity, we will collapse the multitude of processes associated with this phenomenon to the term “coupling”; strong coupling hampers rational molecular design to control tunneling transport⁸ and is most pronounced in tunneling junctions comprising ensembles of molecules, for example, self-assembled monolayers (SAMs).^9,10 The latter are the technologically relevant^11,12 counterparts of single-molecule junctions, but the requisite metal–molecule (usually metal–thiolate) bonds not only bind the molecules to the electrode(s), but, through collective electrostatic effects, shift the occupied states in the SAM toward E_f, pinning the tail of the density of states (DOS).¹³ In order to achieve synthetic control over molecule–electrode coupling, generalizable rules and a simple method for controlling coupling and probing barrier-heights experimentally¹⁴ are needed. The series TnC4, where n is the number of thiophene units of oligothiophenes functionalized with n-butanethiol tails, shown in Figure 1A, accomplishes both goals. The alkyl chain isolates the orbitals at the covalently bound interface, effectively preventing the π-system from coupling to the bottom electrode and preserving the electronic structure of the frontier orbitals, which are localized at the oligo(thiophene)s, even when packed into self-assembled monolayers (SAMs), the most common basis for molecular-ensemble junctions. It also allows efficient tunneling and is flexible enough to drive the formation of densely packed SAMs.¹⁵ When a top-contact of either eutectic Ga–In (EGaIn¹⁶) or an Au-coated Si₃N₄ AFM tip (Au^AFM) is applied, the resulting coupling is relatively weak and does not appreciably perturb the electronic structure in the junction.¹⁷ Moreover, relative to other commonly used aromatic units, the frontier molecular orbital gap of thiophenes decreases particularly rapidly with increasing conjugation length, which has led to numerous observations of unusual length-dependence in a variety of thiophene oligomers.¹⁸⁻²¹ Thus, we expect that the unperturbed, decoupled electronic structure of TnC4 will be expressed in the length-dependence of tunneling charge-transport, which should differ from the parent oligothiophene series significantly.

Figure 1.

(A) Series of alkanes (Cn) and oligothiophenes (TnC4) used in the tunneling junctions. The tunneling distance (d) increases with the number of CH₂ units in the Cn series or the number of thiophene units in TnC4. (B) An energy level diagram for molecular junctions comprising TnC4 molecules between two metal electrodes, showing the fixed barrier-width d_C4 associated with the butanethiol fragment and the increasing d_Tn with n. The shaded regions in blue represent occupied states. The barrier-height (φ) is constant for the alkane series but decreases with increasing n for the TnC4 series.

The simplified Simmons equation describes the length-dependence of tunneling charge-transport

1

where β is the rate of decay of the current I with the width of the barrier d (usually molecular length) and I₀ is the extrapolated conductance when d = 0.²² When a molecular tunneling junction is treated as a rectangular energy barrier, β is related to the average height of that barrier φ (eq 2), which is, in turn, related to the offset between dominant frontier orbital and E_f such that

2

The magnitude of β for n-alkanethiolates is a benchmark in ME because β = (0.7 ± 0.1) Å^–1 [or (1.0 ± 0.1)n_CH2^–1] across many experimental platforms.^11,12,23,24 Through clever molecular design, β can approach zero,²⁵ enabling efficient tunneling transport over tens of nanometers.²⁶ Unusually small values of β occur in disparate molecular motifs and experimental platforms;^27,28 there are no design rules beyond general observations like β ≈ 0.3 Å^–1 for oligophenyleneethynylenes (OPEs), oligoacenes, and oligophenylenes.²⁹⁻³¹ Also, the mechanism is often either speculative or demonstrably switches to hopping,^32,33 at which point β loses physical meaning.

It should not be possible to extract β from the length-dependence of conjugated molecules, in general, because the frontier molecular orbital gap E_g decreases with increasing conjugation length (i.e., d), which changes φ; it is due to coupling that φ remains nearly constant, even for (most) conjugated oligomers. The degree of coupling in this context is variable; it does not mean that the peak positions of the frontier orbitals are completely invariant with length. In cases where φ varies with d (e.g., weak coupling), physical interpretation of the resulting aberrant values of β is erroneous because underlying assumptions in the Simmons model are not valid. However, the relationship between molecular length and tunneling probability is always meaningful as it is still governed by the electronic structure of the tunneling junction.

Results and Discussion

EGaIn Measurements

To examine the influence of decoupling, we grew SAMs from alkanethiols (Cn) and TnC4 on ultrasmooth, template-stripped Ag (Ag^TS) substrates²⁴ and characterized them using ellipsometry, water contact angles, and ultraviolet photoelectron spectroscopy (UPS). These data are summarized in Table S1. We formed tunneling junctions in two different experimental platforms: EGaIn and conducting-probe AFM (CP-AFM). Although both form van der Waals contacts to a SAM, a CP-AFM Au tip (Au^AFM) contacts approximately 100 molecules,³⁴ while a typical EGaIn junction is ∼500 μm²; EGaIn forms large-area junctions, while CP-AFM forms few-molecule junctions.²⁴ To establish a benchmark, we first measured SAMs of Cn (n = 10, 12, 14, 16) on Ag^TS; Figure 2A shows the current-density versus voltage (J/V) plots for Ag^TS/Cn/EGaIn junctions. (Each datum is the peak position of a Gaussian fit of log|j| for that voltage, and the error bars are 95% confidence intervals, with each junction as a degree of freedom; see Figure S13.) The value of J at each bias follows the trend C10 > C12 > C14 > C16, from which we extracted β ≈ 0.7 Å^–1 (Figure 2C). This value is in excellent agreement with the consensus value.^11,23,24

Figure 2.

(A) Plots of log|j| vs V for Ag^TS/Cn//EGaIn (where n = 10, 12, 14, 16) junctions. (B) Plots of log|j| vs V for Ag^TS/TnC4//EGaIn (where n = 1, 2, 3, 4, and corresponds to the number of thiophene rings) junctions. (C) Plots of log|j| vs molecular length with linear fits to eq 1 at different bias: 1.0 V (solid line), −1.0 V (dash-dot line), 0.5 V (dashed line), −0.5 V (dotted line). (D) Plots of log|j| vs molecular length at different biases with lines drawn through the points: 1.0 V (solid line), −1.0 V (dash-dot line), 0.5 V (dashed line), −0.5 V (dotted line). Error bars in all the plots represent 95% confidence intervals from measurements of multiple junctions across multiple substrates.

Figure 2B shows the results of identical measurements on Ag^TS/TnC4/EGaIn junctions for n = 1, 2, 3, 4 (we synthesized n = 5 but it is not soluble enough to form high-quality SAMs). Although both the lengths of the molecules and the measured thickness of the SAMs increases uniformly from T1C4 to T4C4 (Figure S9), the trend in J is T1C4 > T4C4 > T3C4 > T2C4, making it impossible to derive a single value of β for the series. Figure 2D clearly shows that for n > 1 the tunneling probability actually increases exponentially with molecular length; eqs 1 and 2 are inapplicable because the positive slope of log|J| vs molecular length would result in β < 0 for TnC4 where n > 1. Therefore, either φ varies with length (no coupling), or the mechanism of charge-transport is not tunneling. We can rule out the latter explanation due to the lack of thermally activated processes over a range of 210 K (see Figure S15), which also excludes intermolecular charge-transfer.

CP-AFM Measurements and DFT Simulations

To exclude the possibility that the observed length-dependence of TnC4 is specific to EGaIn, we measured Ag^TS/TnC4/Au^AFM junctions (i.e., CP-AFM junctions). Figure 3A shows the resulting I/V plots. (The data were processed identically to the EGaIn data; see Table S5 and Figure S16.) The overall trend is unchanged (I increases with length for n > 1) but is even more striking, as T4C4 is more conductive than T1C4. Whereas EGaIn data are influenced by the entire supramolecular structure of the SAM, CP-AFM data are more likely to reflect the pristine SAM. Pinholes, defects, grain boundaries, etc. widen the histograms of log|j| for large-area junctions,³⁵ but tend to show up as extreme outliers in few-molecule junctions and are often clipped by the current amplifier. These properties enable meaningful simulations of CP-AFM data using models developed for single-molecule junctions. To simulate the I/V data, we generated plots of transmission probability versus electron energy T(E) using density functional theory (DFT) calculations and integrated them over a bias window using

3

where c is a scaling parameter.³⁶ We set E_f to −4.7 eV, selected a value of c to obtain a good fit to the experimental data for T4C4, and used those parameters to simulate the entire series. The resulting simulated I/V curves (Figure 3B) are in remarkably good agreement with the experimental data, reproducing the I/V characteristics (Figure 3A) and length-dependence (Figure 3D). The only substantial deviation is that the calculations predict a much larger Ohmic region for T1C4, which is directly related to the overestimation of the frontier molecular orbital gap. These simulations provide further evidence that the extraordinary length-dependence is intrinsic to the electronic structures of TnC4 and independent of the experimental platform.

Figure 3.

(A) Experimental plots of I vs V for Ag^TS/SAM//Au^AFM junctions for: T1C4 (red), T2C4 (orange), T3C4 (green), and T4C4 (purple). (B) Simulated plots of I vs V derived by integrating the transmission of single-molecule junctions comprising TnC4: T1C4 (red), T2C4 (orange), T3C4 (green), and T4C4 (purple). (C) Experimental plots of log|I| vs molecular length at different biases: 1.5 V (solid line), −1.5 V (dash dot line), 1.0 V (dash line), −1.0 V (dotted line). (D) Simulated plots of log|I| vs molecular length at different bias: 1.5 V (solid line), −1.5 V (dash dot line), 1.0 V (dash line), −1.0 V (dot line). For clarity, the simulated data for log|I| at −1.5 and −1.0 V are shifted by offsets of −0.1 and −0.15 V, respectively.

The experimental data and simulations support the hypothesis that φ varies because, in a junction, transport is dominated by the highest-occupied π-state (HOPS, see Figure S22), which approaches E_f as E_g decreases with increasing n for TnC4. This striking effect of the decoupling of the HOPS from E_f can be seen in the UPS spectra of SAMs of TnC4 (Figure S11) and oligothiophenes in the gas-phase.³⁷ The line-shapes of the SAM and gas-phase spectra are nearly identical, meaning there is no hybridization between the HOPS and metal states. Also, just as the gas-phase peaks shift with decreasing E_g, the DOS in the TnC4 spectra shifts toward E_f with increasing n, which should be affected further by the application of a top-contact. If this situation is indeed preserved in assembled junctions, the HOPS should be visible as peaks in plots of normalized differential conductance (NDC) . In the limiting case of scanning tunneling spectroscopy (STS), where the coupling is zero because there is a vacuum gap between the electrode and the SAM, NDC spectra reveal peaks as the applied bias moves E_f through the density of states (DOS) of surface-bound molecules.³⁸ When molecules are in contact with both electrodes and the coupling is nonzero, as is the case for EGaIn top-contacts, NDC spectra are U-shaped because the DOS never crosses E_f.⁴Figure 4 shows heat-map plots of NDC derived from the same data used to prepare the J/V plots in Figure 2. As expected, the spectrum of C10 is U-shaped; however, the spectra of T1C4 and T2C4 are steeper and begin to curve at ±1 V, while the spectra of T3C4 and T4C4 clearly show peaks that move toward 0 V. (Only junctions of T4C4 were robust enough to scan to ±1.5 V.) This trend is apparent in the evolution gas-phase DOS with n from the DFT simulations (Figure S28). In contrast, the NDC spectra of OPEs, acenes, and fully conjugated bithiophenes are all U-shaped (Figures S19 and S20). Thus, we ascribe the peaks in Figure 4 to the DOS of the HOPS as it approaches E_f across TnC4 (Figure S28). This observation is possible only because of the spatial separation between the bottom electrode and the conjugated segment via the alkyl fragment, which precludes hybridization by preventing the tail of the DOS of the HOPS from pinning to the Fermi-level of the electrode. Thus, the experimental data are clear evidence for the lack of strong coupling through Fermi-level pinning, which would manifest as (nearly) length-independent differential conductance curves.

Figure 4.

Experimental normalized differential conductance (NDC) heat-map plots of Ag^TS/SAM//EGaIn junctions comprising C10 and TnC4. Only junctions of T4C4 were robust enough to scan to ±1.5 V. The NDC plots of the entire Cn series and other, representative, conjugated molecules are shown in the Supporting Information.

Two-Barrier Model

To understand the aforementioned observations, we developed a model that is based on the assumption of piece-wise constant multiple potential barriers.³⁹ As shown in Figure 5A, the first barrier V₂ corresponds to the butanethiol fragment; thus, its length and height are kept constant across TnC4. The second potential barrier V₃ represents the offset between E_f and the energy of the HOPS (E_HOPS). As is the case for organic semiconducting materials (and discussed above), in the absence of strong coupling to the metal electrode, V₃ decreases with the inverse length of the oligothiophene fragment (1/L_T). Thus, the height of the second barrier can be expressed as

4

The parameter Δ^∞ is the relative position of the HOPS as L_T → ∞ in the complete absence of metal–molecule interaction and neglecting the saturation of the ionization potential of oligomers at very large n; notably, it is not unrealistic that Δ^∞ becomes negative, as there is no fundamental reason why the Δ^∞ of a SAM cannot be smaller than the (modified) work function of a metal electrode. β̃ is the slope of the dependence of E_HOPS on 1/L_T (see Figure S24). The max operator ensures that the barrier does not drop below zero, which in the actual junction would be prevented by molecule-to-metal charge transfer (even at very small couplings, as long as thermodynamic equilibrium can be established).⁴⁰

Figure 5.

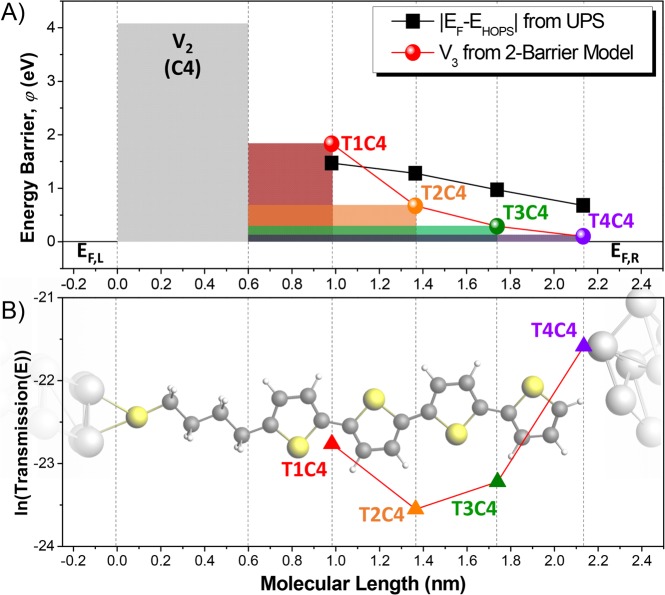
(A) Schematic of the two-barrier model developed to explain the extraordinary length-dependence of TnC4. The gray rectangular barrier depicts the first tunneling potential barrier due to the butanethiol fragment (V₂). The second barrier is defined by the energy offset between the HOPS and the Fermi-level of the electrode (E_f – E_HOPS). Thus, the red, orange, green, and purple spheres represent the second potential barriers (V₃) corresponding to the T1C4, T2C4, T3C4, and T4C4, respectively, illustrating the decrease in barrier-height with the increasing number of thiophene rings. Values of |E_f – E_HOPS| from UPS measurements are plotted with black squares. (B) The length-dependence of transmission derived from the two-barrier model plotted as triangles. The dashed lines drawn through the T4C4 molecule show how the tunneling distance evolves with increasing n.

The tunneling probability as a function of n is calculated as the ratio between electrons transmitted into the right electrode and those emitted from the left electrode into the molecule. It is obtained by evaluating the wave function transmitted through the two-step barrier. We assume the same E_f for both electrodes (i.e., the zero bias situation), which we do not consider to be a serious limitation because the experimental length-dependence of TnC4 discussed above is independent of bias (Figures 2 and 3). These calculations are discussed in detail in section 4.2 of the Supporting Information. For TnC4, the offset between E_HOPS and E_f (Figure 5A) shrinks with L_T corresponding to β̃ = 0.88 eV nm, as obtained from a fit to the UPS data using eq 4 (excluding T1C4, for which the position of the peak is difficult to resolve). Combining this value of β̃ with a suitably chosen Δ^∞ = −0.48 eV yields the n-dependent barriers shown in Figure 5A from which we calculate the transmission probabilities shown in Figure 5B. Negative values of Δ^∞ correspond to cases in which the HOPS would be above E_f for the oligomers greater than a certain value of n (for TnC4, Δ^∞ = −0.48 eV, n > 4). However, in assembled junctions, this situation leads either to ground-state charge transfer between the SAM and the electrode⁴¹ or resonant tunneling,⁴² which is ruled out by the aforementioned variable-temperature measurements.

The two-barrier model very accurately captures the experimentally observed dependence of the tunneling current on the barrier-width defined by the lengths of the molecules. Thus, we conclude that the aberrant length-dependence of TnC4 is the result of a sharp increase in the current when V₃ approaches zero for the longer molecules. In the context of the Simmons model, the drop in transmission due to the increasing barrier-width (d) is surpassed by the shrinking barrier-height (φ), resulting in the experimental observation that β < 0 for n > 1, which is impossible according to eqs 1 and 2. This unusual situation requires that Δ^∞ be negative, which is the result of the intrinsically low ionization potential of oligothiophenes in combination with the weak coupling between the HOPS in the SAM and the electrode.

A requirement for Δ^∞ to become negative is a sufficiently large value for β̃; otherwise, the ionization potential (i.e., E_HOPS) does not decrease fast enough with L_T to yield a negative value of Δ^∞. Thus, the small change in E_HOPS with L_T for OPEs (and other aromatic hydrocarbons) and the effective independence on length for alkanes restores the conventional length-dependence of the transmission. To demonstrate the predictive power of the two-barrier model and to demonstrate its application beyond TnC4, we applied it to a series of ethylenedioxythiophene molecules in section 4.2.5 of the Supporting Information. Unlike the DFT simulations in Figure 3, the two-barrier model does not depend on specific structures or junction geometries; it relies on parameters that describe the well-known relationship between conjugation length and ionization potentials, which can be measured, inferred, or calculated to predict classes of molecules and combinations of π-conjugated and alkyl fragments that will exhibit the desired behavior.

Conclusion

This work is the first to show a trend of increasing tunneling probability with increasing molecular length experimentally. It is the result of the rapid decrease of E_g with length in oligothiophenes and the decoupling of the thiophene π-system, which dominates tunneling charge-transport, from the electrodes. This observation highlights two important design rules for ME: (i) It is possible, over some range of distances, to design molecules that produce a tunneling decay coefficient that is empirically negative. (ii) It is possible to construct molecular tunneling junctions in which molecular states are preserved, varying little from their gas-phase values. Ordinarily, longer molecules lead to very high resistance (and eventually thermally activated, hopping transport), and strong molecule–metal coupling sharply attenuates shifts in molecular states. These two design rules imply that it is possible to manipulate the levels in a junction with simple functional groups (in this case, thienyl rings) and in relatively large molecules. Coupling these functional groups to external stimuli, e.g., via photoswitches, could produce ME devices large enough to be accessed optically that effect significant changes in tunneling currents. Deterministic control over the positions of molecular orbitals in tunneling junctions is also critical to thermoelectrics, which exploit the exponential relationship between tunneling current and orbital/electrode offsets.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b09793.

• Synthetic detail and full characterization data for all new compounds, description of measurement techniques, details of theory and calculation, and additional spectroscopic data on monolayers (PDF)

Author Present Address

^⊥ Department of Chemical Engineering, Massachusetts Institute of Technology, Cambridge, MA 02141, United States.

Author Present Address

^# Macromolecular Materials and Systems, Institute for Technical and Macromolecular Chemistry, RWTH Aachen University, Aachen, Germany.

Author Contributions

^∥ Y.Z. and S.S. contributed equally to this work.

The authors declare no competing financial interest.