Metabolic Modeling of Microbial Community Interactions for Health, Environmental and Biotechnological Applications

Abstract

In nature, microbes do not exist in isolation but co-exist in a variety of ecological and biological environments and on various host organisms. Due to their close proximity, these microbes interact among themselves, and also with the hosts in both positive and negative manners. Moreover, these interactions may modulate dynamically upon external stimulus as well as internal community changes. This demands systematic techniques such as mathematical modeling to understand the intrinsic community behavior. Here, we reviewed various approaches for metabolic modeling of microbial communities. If detailed species-specific information is available, segregated models of individual organisms can be constructed and connected via metabolite exchanges; otherwise, the community may be represented as a lumped network of metabolic reactions. The constructed models can then be simulated to help fill knowledge gaps, and generate testable hypotheses for designing new experiments. More importantly, such community models have been developed to study microbial interactions in various niches such as host microbiome, biogeochemical and bioremediation, waste water treatment and synthetic consortia. As such, the metabolic modeling efforts have allowed us to gain new insights into the natural and synthetic microbial communities, and design interventions to achieve specific goals. Finally, potential directions for future development in metabolic modeling of microbial communities were also discussed.

1. INTRODUCTION

Microbes are ubiquitous across Earth’s biosphere at typical densities of 10⁹ organisms per gram of soil [1] and 10⁶ organisms per milliliter of sea water [2]. They take part in biogeochemical cycles, playing an essential role through their combined metabolic activities [3]. Microbes are also found in different hosts including insects, animals, and plants, interacting among themselves as well as with their hosts [4-6]. In humans, they make up 1-3% of the human body mass, and there is growing evidence of the importance of human gut microbiome and relevance to human health [7, 8]. In addition, microbial communities have been harnessed in diverse applications such as waste water treatment and food production [9, 10].

Microbes can interact with each other and also with hosts in various ways, e.g., sensing of chemical signals, and cross-feeding of metabolites [11-13]. More specifically, microbial communities can produce emergent capabilities through a
complex set of metabolite exchanges that no constituent species can accomplish on isolation. For example, metabolites transferred among microbes link disparate pathways from individual species to render novel metabolic functions [14, 15]. However, it is still difficult to understand microbial communities and their interactions due to the current technical limitations in measuring possible metabolite exchange fluxes between different species in the community [16, 17]. In this regard, metabolic modeling of microbial communities is very useful for addressing some of the questions and gaps left unfilled by the current state-of-the-art. Further integration of mathematical modeling with omics profiling, especially metabolomics, is also a promising avenue to be pursued [18]. Hypotheses can then be derived to design new experiments for probing microbial communities, thereby enhancing our understanding in an iterative manner. In this review, we first summarize the existing methodologies to model metabolic interactions within microbial communities. It is followed by a discussion on their various applications to date. Finally, we suggest potential directions for future work in metabolic modeling of microbial communities.

2. Modeling of microbial communities

Modeling approaches for analyzing microbial communities can be classified on the basis of temporal nature

(static vs. dynamic) and species segregation (compartmentalized vs. lumped network) (Fig. 1). Large-scale static models can be built using the steady-state assumption, which avoids without kinetic parameters that are difficult to be obtained. Static models are typically constrained using measured inputs and outputs, and then solved by assuming a physiologically relevant objective function such as growth maximization [19, 20]. Such computed metabolic flux profile can be used to study the metabolic states in different parts of the community, and examine interactions between member species. Static metabolic networks can also be analyzed to gain insight into the community’s collective metabolic functions. On the other hand, dynamic models allow us to capture the dynamic behaviors such as time-dependent species abundance and metabolite concentrations. They are usually smaller in size, due to the difficulty in obtaining associated kinetic parameters. As few enzymatic parameters are available from enzyme databases, the majority need to be estimated using experimental data.

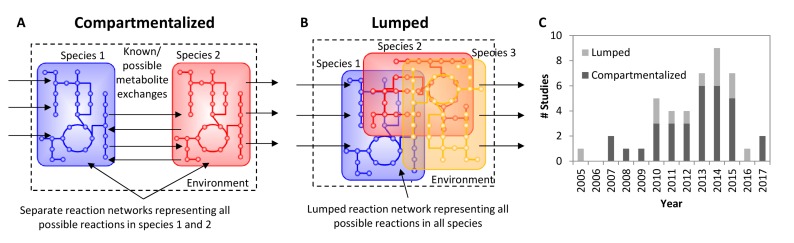
Fig. (1).

The approaches employed to model and study microbial communities can be divided into three major categories: compartmentalized and lumped. A) In a compartmentalized simulation model, each species or functional guild occupies its own distinct compartment. B) In a lumped reaction network simulation model, all reactions are included in a single network with no segregation into distinct subsets. C) The graph summarizes the number of published studies on modeling microbial communities (See supplementary materials for list of collected studies). There is a clear trend of an increasing number of studies published until 2 years ago, where the number of studies fell dramatically.

2.1. Steady-state Metabolic Models

Steady-state metabolic models have been widely used to characterize the metabolic behavior of various microbes [19, 21]. Within the broad classification of steady-state modeling, microbial community models can be compartmentalized or lumped on the basis of species segregation. Compartmentalized network models segregate microbial species or functional guilds into separate compartments in a larger system, while lumped models consider all available enzyme functions within the community as a single network. To construct a compartmentalized community model, metabolic models of member species are first reconstructed individually, and then integrated into a combined model. Species-specific metabolic models can be built typically at genome-scale using available genomic and/or gene expression data [22]. To do so, software pipelines including COBRA, RAVEN, and ModelSEED can be employed for generating an initial draft model, followed by further refinement such as manual curation and gap filling [23-25]. Since model reconstruction and curation is a laborious process, it can be avoided if high quality models of the species are already available on public databases such as BiGG and ModelSEED [25, 26]. Due to the need for detailed species or guild metabolic models, compartmentalized models are usually used to model synthetic consortia or natural communities with well-studied dominant species.

Generally, it is difficult to isolate and characterize most microbes in natural communities [27]. Thus, most compartmentalized metabolic models of natural communities are composed of models constructed from a small number of well-studied individual members, especially dominant species or taxa. On the other hand, large scale simulation models of complex communities adopt a lumped or “enzyme soup” approach when information on individual species is very limited and only meta-omics data is available to identify the community’s metabolic capabilities [28]. The lumped network can be constructed by mapping identified genes in the omics (such as metagenomic and metaproteomic) data to enzymatic reactions [29, 30]. Hence, the community is considered as a single integrated network. The lack of species or guild boundaries often results in linking pathways from different species, which may not reflect actual metabolite exchanges. This may lead to an overestimation of the community’s overall metabolic capabilities. Therefore, it should be viewed as an upper bound that can be tightened as more information is integrated into the model [28].

Tobalina et al. used metaproteomics data to build a static and lumped metabolic network model based on enzyme function present in the community, following a modified procedure of the ModelSEED pipeline [25, 31]. It consists of three steps: The first uses expression data to construct a minimal network capable of producing biomass. The second and third steps add alternate biomass production and non-growth essential reactions respectively, based on the detected proteins. The procedure was used to construct two context specific microbial communities living in polyaromatic hydrocarbon contaminated soil. Similarly, Henry et al. proposed to combine multiple community members into a lumped model after building separate initial draft models by conducting the curation steps on the community model instead of species models [32]. It was argued that by co-curating lumped models, the extraneous gap filling can be reduced as some absent essential metabolic functions may be fulfilled through metabolite exchanges as opposed to adding reactions that may not have experimental evidence.

Despite the different representations of microbial communities as compartmentalized or lumped models, the solution technique for the underlying stoichiometric matrices is the same. To determine the metabolic fluxes flowing across the reaction network, it is assumed that the system is at steady state with no accumulation. Mathematically, this problem can be written as:

where S is the (I × J) stoichiometric matrix, and v is the vector of J reaction fluxes. In typical metabolic reaction networks, there are more reactions than metabolic reactions. This gives rise to an under-determined system of linear equations to be solved.

To obtain a solution to the metabolic state, the flux balance analysis (FBA) approach is commonly employed [19]. FBA assumes that the organism has evolved its metabolic functions to maximize a biological objective such as cellular growth during exponential growth, or ATP production during the stationary phase, while being subjected to nutrient intakes [33]. For a microbial community, a weighted average of all the member species’ biomass equations can be used as the community objective [31]. Therefore, the problem becomes a linear programming (LP) problem in the following form:

Maximize

where LB and UB are vectors of the lower and upper bounds for reaction fluxes v, respectively. w_i and v_biomass,i are the weight and biomass reaction flux for species i, respectively; N is the number of species. The bounds can also be used to restrict the reaction directionality. Such a LP problem can be easily solved using state-of-art solvers [20]. It should be highlighted that when employing the FBA approach in modeling microbial communities, a key consideration is the choice of objective. The weights, w_i can be obtained from experimentally measured microbial abundance [34], or computationally derived based on the assumption of balanced growth in the community [35, 36]. Apart from the general FBA framework with a weighted sum of biomass production, different approaches have been developed to unravel metabolic fluxes within microbial communities. For example, a sophisticated multi-level and multi-objective optimization framework is exemplified by OptCom [37]. Briefly, the community problem is structured as a bi-level optimization problem. Each species in the community has a specific optimization objective (inner problem) that can be biomass maximization (maximum growth rate) or alternatives such as MOMA (minimum adjustment from the wild type state upon mutation). The inner problems are then linked to the overall community objective such as total community biomass maximization. The OptCom framework can be customized by modifying the exchange constraints to model different interactions including mutualism, synergism, commensalism, and parasitism. This framework was used to study the different interactions between species in thermophilic and phototropic microbial mats by quantifying the impact of altruistic and selfish interactions on the growth of individual species and the community [37]. Similar to OptCom, Shoaie et al. developed a multi-level modeling framework to build compartmentalized community models [38]. The procedure first “activates” the network to obtain a feasible flux profile of the community model. Thereafter, the community optimization is performed in a multi-level iterative process where the community objective is first optimized to obtain the optimal resource distribution, which is then used to solve for the organism specific optimal solutions. This procedure adopts a “top down” approach, as opposed to the “bottom up” approach of OptCom. A different multi-objective approach was proposed by Budinich and coworkers to analyze the same phototropic mat community [39]. Instead of computing a single solution, the Pareto solutions were generated from the biomass maximization of different community species to study metabolic interactions.

It should be noted that while maximizing for a particular objective, the resulting flux distribution may not be unique. Therefore, to explore these alternative solutions, flux variability analysis (FVA) can be employed [40]. FVA computes the minimum and maximum fluxes for each reaction while achieving the previously computed optimal objective. As an alternative, a set of possible solutions from the solution space of the metabolic network with measured exchange fluxes can be obtained without any bias via random Monte Carlo flux sampling [41]. Similar to random sampling, elementary mode analysis (EMA) is another method that can analyze the metabolic network in an unbiased manner [42]. This method computes the minimal set of feasible flux vectors in which any valid flux solution is a linear combination of this minimal set. Therefore, this minimal set characterizes the organism’s entire feasible metabolic space. It can be also used to analyze various properties of the network such as metabolic capabilities and structural robustness [43]. When employing this method to analyze segregated community models, the analysis can be performed on the whole community as single model, or in a hierarchical manner by first selecting the elementary modes of each member, which are then pooled together for further analysis [44].

2.2. Dynamic Metabolic Models

Ordinary differential equations (ODEs) are a common mathematical representation to describe dynamic systems with enzyme kinetics in the metabolic reaction network. Typically, ODEs are written in the form:

where x is the vector of system states (nutrients, secreted products, and cell mass), u is the vector of model parameters, and F is the matrix of kinetic functions. For enzymatic reaction kinetics, the popular Michaelis-Menten kinetics, and other forms such as Haldane kinetics, generalized mass action (GMA), and Hill kinetics are considered. These equations contain a large number of parameters to be estimated by regression with time course data, which may be limited in availability. Unlike steady-state models, dynamic models are typically much smaller, and usually cover only the core metabolic network, thus reducing model complexity with a reduced number of kinetic parameters. While large scale dynamic metabolic models have been constructed [45, 46], accurate estimation of parameters from experimental measurements remains the biggest challenge in building predictive kinetic models [47, 48].

Similar to the static approach, dynamic models are also built by either combining the metabolism of multiple species in the community into a single entity or using species specific information to construct individual models which are then linked via exchange reactions. Lumped dynamic models are commonly used to describe microbial communities, especially in the areas of synthetic consortia, wastewater treatment, biogeochemical communities, and gut microbiome [49-52]. This is due to the poor characterization of such communities where only meta-genomic/transcriptomic/proteomic data are available; detailed models of constituent microbes are rarely available. Reed et al. constructed a dynamic Michaelis-Menten based reaction network that successfully mimicked the elemental nitrogen and sulfur cycling in the waters of the Red Sea. They employed a functional genes approach with metagenomics data to estimate the microbes present and their expressed genes, in order to parameterize the model [51]. Notably, these lumped dynamic models focus on specific aspects of microbial functionality such as biodegradation of pollutants, or biochemical production [53-55].

When high quality models of individual species are available, compartmentalized dynamic models can be constructed using dynamic FBA (dFBA), which combines FBA and kinetic modeling approaches [56]. In essence, a set of dynamic equations (ODEs) and a stoichiometric matrix of metabolic reactions are formulated to represent the overall system and intracellular metabolism, respectively. Initially, the stoichiometric model is solved at the start of each time step using FBA to obtain the system input and output rates. The resulting values are then used in the dynamic equations to solve for the concentrations by an explicit method such as Euler’s method. This requires small time steps to be taken in order to keep the solution error within acceptable levels. In the direct approach, the stoichiometric model is solved as part of the right hand side of the ODE system, which allows implicit ODE solvers to be used; the ODE solution errors can thus be controlled. The dFBA formulation can be easily extended to multi-species systems by various approaches that primarily differ in their treatment of the species-specific stoichiometric models [57]. Dynamic multi-species metabolic modeling (DMMM) was first proposed as a multi-species extension of dFBA, where each species’ stoichiometric model is solved separately [58]. DMMM employs the direct approach for dFBA with a stoichiometric matrix for each community member. The members’ flux states are individually solved with objectives such as growth maximization, while the dynamic outer model computes the external metabolite concentration changes. Notably, this formulation does not assume any community wide objective or balanced growth. Alternatively, the species may be integrated as compartments in a single large stoichiometric matrix [59], similar to the multispecies compartment approach in FBA. To compute the solutions of each modeled species during each time interval, the methods discussed above for compartmentalized species models can be adopted with a weighted sum of individual species’ growth rates as the objective function [60]. The dFBA approach avoids the need for a large number of kinetic parameters in a pure kinetic model of similarly scale, while being able to give snapshots of metabolic fluxes across time. dFBA can also be used in conjunction with FVA to quantify alternate solutions in the fluxes computed, which can be used to identify potential biosynthetic capabilities. Recently, d-OptCom (dynamic OptCom), a dynamic extension of OptCom, was proposed to solve multispecies dFBA problems in a bi-level approach, elucidating costly cooperation between community members [61]. Compared to dFBA, the d-OptCom approach offers greater power and flexibility in examining different types of interactions in a dynamic manner.

Natural microbial communities are rarely homogenous; spatial heterogeneity exists in different communities ranging from biofilms to oceanic environments [62, 63]. Such spatial arrangements contribute to influence the interactions between different species or even sub-communities, thus giving rise to unique community functions. To model such structural heterogeneity, the computation of microbial ecosystems in time and space (COMETS) framework was developed [64]. COMETS discretizes space by a two dimensional grid, and each grid box can contain different species of microbes and metabolites. Between different grid boxes, diffusion reactions are used to describe metabolite exchanges, and even biomass. Each grid box is solved separately, followed by calculations of diffusion step using finite difference for metabolite and biomass exchanges. The framework was demonstrated on synthetic consortia of up to three species, simulating the impact of physically segregating two colonies with a third.

3. Applications

3.1. Host Microbiome

The ubiquity of microbes means that microbiota can be found in all multicellular host organisms. Such close proximity invariably results in a multitude of positive, negative, or neutral interactions. There has been growing realization on the microbiota’s impact on human health, especially the human gut microbiome (Fig. 2) [65]. In an early work, Greenblum et al. constructed a lumped metabolic network using published metagenomic data from 124 individuals [29, 66]. Gene abundance data was also used to analyze topological differences correlated with obesity and Inflammatory Bowel Disease (IBD) at the gene and network levels.

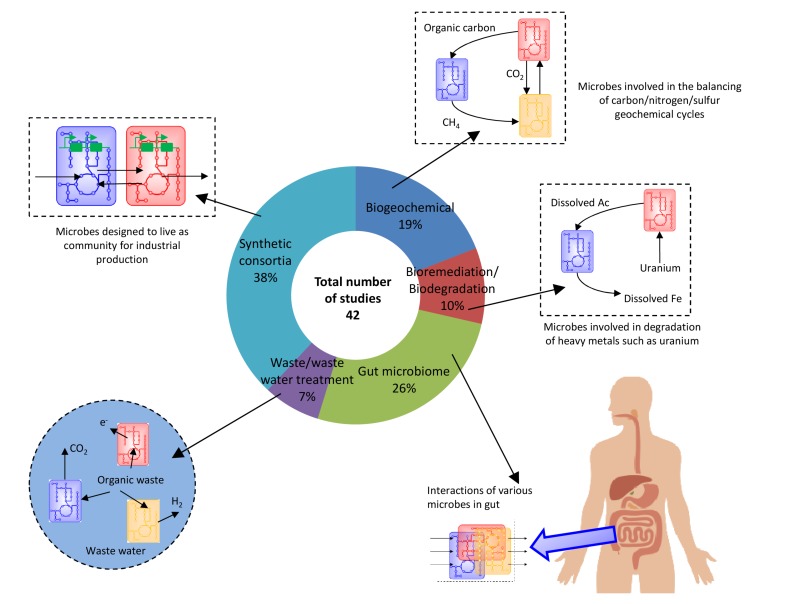
Fig. (2).

The published metabolic community modeling studies are divided into different areas of application: biogeochemical, bioremediation, gut microbiome, waste water treatment, and synthetic consortia.

Constructing stoichiometric models of gut microbes is a necessary step towards quantitative analysis of interactions among microbes, and with their host. In this regard, Shoaie et al. reconstructed genome-scale models of three gut microbes, Bacteroides thetaiotamicron, Eubacterium rectale and Methanobrevibacter smithii [67]. Different combinations of the microbes were simulated and compared with experimental data.

This compartmentalized static model was able to capture the metabolite exchanges and the short-chain fatty acids (acetate, propionate, and butyrate) production during fermentation of dietary fiber in the colon. In particular, butyrate is an important energy source for colon lining cells (colonocytes) with anti-inflammatory properties and its intracellular levels have been found to be inversely correlated with Crohn’s disease susceptibility. El-Semman et al. further focused on gut microbes responsible for butyrate production by reconstructing the genome-scale models of Bifidobacterium adolescentis and Faecalibacterium prausnitzii [68]. In this two members system, B. adolescentis produces acetate, while F. prausnitzii consumes acetate to produce butyrate. The community model accurately simulated the ratio of acetate uptake to butyrate production, and the reliance of F. prausnitzii on acetate for growth. In a more recent work, in silico simulations explored dietary effects on the gut microbiome, and observed its contribution to the changes in free amino acid concentrations in the serum [36].

With the availability of high quality host metabolic models such as human and mouse, host-microbe interactions can be analyzed. In such a pursuit, Heinken et al. developed a two species model containing metabolic networks of mouse and Bacteroides thetaiotaomicron to study their interactions [69]. Here, it should be highlighted that the Bacteroides phylum is one of the biggest constituent in mammalian gut microbiome, with B. thetaiotaomicron being a commonly used representative. The model was simulated using different dietary regimes, thereby confirming known exchange metabolites such as acetate and propionate. The simulations also newly hypothesized that amino acids can be supplied to the host by B. thetaiotaomicron. In a recent work, Heinken and Thiele constructed another compartmentalized static model composed of the human metabolic network, and different combinations of 11 human gut microbes [70]. Five of them are pathogenic while the remaining six are beneficial or commensal. Interestingly, simulation results of the host with commensal microbes support the view that the gut microbiota function as an endocrine organ within the human body as proposed earlier [71].

In addition to the human gut microbiome, the symbiosis between host and microbes has been studied across diverse host species. For example, Ankrah et al. evaluated essential amino acids provisioned by the microbes Portiera aleyrodidarum and Hamiltonella defensa to an insect host, the whitefly (Bemisia tabaci) [72]. The compartmentalized static approach was adopted with both bacteria models exchanging metabolites directly with the host, considering the production of essential amino acids as the objective function. The simulations confirmed known amino acid exchanges, and also predicted other novel metabolite exchanges. Selective disabling of either bacterium showed that H. defensa behaves as a parasite reducing the host’s growth rate, while P. aleyrodidarum is essential to the host’s growth by supplying essential amino acids and participating in nitrogen recycling. Simulation results also confirmed that H. defensa is a nutritional parasite, as it has the metabolic pathways to synthesize essential amino acids for its own growth, but without any excess capacity to supply the host.

Besides positive or commensal host-microbe interactions, some bacteria are pathogenic to their host, e.g., Mycobacterium tuberculosis in human lungs which is responsible for the tuberculosis disease. M. tuberculosis is able to survive phagocytosis by alveolar macrophages to reproduce and spread. To understand the metabolic changes during the infection, Bordbar et al. combined a genome-scale model of M. tuberculosis and a human cell-specific alveolar macrophage model contextualized from the generic human metabolic reconstruction Recon 1 with alveolar macrophage gene expression data [73]. For better accuracy, the biomass equation of the M. tuberculosis model was modified using gene expression data to reflect in vivo conditions within the phagosome. The combined model was then characterized by randomized sampling, an approach extensively used to simulate mammalian genome-scale metabolic models [41]. The simulation results illustrated different metabolic states of the M. tuberculosis model at different stages of infection which can be further studied and even exploited to identify targets for medical interventions. We believe that the greater use of contextualized models will yield more accurate simulation results, especially when applied to more complex eukaryotic host models.

Kinetic approaches have also been used to model microbiota in the human gut. Muñoz-Tamayo et al. considered butyrate production using Eubacterium hallii and Anaerostipes coli in human colon [74]. The constructed model was able to satisfactorily match the experimental data. In another work, Muñoz-Tamayo et al. developed a kinetic model for carbohydrate degradation using the anaerobic digestion model No 1 (ADM1) framework, which was originally created to model anaerobic digestion in waste water treatment [75]. Using the ADM1 framework, the lumen and mucus layers were modeled as a series of three well mixed tank reactors with mass diffusion taking place between the different layers. Both the lumen and mucus layers have four microbial functional groups at different proportions. This approach of spatial segregation allows for more accurate modeling of physically complex systems such as the human gut. Similarly, Kettle et al. aimed to construct a simplified model of the human intestinal microbiota with 10 major microbial functional groups [52]. Within each functional group, there are 10 species with traits (kinetic parameters). The model was then fitted to two data sets by stochastically assigning parameters, and then, the best fitting set was selected from multiple simulations. The model captured changes in the microbiota composition as a result of nutrient composition, as well as changes in metabolite concentration due to pH shifts. While the model reproduced experimental data successfully, the stochastically created individual species in the model hardly matched with observed species, and thus it is difficult to derive mechanistic knowledge from the simulation results.

3.2. Biogeochemical Systems and Bioremediation Communities

Microbial communities play an important role in the earth’s biogeochemical cycles [76, 77]. They are integral in the cycling of carbon, nitrogen, oxygen, and sulfur across the Earth’s surface. With increasing human impact on the environment, a deeper understanding of natural microbial communities is necessary to predict their responses to disturbances, and develop effective methods to manage them. In order to understand the interactions among microbes involved in geochemical cycle, various quantitative models have been developed and analyzed (Fig. 2).

The first static metabolic model of a microbial community was constructed by Stolyar et al., elucidating the interaction between two methanogenic syntrophy microbes (Desulfovibrio vulgaris and Methanococcus maripaludi) which are commonly found in soil, water, and animal digestive systems [34]. Hamilton et al. studied another syntrophy methanogenic co-culture of Syntrophobacter fumaroxidans and Methanospirillum hungatei using their respective genome-scale metabolic models as compartments of the co-culture [78]. It should be highlighted that thermodynamic constraints are added with a modified objective function to correctly elucidate experimental observations of formate and hydrogen exchanges. A similar approach was utilized to model the oxidation process of sulfite minerals by constructing a combined metabolic model of Leptospirillum ferriphilum and Ferroplasma acidiphilum [79].

One important rationale for modeling microbial communities is to study the metabolite exchanges among its members. In this regard, Hunt et al. examined nutrient and energy transfers across different trophic levels [80]. While most studies focus on transfers of low molecular weight metabolite, biomass derived dissolved organic carbon (DOC) was modeled as one of the sources of carbon and energy for heterotrophic consumption. Inclusion of DOC in modeling environmental communities is important since it is a large source of organic carbon [81].

As an alternative to steady state stoichiometric models, Decker et al. constructed a Monod kinetics based dynamic model of oxygen, carbon, and sulfur movement in a hypersaline microbial mat system containing cyanobacteria, purple sulfur bacteria, colorless sulfur bacteria, and sulfate-reducing bacteria [53]. The microbial guilds were connected by the diffusion of selected metabolites. Environmental light and temperature were also included in the model. The simulation results compared favorably with experimental observations, but also highlighted deficiencies in the model that encourage further refinement.

Environmental bioremediation is an area closely related to biogeochemical systems. The system modeled can encompass a large geographic area such as a marine ecosystem. In this regard, Taffi et al. modeled polychlorinated biphenyls (PCB) degradation in the Adriatic Sea by combining both bioaccumulation and PCB degradation pathways [82]. The bioaccumulation model simulated the tropic flux flows through the food web while biodegradation of PCBs was modeled by adding a Pseudomonas putida metabolic model modified with the aerobic PCB degradation pathway. This multi-scale approach based on a bi-level extension of FBA was used to formulate successful bioremediation strategies, and analyze the impact on PCB bioaccumulation in the food web.

Interestingly, Zhuang et al. used a dynamic FBA approach for modeling in situ bioremediation of uranium contaminated ground water [58, 83]. In the first study, a two species community model was constructed with Geobacter sulfurreducens and Rhodoferax ferrireducens. Unlike most works described previously, this study explored microbial competition instead of microbial cooperation. The microbes compete for acetate to grow; ammonium is required by R. ferrireducens but not necessary with G. sulfurreducens. G. sulfurreducens is capable of reducing uranium (VI) to uranium (IV) and precipitate it out of water. Hence, encouraging G. sulfurreducens growth is the ultimate goal for the bioremediation. The microbes showed different growth characteristics, and conditions of high acetate and low ammonium were identified to allow G. sulfurreducens to outcompete R. ferrireducens. In a subsequent work, they examined the problem of G. sulfurreducens population decay following the initial bloom. This population decay was accompanied by the growth of sulfate-reducing bacteria (SRBs) which are poor uranium reducers. This phenomenon was attributed to the depletion of bio-accessible Fe(III), and it was found that the G. sulfurreducens population could be revived by subsequent Fe(III) addition. In this study, the community model was modified to contain an updated metabolic model of G. sulfurreducens, and the core metabolic pathways of SRBs. Dynamic optimization was then applied to the updated community model to solve for the optimal acetate and Fe(III) addition strategy for maximum uranium reduction.

Zomorrodi et al. developed the d-OptCom framework, and used it to simulate a soil community composed of Geobacter sulfurreducens, Rhodoferax ferrireducens, and Shewanella oneidensis [61]. As studied by Zhuang et al. [58], G. sulfurreducens and R. ferrireducens have the abilities of reducing Fe(III) to Fe(II), and U(VI) to U(IV), while S. oneidensis can consume lactate during the acetate production, and reduce U(VI) to U(IV). Both OptCom and d-OptCom were tested to simulate the system, and the newer d-OptCom framework was able to show long term behavior which was not possible with the OptCom methodology.

3.3. Wastewater Treatment

Simplified lumped community models with Monod kinetics is commonly used in the metabolic modeling of wastewater treatment systems. Such an approach assumes specific metabolite flows across organisms based on experimental observations, and thus the community is assumed to be represented by a combined reaction network [84]. Lanham et al. modeled the removal of biological phosphorus removal by an activated sludge process with two main functional guilds, polyphosphate accumulating organisms, and glycogen accumulating organisms [50]. Palatsi et al. used a modified ADM1 model to study the effect of long-chain fatty acids (LCFA) on the anaerobic digestion process in waste water treatment [85]. A new LCFA inhibition kinetics expression was proposed and added to the basic ADM1 to describe experimental results effectively. Such lumped kinetic models are usually constructed based on known metabolic capabilities of the community, and thus rarely offer novel insights into metabolic interactions between microbes.

González-Cabaleiro et al. postulated that bioenergetics maximization was the selection pressure behind the choice of metabolic pathways, and thus influenced the interactions between microbes [86]. They constructed an energy based model that encompasses catabolic activities for energy harvesting, and anabolic activities for biomass growth. The model comprises Monod based kinetics for growth computation with a stoichiometric matrix for bioenergetics calculations. Two microbial communities were modeled, anaerobic fermentation of glucose to methane, and oxidation and reduction of nitrogen (nitrification). When maximizing bioenergetics harvesting, the active pathways and syntrophic relationships corresponded to experimental observations in the glucose to methane fermentation, and both the nitrification and denitrification processes. This study demonstrated how bioenergetics can be used to explain the choice of metabolic pathways and hence microbial interactions within a community.

3.4. Synthetic Consortia

Synthetic consortia are designed to harness the metabolic capabilities of different microbial species for accomplishing complex tasks and balancing the metabolic loads of single species (Fig. 2). These species are often well studied organisms, including engineered strains. A common application of synthetic consortia is to produce desired products from available raw materials. In this regard, Henson and coworkers constructed dynamic FBA models of two synthetic co-culture systems, the first composed of Saccharomyces cerevisiae and engineered Escherichia coli, and the second, S. cerevisiae and Scheffersomyces stipitis [59, 60]. Both co-cultures are constructed to produce ethanol from glucose-xylose mixtures, reflecting lignocellulosic biomass. The latter model was employed to enhance the production of ethanol by identifying optimum concentrations of inoculums and aeration level. Similarly, Ye et al. used a compartmentalized static model to study a synthetic co-culture of Ketogulonicigenium vulgare and Bacillus megaterium employed in vitamin C production [87]. K. vulgare converts the L-sorbose into the vitamin C precursor 2-keto-l-gulonic acid (2-KLG), while the B. megaterium supports growth of K. vulgare and 2-KLG production in co-culture. By fixing the growth rate of one species at experimentally observed rates, the co-culture simulation showed that the other species achieved higher growth rate compared to its mono-culture. These results confirmed the mutualistic relationship observed in experiments. The list of necessary metabolites responsible for enhancing K. vulgare growth was obtained by selective deletion and re-computation of maximal growth rates.

Synthetic consortia are also useful in constructing the theoretical foundation for testing hypotheses of interactions within community behavior. Wintermute and Silver used a set of 46 Escherichia coli auxotrophs to evaluate cross-feeding behavior among different pairs while growing in minimal media [88]. About 17% of the 1,035 pairs were able to show >50 fold greater growth than the monoculture controls by cross-feeding metabolites. These interactions occur spontaneously, defined as synthetic mutualism in trans (SMIT) which is different from the mutualism resulting from adaptive evolution [89]. The SMIT pairs were then modeled mathematically by integrating the contextualized genome-scale models of the auxotrophic E. coli as compartments in a combined model, and solved using MOMA.

As mentioned earlier, quantifying metabolite exchanges, even when the metabolite identities are known, is one of the key challenges in characterizing the behavior of microbial communities. In this respect, Hanemaaijer et al. demonstrated the use of dFBA modeling with experimental data to infer metabolic exchange fluxes between a synthetic co-culture of Clostridium acetobutylicum and Wolinella succinogenes [16].

Metabolic modeling approaches can also be exploited to design synthetic consortia with specific goals by predicting potential interactions and emergent capabilities. Klitgord and Segrè developed an algorithm to predict mutualistic or commensal interactions between pairs of microbes by designing media that did not allow for standalone growth but growth in co-cultures [90]. The method was able to reproduce known co-operations, and predict new interactions. Freilich et al. combined stoichiometric metabolic models with experimental data to quantify the maximal potential for competition and cooperation between microbial pairs under different media conditions [91]. Chiu et al. developed a framework to test ability of newly designed synthetic consortia for emergent biosynthesis capabilities using existing metabolic models [15]. Interestingly, such emergent capabilities in two species communities are more likely to be maximized when the species are at an intermediate functional distance, i.e. neither too close nor too far. This is presumably due to functional close species replicating much of each other’s metabolic functionalities, while functionally distant species share only a few metabolites that can link disparate metabolic pathways. A similar result was observed in another study reporting that metabolic pathway dissimilarities among community members are strongly coupled with metabolite exchanges [92].

4. FUTURE DIRECTIONS OF MICROBIAL COMMUNITY METABOLIC MODELING

Overall, static and dynamic metabolic modeling approaches have been used to describe various microbial communities and the interactions within. It can be further extended to account for other types of signaling interactions, e.g., quorum sensing. For example, microbes such as Pseudomonas sp. produce quorum sensing molecules through which they modulate their growth, motility, and biofilm formation, dynamically interacting with other organisms. In this regard, it may be recommended to use a hybrid approach of combining metabolic and regulatory network models of individual species [93]. Alternatively, metabolic modeling approaches may be combined with other modeling techniques such as game theory or agent based modeling to more comprehensively analyze the dynamic interactions between microbes within a community [94]. Finally, most metabolic models to date do not capture the spatial dimensions that can limit nutrient and growth space availability for a microbial community [64].

As discussed earlier, microbial communities exist in several environmental niches. In addition, several other important processes where microbial communities co-exist can be mathematically modeled to understand their community behavior. These include the human skin microbiome, food fermentation such as yoghurt, cheese, bread, beer, wine, kimchi and sauces, and plant interactions with rhizosphere bacteria and leaf microbiota [95, 96].

The human skin is typically colonized with various microbes including bacteria, fungi and viruses. Similar to the gut microbiome, these microbes also interact among themselves as well as with the host, in both positive and negative ways. However, the role of microbial interactions is crucial under certain disease states such as acne and psoriasis [97, 98]. Therefore, similar to the human gut microbiome, it will be useful to model their interactions for potential health or cosmetic applications.

Using a mixed microbial culture to ferment foods is a common practice employed to achieve the desired flavor, texture, and taste. Typically, the microbial population dynamics, characterized by the dominance of certain microbes during a particular phase, plays a critical role in determining the final food quality. As such, several studies have attempted to link the population dynamics in fermentation culture to product attributes in a mechanistic manner [10]. In this regard, the metabolic modeling approach can be applied to unravel the molecular interactions between different microbes in the consortia, thus elucidating the optimal process conditions to achieve better food quality.

Plant-microbe interactions are quintessential to a plant’s environmental adaptation and growth [96]. Among them, the plant rhizosphere microbial community plays an important role in plant nutrient uptake, and processing the organic matter in soil [99]. Rhizosphere bacteria often grow at high densities near the plant roots, which provide ample access to nutrients and also help plants by fixing atmospheric nitrogen, reduce toxic compounds, and also stimulate phytohormone synthesis, thus enhancing plant growth [100]. Moreover, it has been recently discovered that the composition of rhizosphere microbial community varies between plants, even among its different cultivators, highlighting that soil rhizosphere indeed affects the plant growth and morphogenesis [101]. Therefore, it is important to study the microbial interactions in soil rhizosphere within the microbial community and with plants to develop new strategies for enhancing plant quality and yield in agro-biotechnology.

Conclusion

The use of metabolic modeling to study microbial communities only began in the last decade. There are currently two major approaches, large scale lumped models, and compartmentalized models composed of a small number of well characterized species. In the former approach, individual species are not distinguished from one another, and instead, the focus is more on the community metabolic behaviors and functions, often determined by available meta-omics data. In the latter approach, detailed models of community members are constructed, but this requires a significant amount of information of each individual species (e.g., annotated genomes). With advancements in high-throughput omics technologies and computational capability, we can expect the number of high quality species models to grow [102]. Eventually, both the approaches will merge to result in high quality large scale models. Such high quality models of the human microbiome can be crucial in studying their impact on human health, and the rational design of medical interventions in future [103, 104]. Additionally, more efficient algorithms can be developed to design larger consortia for more sophisticated biosynthetic capabilities that can benefit mankind.

LIST OF ABBREVIATIONS

ADM1

Anaerobic Digestion Model No. 1

ATP

Adenosine triphosphate

COMETS

Computation of Microbial Ecosystems in Time and Space

dFBA

Dynamic Flux Balance Analysis

DMMM

Dynamic Multi-species Metabolic Modeling

DOC

Dissolved Organic Carbon

EMA

Elementary Mode Analysis

FBA

Flux Balance Analysis

Fe

Iron

FVA

Flux Variability Analysis

GMA

Generalized Mass Action

IBD

Inflammatory Bowel Disease

LCFA

Long Chain Fatty Acid

LP

Linear Programming

MO

Multi-objective

MOMA

Minimization of Metabolic Adjustment

ODE

Ordinary Differential Equation

PCB

Polychlorinated biphenyls

SMIT

Synthetic Mutualism in Trans

SRB

Sulfate-reducing Bacteria

U

Uranium

SUPPLEMENTARY MATERIAL

Supplementary material is available on the publisher’s website along with the published article.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors declare no conflict of interest, financial or otherwise.