Abstract
A key challenge in origin-of-life studies is understanding the environmental conditions on early Earth under which abiogenesis occurred. While some constraints do exist (e.g., zircon evidence for surface liquid water), relatively few constraints exist on the abundances of trace chemical species, which are relevant to assessing the plausibility and guiding the development of postulated prebiotic chemical pathways which depend on these species. In this work, we combine literature photochemistry models with simple equilibrium chemistry calculations to place constraints on the plausible range of concentrations of sulfidic anions (HS−, HSO3−, SO32−) available in surficial aquatic reservoirs on early Earth due to outgassing of SO2 and H2S and their dissolution into small shallow surface water reservoirs like lakes. We find that this mechanism could have supplied prebiotically relevant levels of SO2-derived anions, but not H2S-derived anions. Radiative transfer modeling suggests UV light would have remained abundant on the planet surface for all but the largest volcanic explosions. We apply our results to the case study of the proposed prebiotic reaction network of Patel et al. (2015) and discuss the implications for improving its prebiotic plausibility. In general, epochs of moderately high volcanism could have been especially conducive to cyanosulfidic prebiotic chemistry. Our work can be similarly applied to assess and improve the prebiotic plausibility of other postulated surficial prebiotic chemistries that are sensitive to sulfidic anions, and our methods adapted to study other atmospherically derived trace species.
Key Words: : Early Earth, Origin of life, Prebiotic chemistry, Volcanism, UV radiation, Planetary environments
1. Introduction
A key challenge for origins-of-life studies is determining the environmental conditions on early Earth. Environmental conditions (e.g., pH, temperature, pressure, chemical feedstock abundance) play a major role in determining the kinds of prebiotic chemistry that are possible or probable, and hence can help constrain the plausibility of proposed origin-of-life scenarios (e.g., Urey, 1952; Corliss et al., 1981; McCollom, 2013; Ruiz-Mirazo et al., 2014). Consequently, it is critical to understand the range of environmental conditions available on early Earth for abiogenesis to proceed. Work over the past few decades has begun to constrain the environmental conditions that may have been available for abiogenesis, including but not limited to the past presence of liquid water, the availability of UV light at the surface, the mix of gases being outgassed to the atmosphere, the bulk pH of the ocean, and the conditions available at deep-sea hydrothermal vents (Bada et al., 1994; Farquhar et al., 2000; Delano, 2001; Holm and Charlou, 2001; Mojzsis et al., 2001; McCollom and Seewald, 2007; Trail et al., 2011; Mulkidjanian et al., 2012; Beckstead et al., 2016; Sojo et al., 2016; Halevy and Bachan, 2017; Novoselov et al., 2017; Ranjan and Sasselov, 2017).
One challenging environmental factor to constrain is the abundance of trace chemical species on early Earth. These species can be important to proposed prebiotic chemical pathways as feedstocks or catalysts, but their abundances on early Earth can be difficult to determine due to their rarity and hence limited impact on an already scarce rock record. In this paper, we explore the plausible abundances of one such family of molecules: sulfidic anions, that is, sulfur-bearing aqueous anions (e.g., hydrosulfide, HS−; bisulfite, HSO3−; sulfite, SO32−). Our initial interest in these molecules was stimulated by the role they play in the prebiotic chemistry proposed by Patel et al. (2015), but our calculations are applicable to studies of surficial prebiotic chemistry in general. For discussion of the relevance of the surface environment and its attendant processes to prebiotic chemistry, see, for example, Mulkidjanian et al. (2012), Walker et al. (2012), Forsythe et al. (2015), Mutschler et al. (2015), Rapf and Vaida (2016), Deamer and Damer (2017), He et al. (2017). Our results are not relevant to deep-sea origin-of-life scenarios, such as McCollom and Seewald (2007), Larowe and Regnier (2008), Martin et al. (2008), and Sojo et al. (2016).
We specifically explore the atmosphere as a planetary source for sulfidic anions through dissolution of volcanically outgassed SO2 and H2S in small, shallow aqueous reservoirs like lakes. Prebiotic Earth's atmosphere is thought to have been anoxic and more reducing than modern Earth (Kasting, 2014), and volcanism levels have been hypothesized to have been higher (Richter, 1985). Then the abundance of atmospheric H2S and especially SO2 should have been higher compared to modern-day levels, and aqueous reservoirs in equilibrium with the atmosphere would have dissolved some of these gases in accordance with Henry's law, forming sulfidic anions through subsequent dissociation reactions. We use simple equilibrium chemistry combined with literature photochemical modeling to estimate the concentrations of these sulfidic anions as a function of pSO2 and pH2S, and as a function of total sulfur outgassing flux. Elevated levels of atmospheric sulfur can lead to the formation of UV-shielding gases and aerosols; consequently, we use radiative transfer calculations to constrain the surface UV radiation environment as a function of total sulfur outgassing flux. UV light is of interest to prebiotic chemists both as a potential stressor for abiogenesis (Sagan, 1973; Cockell, 2000), as a potential eustressor for abiogenesis (Sagan and Khare, 1971; Mulkidjanian et al., 2003; Pascal, 2012; Sarker et al., 2013; Rapf and Vaida, 2016; Xu et al., 2016), and because of evidence that the nucleobases evolved in a UV-rich environment (Rios and Tor, 2013; Beckstead et al., 2016).
We apply our calculations to the case study of the cyanosulfidic prebiotic systems chemistry of Patel et al. (2015). Building on the work of Powner et al. (2009) and Ritson and Sutherland (2012), Patel et al. (2015) proposed a prebiotic reaction network for the synthesis of activated ribonucleotides, short sugars, amino acids and lipid precursors from a limited set of feedstock molecules in aqueous solution under UV irradiation (at 254 nm). This reaction network is of interest because of the progress it makes toward the longstanding problem of nucleotide synthesis, because it offers the promise of a common origin for many biomolecules, and because it imposes specific geochemical requirements on its environment, which can be compared against what was available on early Earth to constrain and improve the chemistry's prebiotic plausibility (Higgs and Lehman, 2015; Springsteen, 2015; Šponer et al., 2016). Relevant to our work, the Patel et al. (2015) chemistry requires sulfidic anions to proceed, as both a photoreductant and as a feedstock for a subset of the network's reactions. Patel et al. (2015) proposed impactors as a source for the sulfidic anions; while possible, this scenario imposes an additional, local requirement for this chemistry to function. On the other hand, if the atmosphere could supply adequate sulfidic reductant (and feedstock) on a global basis, it would reduce the requirements for parts (or all) of this reaction network to function, and would make it more compelling as an origins-of-life scenario. We evaluate this scenario. While our paper focuses on the chemistry of Patel et al. (2015) as a case study, our work can be used to evaluate and improve the plausibility of any proposed sulfidic anion-sensitive surficial prebiotic chemistry. Our methods can be adapted to study the prebiotic surficial concentrations of other atmospherically sourced aqueous species.
2. Background
2.1. Plausible prebiotic levels of H2S and SO2
The abundances of H2S and SO2 in Earth's atmosphere are set by photochemistry and are sensitive to a variety of factors. One of the most important of these factors is the outgassing rate of these compounds from volcanoes into the atmosphere. Absent biogenic sources, atmospheric photochemistry models typically assume abiotic SO2 outgassing rates of 1–3 × 109 cm−2 s−1 (Kasting et al., 1989; Zahnle et al., 2006; Hu et al., 2013; Claire et al., 2014), consistent with the measured modern mean volcanogenic SO2 outgassing rate of 1.7–2.4 × 109 cm−2 s−1 (Halmer et al., 2002). H2S emission rates are indirectly estimated and much less certain; they range from 3.1 × 108 to 7.7 × 109 cm−2 s−1. A common assumption in atmospheric modeling is that SO2 and H2S are outgassed in a 10:1 ratio (e.g., Zahnle et al., 2006; Claire et al., 2014).
Early Earth is often hypothesized to have been characterized by higher levels of volcanic outgassing compared to modern Earth due to presumed higher levels of internal heat and tectonic activity. Models often assume that Archean SO2 outgassing rates were ∼3× modern (Richter, 1985; Kasting et al., 1989; Zahnle et al., 2006). However, Halevy and Head (2014) point out that during the emplacement of major volcanogenic features such as the terrestrial basaltic plains, sulfur outgassing rates as high as 1010 to 1011.5 cm−2 s−1 are possible, with the upper limit on outgassing rate coming from estimates of sulfur flux during emplacement of the Deccan Traps on Earth (Self et al., 2006).
No firm constraints exist for SO2 and H2S levels on prebiotic Earth. Kasting et al. (1989) modeled a plausible prebiotic atmosphere of 2 bar CO2, 0.8 bar N2 under 0.75× present-day solar irradiation to account for the effects of the faint young Sun at 3.9 Ga. Kasting et al. (1989) assumed that sulfur was outgassed entirely as SO2 at a total sulfur outgassing flux of ΦS = 3 × 109 cm−2 s−1 into an atmosphere overlying an ocean saturated in SO2; this last condition favors accumulation of SO2 in the atmosphere. Claire et al. (2014) modeled an atmosphere of 0.99 bar N2 and 0.01 bar CO2, under irradiation by the 2.5 Ga Sun, with an SO2:H2S outgassing ratio of 10:1, for ΦS = 1 × 108 to 1 × 1010 cm−2 s−1. Hu et al. (2013) modeled an atmosphere consisting of 0.9 bar CO2 and 0.1 bar N2 under irradiation by the modern Sun, with an SO2:H2S emission ratio of 2, for ΦS = 3 × 109 to 1 × 1013 cm−2 s−1. The SO2 and H2S mixing ratios calculated by these models are shown in Table 1; these mixing ratios may be trivially converted to partial pressures by multiplying against the bulk atmospheric pressure. Note that the Claire et al. (2014) and Kasting et al. (1989) values are surface mixing ratios, while the Hu et al. (2013) values are column-integrated mixing ratios. Since H2S and SO2 abundances tend to decrease with altitude due to losses from photochemistry, column-integrated mixing ratios should be somewhat less than the surface mixing ratio. However, since density also decreases with altitude, mixing ratios at lower altitudes are more strongly weighted in the calculation of column-integrated mixing ratios, so the column-integrated mixing ratio tends to be close to the surface mixing ratio.
Table 1.
Mixing Ratios of H2S and SO2 for Different Early Earth Models in the Literature and Different ΦS
| Model | 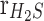 |
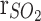 |
|---|---|---|
| Kasting et al. (1989)a, ΦS = 3 × 109 cm−2 s−1 | 2 × 10−10 | 2 × 10−9 |
| Claire et al. (2014)a, ΦS = 3 × 109 cm−2 s−1 | 1 × 10−11 | 5 × 10−11 |
| Hu et al. (2013)b, ΦS = 3 × 109 cm−2 s−1 | 4 × 10−10 | 3 × 10−10 |
| Claire et al. (2014)a, ΦS = 1 × 1010 cm−2 s−1 | 3 × 10−11 | 1 × 10−10 |
| Hu et al. (2013)b, ΦS = 1 × 1010 cm−2 s−1 | 1 × 10−9 | 9 × 10−10 |
Surface mixing ratio.
Column-integrated mixing ratio.
These models broadly agree that SO2 and H2S levels were low and increase with sulfur emission rate, but their estimates for 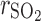 and
and 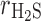 disagree with each other by up to a factor of 400. The Hu et al. (2013) estimates are typically higher than the other estimates considered. The variation in these abundances demonstrates the sensitivity of SO2 and H2S levels to atmospheric parameters such as composition and deposition velocities. Of these models, we find Hu et al. (2013) best matches the current fiducial understanding of conditions on early Earth: an atmosphere dominated by CO2 and N2, with volcanic outgassing of both SO2 and H2S, with oceans not saturated in SO2 (as compared to possibilities for early Mars; see Halevy et al.,
2007). Hu et al. (2013) also has the advantage of calculating atmospheric composition at higher values of sulfur outgassing flux than Kasting et al. (1989) and Claire et al. (2014), encompassing the 1 × 1011.5 cm−2 s−1 flux which is the upper limit of what Halevy and Head (2014) suggest possible for the emplacement of terrestrial basaltic plains. Hu et al. (2013) model processes including wet and dry deposition, formation of H2SO4 and S8 aerosol, and photochemistry and thermochemistry, with >1000 reactions included in their reaction network. We therefore use Hu et al. (2013) as a guide when estimating H2S and SO2 levels as a function of sulfur outgassing flux (see Appendix A), with the understanding that further, prebiotic-Earth-specific modeling is required to constrain this relation with certainty.
disagree with each other by up to a factor of 400. The Hu et al. (2013) estimates are typically higher than the other estimates considered. The variation in these abundances demonstrates the sensitivity of SO2 and H2S levels to atmospheric parameters such as composition and deposition velocities. Of these models, we find Hu et al. (2013) best matches the current fiducial understanding of conditions on early Earth: an atmosphere dominated by CO2 and N2, with volcanic outgassing of both SO2 and H2S, with oceans not saturated in SO2 (as compared to possibilities for early Mars; see Halevy et al.,
2007). Hu et al. (2013) also has the advantage of calculating atmospheric composition at higher values of sulfur outgassing flux than Kasting et al. (1989) and Claire et al. (2014), encompassing the 1 × 1011.5 cm−2 s−1 flux which is the upper limit of what Halevy and Head (2014) suggest possible for the emplacement of terrestrial basaltic plains. Hu et al. (2013) model processes including wet and dry deposition, formation of H2SO4 and S8 aerosol, and photochemistry and thermochemistry, with >1000 reactions included in their reaction network. We therefore use Hu et al. (2013) as a guide when estimating H2S and SO2 levels as a function of sulfur outgassing flux (see Appendix A), with the understanding that further, prebiotic-Earth-specific modeling is required to constrain this relation with certainty.
3. Methods
We consider a gas Z dissolving into a surficial aqueous reservoir (≲1 m deep), through which the UV light required for prebiotic biomolecule synthesis can penetrate (Ranjan and Sasselov, 2016); our archetypal such environment is a shallow lake. To isolate the effects of atmospheric supply of Z, we assume no other source of Z to be present (e.g., no geothermal source at the lake bottom). Henry's law states that the concentration of Z, [Z], in aqueous solution at the air/water interface is proportional to the partial pressure of the gas at that interface. We assume the aqueous reservoir to be well mixed and equilibrated throughout, so that the concentration of [Z] is uniform throughout the reservoir at the surficial value. If the reservoir is not well mixed, then the dissolved gas concentration will vary deeper into the reservoir. Under our assumption of no non-atmospheric source of Z, [Z] would decrease with depth for a poorly mixed aqueous reservoir.
This method of calculating [Z] is predicated on the assumption that the aqueous body is in equilibrium with the atmosphere, that is, that the solution is saturated in Z and the sink and source of Z is outgassing and deposition from the atmosphere. This assumption is valid when there are no other sinks to drive the system away from equilibrium. We discuss the veracity of this assumption in Section 5.2. In brief, this assumption is valid for shallow, well-mixed lakes that are not very acidic or hot, but not valid for deep, acidic, or hot waters. For these scenarios, our calculations provide upper bounds on [Z].
In aqueous solution, H2S undergoes the dissociation reactions
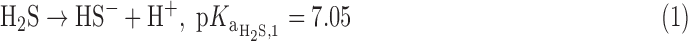 |
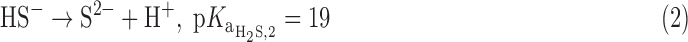 |
where the pKa values are taken from Lide (2009) and can be related to the corresponding equilibrium constants by 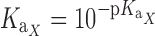 . Similarly, SO2 undergoes the reactions
. Similarly, SO2 undergoes the reactions
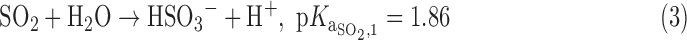 |
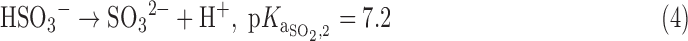 |
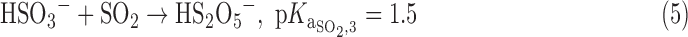 |
where the pKa values are from Neta and Huie (1985).
To compute the abundances of these different sulfur-bearing compounds as a function of [Z], we must make assumptions as to the background chemistry of the aqueous reservoir they are dissolved in, especially its pH. If the reservoir is completely unbuffered (e.g., pure water), its pH (and hence the speciation of S-bearing compounds) will be completely determined by [Z]. At the other extreme, if the reservoir is completely buffered, its pH will be independent of [Z]. Natural waters typically lie in between these two extremes; they are often buffered by mineral or atmospheric interactions toward a certain pH1, but with enough atmospheric supply their buffers can be overwhelmed. We explore these bracketing cases below, with the understanding that the true speciation behavior in nature was most likely somewhere in between.
3.1. Calculating dissolved gas concentration
We use Henry's law, coupled with the well-mixed reservoir assumption, to calculate the concentration of molecules dissolved from the atmosphere. Henry's law states that for a species Z,
 |
where HZ is the gas-specific Henry's law constant and fZ is the fugacity of the gas. Over the range of temperatures and pressures relevant to surficial prebiotic chemistry, the gases in our study are ideal, and consequently fZ = pZ, the partial pressure of Z. We make this simplifying assumption throughout our study.
At T0 = 298.15 K, the Henry's law constants for H2S and SO2 dissolving in pure water are 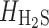 = 0.101 M/bar and
= 0.101 M/bar and 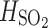 = 1.34 M/bar, respectively. Increasing salinity tends to decrease HG, a process known as salting out. Similarly, increasing temperature also tends to decrease HC. Our overall results are insensitive to variations in temperature of 25 K from T0 and 0 ≤ [NaCl] ≤ 1 M; see Appendix C and Appendix D.1. For simplicity, we therefore neglect the temperature- and salinity-dependence of Henry's law.
= 1.34 M/bar, respectively. Increasing salinity tends to decrease HG, a process known as salting out. Similarly, increasing temperature also tends to decrease HC. Our overall results are insensitive to variations in temperature of 25 K from T0 and 0 ≤ [NaCl] ≤ 1 M; see Appendix C and Appendix D.1. For simplicity, we therefore neglect the temperature- and salinity-dependence of Henry's law.
3.2. Unbuffered solution
Consider an unbuffered solution with dissolved Z, whose properties are determined entirely by the reactions Z and its products undergo. From the definition of equilibrium constant, we can use the H2S and SO2 speciation reactions to write
 |
 |
and
 |
 |
 |
Where aC is the activity of species C. aC is related to the concentration of C, [C], by aC = γC[C], where γC is the activity coefficient (Misra, 2012). The use of activities instead of concentrations accounts for ion-ion and ion-H2O interactions. γ = 1 for a solution with an ionic strength of I = 0. For ionic strengths of 0–0.1 M, we calculate the activity coefficients for each species as a function of solution ionic strength using Extended Debye-Huckel theory (Debye and Huckel, 1923). The activity coefficients in this formalism are calculated by
 |
Here, A and B are constants that depend on the temperature, density, and dielectric constant of the solvent; we use A = 0.5085 M−1/2 and B = 0.3281 M−1/2Å−1, corresponding to 25°C water (Misra, 2012) (our results are robust to this assumption; see Appendix D). zC is the charge of species C. αC is an ion-specific parameter with values related to the hydration radius of the aqueous species; we took our αC values from Misra (2012). We were unable to locate a value of αC for HS2O5− and consequently take 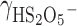 = 1 throughout. I is the ionic strength of the solution, defined as
= 1 throughout. I is the ionic strength of the solution, defined as
 |
We can combine these equations with the equation for water dissociation:
 |
 |
and the requirement for charge conservation:
 |
With [Z] specified by Henry's law and our assumption of a well-mixed reservoir, this system is fully determined, and we can numerically solve it to determine the concentration of each of the species above as a function of pZ and I. A wide range of ionic strengths are possible for natural waters; modern freshwater systems like rivers have typical ionic strengths of order 1 × 10−3 M (Lerman et al., 1995), whereas modern terrestrial oceans have an ionic strength of 0.7 M2. The concentrations of divalent cations, especially Mg2+ and Ca2+, in early oceans have been suggested to be near 10 mM (Deamer and Dworkin, 2005). A more fundamental constraint comes from vesicle formation, which is known to be inhibited at high salt concentrations and hence ionic strengths: Maurer and Nguyen (2016) report that lipid vesicle formation is impeded in solutions with I > 0.1 M. These considerations motivate our focus on low-ionic-strength waters, with I ≤ 0.1 M3.
We calculate the speciation of sulfur-bearing species from dissolved H2S and SO2 for I = 0 and I = 0.1 M; the results are shown in Figs. 1 and 2. I = 0 is the lowest possible ionic strength, and I = 0.1 M corresponds to the limit from lipid vesicle formation.
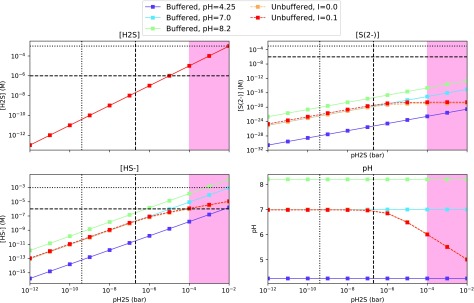
FIG. 1.
Concentrations of sulfur-bearing compounds and pH as a function of pH2S for a well-mixed aqueous reservoir. [H2S] is calculated from Henry's law; the concentrations of HS− and S2− are calculated from equilibrium chemistry for (1) solutions buffered to various pH values and (2) unbuffered solutions with varying ionic strengths. The vertical dotted line demarcates the expected pH2S for an abiotic Earth with a weakly reducing CO2-N2 atmosphere with modern levels of sulfur outgassing, from Hu et al. (2013). The vertical dashed line demarcates the expected pH2S for the same model but with outgassing levels of sulfur corresponding to the upper limit of the estimate for the emplacement of the terrestrial flood basalts. In the red shaded area, pH2S is so high it blocks UV light from the planet surface, meaning UV-dependent prebiotic pathways, e.g., those of Patel et al. (2015), cannot function (Ranjan and Sasselov, 2017). The red curve largely overplots the orange, demonstrating the minimal impact of ionic strength on the calculation for I ≤ 0.1. The horizontal dashed and dotted lines demarcate micromolar and millimolar concentrations, respectively. The cyanosulfidic chemistry of Patel et al. (2015) has been demonstrated at millimolar S-bearing photoreductant concentrations, and at least high micromolar levels of these compounds are thought to be required for high-yield prebiotic chemistry.
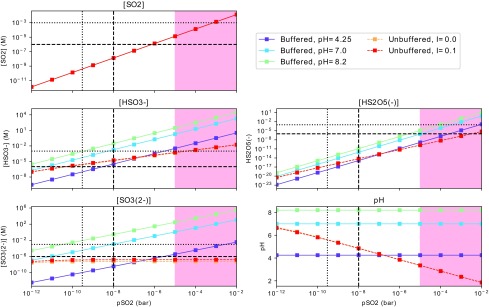
FIG. 2.
Concentrations of sulfur-bearing compounds and pH as a function of pSO2 for a well-mixed aqueous reservoir. [SO2] is calculated from Henry's law; the concentrations of HSO3−, SO32−, and HS2O5− are calculated from equilibrium chemistry for (1) solutions buffered to various pH values and (2) unbuffered solutions with varying ionic strengths. The vertical dotted line demarcates the expected pSO2 for an abiotic Earth with a weakly reducing CO2-N2 atmosphere with modern levels of sulfur outgassing, from Hu et al. (2013). The vertical dashed line demarcates the expected pSO2 for the same model, but with outgassing levels of sulfur corresponding to the upper limit of the estimate for the emplacement of the terrestrial flood basalts. In the red shaded area, pSO2 is so high it blocks UV light from the planet surface, meaning UV-dependent prebiotic pathways, e.g., those of Patel et al. (2015), cannot function (Ranjan and Sasselov, 2017). The red curve largely overplots the orange, demonstrating the minimal impact of ionic strength on the calculation for I ≤ 0.1. The horizontal dashed and dotted lines demarcate micromolar and millimolar concentrations, respectively. The cyanosulfidic chemistry of Patel et al. (2015) has been demonstrated at millimolar S-bearing photoreductant concentrations, and at least high micromolar levels of these compounds are thought to be required for high-yield prebiotic chemistry.
3.3. Buffered solution
Consider now an aqueous reservoir that is buffered to a given pH. For example, the pH of the modern oceans is buffered by calcium carbonate to a global mean value of 8.1–8.2 (Hall-Spencer et al., 2008). Then, we know [H+], and can hence calculate the speciation of dissolved H2S and SO2 from the equilibrium constant Eqs. 7–8 and 9–11 individually. Our results are insensitive to ionic strength for I ≤ 0.1 M (see Figs. 1 and 2, and Appendix B), and I ≤ 0.1 M is required for vesicle formation and other prebiotic chemistry (Maurer and Nguyen, 2016; Deamer and Damer, 2017), motivating us to take I = 0 for simplicity.
With Henry's law and our assumption of a well-mixed reservoir, we can readily calculate the concentration of the above species as a function of pH2S or pSO2 and pH. The results of this calculation are presented in Figs. 1 and 2 for three representative pH values. We selected pH = 8.2, corresponding to modern ocean; pH = 7, corresponding to the near-neutral phosphate-buffered conditions in which Patel et al. (2015) conducted their experiments; and pH = 4.25, corresponding to raindrops in a pCO2∼0.1 bar atmosphere (Halevy et al., 2007). Such high CO2 levels are hypothesized for young Earth in order to power a greenhouse effect large enough to maintain clement surface conditions (Kasting, 1993).
The code used to implement these calculations is available for validation and extension at https://github.com/sukritranjan/RanjanToddSutherlandSasselov2017.git.
4. Results
4.1. H2S versus SO2
Figure 1 shows the speciation of sulfur-bearing compounds from dissolved H2S for an unbuffered reservoir, and reservoirs buffered to various pH values. Over the range of ionic strengths considered, HS− is the dominant anion, and S2− is present at negligible concentrations. As pH2S increases, the pH of the unbuffered reservoir drops, but slowly. This is expected, since H2S is a weak acid.
Figure 2 shows the speciation of sulfur-bearing compounds from dissolved SO2 for an unbuffered reservoir, and reservoirs buffered to various pH values. Because of the lack of O2 in this anoxic era, the first dissociation of SO2 forms sulfite, rather than sulfate. HSO3− and SO32− are present at comparable levels; HS2O5− is negligible. As pSO2 increases, the pH of the unbuffered reservoir falls off rapidly; this is expected since hydrated SO2 is a strong acid.
SO2 is an order of magnitude more soluble than H2S, and its first dissociation is much more strongly favored (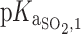 = 1.86 vs.
= 1.86 vs. 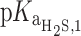 = 7.05). Consequently, far higher concentrations of sulfidic anions can be sustained for a given pSO2 than for the same pH2S (see Figs. 1 and 2). Maintaining micromolar concentrations of HS− requires pH2S ≥ 1 × 10−6 bar at pH = 8.2 (modern ocean), and pH2S ≥ 1 × 10−5 bar for more neutral pH values. Maintaining micromolar concentrations of S2− is impossible over plausible ranges of pH and sulfur outgassing flux (
= 7.05). Consequently, far higher concentrations of sulfidic anions can be sustained for a given pSO2 than for the same pH2S (see Figs. 1 and 2). Maintaining micromolar concentrations of HS− requires pH2S ≥ 1 × 10−6 bar at pH = 8.2 (modern ocean), and pH2S ≥ 1 × 10−5 bar for more neutral pH values. Maintaining micromolar concentrations of S2− is impossible over plausible ranges of pH and sulfur outgassing flux (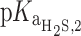 = 19). The concentration of sulfidic anions could be increased by going to higher pH and salinity. However, the reactions of, for example, Patel et al. (2015) have not been demonstrated to proceed under such conditions.
= 19). The concentration of sulfidic anions could be increased by going to higher pH and salinity. However, the reactions of, for example, Patel et al. (2015) have not been demonstrated to proceed under such conditions.
By contrast, dissolved SO2 gives rise to comparatively high concentrations of sulfidic anions due to higher solubility and a more favorable first ionization. Micromolar concentrations of HSO3− are possible for pSO2 > 1 × 10−11 bar for all but very acidic solutions; micromolar concentrations of SO32− are possible for solutions buffered to pH ≥7 over the same range. Millimolar levels of HSO3− and SO32− are possible for solutions buffered to pH ≥8.2 for pSO2 ≳ 10−10 bar, and for pH ≥7 solutions for pSO2 ≳ 10−8 bar. pSO2 ≥ 3 × 10−10 bar is expected for outgassing rates corresponding to the steady state on early Earth according to the model of Hu et al. (2013) (ΦS = 3 × 109 cm−2 s−1). During transient epochs of intense volcanism such as the emplacement of basaltic plains, emission rates might have risen as high as ΦS = 1011.5 cm−2 s−1 (Self et al., 2006; Halevy and Head, 2014), corresponding to pSO2 = 1 × 10−8 bar. We note that estimates based on Hu et al. (2013) are for column-integrated abundances, and the surface abundances were likely modestly larger. Hence, it seems likely that the atmosphere could have supplied micromolar levels of SO2-derived anions for prebiotic chemistry, and perhaps even millimolar concentrations if the solution were buffered to slightly alkaline pH (e.g., pH comparable to the modern ocean).
4.2. H2S and SO2
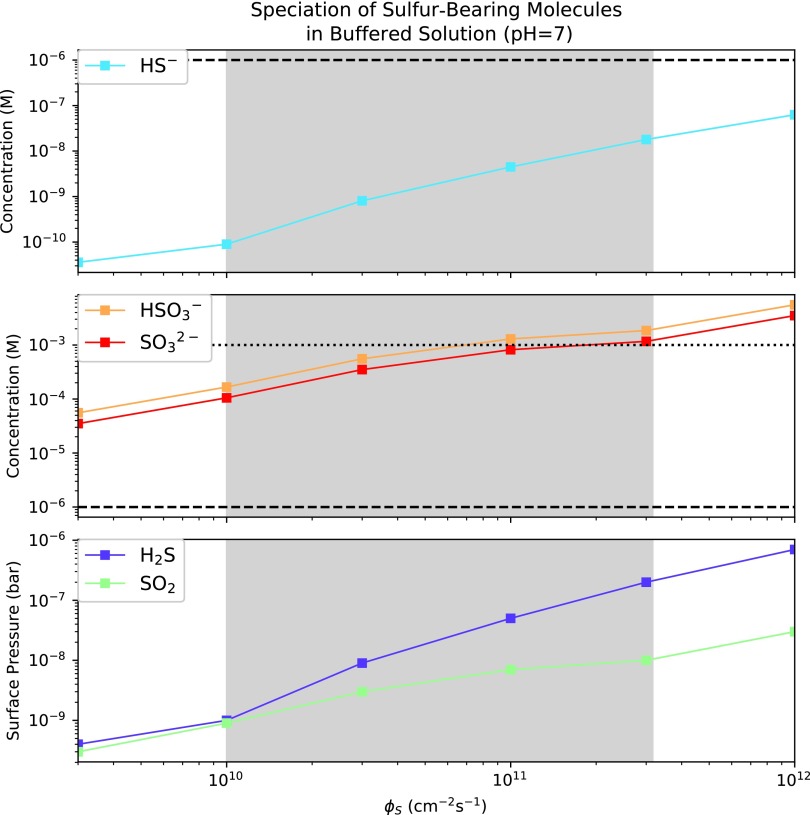
In Section 4.1 we evaluated the prospects for buildup of sulfur-bearing anions from dissolved atmospheric H2S and SO2 in isolation. However, H2S and SO2 are injected simultaneously into the atmosphere by volcanism and would have been present at the same time. Figure 3 presents the speciation of sulfur-bearing molecules from dissolved atmospheric H2S and SO2 in a solution buffered to pH = 7 as a function of total sulfur outgassing rate, ΦS. This pH corresponds approximately to the phosphate-buffered conditions in which the chemistry of Patel et al. (2015) proceeded4. If the solution were buffered to higher pH, sulfidic anion concentrations would be higher due to a more favorable first dissociation, and vice versa.
FIG. 3.
Speciation of sulfur-bearing molecules in an aqueous reservoir buffered to pH = 7 as a function of total sulfur emission flux ΦS. The range of ΦS highlighted by Halevy and Head (2014) for emplacement of basaltic plains on Earth is shaded in gray. Horizontal dashed and dotted lines demarcate micromolar and millimolar concentrations, respectively.
As before, we connected the H2S and SO2 abundances to ΦS by the high-CO2 model calculations of Hu et al. (2013). We took the surface mixing ratio of these gases to equal the column-integrated mixing ratio, which may slightly underestimate the surface mixing ratio of these gases. ΦS = 1–3 × 109 cm−2 s−1 for modern Earth and ΦS = 1010 to 1011.5 cm−2 s−1 have been suggested on a transient (1–10 year) basis for major volcanic episodes like the emplacement of basaltic plains on Earth (Self et al., 2006; Halevy and Head, 2014). As discussed in Section 4.1, SO2-derived anions can build to micromolar levels at modern outgassing rates and can build to millimolar levels during volcanic episodes like the emplacement of basaltic plains, while H2S-derived anions cannot, absent highly alkaline conditions.
4.3. Coupling to the UV surface environment
H2S, SO2, and their photochemical aerosol by-products (S8, H2SO4) are robust UV shields, and at elevated levels their presence can dramatically reduce surface UV radiation (Hu et al., 2013; Ranjan and Sasselov, 2017). This effect could be good for origin-of-life scenarios which do not require UV light, since UV light can photolytically destroy newly formed biomolecules (e.g., Sagan, 1973). On the other hand, it could be bad for UV-dependent prebiotic chemistry, which depends on UV light to power their syntheses (e.g., Ritson and Sutherland, 2012; Patel et al., 2015; Xu et al., 2016). In the latter case, it begs the question whether the elevated levels of SO2 and H2S that could supply the sulfidic anions required for cyanosulfidic chemistry might also quench the UV radiation also required by these pathways.
To explore this question, we calculated the attenuation of incoming 3.9 Ga solar radiation (calculated from the models of Claire et al., 2012) by a CO2-N2-SO2-H2S atmosphere, using a two-stream radiative transfer model (Ranjan and Sasselov, 2017; Ranjan et al., 2017). We set the solar zenith angle to 48.2°, corresponding to the insolation-weighted mean value (Cronin, 2014), and the albedo to 0.2, a representative value for rocky planets consistent with past modeling5 (Segura et al., 2003; Rugheimer et al., 2015). We once again used the work of Hu et al. (2013) to connect H2S and SO2 abundances to ΦS, and for consistency we assumed inventories of CO2 and N2 matching those assumed by Hu et al. (2013) (their high-CO2 case). Our radiative transfer calculations are insensitive to the atmospheric T/P profile, because atmospheric emission is negligible at UV wavelengths and our UV cross-sections vary minimally as a function of temperature (Ranjan et al., 2017); consequently, we assume a simple exponential profile to the vertical number density of the atmosphere. We also used the work of Hu et al. (2013) to estimate the total S8 and H2SO4 aerosol loading in the atmosphere for each ΦS, and calculated aerosol optical parameters using the same size distributions and complex indices of refraction as they did. Lacking detailed atmospheric profiles of the aerosol abundance as a function of altitude, we assumed the aerosols were distributed exponentially, with a scale height equal to the bulk atmospheric scale height (i.e., well mixed). In practice, sulfur aerosols tend to form photolytically at higher altitudes, meaning our approach places more aerosol at low altitude and less aerosol at high altitude. Since the radiative impact of aerosol absorption is amplified lower in the atmosphere due to enhanced scattering, this means our treatment should slightly overestimate UV attenuation due to aerosols. Similarly, Hu et al. (2013) assume an aerosol size distribution with surface area mean diameter DS = 0.1 μm, at the lower end of the plausible DS = 0.1–1 μm range, which maximizes the possible radiative impact of the sulfur aerosols. Consequently, our results should be interpreted as a lower bound on the true UV fluence.
Figure 4 presents the UV fluence available on the surface of the prebiotic Earth as a function of ΦS under these assumptions. For ΦS ≤ 1 × 1011 cm−2 s−1, UV radiation remains abundant on the planet surface. Millimolar levels of SO32− and HSO3− are available in aqueous reservoirs buffered to pH ≥7 for ΦS = 1 × 1011 cm−2 s−1. Consequently, volcanism could supply prebiotically relevant levels of SO32− and HSO3− without blocking off the UV radiation required by UV-dependent prebiotic pathways for sulfur emission fluxes up to ΦS ≤ 1 × 1011 cm−2 s−1 (near the upper edge of what is considered plausible for major terrestrial volcanic episodes). On the other hand, for ΦS ≥ 3 × 1011 cm−2 s−1, atmospheric sulfur-bearing gases and aerosols, especially the UV-absorbing S8, suppress surface UV radiation by an order of magnitude or more; this paucity of UV radiation may pose a challenge for UV-dependent prebiotic chemistry but could create a very clement surface environment for UV-independent prebiotic chemistries. If one accepts the idea that the nucleobases show evidence of UV selection pressure (Crespo-Hernández et al., 2004; Serrano-Andres and Merchan, 2009; Rios and Tor, 2013; Beckstead et al., 2016; Pollum et al., 2016), this suggests the biogenic nucleobases evolved in an epoch with ΦS ≤ 1 × 1011 cm−2 s−1.
FIG. 4.
UV surface radiance for early Earth as a function of ΦS, using the models of Hu et al. (2013). The black solid line indicates the top-of-atmosphere (TOA) flux, i.e., the irradiation incident at the top of the atmosphere from the young Sun. The vertical dashed line demarcates 254 nm, the wavelength at which the low-pressure mercury lamps commonly used in prebiotic chemistry experiments emit.
5. Discussion
5.1. Sulfidic anion concentrations in surficial waters on early Earth
We have shown that terrestrial volcanism could have globally supplied the sulfidic anions SO32− and HSO3−, derived from the dissolution of SO2 into aqueous solution, to shallow surficial aqueous reservoirs on early Earth. These compounds would have been available at micromolar levels for volcanic outgassing rates comparable to the modern day. During episodes of high volcanism, such as those responsible for emplacement of basaltic plains (ΦS≈1 × 1011 cm−2 s−1), these compounds could have built up to the millimolar levels in shallow aqueous reservoirs buffered to pH ≥7. On the other hand, due to its lower solubility and unfavorable first dissociation, sulfidic anions derived from dissolving atmospheric H2S can only be supplied at low concentrations (sub-micromolar) across the plausible range of pH2S and pH6. Therefore, other mechanisms must be invoked for supply of such anions, if required by a proposed prebiotic chemical pathway.
We conducted our calculations assuming a temperature of T = 25°C. We investigate the sensitivity of our results to temperatures ranging from T = 0°C to 50°C in Appendix D, including temperature effects on both the reaction rate and the Henry's law coefficient. While H2S-derived anion concentrations are not significantly affected by temperature variations in this range, SO2-derived anion concentrations are. This is because 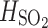 decreases with temperature and
decreases with temperature and 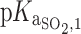 increases with temperature7; both effects favor decreased concentrations of HSO3− and its derivatives with increasing temperature, assuming a not highly acidic (pH >2.5) solution. We find that while our overall conclusions are unchanged, concentrations of the SO2-derived anions HSO3− and SO32− are an order of magnitude higher for T ≈ 0°C relative to T = 25°C, and an order of magnitude lower for T ≈ 50°C, assuming a near-neutral reservoir. Consequently, cooler waters are more favorable environments for prebiotic chemistry which invokes HSO3− or SO32−.
increases with temperature7; both effects favor decreased concentrations of HSO3− and its derivatives with increasing temperature, assuming a not highly acidic (pH >2.5) solution. We find that while our overall conclusions are unchanged, concentrations of the SO2-derived anions HSO3− and SO32− are an order of magnitude higher for T ≈ 0°C relative to T = 25°C, and an order of magnitude lower for T ≈ 50°C, assuming a near-neutral reservoir. Consequently, cooler waters are more favorable environments for prebiotic chemistry which invokes HSO3− or SO32−.
Sulfur-bearing gases and aerosols, in particular S8, are strong UV absorbers, and if present at high enough levels could suppress UV-sensitive prebiotic chemistry. For ΦS ≤ 1 × 1011 cm−2 s−1, corresponding to most of the plausible range of sulfur emission fluxes on early Earth, surface UV fluxes (200–300 nm) are not significantly attenuated by atmospheric absorbers, meaning that in the steady state and for most volcanic eruptions, abundant UV light should have reached Earth's surface to power UV-dependent prebiotic chemistry. However, for the very largest volcanic eruptions, corresponding to the uppermost end of the plausible range of sulfur outgassing fluxes during terrestrial basaltic flood plain emplacement (ΦS = 3 × 1011 cm−2 s−1), surface UV fluence (200–300 nm) may be reduced by an order of magnitude or more. Hence, the very largest volcanic events8 might create an especially clement surficial environment for UV-independent prebiotic chemistry.
These results were derived using the high-CO2 model of Hu et al. (2013), which, while plausible, assumes more CO2 and less N2 than other models of prebiotic Earth (e.g., Rugheimer et al., 2015) and is hence comparatively oxidizing. We explored the sensitivity of our results to this assumption via the N2-rich model of Hu et al. (2013). This model assumes 1 bar of N2 and negligible CO2 and is hence an unrealistic approximation to early Earth, because an appreciable CO2 inventory is expected due to climate constraints (Kasting, 1993; Wordsworth and Pierrehumbert, 2013) and due to volcanic outgassing of CO2. Hence, this model serves as an extreme bounding case. Assuming this model, we find that H2S and SO2 levels are lower than for the high-CO2 case. SO2-derived anions remain available at micromolar levels over the plausible range of ΦS but in order to build to millimolar levels require the assumption of reservoirs buffered to slightly alkaline pH (e.g., pH ∼8.2, modern ocean). HS− levels are even lower than in the CO2-rich case. UV fluences are lower than in the CO2-rich case, due to elevated levels of S8 formation in this more reducing atmosphere; surface UV fluence (200–300 nm) is suppressed by an order of magnitude or more for ΦS ≥ 1 × 1011 cm−2 s−1. Overall, this boundary case suggests that our finding that the atmosphere can supply prebiotically relevant levels of SO2-derived anions but not H2S-derived anions in conjunction with UV light remains true across a broad range of CO2 and N2 abundances, though both sulfidic anion abundances and UV are lower for more reducing, N2-rich atmospheres. However, a detailed exploration of the pCO2-pN2 parameter space with photochemical models is required to be certain of these findings.
5.2. Impact of other sinks
Our analysis is predicated on the assumption that [Z] is set by Henry equilibrium, that is, that the aqueous reservoir is saturated in H2S and SO2. This assumes no major sinks other than outgassing to the atmosphere. In this section, we examine the sensitivity of our results to this assumption. Microbial sinks (e.g., Halevy, 2013) are not relevant since we are concerned with prebiotic Earth; neither are oxic sinks, since the surface of early Earth was anoxic (Kasting and Walker, 1981; Kasting, 1987; Farquhar et al., 2001; Pavlov and Kasting, 2002; Li et al., 2013). However, reactions with metal cations to produce insoluble precipitates and redox reactions could have been relevant; we explore these sinks.
5.2.1. Precipitation reactions with metal cations
We explored the possibility that reactions of S anions with metal cations might lead to formation of insoluble precipitates, which would act as a sink on S-anion concentrations. Such cations might have been delivered to aqueous reservoirs via weathering of rocks and minerals.
Under standard conditions, Fe2+ and Cu2+ react with H2S(aq) to generate insoluble precipitates, like CuS and FeS2 (Rickard and Luther, 2007; Rumble, 2017). Interaction of copper sulfides with cyanide solution can liberate HS− (Coderre and Dixon, 1999), as invoked by Patel et al. (2015). In general, high-Cu/Fe waters (e.g., due to interaction with ores) will be even more HS−-poor than we have modeled, with the caveat that specific local environmental factors (like the presence of aqueous cyanide) can prevent sulfide depletion due to precipitation. This reinforces our conclusion that HS− concentrations are unlikely to have reached prebiotically relevant levels on early Earth, absent unique local factors. For example, the aqueous cyanide required as a feedstock in the pathways of Patel et al. (2015) would also permit elevated HS− levels.
Ca2+, produced by mineral weathering, reacts with sulfite to produce insoluble CaSO3. Studying the Ca2+-SO2− system requires considering the effects of carbonate (CO32−) as well, because Ca2+ forms precipitate with this anion as well, and because high levels of carbonate are expected in natural waters on early Earth due to elevated levels of atmospheric CO2 required to solve the faint young Sun paradox (Kasting, 1987). While precisely modeling this geochemical system requires use of a geochemical model capable of accounting for all reactions involving sulfites and carbonates and their kinetics, we can get a first-order estimate of the impact of Ca2+, as follows. Assuming parameters from Hu et al. (2013), the flux of carbonates into solution due to deposition and speciation of atmospheric CO2 is 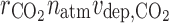 = 2 × 1015 cm−2 s−1 on the CO2-rich early Earth, which exceeds the mean flux of Ca due to mineral weathering (1–5 × 1010 cm−2 s−1; Watmough and Aherne, 2008; Taylor et al.,
2012) by 5 orders of magnitude; thus, it is reasonable to assume the solution is saturated in CO2 with abundance dictated by Henry's law of (3.3 × 10−2
M/bar)(0.9 bar) = 0.03 M (Sander, 2015). Then, [CO32−] = (0.03 M)(107–6.35)(107–10.33) = 6 × 10−5
M at neutral pH (dissociation constants
= 2 × 1015 cm−2 s−1 on the CO2-rich early Earth, which exceeds the mean flux of Ca due to mineral weathering (1–5 × 1010 cm−2 s−1; Watmough and Aherne, 2008; Taylor et al.,
2012) by 5 orders of magnitude; thus, it is reasonable to assume the solution is saturated in CO2 with abundance dictated by Henry's law of (3.3 × 10−2
M/bar)(0.9 bar) = 0.03 M (Sander, 2015). Then, [CO32−] = (0.03 M)(107–6.35)(107–10.33) = 6 × 10−5
M at neutral pH (dissociation constants 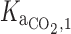 = 6.35 and
= 6.35 and 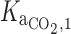 = 10.33 from Rumble [2017]9). Since CaCO3 (Ksp = 3.36 × 10−9
M2, Rumble, 2017) is 2 orders of magnitude less soluble than CaSO3 (Ksp = 3.1 × 10−7
M2, Rumble, 2017) and the sulfite flux is much less than the carbonate flux, we can assume that [Ca2+] is dictated to first order by equilibrium with carbonate mineral, that is, [Ca2+] = 3.36 × 10−9
M2/6 × 10−5
M = 6 × 10−5
M. At this [Ca2+], CaSO32−(s) will begin to form at [SO32−] = 3.1 × 10−7
M2/6 × 10−5
M = 5 × 10−3
M. The [SO32−] we calculate does not exceed this threshold value across the plausible range of sulfur outgassing fluxes in our calculation, meaning the solution is unsaturated in CaSO3 and precipitate does not form. Were pCO2 lower, for example, pCO2 = 0.2 bar10, CaSO3 precipitate formation begins at [SO32−] = 1 × 10−3
M. However, if pH were low, the carbonate solubility would exceed sulfite solubility, and sulfite precipitates would form (Halevy et al.,
2007); hence, at low pH, sulfite and bisulfite concentrations will be below the values we calculate. Overall, our results are unaffected by CaSO3 precipitation across most of parameter space, but CaSO3 precipitation might be a significant sink on aqueous sulfite levels for acid solutions and/or for very low atmospheric CO2-levels; calculations with a more thorough geochemical model (e.g., PHREEQC, Parkhurst and Appelo, 2013) are required to constrain S-anion concentrations in this regime.
= 10.33 from Rumble [2017]9). Since CaCO3 (Ksp = 3.36 × 10−9
M2, Rumble, 2017) is 2 orders of magnitude less soluble than CaSO3 (Ksp = 3.1 × 10−7
M2, Rumble, 2017) and the sulfite flux is much less than the carbonate flux, we can assume that [Ca2+] is dictated to first order by equilibrium with carbonate mineral, that is, [Ca2+] = 3.36 × 10−9
M2/6 × 10−5
M = 6 × 10−5
M. At this [Ca2+], CaSO32−(s) will begin to form at [SO32−] = 3.1 × 10−7
M2/6 × 10−5
M = 5 × 10−3
M. The [SO32−] we calculate does not exceed this threshold value across the plausible range of sulfur outgassing fluxes in our calculation, meaning the solution is unsaturated in CaSO3 and precipitate does not form. Were pCO2 lower, for example, pCO2 = 0.2 bar10, CaSO3 precipitate formation begins at [SO32−] = 1 × 10−3
M. However, if pH were low, the carbonate solubility would exceed sulfite solubility, and sulfite precipitates would form (Halevy et al.,
2007); hence, at low pH, sulfite and bisulfite concentrations will be below the values we calculate. Overall, our results are unaffected by CaSO3 precipitation across most of parameter space, but CaSO3 precipitation might be a significant sink on aqueous sulfite levels for acid solutions and/or for very low atmospheric CO2-levels; calculations with a more thorough geochemical model (e.g., PHREEQC, Parkhurst and Appelo, 2013) are required to constrain S-anion concentrations in this regime.
5.2.2. Redox reactions
We explored the possibility that redox reactions (disproportionation, comproportionation) might have acted as sinks to S-anion concentrations in shallow aqueous reservoirs on prebiotic Earth, or might otherwise affect the distribution of sulfidic anions. We identified the following reactions that are spontaneous near standard conditions (Siu and Jia, 1999; Halevy, 2013):
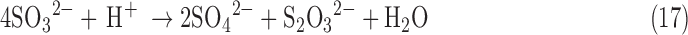 |
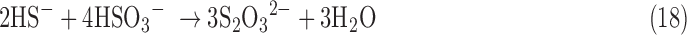 |
The kinetics of Reaction 17 are not well characterized near standard temperature and are an active topic of research (Mirzoyan and Halevy, 2014; Amshoff et al., 2016). Meyer et al. (1982) report sulfite and bisulfite are stable on timescales ≥1 year in anoxic conditions, while Guekezian et al. (1997) report decay of sulfite in days at pH ≥12.8. Halevy (2013) propose that rate coefficients in the range 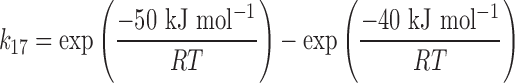 s−1 are plausible; at 293 K, this corresponds to 1 × 10−9 to 7 × 10−8 s−1, which correspond to timescales of 0.5–30 years. The kinetics of Reaction 18 have been determined as a function of temperature at pH = 9 and I = 0.2 M by Siu and Jia (1999). At 293 K, the rate coefficient is k18 = 4 × 103
M −2 s−1. At the S-anion concentrations relevant to our work11, the timescale of this reaction is ≳1 year. For comparison, putative prebiotic chemistry in laboratory studies often occurs on timescales of hours to days (Patel et al., 2015; Xu et al., in press, e.g.).
s−1 are plausible; at 293 K, this corresponds to 1 × 10−9 to 7 × 10−8 s−1, which correspond to timescales of 0.5–30 years. The kinetics of Reaction 18 have been determined as a function of temperature at pH = 9 and I = 0.2 M by Siu and Jia (1999). At 293 K, the rate coefficient is k18 = 4 × 103
M −2 s−1. At the S-anion concentrations relevant to our work11, the timescale of this reaction is ≳1 year. For comparison, putative prebiotic chemistry in laboratory studies often occurs on timescales of hours to days (Patel et al., 2015; Xu et al., in press, e.g.).
We test the effects of redox reactions on S-anion concentrations by carrying out a dynamical equilibrium calculation for a shallow lake buffered to pH = 7, with source the atmosphere and sink these redox reactions. Following the treatment of Halevy (2013), the equilibrium equations can be written:
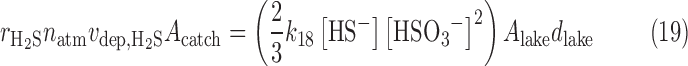 |
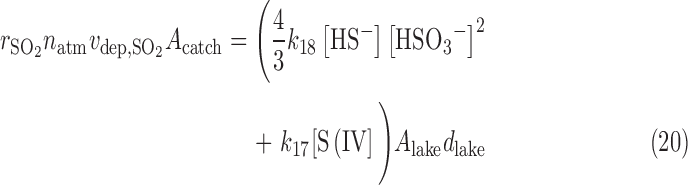 |
For consistency with Hu et al. (2013), we adopt 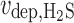 = 0.015 cm s−1,
= 0.015 cm s−1, 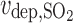 = 1 cm s−1, T = 288 K, and natm =
= 1 cm s−1, T = 288 K, and natm = 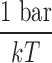 = 2.4 × 1019 cm−3. Since we are concerned with shallow, well-mixed lakes, we take the lake depth dlake = 102 cm. Acatch is the catchment area of the lake, and Alake is the surface area of the lake; we conservatively adopt Acatch = Alake, which likely underestimates sulfur supply since the catchment area is often larger than the lake area. [S(IV)] refers to the total concentration of S(IV) atoms in solution, and is calculated as [S(IV)] = [SO2] + [HSO3−] + [SO32−] + 2[HS2O5−] ≈ [SO2(aq)] + [HSO3−] + [SO32−]12. Since we have specified pH = 7 and know the relevant pKa values, we can calculate [HSO3−] from [S(IV)] and vice versa. With
= 2.4 × 1019 cm−3. Since we are concerned with shallow, well-mixed lakes, we take the lake depth dlake = 102 cm. Acatch is the catchment area of the lake, and Alake is the surface area of the lake; we conservatively adopt Acatch = Alake, which likely underestimates sulfur supply since the catchment area is often larger than the lake area. [S(IV)] refers to the total concentration of S(IV) atoms in solution, and is calculated as [S(IV)] = [SO2] + [HSO3−] + [SO32−] + 2[HS2O5−] ≈ [SO2(aq)] + [HSO3−] + [SO32−]12. Since we have specified pH = 7 and know the relevant pKa values, we can calculate [HSO3−] from [S(IV)] and vice versa. With 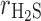 and
and 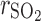 specified from Hu et al. (2013), we have a system of two equations in two variables that we can solve. Figure 5 shows the resultant S-anion concentrations as a function of ΦS.
specified from Hu et al. (2013), we have a system of two equations in two variables that we can solve. Figure 5 shows the resultant S-anion concentrations as a function of ΦS.
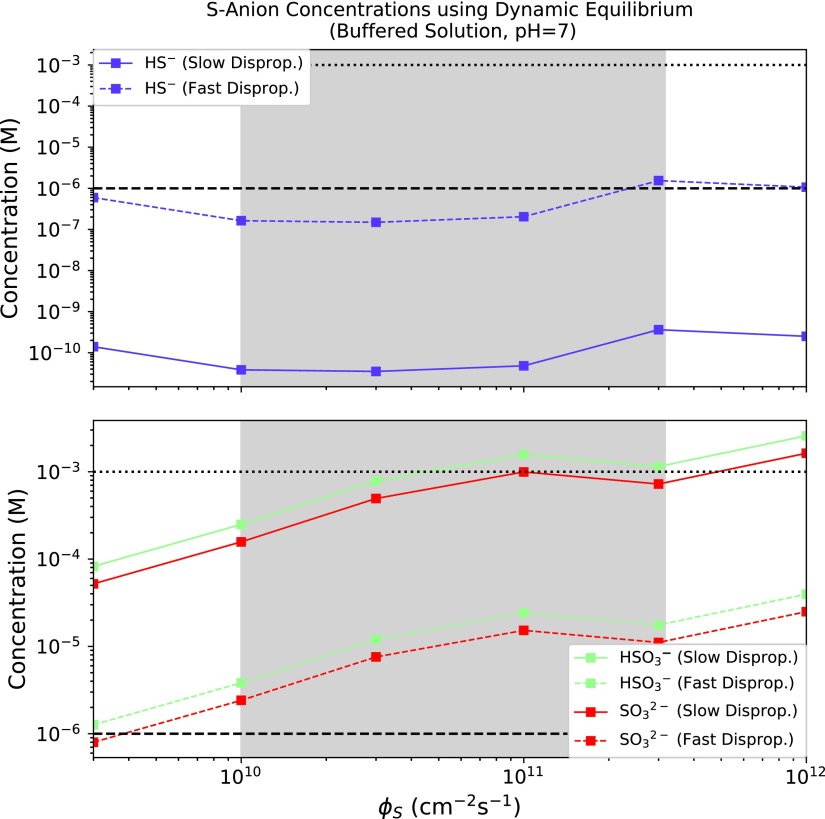
FIG. 5.
Speciation of sulfur-bearing molecules in a shallow lake buffered to pH = 7 as a function of total sulfur emission flux ΦS, using a dynamic calculation with source atmospheric deposition and sink redox reactions. The range of ΦS highlighted by Halevy and Head (2014) for emplacement of basaltic plains on Earth is shaded in gray. Horizontal dashed and dotted lines demarcate micromolar and millimolar concentrations, respectively. [HS−] would not be able to achieve the high concentrations calculated here for the slow disproportionation (low k17) case due to solubility constraints.
The dynamic calculation is very sensitive to the uncertainty in k17, with sulfite and bisulfite concentrations varying by 2 orders of magnitude and hydrosulfide concentrations varying by 4 across the range of k17 suggested by Halevy (2013). However, even with this uncertainty it is clear that prebiotically relevant levels (≥1 μM) of SO2-derived anions are available across the range of plausible sulfur outgassing fluxes, with concentrations ∼1–10 μM if sulfite disproportionation is fast and ∼100–1000 μM if sulfite disproportionation is slow. Note depending on k17, it is possible for [HS−] in the dynamic calculation to exceed the value calculated from solubility constraints; in reality, in well-mixed solution H2S would de-gas when it reached the solubility limit, voiding Eq. 19. In these cases, [HS−] is lower than the value calculated from the dynamic method, modestly increasing sulfite and bisulfite concentrations since Reaction 18 is slower. S-anion concentrations increase as dlake and T decrease, and are ultimately limited by gas solubility. Overall, our finding that prebiotically relevant levels of SO2-derived anions were available in shallow well-mixed lakes on early Earth is robust to the effect of redox reactions, but it is possible for the precise concentrations to be lower than from our equilibrium calculation depending on the depth and temperature of the lake, and especially on the rate of sulfite disproportionation k17. Constraining k17 is key to improved modeling of abiotic sulfur chemistry.
5.3. Case study: Implications for cyanosulfidic systems chemistry of Patel et al. (2015)
The cyanosulfidic prebiotic chemistry of Patel et al. (2015) requires cyanide and sulfur-bearing anions, both as feedstocks and as sources of hydrated electrons through UV-driven photoionization. Patel et al. (2015) used HS− as their sulfidic anion, and propose impact-derived sources of metal sulfides (both from the impactor and from subsequent metallogenesis) and evaporatively concentrated iron sulfides as a source for HS−. This postulated mechanism requires specific, local environmental conditions to function. By contrast, simple exposure of a non-acidic lake to the atmosphere anywhere on the planet would supply HSO3− and SO32− at prebiotically relevant levels to either supplement the photochemical reducing capacity of HS− or function as sole sources of hydrated electrons in the Patel et al. (2015) chemistry. Indeed, recent work by the same group suggests that HSO3− and SO32− can replace HS− as the source of hydrated electrons upon UV irradiation, and thus drive those parts of the reaction network that do not rely on HS− as a feedstocks (Xu et al., in press). Reducing or eliminating the dependence of the Patel et al. (2015) chemistry on HS− in favor of HSO3− or SO32− increases the robustness of this chemistry, because no special local circumstances need to be invoked. This illustrates how geochemistry can inform improvements of the plausibility of prebiotic pathways.
Indeed, volcanism can be a source of more than sulfidic anions. Volcanism can also be a source of phosphates through partial hydrolysis of volcanically outgassed polyphosphates (Yamagata et al., 1991), and a supplementary source of HCN through photochemical reprocessing of volcanically outgassed reducing species like CH4 (Zahnle, 1986)13. Volcanism could thereby supply or supplement many of the C-, H-, O-, N-, P-, and S-containing feedstock molecules and photoreductants required by the Patel et al. (2015) chemistry. The UV light also required by the Patel et al. (2015) chemistry would be available at Earth's surface for all but the largest volcanic episodes (ΦS ≥ 3 × 1011 cm−2 s−1). Hence, epochs of moderately high volcanism may have been uniquely conducive to cyanosulfidic prebiotic chemistry like that of Patel et al. (2015), especially if they can be adapted to work with HSO3− or SO32− instead of HS−.
We considered alternate planetary sources for HS− for the Patel et al. (2015) chemistry. We explored whether shallow hydrothermal systems, such as hot springs, might provide prebiotically relevant levels of HS−. These sources are high-sulfur systems on modern Earth, and, if shallow, prebiotic chemistry in them might retain access to UV light while accessing high concentrations of sulfidic anions. Surveys of modern hydrothermal systems reveal examples of surficial systems that exhibit micromolar or even millimolar concentrations of HS− (Xu et al., 1998; Vick et al., 2010; Kaasalainen and Stefánsson, 2011). However, high concentrations of HS− appear to only be achieved in hot systems14 (T > 60°C, and typically higher). Similarly, studies of geothermal waters in Yellowstone National Park suggest sulfite availability at the 0.4–5 μM level. However, such levels of sulfite were again accessed only in hot waters (Kamyshny et al., 2014). It is not clear how compatible such conditions are with prebiotic chemistry; for example, most of the cyanosulfidic chemistries of Patel et al. (2015) and Xu et al. (2016) were conducted at room temperature (25°C), and in general many molecules thought to be relevant to the origin of life, such as ribozymes, RNA, and their components, are more stable and function better at cooler temperatures (Levy and Miller, 1998; Attwater et al., 2010; Kua and Bada, 2011; Akoopie and Müller, 2016). However, for hot origin-of-life scenarios, e.g., those at deep-sea hydrothermal vents, hydrothermal systems may be compelling venues for cyanosulfidic reaction networks like that of Patel et al. (2015), reinforcing the utility of volcanism for prebiotic chemistry.
6. Conclusion and Next Steps
Constraining the abundances of trace chemical species on early Earth is important to understanding whether postulated prebiotic pathways which are dependent on them could have proceeded. Here, we show that prebiotically relevant levels of certain sulfidic anions are globally available in shallow, well-mixed aqueous reservoirs due to dissolution of sulfur-bearing gases that are volcanically injected into the atmosphere of early Earth. In particular, anions derived from SO2 are available at ≥1 μM levels in non-acidic reservoirs for SO2 outgassing rates corresponding to modern Earth and higher. During episodes of intense volcanism, like the emplacement of basaltic fields like the Deccan Traps, SO2-derived anions may be available at ≥1 mM levels for reservoirs buffered to pH ≥7 (e.g., the modern ocean at pH = 8.2) and at a temperature of T = 25°C, though sulfite disproportionation may have ultimately limited concentrations to the ∼10 μM level; better constraints on sulfite disproportionation reaction rates are required to constrain this possibility. At cooler temperatures, even higher concentrations of these anions would have been available. Formation of mineral precipitate should not inhibit sulfite concentrations until ≥1 mM concentrations so long as the reservoir is not acidic, but might suppress sulfite levels in acidic waters. On the other hand, anions derived from H2S would not have been available at micromolar levels across the plausible range of volcanic outgassing due to low solubility of H2S and an unfavorable dissociation constant, and prebiotic chemistry invoking such anions must invoke local, specialized sources. Radiative transfer calculations suggest that NUV radiation will remain abundant at the planet surface for ΦS ≤ 1 × 1011 cm−2 s−1 but will be suppressed for ΦS ≥ 3 × 1011 cm−2 s−1; such epochs may be especially clement for surficial, UV-independent prebiotic chemistry. We applied our results to the case study of the proposed prebiotic reaction network of Patel et al. (2015). The prebiotic plausibility of this network can be improved if it can be adapted to use SO2-derived anions like HSO3− or SO32− instead of HS−, since the atmosphere is capable of supplying prebiotically relevant levels of the former directly but more localized sources must be invoked for adequate supply of the latter. Coupled with the potential for volcanogenic synthesis of feedstock molecules like HCN and phosphate (Zahnle, 1986; Yamagata et al., 1991), it appears that episodes of moderately intense volcanism (ΦS ≈ 1 × 1011 cm−2 s−1) might have been especially clement for cyanosulfidic prebiotic chemistry which exploits SO2-derived anions (e.g., HSO3−). Avenues for future work include simulating these scenarios experimentally and/or with a large general-purpose aqueous geochemistry code, improving measurements of the sulfite disproportionation reaction rate constant, and further photochemical modeling to improve constraints on the expected concentrations of SO2 and H2S on early Earth.
A. Atmospheric Sulfur Speciation
We use the work of Hu et al. (2013) to connect the sulfur emission flux ΦS to the speciation of atmospheric sulfur. Table A1 presents H2S and SO2 mixing ratios as a function of ΦS from Hu et al. (2013) (their Fig. 5, CO2-dominated atmosphere case).
Table A1.
Column-Integrated Mixing Ratios of H2S and SO2 as a Function of ΦS from Hu et al. (2013) (Their Fig. 5, CO2-Dominated Case)
B. Activity Coefficient Calculation
This appendix describes the calculation of the activity coefficients of the ions involved in equilibria reactions for SO2 and H2S.
We use the Extended Debye-Huckel theory to calculate activity coefficients (γi) for the ions in our study. Extended Debye-Huckel theory is valid for ionic strengths up to 0.1 M, which is the highest ionic strength we consider, motivated by the fact that lipid vesicle formation is inhibited at ionic strengths above 0.1 M (Maurer and Nguyen, 2016).
Extended Debye Huckel theory states that
 |
where A and B depend on the temperature, density, and dielectric constant of the solvent (in our case water), and αi is an ion-specific parameter. We took A = 0.5085 M−1/2 and B = 0.3281 M−1/2Å−1, corresponding to T = 25°C; Appendix D describes the sensitivity of our analysis to this assumption. Table B1 summarizes the αi used in our study, taken from Misra (2012). We were unable to locate a value of αC for HS2O5− and consequently take 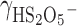 = 1 throughout (i.e., we do not correct for its activity). Since in our analysis the supply of SO2 is not limited (the atmosphere is treated as an infinite reservoir),
= 1 throughout (i.e., we do not correct for its activity). Since in our analysis the supply of SO2 is not limited (the atmosphere is treated as an infinite reservoir), 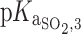 affects only the abundance of H2SO5−, which is a trace compound in our analysis (see Fig. 2).
affects only the abundance of H2SO5−, which is a trace compound in our analysis (see Fig. 2).
Table B1.
Values for the Ion-Specific Parameter α (Related to the Hydration Sphere of the Ion) Used to Calculate Activity Coefficients
| Ion | αi(Å) |
|---|---|
| HSO3− | 4.0 |
| SO32− | 4.5 |
| HS− | 3.5 |
| S2− | 5.0 |
| OH− | 3.5 |
| H+ | 9.0 |
Table B2 shows the activity coefficients for the relevant ions at the two ionic strengths considered in our study.
Table B2.
Per-Ion Activity Coefficients for Different Ionic Strengths
| Ion | I = 0 M | I = 0.1 M |
|---|---|---|
| HSO3− | 1.0 | 0.770 |
| SO32− | 1.0 | 0.364 |
| HS− | 1.0 | 0.762 |
| S2− | 1.0 | 0.377 |
| OH− | 1.0 | 0.762 |
| H+ | 1.0 | 0.826 |
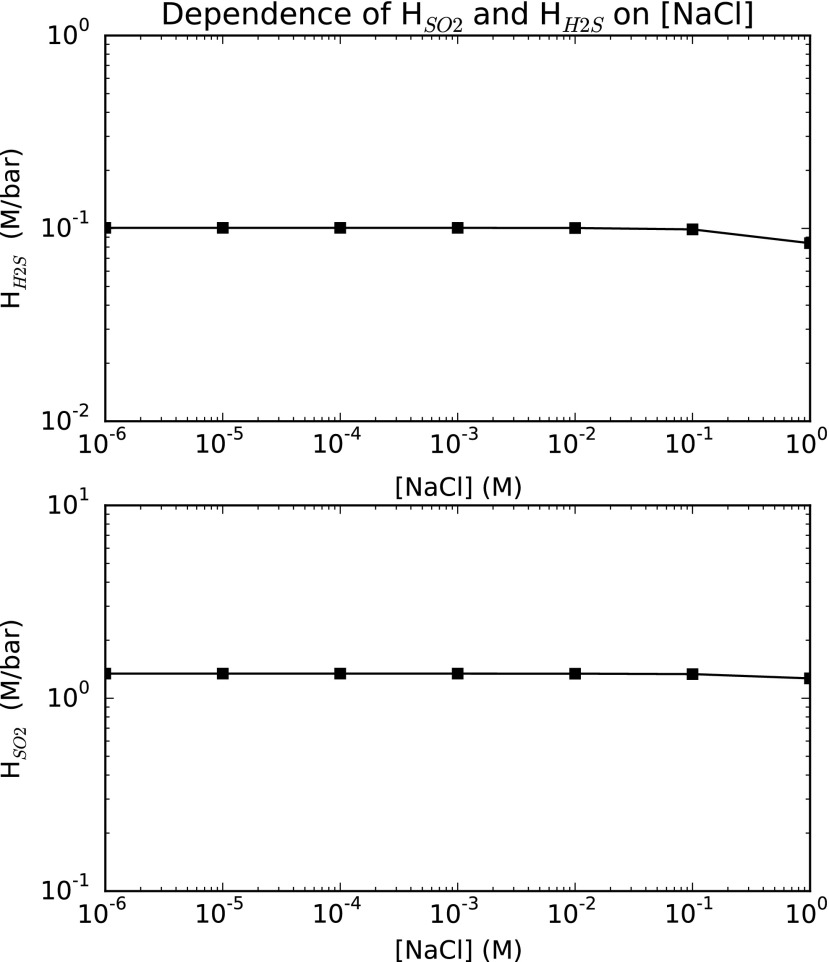
C. Sensitivity of Henry's Law Constants to Salinity
This appendix describes our assessment of the sensitivity of the Henry's law coefficients for SO2 and H2S to salinity.
We account for the effect of salinity on HG using the Schumpe-Sechenov method, as outlined in Burkholder et al. (2015):
 |
where H0 is the Henry's law constant in pure water, H is the Henry's law constant in saline solution, ci is the concentration of the ion i, hi is an ion-specific constant, and hG is a gas-specific constant. hG is temperature dependent, via hG = h0 + hT (T-298.15 K). NaCl is the dominant salt in Earth's oceans; we approximate NaCl as the sole source of salinity in our calculations. Table C1 summarizes the values of these parameters used for this study, all taken from the compendium of Burkholder et al. (2015). We were unable to locate a value for hT for H2S in our literature search, and assumed hT = 0 for this case.
Table C1.
Parameters Used to Estimate the Dependence of Henry's Law Constants on [NaCl]
| Parameter | H2S | SO2 | Na+ | Cl− |
|---|---|---|---|---|
| H0 (M/bar) | 0.101 | 1.34 | — | — |
| h0 (M−1) | −0.0333 | −0.0607 | — | — |
| hT (M−1) | 0a | 0.000275 | — | — |
| hi (M−1) | — | — | 0.1143 | 0.0318 |
Value not found in literature search; assumed to be 0.
The Henry's law constants for these gases as a function of [NaCl] at T = 298.15 K are shown in Fig. C1. In this study, we consider ionic strengths I ≤ 0.1 M, corresponding to [NaCl] ≤0.1 M. At such levels, salinity has a negligible effect on Henry's law solubility, and we consequently neglect it in our calculations.
FIG. C1.
Dependence of Henry's law constants for H2S and SO2 on [NaCl], calculated using the formalism from Burkholder et al. (2015). 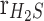 and
and 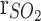 are insensitive to [NaCl] for [NaCl] <1 M.
are insensitive to [NaCl] for [NaCl] <1 M.
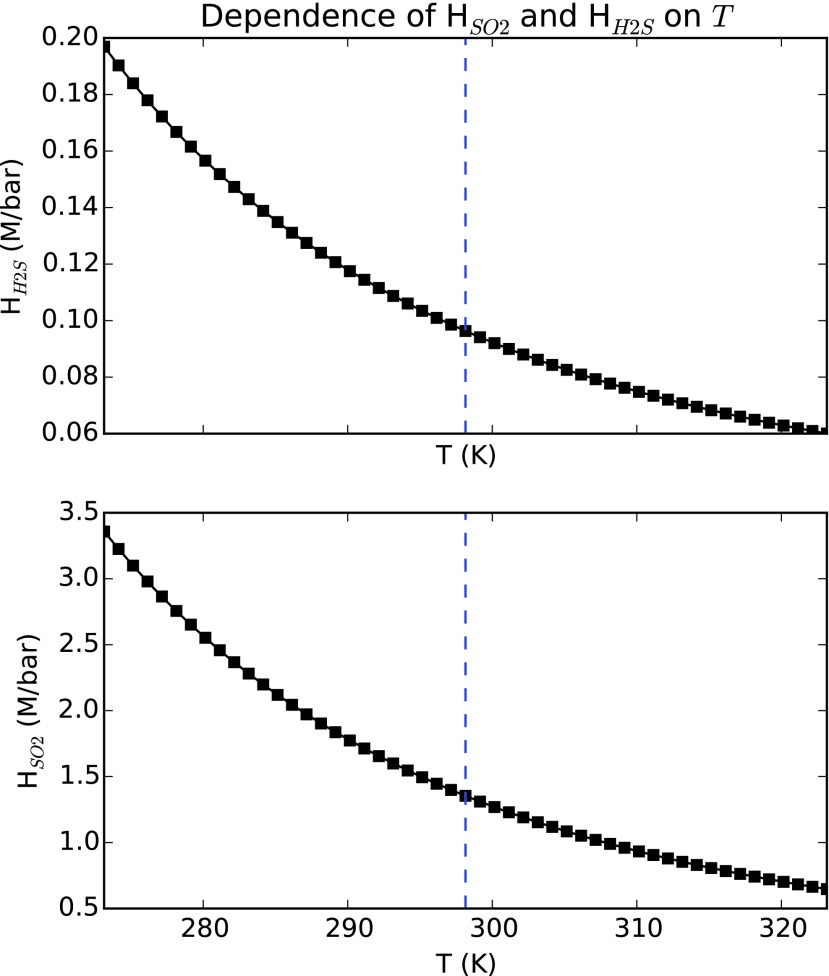
D. Sensitivity of Analysis to Temperature
This appendix describes our assessment of the sensitivity of our calculations to the temperature of the aqueous reservoir in which the equilibrium chemistry proceeds.
D.1. Sensitivity of Henry's law constants to temperature
We calculated the effect of temperature on Henry's law using the three-term empirical fit outlined in Burkholder et al. (2015), that is, ln(H) = A + B/T + C ln(T), where H is in units of M/atm and A, B, and C are gas-specific coefficients of an empirical fit. The values of these coefficients for H2S and SO2 were taken from Burkholder et al. (2015) and are summarized in Table D1. H(T) for H2S and SO2 is plotted in Fig. D1. For temperatures ranging from 0°C to −50°C (273.15 to 323.15 K), the Henry's law constants vary by less than a factor of 2.5 relative to their values at 25°C (293.15 K), which is small compared to the order-of-magnitude variations in concentration we focus on in this study. We also estimated the temperature dependence using the van't Hoff equation as outlined in Sander (2015) and obtained similar results.
FIG. D1.
Temperature dependence of Henry's law constants for H2S and SO2, calculated using the formalism from Burkholder et al. (2015). Varying the temperature by 25 K relative to the reference temperature of 298.15 K (blue line) affects the value of 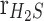 and
and 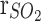 by less than a factor of 2.5.
by less than a factor of 2.5.
Table D1.
Parameters Used to Estimate Dependence of Henry's Law Constant on Temperature
| Parameter | H2S | SO2 |
|---|---|---|
| A | −145.2 | −39.72 |
| B | 8120 | 4250 |
| C | 20.296 | 4.525 |
D.2. Sensitivity of reaction rates to temperature
In order to assess the temperature dependence of acid dissociation pKa values, we use the van't Hoff equation:
 |
where K0 is the equilibrium constant, T is temperature, ΔH0 is the change in enthalpy, and R = 8.314 × 10−3 kJ/mol/K. Solving this differential equation, assuming temperature-invariant enthalpy of solution15, gives
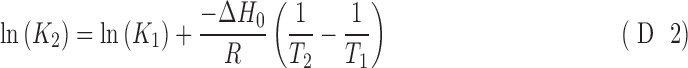 |
With this equation, the acid dissociation constant K2 can be estimated at a given temperature T2, provided its value K1 is known at a reference temperature T1. ΔH is the change in enthalpy of the reaction, given by
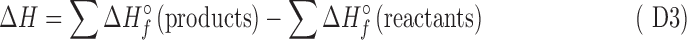 |
The enthalpies of formation for the products and reactants of the first two acid dissociation reactions for H2S and SO2 are taken from Lide (2009) and are shown in Table D2. Note that ΔHf° = 0 for H+, by definition. We were unable to locate an enthalpy of formation for H2SO5− and consequently are unable to calculate the temperature dependence of 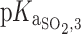 . Since in our analysis the supply of SO2 is not limited (the atmosphere is treated as an infinite reservoir),
. Since in our analysis the supply of SO2 is not limited (the atmosphere is treated as an infinite reservoir), 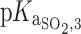 affects only the abundance of H2SO5−, which is a trace compound in our analysis (see Fig. 2).
affects only the abundance of H2SO5−, which is a trace compound in our analysis (see Fig. 2).
Table D2.
Enthalpies of Formation Used in the van't Hoff Equation Calculation
| Molecule | ΔHf° (kJ/mol) |
|---|---|
| HSO3− | −626.2 |
| SO32− | −635.5 |
| SO2 | −296.8 |
| HS− | −17.6 |
| S2− | 33.1 |
| H2S | −20.6 |
| H2O | −285.8 |
Using these values and the van't Hoff equation, we calculated the temperature dependence of the first two acid dissociation constants for aqueous H2S and SO2. Table D3 shows these pKa values for SO2 and H2S at 0°C, 25°C, and 50°C.
Table D3.
pKa at Temperatures of 0°C, 25°C, and 50°C and Reaction Enthalpies
| T = 0°C | T = 25°C | T = 50°C |
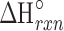 (kJ/mol) (kJ/mol)
|
|
|---|---|---|---|---|
| H2S, pKa1 | 7.098 | 7.05 | 7.009 | 3.0 |
| H2S, pKa2 | 19.81 | 19.0 | 18.31 | 50.7 |
| SO2, pKa1 | 1.160 | 1.86 | 2.452 | −43.6 |
| SO2, pKa2 | 7.051 | 7.2 | 7.326 | −9.3 |
The variation in pKa is negligible for all reactions except the first dissociation of SO2; 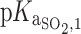 increases significantly with temperature. This implies that in non-acidic solutions, the concentrations of SO2-derived anions should decrease, and conversely that as temperature decreases they should increase.
increases significantly with temperature. This implies that in non-acidic solutions, the concentrations of SO2-derived anions should decrease, and conversely that as temperature decreases they should increase.
D.3. Sensitivity of activity coefficients to temperature
Temperature dependence enters the calculation of the activity coefficients through the parameters A and B (see Appendix B for details). For water, at T = 0°C, A = 0.4883 M−1/2 and B = 0.3241 M−1/2Å−1; at T = 25°C, A = 0.5085 M−1/2 and B = 0.3281 M−1/2Å−1; and at T = 50°C, A = 0.5319 M−1/2 and B = 0.3321 M−1/2Å−1 (Misra, 2012). From T = 0–50°C, the activity coefficients varied by <8% for I ≤ 0.1 M.
D.4. Overall sensitivity of analysis to temperature
We evaluated the overall sensitivity of our analysis to our assumption of T = 25°C by repeating our analysis at T = 0°C and T = 50°C, and including the effects of temperature on Henry's law constant, the reaction pKa values, and the activity coefficients, simultaneously. Across the tested range, temperature had a negligible impact on the abundances of the H2S-derived anions but a significant impact on the abundances of the SO2-derived anions. 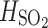 decreases with temperature, and
decreases with temperature, and 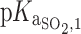 increases with temperature; both effects serve to increase the concentration of HSO3− and its derivatives in non-acidic (pH > 2.5) waters. At T = 0°C, HSO3− and SO32− concentrations are an order of magnitude higher than at T = 25°C. Similarly, at T = 50°C, HSO3− and SO32− concentrations are an order of magnitude lower than at T = 25°C. Our overall conclusions are robust to these variations. However, this study does imply that significantly higher concentrations of SO2-derived anions are available to prebiotic chemistry in cooler waters, and inversely that hotter waters would have access to lower levels of SO2-derived anions.
increases with temperature; both effects serve to increase the concentration of HSO3− and its derivatives in non-acidic (pH > 2.5) waters. At T = 0°C, HSO3− and SO32− concentrations are an order of magnitude higher than at T = 25°C. Similarly, at T = 50°C, HSO3− and SO32− concentrations are an order of magnitude lower than at T = 25°C. Our overall conclusions are robust to these variations. However, this study does imply that significantly higher concentrations of SO2-derived anions are available to prebiotic chemistry in cooler waters, and inversely that hotter waters would have access to lower levels of SO2-derived anions.
Acknowledgments
We thank A. Levi for his insight regarding equilibrium chemistry, and D. Catling, I. Halevy, M. Claire, J. Szostak, T. Bosak, and T. Vick for answers to many questions and/or comments on the manuscript. We especially thank J. Toner for extensive discussion and feedback. We thank M. Claire for sharing sulfur aerosol cross-sections for validation purposes. This research has made use of NASA's Astrophysics Data System Bibliographic Services and the MPI-Mainz UV-VIS Spectral Atlas of Gaseous Molecules. S.R., Z.R.T., D.D.S., and J.D.S. gratefully acknowledge support from the Simons Foundation (S.R., Z.R.T., D.D.S.: grant no. 290360; S.R.: grant no. 495062; J.D.S.: grant no. 290362).
Author Disclosure Statement
The authors declare no competing financial interests.
For example, the oceans on modern Earth are buffered to a pH of 8.1–8.2 due primarily to carbonate buffering (Hall-Spencer et al., 2008; Zeebe and Wolf-Gladrow, 2009); estimates of ancient ocean pH vary but often invoke slightly lower pH due to posited higher CO2 levels early in Earth's history (see, e.g., Morse and Mackenzie, 1998; Amend and McCollom, 2009; Halevy and Bachan, 2017, and sources therein). Smaller bodies, like lakes, can have an even wider range of pH values due to local conditions; lakes on modern Earth can have pH < 1 (e.g., Kawah Ijen crater lake; Löhr et al., 2005) and pH > 11 (e.g., Lake Natron; Grant and Jones, 2000).
http://www.aqion.de/site/69, accessed 29 November 2016.
A further practical challenge with extending our calculations to higher ionic strengths is that the parameters required to compute the activity coefficients at high ionic strengths (e.g., via the Truesdell and Jones, 1974 formalism) are not available for many of the species we consider.
It is thought that these chemistries should proceed over a broad range of pH. However, they will proceed best for pH ≲9.2 (so that HCN tends to remain protonated) and pH ≳7 (so that the sulfidic anions tend to remain deprotonated)
Our results are insensitive to the precise choice of albedo or solar zenith angle.
Our results are relevant to shallow, aqueous bodies of water, like lakes. By contrast, in the ocean, volcanoes vent directly into the water, and the turnover time can be long. Consequently, one could envision significant buildup of H2S near deep-ocean volcanoes. This scenario is beyond the scope of this work but may be worthy of consideration for HS--dependent chemistry.
The exothermic first dissociation of SO2 is disfavored at higher temperatures.
However, even in this case there may be a window in which prebiotic chemistry experiences both elevated SO2 levels and plenty of UV light, since aerosol formation is not instantaneous. Detailed photochemical modeling is required to determine the timescale of aerosol formation after a large volcanic eruption on early Earth; absent such modeling, we note that on modern Earth, formation of sulfate aerosols from volcanic eruptions occurs on a timescale of weeks (Robock, 2000); we may speculate a similar timescale for aerosol formation on early Earth.
Using pKa values for CO2 dissociation from modern seawater, e.g., Zeebe and Wolf-Gladrow (2009), results in much higher carbonate levels, much lower Ca levels, and a much higher threshold for CaSO3 saturation, so this treatment is conservative.
Corresponding to the lower limit suggested by Kasting (1987) from climate considerations.
[HS−] ≲ 10−8 M, [HSO3−] ≲ 10−3 M.
[HS2O5−] is negligible for dilute [SO2].
Though some concentration mechanism would be required to achieve prebiotically relevant levels of HCN via this pathway.
We speculate that HS--rich shallow hydrothermal systems tend to be hot because the same volcanism that supplies elevated levels of HS- also supplies elevated levels of heat.
We expect this assumption to be reasonable because of the limited range of temperatures that are plausible for our surface aqueous reservoir scenario.
References
- Akoopie A. and Müller U.F. (2016) Lower temperature optimum of a smaller, fragmented triphosphorylation ribozyme. Phys Chem Chem Phys 18:20118–20125 [DOI] [PubMed] [Google Scholar]
- Amend J.P. and McCollom T.M. (2009) Energetics of biomolecule synthesis on early Earth. In Chemical Evolution II: From the Origins of Life to Modern Society, edited by Zaikowski L., Friedrich J.M., and Seidel S.R., American Chemical Society, Washington, DC, pp 63–94 [Google Scholar]
- Amshoff P., Weger T., and Ostertag-Henning C. (2016) SO2 solution, hydrolysis and disproportionation at geological storage conditions in the system CO2-SO2-H2O. In Goldschmidt Conference Abstracts
- Attwater J., Wochner A., Pinheiro V.B., Coulson A., and Holliger P. (2010) Ice as a protocellular medium for RNA replication. Nat Commun 1, doi: 10.1038/ncomms1076 [DOI] [PubMed] [Google Scholar]
- Bada J.L., Bigham C., and Miller S.L. (1994) Impact melting of frozen oceans on the early Earth: implications for the origin of life. Proc Natl Acad Sci USA 91:1248–1250 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckstead A.A., Zhang Y., de Vries M.S., and Kohler B. (2016) Life in the light: nucleic acid photoproperties as a legacy of chemical evolution. Phys Chem Chem Phys 18:24228–24238 [DOI] [PubMed] [Google Scholar]
- Burkholder J., Abbatt J., Huie R., Kolb C., Orkin V., Wine P., Sander S., Barker J., Kurylo M., and Wilmouth D. (2015) Chemical Kinetics and Photochemical Data for Use in Atmospheric Studies: Evaluation Number 18, JPL Publication 15-10, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA [Google Scholar]
- Claire M.W., Sheets J., Cohen M., Ribas I., Meadows V.S., and Catling D.C. (2012) The evolution of solar flux from 0.1 nm to 160 μm: quantitative estimates for planetary studies. Astrophys J 757, doi: 10.1088/0004-637X/757/1/95 [DOI] [Google Scholar]
- Claire M.W., Kasting J.F., Domagal-Goldman S.D., Stüeken E.E., Buick R., and Meadows V.S. (2014) Modeling the signature of sulfur mass-independent fractionation produced in the Archean atmosphere. Geochim Cosmochim Acta 141:365–380 [Google Scholar]
- Cockell C. (2000) The ultraviolet history of the terrestrial planets: implications for biological evolution. Planet Space Sci 48:203–214 [Google Scholar]
- Coderre F. and Dixon D.G. (1999) Modeling the cyanide heap leaching of cupriferous gold ores: Part 1: Introduction and interpretation of laboratory column leaching data. Hydrometallurgy 52:151–175 [Google Scholar]
- Corliss J.B., Baross J., and Hoffman S. (1981) An hypothesis concerning the relationships between submarine hot springs and the origin of life on Earth. Oceanologica Acta 4(suppl):59–69 [Google Scholar]
- Crespo-Hernández C.E., Cohen B., Hare P.M., and Kohler B. (2004) Ultrafast excited-state dynamics in nucleic acids. Chem Rev 104:1977–2020 [DOI] [PubMed] [Google Scholar]
- Cronin T.W. (2014) On the choice of average solar zenith angle. Journal of the Atmospheric Sciences 71:2994–3003 [Google Scholar]
- Deamer D. and Damer B. (2017) Can life begin on Enceladus? A perspective from hydrothermal chemistry. Astrobiology 17:834–839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deamer D.W. and Dworkin J.P. (2005) Chemistry and physics of primitive membranes. In Prebiotic Chemistry, Springer, Berlin, pp 1–27 [Google Scholar]
- Debye P. and Huckel E. (1923) On the theory of electrolytes. I. Freezing point depression and related phenomena. Physik Z 24:185–206 [Google Scholar]
- Delano J. (2001) Redox history of the Earth's interior since ∼3900 Ma: implications for prebiotic molecules. Orig Life Evol Biosph 31:311–341 [DOI] [PubMed] [Google Scholar]
- Farquhar J., Bao H., and Thiemens M. (2000) Atmospheric influence of Earth's earliest sulfur cycle. Science 289:756–759 [DOI] [PubMed] [Google Scholar]
- Farquhar J., Savarino J., Airieau S., and Thiemens M.H. (2001) Observation of wavelength-sensitive mass-independent sulfur isotope effects during SO2 photolysis: implications for the early atmosphere. J Geophys Res 106:32829–32840 [Google Scholar]
- Forsythe J.G., Yu S.-S., Mamajanov I., Grover M.A., Krishnamurthy R., Fernandez F.M., and Hud N.V. (2015) Ester-mediated amide bond formation driven by wet–dry cycles: a possible path to polypeptides on the prebiotic Earth. Angew Chem Int Ed Engl 54:9871–9875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant W. and Jones B. (2000) Alkaline Environments, Vol. 1, Academic Press, New York, pp 126–133 [Google Scholar]
- Guekezian M., Coichev N., Suarez-Iha M.E.V., and de Almeida Neves E. (1997) Stability of sulfur(IV) solutions in the presence of amines and the tendency of sulfite ions to disproportionate in stock solutions. Anal Lett 30:1423–1436 [Google Scholar]
- Halevy I. (2013) Production, preservation, and biological processing of mass-independent sulfur isotope fractionation in the Archean surface environment. Proc Natl Acad Sci USA 110:17644–17649 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halevy I. and Bachan A. (2017) The geologic history of seawater pH. Science 355:1069–1071 [DOI] [PubMed] [Google Scholar]
- Halevy I. and Head J.W., III. (2014) Episodic warming of early Mars by punctuated volcanism. Nat Geosci 7:865–868 [Google Scholar]
- Halevy I., Zuber M.T., and Schrag D.P. (2007) A sulfur dioxide climate feedback on early Mars. Science 318:1903–1907 [DOI] [PubMed] [Google Scholar]
- Hall-Spencer J.M., Rodolfo-Metalpa R., Martin S., Ransome E., Fine M., Turner S.M., Rowley S.J., Tedesco D., and Buia M.-C. (2008) Volcanic carbon dioxide vents show ecosystem effects of ocean acidification. Nature 454:96–99 [DOI] [PubMed] [Google Scholar]
- Halmer M., Schmincke H.-U., and Graf H.-F. (2002) The annual volcanic gas input into the atmosphere, in particular into the stratosphere: a global data set for the past 100 years. Journal of Volcanology and Geothermal Research 115:511–528 [Google Scholar]
- He C., Gállego I., Laughlin B., Grover M.A., and Hud N.V. (2017) A viscous solvent enables information transfer from gene-length nucleic acids in a model prebiotic replication cycle. Nat Chem 9:318–324 [DOI] [PubMed] [Google Scholar]
- Higgs P.G. and Lehman N. (2015) The RNA world: molecular cooperation at the origins of life. Nat Rev Genet 16:7–17 [DOI] [PubMed] [Google Scholar]
- Holm N.G. and Charlou J.L. (2001) Initial indications of abiotic formation of hydrocarbons in the Rainbow ultramafic hydrothermal system, Mid-Atlantic Ridge. Earth Planet Sci Lett 191:1–8 [Google Scholar]
- Hu R., Seager S., and Bains W. (2013) Photochemistry in terrestrial exoplanet atmospheres. II. H2S and SO2 photochemistry in anoxic atmospheres. Astrophys J 769, doi: 10.1088/0004-637X/769/1/6 [DOI] [Google Scholar]
- Kaasalainen H. and Stefánsson A. (2011) Sulfur speciation in natural hydrothermal waters, Iceland. Geochim Cosmochim Acta 75:2777–2791 [Google Scholar]
- Kamyshny A., Druschel G., Mansaray Z.F., and Farquhar J. (2014) Multiple sulfur isotopes fractionations associated with abiotic sulfur transformations in Yellowstone National Park geothermal springs. Geochem Trans 15, doi: 10.1186/1467-4866-15-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasting J.F. (1987) Theoretical constraints on oxygen and carbon dioxide concentrations in the Precambrian atmosphere. Precambrian Res 34:205–229 [DOI] [PubMed] [Google Scholar]
- Kasting J.F. (1993) Earth's early atmosphere. Science 259:920–926 [DOI] [PubMed] [Google Scholar]
- Kasting J. (2014) Atmospheric composition of Hadean–early Archean Earth: the importance of CO. Geological Society of America Special Papers 504:19–28 [Google Scholar]
- Kasting J.F. and Walker J.C.G. (1981) Limits on oxygen concentration in the prebiological atmosphere and the rate of abiotic fixation of nitrogen. J Geophys Res 86:1147–1158 [Google Scholar]
- Kasting J.F., Zahnle K.J., Pinto J.P., and Young A.T. (1989) Sulfur, ultraviolet radiation, and the early evolution of life. Orig Life Evol Biosphere 19:95–108 [DOI] [PubMed] [Google Scholar]
- Kua J. and Bada J.L. (2011) Primordial ocean chemistry and its compatibility with the RNA world. Orig Life Evol Biosph 41:553–558 [DOI] [PubMed] [Google Scholar]
- Larowe D.E. and Regnier P. (2008) Thermodynamic potential for the abiotic synthesis of adenine, cytosine, guanine, thymine, uracil, ribose, and deoxyribose in hydrothermal systems. Orig Life Evol Biosph 38:383–397 [DOI] [PubMed] [Google Scholar]
- Lerman A., Imboden D., and Gat J., editors. (1995) Physics and Chemistry of Lakes, 2nd ed., Springer, Berlin [Google Scholar]
- Levy M. and Miller S.L. (1998) The stability of the RNA bases: implications for the origin of life. Proc Natl Acad Sci USA 95:7933–7938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li W., Czaja A.D., Van Kranendonk M.J., Beard B.L., Roden E.E., and Johnson C.M. (2013) An anoxic, Fe (II)-rich, U-poor ocean 3.46 billion years ago. Geochim Cosmochim Acta 120:65–79 [Google Scholar]
- Lide D.R., editor. (2009) CRC Handbook of Chemistry and Physics, 90th ed., CRC Press, Boca Raton, FL [Google Scholar]
- Löhr A., Bogaard T., Heikens A., Hendriks M., Sumarti S., Bergen M.v., Gestel K.C.v., Straalen N.v., Vroon P., and Widianarko B. (2005) Natural pollution caused by the extremely acid crater lake Kawah Ijen, East Java, Indonesia. Environ Sci Pollut Res Int 12:89–95 [DOI] [PubMed] [Google Scholar]
- Martin W., Baross J., Kelley D., and Russell M.J. (2008) Hydrothermal vents and the origin of life. Nat Rev Microbiol 6:805–814 [DOI] [PubMed] [Google Scholar]
- Maurer S.E. and Nguyen G. (2016) Prebiotic vesicle formation and the necessity of salts. Orig Life Evol Biosph 46:215–222 [DOI] [PubMed] [Google Scholar]
- McCollom T.M. (2013) Miller-Urey and beyond: what have we learned about prebiotic organic synthesis reactions in the past 60 years? Annu Rev Earth Planet Sci 41:207–229 [Google Scholar]
- McCollom T.M. and Seewald J.S. (2007) Abiotic synthesis of organic compounds in deep-sea hydrothermal environments. Chem Rev 107:382–401 [DOI] [PubMed] [Google Scholar]
- Meyer B., Rigdon M., Burner T., Ospina M., Ward K., and Koshlap K. (1982) Thermal decomposition of sulfite, bisulfite, and disulfite solutions. In Flue Gas Desulfurization, Vol. 188, edited by Hudson J.L. and Rochelle G.T., American Chemical Society, Washington, DC, pp 113–125 [Google Scholar]
- Mirzoyan N. and Halevy I. (2014) Kinetics of sulfite disproportionation and thiosulfate acid dissociation [abstract 1701]. In Goldschmidt Conference Abstracts [Google Scholar]
- Misra K.C. (2012) Introduction to Geochemistry: Principles and Applications, Wiley-Blackwell, Chichester, UK [Google Scholar]
- Mojzsis S.J., Harrison T.M., and Pidgeon R.T. (2001) Oxygen-isotope evidence from ancient zircons for liquid water at the Earth's surface 4,300 Myr ago. Nature 409:178–181 [DOI] [PubMed] [Google Scholar]
- Morse J.W. and Mackenzie F.T. (1998) Hadean ocean carbonate geochemistry. Aquat Geochem 4:301–319 [Google Scholar]
- Mulkidjanian A.Y., Cherepanov D.A., and Galperin M.Y. (2003) Survival of the fittest before the beginning of life: selection of the first oligonucleotide-like polymers by UV light. BMC Evol Biol 3, doi: 10.1186/1471-2148-3-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mulkidjanian A.Y., Bychkov A.Y., Dibrova D.V., Galperin M.Y., and Koonin E.V. (2012) Origin of first cells at terrestrial, anoxic geothermal fields. Proc Natl Acad Sci USA 109:E821–E830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mutschler H., Wochner A., and Holliger P. (2015) Freeze–thaw cycles as drivers of complex ribozyme assembly. Nat Chem 7:502–508 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neta P. and Huie R.E. (1985) Free-radical chemistry of sulfite. Environ Health Perspect 64:209–217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novoselov A.A., Silva D., Schneider J., Abrevaya X.C., Chaffin M.S., Serrano P., Navarro M.S., Conti M.J., and de Souza Filho C.R. (2017) Geochemical constraints on the Hadean environment from mineral fingerprints of prokaryotes. Sci Rep 7, doi: 10.1038/s41598-017-04161-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parkhurst D.L. and Appelo C.A.J. (2013) Description of input and examples for PHREEQC version 3—a computer program for speciation, batch-reaction, one-dimensional transport, and inverse geochemical calculations. Chapter 43 in Section A, Groundwater. Book 6, Modeling Techniques, Techniques and Methods 6-A43, U.S. Geological Survey, Denver, CO [Google Scholar]
- Pascal R. (2012) Suitable energetic conditions for dynamic chemical complexity and the living state. J Syst Chem 3, doi: 10.1186/1759-2208-3-3 [DOI] [Google Scholar]
- Patel B.H., Percivalle C., Ritson D.J., Duffy C.D., and Sutherland J.D. (2015) Common origins of RNA, protein and lipid precursors in a cyanosulfidic protometabolism. Nat Chem 7:301–307 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlov A.A. and Kasting J.F. (2002) Mass-independent fractionation of sulfur isotopes in Archean sediments: strong evidence for an anoxic Archean atmosphere. Astrobiology 2:27–41 [DOI] [PubMed] [Google Scholar]
- Pollum M., Ashwood B., Jockusch S., Lam M., and Crespo-Hernández C.E. (2016) Unintended consequences of expanding the genetic alphabet. J Am Chem Soc 138:11457–11460 [DOI] [PubMed] [Google Scholar]
- Powner M.W., Gerland B., and Sutherland J.D. (2009) Synthesis of activated pyrimidine ribonucleotides in prebiotically plausible conditions. Nature 459:239–242 [DOI] [PubMed] [Google Scholar]
- Ranjan S. and Sasselov D.D. (2016) Influence of the UV environment on the synthesis of prebiotic molecules. Astrobiology 16:68–88 [DOI] [PubMed] [Google Scholar]
- Ranjan S. and Sasselov D.D. (2017) Constraints on the early terrestrial surface UV environment relevant to prebiotic chemistry. Astrobiology 17:169–204 [DOI] [PubMed] [Google Scholar]
- Ranjan S., Wordsworth R., and Sasselov D.D. (2017) Atmospheric constraints on the surface UV environment of Mars at 3.9 Ga relevant to prebiotic chemistry. Astrobiology 17:687–708 [DOI] [PubMed] [Google Scholar]
- Rapf R.J. and Vaida V. (2016) Sunlight as an energetic driver in the synthesis of molecules necessary for life. Phys Chem Chem Phys 18:20067–20084 [DOI] [PubMed] [Google Scholar]
- Richter F.M. (1985) Models for the Archean thermal regime. Earth Planet Sci Lett 73:350–360 [Google Scholar]
- Rickard D. and Luther G.W. (2007) Chemistry of iron sulfides. Chem Rev 107:514–562 [DOI] [PubMed] [Google Scholar]
- Rios A.C. and Tor Y. (2013) On the origin of the canonical nucleobases: an assessment of selection pressures across chemical and early biological evolution. Isr J Chem 53:469–483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ritson D. and Sutherland J.D. (2012) Prebiotic synthesis of simple sugars by photoredox systems chemistry. Nat Chem 4:895–899 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robock A. (2000) Volcanic eruptions and climate. Rev Geophys 38:191–219 [Google Scholar]
- Rugheimer S., Segura A., Kaltenegger L., and Sasselov D. (2015) UV surface environment of Earth-like planets orbiting FGKM stars through geological evolution. Astrophys J 806, doi: 10.1088/0004-637X/806/1/137 [DOI] [Google Scholar]
- Ruiz-Mirazo K., Briones C., and de la Escosura A. (2014) Prebiotic systems chemistry: new perspectives for the origins of life. Chem Rev 114:285–366 [DOI] [PubMed] [Google Scholar]
- Rumble J.R., editor. (2017) CRC Handbook of Chemistry and Physics, 98th ed., CRC Press, Boca Raton, FL [Google Scholar]
- Sagan C. (1973) Ultraviolet selection pressure on the earliest organisms. J Theor Biol 39:195–200 [DOI] [PubMed] [Google Scholar]
- Sagan C. and Khare B.N. (1971) Long-wavelength ultraviolet photoproduction of amino acids on the primitive Earth. Science 173:417–420 [DOI] [PubMed] [Google Scholar]
- Sander R. (2015) Compilation of Henry's law constants (version 4.0) for water as solvent. Atmos Chem Phys 15:4399–4981 [Google Scholar]
- Sarker P.K., Takahashi J.-i., Obayashi Y., Kaneko T., and Kobayashi K. (2013) Photo-alteration of hydantoins against UV light and its relevance to prebiotic chemistry. Adv Space Res 51:2235–2240 [Google Scholar]
- Segura A., Krelove K., Kasting J.F., Sommerlatt D., Meadows V., Crisp D., Cohen M., and Mlawer E. (2003) Ozone concentrations and ultraviolet fluxes on Earth-Like planets around other stars. Astrobiology 3:689–708 [DOI] [PubMed] [Google Scholar]
- Self S., Widdowson M., Thordarson T., and Jay A.E. (2006) Volatile fluxes during flood basalt eruptions and potential effects on the global environment: a Deccan perspective. Earth Planet Sci Lett 248:518–532 [Google Scholar]
- Serrano-Andres L. and Merchan M. (2009) Are the five natural DNA/RNA base monomers a good choice from natural selection?: a photochemical perspective. Journal of Photochemistry and Photobiology C: Photochemistry Reviews 10:21–32 [Google Scholar]
- Siu T. and Jia C.Q. (1999) Kinetic and mechanistic study of reaction between sulfide and sulfite in aqueous solution. Ind Eng Chem Res 38:3812–3816 [Google Scholar]
- Sojo V., Herschy B., Whicher A., Camprubí E., and Lane N. (2016) The origin of life in alkaline hydrothermal vents. Astrobiology 16:181–197 [DOI] [PubMed] [Google Scholar]
- Šponer J.E., Szabla R., Góra R.W., Saitta A.M., Pietrucci F., Saija F., Di Mauro E., Saladino R., Ferus M., Civiš S., and Šponer J. (2016) Prebiotic synthesis of nucleic acids and their building blocks at the atomic level–merging models and mechanisms from advanced computations and experiments. Phys Chem Chem Phys 18:20047–20066 [DOI] [PubMed] [Google Scholar]
- Springsteen G. (2015) Reaching back to jump forward: recent efforts towards a systems-level hypothesis for an early RNA world. ChemBioChem 16:1411–1413 [DOI] [PubMed] [Google Scholar]
- Taylor L.L., Banwart S.A., Valdes P.J., Leake J.R., and Beerling D.J. (2012) Evaluating the effects of terrestrial ecosystems, climate and carbon dioxide on weathering over geological time: a global-scale process-based approach. Philos Trans R Soc Lond B Biol Sci 367:565–582 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trail D., Watson E.B., and Tailby N.D. (2011) The oxidation state of Hadean magmas and implications for early Earth's atmosphere. Nature 480:79–82 [DOI] [PubMed] [Google Scholar]
- Truesdell A.H. and Jones B.F. (1974) WATEQ, a computer program for calculating chemical equilibria of natural waters. Journal of Research of the U.S. Geological Survey 2:233–248 [Google Scholar]
- Urey H.C. (1952) On the early chemical history of the Earth and the origin of life. Proc Natl Acad Sci USA 38:351–363 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vick T., Dodsworth J.A., Costa K., Shock E., and Hedlund B.P. (2010) Microbiology and geochemistry of Little Hot Creek, a hot spring environment in the Long Valley caldera. Geobiology 8:140–154 [DOI] [PubMed] [Google Scholar]
- Walker S.I., Grover M.A., and Hud N.V. (2012) Universal sequence replication, reversible polymerization and early functional biopolymers: a model for the initiation of prebiotic sequence evolution. PLoS One 7, doi: 10.1371/journal.pone.0034166 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watmough S.A. and Aherne J. (2008) Estimating calcium weathering rates and future lake calcium concentrations in the Muskoka–Haliburton region of Ontario. Can J Fish Aquat Sci 65:821–833 [Google Scholar]
- Wordsworth R. and Pierrehumbert R. (2013) Hydrogen-nitrogen greenhouse warming in Earth's early atmosphere. Science 339:64–67 [DOI] [PubMed] [Google Scholar]
- Xu J., Tsanakopoulou M., Magnani C.J., Szabla R., Šponer J.E., Šponer J., Góra R.W., and Sutherland J.D. (2016) A prebiotically plausible synthesis of pyrimidine β-ribonucleosides and their phosphate derivatives involving photoanomerization. Nat Chem 9:303–309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J., Ritson D.J., Ranjan S., Todd Z.R., Sasselov D.D., and Sutherland J.D. (2018) Photochemical reductive homologation of hydrogen cyanide using sulfite and ferrocyanide. Chemical Communications, in press [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y., Schoonen M.A.A., Nordstrom D.K., Cunningham K.M., and Ball J.W. (1998) Sulfur geochemistry of hydrothermal waters in Yellowstone National Park: I. The origin of thiosulfate in hot spring waters. Geochim Cosmochim Acta 62:3729–3743 [Google Scholar]
- Yamagata Y., Watanabe H., Saitoh M., and Namba T. (1991) Volcanic production of polyphosphates and its relevance to prebiotic evolution. Nature 352:516–519 [DOI] [PubMed] [Google Scholar]
- Zahnle K., Claire M., and Catling D. (2006) The loss of mass-independent fractionation in sulfur due to a Palaeoproterozoic collapse of atmospheric methane. Geobiology 4:271–283 [Google Scholar]
- Zahnle K.J. (1986) Photochemistry of methane and the formation of hydrocyanic acid (HCN) in the Earth's early atmosphere. J Geophys Res 91:2819–2834 [Google Scholar]
- Zeebe R.E. and Wolf-Gladrow D.A. (2009) Carbon Dioxide, Dissolved (Ocean), Springer, Dordrecht, the Netherlands, pp 123–127 [Google Scholar]