Assessing the Performance of Ks Plots for Detecting Ancient Whole Genome Duplications

Abstract

Genomic data have provided evidence of previously unknown ancient whole genome duplications (WGDs) and highlighted the role of WGDs in the evolution of many eukaryotic lineages. Ancient WGDs often are detected by examining distributions of synonymous substitutions per site (Ks) within a genome, or “Ks plots.” For example, WGDs can be detected from Ks plots by using univariate mixture models to identify peaks in Ks distributions. We performed gene family simulation experiments to evaluate the effects of different Ks estimation methods and mixture models on our ability to detect ancient WGDs from Ks plots. The simulation experiments, which accounted for variation in substitution rates and gene duplication and loss rates across gene families, tested the effects of WGD age and gene retention rates following WGD on inferring WGDs from Ks plots. Our simulations reveal limitations of Ks plot analyses. Strict interpretations of mixture model analyses often overestimate the number of WGD events, and Ks plot analyses typically fail to detect WGDs when ≤10% of the duplicated genes are retained following the WGD. However, WGDs can accurately be characterized over an intermediate range of Ks. The simulation results are supported by empirical analyses of transcriptomic data, which also suggest that biases in gene retention likely affect our ability to detect ancient WGDs. Although our results indicate mixture model results should be interpreted with great caution, using node-averaged Ks estimates and applying more appropriate mixture models can improve the accuracy of detecting WGDs.

Introduction

Genomic data have revealed evidence for previously undetected ancient whole genome duplications (WGDs) in many eukaryotic lineages, including angiosperms (Schlueter et al. 2004; Cui et al. 2006; McKain et al. 2012; Vanneste et al. 2014), gymnosperms (Li et al. 2015; Guan et al. 2016), ferns (Vanneste et al. 2015), mosses (Rensing et al. 2007; Szövényi et al. 2015; Devos et al. 2016; Johnson et al. 2016), teleost fishes (Taylor et al. 2003; Jaillon et al. 2004; Crête-Lafrenière et al. 2012), horseshoe crabs (Nossa et al. 2014; Kenny et al. 2016), and spiders (Clark et al. 2015; Schwager et al. 2017). Analysis of completely sequenced genomes also supported long-standing hypotheses regarding two rounds of polyploidy predating the common ancestor of vertebrates (Ohno 1970; see Dehal and Boore 2005; Nakatani et al. 2007; Holland et al. 2008). Ancient WGDs often are detected by examining the distribution of synonymous substitutions per site (Ks) among paralogous genes within a genome, which can be visualized in a “Ks plot” (Cui et al. 2006; Barker et al. 2008; Vanneste et al. 2014). In the absence of WGDs or large episodic duplications, the synonymous substitutions between paralogs within a genome should follow an exponential distribution (Lynch and Conery 2003). WGDs should produce additional normally distributed peaks in the Ks plots (Blanc and Wolfe 2004; Schlueter et al. 2004). The age of the ancient WGDs can be estimated from the number of synonymous substitutions at these peaks (Maere et al. 2005).

Ks plot analyses require only genomic or transcriptomic sequence data from a single taxon and can be relatively quick and easy, especially with the aid of bioinformatic pipelines (Lyons et al. 2008; Barker et al. 2010). However, Ks plots can be difficult to interpret, and the accuracy of WGD identification from Ks plots is unclear. For example, Ks plot analyses sometimes fail to detect peaks from established ancient WGDs (Johnson et al. 2016). Alternately, substitutional saturation can produce peaks in the Ks plots that do not reflect WGDs (Vanneste et al. 2013). Many studies construct Ks plots using pairwise estimates of Ks (Schlueter et al. 2004; Ming et al. 2013; Kim et al. 2014; Nossa et al. 2014; Johnson et al. 2016), which are susceptible to saturation (Yang 1994) and introduce many more data points into Ks plots than there are duplicated genes (Blanc and Wolfe 2004; Cui et al. 2006; Rensing et al. 2007; Barker et al. 2008). Using the average Ks estimates for nodes of hierarchical clusters computed from pairwise Ks estimates (Blanc and Wolfe 2004; Maere et al. 2005; Cui et al. 2006; Barker et al. 2008) or phylogenetic estimates of Ks (Rensing et al. 2007; Olsen et al. 2016) may reduce problems caused by using pairwise Ks estimates. The effects of saturation also may be ameliorated by cropping high Ks estimates from the Ks plots (Lynch and Conery 2000; Cui et al. 2006; Barker et al. 2008; Tang et al. 2010; Vanneste et al. 2013, 2014).

The age of a WGD also may impact the efficacy of Ks plot analyses. For example, relatively recent WGDs with peaks at low Ks values can be difficult to identify, especially when few genes are retained from the WGD, because the small evolutionary distances between homeologs resulting from the WGD can be masked by recently duplicated genes (Cui et al. 2006). A WGD also could be too old to be detected with a Ks plot if too many duplicate genes from the ancient WGD are lost (Paterson et al. 2004; Conant et al. 2014). One approach to highlight a weak WGD signal from Ks plots is to include only paralogs that likely emerged from a WGD. A WGD can produce large syntenic segments within a genome (Kellis et al. 2004; Tuskan et al. 2006), and constructing Ks plots using only syntenic paralogs can accentuate the peaks from WGDs (Tang et al. 2008, 2010; Amborella genome project 2013; Myburg et al. 2014).

The null hypothesis for Ks plot analyses assumes exponentially distributed evolutionary distances among paralogs, implying that gene duplication and loss rates have remained constant over time (Cui et al. 2006; Soltis et al. 2011). Variation in gene duplication and loss rates through time, including any episodic burst of gene duplication, conceivably could affect the interpretation of Ks plots. Large segmental duplications often are invoked as alternative explanations for peaks in Ks plots (Al-Mssallem et al. 2013), but biased retention of other small-scale gene duplications also can potentially confound Ks plot analyses. For example, Blanc and Wolfe (2004) detected a modest Ks peak from Arabidopsis thaliana genomic data that was caused by tandemly duplicated genes. More recently, episodic expansion of many gene families caused peaks in the Ks plots from the Octopus bimaculoides genome, but synteny analyses suggested that recently expanded tandem duplications have increased the prominence of these peaks (Albertin et al. 2015).

WGDs often are identified by visual inspection of Ks plots (Yang et al. 2015). Yet an accurate, scalable, and less subjective approach is desirable. Univariate mixture models can be used to identify and estimate the timing of WGDs (Schlueter et al. 2004; Cui et al. 2006; Barker et al. 2008, 2016; Vanneste et al. 2014). The most commonly used approach is to maximize a likelihood function that fits one or more (k) normal probability distributions to a Ks plot. Each normal distribution for k >1 represents a putative WGD. However, this approach can overfit distributions (Johnson et al. 2016), leading to overestimates of the number of ancient WGDs., and consequently, the results often are ignored, sometimes in favor of nonparametric approaches that may be less susceptible to overfitting (Vanneste et al. 2015).

In this study, we used gene family simulation experiments to explore the effects of WGD age and gene retention rate following WGDs on our ability to infer and estimate the ages of WGDs from Ks plots with mixture models. We varied the age of WGDs to evaluate the range of evolutionary distances at which Ks plot analyses are effective. We also explored how much gene retention is necessary to produce a peak in a Ks plot analysis and evaluated different methods to construct Ks distributions and infer WGDs from Ks plots, including using pairwise or phylogeny-based (i.e., node-averaged) estimates of Ks, different mixture models, and limiting the Ks plots to genes involved in the WGD.

Materials and Methods

The goals of this study were to characterize and evaluate the performance of mixture model approaches for detecting WGDs from Ks plots under different evolutionary scenarios. We simulated gene family evolution, including WGDs, while varying the age of the WGDs, the gene retention rate following WGDs, and the background rates of gene duplication and loss. Our simulations also account for variation in gene duplication and loss rates across gene families as well as heterogeneity in substitution rate across branches in each gene family. We used node-averaged and pairwise estimators to generate the Ks distributions from the simulated gene families and applied two different mixture models to estimate the number of WGDs and their age. We also performed analyses using all paralogous gene pairs and only those resulting from WGDs alone. The simulation process is graphically depicted in figure 1. Finally, we compared our simulation results with analyses of several published data sets from angiosperms.

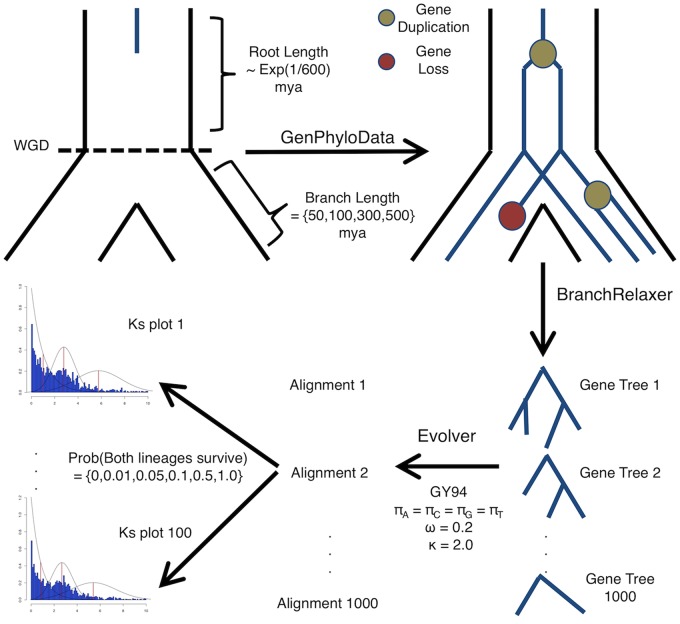
Fig. 1.

—Stylized workflow for simulating gene trees with a known WGD under a known retention rate. Gene families with an explicit WGD are simulated similar to gene trees evolving within a species tree. The branch length of the root of the species tree is drawn from a distribution so not all gene families are single copy before the WGD. The branch lengths following the WGD either are 15, 50, 100, 200, 300, or 500 Ma, which correspond to Ks of 0.15, 0.5, 1.0, 2.0, 3.0, and 5.0, respectively. Gene trees then evolve under variable rates of gene duplication and loss, followed by relaxation of branches to account for substitution rate variation. Sequence data was then simulated on these relaxed gene trees. We implemented a nonstandard data resampling procedure here that allowed for random gene loss. Individual gene trees were not resampled, but the probability that both lineages following a WGD survived was resampled. One hundred Ks plots were then generated from the 100 resampled data sets of 1000 trees.

Simulating Gene Family Evolution

We simulated gene families with WGDs within a single species using GenPhyloData (Sjöstrand et al. 2013) by allowing gene trees to evolve under a gene duplication and loss process within a species tree, but interpreting speciation events as WGDs. Like a speciation event, a WGD (or at least an autopolyploidy event) results in a split in each gene lineage. We generated six sets of gene trees with a single WGD at different ages (15, 50, 100, 200, 300, and 500 Ma, which, in our simulations, corresponds to Ks = 0.15, 0.5, 1.0, 2.0, 3.0, and 5.0). For each set, each gene tree had a single gene duplication rate (λ) and a loss rate (μ) for all branches. We incorporated variation in λ and μ among gene trees by allowing λ and μ to be independently distributed as β(4, 2460) and β(4, 2053), respectively. The distributions of λ and μ have means of 0.00162 and 0.00194, which were estimated from land plant genomes based on a model of gene copy number evolution (Tiley et al. 2016), with assumed equal variances of 1e10⁻⁶. Additionally, we simulated variation in the size of the gene families by altering the number of genes at the root of each gene tree by allowing the root age to be exponentially distributed with a mean of 600 Ma. We simulated 1,000 gene trees for each of the six WGD ages.

For each simulated gene tree, we simulated codon sequences using the EVOLVER program within PAML v4.8a (Yang 2007). First, to introduce among branch variation in substitution rates, we relaxed the branch lengths using BRANCHRELAXER (Sjöstrand et al. 2013). We chose to make rates consistent with the autocorrelated lognormal model of Rannala and Yang (2007) with mean of 1 and drift distributed as Γ(1, 1,000), such that drift had a mean of 0.001 and variance of 1e10⁻⁶. This model of rate variation allowed for different rates of evolution among branches, but not shifts in rates within branches. We simulated the codon sequence data for each simulated gene tree using a Goldman–Yang (GY94) model of codon evolution (Goldman and Yang 1994; Nielsen and Yang 1998) with equal equilibrium codon frequencies, a transition/transversion rate ratio (κ) of 2, a global dN/dS (ω) of 0.2, and an alignment length of 1,000 codons. We set the per site evolutionary distance (t) for simulations to 0.01268182, so that Ks = 0.01/Myr (see Supplementary Material online).

Duplicate gene retention following WGD in plants is highly heterogeneous, with estimates ranging from 1% to 75% of genes retained (Tiley et al. 2016). To assess the performance of mixture models under varying degrees of gene loss following WGDs, we pruned gene trees such that both gene copies following a WGD had probability of surviving in 0%, 1%, 5%, 10%, 30%, 50%, and 100% of the gene trees. A 0% survival probability, or retention rate, means there is no evidence of the WGD (i.e., all new gene copies from the WGD are immediately lost), and a 100% survival probability, or retention rate, indicates that there is no instantaneous gene loss following the WGD. In the simulations, gene loss was instantaneous, preventing any further duplication events from occurring on a branch that was created by the WGD and then lost. We created 100 replicated data sets of Ks for each WGD age and gene retention combination by allowing random instantaneous loss on 1,000 gene trees to proceed 100 times. If a gene tree was randomly chosen to lose a gene from the WGD, then the left and right subtree had equal probability of being removed from the gene tree.

Our simulation experiments implicitly assumed autopolyploidy. For autopolyploidy, the Ks plot peak should represent the time of WGD. In the case of allopolyploidy, the Ks plot peak represents speciation of the parents rather than the hybridization event leading to polyploidy (Thomas et al. 2017). However, both autopolyploidy and allopolyploidy are expected to create peaks in Ks plots, and our simulations are relevant to both cases.

Estimating Synonymous Substitution Rates

We estimated substitution model parameters from the simulated nucleotide alignments using the GY94 model (Goldman and Yang 1994; Nielsen and Yang 1998) with the empirical (i.e., observed) codon frequencies (F3x4). We implemented the GY94-F3x4 estimator using codeml within PAML v4.8a (Yang 2007). We obtained node-averaged Ks values by optimizing model parameters on the gene tree used to simulate the data using the simulated sequence data. For each internal node, from the tips to the root, node Ks = ((distance to left child+left child node Ks)+(distance to right child+right child node Ks))/2 (see supplementary fig. S1, Supplementary Material online). We extracted the node-averaged Ks using Perl scripts from Newick trees with Ks branch lengths. We obtained pairwise Ks estimates by optimizing the ML estimator parameters for each pair of sequences from a gene tree with PAML 4.8a (Yang 2007).

We also constructed Ks plots only from nodes in gene trees that resulted from the WGD. For example, consider that following a WGD there is both an A and B subgenome. If a node is the most recent common ancestor of a gene from the A subgenome and a gene from the B subgenome, then that node must have been generated by a WGD (supplementary fig. S1, Supplementary Material online). We then constructed Ks plots using only these node-averaged Ks values that were generated by the WGD event. These genes could represent sequences located on large syntenic blocks within a genome resulting from ancient WGDs. Using only nodes from WGDs allowed us to assess the value of syntenic data or data enriched for WGD duplicates for Ks plot analyses.

Discriminate Analyses and Fitting Mixture Models

We fit univariate mixture models to simulated distributions of Ks by expectation maximization using R (R Core Team 2015) with in-house source code (https://github.com/gtiley/Ks_plots; last accessed June 24, 2018) that uses the finite mixture expectation maximization algorithm implemented by Benaglia et al. (2009). For each Ks plot, we fit three models with k mixing components: 1) k normal components (McLachlan et al. 1999), as used in numerous previous studies (Schlueter et al. 2004; Cui et al. 2006; Barker et al. 2008), 2) an exponential distribution with k−1 normal components, to better account for the contributions of background gene duplication and loss, and 3) an exponential distribution with k−1 lognormal components, as lognormal distributions may be more appropriate for evolutionary distances than normal distributions (Morrison 2008). Distributions of syntenic data (i.e., nodes resulting from WGDs) were only analyzed with a mixture of normal distributions, as the exponential distribution from background duplication and loss was no longer present. We used 100 random starts to find the optimal mixing components for each number of distributions. The number of components (k) was inferred using the ΔBIC. Due to the large number of simulations performed here, it was not possible to use nonparametric bootstrapping to develop an empirical null distribution of likelihood ratio test statistics (McLachlan 1987). Although ΔBIC does not provide a formal hypothesis test, it can guide model selection and is often used in Ks plot analyses (Barker et al. 2008). We assumed that the ΔBIC between nested models provides an approximation of Bayes factors, and we used ΔBIC <3.2 as a stopping criterion (Kass and Raftery 1995). Functions for automating the selection of the optimal number of mixing components based on ΔBIC are implemented in the R source code (https://github.com/gtiley/Ks_plots; last accessed June 24, 2018) as bic.test.wgd.

Comparisons with Empirical Data

To assess whether our simulation results were consistent with analyses of empirical data, we reanalyzed Ks plots for putative ancient WGDs that occurred before the diversification of Actinidiaceae (Shi et el. 2010), most Asteraceae (Barker et al. 2016), and the common ancestor of Asteraceae and Calyceraceae (Barker et al. 2016). For the Actinidiaceae WGD, we reanalyzed Ks plots constructed using both node-averaged and pairwise Ks from Actinidia chinensis and Actinidia deliciosa EST data sets (Shi et el. 2010). We also reanalyzed Ks plots built using node-averaged and pairwise Ks from an Artemisia annua transcriptome for the Asteraceae-specific ancient WGD, as well as transcriptomes from Barnadesia spinosa and Acicarpha spathulata for the WGD shared by Asteraceae and Calyceraceae (Barker et al. 2016). All Ks estimates >5 and <0.0001 were not included for mixture model analyses. As with the simulated data sets, we estimated the optimal number of mixing components and the mean age in Ks of each component using the bic.test.wgd R function for the exponential+normal and normal mixture models using 100 random starts with a maximum of five components.

Results

Detecting WGDs Using Node-Averaged Ks

Accurately estimating the number of WGD events using mixture models is challenging under many conditions. The mixture model analyses had difficulty identifying the correct number of WGDs and the age of the WGDs, regardless of whether we used the known simulated values of Ks or Ks values estimated with maximum likelihood (ML). The error in analyses using the true Ks values demonstrates that there was error inherent to the mixture model analyses, and does not result only from error in Ks values.

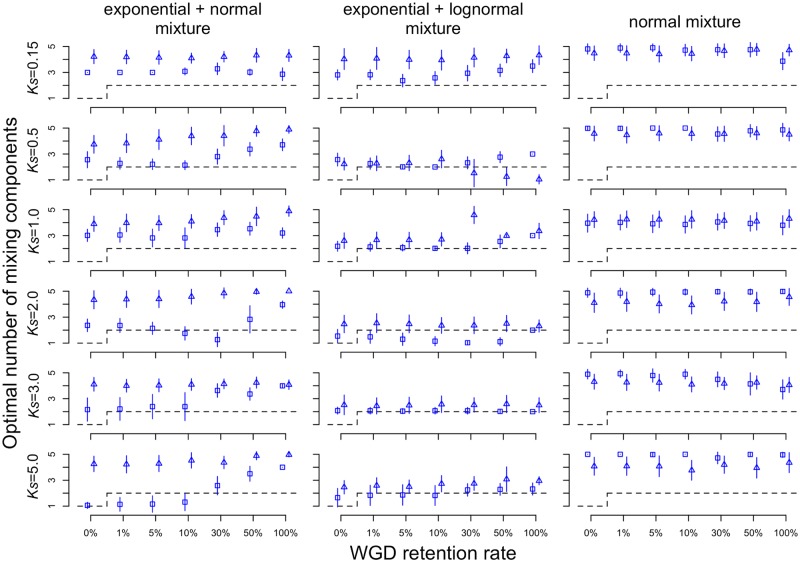
In our simulations, if the retention rate was >0, we expected to detect two peaks in the distribution of Ks for all paralogs, one representing the WGD and one representing the background duplications. However, we frequently detected more than two peaks, even in the absence of a WGD (i.e., retention rate = 0), especially if we were using the normal mixture model (fig. 2 and supplementary fig. S2 and table S1, Supplementary Material online). For the exponential+normal model, we only obtained accurate estimates of the number of WGDs in ≥ 50% of the simulations when Ks = 0.5 or 2.0 and the retention rate was ≤ 0.1 (tables 1 and 2). The only times we failed to detect a WGD with an exponential+normal model was when the Ks value for the WGDs was ≥ 3.0 and the retention rate was ≤ 0.1 (fig. 2 and tables 1 and 2). Otherwise, in most other cases, the exponential+normal model overestimated the number of WGDs, and except when Ks = 5.0, it also generally inferred at least one WGD when there was none (i.e., retention rate = 0; fig. 2). The exponential+lognormal model generally estimated the expected number of components more accurately than the exponential+normal or the normal mixture models (fig. 2; supplementary fig. S2, Supplementary Material online; and tables 1 and 2). However, the exponential+lognormal model also estimated multiple components in the absence of a WGD (fig. 2). Using mixtures of normal distributions always results in more components than the exponential+normal model or exponential+lognormal model (fig. 2 and supplementary fig. S2 and table S1, Supplementary Material online).

Fig. 2.

—The average number of components for simulated WGD events at different ages and retention rates. Results for node-averaged estimates of Ks are squares and pairwise Ks estimates are triangles. Error bars represent one standard deviation. The dashed line represents the expected number of components if Ks plots can be described by a single background distribution and peaks from WGDs alone.

Table 1.

Detection and Age of WGD Peaks for Distributed Duplication and Loss Rates with Simulated Node Ks

WGD Age	Retention	Exp+Norm Replicates with Optimal k = 2	Exp+LogNorm Replicates with Optimal k = 2	Norm Replicates with Optimal k = 2	Exp+Norm Mean for k = 2	Exp+LogNorm Mean for k = 2	Norm Mean for k = 2
0.15	0	0	0.98	0	3.03±0.21	3.14±0.21	2.16±0.24
	0.01	0	0.97	0	2.97±0.22	2.94±0.23	2.13±0.25
	0.05	0	0.69	0	2.73±0.23	2.60±0.25	1.99±0.25
	0.1	0	0.23	0	2.53±0.23	2.42±0.26	1.85±0.25
	0.3	0	0.02	0	2.30±0.24	2.29±0.27	1.77±0.25
	0.5	0	0.14	0	2.25±0.24	2.27±0.27	1.75±0.25
	1	0.29	0	0.01	2.23±0.24	2.27±0.27	1.66±0.25
0.5	0	0.01	0.03	0	3.16±0.20	3.61±0.14	2.10±0.24
	0.01	0.04	0.13	0	3.18±0.20	3.95±0.11	2.12±0.24
	0.05	0.18	0.55	0	3.22±0.20	4.17±0.09	2.11±0.24
	0.1	0.24	0.48	0	3.26±0.19	4.08±0.10	2.10±0.24
	0.3	0.43	0.42	0	3.31±0.19	3.45±0.15	2.06±0.24
	0.5	0.36	0.22	0	3.13±0.17	2.31±0.19	2.03±0.24
	1	0.92	0	0	0.46±0.02	0.77±0.18	1.96±0.23
1	0	0.25	0.93	0	3.31±0.17	3.94±0.09	2.09±0.23
	0.01	0.35	0.93	0	3.42±0.16	3.98±0.09	2.17±0.23
	0.05	0.72	0.9	0	3.61±0. 14	4.01±0.09	2.36±0.23
	0.1	0.8	0.81	0	3.72±0.12	4.08±0.08	2.42±0.23
	0.3	0.04	0.76	0	3.52±0.09	4.11±0.08	2.48±0.22
	0.5	0	0.51	0	0.99±0.04	3.08±0.13	2.48±0.22
	1	0	0	0	0.91±0.04	1.28±0.20	2.45±0.22
2	0	0.83	0.83	0	5.51±0.39	5.81±0.35	3.57±0.42
	0.01	0.86	0.86	0	5.62±0.38	5.89±0.34	3.61±0.42
	0.05	0.59	0.59	0	6.21±0.34	7.00±0.24	3.68±0.42
	0.1	0.21	0.21	0	6.71±0.29	7.14±0.21	3.76±0.42
	0.3	0.24	0.24	0	5.34±0.14	3.45±0.34	4.04±0.42
	0.5	0.97	0.97	0	2.08±0.08	2.39±0.34	4.15±0.42
	1	1	1	0	1.86±0.09	1.94±0.10	4.33±0.43
3	0	0.01	0.98	0	5.08±0.39	3.90±0.42	3.20±0.40
	0.01	0.03	0.97	0	5.03±0.40	3.88±0.42	3.21±0.40
	0.05	0	0.95	0	4.65±0.34	3.76±0.40	3.12±0.39
	0.1	0	0.98	0	3.74±0.20	3.67±0.39	3.05±0.38
	0.3	0	0.94	0	3.00±0.12	3.50±0.36	2.95±0.37
	0.5	0	0.92	0	2.95±0.12	3.44±0.34	2.89±0.35
	1	0	0.2	0	2.90±0.12	3.34±0.31	2.82±0.34
5	0	0.23	0.82	0	5.13±0.17	4.24±0.39	3.49±0.44
	0.01	0.29	0.84	0	5.06±0.17	4.32±0.38	3.51±0.44
	0.05	0.5	0.74	0	4.97±0.19	4.50±0.38	3.59±0.45
	0.1	0.44	0.65	0	4.95±0.18	4.66±0.36	3.64±0.45
	0.3	0.06	0.42	0	4.66±0.34	4.84±0.34	3.62±0.40
	0.5	0.02	0.25	0	4.87±0.20	4.92±0.33	3.89±0.46
	1	0	0.27	0	4.85±0.21	4.97±0.32	4.00±0.45

Note.—The proportion of replicates with and optimal number of 2 components (k) and the mean Ks when k is constrained to 2 is displayed. 95% confidence intervals are given for WGD peak means.

Table 2.

Detection and Age of WGD Peaks for Distributed Duplication and Loss Rates with Estimated Node Ks

WGD Age	Retention	Exp+Norm Replicates with Optimal k = 2	Exp+LogNorm Replicates with Optimal k = 2	Norm Replicates with Optimal k = 2	Exp+Norm Mean for k = 2	Exp+LogNorm Mean for k = 2	Norm Mean for k = 2
0.15	0	0	0.19	0	2.92±0.22	3.82±0.12	2.17±0.24
	0.01	0	0.18	0	2.86±0.22	3.22±0.17	2.13±0.24
	0.05	0	0.63	0	2.66±0.23	2.59±0.22	1.94±0.24
	0.1	0	0.42	0	2.49±0.23	2.40±0.24	1.85±0.24
	0.3	0	0.19	0	2.29±0.23	2.27±0.25	1.77±0.25
	0.5	0.02	0.01	0	2.25±0.23	2.25±0.25	1.72±0.25
	1	0.2	0	0	2.23±0.24	2.02±0.27	1.64±0.24
0.5	0	0.51	0.43	0	3.12±0.21	3.58±0.16	2.15±0.24
	0.01	0.72	0.74	0	3.17±0.20	3.68±0.15	2.16±0.24
	0.05	0.79	0.99	0	3.28±0.19	3.77±0.14	2.17±0.24
	0.1	0.86	1	0	3.33±0.19	3.77±0.14	2.15±0. 24
	0.3	0.29	0.68	0	3.43±0.18	3.71±0.14	2.12±0. 24
	0.5	0.02	0.24	0	2.40±0.12	3.70±0.13	2.08±0.23
	1	0	0	0	0.49±0.03	0.81±0.17	2.01±0.23
1	0	0.1	0.82	0	3.39±0.18	4.14±0.09	2.13±0.24
	0.01	0.13	0.87	0	3.50±0.17	4.18±0.08	2.15±0.24
	0.05	0.34	0.93	0	3.74±0.14	4.18±0.08	2.38±0.24
	0.1	0.41	0.98	0	3.91±0.11	4.20±0.08	2.55±0.23
	0.3	0.01	0.82	0	3.64±0.08	3.70±0.07	2.63±0.23
	0.5	0	0.45	0	1.22±0.05	2.46±0.07	2.65±0.22
	1	0	0	0	1.03±0.06	1.28±0.18	2.61±0.22
2	0	0.63	0.52	0	5.46±0.39	7.52±0.19	3.70±0.42
	0.01	0.64	0.48	0	5.48±0.39	7.57±0.18	3.71±0.42
	0.05	0.79	0.28	0	5.80±0.36	7.36±0.20	3.74±0.41
	0.1	0.67	0.15	0	6.51±0.30	7.85±0.17	3.82±0.42
	0.3	0.2	0.03	0	6.91±0.18	7.82±0.16	3.99±0.42
	0.5	0.32	0.11	0	2.60±0.09	5.43±0.26	4.13±0.42
	1	0.02	1	0	1.89±0.09	2.41±0.34	4.30±0.42
3	0	0.42	0.92	0	4.68±0.37	3.96±0.40	3.18±0.39
	0.01	0.37	0.93	0	4.66±0.37	3.95±0.40	3.16±0.39
	0.05	0.24	0.96	0	4.51±0.35	3.90±0.39	3.14±0.38
	0.1	0.08	0.93	0	4.31±0.31	3.79±0.39	3.12±0.38
	0.3	0	0.93	0	3.95±0.20	4.36±0.39	3.54±0.41
	0.5	0	0.98	0	3.38±0.20	3.62±0.37	3.02±0.37
	1	0	1	0	3.21±0.19	3.59±0.36	3.00±0.36
5	0	0.06	0.37	0	4.91±0.37	5.54±0.29	3.37±0.40
	0.01	0.04	0.37	0	4.97±0.37	5.43±0.30	3.41±0.40
	0.05	0.04	0.36	0	4.98±0.37	5.48±0.31	3.47±0.40
	0.1	0.15	0.38	0	5.00±0.37	5.22±0.32	3.55±0.41
	0.3	0.55	0.71	0	5.06±0.38	5.27±0.33	3.77±0.42
	0.5	0.03	0.71	0	5.08±0.38	5.32±0.33	3.88±0.42
	1	0	0.68	0	5.11±0.38	5.42±0.32	4.02±0.43

Note.—The proportion of replicates with and optimal number of 2 components (k) and the mean Ks when k is constrained to 2 is displayed. 95% confidence intervals are given for WGD peak means.

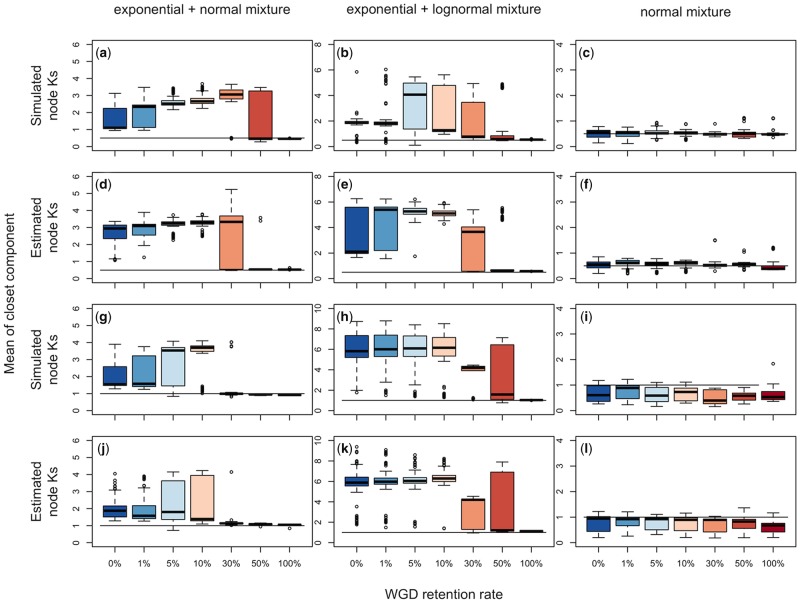
Mixture models often fit the tail of a Ks distribution with one or more extra components, and the maximum Ks cut-off can affect the number of components inferred from Ks plot analyses (Barker et al. 2008; Vanneste et al. 2015). Thus, rather than strictly interpreting any identified component as evidence for a WGD, we also examined only the component whose mean Ks was closest to the actual age of the WGD. We compared the mean Ks values of gene pairs comprising these components to the Ks value of the WGD that was used to simulate the data. Using the exponential+normal mixture model, a WGD often was only detectable, meaning that the estimated mean of a component in the mixture model corresponded to the true age of the simulated WGD, near the true Ks value when the gene retention rate was ≥ 0.3 (fig. 3). When retention rates were ≤ 0.1 for the exponential+normal mixture model, the closest mean Ks for the putative WGD component generally far exceeded the Ks of the WGD, and it overlapped with the component observed when there was no WGD (i.e., retention rate = 0) when Ks was between 0.5 and 2.0 (fig. 3 and supplementary figs. S4–S6, Supplementary Material online). The exponential+lognormal model was able to detect WGD events between Ks = 0.15 and 2.0 with 30% gene retention, except at Ks = 1.0, which required 50% gene retention (fig. 3 and supplementary figs. S3–S6, Supplementary Material online). While the mean node-averaged Ks from the putative WGD component from the normal mixture model analyses overlapped with the true age of the WGD when Ks ≤ 1.0, a peak also was present in the case of no WGD (fig. 3 and supplementary figs. S3–S8, Supplementary Material online). All mixture models had a component mean that overlapped with the simulated WGD Ks = 3.0 and 5.0; however, a component would have been expected at these evolutionary distances even in the complete absence of a WGD (supplementary figs. S7 and S8, Supplementary Material online).

Fig. 3.

—Distributions of the mean Ks of gene pairs comprising the components closest to the true age of the WGD at Ks = 0.5 and Ks = 1.0, when the number of components for each mixture model is optimized by ML. Horizontal black lines represent the true age of a WGD. Panels a–f represent WGDs at Ks = 0.5, and panels g–l are WGD at Ks = 1.0. Results for known simulated node-averaged Ks when a WGD is at Ks = 0.5 are shown in panels (a), (b), and (c) for the exponential+normal, exponential+log normal, and normal mixture model, respectively. Results for the WGD at Ks = 0.5 for estimated Ks are in panels (d), (e), and (f). The distributions of means of components closest to the true WGD age when the WGD is at Ks = 1.0 is given in panels (g), (h), and (i) for known simulated Ks, and panels (j), (k), and (l) for estimated Ks.

In the simulations with a WGD peak mean of Ks = 0.15, the exponential+normal and normal models were not able to detect the WGD even with 100% gene retention, but the exponential+lognormal model detected this component for a gene retention rate ≥ 0.3 (supplementary fig. S3, Supplementary Material online). For a WGD peak mean of Ks = 0.5, the WGD was detectable using the exponential+normal model when the retention rate was 1.0 and the Ks values of the gene pairs were known. In the simulations when the WGD was Ks = 0.5 and the retention rate was 0.5, we could distinguish a WGD in some resampled data sets, which represented a set of possible random gene loss scenarios following WGD, when we knew the node-averaged Ks values, although there was much overall error (fig. 3a and supplementary fig. S4, Supplementary Material online). However, when we used estimated node-averaged Ks values, the WGD was detectable with little error when the retention rate was 0.5 or 1.0, and in some replicates for a retention rate of 0.3 (fig. 3d and supplementary fig. S4, Supplementary Material online). When Ks = 0.5, the normal mixture model found the WGD when optimizing the number of components, but this peak was also found at the same location in simulations without a WGD (i.e., retention rate = 0; fig. 3c and f;supplementary fig. S4, Supplementary Material online). The exponential+lognormal model performed similarly to the exponential+normal model at Ks = 0.5 (fig. 3b and e;supplementary fig. S4, Supplementary Material online).

For simulations with a WGD at Ks = 1.0, the WGD was detectable when optimizing the number of mixing components using the exponential+normal model when retention rates were ≥ 0.3 (fig. 3g and j;supplementary fig. S5, Supplementary Material online). The exponential+lognormal model was less accurate than the exponential+normal model at characterizing the true WGD age at Ks = 1.0, only able to recover the simulated WGD for a few replicates at 30% gene retention with some error at 50% gene retention (fig. 3h and m;supplementary fig. S5, Supplementary Material online). The mixture of normal distributions identified the WGD peaks at high retention rates when the WGD is at Ks = 1.0, but they were also present when there was no WGD (fig. 3i and l;supplementary fig. S5, Supplementary Material online). For the WGD at Ks = 2.0, the exponential+normal model had even higher precision for a retention rate of 0.3 and the exponential+lognormal model could detect WGDs at a retention rate of 0.1 (supplementary fig. S6, Supplementary Material online). As the WGD age increased to Ks = 3.0 and Ks = 5.0, all mixture models performed similarly; peaks detected with 100% gene retention, possibly at the same Ks as the WGD, were also found in the complete absence of a WGD (supplementary figs. S7 and S8, Supplementary Material online).

Instead of optimizing the number of components in the mixture models, we also constrained the number of components to 2 (i.e., the expected number of components when the retention rate is >0) and optimized the mixing distribution parameters to reveal scenarios where WGDs were most consistently detectable (supplementary figs. S9–S14, Supplementary Material online). The most recent WGD in the simulations, Ks = 0.15, was outside of the 95% confidence interval for all mixture models even with complete gene retention following the WGD (tables 1 and 2; supplementary fig. S9, Supplementary Material online). When a WGD occurred at Ks = 0.5, the second component mean was outside of the 95% confidence interval when the retention rate was 0.5 (supplementary fig. S10, Supplementary Material online), but a WGD with a retention rate of 1.0 was identified separately from the background distribution for the exponential+normal and exponential+lognormal models (tables 1 and 2; supplementary fig. S10, Supplementary Material online). The exponential+normal model detected the WGD peak for Ks = 1.0 (supplementary fig. S11, Supplementary Material online) and Ks = 2.0 (supplementary fig. S12, Supplementary Material online) at retention rates of 0.5 and 1.0, but only at a retention rate of 1.0 for the exponential+lognormal model (tables 1 and 2; supplementary figs. S11 and S12, Supplementary Material online). For WGDs at Ks = 3.0 and Ks = 5.0, the exponential+normal and normal mixture models performed similarly, at least for the mean Ks ML estimates (supplementary figs. S13 and S14, Supplementary Material online). When a WGD was at Ks = 3.0 with retention of 0.5 or 1.0, the second component mean was slightly older than the true value of 3.0 (tables 1 and 2; supplementary fig. S13, Supplementary Material online). The true WGD age was within the distribution of second component means for Ks = 5.0; however, a second peak was also detected at Ks = 5.0 when there was no retention of duplicates from the WGD (tables 1 and 2; supplementary fig. S14, Supplementary Material online). The WGD was always outside of the 95% confidence interval for the second component mean for the normal mixture model or overlapped with the 0% gene retention case (supplementary figs. S9–S14, Supplementary Material online).

Detecting WGDs Using Pairwise Ks

Inferring the presence and age of a WGD using pairwise estimates of Ks was less accurate than using node-averaged Ks (fig. 2). When applying the exponential+normal or exponential+lognormal model, we generally inferred more components than when we estimated in the node-averaged analyses (fig. 2 and supplementary fig. S2, Supplementary Material online). When analyzing the means of the components closest to the true ages of the WGDs across replicates, for WGDs at Ks = 0.5 or Ks = 1.0 pairwise distances detected a peak in the distribution that corresponded to the WGD event when retention rates were 0.5 or 1.0 and for some replicates with a retention rate of 0.3 or 0.1, but they overestimated the WGD age (supplementary figs. S4 and S5, Supplementary Material online). All models failed to detect a WGD at Ks = 0.15, even with complete gene retention (supplementary fig. S3, Supplementary Material online). For older WGDs at Ks = 2.0, 3.0, and 5.0, we detected a peak in the Ks distribution at the same evolutionary distance even when there was no WGD (i.e., retention rate = 0; supplementary figs. S6–S8, Supplementary Material online). For the exponential+normal model, when the WGD was at Ks = 2.0, there was less variation in the distribution of component means when using the known pairwise Ks values than when using the estimated pairwise Ks values (supplementary fig. S6, Supplementary Material online), but the converse was observed for Ks = 3.0 (supplementary fig. S7, Supplementary Material online) and Ks = 5.0 (supplementary fig. S8, Supplementary Material online). This result was likely due to saturation, which may have been mitigated by gene trees in the node-averaged distributions, especially when Ks ≥ 3.0 (supplementary figs. S12–S14 and tables S2 and S3, Supplementary Material online). Across all simulation conditions, we could not identify a WGD from the pairwise distances of all paralogs using two components, particularly when using Ks estimated from gene pairs. There was little difference in the qualitative performance of the three mixture models when using pairwise Ks estimates (supplementary figs. S3–S14 and tables S2 and S3, Supplementary Material online).

Analyzing “Syntenic” Data instead of All Paralogs

We examined whether using Ks plots built from only paralogs resulting from a WGD can be used to detect and date ancient WGDs more accurately than using Ks plots built from all paralogs. In these experiments, we removed all data points representing paralogs that were not from WGDs, so that the remaining genes represented paralogs from large syntentic regions within a genome, and we only used node-averaged estimates of Ks. We did not use simulations with retention rates of 0 and 0.01 because there were no genes resulting from the WGD when the retention rate was 0 and too few genes resulting from the WGD when the retention rate was 0.01 (<30 duplication nodes across 1,000 gene trees). Because the syntenic data lacks the background duplicates that we attempted to fit with an exponential distribution in prior analyses, we only applied the normal mixture model to these data.

Overfitting distributions remained an issue with the syntenic node-averaged data (fig. 4 and supplementary fig. S15, Supplementary Material online). Only a single component was expected in these analyses, since all the duplications resulted from the WGD. However, when the retention rate was 0.05, a single component was chosen for estimated distributions of Ks 14%, 15%, 22%, 34%, 53%, and 67% of the time for a WGD at Ks = 0.15, 0.5, 1.0, 2.0, 3.0, and 5.0, respectively. The number of resampled data sets with a single component decreased when the retention rate was 0.1; a single component was chosen 0%, 1%, 8%, 10%, 26%, and 47% of the time when Ks = 0.15, 0.5, 1.0, 2.0, 3.0, and 5.0, respectively (fig. 4). A single normal component was never chosen using ΔBIC for retention rates ≥ 0.3, except in 53% of the replicates for a WGD at Ks = 5.0 with 30% gene retention (supplementary table S4, Supplementary Material online). Analyses using known Ks values estimated from gene pairs followed a similar pattern (supplementary table S4, Supplementary Material online).

Fig. 4.

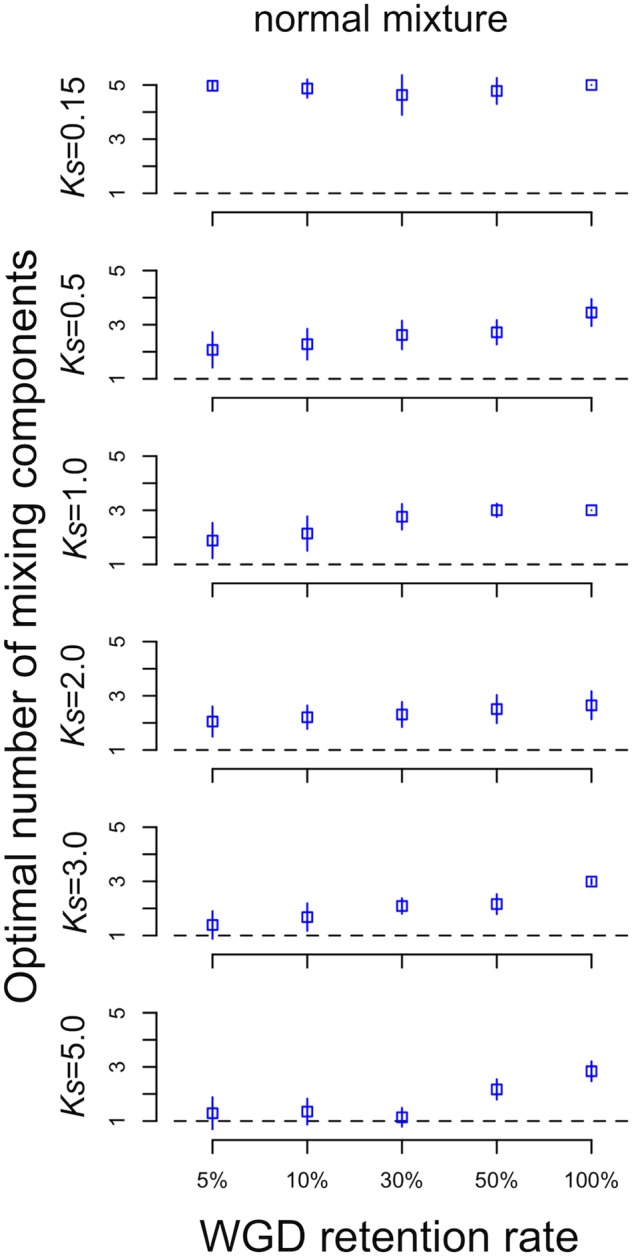
—The average number of components for simulated WGD events at different ages and retention rates when only using gene pairs that are products of a WGD event. Results for node-averaged estimates of Ks are squares and pairwise Ks estimates are triangles. Error bars represent one standard deviation. The dashed line represents the expected number of components, which is always one in the case of a single WGD event and syntenic data.

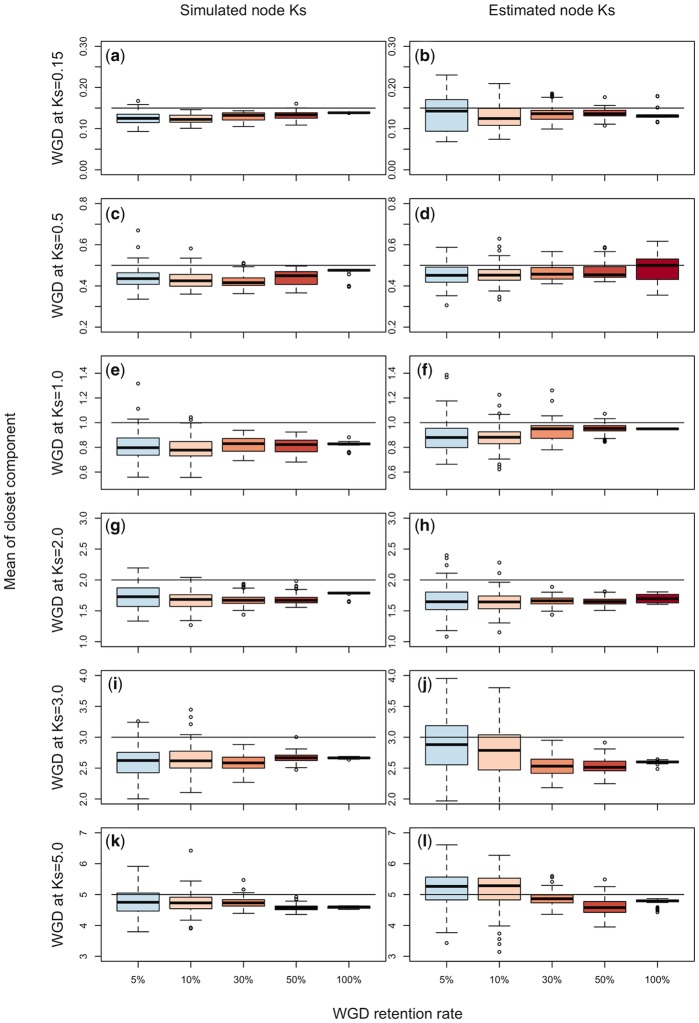
Again, the true WGD still may be detectable even if the optimal number of components does not reflect the number of WGDs. For both the known and estimated node-averaged Ks, the WGD peak was detectable, within or very close to the upper quartile of the estimated component means, when gene retention rates were 0.05, 0.1, 0.3, 0.5, and 1.0 across all WGD ages (fig. 5). Still, the mean of the component generally underestimated the true age of the WGD, except when analyzing the ML estimates of Ks for retention rates of 0.05 and 0.1 when the WGD was at Ks = 5.0. Although there was some uncertainty in the timing of the WGDs when retention rates were 0.05 and 0.1 (fig. 5), the WGD was discernable using normal mixture models on our simulations. However a single WGD using only syntenic data did not fit the expectation of a single normal distribution, with a bias toward Ks values more recent than the expected WGD that may have been a product of the lognormal distributed rates of evolution used in the simulations (Rannala and Yang 2007; supplementary fig. S16, Supplementary Material online).

Fig. 5.

—Distributions of the means of components closest to the true age of the WGD at Ks = 0.15, 0.5, 1.0, 2.0, 3.0, and 5.0, when the number of components for a normal mixture model is optimized by ML. Distributions are shown for known and estimated node-averaged Ks of syntenic data. Horizontal black lines represent the true age of a WGD.

Performance of Mixture Models on Empirical Transcriptomic Data

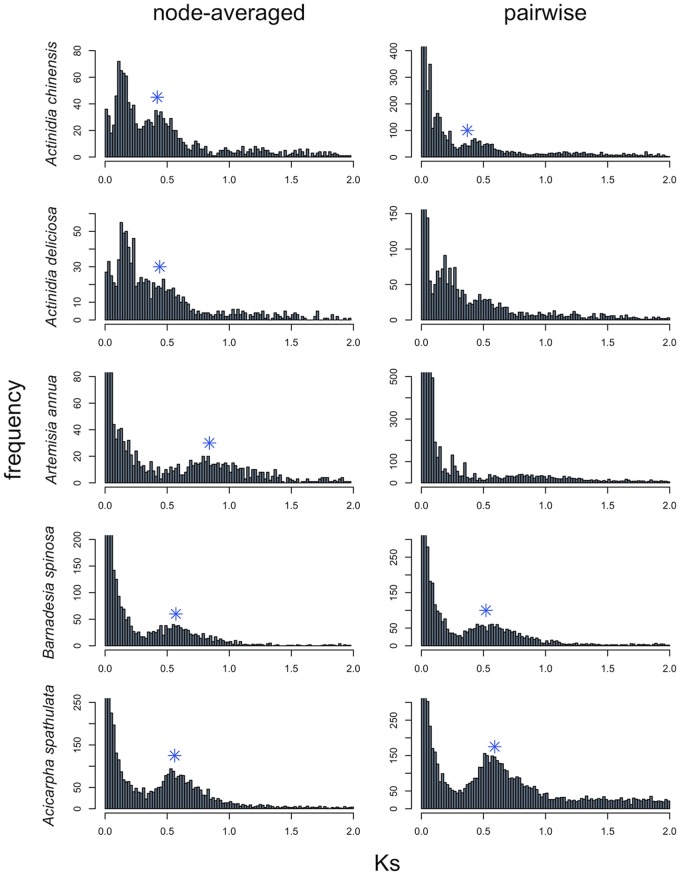
Mixture model analyses of Ks plots from several transcriptomic data sets used to identify ancient WGDs (Shi et al. 2010; Barker et al. 2016) generally were consistent with the simulation results. The normal mixture model fit at least as many components as the exponential+normal mixture model (supplementary table S5, Supplementary Material online). However, the exponential+lognormal mixture model sometimes fit fewer components than the exponential+normal and normal mixture models (supplementary table S5, Supplementary Material online). In spite of overfitting, the WGD peak was detectable in all five empirical cases with all three mixture models for node-averaged Ks estimates, while the mixture models failed to detect putative WGD peaks in two out of the five empirical Ks plots with pairwise Ks estimates (fig. 6 and supplementary table S5, Supplementary Material online). The peaks identified in the node-averaged data correspond to WGDs characterized in previous studies (Shi et al. 2010; Barker et al. 2016); however, the exponential+normal model failed to identify a prominent peak near Ks = 0.15 in both Actinidia chinensis and Actinidia deliciosa (fig. 6 and supplementary table S5, Supplementary Material online), which was expected given our simulation results (supplementary figs. S3 and S9, Supplementary Material online). This peak at Ks = 0.15 for Actinidia chinensis was detected by the exponential+lognormal model for node-averaged data as well as the normal mixture model (supplementary table S5, Supplementary Material online). Although, the normal mixture model likely has an inflated estimate of the proportion of data that corresponds to the peak near Ks = 0.15 by not accounting for the background duplicates with an exponential component (supplementary table S5, Supplementary Material online). Peaks consistently identified in pairwise data for Barnadesia spinosa and Acicarpha spathulata were close to their node-averaged estimates (fig. 6 and supplementary table S5, Supplementary Material online).

Fig. 6.

—Ks plots for five previously published transcriptome sequences or EST data sets. Node-averaged ML estimates are shown on the left while pairwise ML estimates are shown on the right. Plots are truncated at Ks = 2 and arbitrarily on the y-axis to ease visualization. Blue asterisks indicated a component mean that was identified by all three mixture model analyses. Complete mixture model results are given in supplementary table S5, Supplementary Material online.

Discussion

Although our simulations indicate that mixture model analyses of Ks plot distributions should be interpreted with great caution, they can detect ancient WGDs under some conditions. For example, we detected simulated WGDs in Ks plots when the Ks distance was between 0.5 and 2.0 and at least 30% of duplicate genes were retained from the WGD (fig. 3 and supplementary figs. S3–S8, Supplementary Material online). We were able to detect simulated WGDs in this range using only two component for the exponential+normal and exponential+lognormal in the presence of complete gene retention, suggesting that the mean of the components associated with the WGDs was unlikely to change regardless of how many additional components were introduced into the mixture models. The exponential+lognormal model also had the benefit of detecting simulated WGDs as recent as Ks = 0.15 when freely optimizing the number of components. In our simulations, it was difficult to detect WGDs when the gene retention rate following the WGD was ≤ 10%, especially when the WGD is relatively recent (Ks ≤ 0.5 in our simulations). Although estimates of gene retention rates following ancient WGDs based on genome sequences from some angiosperms are <10% (Tiley et al. 2016), estimates of ≥ 10% duplicate gene retention are not uncommon (Maere et al. 2005; Barker et al. 2009; Yang et al. 2015).

Perhaps the most troubling aspect of mixture model analyses from Ks plots is their tendency to falsely detect WGDs. Mixture model analyses of gene age distributions often overfit the number of components (fig. 2). When analyzing WGDs with low (≤ 10%) retention rates with the exponential+normal mixture model, not only was the estimated number of components and ages of the components inaccurate (fig. 2) but also the results were indistinguishable from the simulations with no WGD (i.e., 0% genes retention; fig. 3 and supplementary figs. S3–S8, Supplementary Material online). Clearly a strict interpretation of optimal mixture model components can lead to false positives for the signal of ancient WGDs, even when limiting the Ks plot analyses to include only paralogs involved in the WGD (fig. 4 and supplementary fig. S15, Supplementary Material online). Moreover, the number of components estimated by the mixture model appears to often lack biological meaning (Vanneste et al. 2014; Johnson et al. 2016). The extra components that do not correspond to either the WGD or background distribution generally fit the tails of Ks plots and account for a small proportion of the data, as also seen with our empirical analyses (supplementary table S5, Supplementary Material online). Cases where WGD peaks could be detected in our simulations by the exponential+normal mixture also required multiple distributions to account for the tail (supplementary table S1 and figs. S4–S6 and S17–S19, Supplementary Material online). Normal mixture models sometimes required more than one component to fit the background distribution alone, which contributed to the overall increased number of components estimated for normal mixture models compared with the exponential+normal mixture models in both the simulated and empirical data (supplementary figs. S4–S6 and S17–S19 and table S5, Supplementary Material online). These results indicated that the ΔBIC score often does not provide accurate estimates of the number of components (i.e., ancient WGDs). Similar criticisms of ΔBIC for model selection have been previously shown for generalized linear mixed models (Naik et al. 2007), and the overfitting of parametric mixture models likely is exacerbated in Ks plots because they are bounded at zero (Morrison 2008). Alternative model selection approaches, such as generating null distributions of LRTs with nonparametric bootstrapping, may be more appropriate for detecting ancient WGDs from Ks plots (McLachlan 1987); however, they can be intensely computationally demanding.

Although our results suggested that extremely ancient WGDs (i.e., Ks = 5.0) could be identified with mixture models when using node-based estimates of Ks (supplementary fig. S8, Supplementary Material online; tables 1 and 2), we found that a second peak would manifest at Ks = 5.0 regardless of whether a WGD occurred or not, similar to Vanneste et al. (2013). Ks = 5.0 is outside of the range of values considered for most Ks plot analyses; however, the location of the erroneous second peak depends on where a user truncates the Ks plot, and the presence of a tail that may require additional normal components. For example, more than two peaks manifested in nearly all of the Ks plots in our simulation experiments; Ks plots were truncated at 5.0 for WGDs at Ks = 0.15, Ks = 0.5, and Ks = 1.0, which all showed a second distribution mean near Ks = 3.0 in the absence of a WGD for the exponential+normal model (supplementary figs. S9–S11, Supplementary Material online). Truncating Ks plots to lower values will likely push these arbitrary distribution means into biologically plausible ranges. Thus, no matter how the Ks plot is constructed, it is important to distinguish between arbitrary model fitting and lines of evidence for a WGD.

Our simulations confirmed findings from previous research (Cui et al. 2006; Vanneste et al. 2013) that Ks plots perform best at a limited range of ages and levels of gene retention (fig. 3 and supplementary figs. S3–S14, Supplementary Material online). Thus, we might expect Ks plot analyses alone to produce a biased view that ancient WGDs are clustered in time. Many WGDs in angiosperms appear to coincide with the Cretaceous-Paleogene boundary based on a second Ks peak generally falling between 0.5 and 1.0 (Fawcett et al. 2009; Vanneste et al. 2014; Lohaus and Van de Peer 2016), within the range where Ks plot analyses appear optimal, between Ks = 0.5 and 2.0, in our simulations. Although, this range of Ks can cover a large amount of absolute time, considering that variation in substitution rates, such as in Pinus, can cause a Ks peak of 0.25 to correspond to >200 Ma (Li et al. 2015). Thus, the efficacy of Ks plots for certain windows of divergence does not mean that that WGDs are not clustered in this window (e.g., near the Cretaceous-Paleogene boundary). In fact, many of the primary Ks plot results in plants (Schlueter et al. 2004; Tuskan et al. 2006; Schmutz et al. 2010) are supported through analyses of gene trees using genes of putative WGD origin based on syntenic evidence and absolute dating with the multispecies coalescent model (Fawcett et al. 2009; Vanneste et al. 2014; Lohaus and Van de Peer 2016). However, many other WGDs may go unobserved in Ks plot analyses alone if they are younger than Ks = 0.15 or older than Ks = 3.0. As more genomic data for plants, especially nonmodel taxa that may lack near-chromosome level assemblies, becomes available, methods that characterize ancient WGDs in a phylogenetic context (Cannon et al. 2015; Li et al. 2015; Yang et al. 2015; McKain et al. 2016) may be better able to test hypotheses regarding the clustering of WGDs and their association with evolutionary innovation as well as the survival and diversification of major plant groups (Tank et al. 2015; Kellogg 2016).

Although our simulation results provided many reasons to question the strict interpretation of mixture model analyses of Ks plots, they also offer some guidance on ways to optimize the inference of WGDs. For example, it is always better to use node-based estimates of Ks distance than pairwise distance estimates. Criticisms of pairwise Ks estimates arose early in the ancient WGD literature (Blanc and Wolfe 2004), and consequently, many studies have corrected for the redundancy of pairwise estimators with neighbor-joining trees made from pairwise Ks (Blanc and Wolfe 2004; Maere et al. 2005; Cui et al. 2006; Barker et al. 2008; Vanneste et al. 2013; Devos et al. 2016), with few using phylogenetic estimates of evolutionary distances (Rensing et al. 2007; Olsen et al. 2016). However, the use of pairwise estimates in Ks plot analyses still persists (Ming et al. 2013; Kim et al. 2014; Nossa et al. 2014; Johnson et al. 2016). Our simulations indicated that pairwise Ks distances are limiting compared with node-averaged estimates; a WGD with 100% gene retention cannot be distinguished from the absence of a WGD (i.e., 0% gene retention) regardless of the WGD age (supplementary figs. S3–S8, Supplementary Material online). However, a WGD at Ks = 2.0 could be accurately characterized with the exponential+normal or exponential+lognormal mixture model when gene retention rates were 30%, and possibly less (supplementary fig. S6, Supplementary Material online). Pairwise estimators can perform well in some empirical cases though. The differences between node-based and pairwise Ks distributions are generally greater in our simulations than in our empirical analyses (fig. 6 and supplementary figs. S9–S14, Supplementary Material online), but given that the computation cost for node-averaged estimates is low, our experiments suggest there is little reason to use pairwise distances in Ks plot analyses.

Using the exponential+normal and exponential+lognormal mixture model typically fit fewer components, and thus resulted in fewer false positives, than using the normal mixture model (fig. 2 and supplementary fig. S2, Supplementary Material online). As observed in many empirical studies (Szövényi et al. 2015; Johnson et al. 2016), normal mixture models generally overfit components (fig. 2). The normal mixture model could always recover a peak that corresponded to the true age of the simulated WGD for Ks between 0.15 and 1.0 (fig. 3 and supplementary figs. S3–S5, Supplementary Material online), but the overlap between component means at complete gene retention and no gene retention suggested that these peaks were not caused by the WGD (supplementary figs. S17–22, Supplementary Material online). Even when the gene retention rate was high, the age of a WGD often could be accurately characterized with only two components by the exponential+normal or exponential+lognormal, but not the normal mixture model between Ks = 0.5 and 3.0 (supplementary figs. S10–S13, Supplementary Material online). This result provides additional evidence that while more components may be preferred by the ΔBIC, the extra components are likely fitting the tails of the distributions for the exponential+normal and exponential+lognormal mixtures. One strategy to improve detection of WGDs is to look for consistency in a component mean, that is, cases when the estimates of a component mean are similar, regardless of how many mixing distributions are incorporated into the model. For example, we demonstrated consistency for analyses of all paralogs by comparing the exponential+normal mixture model where k was constrained to 2 with the exponential+normal mixture model where k was freely optimized. A peak was detectable at the age of the WGD with only two components (supplementary figs. S9–S14, Supplementary Material online), and the approximate age of this peak remained unchanged, even with the addition of more components when k was freely optimized (figs. 2 and 3; supplementary figs. S3–S8, Supplementary Material online). Additionally, peaks corresponding to ancient WGDs in empirical Ks plots were detectable in all three mixture models, while other component means were not associated with a visible peak in the Ks distributions (fig. 6 and supplementary table S5, Supplementary Material online).

The best performance in our simulations resulted from using Ks plots built only from paralogs that diverged at an ancient WGD (e.g., paralogs on large syntenic regions within a genome). Syntenic data alone can be interpreted as evidence of a WGD (Kellis et al. 2004; Aury et al. 2006; Tang et al. 2008), and in these cases, the Ks plot analyses may be viewed as corroborating evidence for an ancient WGD or as a means to date the WGD. Ks plots built from syntenic data have helped resolve the absolute timing of notable WGD events such as two ancient WGDs shared by all Brassicaceae (Bowers et al. 2003), the papilionoid legume WGD (Schmutz et al. 2010), the ancestral eudicot triplication (Tang et al. 2008), a WGD predating angiosperms (Amborella genome project 2013), and at least two WGDs shared by most grasses (McKain et al. 2016). In contrast to analyses that used all paralogs, when using only paralogs from a WGD, the WGD peak was consistently prominent across all ages, even when there was only a 5% gene retention rate following the WGD (fig. 5 and supplementary fig. S16, Supplementary Material online). Ks plot analyses of syntenic duplicates also could detect a distinct WGD component at Ks = 0.15, where the WGD peak is absorbed into the background duplication distribution in analyses of all paralogs for the exponential+normal model, and detect ancient WGDs even beyond Ks = 3.0. Unfortunately, syntenic data are available from relatively few taxa with near-complete genome assemblies, and therefore, these simulations are applicable to a limited number of taxa.

In spite of our cautionary assessment of mixture model analyses of Ks plots under a number of conditions, they have helped characterize many well-accepted ancient WGDs across plants (Schlueter et al. 2004; Cui et al. 2006; Rensing 2007; Barker 2008; Vanneste et al. 2014; Szövényi et al. 2015; Johnson et al. 2016). This raises the question whether Ks plot analyses may perform better on empirical rather than simulated data. Several empirical studies have detected peaks with ranges of Ks = 0.1 to Ks = 0.3 from analyses of all paralogs, such as in Zea mays (Schlueter et al. 2004; Vanneste et al. 2014), Glycine max (Cui et al. 2006; Vanneste et al. 2014), and Helianthus (Barker et al. 2008). This suggests that background duplicate gene loss, especially of recent duplicates, may be faster than we modeled with a simple stochastic birth and death process. Consequently, our simulations may have retained too many genes from background duplications. For instance, Li et al. (2016) showed that putative single-copy orthologous groups tend to revert to a single-copy state rapidly following WGD across angiosperms. Notably, our simulated distributions lack the distinct sharp increase of recent paralogs (supplementary figs. S17–S22, Supplementary Material online) found in many empirical data sets, including those reanalyzed here (fig. 6; Barker et al. 2008; Shi et al. 2010). The assumptions made in order to simulate gene family evolution while accounting for gene retention following a WGD event certainly oversimplified the biological complexities of gene gain and loss, which may have led to simulated distributions of Ks with much weaker WGD signals than empirical cases. Gene copies that survive the fractionation process following a WGD typically maintain unique balances of gene products (Edger and Pires 2009; Freeling 2009; Conant et al. 2014). The biases in gene retention following a WGD may contribute to evidence for ancient WGDs from Ks plots, as there are typically enrichments in gene ontology categories among genes corresponding to Ks plot peaks, such as in Arabidopsis thaliana (Maere et al. 2005) and Physcomitrella patens (Rensing et al. 2007). Additionally, many Ks plot analyses are based on transcriptomic data. If duplicates from WGDs are more frequently expressed than duplicates from small-scale duplication events (Casneuf et al. 2006), transcriptomic data may be enriched for WGD duplicates compared with genomic data, and our simulations suggest that enriching a data set for WGD duplicates typically should improve our ability to detect ancient WGDs.

Based on our results, mixture model analyses of Ks plots should be considered, at most, a hypothesis-generating tool for ancient WGDs. Evidence of a peak from Ks plot analyses should not be considered proof of an ancient WGD, nor should the absence of evidence of a peak from a Ks plot be considered proof of the absence of an ancient WGD. Multiple lines of evidence, ideally including syntenic evidence and phylogenetic tests for a WGD, should be used to identify and characterize ancient WGDs. For example, as more comparative genomic and transcriptomic data becomes available, combined analyses of Ks plots and gene tree reconciliation likely will improve the phylogenetic placement of WGDs (Barker et al. 2009, 2016; Jiao et al. 2011; Li et al. 2015; Yang et al. 2015). In addition, probabilistic models of gene gain and loss (Rabier et al. 2014; Tiley et al. 2016) enable rigorous statistical tests for ancient WGDs. Still, Ks plots are computationally inexpensive and do not require comparative genomic data or ultrametric phylogenetic trees. Ks plots also appear to perform well identifying and dating some ancient WGDs (Cui et al. 2006; Barker et al. 2009; Vanneste et al. 2014), especially when combined with absolute dating of gene trees (Vanneste et al. 2014). Furthermore, simple methodological choices, such as using node-averaged estimates of Ks and diagnosing consistency in mixture model results, can help evolutionary biologists maximize the performance of mixture model analyses of Ks plots.