Concordant Changes in Gene Expression and Nucleotides Underlie Independent Adaptation to Hydrogen-Sulfide-Rich Environments

Abstract

The colonization of novel environments often involves changes in gene expression, protein coding sequence, or both. Studies of how populations adapt to novel conditions, however, often focus on only one of these two processes, potentially missing out on the relative importance of different parts of the evolutionary process. In this study, our objectives were 1) to better understand the qualitative concordance between conclusions drawn from analyses of differential expression and changes in genic sequence and 2) to quantitatively test whether differentially expressed genes were enriched for sites putatively under positive selection within gene regions. To achieve this, we compared populations of fish (Poecilia mexicana) that have independently adapted to hydrogen-sulfide-rich environments in southern Mexico to adjacent populations residing in nonsulfidic waters. Specifically, we used RNA-sequencing data to compare both gene expression and DNA sequence differences between populations. Analyzing these two different data types led to similar conclusions about which biochemical pathways (sulfide detoxification and cellular respiration) were involved in adaptation to sulfidic environments. Additionally, we found a greater overlap between genes putatively under selection and differentially expressed genes than expected by chance. We conclude that considering both differential expression and changes in DNA sequence led to a more comprehensive understanding of how these populations adapted to extreme environmental conditions. Our results imply that changes in both gene expression and DNA sequence—sometimes at the same loci—may be involved in adaptation.

Introduction

Changes in protein coding DNA sequence, gene expression, or both, often occur when populations colonize and adapt to new environments (Rosenblum et al. 2004; Chan et al. 2010; Pavey et al. 2010; Jones et al. 2012). There are ongoing debates about whether adaptation to novel environments is more frequently driven by changes in protein structure or gene expression, and about the relative roles of regulatory versus structural (nonsynonymous) changes in the adaptive process (King and Wilson 1975; Stern 2000; Hoekstra and Coyne 2007; Wray 2007; Haygood et al. 2010; Jones et al. 2012; Pespeni et al. 2012; Fraser 2013; Halligan et al. 2013). Previously, separate molecular techniques were required to analyze sequence level changes (e.g., Sanger sequencing) and differences in gene expression (e.g., quantitative polymerase chain reaction) between populations. With the advent of RNA-sequencing (RNA-seq), however, it is feasible to simultaneously obtain information about both positive selection on gene sequences and expression variation in expressed regions of the genome. RNA-seq has proven to be a powerful technique for elucidating the molecular basis of adaptation to new environments (Chapman et al. 2013; De Wit and Palumbi 2013; Hodgins et al. 2016; Zhang et al. 2017). RNA-seq gives researchers the ability to detect two potentially important molecular signatures that give insight into the adaptive process: differential expression (Huang et al. 2016; Kelley et al. 2016) and positive selection on gene sequences (De Wit and Palumbi 2013; Tong et al. 2017).

During adaptation to novel environments, these two mechanisms may work in concert (sequence changes within regulatory regions of a gene could lead to differential expression directly, or both types of changes could be favorable), leading to genes showing both high sequence divergence and differential expression. Alternatively, gene expression changes may be important for adaptation in different biological pathways than changes in protein coding sequence, leading to a different set of candidate genes depending on the analysis performed. For example, gene expression changes may be required in instances where strong constraints prevent changes to protein coding sequences, whereas gene sequence changes may be required in situations where protein structural changes are necessary for adaptation. Some studies have indicated that these two mechanisms act independently more often than they work in tandem. A recent study comparing two conifer species found that genes under positive selection were not more likely to be differentially expressed than expected by chance (Hodgins et al. 2016). Similarly, studies of yeast strains from different environments indicate no correlation between gene sequence divergence and gene expression divergence (Tirosh and Barkai 2008; Li YD et al. 2009). The discordance between differential expression and evidence for positive selection has also been observed between humans and chimpanzees, though genes involved in certain processes (e.g., spermatogenesis) show signatures of both high sequence differentiation and differential expression (Nielsen et al. 2005). There have been a few studies, however, that have found a correlation between differential expression and sequence divergence. Differentially expressed genes between ragwort populations living at different altitudes showed increased levels of differentiation between populations (F_ST) compared with genes that showed no evidence for differential expression (Chapman et al. 2013). A comparison of transcriptomic data from two frog species indicated a correlation between gene sequence divergence and differential expression levels (i.e., genes with larger fold changes in expression were also more divergent in sequence; Sartor et al. 2006). Most of the studies mentioned earlier have involved comparisons between expression and genetic profiles of populations and species with high levels of differentiation. In fact, one hypothesis to explain the association between expression and sequence divergence documented by Sartor et al. (2006) is that the genes might have become so divergent at the sequence level that they changed function, leading to concomitant differences in expression levels. Comparisons between closely related populations where divergence is unlikely to have led to entirely new function are largely unexplored. Comparing putatively ancestral populations to populations that have recently colonized a new environment with clear, strong selective pressures could lead to a better understanding of genomic responses at both the expression and sequence level during the early stages of adaptation and speciation.

Populations of a small livebearing fish (Poecilia mexicana) have recently (<100,000 years ago) colonized multiple springs with extremely high concentrations of toxic hydrogen sulfide (H₂S) in southern Mexico (Tobler et al. 2011; Pfenninger et al. 2014). These populations are suited for investigating whether there is a correlation between differential expression and differentiation outliers during the early phases of adaptation. There have been multiple colonizations of sulfide springs, including independent events in the Puyacatengo and Tacotalpa river drainages (see fig. 1;Tobler et al. 2011). Populations residing in the sulfide springs are locally adapted to their environment (Tobler et al. 2018), and gene flow between adjacent sulfidic and nonsulfidic populations is suppressed due to strong natural and sexual selection against migrants (Tobler et al. 2009; Plath et al. 2013). H₂S is toxic at low concentrations to metazoans (Beauchamp et al. 1984; Bagarinao 1992; Reiffenstein et al. 1992; Tobler et al. 2016), mostly because it inhibits cytochrome c oxidase (COX), which stops aerobic ATP production (Petersen 1977; Cooper and Brown 2008). COX is a candidate for adaptive changes, because changes in this complex could allow organisms to overcome the toxic effects of H₂S (Pfenninger et al. 2014). Another candidate pathway that is likely to have played a role in adaptation to the sulfidic environments is the sulfide: quinone oxidoreductase (SQR) pathway, which allows metazoans to enzymatically oxidize small amounts of H₂S to nontoxic forms that can be excreted (Hildebrandt and Grieshaber 2008; Lagoutte et al. 2010). H₂S detoxification is primarily mediated by three genes: sulfide: quinone oxidoreductase (SQRDL), persulfide dioxygenase (ETHE1), and thiosulfate sulfurtransferase (TST) (Lagoutte et al. 2010). A recent study identified genes that were differentially expressed between adjacent sulfidic and nonsulfidic populations using RNA-seq data, but did not attempt to identify sites potentially under positive selection (Kelley et al. 2016). Another study analyzed patterns of genomic divergence between adjacent sulfidic and nonsulfidic populations using pooled whole-genome sequencing data, but included no analyses of differential expression (Pfenninger et al. 2015). Therefore, it remains to be tested how well candidate genes for adaptation identified by those analyses overlap with one another. Here, we use transcriptome data from Kelley et al. (2016) to ask whether differential expression and differentiation outlier analyses lead to similar conclusions about how these populations have adapted to the sulfidic environments, and whether there is higher overlap between genes with evidence of differential expression and positive selection than expected by chance. Specifically, our study addresses the following questions: 1) Qualitatively, do the results from an outlier scan match those from a differential expression analysis? We identified highly differentiated sites in the transcriptome between adjacent sulfidic and nonsulfidic populations of Poecilia mexicana in the Puyacatengo and Tacotalpa river drainages and identified enriched functional categories in the set of genes that contained these sites. We then compared the general conclusions from our analysis to conclusions from a study on differential gene expression in the same individuals (Kelley et al. 2016). 2) Are differentially expressed genes more likely to contain highly differentiated sites than expected? We quantitatively tested whether the differentially expressed genes were more likely to contain highly differentiated sites than expected.

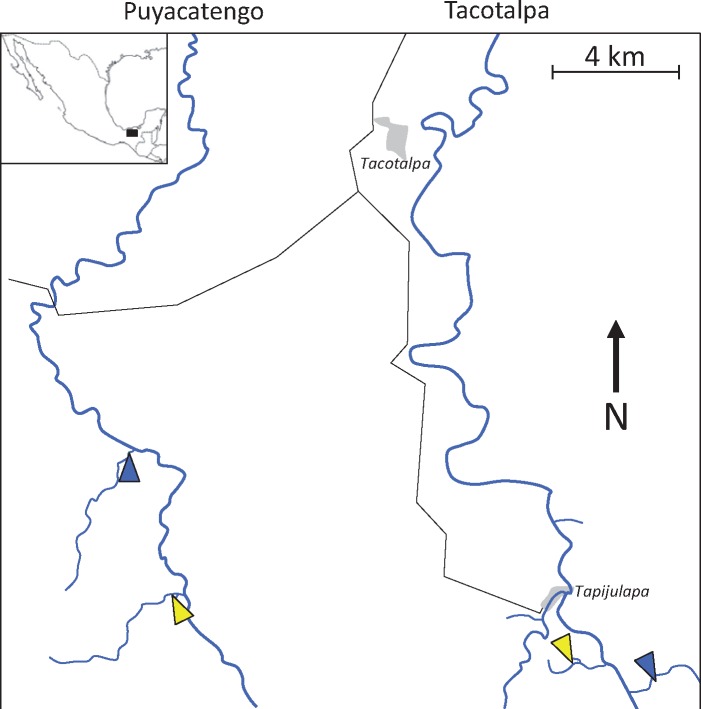
Fig. 1.

—Map of Poecilia mexicana system in southern Mexico near the Sierra Madre de Chiapas mountain range. The water flows north toward the Gulf of Mexico. Yellow triangles represent populations from sulfidic environments, whereas blue triangles represent populations from nonsulfidic environments.

Materials and Methods

Study Sites and Sample Collection

Poecilia mexicana samples for sequencing were collected from sulfidic springs and nearby nonsulfidic streams near Teapa (Tabasco, Mexico) in the Sierra Madre de Chiapas mountain range (fig. 1) for a previous study (Kelley et al. 2016). Sampling sites were distributed in two tributaries of the Río Grijalva (Ríos Tacotalpa and Puyacatengo), representing independent colonizations of H₂S-rich springs (Tobler et al. 2011) (fig. 1).

RNA Isolation and RNA-Seq Library Construction

RNA was isolated from gill tissue and libraries were prepared on a per individual basis for a previous study (see Kelley et al. 2016) for full details on RNA isolation and RNA-seq library construction. Libraries were sequenced on an Illumina HiSeq 2000 with paired-end 101 basepair (bp) reads at the Stanford Center for Genomics and Personalized Medicine. RNA-seq data from a total of 23 individuals (Tacotalpa sulfidic: n = 6 sulfidic, nonsulfidic: n = 6; Puyacatengo sulfidic: n = 5, nonsulfidic: n = 6) were used in the present study. Sequencing yielded between 6.2 and 28.5 million paired-end reads per individual (between 629 and 2,848 megabases [Mb] of raw data per individual). Additional descriptive statistics for the data set are provided in Table S1 of Kelley et al. (2016). Differentially expressed genes between adjacent populations (sulfidic vs nonsulfidic) in the Puyacatengo and Tacotalpa drainages were also pulled directly from Kelley et al. 2016.

SNP Calling from RNA-Seq Data

Raw RNA-seq reads from Kelley et al. 2016 (study accession ID: PRJNA290391) were sorted by barcode and dynamically trimmed to quality 20 using Trim Galore! (http://www.bioinformatics.babraham.ac.uk/projects/trim_galore/; last accessed September 24, 2018). Only paired reads with at least 50 bp for each read were retained for the analysis. Trimmed reads were mapped using Stampy (version 1.0.23) (Lunter and Goodson 2011) to the platyfish (Xiphophorus maculatus) genome (v 4.4.2 release-75), which was the closest well-annotated published genome available (Schartl et al. 2013).

Mapped reads were used to identify single nucleotide polymorphisms (SNPs) from the RNA-seq data. Read groups were added to individual Stampy mapped bam files. SNPs were called per population using the Genome Analysis Toolkit (GATK) (v3.2.2) (McKenna et al. 2010). SNP and insertion/deletion (INDEL) discovery and genotyping was accomplished using standard hard filtering parameters according to the GATK Best Practices recommendations (DePristo et al. 2011; Van der Auwera et al. 2013). Initially all confident sites were emitted to facilitate merging of population variant call format (vcf) files. Population vcf files were compressed using bgzip and indexed using tabix from the htslib repository (v 1.2.1), which is part of the samtools suite (Li H et al. 2009). The compressed population vcf files were then merged using the vcf-merge utility from vcftools (v 0.1.12b) (Danecek et al. 2011). The merged vcf files were filtered using vcftools (Danecek et al. 2011). Sites that passed our filters were biallelic (–min-alleles 2, –max-alleles 2), had at least 8x coverage per individual (–minDP 8), and had sufficient coverage for at least 90% of individuals (–max-missing 0.9). We also filtered out sites where at least 70% of the individuals across all four populations were heterozygous. Such sites with extremely high levels of heterozygosity across multiple populations are likely the result of a gene duplication.

DNA Isolation and DNA-Seq Whole Genome Library Construction

Given that SNPs were called and analyzed from RNA-seq data, we attempted to validate any site that was putatively a fixed difference in our data set between adjacent populations using low-fold whole-genome sequencing data from the same individuals. DNA was isolated from the second gill arch from the same individuals included in the RNA-seq experiment (except for one individual from the sulfidic Tacotalpa population for which there was no second gill arch available). Liquid nitrogen frozen gill tissue (45–60 mg) was pulverized with a Covaris Cryoprep at setting 3. DNA was extracted using Qiagen Gentra Purgene Tissue Kit. DNA-sequencing libraries were generated using the Epicentre (Illumina) Nextera protocol with dual-barcodes. After using qPCR to determine library concentrations, one equimolar pool was created and sequenced on two lanes of an Illumina HiSeq 2000, resulting in 101-bp reads. Sequencing yielded between 13 and 45 million paired-end reads per individual (between 1,370 and 4,553 Mb of raw data per individual). Additional descriptive statistics for the DNA sequencing are provided in supplementary table S1, Supplementary Material online.

SNP Calling from DNA-Seq Data

The quality of the DNA-seq data was inspected using FastQC (Andrews 2010). We dynamically trimmed reads to quality 20 and trimmed sixteen bases off of the 5′ end of each read using Trim Galore! due to skewed per base sequence composition at the beginning of the reads (Krueger 2014). Only paired reads with at least 50 base pairs for each read were retained for the analysis. Trimmed reads were mapped to the platyfish genome (v 4.4.2 release-75) (Schartl et al. 2013). Reads were mapped using BWA (v 0.7.10) (Li and Durbin 2009). Given that each individual sample had two bam files (one for each sequencing lane), bam files for the same individuals were merged using the merge option in samtools (v 1.0) (Li H et al. 2009). SNPs were called per population using GATK (v 3.2.2) (McKenna et al. 2010). As with the RNA-seq data, SNP and insertion/deletion (INDEL) discovery and genotyping was accomplished using standard hard filtering parameters according to GATK Best Practices recommendations (DePristo et al. 2011; Van der Auwera et al. 2013). To prepare for merging, the population vcf files were then compressed using bgzip and indexed using tabix from the htslib repository (Li H et al. 2009). The compressed vcf files were then merged using the vcf-merge option in vcftools (Danecek et al. 2011). Since our interest was in validating the SNP calls from the RNA-seq data, only sites that were identified as SNPs in the RNA-seq data were kept in the DNA-seq data. All other sites were filtered out using the –positions option in vcftools (v 0.1.12b) (Danecek et al. 2011).

Validating Fixed Differences between Our Samples of Adjacent Populations

After computing pairwise F_ST values per site for each drainage (sulfidic vs nonsulfidic) using vcftools (–weir-fst-pop) (Danecek et al. 2011), we validated fixed differences between our samples of adjacent populations called from our RNA-seq data using our low-fold whole genome DNA-seq data from the same individuals. The only sites that we considered potential candidates for validation were sites where at least two individuals per population in the pairwise comparison had at least 4X coverage in the DNA-seq data set. If a fixed difference in our RNA-seq data set had a high F_ST (>0.5) in our DNA-seq data set, then we considered this to be a valid site putatively under selection. Of the sites with high enough coverage for validation (86.8% of all fixed differences), 99.7% (325 out of 326) of fixed sites in our RNA-seq data set were either fixed or high F_ST in our DNA-seq data set. We removed the one invalidated site from the Puyacatengo drainage from the analysis. Because 99.7% of sites with sufficient coverage were validated, we also retained all fixed differences in the RNA-seq data set without sufficient coverage in the DNA-seq data set to validate (13.2% of fixed sites fell into this category).

Estimating Demographic Models, Simulating Neutral Distributions of F_ST, and Identifying F_ST Outliers

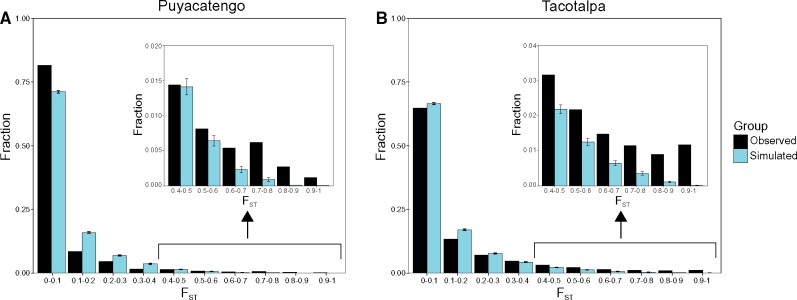
To identify sites with evidence for selection, we compared our empirical F_ST distribution to neutral simulations based on estimated demographic models. To estimate demographic models for each population, we used paired-end, pooled, whole genome sequencing data from a separate study (downloaded from the European Nucleotide Archive, accession PRJEB8912; Pfenninger et al. 2015). Each population included in this study was represented by one pool in the pooled sequencing data. Each pool included 100–200 individuals with an average genome-wide coverage of 20X. Raw read quality was inspected using FastQC (Andrews 2010), and reads were dynamically trimmed to quality 20 using Trim Galore! (Krueger 2014). Trimmed reads were then mapped to the platyfish genome using BWA (v 0.7.10) (Li and Durbin 2009). Following the PoPoolation2 manual (Kofler et al. 2011), SNPs were called on a per drainage basis using samtools mpileup (Li H et al. 2009), resulting in one mpileup file per drainage for comparison between adjacent sulfidic and nonsulfidic populations. Using mpileup2sync.pl (a script included in the PoPoolation2 distribution), mpileup files were converted to PoPoolation2 sync files containing allele counts for each site in the genome for each population. Using custom bash scripts (code for all analyses can be found at: https://github.com/jokelley/Pmex-Expression-vs-Selection; last accessed September 24, 2018), sites that were not biallelic or that contained fewer than 20 allele counts per population were removed. To construct a joint site frequency spectrum for each drainage, count data were then standardized such that each site that passed the filters had allele counts that added up to 20 per population. Sites were then binned based on counts in each population. The joint site frequency spectra were then used to estimate demographic models using δaδi (Gutenkunst et al. 2009). Demographic parameters were estimated on a per drainage basis, including migration rates, effective population sizes, divergence time, and population growth/decline rates. Twenty different models were tested; models differed in the parameters that were included (see supplementary table S2, Supplementary Material online, for details). We performed 20 iterations for each model, with each iteration starting at a different place in the parameter space. The best fit model was determined using the Akaike information criterion (Akaike 1974) with corrections for finite sample size (AICc) (Cavanaugh 1997). We used ΔAICc > 2 as our threshold for selecting the best model (see supplementary table S2, Supplementary Material online, for AICc values for the best run of each model). Migration parameters from δaδi were converted to number of individuals per year by assuming a generation time of six months (Jourdan et al. 2014; Riesch et al. 2014). Effective population size estimates were converted to number of individuals by assuming a mutation rate of 6.6×10⁻⁸ mutations per site per generation (Recknagel et al. 2013) (see supplementary fig. S1, Supplementary Material online, for the best fit demographic model for each drainage, and supplementary figs. S2 and S3, Supplementary Material online, for residuals between the models and the observed data). We then performed 1,000 neutral simulations of these models per drainage using ms (Hudson 2002), and calculated F_ST from simulated SNPs using msstatsFST (Thornton 2003; Eckert et al. 2010) (see simulated distributions in fig. 2). In order to take the relatively small sample size of our RNA-seq data set into account, we matched the number of individuals we sampled in the neutral distribution to the number of samples we had for our empirical distribution (n = 6 for the two Tacotalpa populations and the Puyacatengo nonsulfidic population, n = 5 for the Puyacatengo sulfidic population). We also matched the number of SNPs per drainage in our simulations to the number of SNPs in our empirical data set (50,394 in Tacotalpa, 42,607 in Puyacatengo). We calculated empirical F_ST values for each drainage (sulfidic vs nonsulfidic) using vcftools (Danecek et al. 2011). Sites in our empirical F_ST distributions that fell above the average 99.9th percentile across the 1,000 simulations per drainage were considered potentially under selection, as implemented in Reid et al. (2016).

Fig. 2.

—Simulated and observed F_ST distributions for SNPs between the adjacent sulfidic and nonsulfidic populations in the (A) Puyacatengo drainage (observed mean = 0.064) and in the (B) Tacotalpa drainage (observed mean = 0.111). Insets show the right-hand tail of the F_ST distributions for the Puyacatengo and the Tacotalpa drainages, respectively. Simulated F_ST distributions were generated using ms (Hudson 2002), based on the best fit demographic models estimated using δaδi (Gutenkunst et al. 2009). The distributions shown here are averages of 1,000-ms simulations. Error bars represent 95% confidence intervals for the simulated F_ST distributions.

Annotating Sites Putatively under Selection

After compiling our list of highly differentiated sites, which are putatively under selection for each drainage, we used the platyfish annotation in SnpEff (v 4.1) (Cingolani, Platts, et al. 2012) to functionally annotate the sites (supplementary tables S3 and S4, Supplementary Material online). In our analysis, we considered a gene putatively under selection if it had at least one site putatively under selection. Additionally, SnpSift (v 4.1) (Cingolani, Patel, et al. 2012) was used to separate the outlier SNPs based on whether they were nonsynonymous, synonymous, or noncoding but still within a gene (e.g., untranslated regions). We generated a list of genes that had at least one nonsynonymous site putatively under selection for each drainage (supplementary table S5, Supplementary Material online) so that we could test whether genes containing at least one nonsynonymous site under selection were more likely to be differentially expressed than genes containing only synonymous or noncoding sites putatively under selection.

Testing Whether Differentially Expressed Genes Were More Likely to Be under Selection than Expected by Random Chance

We compared the genes putatively under selection to the genes that were differentially expressed in each drainage (differentially expressed genes were obtained from Kelley et al. 2016). Only genes that had callable sites given our filtering (described above) were included in this analysis (6,361 genes in total), which means that genes that were expressed highly in one population but were either lowly expressed or not expressed at all in the adjacent population were not included in the analysis due to insufficient coverage. Out of the 6,361 genes, 360 were differentially expressed in the Tacotalpa and 274 were differentially expressed in the Puyacatengo. Additionally, we tested whether stratifying the data (including only nonsynonymous or synonymous sites, upregulated or downregulated genes, or fixed or not fixed sites) changed whether there was a significant correlation between differentially expressed genes and genes putatively under selection. Fisher’s exact test was used to determine whether each 2x2 contingency table differed significantly from the null hypothesis that the two categories were independent (P < 0.05). We also performed a Mantel–Haenzel test (Mantel and Haenszel 1959) for each drainage to determine whether there was a significant association between differentially expressed genes and genes putatively under selection after taking the stratification of the data into account. Additionally, we performed a Woolf test (Woolf 1955) and a Breslow–Day test (Breslow and Day 1980) to determine whether the relationship between differential expression and selection differed based on which stratification we tested. All tests were conducted in R. We also applied a Bonferroni correction given that multiple subsets of the data were evaluated for enrichment.

Gene Ontology Enrichment Analyses

To identify overrepresented Gene Ontology (GO) terms, we used WebGestalt (last updated May 20, 2014) (Wang et al. 2013). We used the human orthologs of genes that were expressed in our data set as the reference set. For each drainage, we performed GO enrichment analyses on two sets of genes. First, we used the set of genes putatively under selection in each drainage as a test set. Second, to identify enriched GO terms in candidate genes identified from both differential expression and selection analyses, we used the set of genes that were both putatively under selection and differentially expressed in each drainage as a test set. Each test set was generated using the SNPEff (v 4.1) (Cingolani, Platts, et al. 2012) platyfish annotation; these gene names were then converted to the human ortholog name using the biomart conversion tool (Smedley et al. 2015), because WebGestalt only uses gene names from model organisms. Therefore, only genes with a human ortholog were included in the analysis. Significantly overrepresented GO terms (represented by at least two genes) were identified at an adjusted P value <0.05 (Benjamini and Hochberg 1995).

Results

SNP Calling and Validating Fixed Differences between Adjacent Populations

We identified single nucleotide polymorphisms (SNPs) by mapping gill RNA-seq libraries from sulfidic and nonsulfidic populations from two different drainages (Puyacatengo and Tacotalpa) to the platyfish genome. A total of 98,564 SNPs passed our filtering criteria. To validate the quality of our RNA-seq SNP set, we tested for concordance between the low-fold DNA-seq and RNA-seq data sets. Of the 98,564 high-quality SNPs retained from the RNA-seq data set, 74,841 of those sites were polymorphic in the DNA-seq data set (75.9%). Of the 74,841 sites, 99.65% had the same alternative allele in the DNA-seq data set as they did in the RNA-seq data set. Of the 260 sites that did not have the same alternative allele, 133 had multiple alternative alleles, and 127 had different alternative alleles. At the sites that had the same alternative allele, the same genotype was inferred from both data sets 89.2% of the time (at sites where individuals had at least 4x coverage in the DNA-seq data set). For the SNPs identified in the RNA-seq data set that were not identified in the DNA-seq data set (23,723 sites), the majority were singletons in the RNA-seq data set (67%). There was no significant difference in average coverage for sites that had an alternative allele in the RNA-seq data set but not in the DNA-seq data set and sites that had alternative alleles in both data sets. Overall, these results provided confidence for using the RNA-seq data set for identifying sites under selection. Only one fixed difference (out of 326) was excluded, because it was highly differentiated in the RNA-seq data set and not highly differentiated in the DNA-seq data set (see Methods).

Sites with Evidence for Selection

We identified highly differentiated sites between adjacent sulfidic and nonsulfidic populations (two pairwise comparisons). Sites above the average 99.9th percentile across the 1,000 simulations per drainage of the F_ST distribution, including fixed differences in our data set, were considered potentially under selection. Average empirical F_ST (± standard error) values were 0.064 (± 0.006) and 0.111 (± 0.001) for the Puyacatengo and Tacotalpa, respectively, while the 99.9% cutoffs were 0.692 and 0.836 for the Puyacatengo and Tacotalpa, respectively (table 1). For comparison, the average simulated F_ST values were 0.069 (± 0.001) for the Puyacatengo and 0.108 (± 0.001) for the Tacotalpa. The average observed within population nucleotide diversities (π) at polymorphic sites were 0.112 (± 0.001) in the Puyacatengo nonsulfidic, 0.111 (± 0.001) in the Puyacatengo sulfidic population, 0.130 (± 0.001) in the Tacotalpa nonsulfidic, and 0.080 (± 0.001) for the Tacotalpa sulfidic. The average simulated π at polymorphic sites for each population were 0.108 (± 0.001) for the Puyacatengo nonsulfidic, 0.111 (± 0.001) for the Puyacatengo sulfidic, 0.123 (± 0.001) for the Tacotalpa nonsulfidic, and 0.084 (± 0.001) for the Tacotalpa sulfidic. For the Puyacatengo drainage, 429 empirical sites were above the average 99.9th percentile of the neutral F_ST distributions (fig. 2 and supplementary table S3, Supplementary Material online). For the Tacotalpa drainage, 614 empirical sites were above the average 99.9th percentile of the neutral distributions (fig. 2 and supplementary table S4, Supplementary Material online). Each empirical distribution contained more high-F_ST sites than the average neutral distribution (fig. 2). Six sites were under selection in both drainages, which is not significantly different than the number expected by chance (Fisher’s exact test, P = 0.18), and included one nonsynonymous site (supplementary table S5, Supplementary Material online). Two sites (including the nonsynonymous site) were in the SQRDL gene, a major component in H₂S detoxification (Hildebrandt and Grieshaber 2008), one was in a ribosomal processing gene (RRP36), one was in an unannotated gene (ENSXMAG00000006432), and two were in intergenic regions (which could be in novel, unannotated genes).

Table 1.

Number of Polymorphic Sites and F_ST Outliers in Pairwise Comparisons of Adjacent Sulfidic and Nonsulfidic Populations in Each Drainage

Drainage	Number of Polymorphic Sites	FST Outliers (FST<1)	Fixed Differences (FST=1)	Total Number of FST Outliers	Average Empirical FST
Tacotalpa	50,394	326	288	614	0.111
Puyacatengo	42,607	392	37	429	0.064

Genes Putatively under Selection

To better understand the putative functional effects of these genomic changes, we also summarized which genes had evidence for selection. Genes putatively under selection were defined as containing at least one outlier site, meaning that the same gene could be under selection in both drainages even if different sites were highly differentiated in each drainage. There were 129 genes with evidence for at least one highly differentiated site in the Puyacatengo drainage, and 338 such genes in the Tacotalpa drainage (supplementary tables S3 and S4, Supplementary Material online). Twelve genes had evidence for selection in both drainages, including SQRDL. Other notable genes putatively under selection in both drainages include another gene involved with sulfide detoxification (ETHE1) and a calcium-transporting ATPase (ATP2C1).

Comparison between Differentially Expressed Genes and Genes Putatively under Selection

To quantitatively determine whether differentially expressed genes were more likely to show evidence of selection than expected by chance, we performed Fisher’s exact tests. Contingency tables were constructed for each drainage (Puyacatengo: table 2, Tacotalpa: table 3). When considering the full data set, the observed contingency tables were significantly different from the expected (P < 0.001) for each drainage. There were more genes that were both putatively under selection and differentially expressed than expected in each drainage.

Table 2.

Contingency Table Analysis for Puyacatengo

Puyacatengo Drainage
Data Included		Under Selection	Not Under Selection	Odds Ratio	P Value
All genes	DE	18	256	3.78547	<0.0001**
	Not DE	111	5,976
Nonsynonymous	DE	9	265	5.55329	<0.0001**
	Not DE	37	6,050
Synonymous	DE	9	265	2.75966	<0.0001**
	Not DE	74	6,013
Upregulated	DE	12	117	5.36051	<0.0001**
	Not DE	117	6,115
Downregulated	DE	6	139	2.13827	0.0737
	Not DE	123	6,093
Fixed	DE	2	272	4.96569	0.0787
	Not DE	9	6,078
Not fixed	DE	16	258	3.71287	<0.00001**
	Not DE	100	5,987

Note.—The leftmost column denotes the genes that are included in specific categories. “All genes” includes all differentially expressed genes in the “DE” category and all genes with at least one site under selection in the “Under selection” category. “Nonsynonymous” includes only genes containing at least one nonsynonymous site under selection in the “Under Selection” category. “Synonymous” includes only genes containing no nonsynonymous sites under selection in the “Under Selection” category. “Upregulated” includes only genes that were upregulated in the sulfidic population in the “DE” category. “Downregulated” includes only genes that were downregulated in the sulfidic population in the “DE” category. “Fixed” includes only genes that contained at least one fixed difference between sulfidic and nonsulfidic populations in the “Under selection” category. “Not fixed” includes only genes that did not contain any fixed differences, but had other sites under selection in the “Under Selection” category. The second through fourth columns from the left show the observed tables for each set of genes. The fifth column shows the odds ratio, and the last column shows the P value.

^*P value <0.05, **P value <0.005.

Table 3.

Contingency Table Analysis for Tacotalpa

Tacotalpa Drainage
Data Included		Under Selection	Not Under Selection	Odds Ratio	P Value
All genes	DE	34	326	1.95449	0.0009**
	Not DE	304	5,697
Nonsynonymous	DE	13	347	2.88229	0.0015**
	Not DE	77	5,924
Synonymous	DE	21	339	1.57569	0.0662
	Not DE	227	5,774
Upregulated	DE	19	153	2.28512	0.0026**
	Not DE	319	5,870
Downregulated	DE	15	173	1.57036	0.0991
	Not DE	323	5,850
Fixed	DE	17	343	1.93328	0.0164*
	Not DE	150	5,851
Not fixed	DE	17	343	1.88177	0.0268*
	Not DE	154	5,847

Note.—Refer to the footnote of table 2 for further information.

^*P value <0.05, **P value <0.005.

In an attempt to better understand the patterns observed in the full data set, we subset the data to examine whether different groups of genes were more likely to show concordance than others. When we limited the genes under selection to only genes that had evidence for selection at a nonsynonymous site, the observed contingency tables were still significantly different than expected (tables 2 and 3). When considering only genes with synonymous sites (or sites within 3′- or 5′-untranslated regions), the observed and expected tables were significantly different for the Puyacatengo drainage, but not for the Tacotalpa drainage (tables 2 and 3). When we partitioned the differentially expressed genes based on whether they were upregulated or downregulated in sulfidic environments, observed contingency tables were significantly different than expected for upregulated genes in each drainage, but not for downregulated genes in each drainage (tables 2 and 3). In every comparison described in this section, the number of genes that were simultaneously under selection and differentially expressed was greater than expected, even in the cases where the observed contingency tables were not significantly different from the expected table. We also tested whether—given the stratification the data—there was a significant association between differentially expressed genes and genes putatively under selection with a Mantel–Haenszel test (Mantel and Haenszel 1959). Mantel–Haenszel tests were significant for each drainage (P = 1.2×10⁻⁹ for Tacotalpa, P = 2.2×10⁻¹⁶ for Puyacatengo). Lastly, we tested whether there were significant differences in the odds ratios between the stratifications (i.e., the null hypothesis was that the associations were the same regardless of which categories we were testing) using a Woolf test (Woolf 1955) and a Breslow–Day test (Breslow and Day 1980). Neither Woolf tests (P = 0.62 for Tacotalpa, P = 0.43 for Puyacatengo) nor Breslow–Day tests (P = 0.62 for Tacotalpa, P = 0.41 for Puyacatengo) were significant, indicating that subsetting the data generally had no effect on the significance of the relationship between differential expression and selection.

Gene Ontology Enrichment Analyses on Genes Putatively under Selection in Each Drainage

We identified GO terms that were enriched in the set of genes putatively under selection in each drainage using WebGestalt (last updated May 20, 2014) (Wang et al. 2013). We detected seven significantly enriched GO terms in the set of genes putatively under selection in the Puyacatengo drainage (zero biological process, four molecular function, and three cellular component), all of which were enriched only in this drainage (supplementary table S6, Supplementary Material online). Of the seven significantly enriched GO terms, three were related to mitochondrial cellular components (e.g., respiratory chain complex IV), one was the molecular function GO term cytochrome-c oxidase activity, and two were likely related to sulfide detoxification (oxidoreductase activity, acting on a heme group of donors [molecular function], and oxidoreductase activity, acting on a heme group of donors, oxygen as acceptor [molecular function]).

There were 15 significantly enriched GO terms in the set of genes putatively under selection in the Tacotalpa drainage (0 biological process, 3 molecular function, and 12 cellular component). All 15 of these GO terms were enriched solely in this drainage (supplementary table S6, Supplementary Material online). Five of these terms were related to cell junctions (e.g., adherens junction [cellular component] and cell junction [cellular component]), while four of these terms were related to adhesion (e.g., cadherin binding involved in cell–cell adhesion [molecular function] and focal adhesion [cellular component]). There was one enriched cellular component GO term that is likely related to sulfide detoxification (oxidoreductase complex).

Genes with Evidence for Both Selection and Differential Expression

To identify genes that were differentially expressed and contained highly differentiated sites in both drainages, we examined the overlapping results from the two separate analyses. A total of 18 genes were both differentially expressed and under selection in the Puyacatengo drainage, whereas 34 genes fit the same criteria in the Tacotalpa drainage. Only two genes showed evidence of both differential expression and selection in both drainages (supplementary table S7, Supplementary Material online): ETHE1 and SQRDL. As mentioned previously, both of these genes are involved in H₂S detoxification (Hildebrandt and Grieshaber 2008).

For each drainage, we also tested for overrepresented GO terms in genes that were putatively under selection and differentially expressed to determine whether any biological processes were affected by both mechanisms more than expected by chance. Only one GO term was significantly overrepresented in this set of genes in the Puyacatengo drainage (hydrogen sulfide metabolic process [biological process]) and four in the Tacotalpa drainage (cofactor metabolic process [biological process], sulfur compound metabolic process [biological process], sulfide oxidation [biological process], and sulfide oxidation, using sulfide: quinone oxidoreductase [biological process]) (supplementary table S8, Supplementary Material online). No overrepresented GO terms were shared between the drainages in genes that were both putatively under selection and differentially expressed. There were, however, overrepresented GO terms related to sulfur in genes that were putatively under selection and differentially expressed for each drainage individually.

Discussion

Recent studies on differential expression (Kelley et al. 2016) and selection (Pfenninger et al. 2015) between sulfidic and nonsulfidic populations of Poecilia mexicana made this system ideal for comparing inferences about adaptive mechanisms based on differential expression and selection analyses. Though studies of molecular adaptation typically rely on either differential expression or selection analyses from RNA-seq data, we found that considering results from both analyses gave a more comprehensive view of how separate populations have adapted to independent, hydrogen-sulfide-rich environments. Our RNA-seq approach allowed us to test whether differentially expressed genes were enriched for genes putatively under selection. Though we had relatively small sample sizes (like many RNA-seq studies), we argue that we have minimized this issue in our outlier analyses by comparing our empirical F_ST values to a neutral distribution of F_ST values from samples of the same size from neutral simulations. Unlike results from other systems (Nielsen et al. 2005; Li YD et al. 2009; Hodgins et al. 2016), we found more genes that simultaneously displayed signatures of differential expression and selection than expected by chance.

Qualitatively, Do the Results from an Outlier Scan Match Those from a Differential Expression Analysis?

Overall, analyses of sites putatively under selection and differential expression led to similar conclusions about the physiological mechanisms putatively underlying adaptation to H₂S. As evidenced in both this study and other studies (Tobler et al. 2014; Kelley et al. 2016), changes in genes associated with H₂S detoxification appear to underlie adaptation to toxic environments in P. mexicana populations. In a previous study on differential expression between adjacent P. mexicana populations that used the same RNA-seq data as this study, upregulated genes in sulfidic populations were enriched for several GO terms related to sulfide detoxification, such as sulfide oxidation using sulfide: quinone oxidoreductase (biological process) and hydrogen sulfide metabolic process (biological process) (Kelley et al. 2016). From our present study, we also identified enriched GO terms related to sulfide detoxification in each drainage (e.g., oxidoreductase activity, acting on a heme group of donors, oxygen as acceptor [molecular function] in the Puyacatengo and oxidoreductase complex [cellular component] in the Tacotalpa) (supplementary table S6, Supplementary Material online), indicating that the general conclusions drawn from these separate analyses are similar.

In both drainages, we identified two genes involved in sulfide detoxification that were potentially under selection: SQRDL (sulfide: quinone oxidoreductase) and ETHE1 (sulfur dioxygenase). SQRDL was also identified as a target of selection in a recent study on these same populations (Pfenninger et al. 2015). These genes are two of the main components of the sulfide: quinone oxidoreductase (SQR) pathway that detoxifies H₂S (Hildebrandt and Grieshaber 2008; Shahak and Hauska 2008). The only two genes that were differentially expressed and putatively under selection in both drainages were these two genes (ETHE1 and SQRDL), further supporting the hypothesis that major changes in sulfide detoxification underlie adaptation in these populations. Importantly, expression differences in genes involved in H₂S detoxification are retained even when individuals are raised in laboratory environments that lack H₂S (Tobler et al. 2014; Passow, Henpita, et al. 2017), indicating that the upregulation of these genes is not simply a plastic response to H₂S exposure.

Our data suggest that mitochondrial electron transport chain genes (including subunits of NADH dehydrogenase and COX) are putatively under selection in only one of the two drainages (Puyacatengo). Several mitochondrial genes involved in the electron transport chain (three subunits of COX, two subunits of NADH dehydrogenase, and CYTB) contain highly differentiated SNPs between adjacent populations in the Puyacatengo drainage. Eight out of ten of these SNPs were nonsynonymous changes. None of these genes, however, contain highly differentiated sites in the Tacotalpa drainage (though one nuclear encoded subunit of COX contains a highly differentiated site). While certain components in the electron transport chain were consistently upregulated in sulfidic populations (including cytochrome c), there were no mitochondrially encoded subunits of COX that were differentially expressed between sulfidic and nonsulfidic populations in either of the drainages (Kelley et al. 2016). Based on these findings, differential expression of COX subunits may be less important than changes in the amino acid sequence of the proteins. Fixed differences in amino acid sequence of COX1 between sulfidic and nonsulfidic populations in the Puyacatengo drainage have been shown to reduce binding of H₂S to the COX active site (Pfenninger et al. 2014). In the case of COX1 in the sulfidic Puyacatengo population, it appears that adaptation has been mediated by changes in protein structure rather than changes in expression. However, upregulated genes were enriched for genes involved in the transfer of electrons from cytochrome c to oxygen (Kelley et al. 2016), so changes in expression of other genes associated with the electron transport chain may be adaptive. Cytochrome c can hold on to electrons until COX can process them (Hatefi 1985; Saraste 1999), so Kelley et al. (2016) hypothesized that the upregulation of cytochrome c could act as a buffer against changes in the stoichiometric balance of the complexes involved in the electron transport chain that can occur due to the blockage of COX by H₂S (Lagoutte et al. 2010).

Interestingly, populations in the Puyacatengo drainage are more genetically similar than the populations from the Tacotalpa drainage (fig. 2; Plath et al. 2013; Pfenninger et al. 2015; also see Figure S6 from Passow et al. 2017), implying that the Puyacatengo sulfide spring may have been colonized more recently and/or that there is more gene flow between adjacent populations in the Puyacatengo. Our best fit demographic models imply that the higher genetic similarity between populations is due to a more recent colonization of the Puyacatengo sulfide spring (supplementary fig. S1, Supplementary Material online). Given the more recent colonization of the Puyacatengo sulfide spring, one hypothesis would be that fewer pathways to adaptation (e.g., sulfide detoxification and/or changes in cellular respiration) would be utilized in the Puyacatengo compared with the Tacotalpa. This is exactly the opposite of what our data suggests, as it appears that changes in both biological pathways occurred in the Puyacatengo, whereas changes primarily in sulfide detoxification seem to underlie adaptation in the Tacotalpa sulfidic population. HIG1, which has been shown to be a positive regulator of COX (Hayashi et al. 2015), was also putatively under selection and differentially expressed in the Puyacatengo drainage, whereas it was only differentially expressed in the Tacotalpa drainage. An increase in COX activity due to more frequent interactions with HIG1 may be sufficient for sulfidic individuals in the Tacotalpa to overcome H₂S toxicity. Another nonmutually exclusive hypothesis is that individuals from the sulfidic Tacotalpa population are more efficient at H₂S detoxification than individuals from the Puyacatengo sulfidic population. These changes (whether on their own or in concert) may have been sufficient to render structural changes to COX unnecessary in the sulfidic Tacotalpa population. Enzyme activity assays on SQRDL and ETHE1 from these populations will illuminate any differences between populations in how effectively they detoxify H₂S.

Genes putatively under selection and differentially expressed were enriched for GO terms related to H₂S detoxification in both drainages. While no GO terms were enriched simultaneously in both drainages, hydrogen sulfide metabolic process (biological process) was enriched in genes both differentially expressed and putatively under selection in the Puyacatengo, and sulfide oxidation, using sulfide: quinone oxidoreductase (biological process) was enriched in genes both differentially expressed and under selection in the Tacotalpa (supplementary table S8, Supplementary Material online). There is evidence to suggest that increases in both activity (Hildebrandt and Grieshaber 2008) and expression (Liu et al. 2015) of sulfide detoxification enzymes may be adaptive responses to life in high H₂S concentrations. Our analysis suggested that sulfidic P. mexicana populations have higher expression levels of sulfide detoxification genes, and that those detoxification enzymes are potentially more efficient in sulfidic populations than nonsulfidic populations. While all of the enriched GO terms in the genes putatively under selection in the Puyacatengo were at least loosely related to either cellular respiration/mitochondrial components or sulfide detoxification, there were several enriched GO terms in the genes putatively under selection in the Tacotalpa that were likely not related to either of those processes, including multiple related to cell adhesion (supplementary table S6, Supplementary Material online). H₂S has been shown to reduce cell adhesion in human cells (Szabo 2007; Gobbi et al. 2009; Perna et al. 2013), indicating that changes in genes involved in cell adhesion may have been important for adaptation to the sulfidic environment solely in the Tacotalpa. No GO terms containing the word “adhesion” were enriched in the differentially expressed genes in the Tacotalpa (see Tables S5 and S6 in Kelley et al. 2016), so perhaps changes in the actual sequence rather than expression levels were more functionally relevant for dealing with the effects of H₂S. This evidence for selection at multiple levels highlights the need for integrative studies to fully understand the multifaceted nature of adaptation to novel environments.

Overall, both approaches—the identification of differentially expressed genes and the differentiation outlier approach—led to the conclusion that changes in sulfide detoxification and the electron transport chain are important for adaptation to extremely sulfidic environments. While specific components of the electron transport chain seem more important to adaptation depending on which approach was employed, the results imply that the general conclusions from these two different analyses are similar for this particular system. We argue that performing both analyses led to a more comprehensive understanding of the molecular basis of adaptation to extremely sulfidic environments, and we expect this to be true of any other studies attempting to better understand adaptation to novel conditions.

Are Differentially Expressed Genes More Likely to Be under Selection than Expected?

When considering all of the data for each drainage, we detected signatures of selection in differentially expressed genes more frequently than expected by chance for each drainage. Our Woolf tests and Breslow–Day tests indicated that there were no significant differences in the odds ratios between stratifications for both drainages, essentially indicating that the general result of an association between genes putatively under selection and differentially expressed genes holds regardless of how we subset the data. Overall, these results imply that certain physiological processes may have been under such strong selection that both differential expression and changes in protein sequence were required for colonization of these new, harsh environments, or that evolutionary constraint led to drastic changes in a few biological pathways. We found similar relationships between differentially expressed genes and genes potentially under selection in both drainages despite growing evidence that the populations are on independent evolutionary trajectories (e.g., COX modifications in the Puyacatengo, but not in the Tacotalpa) (Pfenninger et al. 2014, 2015). For the most part, different genes led to the correlation in each drainage, implying that the repeated observation of a correlation between differential expression and selection in the two drainages was not merely a result of parallel evolution.

There are a few scenarios that could lead to the inference of differential expression and selection in the same gene. First, neutral differences in the sequence of a gene could be linked to adaptive changes in nearby regulatory regions that led to differential gene expression (Sato et al. 2016). Second, there could simultaneously be a beneficial change in protein structure and the amount of protein produced. In this case, we might expect more highly differentiated nonsynonymous sites in differentially expressed genes, since nonsynonymous affect the structure of the protein (Studer et al. 2013). Third, synonymous changes may affect translation rate (Gouy and Gautier 1982; Hershberg and Petrov 2008), meaning that selection could be simultaneously acting on both transcription (detected via differential expression analyses) and translation rates. Fourth, synonymous changes can affect the stability of mRNAs (Trotta 2013; Presnyak et al. 2015), implying that synonymous changes could be selectively favorable because of their direct impact on mRNA levels. Given that we found no significant difference in odds ratios for our different stratifications for either of our drainages, it is possible that broad patterns of selection in the Puyacatengo and the Tacotalpa are due mostly to linkage with adaptive changes in regulatory regions or that some combination of the mechanisms listed above led to an apparent correlation between selection and expression.

Few other studies have reported a positive correlation between differential expression and gene sequence divergence (with a study comparing ragwort populations; Chapman et al. 2013, and another comparing frog species; Sartor et al. 2006, being notable exceptions), but that may partially be explained by differences in methodology. Importantly, other studies have typically relied on detecting positive selection using a comparison between the rate of nonsynonymous substitutions and the rate synonymous substitutions (d_N/d_S ratios) (Li YD et al. 2009; Hodgins et al. 2016). A d_N/d_S ratio significantly >1 implies a gene has been subject to positive selection. This analysis was designed for analyzing sequence differences between divergent species, and this ratio is highly sensitive to violations of this principle, for example, when applied to population data (Kryazhimskiy and Plotkin 2008). Because our populations of interest are the same species (P. mexicana) that have recently diverged (Pfenninger et al. 2014), the d_N/d_S approach is inappropriate for detecting selection in this system. We instead used a site-based F_ST outlier approach to identify putative genes under selection; the differences in approaches and divergence times between species compared may explain why we found a correlation between differential expression and selection whereas other studies generally have not.

Another possibility is that this correlation is relatively unique to the P. mexicana system, or specifically that this correlation is highly dependent on the target tissue selected (gill) and the presumed selective pressure (H₂S). A study of differential expression between these populations in various tissues found the highest number of differentially expressed genes in gill tissue, and that genes involved in sulfide detoxification were primarily differentially expressed in the gills rather than in the brain or liver (Passow, Brown, et al. 2017). Based on these results, the authors suggested that the majority of sulfide is detoxified in the gill tissue (Passow, Brown, et al. 2017), therefore it is possible that gill-specific changes in gene expression led to our detection of a correlation between differential expression and positive selection. Genes in humans with highly tissue specific expression have undergone more coding sequence changes than genes that are expressed in multiple tissues (Haygood et al. 2010), and tissue specificity was positively correlated with signatures of positive selection in comparisons among three sunflower species (Renaut et al. 2012). Since expression changes in potentially vital pathways were found primarily in gill tissue, changes in DNA sequence in these genes may have been less constrained than for genes that increased in expression across multiple tissues. Our focus on gill tissue may have led to a better chance of detecting a correlation between differential expression and positive selection. Alternatively, strong selection should lead to higher levels of linkage disequilibrium (Smith and Haigh 1974), meaning that linkage between favorable changes in regulatory regions and neutral variants within gene sequences may generally be more likely during transitions into extreme environments, regardless of how broadly across tissues a gene is expressed. Future work examining linkage between changes in regulatory regions and F_ST outliers within gene sequences could help explain these findings.

Conclusions

Analyzing both differential expression and selection on gene sequences in population pairs of sulfidic and nonsulfidic Poecilia mexicana from southern Mexico led to a more complete understanding of how the sulfidic populations survive in such toxic environments. Changes in sulfide detoxification at both the expression and sequence levels appear to underlie adaptation in both sulfidic populations, whereas sequence changes in mitochondrially encoded cellular respiration genes appear to contribute to adaptation in only one of the two sulfidic populations (Puyacatengo). Additionally, we found more genes that were differentially expressed and putatively under selection than expected by random chance, implying a potential mechanistic link between expression levels and changes in gene sequence during colonization of sulfidic environments. Our study demonstrates how incorporating multiple molecular analyses improves our understanding of how populations adapt to novel, extreme environments.