Stochastic modeling of tumor progression and immune evasion

Abstract

It is now well-established that the host’s adaptive immune system plays an important role in identifying and eliminating cancer cells in much the same way that intracellular pathogens are cleared during an adaptive immune response to infection. From a therapeutic standpoint, the adaptive immune system is unique in that it can co-evolve alongside a developing tumor. Tumor acquisition of immune evasive phenotypes, such as class-I MHC down-regulation, remains a major limitation of successful T-cell immunotherapy. Here, we consider a population dynamical model coupling tumor and adaptive immune compartments in order to study the dynamics and survival of an evolving threat when faced with adaptive immune pressure. We demonstrate that predicted optimal growth strategies depend on whether or not the threat may acquire an immune-evasive phenotype as well as the mode of immune detection. We parameterize adaptive immune functioning by T-cell turnover and repertoire diversity and predict that decreases in the latter quantity which occur in advanced age may substantially affect the ability to recognize, and therefore control, an immune evasive threat like cancer. This framework recapitulates general features of age-dependent AML incidence, thereby providing a probable association between cancer frequency and adaptive immune functioning. Lastly, we quantify therapeutic efficacy of adjuvant immunotherapeutic strategies, and predict their benefits and limitations with regard to handling immune evasion. Our model generates survival behavior consistent with known growth-dependent characteristics, and serves as a first attempt at modeling stochastic cancer evolution alongside an adaptive immune compartment.

Graphical Abstract

1. Introduction

The lack of successful treatment options that lead to durable remission outcomes still remains an ongoing challenge for curing many malignancies. However, there have been significant advances made most recently in targeted and immune therapeutic strategies (Couzin-Frankel, 2013). It is now well-established that the CD8+ T-cell compartment of the human adaptive immune system plays an integral role in immunoediting, and tumor progression therefore necessarily requires successful evasion of adaptive immune surveillance (Fridman et al., 2011; Dunn et al., 2002). Immunotherapy is responsible for recent breakthroughs in cancer treatment and encompasses strategies aimed at enhancing the patient’s immune system, via tumor antigen vaccines (Fritsch et al., 2014; Ott et al., 2017; Hellmann and Snyder, 2017; Sahin et al., 2017), immune checkpoint inhibition (Alsaab et al., 2017; Leach et al., 1996), and introduction of tumor-specific immune cells, as is the case in CAR T-cell therapy (Sadelain et al., 2017; Wang and Rivière, 2016; Martin et al., 2016).

Despite these advances, tumors may acquire treatment- resistant clones during disease progression (Iwasa et al., 2006), thus limiting treatment efficacy. Cancer cells exploit a variety of strategies that facilitate CD8+ T-cell immune evasion (Bronte and Mocellin, 2009), including up-regulation of immune inhibitory genes like PD-L1 and HLA-G (Herbst et al., 2014; Driessens et al., 2009; Sheu and Shih, 2010; Lin and Yan, 2015), reduced immunoproteasome expression (Tripathi et al., 2016), and complete evasion of CD8+ recognition via loss of MHC-I (Garrido et al., 2016; Carretero et al., 2008; del Campo et al., 2014; Straten and Garrido, 2016). Such evasive tactics occur alongside active immunosurveillance by an adaptive T-cell repertoire. Naïve T-cell turnover can, in theory, lead to recognition of a dividing cancer cell population prior to acquisition of an immune-evasive phenotype. Previous studies have considered systems level interactions between the tumor and host adaptive immune system (Son-tag, 2017; Khailaie et al., 2013; Andrew et al., 2007; Nani and Ouztöreli, 1994; Kirschner and Panetta, 1998), while a separate effort has gone into understanding the acquisition of drug-resistant subpopulations during clonal evolution (Iwasa et al., 2006; Michor et al., 2004). At present, the temporal dynamics of acquired immune evasion on tumor development under adaptive immune pressure remains uncharacterized. Filling this gap is of fundamental importance to better understand tumor progression. Additionally, an improved quantitative framework for describing the successes, and failures, of adaptive immune targeting of cancer cells would enable more accurate predictions of treatment success rates.

Here, we propose a foundational model of adaptive immune system and tumor co-evolution wherein tumor cells may be recognized by the immune system, but may also acquire an immune-evasive phenotype. We account for key empirical behavior, including the growth-threshold conjecture which predicts initiation of an immune response depends on threat net growth rates instead of absolute threat size (Arias et al., 2015; Pradeu et al., 2013; Grossman and Paul, 1992; Johansen et al., 2008). For threats like cancer which may acquire an immune evasive phenotype, we show that the model supports the experimental observation of ‘sneak-through’ wherein threats with either large or small net growth rates have a preferential advantage over their intermediate-growth counterparts (Bocharov et al., 2004). We apply this model to study AML incidence as a function of immune turnover and repertoire diversity, and accurately characterize increased incidence as a result of an aging immune system in addition to chronic immunosuppression. We conclude our analysis by quantifying the benefit of certain types of T-cell immunotherapy and predicting treatment-specific advantages based on tumor growth rates and patient immune status.

2. Model Development

We conceptualize the dynamics between a foreign threat and the host immune system as a time-continuous birth process, where the state variable, X, represents the total number of cancerous or infected cells. In our model, these cells grow at net rate r per cell until either exceeding a critical size, M ≫ 1, or until the immune system mounts a response at a (possibly random) population size X = m and time S₁. If recognized, the population undergoes net death at a per-cell rate of $\tilde{r}=d-r$ so that d characterizes per-cell immune system killing rate. We assume d is large enough to handle threats with a variety of growth rates so that r < d always. States 0 and M + 1 are absorbing. A more precise model would separately track birth and death rates both before and after treatment. We have opted for this simpler form to enable analytic investigations.

2.1. Static Threats

Static threats are those unable to acquire an immune evasive phenotype. These dynamics are most appropriate for investigating intracellular microbial pathogens that grow, divide, and infect host cells. In this case the process evolves according to the following transitions:

$$\begin{array}{ll}t<S_1:\hfill & x\to x+1\text{ at rate }rx\hfill \\ t\ge S_1:\hfill & x\to x-1\text{ at rate }\tilde{r}x\hfill \end{array}$$ (1)

2.2. Dynamic Threats

Dynamic threats, including cancer, may randomly acquire an immune evasive phenotype that enables its members to avoid immune recognition targeting the initial population. We therefore consider two cell populations: a non-evasive population, X₁, and an immune evasive population, X₂ that broadly represents cells adopting a variety of CD8+ T-cell evasion strategies commonly observed during cancer progression. We assume that immune evasive cells are randomly acquired at rate μ ≪ 1 per cell division. Transitions are described by:

$$\begin{array}{l}t\text{ < }{S}_{\text{1}}\text{:}\\ \left(x_1,x_2\right)\to \left(x_1,x_2+1\right)\text{ at rate }\mu r{x}_1+r{x}_2\\ \left(x_1,x_2\right)\to \left(x_1+1,x_2\right)\text{ at rate }(1-\mu )r{x}_1\approx r{x}_1\\ t\ge S_1:\\ \left(x_1,x_2\right)\to \left(x_1,x_2+1\right)\text{ at rate }\mu r{x}_1+r{x}_2\\ \left(x_1,x_2\right)\to \left(x_1-1,x_2\right)\text{ at rate }[d-(1-\mu )r]x_1\approx \tilde{r}{x}_1\end{array}$$ (2)

We assume that successful immune responses occur quickly and are not limited at large population sizes for both the static and dynamic cases.

2.3. Detection Limit

We assume that immune recognition at size X₁ = m may only occur after the population reaches a lower detection limit, m₀, based either on the population size or the population total net growth rate. We will refer to the former assumption as the size threshold or size-limited case (m₀ = m_c), and the latter as the growth-threshold or growth-limited case (m₀ = m₀(r) such that the total net growth rate first exceeds R), where appropriate. The growth-threshold conjecture is supported by empirical and theoretical observations (Sontag, 2017; Arias et al., 2015; Pradeu et al., 2013; Grossman and Paul, 1992; Johansen et al., 2008). We will argue later that a size-limited model is perhaps most appropriate for modeling CAR T-cell infusions, as CAR T self-activation is engineered directly in this case.

2.4. ·Recognition Mode

In the primary case of interest we model the response of an adaptive immune compartment whose present and future CD8+ T-cell repertoire may contain a T-cell capable of recognizing an immune susceptible threat X₁. There is continual opportunity for the sensitive population to be recognized as its growth trajectory exceeds m₀ and continues growing to final size M. We refer to this case hereafter as stochastic or adaptive recognition. Recognition depends on both the T-cell repertoire and turnover of new T-cell clones. The population at size m₀ evades the current immune repertoire, due in part to a lack of sufficient levels of detectable antigen or recognizing T-cells, with a background escape probability p_b, which we use to represent the clonal diversity of the TCR repertoire (larger p_b implies lower diversity). We model the arrival of a recognizing T-cell clone as a Poisson process with rate k, corresponding to the thymic turnover rate of naïve CD8+ T-cells. It is also convenient to analyze a simpler process wherein a growing threat is (deterministically) recognized at threshold size m₀, which applies for example to innate immune recognition of, or memory reactivation to, a previously encountered threat. We refer to this case as deterministic recognition.

2.5. Mathematical Analysis

Here we provide a broad outline of our general strategy, with the primary goal of calculating the probability that a threat either escapes immune detection, or acquires an evasive phenotype, or is controlled by the immune system. Complete derivations are included in the SI. We let E_e denote the event that a threat escapes recognition and exceeds size M with corresponding probability P_e. For dynamic threats, Ε_𝜇 denotes the event that an immune evader arrives with probability Ρ_𝜇. All events may be partitioned by: E_e,μ ≡ E_e ∩ E_μ, $E_{e,{\mu }^c}\equiv E_e\cap E_{\mu }^c,E_{e^c,\mu }\equiv E_e^c\cap E_{\mu }$, and $E_{e^c,{\mu }^c}\equiv E_e^c\cap E_{\mu }^c$ with corresponding probabilities P_e,μ,$P_{e,{\mu }^c},P_{e^c,\mu }$ , and P_ι (a threat loses if it neither escapes nor acquires an evader, see SI Sec. S5).

Pe is determined by relating the immune turnover and size parameters to recognition probabilities (Sec. 3.1). This may be obtained by solving for the probability that detection occurs at size m ≥ m₀, denoted by p_r (m; m₀) (SI Sec. S3). The calculation of $P_{e^c,\mu }$ is more involved, and so we begin first by evaluating this quantity under deterministic recognition at fixed size m, denoted $P_{e^c,\mu }$ . We recall that S₁ denotes type-1 arrival time. If τ₂ is the type- 2 arrival time, and ${\tilde{S}}_1$ the type-1 extinction time, then the probability of interest is of the form

$$\begin{gathered} P_{e^c,\mu }(m)=\mathbb{P}\left({\tau }_2<S_1|X_1\left(S_1\right)=m\right) \\ +\mathbb{P}\left(S_1\le {\tau }_2<{\tilde{S}}_1|X_1\left(S_1\right)=m\right), \end{gathered}$$ (3)

with both terms amenable to exact calculation by conditioning on the exponential inter-arrival times of each birth/death event (SI Sec. S5.1). The corresponding probability under adaptive recognition with variable detection size, denoted $P_{e^c,\mu }\left(m_0\le m\le M\right)$ , may be calculated by taking weighted averages of each estimate conditioned on size m recognition via

$$P_{e^c,\mu }\left(m_0\le m\le M\right)=\sum _{m=m_0}^M{P}_{e^{c{,}_{\mu }}}(m)\cdot p_r\left(m;m_0\right),$$ (4)

provided m₀ < M (SI Sec. S5.3). In all cases, P_ι is calculated indirectly via

$$P_l=1-\left(P_{e^c,\mu }+P_e\right).$$ (5)

We obtain a solution in the adaptive recognition mode by weighting by the distribution of recognition sizes, calculated subsequently.

Under deterministic recognition, we also characterize the mean first time of type-2 arrival conditioned on acquired evasion, given by $T_{\mu }(m)\equiv \mathbb{E}\left[{\tau }_2|{\tau }_2<{\tilde{S}}_1\right]$ . Using the usual indicator random variable notation

$$I_{\left[{\tau }_2<{\tilde{S}}_1\right]}=\{\begin{array}{ll}1,\hfill & {\tau }_2<{\tilde{S}}_1;\hfill \\ 0,\hfill & {\tau }_2\nless {\tilde{S}}_1.\hfill \end{array}$$ (6)

This quantity may be calculated using the definition of conditional probability

$$T_{\mu }(m)=\frac{\mathbb{E}\left[{\tau }_2{I}_{\left[{\tau }_2<{\tilde{S}}_1\right]}\right]}{\mathbb{P}\left({\tau }_2<{\tilde{S}}_1\right)},$$ (7)

and is derived to first order in μ following a similar strategy for characterizing $P_{e^c,\mu }$ , here instead assuming each inter-arrival time is well-characterized by its mean value (SI Sec. S5.2). This framework permits analytical comparisons between predicted evasion behavior for the various assumptions on detection limit and recognition mode. We apply this framework to study AML, a hematological malignancy, as our model disease due to its low mutation rate, relative immune accessibility, and rapid growth. We compare model predictions to AML incidence data, comparing our theory with the alternative ‘multi-stage’ theory of cancer incidence (Armitage and Doll, 1954), and conclude by expanding the analysis to predict post-immunotherapy treatment success probabilities.

3. Tumor Progression

The following sections present the main findings of our analysis. Full mathematical details are provided in the SI. In an effort to organize subsequent analyses, we subdivide outcomes of the process based on relevant events.

3.1. Adaptive repertoire and detection limit determine escape probability

This section focuses on static threats (Ρ_𝜇 = 0). If recognition is deterministic, then P_e = 0 trivially. Adaptive recognition in contrast permits a threat to grow past minimal detection before recognition and subsequent elimination (Fig. 1), as long as m₀ < M (for large simulation trajectories illustrating mean-variance behavior, see Fig. 1 in (George and Levine, 2018)). In this case a population’s survival probability is inversely related to its mean sojourn time on {m₀,..., M}, given by

$$\Delta t_s(r)\approx \log \left(M/m_0\right)r^{-1}.$$ (8)

Recognition probability at size m is given by

$$p_r\left(m;m_0\right)\approx \{\begin{array}{cc}0,& m<m_0;\\ 1-p_b{e}^{-\frac{k}{r{m}_0}},& m=m_0;\\ p_b\left(1-e^{-\frac{k}{rm}}\right){\left(\frac{m_0}{m}\right)}^{\frac{k}{r}},& m_0<m\le M.\end{array}$$ (9)

From this formula, we observe that the escape probability to size m > m₀ is

$$p_e\left(m;m_0\right)=p_b{\left(\frac{m_0}{m}\right)}^{k/r}.$$ (10)

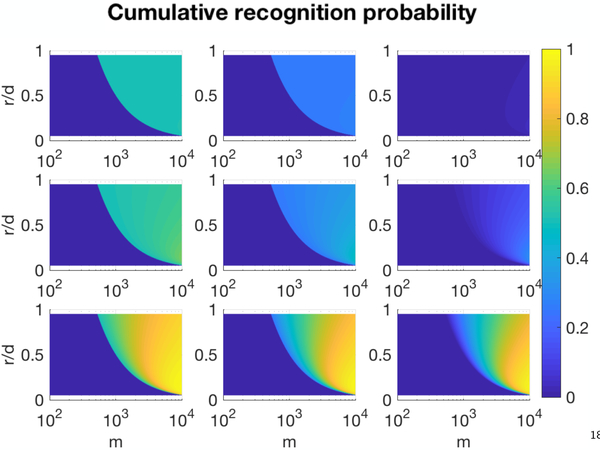
It is clear from the above that optimal growth rates of immune evaders balance the size of earliest detection with the amount of time spent under immunosurveillance. Faster growing threats always have higher escape probabilities if detection is size-limited. However, under growth-limited detection the existence of a slow-growth window r ϵ (0, eR/M) enables threats with slow growth rates to increase escape by minimizing surveillance time (Table S1). Thus, growth-limited detection of a static threat is consistent with the phenomena of ‘sneak-through’ (Arias et al., 2015; Pradeu et al., 2013; Grossman and Paul, 1992; Johansen et al., 2008; Bocharov et al., 2004). Analogously, if m_c > M in the size-limited case, then clearly threats of all growth rates escape detection. Cumulative recognition probabilities, given by 1 - p_e (m; m₀), are presented for a variety of immune parameters (Fig. 2), indicating the relevance of repertoire diversity and T-cell turnover to tumor recognition.

Figure 1:

Dynamics under adaptive immune detection. Stochastic population trajectories obeying Eqs. 1 that are ultimately recognized and eliminated. Red trajectories illustrate recognition at detection limit m₀ (dashed line) (r = 0.1, d = 0.2, m₀ = 10², p_b = 0.75, k = 0.1).

Figure 2:

Growth-limited cumulative recognition. Cumulative recognition probability 1 - pe (m; m₀) as a function of population size m and relative growth rate r/d for various values of immune turnover (rows bottom-to-top: k={10⁻¹, 10⁻², 10⁻³}) and repertoire diversity (columns left-to-right: p_b={0.5, 0.75,1.0}) (d = 0.2, R = 10²).

3.2. Cancer ‘sneak-through’ predicted by detection limited by growth, not size

Non-escape $E_e^c$ occurs with certainty under deterministic recognition. However, a dynamic threat may acquire an immune evader $\left(\text{event }{E}_{e^c,\mu }\right)$ . The probability of evader acquisition as a function of deterministic detection at size m is given by

$$P_{e^c,\mu }(m)=1-{(1-\mu )}^{m-1}{\left(\frac{d-(1-\mu )r}{d-(1-2\mu )r}\right)}^m.$$ (11)

This arrival probability is plotted in Fig. 3 alongside mean evader arrival times as a function of net growth rates r for size- and growth-limited detection assumptions (see SI for full details). Immune evaders rarely emerge for slow-growing threats under size-limited detection, and only do so on average over large time scales. This contrasts with growth-limited detection, for which immune evaders arrive with high probability for both large and small r, and do so with comparable time scales of arrival. Evasion behavior under the latter detection mode predicts for the first time a novel mechanism of sneak-through resulting exclusively from acquired immune evasion. A corollary to this implies that the enhancement of immune killing (via increased d) alone cannot eliminate the risk of immune evader arrival, and the effects of such immunomodulation are diminished for slow-growth cancers. This prediction corroborates known experimental observations linking growth-rate with immune resiliency, including slow-growth melanoma variants with known T-cell exclusion (Spranger et al., 2015), and are reminiscent of the state of reduced proliferation with concomitant survival phenotypes characteristic of drug tolerant persisters (Chisholm et al., 2015), as well as the observed concave relationship between viral growth rate and peak CD8+ T-cell response (Bocharov et al., 2004) . We focus next on the case of a dynamic threat under adaptive immune recognition in subsequent sections.

Figure 3:

‘Sneak-through’ via immune evasion under deterministic detection. (A) Immune evader arrival probability and (B) mean time of evader arrival for both growth-limited (blue, R = 10²) and size-limited (red, m_c = 10³) detection assumptions (d = 0.2, μ = 10⁻⁶).

3.3. Acquired evasion and immune escape predicted with diminishing adaptive immune repertoire

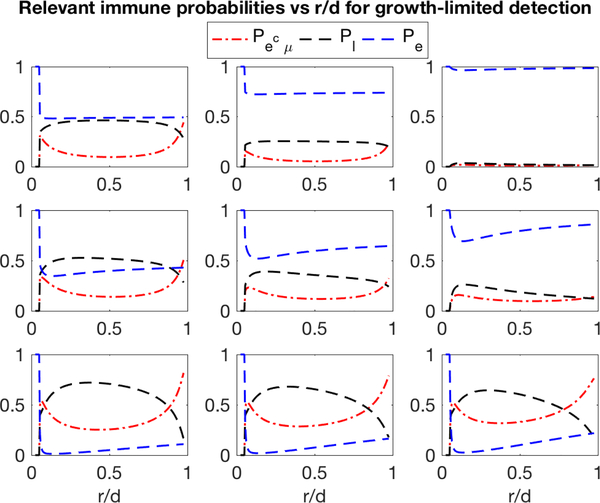
In contrast with the prior examples, a dynamic threat faced with an adaptive immune system has nontrivial likelihood of events E_e and Ε_μ. We focus here on escape E_e, immune evasion $E_{e^c,\mu }$, and cancer loss (immune victory) $E_{e^c,{\mu }^c}$ with respective probabilities P_e, $P_{e^c,\mu }$, and P_l. A similar analysis (Eq. S49) that marginalizes over the deterministic detection sizes in Eq. 11 is depicted for various immune parameters under growth-limited detection (Fig. 4). Under competent immune surveillance (high k, low p_b) disease stems almost exclusively from acquired immune evasion, and the majority of threats are expected to be cleared. As turnover rate and repertoire diversity are compromised, immune escape is predicted to dominate over acquired evasion in its overall contribution to disease. Here, the overall predicted success probability of disease clearance, P_l, is again maximal for large and small r. In all cases, ‘sneak through’ is observed for slow growth threats, further supporting the growth-threshold conjecture under adaptive immune surveillance.

Figure 4:

Probability estimates of relevant immune outcomes. Dynamic threat escape, evasion, and loss probabilities as a function of relative net growth rate r/d for various values of immune turnover (rows bottom-to-top: k={10⁻¹, 10⁻²,10⁻³}) and repertoire diversity (columns left-to-right: p_b={0.5, 0.75, 1.0}) (d = 0.20, μ = 10⁻⁶, R = 10⁴, M = 10⁶).

The dependence of disease mechanism on immune status predicts an essential role of immune recognition in the ability to control adaptive threats. Motivated by this, we apply our model to predict cancer incidence as a function of an aging immune compartment. We select AML as a representative case due to the large amount of available incidence data, its low mutation burden, association with advanced age, and, unlike solid malignancies, relative accessibility by the adaptive immune compartment (Alexandrov et al., 2013). Empirically observed decreases in thymic output in middle age and T-cell repertoire diversity in advanced age (Naylor et al., 2005) are modeled by decreasing Hill functions of k and 1 - p_b, respectively. While the absolute mapping between recognition probabilities via p_r (m; m₀) and TCR diversity and turnover rates remains an open problem, we may use the known relative decreases in each of these parameters as a function of age in order to estimate potential immune impairment. The model assumes equal cancer risk for every age and estimates escape probability by incorporating the total number of T-cell clones, N_t, and the probability of a single T-cell recognizing individual antigenic peptide, $\tilde{p}$, via $p_b={(1-\tilde{p})}^{N_t}$ as done previously (George et al., 2017). Incidence (defined as 1–P_ι) for a particular set of parameters explains empirical AML data well, outperforming the standard multi-hit model of cancer incidence (Fig. 5A).

Figure 5:

AML incidence vs immune function. (A) Bar plot of empirical data (gray) is compared to model-derived AML estimates $P_e+P_e{c}_{,\mu }$ (red dashed line) that assumes constant cancer incidence and decreasing immunity vs age. Thymic turnover rates and effective clone sizes are modeled as Hill functions. Escape probability is approximated using $p_b\approx 1-{(1-\tilde{p})}^{N_s}$ , where $\tilde{p}~{10}^{-6}$ is the probability of a single TCR recognizing the immune sensitive population and N_s is the effective number of distinct clones (See SI for details). This estimate is compared to the least squares best-fit models of multi-stage incidence (solid lines), where incidence is assumed to be approximately proportional to tⁿ, for age t and n number of hits.; (B) Predicted cumulative incidence over 10 years assuming chronic immunosuppression (1-p_b and k scaled by α=0.9) and mean age of 43 prior to treatment.

The model agreement with age-specific incidence data (Cancer Research UK) would suggest that age-incidence may be partitioned into three categories: Early, unfortunate disease due to the (rare) arrival of immune evaders that escape immune detection, slightly increased incidence in middle age secondary to lower turnover rates, and dramatic, late-onset increases in risk as a result of decreasing TCR repertoire diversity. Our results are consistent with recent independent efforts to quantify immune-related cancer incidence (Palmer et al., 2018). The same parameter choice, assuming mild (~10%) decreases in T-cell recognition, is applied to characterize predicted AML incidence in the setting of chronic immunosuppression (Fig. 5B) and we find general agreement with large (n ~ 3 · 10⁵) empirical datasets of heart and lung transplant recipients and healthy controls (Offman et al., 2004).

4. Applications to Immunotherapy

We now turn to the setting of adjuvant immunotherapy with the goal of estimating the therapeutic benefit of chimeric antigen receptor (CAR) T-cell and tumor antigen vaccination therapies. We introduce E to denote the event of overall disease elimination with corresponding probability equal to the sum of tumor loss probability due to immune system elimination (P_l above) and treatment probability, denoted by Pt . Treatment probability may be expanded by conditioning on relevant events:

$$\begin{gathered} P_T=\mathbb{P}(E|E_{e,\mu })P_{e,\mu }+\mathbb{P}(E|E_{e,{\mu }^c})P_{e,{\mu }^c} \\ +\mathbb{P}(E|E_{e^c,\mu })P_{e^c,\mu }. \end{gathered}$$ (12)

where the necessary conditioning probabilities are given in SI. We assume that radio- (or chemo-) ablative therapy administered at time of detection T_D prior to adjuvant immunotherapy reduces the population to a minimal residual level m_mrd ≪ M.

4.1. CAR T-cell therapy

Chimeric Antigen Receptor (CAR) T-cells are a class of ex-vivo engineered T-cells with artificial receptors and co-stimulatory signals designed to target an epitope differentially expressed by cancer cells (Sadelain et al., 2017). Their use has been particularly effective against hematological malignancies, wherein a variety of B-cell lymphomas demonstrate response to anti-CD-19 CAR T-cells (Brudno and Kochenderfer, 2018). Importantly, the CAR T receptor is not limited to MHC-I recognition and can identify a variety of preferentially expressed tumor cell signatures, including surface proteins and carbohydrates (Yu et al., 2017). Thus, CAR T-cell therapy is effective in settings such as acute lymphoblastic leukemia, where mutation burden is low (Wang and Rivière, 2016; Martin et al., 2016). Its success in solid malignancies requires selection of preferentially over-expressed tumor-specific epitopes in the bulk tumor (Brown and Adusumilli, 2016; Newick et al., 2016).

Our analysis considers the case where a CAR T-cell clone has been engineered with recognition directed against a pre-identified tumor-specific epitope. We assume the CAR-T detection limit, m_car, is sufficiently low so that m_car ≤ m_mrd (See SI for details). Deterministic detection therefore occurs immediately at size m_mrd for some fixed dosage of CAR T-cells as a result of built-in co-stimulation that occurs automatically with receptor binding. We allow for the arrival of CAR epitope-evasive cells at rate 𝜇_car following treatment, and neglect the event that an epitope-evasive clone is present prior to treatment. Since CAR T-cells target all cancer cells at detection, successful treatment proceeds identically independent of how the cancer population arrived at detection (escape vs. evasion). Therefore, the conditional probabilities of Eq. 12 reduce to deterministic recognition with detection limit at starting size m_mrd, and may be written as a generalized version of Eq. 11.

Analytical estimates of CAR T-cell P_E are plotted over all growth ranges for a variety of immune states in Fig. 6. 𝜇_car~10⁻⁴ was chosen large to best illustrate CAR T efficacy vs growth rate. In reality, 𝜇_car could be significantly less than μ depending on the CAR T target, so that Fig. 6 underestimates CAR T benefit. Intuitively, CAR T therapy is predicted to impart substantial treatment benefit independent of immune functioning because CAR T cancer elimination does not rely upon the host immune system. Detection at m_mrd is effectively size-limited, and so this therapy is also less effective against threats with larger net growth rates.

Figure 6:

Predicted disease elimination probability (P_l+ Pe). CAR T (green) neoantigen vaccine (red) therapy benefit is compared to non-treatment survival predictions (black) as a function of relative net growth rate r/d for various values of immune turnover (rows bottom-to-top: k={10⁻¹, 10⁻²,10⁻³}) and repertoire diversity (columns left-to-right: p_b={0.5, 0.75, 1.0}) (d = 0.20, μ = 10⁻⁶, R = 10⁴, M = 10⁶, m_mrd = 10³, R = 0 for neoantigen vaccine case, μcαr = 10⁻⁴).

4.2. Autologous neoantigen vaccines

Autologous neoantigen vaccines are another type of immunotherapy which relies on the delivery of tumor antigens to the cell in order to augment or enhance the effect of neoantigen-specific CD8+ T-cells (Fritsch et al., 2014). Contrasting their reduced efficacy in tumors with lower mutation rates (Martin et al., 2016), neoantigen vaccines have been effective against highly mutagenic tumors, such as melanoma, where the neoantigen burden is significant (Ott et al., 2017; Hellmann and Snyder, 2017; Sahin et al., 2017). In our framework, successful immune priming occurs if sufficient levels of vaccine-delivered antigen suddenly become available for activating T-cells, effectively reducing the detection threshold R. For simplicity we assume that a sufficient level of tumor antigens are present so that R = 0 and any residual cancer size can be targeted.

Unlike CAR T treatment, vaccine therapy is only successful when there is an absence of immune evasive cells both prior to and following treatment $\left(\text{i}.\text{e}.\text{ on }{E}_{{\mu }^{\text{c}}}\right)$, since type-2 cells can still evade vaccine-sensitized host T-cells. The only conditional probability in Eq. 12 that contributes to treatment success is $\mathbb{P}(E|E_{e,{\mu }^c})$ , which is none other than P_l in the adaptive model with detection and initial population size both equal to m_mrd (see SI). The final required quantity is the factor $P_{e,{\mu }^c}$ calculated as follows:

$$P_{e,{\mu }^c}=\mathbb{P}\left(E_{{\mu }^c}|E_e\right)P_e={(1-\mu )}^M\cdot P_e\left(M;m_0\right).$$ (13)

Vaccine treatment efficacy is plotted alongside CAR T therapy in Fig. 6. There is minimal predicted treatment benefit in immunocompromized patients, consistent with the fact that vaccine strategies are reliant upon proper immune recognition. The treatment benefit appears to be maximal for patients with preserved repertoire diversity and low T-cell turnover, presumably the result of allowing more time to pass, and hence immune turnover to occur, at low population sizes. Elimination of slow-growth threats that would normally sneak-through immune detection are increased, since there is no post-treatment detection limit.

5. Discussion

Our findings support the importance of the growth-threshold conjecture as an essential aspect of empirical recognition dynamics, since size-limited detection predicts an exclusive preference for fast-growing threats. In addition to static growth and recognition, ‘sneak-through’ is predicted by a new mechanism that involves preferential acquisition of immune evasion for slow and large growth rates.

Application of this relatively simple model to AML provides a quantification of the trade-off between T-cell turnover and repertoire size and control of malignancy. Moreover,the assumption that incidence carries equal risk through time places no mechanistic restrictions on the molecular generation of tumor development, and stands as a prediction of tumor generation largely orthogonal to the canonical ‘multi-hit’ hypothesis (Armitage and Doll, 1954). We find not only that this model agrees more closely with the data when compared to the best-fit multihit predictions, but that the immune incidence curve also accurately reproduces the sigmoid shape of AML incidence in a way that is impossible for the convex multi-hit model. It is also interesting that gender-specific differences in thymic output (favoring females) also correlate with a systematic reduction in AML incidence (Pido-Lopez et al., 2001). From a clinical standpoint, the prediction of maximizing immune health in order to mitigate incidence is broadly quantified for tumors that may adopt immune evasion strategies, as well as more general immune threats. In the case of treatment-refractory AML with subsequent hematopoietic stem cell transplant, our results would suggest that an emphasis be placed on maintaining repertoire diversity and, where possible, thymic turnover (Holländer et al., 2010).

In an attempt to provide an initial and straightforward presentation, we assumed pure birth in the recognition and death phase. Future analysis using the more complicated birth-death process would likely increase the rate of immune evasion generation during immune killing. We have also assumed immune killing ability occurs quickly and to a sufficient level for all threat sizes. We have also inherently assumed in this analysis that the threat net growth rate is fixed. We believe that this is a reasonable assumption for studying a rapidly growing threat such as AML, where reduced growth occurs only in advanced disease Akinduro et al. (2018). Other dynamic threats including many solid tumors, characterized by complicated, time-varying growth rates, are analytically intractable in this framework, necessitating a more extensive reliance on numerical simulation. In general, for sigmoid growth, the above results assuming mean exponential growth provide an upper-estimate on tumor escape, while evasion under growth-limited detection inherently depends on the functional form of the growth rate. Though an approximation, we believe these dynamics are reasonable as a naïve T-cell clone expands rapidly, though not instantaneously, to become a dominant clone during proper immune activation (Desponds et al., 2016).

We selected AML as a model disease for initial assessment of our model owing to several applicable features. Its rapid growth is well-approximated by a growth rate homogeneous in time and size. Unlike their solid counterparts, the immune cells have no difficulty interfacing with hematological cancer cells. Lastly, AML’s characteristically low mutational burden enables us to estimate immune evasion in the simplified framework above without the risk of ignoring possibly many intermediate phenotypes with mild evasion potential. It is likely however that the tumor-immune co-evolution described here applies broadly to many cancer types, and therefore warrants careful consideration of other relevant factors, such as mutational burden and immune infiltration, in future analyses (Blank et al., 2016).

The advantage of antigen vaccine strategies studied here resulted from augmented immune priming of the T-cell repertoire, thereby allowing recognition to overcome detection limits. Variations due to cancer subtype, including antigenicity and (for solid tumors) T-cell infiltration, may substantially affect immune priming, and hence vaccine efficacy, but are not considered here. In particular, the subclonal neoantigen landscape is an important consideration that warrants further analysis for a more complete understanding. Future studies will further distinguish between clones of differing fitnesses dependent upon their antigenicity and intermediate levels of immune evasion in an attempt to better characterize the co-evolution between a dynamic tumor and adaptive immune compartment.

Highlights.

• Stochastic analysis of cancer growth in the face of adaptive immune pressure

• Effects of immune recognition on tumor progression and acquired evasion are studied

• Immune detection limited by size supports sneak- through of slow-growth threats

• Cancer immune elimination and evasion probabilities are analytically estimated

• Effects of decreased immune functioning explain AML age-incidence data