Approaching protein design with multisite λ dynamics: Accurate and scalable mutational folding free energies in T4 lysozyme

Abstract

The estimation of changes in free energy upon mutation is central to the problem of protein design. Modern protein design methods have had remarkable success over a wide range of design targets, but are reaching their limits in ligand binding and enzyme design due to insufficient accuracy in mutational free energies. Alchemical free energy calculations have the potential to supplement modern design methods through more accurate molecular dynamics based prediction of free energy changes, but suffer from high computational cost. Multisite λ dynamics (MSλD) is a particularly efficient and scalable free energy method with potential to explore combinatorially large sequence spaces inaccessible with other free energy methods. This work aims to quantify the accuracy of MSλD and demonstrate its scalability. We apply MSλD to the classic problem of calculating folding free energies in T4 lysozyme, a system with a wealth of experimental measurements. Single site mutants considering 32 mutations show remarkable agreement with experiment with a Pearson correlation of 0.914 and mean unsigned error of 1.19 kcal/mol. Multisite mutants in systems with up to five concurrent mutations spanning 240 different sequences show comparable agreement with experiment. These results demonstrate the promise of MSλD in exploring large sequence spaces for protein design.

Introduction

The estimation of changes in free energy upon mutation is one of the central problems of protein design. Relevant free energies include the folding free energy, ligand binding free energy, catalytic transition state binding free energy, protein–protein association free energy, and others. These free energies can be used to design proteins with desired stability, ligand binding, catalytic, and dimerization properties, respectively. Estimation of the appropriate free energy can guide in silico evolution, through Monte Carlo sampling of sequence space at some selection temperature1, 2 to optimize the property of interest.

Modern protein design algorithms, such as Rosetta3, 4 and others,5, 6, 7, 8 typically estimate free energies for a particular sequence and conformation using heuristic or empirical free energy estimates. Sequence and conformational space are explored simultaneously through Monte Carlo sampling of rotamer libraries of various side chains. This general approach has had remarkable success in designing new sequences with desired structural properties,9 as well as moderate success in designing sequences with desired dimerization,10 ligand binding,11 and catalytic properties.12, 13

In spite of this success, several unmet challenges remain in ligand binding14 and enzyme design that would benefit from improved predictions of free energy differences. Designed enzymes continue to show much lower activity than natural enzymes,15, 16, 17 but typically possess enough initial activity that their efficiency may be raised to moderate levels through directed evolution.12, 13 Although directed evolution can improve catalytic efficiency, better design algorithms are highly desirable, because better initial enzyme designs also tend to possess superior activities after directed evolution.13 Current enzyme design methods suffer from a variety of limitations and approximations. Limitations include the inability to dock theozymes18 with more than about four catalytic residues into candidate protein scaffolds,16 which limits designed enzymes to simple reactions. Approximations include implicit solvent energy functions, lack of long range electrostatics, and the neglect of backbone flexibility during the design process.17 Due to these approximations, many enzyme active sites are no longer stable after redesign. In contrast, explicit solvent molecular dynamics (MD) simulations utilize more accurate energy functions and explicitly account for protein flexibility. Indeed, long MD simulations are frequently used in a diagnostic fashion to assess the kinetic stability of designed sequences before experimental testing.15, 19

Alchemical free energy methods can make rigorous estimates of thermodynamic stability using MD simulations. Free energy methods include free energy perturbation (FEP),20 thermodynamic integration (TI),21 multisite λ dynamics (MSλD),22, 23, 24 enveloping distribution sampling,25, 26 and many others.27, 28 These methods have most commonly been applied to compute solvation free energies of ligands,22, 29, 30 drug binding free energies,31, 32 and pKa values of titratable groups in proteins.33, 34, 35, 36 Studies using free energy methods to estimate changes in peptide and protein free energy upon side chain mutation are much rarer.37, 38, 39, 40, 41 Last year, two large‐scale applications of free energy methods to protein folding and binding upon mutation appeared.42, 43 Such studies could in principle be used to guide protein design, but in practice are far too slow to be of practical use in driving design. However, in one case, rigorous alchemical free energy calculations were used in post‐design evaluation to assess thermodynamic stability and eliminate a less promising sequence.41

MSλD is a unique free energy technique with several features that make it sufficiently efficient to drive protein design. First, MSλD is highly efficient, and requires one to two orders of magnitude less computation than other free energy methods to achieve comparable levels of precision.24, 38 Second, MSλD can be tuned to screen the most promising sequences from a larger set without wasting sampling on the remaining sequences.22, 44 Third, MSλD is highly scalable, allowing the comparison of hundreds of physical systems in a single simulation,45 whereas conventional techniques like FEP and TI require independent simulations for each pairwise comparison of physical states. Scalability to combinatorial sequence spaces allows MSλD to mitigate the high cost of MD simulations by searching much larger swaths of sequence space than FEP or Rosetta during each in silico evolutionary step. λ dynamics is over two decades old, but has matured substantially in recent years via generalization to multiple sites,24 the use of implicit constraints to focus sampling on physical endpoint states,46 enhanced sampling with biasing potential replica exchange (BP‐REX),47 adaptive landscape flattening (ALF) to remove alchemical barriers,48 and the use of soft‐core interactions.48, 49

In this study, we seek to assess the accuracy limits and demonstrate the scalability of MSλD for use in future protein design projects. T4 lysozyme is an ideal test system, as changes in folding free energy have been measured for hundreds of mutants through the work of Brian Matthews and coworkers.50 T4 lysozyme residue L133 was also the system used by Kollman in the first free energy simulations of protein mutation.37, 51, 52 We begin by computing single site mutational free energies at seven sites, A42, A98, L99, M102, M106, V149, and F153, which were chosen because they possessed multiple mutants and a large range of folding free energy changes. Predicted ΔΔG_Folding agree well with experiment (Pearson correlation of 0.914 and mean unsigned error of 1.19 kcal/mol). Next, we turned our attention to simultaneous mutations at multiple sites exploring up to 240 sequences concurrently. Agreement for these systems is of roughly equal quality (Pearson correlation of 0.860 and mean unsigned error of 1.12 kcal/mol). The ability of MSλD to predict protein stability with high accuracy in these large combinatorial sequence spaces suggests this method holds promise for identifying the most favorable mutations in future protein design projects.

Results

Single site mutants

Mutation sites were chosen from and compared against the experimental data in Reference [50]. Single site mutants were chosen according to several criteria: first, stabilities at a particular site must have been measured at the same pH in the C54T/C97A background, a mutant with the one native disulfide bond between C54 and C97 removed. Second, at least three sequences (native and two mutants), excluding G and P for technical reasons, must have been measured. Finally, the range of stabilities must be at least 3.5 kcal/mol. Seven sites, listed in Table 1, met these criteria.

Table 1.

Single Site Mutants

Site	Mutations	pH
A42	FILSV	3.0
A98	CFILMSVW	3.0
L99	AFIMV	3.0
M102	AK	5.4
M106	KL	3.0
V149	CIMST	5.4a
F153	AILMV	3.0

^aV149T was measured at a different pH (3.0) from other mutations at this site

MSλD simulations were run on each of the seven single site mutants featuring three to nine side chains per simulation, each scaled by its own λ variable, according to the procedure outlined in Methods. Briefly, the landscape was flattened using an updated ALF framework to optimize sampling, and then five independent trial simulations were run for each site for either 40 ns without variable bias replica exchange (VB‐REX, see Methods) or 20 ns with VB‐REX. The entire procedure was run once with force switching (FSWITCH) electrostatics53 and once with particle mesh Ewald (PME) electrostatics36, 54, 55 to explore the influence of long range electrostatics on the free energy changes.

The overall agreement with experiment is shown in Figure 1. FSWITCH and PME yielded comparable accuracy with Pearson correlations of 0.914/0.893, mean unsigned error (MUE) of 1.19/1.10 kcal/mol, and root mean squared error (RMSE) of 1.39/1.50 kcal/mol, respectively.

Figure 1.

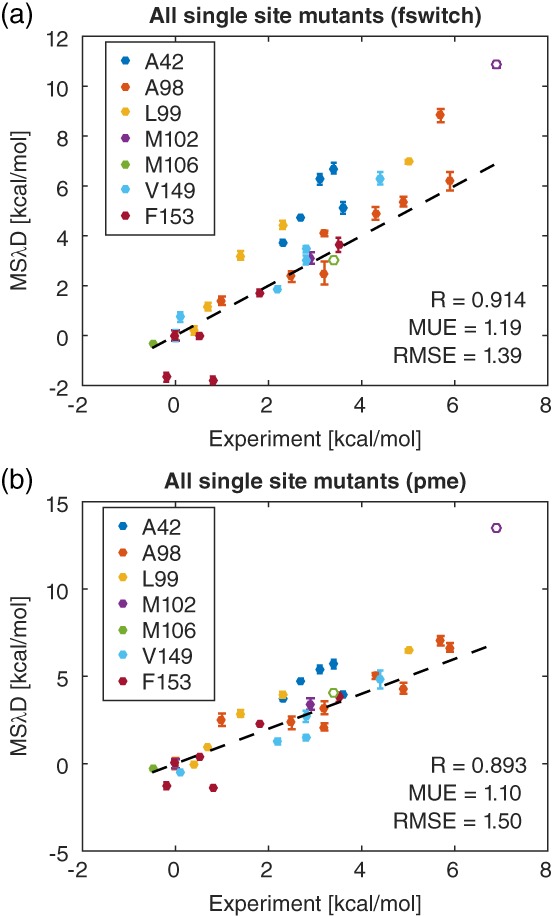
Comparison between predicted MSλD and experimental folding free energies at all seven mutation sites using (a) FSWITCH and (b) PME electrostatics. Open circles denote charged mutants M102K and M106K. Dashed lines denote y = x, and free energies are plotted relative to wild type with C54T/C97A.

In most cases, mutations within an individual site had substantially higher correlations and lower RMSE than when all the sites were combined (Table 2). Three sites, A42, A98, and M102, proved difficult to sample in preliminary simulations, consequently VB‐REX was employed to sample these sites more aggressively. These sites proved difficult for two reasons. M102 involved a charge change, which is known to cause serious artifacts in free energy calculations,56 via mutation to a buried lysine. A42 and A98 both involved mutations from small to large residues in the protein core, which in general may require relaxation of slow degrees of freedom to accommodate the extra steric bulk.

Table 2.

Site Specific Results

Site	RMSEa	R
FSWITCH
A42	1.12	0.952
A98	1.01	0.938
L99	0.97	0.968
M102	1.82	0.989
M106	0.25	1.000
V149	0.71	0.960
F153	0.98	0.884
All	1.39	0.914
PME
A42	0.92	0.920
A98	0.82	0.926
L99	0.82	0.970
M102	2.99	0.983
M106	0.29	0.999
V149	0.59	0.944
F153	0.91	0.897
All	1.50	0.893

^aCentered RMSE in kcal/mol: (〈(ΔΔG_MSλD − ΔΔG_Exp)²〉 − 〈ΔΔG_MSλD − ΔΔG_Exp〉²)^1/2

To investigate whether relaxation of slow degrees of freedom limited convergence in these particular mutations, crystal structures for each of the seven sites57, 58, 59, 60, 61, 62, 63, 64, 65 were visually inspected to identify distances that correlate with mutation for use as structural reaction coordinates. Distances averaged over all frames where a particular substituent was on (λ>0.99) agreed fairly well with the crystal structures, though slight thermal expansion of about 0.1 Å was seen in simulations and distances for S and T were overestimated by 0.5 Å (Supporting Information Table S3). Crystal structure analysis also suggests a possible explanation for the large error in M102K: although M102K remains buried, S_δ in M106 reorients to directly contact M102K. Interaction with a polarizable sulfur atom likely ameliorates the cost of charge burial but is neglected in our fixed charge models.

As all reaction coordinates identified in crystals were demonstrated to correlate with λ in our simulations (Supporting Information Table S3), the autocorrelation time in these reaction coordinates gives a lower bound for time scale of relaxations that are necessary to obtain converged estimates of free energy. Autocorrelation times are shown in Figure 2 and show a clear split between more rapidly relaxing sites (L99, M106, and V149) and more slowly relaxing sites (A42, A98, M102, and F153). Notably, three out of four of the more slowly relaxing sites were sites that required VB‐REX for efficient sampling. These results also suggest that A98 sampling could use further improvement due to its long autocorrelation time.

Figure 2.

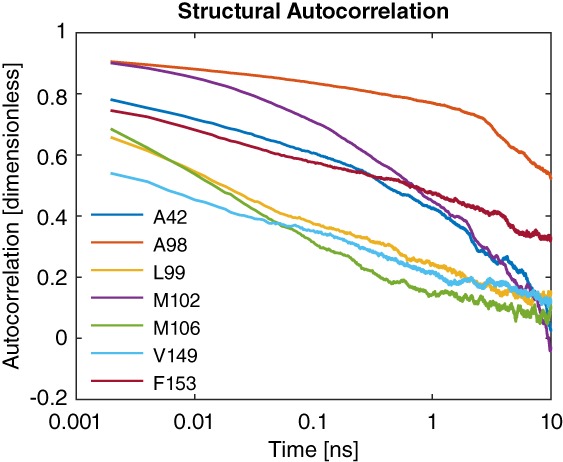
Autocorrelation in structural reaction coordinates at all seven sites (see Supporting Information for reaction coordinate definitions). Sites divide into three groups: L99, M106, and V149 decay rapidly; A42, M102, and F153 decay more slowly; and A98 decays very slowly. This division roughly parallels the sites requiring VB‐REX and the sites not requiring VB‐REX. At sites A42 and M102 two distances were chosen to capture the variety of structural changes observed. The autocorrelation in the distance more strongly correlated with λ is plotted; the other autocorrelation decays more rapidly in both cases.

Multisite mutants

Encouraged by our findings from the single site mutation studies, we turned our attention to multisite mutants. Three systems comprising 3, 4, and 5 mutation sites were selected from methionine scan and core redesign studies (Table 3). The three site, four site, and five site systems comprised 8 (2 × 2 × 2), 24 (2 × 2 × 3 × 2), and 240 (3 × 5 × 4 × 2 × 2) sequences with all combinatorial permutations of the individual mutations in Table 3. Of these 8, 24, and 240 sequences, only 6, 14, and 9 have been experimentally measured at the same pH,50 (see Supporting Information Tables S5–S9 for identities of these sequences), so only results for these sequences are compared with experiment.

Table 3.

Multisite Mutants

Site	Mutations
3 Site pH = 5.4
I17	M
I27	M
L33	M
4 Site pH = 3.0
L99	F
M102	L
V111	FI
F153	L
5 Site pH = 3.0
L121	AI
A129	LMVW
L133	AMV
V149	I
F153	L

Interactions between side chains at different sites are scaled by the product of their λ variables, so mutating side chains at two sites only interact when they are both on, which allows MSλD to explicitly account for coupling between sites. VB‐REX was applied to all systems to increase sampling near the alchemical endpoints, otherwise most endpoints were not sampled using a λ cutoff of 0.99 in the five site system.

Results are shown in Figure 3 and Table 4. The four site system had a narrower range of stabilities than the other two systems and consequently had a lower Pearson correlation with experiment; however, the four site system also had a lower RMSE with experiment, demonstrating the ability of MSλD to quantify the small effect of these mutations. Overall, Pearson correlations were 0.860/0.845, the RMSEs were 1.28/1.11 kcal/mol, and the MUEs were 1.12/1.02 kcal/mol when FSWITCH and PME respectively were compared with experiment. The agreement with experiment of these multisite mutational results are strikingly comparable with the single site results, suggesting errors do not increase rapidly with the number of mutations.

Figure 3.

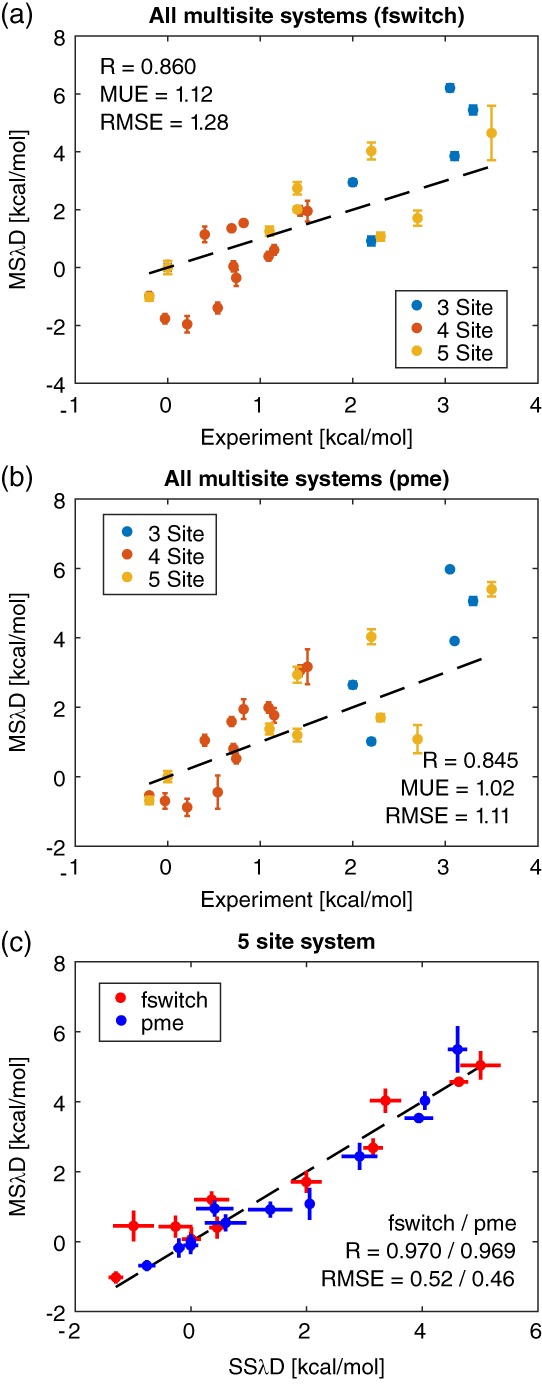
Accuracy of MSλD in multisite systems. Comparison of multisite mutant results with experiment using (a) FSWITCH and (b) PME electrostatics. (c) Comparison of 5 site results from MSλD dynamics with more converged results run on a single site only (SSλD). Comparison with SSλD is only affected by sampling errors, comparison with experiment is affected by sampling and force field errors. Dashed lines denote y = x, and free energies are plotted relative to wild type with C54T/C97A.

Table 4.

Multisite Results

System	SSλDa		Experimentb
	RMSEc	R	RMSEd	R
FSWITCH
3 site	0.04	1.000	1.43	0.841
4 site	0.47	0.946	0.98	0.726
5 site	0.52	0.970	1.03	0.806
All			1.28	0.860
PME
3 site	0.10	0.999	1.29	0.856
4 site	0.24	0.981	0.87	0.904
5 site	0.46	0.969	1.15	0.790
All			1.11	0.845

^aErrors due to only sampling

^bErrors due to force field, pentapeptide approximation of unfolded ensemble, and sampling

^cCentered RMSE in kcal/mol: (〈(ΔΔG_MSλD − ΔΔG_SSλD)²〉 − 〈ΔΔG_MSλD − ΔΔG_SSλD〉²)^1/2

^dCentered RMSE in kcal/mol: (〈(ΔΔG_MSλD − ΔΔG_Exp)²〉 − 〈ΔΔG_MSλD − ΔΔG_Exp〉²)^1/2

Table 5.

Comparison of Alchemical Methods

Method	Mutants	R	RMSE	MUE
All Point Mutants
FEP (Reference [42])	712	0.63	2.06a	1.58
MSλD with FSWITCH	32	0.914	1.39	1.15
MSλD with PME	32	0.893	1.50	1.07
Charge Conserving Point Mutants
FEP (Reference [42])	534	0.69	1.84b	1.38
MSλD with FSWITCH	30	0.901	1.30	1.12
MSλD with PME	30	0.896	1.09	0.93

^aThe originally cited RMSE of 2.27 was uncentered

^bThe originally cited RMSE of 2.07 was uncentered

In order to determine how much error came from the force field and how much came from sampling, each of the sites was mutated individually in single site λ dynamics simulations (SSλD) run with VB‐REX. These point mutations were then compared against the same point mutations in the MSλD ensemble (Fig. 3(c)) and Supporting Information (Fig. S1). SSλD and MSλD agreed closely in the three site system (Supporting Information Fig. S1). Differences for the four site and five site systems were slightly outside of statistical uncertainty, suggesting there are reproducible differences that we attribute to lack of sampling in the MSλD simulations. These differences are substantially smaller than the deviation from experiment, suggesting most of the deviation is due to force field errors or shared approximations of the unfolded ensemble.

It should be noted that of the 240 sequences in the five site system, either five or two sequences were not sampled and 23 or 13 sequences were insufficiently sampled across all independent trials to estimate statistical significance in the FSWITCH or PME simulations, respectively (Supporting Information Tables S7–S9). The sequences exhibiting these characteristics were all less stable than the average of the other 210 sequences, typically by 2–3 kcal/mol. This outcome is likely due to cooperative effects between pairs of conflicting mutations. Since such sequences are particularly unstable, they are of less interest in protein design, and inability to sample them within the context of an MSλD design process is only a minor concern.

Discussion

Comparison with other methods

Due to the importance of changes in protein stability upon mutation, a wide variety of techniques exist to predict ΔΔG_Folding(S₁ → S₂). Techniques range from fast physics‐based, knowledge‐based, and machine learning approaches3, 66, 67; to implicit solvent methods68, 69; to rigorous alchemical free energy calculations in explicit solvent.37, 38, 39, 40, 41, 42, 43

In one study comparing a variety of fast prediction methods including Rosetta,3 FoldX,67 CC/PBSA68 and others, MUEs ranged from 1.00 to 1.68 kcal/mol and Pearson correlations ranged from 0.26 to 0.59.66 While some of these methods may appear to be competitive with MSλD in terms of MUE, this is because these methods are designed to minimize error and thus make conservative estimates, while most errors by MSλD are overestimates. Consequently, the Pearson correlations, which normalize out overprediction and underprediction, reveal MSλD clearly gives superior predictions. It is noteworthy that the worst performing algorithm was Rosetta, which suggests current design algorithms are still able to design highly stable foldable proteins despite poor prediction of free energies because they capture the underlying physics of hydrophobic burial and side chain packing. Consequently, MSλD may enable even more accurate design of proteins, because in addition to these effects, it also captures backbone flexibility and ligand binding energetics, which are poorly modeled by current design algorithms.14, 17, 70, 71

It is also instructive to compare MSλD directly to other alchemical free energy methods. Most alchemical free energy studies of protein mutations have been small37, 38, 39, 40, 41; however, two large scale tests of FEP for calculating folding free energies42 and protein–protein binding free energies43 recently appeared. The binding free energy study achieved excellent accuracy (0.68 kcal/mol RMSE, Pearson correlation 0.70) due to the small data range, aggressive sampling (100 ns per window in some cases), neglect of charge changing mutations, and ability to ignore the unfolded ensemble.43 ^{, *}

The FEP folding free energy study allows a more direct comparison with our results because both studies must grapple with the unfolded ensemble. In a survey of 712 mutations in 10 proteins, that study achieved a Pearson correlation of 0.63, an RMSE of 2.06 kcal/mol, ^† and an MUE of 1.58 kcal/mol.42 MSλD achieved superior results with Pearson correlations of 0.914/0.893, RMSEs of 1.39/1.50 kcal/mol, and MUEs of 1.15/1.07 kcal/mol for FSWITCH/PME, but the differences in the mutation sets call for a more nuanced comparison. First, 25% of the mutations in the FEP study involved charge changes, while only 6.3% of mutations in the present study did. Removing these mutants gives FEP a correlation coefficient of 0.69, an RMSE of 1.84 kcal/mol, ^‡ and an MUE of 1.38 kcal/mol. MSλD results improve to correlation coefficients of 0.901/0.896, RMSEs of 1.30/1.09 kcal/mol, and MUEs of 1.12/0.93 kcal/mol for FSWITCH/PME. Another noteworthy difference is in the relative number of large to small mutations (decreasing number of heavy atoms), which may simply leave a void, versus small to large mutations (increasing number of heavy atoms), which may require slow relaxation of the protein core to relieve a steric clash. The FEP dataset is comprised of mostly large to small mutations derived from alanine and glycine scans; on average, mutations involved loss of three heavy atoms, and only 7.6% mutations involved an equally sized or larger side chain. In the MSλD dataset, 68.8% of the mutations were to an equally sized or larger side chain. The small to large mutants were harder to sample and gave larger errors, suggesting the MSλD dataset is a more challenging dataset. Removing the large to small and equal‐sized mutants from the MSλD dataset gives roughly the same agreement with experiment as removing the charge change mutants, and does not result in further improvements because only 10 mutants remain, and of these, half are to F153, where the force field may not fully capture aromatic interactions.

The improved accuracy of MSλD relative to conventional FEP may be attributed to a variety of causes. First, while both studies are large systematic studies, the FEP study tackled more than an order of magnitude more mutations. Consequently, the FEP study merely identified poorly converged mutants and noted that they degraded the quality of the results. In contrast, due to its smaller scope, the present study could identify poorly converged mutants and focus sampling on them with VB‐REX and reoptimization of biasing potential parameters. Second, the accuracy of both methods is limited by the force field used, and it is possible that the CHARMM36 force field used here is more accurate than OPLS3, though at least one study suggests that the two force fields to have comparable accuracy.43 Finally, MSλD is more computationally efficient; one study cites a factor of 20–3045; see Supporting Information for further discussion. Here, MSλD requires 0.22 simulations per mutant (32 mutants in 7 simulations), while FEP requires 12–16 simulations per mutant (55–73 times more simulations per mutant). ^§ This allows MSλD to use longer 20–40 ns simulations with multiple independent trials, while FEP was limited to a single trial of 5 ns per simulation per window. As in Methods, substantial differences were noted between the biasing potentials obtained during the 5 ns flattening runs and the optimal biases in MSλD production, suggesting the system was still relaxing after 5 ns. Autocorrelations in structural reaction coordinates confirm this for some sites (Fig. 2). Consequently, the FEP simulations likely did not fully relax to equilibrium.

Looking forward

The present study allows a comparison of FSWITCH and PME electrostatics. In the systems considered here, FSWITCH and PME achieved comparable agreement with experiment. While the differences are small, FSWITCH performed better for single site mutants until charge mutations (which PME was not corrected for) were removed. For multisite mutants, PME performed better in terms of RMSE. Moving forward it will be worthwhile to monitor the relative performance of the two methods, as each has advantages. PME is more computationally efficient than FSWITCH because shorter cutoffs may be used. PME appears to perform worse if uncorrected for charge changes,56 but likely stabilizes the rest of the protein structure more effectively.

Currently, MSλD does not treat all amino acid mutations equally. In particular, charge changes are handled less well than charge conserving mutations, and mutations to or from G and P have been avoided due to technical challenges. Corrections for charge changes with PME electrostatics have been derived,56 but the recent FEP folding study demonstrated that large errors remain even when these corrections are applied.42 Such errors have been attributed to sampling,42 but some error would remain even with perfect sampling due to the fixed protonation state of mutating and surrounding residues. MSλD is ideally poised to consider such protonation changes with the use of constant pH MD simulations, which utilize the same MSλD formalism.33, 34, 35, 36 Glycine mutations, which were considered in the FEP studies,42, 43 require the ability to change the charge on the C_α atom and to scale CMAP interactions72, 73 by λ, which are not currently implemented in the CHARMM molecular dynamics package. Proline mutations are even more challenging, requiring topology changes via the opening of a ring.74 Such mutations could be allowed through the use of soft bonds75, 76 and other advances. Overcoming these limitations with charged, G, and P mutants represents an important direction for future MSλD development.

The present study aimed to assess the level of accuracy attainable with MSλD, not necessarily to obtain the desired free energy changes with the greatest efficiency. In particular, full production was run with five independent trials, and then discarded if the biasing potentials were determined to be suboptimal. Running fewer production runs to see if biases were converged before launching all five trials ^∥ or combining subsequent production runs together with the weighted histogram analysis method (WHAM)77 would likely allow comparable precision with even less computational expense and should be considered in the future.

Sampling is a constant concern, and it is worth noting the sampling difficulties encountered with this approach. While MSλD gives good results for even the nine sequence A98 system, the very long structural autocorrelation time in this system (Fig. 2) reveals sampling difficulties that are obscured by VB‐REX. Individual replicas are either trapped in a state transitioning slowly between W and F or in a state rapidly transitioning between the remaining seven side chains. As both states are included in the full set of replicas, reasonable free energy estimates can still be obtained. However, advanced sampling techniques beyond VB‐REX, such as orthogonal space random walk (OSRW)27 or replica exchange with solute tempering (REST)78 may allow more facile transitions between all mutants and yield superior results. In addition, biasing potentials changed between the 5 ns flattening simulations and the full length production simulations, which suggests that the system does not fully relax in 5 ns. It is likely the system is still not fully relaxed after 20–40 ns, so longer production simulations might allow further relaxation, which could improve agreement with experiment.

Prospects of MSλD for protein design

The FEP folding study offered discouraging prospects for computational protein design, suggesting that favorable mutations could only be enriched by a factor of three above random, or possibly more if aggressive filtering were used.42 Such a strategy is not accurate enough to generate new stable sequences and thus requires constant experimental testing, and is of use primarily for designing enriched libraries for directed evolution. While useful, this may represent a step backward from the current state of the art in enzyme design, because it is perturbative and requires an existing enzyme with initial activity as a starting point, whereas programs like Rosetta are generative and can propose an enzyme with a new function as a starting point for directed evolution.12, 13, 79

We believe the present study offers more potential for two reasons. First, errors are smaller, suggesting MSλD can enrich favorable mutations at a greater rate. Second, errors for multisite mutants are comparable with errors for single site mutants, so errors appear not to compound significantly. This suggests that while the force field and experiment may disagree slightly, they capture the same physical effects, and do not diverge rapidly as one moves through sequence space. Therefore, MSλD offers the ability to accurately search combinatorially large sequence spaces, which is computationally intractable with FEP. Consequently, by searching larger regions of sequence space, MSλD possesses more potential for finding favorable cooperative mutations that can be aggressively screened.

The strength of MSλD lies in its ability to consider large combinatorial sequence spaces. Modern protein design algorithms function through a Monte Carlo annealing search of sequence space, in which tens to hundreds of thousands of point mutations are proposed sequentially80 with dozens to hundreds of alternative designs attempted in parallel.9, 11 The improved accuracy of alchemical free energy approaches comes at a high computational cost: multisite simulations with MSλD required 54 h for flattening and 26 h for production, which limits alchemical simulations to several dozen steps in sequence space. The point mutations considered by FEP are inadequate to optimize a protein sequence in such a small number of steps; however, MSλD enables much larger jumps in sequence space which may allow sequence optimization in a small number of steps.

The ability of MSλD to consider concurrent mutations is critical for efficiently navigating the topological complexities of sequence space81, 82 such as fitness valleys. A simple example of a fitness valley is a case where a small and a large residue are in contact in a well‐packed core. Even if switching the residue sizes is favorable, the pathways to do so lie through a fitness valley because either an unfavorable void or steric clash is introduced before the second compensating mutation can occur. Current design algorithms can cross fitness valleys of several ${\mathit{kT}}_{\text{Selection}}$ through the sheer number Monte Carlo steps. In contrast, alchemical methods like FEP that only propose point mutations cannot cross fitness valleys in the small number of Monte Carlo steps available. MSλD can overcome this limitation by considering concurrent mutations, which allow movement directly to the other side of the fitness valley in a single Monte Carlo step.

Conclusions

Multisite λ dynamics is a highly efficient and scalable alchemical free energy method that allows high accuracy estimation of changes in folding free energy for both single site and multisite mutants. The efficiency enables longer simulations that appear to relax more closely to equilibrium, while scalability allows the exploration of large combinatorial sequence spaces. This study represents a first step towards protein design with MSλD by quantifying the accuracy of MSλD and demonstrating its scalability to large sequence spaces.

Additional work is required to extend MSλD to poorly treated charged residues and technically excluded G and P residues. Extension of MSλD to charged residues will be aided by the identical formalism underlying MSλD and constant pH MD. These advances will enable protein design with the full palette of amino acids.

The strength of MSλD lies in its ability to consider large combinatorial sequence spaces, and find cooperative mutations within them that enable efficient navigation of the protein sequence landscape. This scalability is essential due to the high cost of alchemical free energy calculations. The accuracy, efficiency, and combinatorial scalability of MSλD suggest it will become a powerful tool for protein design in the future.

Methods

Multisite λ dynamics

Like most free energy methods, MSλD relies on a thermodynamic scheme such as the one shown in Figure 4 to calculate free energy differences. As free energy is a state function, sequences S ₁ and S ₂ can be compared by calculating ΔΔG_Folding(S₁ → S₂) in one of the two ways:

$$\mathrm{\Delta \Delta }{G}_{\text{Folding}}\left(S_1\to S_2\right)=\mathrm{\Delta }{G}_{\text{Folding}}\left(S_2\right)-\mathrm{\Delta }{G}_{\text{Folding}}\left(S_1\right)$$

$$=\mathrm{\Delta }{G}_{\text{Folded}}\left(S_1\to S_2\right)-\mathrm{\Delta }{G}_{\text{Unfolded}}\left(S_1\to S_2\right)$$ (1)

Figure 4.

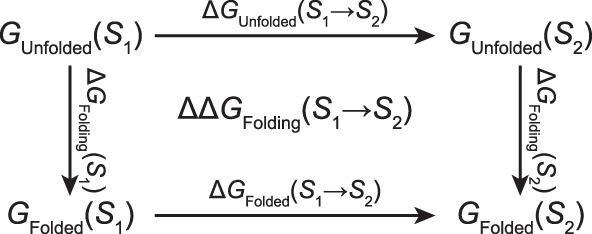
Thermodynamic scheme that enables the calculation of ΔΔG_Folding(S₁ → S₂), the change in folding free energy upon mutation from sequence S ₁ to sequence S ₂. The folded ensemble is modeled starting from the crystal structure, the unfolded ensemble is modeled using a capped pentapeptide.

While the first expression converges slowly because many folding transitions are required for convergence, the second expression converges rapidly and is readily obtained by alchemically transforming from S ₁ to S ₂ in both the folded and unfolded ensembles.

Alchemical free energy methods accomplish this transformation through a coupling parameter λ, which tunes the potential energy function from sequence S ₁ at λ = 0 through nonphysical intermediates to sequence S ₂ at λ = 1. In traditional alchemical methods, several MD simulations are run at closely spaced fixed values of λ, and free energy differences are then estimated using FEP,20 TI,21 or multistate Bennett acceptance ratio (MBAR).83

In MSλD, λ is not fixed, but is rather a dynamic variable with a pseudomass and velocity that is propagated along with the other coordinates in the equations of motion. Consequently, MSλD only requires two simulations to estimate ΔΔG_Folding(S₁ → S₂), one for the folded ensemble and one for the unfolded ensemble. Furthermore, while traditional free energy methods are limited to pairwise comparisons between sequences, MSλD can evaluate multiple mutations at the same site or even multiple sites using a multidimensional λ space.24

Updated techniques

Recently, landscape flattening and soft‐core interactions have been shown to give marked improvements in MSλD predictions of ΔΔG.48 Those methods are used here with several important updates, including a new biasing potential that better flattens soft‐core landscapes and a more general flattening algorithm. A generalization of BP‐REX47 called VB‐REX is introduced to improve sampling on multisite systems. Finally, we extend the treatment of electrostatics from FSWITCH to PME following the work of Shen.36 See Supporting Information for full details.

The previous set of biasing potentials were designed to flatten alchemical free energy landscapes observed with hard‐core interactions. An additional biasing potential of the form

$$V_{\text{Skew}}=\sum _s^M\sum _i^{N_s}\sum _{j\ne i}^{N_s}{\chi }_{\mathit{si},\mathit{sj}}{\lambda }_{\mathit{sj}}\left(1-\exp \left(-{\lambda }_{\mathit{si}}/\sigma \right)\right),$$ (2)

with σ = 0.18, was found to give improved fits to free energy profiles obtained with soft‐core interactions. The previous flattening algorithm handled a variety of special cases on an individual basis, and could not be easily modified to accommodate additional biasing potentials such as Equation (2).

In the present work a more generalizable approach was used to learn biasing potential parameters to flatten the landscape. Free energy profiles are computed from several recent sampling iterations using WHAM,77 the entropy of the implicit constraints is subtracted,46 and changes in the biasing potential parameters Δφ_si,  Δψ_{si, sj},  Δχ_{si, sj}, and Δω_{si, sj} are computed for the next round of sampling. A scoring function for proposed changes in parameters at each site s is constructed as

$$E=\sum _p^{\text{Profiles}}\sum _b^{\text{Bins}}\frac{w_{\mathit{pb}}}{2}{\left(G_{\mathit{pb}}+\mathrm{\Delta }{G}_{\mathit{pb}}-{\overline{G}}_p\right)}^2+\sum _i^{\text{Biases}}\frac{k}{2{{\gamma }_0}^2}\mathrm{\Delta }{{\gamma }_i}^2$$ (3)

$$\mathrm{\Delta }{G}_{\mathit{pb}}=\sum _i^{\text{Biases}}\frac{\partial G_{\mathit{pb}}}{\partial {\gamma }_i}\mathrm{\Delta }{\gamma }_i,$$ (4)

where γ _i runs over all biasing potential parameters in the set {φ_si, ψ_{si, sj}, χ_{si, sj}, ω_{si, sj}}. The first term of Equation (3) assesses landscape flatness and predicts the effects of changes in biasing parameters on landscape flatness through the linear approximation of ΔG_pb, and the second term prevents overfitting. The scoring function is minimized at each site s independently using least squares with ${\overline{G}}_{\mathit{pb}}$ and Δγ_i as free parameters. This flattening algorithm can be easily generalized to other biasing potentials.

As in the previous version of ALF,48 50 cycles of optimization were run with 100 ps of equilibration and 100 ps of sampling, followed by 10 cycles of optimization with 100 ps of equilibration and 1 ns of sampling. We observed that biasing potentials at the end of the 1 ns cycles were still suboptimal for some of the more slowly converging sites (e.g. A42, A98, and M102), so an additional phase with three cycles of 2 ns of equilibration and 5 ns of sampling were added to the protocol for all sites. For production, five independent simulations were run for 40 ns each, or 20 ns when using VB‐REX. It was observed often that some substituents stopped being sampled after the system had relaxed, therefore the first quarter of all production runs was discarded as equilibration. If sampling was poor during the remainder of production, landscape flattening parameters were reestimated and an additional one to three rounds of production were run, until all substituents were being sampled efficiently during the remainder of production. (See Supporting Information Table S2 for details.)

Inspired by BP‐REX,47 a new form of biasing potential replica exchange on the variable biases (VB‐REX) was implemented to encourage interconversion of side chains in low replicas, and endpoint sampling in high replicas. This was achieved by changing the biasing potential parameters between neighboring replicas by Δψ_{si, sj} = 2B and Δω_{si, sj} = 0.5B for all si‐sj combinations, in order to change the barrier height by B. Parameters vary with the number of sites, where B is tuned to optimize exchange rates, while the number of replicas and the replica flattened by ALF are tuned to sample primarily physical endpoint states in the final replica. For the five mutation site system, even the small 1.8 kcal/mol barrier in the final replica was adequate to increase the sampling of approximately physical states (λ > 0.99 at all sites) by about two orders of magnitude.

Three different electrostatic models were considered in this work: force shifting (FSHIFT), FSWITCH, and PME. In preliminary simulations, FSHIFT showed poorer correlation with experiment and roughly 0.5 kcal/mol greater RMSE, so only FSWITCH and PME results are reported. FSWITCH multiplies the electrostatic force by a function that decays smoothly from one to zero within a narrow range, but neglects long range electrostatics.53 PME splits the electrostatic potential into a short range piece accurately calculated with cutoffs and a smooth long range piece accurately calculated in Fourier space.54, 55 Using PME in MSλD simulations is not trivial, and we follow the approach of Shen.36 Alchemical simulations involving a net change in charge can result in significant artifacts.84, 85, 86 While corrections for these effects have been devised for PME,56 they were not applied in the present work as only two of the considered mutants involved a charge change. Application of these corrections is deferred until it can be tested more systematically.

Simulation details

Simulations began from the T4 lysozyme structure with the disulfide C54T/C97A mutated out (PDB ID: http://firstglance.jmol.org/fg.htm?mol=1L63).87 The unfolded ensemble was modeled through the use of short capped pentapeptides starting from their conformation in the crystal structure. The pentapeptide N‐terminus was capped with an acetyl group (—COCH₃) and the C‐terminus was capped with an amide group (—NH₂). The unfolded ensemble for multisite systems was treated as an independent sum of the pentapeptide systems for each individual mutation site. Folded lysozyme and unfolded pentapeptides were solvated with TIP3P88 in 72 Å and 40 Å cubic boxes respectively giving margins of at least 10 Å on each side. Residues were protonated according to pKa predictions by PropKa89 at pH values corresponding to experimental measurements, either 3.0 or 5.4. At a pH of 5.4, all K, R, and H were positive, and all D and E were negative. At a pH of 3.0, only D47, E62, D89, D92, and D159 remained negative. NaCl ions were added to a molality of 100 millimolal, and the system was neutralized by switching an appropriate number of Na⁺ to Cl⁻.

Simulations were run with the CHARMM molecular dynamics engine90, 91 using the DOMDEC module92 for GPU. Folded simulations achieved roughly 18 ns/day and unfolded pentapeptide simulations achieved 67 ns/day with each replica using four OpenMP threads on an Intel Xeon E5‐2650 v3 CPU and an Nvidia GeForce GTX 980 GPU. Simulations used the CHARMM36 force field.73, 93 Mutating residues were modeled using the patch facility of CHARMM. Every mutation site had a single C_α atom and side chains for each mutation were attached starting at the C_β atom with appropriate bonds, angles, dihedrals, impropers, and 1–4 interactions. Each side chain is assigned to a different block in the CHARMM block module. The nonbonded potential terms of each side chain are scaled by the appropriate λ (or product of λs for site‐site interactions) and do not interact with other side chains at the same site. Soft‐core nonbonded interactions were used as described in Reference [48]. Most bonded interactions are not scaled by λ in order to maintain side chain geometry when it is in the off state. Historically, dihedrals have not been scaled in MSλD, but scaling dihedrals that include side chain atoms was necessary here, otherwise the side chain C_β—C_α—NH—C and C_β—C_α—C—O dihedrals (with dihedral amplitudes of 1.8 and 1.4 kcal/mol) would be double counted by the number of side chains at a site. As these dihderals involve the same rotatable bonds as protein backbone φ and ψ angles, respectively, such double counting would have adverse consequences on the protein backbone conformations. CMAP interactions72, 73 do not include side chain atoms, so only one CMAP interaction is present per residue, and scaling it is unnecessary.

Supporting information

Appendix S1: Supporting Information