Abstract
The R package frailtySurv for simulating and fitting semi-parametric shared frailty models is introduced. Package frailtySurv implements semi-parametric consistent estimators for a variety of frailty distributions, including gamma, log-normal, inverse Gaussian and power variance function, and provides consistent estimators of the standard errors of the parameters’ estimators. The parameters’ estimators are asymptotically normally distributed, and therefore statistical inference based on the results of this package, such as hypothesis testing and confidence intervals, can be performed using the normal distribution. Extensive simulations demonstrate the flexibility and correct implementation of the estimator. Two case studies performed with publicly available datasets demonstrate applicability of the package. In the Diabetic Retinopathy Study, the onset of blindness is clustered by patient, and in a large hard drive failure dataset, failure times are thought to be clustered by the hard drive manufacturer and model.
Keywords: shared frailty model, survival analysis, clustered data, frailtySurv, R
1. Introduction
The semi-parametric Cox proportional hazards (PH) regression model was developed by Sir David Cox (1972) and is by far the most popular model for survival analysis. The model defines a hazard function, which is the rate of an event occurring at any given time, given the observation is still at risk, as a function of the observed covariates. When data consist of independent and identically distributed observations, the parameters of the Cox PH model are estimated using the partial likelihood (Cox 1975) and the Breslow (1974) estimator.
Often, the assumption of independent and identically distributed observations is violated. In clinical data, it is typical for survival times to be clustered or depend on some unobserved covariates. This can be due to geographical clustering, subjects sharing common genes, or some other predisposition that cannot be observed directly. Survival times can also be clustered by subject when there are multiple observations per subject with common baseline hazard. For example, the Diabetic Retinopathy Study was conducted to determine the time to the onset of blindness in high risk diabetic patients and to evaluate the effectiveness of laser treatment. The treatment was administered to one randomly-selected eye in each patient, leaving the other eye untreated. Obviously, the two eyes’ measurements of each patient are clustered by patient due to unmeasured patient-specific effects.
Clustered survival times are not limited to clinical data. Computer components often exhibit clustering due to different materials and manufacturing processes. The failure rate of magnetic storage devices is of particular interest since component failure can result in data loss. A large backup storage provider may utilize tens of thousands of hard drives consisting of hundreds of different hard drive models. In evaluating the time until a hard drive becomes inoperable, it is important to consider operating conditions as well as the hard drive model. Hard drive survival times depend on the model since commercial grade models may be built out of better materials and designed to have longer lifetimes than consumer grade models. The above two examples are used in Section 5 for demonstrating the usage of the frailtySurv package (Monaco, Gorfine, and Hsu 2018).
Clayton (1978) accounted for cluster-specific unobserved effects by introducing a random effect term into the proportional hazards model, which later became known as the shared frailty model. A shared frailty model includes a latent random variable, the frailty, which comprises the unobservable dependency between members of a cluster. The frailty has a multiplicative effect on the hazard, and given the observed covariates and unobserved frailty, the survival times within a cluster are assumed independent.
Under the shared frailty model, the hazard function at time t of observation j of cluster i is given by
| (1) |
where ωi is an unobservable frailty variate of cluster i, λ0(t) is the unknown common baseline hazard function, β is the unknown regression coefficient vector, and Zij is the observed vector of covariates of observation j in cluster i. The frailty variates ω1,…,ωn, are independent and identically distributed with known density f (‧;θ) and unknown parameter θ.
There are currently several estimation techniques available with a corresponding R package (R Core Team 2018) for fitting a shared frailty model, as shown in Table 1. In a parametric model, the baseline hazard function is of known parametric form, with several unknown parameters. Parameter estimation of parametric models is performed by the maximum marginal likelihood (MML) approach (Duchateau and Janssen 2007; Wienke 2010). The parfm package (Munda, Rotolo, and Legrand 2012) implements several parametric frailty models. In a semi-parametric model, the baseline hazard function is left unspecified, a highly important feature, as often in practice the shape of the baseline hazard function is unknown. Under the semi-parametric setting, the top downloaded packages, survival (Therneau 2018b) and coxme (Therneau 2018a), implement the penalized partial likelihood (PPL). frailtypack parameter estimates are obtained by nonlinear least squares (NLS) with the hazard function and cumulative hazard function modeled by a 4th order cubic M-spline and integrated M-spline, respectively (Rondeau, Mazroui, and Gonzalez 2012). Since the frailty term is a latent variable, expectation maximization (EM) is also a natural estimation strategy for semi-parametric models, implemented by phmm (Donohue and Xu 2017). More recently, a hierarchical-likelihood (h-likelihood, or HL) method (Do Ha, Lee, and kee Song 2001) has been used to fit hierarchical shared frailty models, implemented by frailtyHL (Do Ha, Noh, and Lee 2018). Both R packages R2BayesX (Brezger, Kneib, and Lang 2005; Gu 2014) and gss (Hirsch and Wienke 2012) can fit a shared frailty model and support only Gaussian random effects with the baseline hazard function estimated by penalized splines.
Table 1:
R functions for fitting shared frailty models. NP = nonparametric, P = parametric, PPL = penalized partial likelihood, NLS = nonlinear least squares, EM = expectation maximization, PFL = pseudo full likelihood, HL = h-likelihood, MML = maximum marginal likelihood, LN = log-normal, LT = log-t, IG = inverse Gaussian, PS = positive stable. Weekly downloads are averages from the time the package first appears on the RStudio CRAN mirror through 2016-06-01, as reported by the RStudio CRAN package download logs: http://cran-logs.rstudio.com/.
| package: :function | λ0 | Estimation procedure | Frailty distributions | Weekly downloads |
|---|---|---|---|---|
| survival: :coxph | NP | PPL | Gamma, LN, LT | 3905 |
| gss: : sscox | NP | PPL | LN | 1120 |
| coxme: :coxme | NP | PPL | LN | 260 |
| frailtypack: :frailtyPenal | NP | NLS | Gamma, LN | 98 |
| R2BayesX: :bayesx | NP | PPL | LN | 58 |
| phmm: :phmm | NP | EM | LN | 52 |
| frailtySurv: :fitfrail | NP | PFL | Gamma, LN, IG, PVF | 50 |
| frailtyHL: :frailtyHL | NP | HL | Gamma, LN | 50 |
| parfm: :parfm | P | MML | Gamma, PS, IG | 49 |
| survBayes: :survBayes | NP | Bayes | Gamma, LN | 28 |
This work introduces the frailtySurv R package, an implementation of Gorfine, Zucker, and Hsu (2006) and Zucker, Gorfine, and Hsu (2008), wherein an estimation procedure for semi-parametric shared frailty models with general frailty distributions was proposed. Gorfine et al. (2006) addresses some limitations of other existing methods. Specifically, all other available semi-parametric packages can only be applied with gamma, log-normal (LN), and log-t (LT) frailty distributions. In contrast, the semi-parametric estimation procedure used in frailtySurv supports general frailty distributions with finite moments, and the current version of frailtySurv implements gamma, log-normal, inverse Gaussian (IG), and power variance function (PVF) frailty distributions. Additionally, the asymptotic properties of most of the semi-parametric estimators in Table 1 are not known. In contrast, the regression coefficients’ estimators, the frailty distribution parameter estimator, and the baseline hazard estimator of frailtySurv are backed by a rigorous large-sample theory (Gorfine et al. 2006; Zucker et al. 2008). In particular, these estimators are consistent and asymptotically normally distributed. A consistent covariance-matrix estimator of the regression coefficients’ estimators and the frailty distribution parameter’s estimator is provided by Gorfine et al. (2006) and Zucker et al. (2008), also implemented by frailtySurv. Alternatively, frailtySurv can perform variance estimation through a weighted bootstrap procedure. Package frailtySurv is available from the Comprehensive R Archive Network (CRAN) at https://CRAN.R-project.org/package=frailtySurv.
While some of the packages in Table 1 contain synthetic and/or real-world survival datasets, none of them contain functions to simulate clustered data. There exist several other packages capable of simulating survival data, such as the rmultime function in the MST package (Calhoun, Su, Nunn, and Fan 2018), the genSurv function in survMisc (Dardis 2016), and survsim (Moriña and Navarro 2014), an R package dedicated to simulating survival data. These functions simulate only several frailty distributions. frailtySurv contains a rich set of simulation functions, described in Section 2, capable of generating clustered survival data under a wide variety of conditions. The simulation functions in frailtySurv are used to empirically verify the implementation of unbiased (bug-free) estimators through several simulated experiments.
The rest of this paper is organized as follows. Sections 2 and 3 describe the data generation and model estimation functions of frailtySurv, respectively. Section 4 demonstrates simulation capabilities and results. Section 5 is a case study of two publicly available datasets, including high-risk patients from the Diabetic Retinopathy Study and a large hard drive failure dataset. Finally, Section 6 concludes the paper. The currently supported frailty distributions are described in Appendix A, full simulation results are presented in Appendix B, and Appendix C contains an empirical analysis of runtime and accuracy.
2. Data generation
The genfrail function in frailtySurv can generate clustered survival times under a wide variety of conditions. The survival function at time t of the jth observation of cluster i, given time-independent covariate Zij and frailty variate ωi, is given by
| (2) |
where is the unspecified cumulative baseline hazard function. In the following sections we describe in detail the various options for setting each component of the above conditional survival function.
2.1. Covariates
Covariates can be sampled marginally from normal, uniform, or discrete uniform distributions, as specified by the covar.distr parameter. The value of β is specified to genfrail through the covar.param parameter. User-supplied covariates can also be passed as the covar.matrix parameter. There is no limit to the covariates’ vector dimension. However, the estimation procedure requires the number of clusters to be much higher than the number of covariates. These options are demonstrated in Section 2.7.
2.2. Baseline hazard
There are three ways the baseline hazard can be specified to generate survival data: as the inverse cumulative baseline hazard , the cumulative baseline hazard Λ0, or the baseline hazard λ0. If the cumulative baseline hazard function can be directly inverted, then failure times can be computed by
| (3) |
where Uij ~ U (0, 1) and is the failure time of member j of cluster i. Consequently, if is provided as parameter Lambda_0_inv in genfrail, then survival times are determined by Equation 3. This is the most efficient way to generate survival data.
When Λ0 cannot be inverted, one can use a univariate root-finding algorithm to solve
| (4) |
for failure time . Alternatively, taking the logarithm and solving
| (5) |
yields greater numerical stability. Therefore, genfrail uses Equation 5 when Λ0 is provided as parameter Lambda_0 in genfrail and uses the R function uniroot, which is based on Brent’s algorithm (Brent 2013).
If neither or Λ0 are provided to genfrail, then the baseline hazard function λ0 must be passed as parameter lambda_0. In this case,
| (6) |
is evaluated numerically. Using the integrate function in the stats package (R Core Team 2018), which implements adaptive quadrature, Equation 5 can be numerically solved for . This approach is the most computationally expensive since it requires numerical integration to be performed for each observation ij and at each iteration in the root-finding algorithm.
Section 2.7 demonstrates generating data using each of the above methods, which all generate failure times in the range [0, ∞). The computational complexity of each method is O (n) under the assumption that a constant amount of work needs to be performed for each observation. Despite this, the constant amount of work per observation varies greatly depending on how the baseline hazard is specified. Using the inverse cumulative baseline hazard, there exists an analytic solution for each observation and only arithmetic operations are required. Specifying the cumulative baseline hazard requires root finding for each observation, and specifying the baseline hazard requires both root finding and numerical integration for each observation. Since the time to perform root finding and numerical integration is not a function of n, the complexity remains linear in each case. Appendix C.1 contains benchmark simulations that compare the timings of each method.
2.3. Shared frailty
Shared frailty variates ω1,…,ωn are generated according to the specified frailty distribution, through parameters frailty and theta of genfrail, respectively. The available distributions are gamma with mean 1 and variance θ; PVF with mean 1 and variance 1 − θ; log-normal with mean exp(θ/2) and variance exp(2θ) − exp(θ); and inverse Gaussian with mean 1 and variance θ. genfrail can also generate frailty variates from a positive stable (PS) distribution, although estimation is not supported due to the PS having an infinite mean. The supported frailty distributions are described in detail in Appendix A. Specifying parameters that induce a degenerate frailty distribution, or passing frailty = “none”, will generate non-clustered data. Hierarchical clustering is currently not supported by frailtySurv.
The dependence between two cluster members can be measured by Kendall’s tau1, given by
| (7) |
where is the Laplace transform of the frailty distribution and , m = 1, 2,… are the mth derivatives of . If failure times of the two cluster members are independent, κ = 0. Figure 1 shows the densities of the supported distributions for various values of κ. Note that gamma, IG, and PS are special cases of the PVF. For gamma, LN, and IG, κ = 0 when θ = 0, and for PVF, κ = 0 when θ = 1. Also, for gamma and LN, limθ→∞ κ = 1, for IG limθ→∞ κ = 1/2, for PVF limθ→∞ κ = 1/3, and for PS κ = 1 − θ.
Figure 1:
Frailty distribution densities.
2.4. Cluster sizes
In practice, the cluster sizes mi, i = 1,…,n, can be fixed or may vary. For example, in the Diabetic Retinopathy Study, two failure times are observed for each subject, corresponding to the left and right eye. Hence, observations are clustered by subject, and each cluster has exactly two members. If instead the observations were clustered by geographical location, the cluster sizes would vary, e.g., according to a discrete power law distribution. genfrail is able to generate data with fixed or varying cluster sizes.
For fixed cluster size, the cluster size parameter K of genfrail is simply an integer. Alternatively, the cluster sizes may be specified by passing a length-N vector of the desired cluster sizes to parameter K. To generate varied cluster sizes, K is the name of the distribution to generate from, and K.param specifies the distribution parameters.
Cluster sizes can be generated from a κ-truncated Poisson with K = “poisson” (Geyer 2018). The truncated Poisson is used to ensure there are no zero-sized clusters and to enforce a minimum cluster size. The expected cluster size is given by
| (8) |
where λ is a shape parameter and k is the truncation point such that min {m1,…,mn} > k. The typical case is with k = 0 for a zero-truncated Poisson. For example, with λ = 2 and k = 0, the expected cluster size equals 2.313. The parameters of the k-truncated Poisson are determined in K.param = c(lambda, k) of genfrail.
A discrete Pareto (or zeta) distribution can also be used to generate cluster sizes with K = “pareto”. Accurately fitting and generating from a discrete power-law distribution is generally difficult, and genfrail uses a truncated discrete Pareto to avoid some of the pitfalls as described in Clauset, Shalizi, and Newman (2009). The probability mass function is given by
| (9) |
where ζ (s) is the Riemann zeta function, s is a scaling parameter, l is the noninclusive lower bound, and u is the inclusive upper bound. With large enough u and s ≫ 1, the distribution behaves similar to the discrete Pareto distribution and the expected cluster size equals . The distribution parameters are specified as K.param = c(s, u, l). Finally, a discrete uniform distribution can be specified by K = “uniform” in genfrail. The respective parameters to K.param are c(l, u), where l is the noninclusive lower bound and u is the inclusive upper bound. Similar to the truncated zeta, the support is {l + 1,…,u} while each cluster size is uniformly selected from this set of values. Since the lower bound is noninclusive, the expected cluster size equals (1 + l + u)/2.
2.5. Censoring
The observed times Tij and failure indicators δij are determined by the failure times and right-censoring times Cij such that the observed time of observation ij is given by
| (10) |
and the failure indicator is given by
| (11) |
Currently, only right-censoring is supported by frailtySurv. The censoring distribution is specified by the parameters censor.distr and censor.param for the distribution name and parameters’ vector, respectively. A normal distribution is used by default. A log-normal censoring distribution is specified by censor.distr = “lognormal” and censor.param = c(mu, sigma), where mu is the mean and sigma is the standard deviation of the censoring distribution. Lastly, a uniform censoring distribution can be specified by censor.distr = “uniform” and censor.param = c(lower, upper) for the lower and upper bounds on the interval, respectively.
Sometimes a particular censoring rate is desired. Typically, the censoring distribution parameters are varied to obtain a desired censoring rate. genfrail can avoid this effort on behalf of the user by letting the desired censoring rate be specified instead. In this case, the appropriate parameters for the censoring distribution are determined to achieve the desired censoring rate, given the generated failure times.
Let F and G be the failure time and censoring time cumulative distributions, respectively. Then, the censoring rate equals
| (12) |
where the expectation of equals the expectation of any random subject from the population. The above formula can be estimated by
| (13) |
where is the empirical cumulative distribution function. To obtain a particular censoring rate 0 < R < 1, as a function of the parameters of G, one can solve
| (14) |
For example, if G is the normal cumulative distribution function with mean μ and variance σ2, σ2 should be pre-specified (otherwise the problem is non-identifiable), and Equation 14 is solved for μ. This method works with any empirical distribution of failure times. genfrail uses this approach to achieve a desired censoring rate, specified by censor.rate, with normal, log-normal, or uniform censoring distributions. Lastly, user-supplied censorship times can be supplied through the censor.time parameter, which must be a vector of length N ∗ K, where N is the number of clusters and K is the size of each cluster. Because of this, censor.time cannot be used with variable-sized clusters.
2.6. Rounding
In some applications the observed times are rounded and tied failure times can occur. For example, the age at onset of certain diseases are often recorded as years of age rounded to the nearest integer. To simulate tied data, the simulated observed times may optionally be rounded to the nearest integer of multiple of B by
| (15) |
If B = 1, the observed times are simply rounded to the nearest integer. The value of B is specified by the parameter round.base of genfrail, with the default being the non-rounded setting.
2.7. Examples
The best way to see how genfrail works is through examples. R and frailtySurv versions are given by the following commands.
R> R.Version()$version.string
[1] “R version 3.4.3 (2017-11-30)”
R> packageDescription(“frailtySurv”, fields = “Version”)
[1] “1.3.5”
Consider the survival model defined in Equation 2 with baseline hazard function
| (16) |
where c = 0.01 and d = 4.6. Let Gamma (2) be the frailty distribution, two independent standard normally distributed covariates, and N (130, 152) the censoring distribution. The resulting survival times are representative of a late onset disease and with ~ 40% censoring rate. Generating survival data from this model, with 300 clusters and 2 members within each cluster, is accomplished by2
R> set.seed(2015)
R> dat <- genfrail(N = 300, K = 2, beta = c(log(2), log(3)),
+ frailty = “gamma”, theta = 2,
+ lambda_0 = function(t, c = 0.01, d = 4.6) (d * (c * t) ^ d) / t)
R> head(dat, 3)
family rep time status Z1 Z2
1 1 1 87.95447 1 −1.5454484 0.9944159
2 1 2 110.04615 0 −0.5283932 −0.9053164
3 2 1 119.94127 1 −1.0867588 0.5240979
Similarly, to generate survival data with uniform covariates from, e.g., 0.1 to 0.2, specify covar.distr = “uniform” and covar.param = c(0.1, 0.2) in the above example. The covariates may also be specified explicitly in a c(N ∗ K, length(beta)) matrix as the covar.matrix parameter.
In the above example, the baseline hazard function was specified by the lambda_0 parameter. The same dataset can be generated more efficiently using the Lambda_0 parameter if the cumulative baseline hazard function is known. This is accomplished by integrating Equation 16 to get the cumulative baseline hazard function
| (17) |
and passing this function as an argument to Lambda_0 when calling genfrail:
R> set.seed(2015)
R> dat.cbh <- genfrail(N = 300, K = 2, beta = c(log(2),log(3)),
+ frailty = “gamma”, theta = 2,
+ Lambda_0 = function(t, c = 0.01, d = 4.6) (c * t) ^ d)
R> head(dat.cbh, 3)
family rep time status Z1 Z2
1 1 1 87.95447 1 −1.5454484 0.9944159
2 1 2 110.04615 0 −0.5283932 −0.9053164
3 2 1 119.94127 1 −1.0867588 0.5240979
The cumulative baseline hazard in Equation 17 is invertible and it would be even more efficient to specify as
| (18) |
This avoids the numerical integration, required by Equation 6, and root finding, required by Equation 5. Equation 18 should be passed to genfrail as the Lambda_0_inv parameter, again producing the same data when the same seed is used:
R> set.seed(2015)
R> dat.inv <- genfrail(N = 300, K = 2, beta = c(log(2),log(3)),
+ frailty = “gamma”, theta = 2,
+ Lambda_0_inv = function(t, c = 0.01, d = 4.6) (t ^ (1 / d)) / c)
R> head(dat.inv, 3)
family rep time status Z1 Z2
1 1 1 87.95447 1 −1.5454484 0.9944159
2 1 2 110.04615 0 −0.5283932 −0.9053164
3 2 1 119.94127 1 −1.0867588 0.5240979
A different frailty distribution can be specified while ensuring an expected censoring rate by using the censor.rate parameter. For example, consider a PVF (0.3) frailty distribution while maintaining the 40% censoring rate in the previous example. The censoring distribution parameters are determined by genfrail as described in Section 2.5 by specifying censor.rate = 0.4. This avoids the need to manually adjust the censoring distribution to achieve a particular censoring rate. The respective code and output are:
R> set.seed(2015)
R> dat.pvf <- genfrail(N = 300, K = 2, beta = c(log(2),log(3)),
+ frailty = “pvf”, theta = 0.3, censor.rate = 0.4,
+ Lambda_0_inv = function(t, c = 0.01, d = 4.6) (t ^ (1 / d)) / c)
R> summary(dat.pvf)
genfrail created : 2018-06-14 13:46:36
Observations : 600
Clusters : 300
Avg. cluster size : 2.00
Right censoring rate : 0.39
Covariates : normal(0, 1)
Coefficients : 0.6931, 1.0986
Frailty : pvf(0.3)
Baseline hazard : Lambda_0 = function (t, tau = 4.6, C = 0.01) (t^(1/tau))/C
3. Model estimation
The fitfrail function in frailtySurv estimates the regression coefficient vector β, the frailty distribution’s parameter θ, and the non-parametric cumulative baseline hazard Λ0. The observed data consist of {Tij, Zij, δij} for i = 1,…,n and j = 1,…,mi, where the n clusters are independent. fitfrail takes a complete observation approach, and observations with missing values are ignored with a warning.
There are two estimation strategies that can be used. The log-likelihood can be maximized directly, by using control parameter fitmethod = “loglik”, or a system of score equations can be solved with control parameter fitmethod = “score”. Both methods have comparable computational requirements and yield comparable results. In both methods, the estimation procedure consists of a doubly-nested loop, with an outer loop that evaluates the objective function and gradients and an inner loop that estimates the piecewise constant hazard, performing numerical integration at each time step if necessary. As a result, the estimator implemented in frailtySurv has computationally complexity on the order of O (n2)
3.1. Log-likelihood
The full likelihood can be written as
| (19) |
where τ is the end of follow-up period, f is the frailty’s density function,Nij (t) = δijI (Tij ≤ t), , and , j = 1,…,mi, i = 1,…,n. Note that the mth derivative of the Laplace transform evaluated at Hi. (τ) equals , i = 1,…,n. the log-likelihood equals
| (20) |
Evidently, to obtain estimators and based on the log-likelihood, an estimator of Λ0, denoted by , is required. For given values of β and θ, Λ0 is estimated by a step function with jumps at the ordered observed failure times τk, k = 1,…,K, defined by
| (21) |
where dk is the number of failures at time τk, i (γ, Λ, t) = ϕ2i (γ, Λ, t) /ϕ1i (γ, Λ, t), Yij (t) = I (Tij ≥ t), and
For the detailed derivation of the above baseline hazard estimation the reader is referred to Gorfine et al. (2006). The estimator of the cumulative baseline hazard at time τk is given by
| (22) |
and is a function of , i.e., at each τk, the cumulative baseline hazard estimator is a function of with t < τk. Then, for obtaining and , is substituted into ℓ(β, θ, Λ0).
In summary, the estimation procedure of Gorfine et al. (2006) consists of the following steps:
Step 1. Use standard Cox regression software to obtain initial estimates of β, and set the initial value of θ to be its value under within-cluster independence or under very week dependency (see also the discussion at the end of Section 3.2).
Step 2. Use the current values of β and θ to estimate Λ0 based on the estimation procedure defined by Equation 21.
Step 3. Using the current value of , estimate β and θ by maximizing l(β, θ, ).
Step 4. Iterate between Steps 2 and 3 until convergence.
For frailty distributions with no closed-form Laplace transform, the integral can be evaluated numerically. This adds a considerable overhead to each iteration in the estimation procedure since the integrations must be performed for the baseline hazard estimator that is required for estimating β and θ, as .
With control parameter fitmethod = “loglik”, the log-likelihood is the objective function maximized directly with respect to γ = (β⊤, θ)⊤, for any given Λ0, by optim in the stats package using the L-BFGS-B algorithm (Byrd, Lu, Nocedal, and Zhu 1995). Box constraints specify bounds on the frailty distribution parameters, typically θ ∈ (0, ∞) except for PVF which has θ ∈ (0, 1). Convergence is determined by the relative reduction in the objective function through the reltol control parameter. By default, this is 10−6.
As an example, consider fitting a model to the data generated in Section 2. The following result shows that convergence is reached after 11 iterations and 15.8 seconds, running Red Hat 6.5, R version 3.2.2, and 2.6 GHz Intel Sandy Bridge processor:
R> fit <- fitfrail(Surv(time, status) ~ Z1 + Z2 + cluster(family),
+ dat, frailty = “gamma”, fitmethod = “loglik”)
R> fit
Call: fitfrail(formula = Surv(time, status) ~ Z1 + Z2 + cluster(family),
dat = dat, frailty = “gamma”, fitmethod = “loglik”)
Covariate Coefficient
Z1 0.719
Z2 1.194
Frailty distribution gamma(1.716), VAR of frailty variates = 1.716
Log-likelihood −2507.725
Converged (method) 11 iterations, 6.75 secs (maximized log-likelihood)
3.2. Score equations
Instead of maximizing the log-likelihood, one can solve the score equations. The score function with respect to β is given by
| (23) |
Note that corresponds to ψi in with Gorfine et al. (2006). The score function respect to θ is given by
| (24) |
The score equations are given by U(β, θ, Λ0) = (Uβ, Uθ) = 0 and the estimator of γ = (β⊤, θ) is defined as the value of (β⊤, θ) that solves the score equations for any given Λ0. Specifically, the only change required in the above summary of the estimation procedure, is to replace Step 3 with the following
Step 3’. Using the current value of , estimate β and θ by solving U(β, θ, ) = 0.
frailtySurv uses Newton’s method implemented by the nleqslv package to solve the system of equations (Hasselman 2017). Convergence is reached when the relative reduction of each parameter estimate or absolute value of each normalized score is below the threshold specified by reltol or abstol, respectively. The default is a relative reduction of less than 10−6, i.e., reltol = 1e-6.
As an example, in the following lines of code and output we consider again the data generated in Section 2. The results are comparable to the fitted model in Section 3.1. The score equations can usually be solved in fewer iterations than maximizing the likelihood, although solving the system of equations requires more work in each iteration. For this reason, maximizing the likelihood is typically more computationally efficient for large datasets when a permissive convergence criterion is specified.
R> fit.score <- fitfrail(Surv(time, status) ~ Z1 + Z2 + cluster(family),
+ dat, frailty = “gamma”, fitmethod = “score”)
R> fit.score
Call: fitfrail(formula = Surv(time, status) ~ Z1 + Z2 + cluster(family),
dat = dat, frailty = “gamma”, fitmethod = “score”)
Covariate Coefficient
Z1 0.719
Z2 1.194
Frailty distribution gamma(1.716), VAR of frailty variates = 1.716
Log-likelihood −2507.725
Converged (method) 10 iterations, 6.50 secs (solved score equations)
L-BFGS-B, used for maximizing the log-likelihood, allows for (possibly open-ended) box constraints. In contrast, Newton’s method, used for solving the system of score equations, does not support the use of box constraints and, therefore, has a risk of converging to a degenerate parameter value. In this case, it is more important to have a sensible starting value. In both estimation methods, the regression coefficient vector β is initialized to the estimates given by coxph with no shared frailty. The frailty distribution parameters are initialized such that the dependence between members in each cluster is small, i.e, with κ ≈ 0.3.
3.3. Baseline hazard
The estimated cumulative baseline hazard defined by Equation 22 is accessible from the resulting model object through the fit$Lambda member, which provides a data.frame with the estimates at each observed failure time, or the fit$Lambda.fun member, which defines a scalar R function that takes a time argument and returns the estimated cumulative baseline hazard. The estimated survival curve or cumulative baseline hazard can also be summarized by the summary method for objects returned by fitfrail resulting in a data.frame. In the example below, the n.risk column contains the number of observations still at risk at time t− and the n.event column contains the number of failures from the previous time listed to time t+. The output is similar to that of the summary method for ‘survfit’ objects in the survival package.
R> head(summary(fit), 3)
time n.risk n.event surv
1 23.37616 600 1 0.9992506
2 24.38503 599 1 0.9984604
3 25.14435 598 1 0.9976600
R> tail(summary(fit), 3)
time n.risk n.event surv
384 139.5629 42 1 0.0016570493
385 140.5862 39 1 0.0011509892
386 141.3295 36 1 0.0007665802
By default, the survival curve estimates at observed failure times are returned. Estimates at the censored observed times are included if censored = TRUE is passed to the summary method for ‘fitfrail’ objects. The cumulative baseline hazard estimates are summarized by parameter type = “cumhaz”. The estimates can also be evaluated at specific times passed to the summary method for ‘fitfrail’ objects through the Lambda.times parameter, demonstrated by:
R> summary(fit, type = “cumhaz”, Lambda.times = c(20, 50, 80, 110))
time n.risk n.event cumhaz
1 20 600 0 0.00000000
2 50 566 34 0.03248626
3 80 439 127 0.33826069
4 110 274 147 1.69720757
3.4. Standard errors
There are two ways the standard errors can be obtained for a fitted model. The covariance matrix of , the estimators of the regression coefficients and the frailty parameter, can be obtained explicitly based on the sandwich-type consistent estimator described in Gorfine et al. (2006) and Zucker et al. (2008). The covariance matrix is calculated by the vcov function applied to the ‘fitfrail’ object returned by fitfrail. Optionally, standard errors can also be obtained in the call to fitfrail by passing se = TRUE. Using the above fitted model, the covariance matrix of is obtained by
R> COV.est <- vcov(fit)
R> sqrt(diag(COV.est))
Z1 Z2 theta.1
0.09343685 0.12673624 0.36020143
frailtySurv can also estimate standard errors through a weighted bootstrap approach, in which the variance of both and are determined3. The weighted bootstrap procedure consists of independent and identically distributed positive random weights applied to each cluster. This is in contrast to a nonparametric bootstrap, wherein each bootstrap sample consists of a random sample of clusters with replacement. The resampling procedure of the nonpara-metric bootstrap usually yields an increased number of ties compared to the original data, which sometimes causes convergence problems. Therefore, we adopt the weighted bootstrap approach which does not change the number of tied observations in the original data. The weighted bootstrap is summarized as follows.
Sample n random values from an exponential distribution with mean 1. Standardize the values by the empirical mean to obtain standardized weights v1,…,vn.
In the estimation procedure, each function of form is replaced be the be the corresponding weighted function , where , and , i = 1,…,n.
Repeat Steps 1–2 B times and take the empirical variance (and covariance) of the B parameter estimates to obtain the weighted bootstrap variance (and covariance).
For smaller datasets, this process is generally more time-consuming than the explicit estimator. If the parallel package is available, all available cores are used to obtain the bootstrap parameter estimates in parallel (R Core Team 2018). Without the parallel package, vcov runs in serial.
R> set.seed(2015)
R> COV.boot <- vcov(fit, boot = TRUE, B = 500)
R> sqrt(diag(COV.boot))[1:8]
Z1 Z2 theta.1 Lambda. 0.00000
0.0742560635 0.0984509739 0.2568936409 0.0000000000
Lambda. 23.37616 Lambda. 24.38503 Lambda. 25.14435 Lambda. 25.33731
0.0006340182 0.0010267995 0.0012781985 0.0014768459
In the preceding example, the full covariance matrix for is obtained. If only certain time points of the estimated cumulative baseline hazard function are desired, these can be specified by the Lambda.times parameter Since calls to vcov method for ‘fitfrail’ objects are typically computationally expensive, the results are cached when the same arguments are provided.
3.5. Control parameters
Control parameters provided to fitfrail determine the speed, accuracy, and type of estimates returned. The default control parameters to fitfrail are given by calling the function fitfrail.control(). This returns a named list with the following members.
fitmethod: Parameter estimation procedure. Either “score” to solve the system of score equations or “loglik” to estimate using the log-likelihood. Default is “loglik”.
abstol: Absolute tolerance for convergence. Default is 0 (ignored).
reltol: Relative tolerance for convergence. Default is 1e-6.
maxit: The maximum number of iterations before terminating the estimation procedure.Default is 100.
int.abstol: Absolute tolerance for numerical integration convergence. Default is 0 (ignored).
int.reltol: Relative tolerance for numerical integration convergence. Default is 1.
int.maxit: The maximum number of function evaluations in numerical integration. Default is 1000.
verbose: If verbose = TRUE, the parameter estimates and log-likelihood are printed at each iteration. Default is FALSE.
The parameters int.abstol, int.reltol, and int.maxit are only used for frailty distributions that require numerical integration, as they specify convergence criteria of numerical integration in the estimation procedure inner loop. These control parameters can be adjusted to obtain an speed-accuracy tradeoff, whereby lower int.abstol and int.reltol (and higher int.maxit) yield more accurate numerical integration at the expense of more work performed in the inner loop of the estimation procedure.
The abstol, reltol, and maxit parameters specify convergence criteria of the outer loop of the estimation procedure. Similar to the numerical integration convergence parameters, these can also be adjusted to obtain a speed-accuracy tradeoff using either estimation procedure (fitmethod = “loglik” or fitmethod = “score”). If fitmethod = “loglik”, convergence is reached when the absolute or relative reduction in log-likelihood is less than abstol or reltol, respectively. Using fitmethod = “score” and specifying abstol > 0 (with reltol = 0), convergence is reached when the absolute value of each score equation is below abstol. Alternatively, using fitmethod = “score” and specifying reltol > 0 (with abstol = 0), convergence is reached when the relative reduction of parameter estimates is below reltol. Note that with fitmethod = “score”, abstol and reltol correspond to parameters ftol and xtol of nleqslv::nleqslv, respectively. The default convergence criteria were chosen to yield approximately the same results with either estimation strategy.
3.6. Model object
The resulting model object returned by fitfrail contains the regression coefficients’ vector, the frailty distribution’s parameters, and the cumulative baseline hazard. Specifically:
beta: Estimated regression coefficients’ vector named by the input data columns.
theta: Estimated frailty distribution parameter.
loglik: The resulting log-likelihood.
Lambda: data.frame with the cumulative baseline hazard at the observed failure times.
Lambda.all: data.frame with the cumulative baseline hazard at all observed times.
Lambda.fun: Scalar R function that returns the cumulative baseline hazard at any time point.
The model object also contains some standard attributes, such as call for the function call. If se = TRUE was passed to fitfrail, then the model object will also contain members se.beta and se.theta for the standard error of the regression coefficients’ vector and frailty parameter estimates, respectively.
4. Simulation
As an empirical proof of implementation, and to demonstrate flexibility, several simulations were conducted. The simfrail function can be used to run a variety of simulation settings. Simulations are run in parallel if the parallel package is available, and the mc.cores parameter specifies how many processor cores to use. For example,
R> set.seed(2015)
R> sim <- simfrail(1000,
+ genfrail.args = alist(beta = c(log(2),log(3)), frailty = “gamma”,
+ censor.rate = 0.30, N = 300, K = 2, theta = 2,
+ covar.distr = “uniform”, covar.param = c(0, 1),
+ Lambda_0 = function(t, c = 0.01, d = 4.6) (c * t) ^ d),
+ fitfrail.args = alist(
+ formula = Surv(time, status) ~ Z1 + Z2 + cluster(family),
+ frailty = “gamma”), Lambda.times = 1:120)
R> summary(sim)
Simulation: 1000 reps, 300 clusters (avg. size 2), gamma frailty
Serial runtime (s): 9680.18 (9.68 +/− 1.53 per rep)
beta.1 beta.2 theta.1 Lambda.30 Lambda.60 Lambda.90
value 0.6931 1.0986 2.0000 0.003933 0.09539 0.6159
mean.hat 0.6821 1.0929 1.9752 0.003995 0.09716 0.6236
sd.hat 0.2472 0.2529 0.2659 0.001876 0.02248 0.1387
mean.se 0.3130 0.3156 0.3442 NA NA NA
cov.95CI 0.9890 0.9850 0.9780 NA NA NA
The above results indicate that the empirical coverage rates are reasonably close to the nominal 95% coverage rate. These results can also be compared to the estimates obtained by coxph which applies the PPL approach with gamma frailty model:
R> set.seed(2015)
R> sim.coxph <- simcoxph(1000,
+ genfrail.args = alist(beta = c(log(2), log(3)), frailty = “gamma”,
+ censor.rate = 0.30, N = 300, K = 2, theta = 2,
+ covar.distr = “uniform”, covar.param = c(0, 1),
+ Lambda_0 = function(t, c = 0.01, d = 4.6) (c * t) ^ d),
+ coxph.args = alist(
+ formula = Surv(time, status) ~ Z1 + Z2 + frailty.gamma(family)),
+ Lambda.times = 1:120)
R> summary(sim.coxph)
Simulation: 1000 reps, 300 clusters (avg. size 2), gamma frailty
Serial runtime (s): 113.27 (0.11 +/− 0.02 per rep)
beta.1 beta.2 theta.1 Lambda.30 Lambda.60 Lambda.90
value 0.6931 1.0986 2.0000 0.003933 0.09539 0.6159
mean.hat 0.6783 1.0913 1.9843 0.004003 0.09754 0.6282
sd.hat 0.2447 0.2522 0.2665 0.001869 0.02221 0.1375
mean.se 0.2456 0.2468 NA NA NA NA
cov.95CI 0.9470 0.9440 NA NA NA NA
The above output indicates that the frailtySurv and PPL approach with gamma frailty distribution provide similar results. Note that the theta.1 mean SE and coverage rate are NA since coxph does not provide the SE for the estimated frailty distribution parameter.
The correlation between regression coefficient and frailty distribution parameter estimates of both methods is given by
R> sapply(names(sim)[grepl(“^hat.beta|^hat.theta”, names(sim))],
+ function(name) cor(sim[[name]], sim.coxph[[name]]))
hat.beta.1 hat.beta.2 hat.theta.1
0.9912442 0.9911590 0.9982390
The mean correlation between cumulative baseline hazard estimates is given by
R> mean(sapply(names(sim)[grepl(“^hat.Lambda”, names(sim))],
+ function(name) cor(sim[[name]], sim.coxph[[name]])), na.rm = TRUE)
[1] 0.9867021
Full simulation results are provided in Appendix B and include the following settings: gamma frailty with various number of clusters; large cluster size; discrete observed times; oscillating baseline hazard; PVF frailty with fixed and random cluster size; log-normal frailty; and inverse Gaussian frailty. It is evident that for all the available frailty distributions our estimation procedure and implementation work very well in terms of bias, and the sandwich-type variance estimator is dramatically improved as the cluster size increases (for example, from 2 to 6). The bootstrap variance estimators are shown to be accurate even with small cluster size.
5. Case study
To demonstrate the applicability of frailtySurv, results are obtained for two different datasets. The first is a clinical dataset, for which several benchmark results exist. The second is a hard drive failure dataset from a large cloud backup storage provider. Both datasets are provided with frailtySurv as data(“drs”, package = “frailtySurv”) and data(“hdfail”, package = “frailtySurv”), respectively.
5.1. Diabetic Retinopathy Study
The Diabetic Retinopathy Study (DRS) was performed to determine whether the onset of blindness in 197 high-risk diabetic patients could be delayed by laser treatment (The Diabetic Retinopathy Study Research Group 1976). The treatment was administered to one randomly-selected eye in each patient, leaving the other eye untreated. Thus, there are 394 observations which are clustered by patient due to unobserved patient-specific effects. A failure occurred when visual acuity dropped to below 5/200, and approximately 61% of observations are right-censored. All patients had a visual acuity of at least 20/100 at the beginning of the study. A model with gamma shared frailty is estimated from the data.
R> data(“drs”, package = “frailtySurv”)
R> fit.drs <- fitfrail(Surv(time, status) ~ treated + cluster(subject_id),
+ drs, frailty = “gamma”)
R> COV.drs <- vcov(fit.drs)
R> fit.drs
Call: fitfrail(formula = Surv(time, status) ~ treated + cluster(subject_id),
dat = drs, frailty = “gamma”)
Covariate Coefficient
treated −0.918
Frailty distribution gamma(0.876), VAR of frailty variates = 0.876
Log-likelihood −1005.805
Converged (method) 7 iterations, 1.36 secs (maximized log-likelihood)
R> sqrt(diag(COV.drs))
treated theta.1
0.1975261 0.3782775
The regression coefficient for the binary treated variable is estimated to be −0.918 with 0.198 estimated standard error, which indicates a 60% decrease in hazard with treatment. The p value for testing the null hypothesis that the treatment has no effect against a two sided alternative equals 3.5×10−6 (calculated by 2 ∗ pnorm(−0.918/0.198)). The parameter trace can be plotted to determine the path taken by the optimization procedure, as follows (see Figure 2):
Figure 2:
Parameter and log-likelihood trace.
R> plot(fit.drs, type = “trace”)
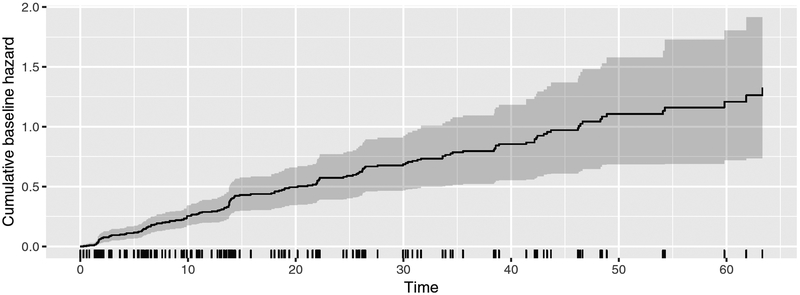
The long stretch of nearly-constant parameter estimates and log-likelihood indicates a local maximum in the objective function. In general, a global optimum solution is not guaranteed with numerical techniques. The estimated baseline hazard with point-wise 95% bootstrapped confidence intervals is given by (see Figure 3):
Figure 3:
Estimated baseline hazard with point-wise 95% bootstrapped confidence intervals.
R> set.seed(2015)
R> plot(fit.drs, type = “cumhaz”, CI = 0.95)
where the seed is used to generate the weights in the bootstrap procedure of the cumulative baseline hazard plot function. Individual failures are shown by the rug plot directly above the time axis. Note that any other CI interval can be specified by the CI parameter of the plot method for ‘fitfrail’ objects. Subsequent calls to the vcov method for ‘fitfrail’ objects with the same arguments will use a cached value and avoid repeating the computationally-expensive bootstrap or sandwich variance estimation procedures.
For comparison, the following results were obtained with coxph in the survival package based on the PPL approach:
R> library(“survival”)
R> coxph(Surv(time, status) ~ treated + frailty.gamma(subject_id), drs)
Call:
coxph(formula = Surv(time, status) ~ treated + frailty.gamma(subject_id),
data = drs)
coef se(coef) se2 Chisq DF p
treated −0.910 0.174 0.171 27.295 1.0 1.7e-07
frailty.gamma(subject_id) 114.448 84.6 0.017
Iterations: 6 outer, 30 Newton-Raphson
Variance of random effect= 0.854 I-likelihood = −850.9
Degrees of freedom for terms= 1.0 84.6
Likelihood ratio test=201 on 85.6 df, p=2.57e-11 n= 394
5.2. Hard drive failure
A dataset of hard drive monitoring statistics and failure was analyzed. Daily snapshots of a large backup storage provider over two years were made publicly available4. On each day, the Self-Monitoring, Analysis, and Reporting Technology (SMART) statistics of operational drives were recorded. When a hard drive was no longer operational, it was marked as a failure and removed from the subsequent daily snapshots. New hard drives were also continuously added to the population. In total, there are over 52,000 unique hard drives over approximately two years of follow-up and 2885 (5.5%) failures.
The data must be pre-processed in order to extract the SMART statistics and failure time of each unique hard drive. In some cases, a hard drive fails to report any SMART statistics up to several days before failing and the most recent SMART statistics before failing are recorded. The script for pre-processing is publicly available5. Although there are 40 SMART statistics altogether, many (older) drives only report a partial list. The current study is restricted to the covariates described in Table 2, which are present for all but one hard drive in the dataset.
Table 2:
Hard drive failure covariates.
| Name | Description |
|---|---|
| temp | Continuous covariate, which gives the internal temperature in °C. |
| rer | Binary covariate, where 1 indicates a non-zero rate of errors that occur in hardware when reading from data from disk. |
| rsc | Binary covariate, where 1 indicates sectors that encountered read, write, or verification errors. |
| psc | Binary covariate, where 1 indicates there were sectors waiting to be remapped due to an unrecoverable error. |
The hard drive lifetimes are thought to be clustered by model and manufacturer. There are 85 unique models ranging in capacity from 80 gigabytes to 6 terabytes. The cluster sizes loosely follow a power-law distribution, with anywhere from 1 to over 15,000 hard drives of a particular model.
For a fair comparison, the hard drives of a single manufacturer were selected. The subset of Western Digital hard drives consists of 40 different models with 178 failures out of 3530 hard drives. The hard drives are clustered by model, and cluster sizes range from 1 to 1190 with a mean of 88.25. A gamma shared frailty model was fitted to the data using the “score” fit method and default convergence criteria.
R> data(“hdfail”, package = “frailtySurv”)
R> hdfail.sub <- subset(hdfail, grepl(“WDC”, model))
R> fit.hd <- fitfrail(
+ Surv(time, status) ~ temp + rer + rsc + psc + cluster(model),
+ hdfail.sub, frailty = “gamma”, fitmethod = “score”)
R> fit.hd
Call: fitfrail(formula = Surv(time, status) ~ temp + rer + rsc + psc +
cluster(model), dat = hdfail.sub, frailty = “gamma”, fitmethod = “score”)
Covariate Coefficient
temp −0.0145
rer 0.7861
rsc 0.9038
psc 2.4414
Frailty distribution gamma(1.501), VAR of frailty variates = 1.501
Log-likelihood −1305.134
Converged (method) 10 iterations, 15.78 secs (solved score equations)
Bootstrapped standard errors for the regression coefficients and frailty distribution parameter are given by
R> set.seed(2015)
R> COV <- vcov(fit.hd, boot = TRUE)
R> se <- sqrt(diag(COV)[c(“temp”, “rer”, “rsc”, “psc”, “theta.1”)])
R> se
temp rer rsc psc theta.1
0.03095664 0.62533725 0.18956662 0.36142850 0.32433275
Significance of the regression coefficient estimates are given by their corresponding p values,
R> pvalues <- pnorm(abs(c(fit.hd$beta, fit.hd$theta)) / se,
+ lower.tail = FALSE) * 2
R> pvalues
temp rer rsc psc theta.1
6.400162e-01 2.087038e-01 1.861996e-06 1.429667e-11 3.690627e-06
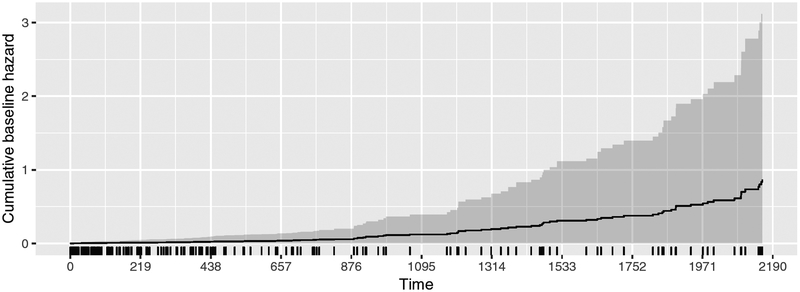
Only the estimated regression coefficients of the reallocated sector count (rsc) and pending sector count (psc) are statistically significant at the 0.05 level. Generally, SMART statistics are thought to be relatively weak predictors of hard drive failure (Pinheiro, Weber, and Barroso 2007). A hard drive is about twice as likely to fail with at least one previous bad sector (given by rsc > 0), while the hazard increases by a factor of 11 with the presence of bad sectors waiting to be remapped. The estimated baseline hazard with 95% CI is also plotted, up to 6 years, in Figure 4. This time span includes all but one hard drive that failed after 15 years (model: WDC WD800BB).
Figure 4:
Estimated baseline hazard with 95% confidence interval.
R> plot(fit.hd, type = “cumhaz”, CI = 0.95, end = 365 * 6)
6. Discussion
frailtySurv provides a suite of functions for generating clustered survival data, fitting shared frailty models under a wide range of frailty distributions, and visualizing the output. The semi-parametric model has better asymptotic properties than most existing implementations, including consistent and asymptotically-normal estimators, which penalized partial likelihood estimation lacks. Moreover, this is the first R package that implements semi-parametric estimators with inverse Gaussian and PVF frailty models. The complete set of supported frailty distributions, including implementation details, are described in Appendix A. The flexibility and robustness of data generation and model fitting functions are demonstrated in Appendix B through a series of simulations.
The main limitation of frailtySurv is the computational complexity, which is approximately an order of magnitude greater than PPL. Despite this, critical sections of code have been optimized to provide reasonable performance for small and medium sized datasets. Specifically, frailtySurv caches computationally-expensive results, parallelizes independent computations, and makes extensive use of natively-compiled C++ functions through the Rcpp R package (Eddelbuettel and François 2011). As a remedy for relatively larger computational complexity, control parameters allow for fine-grained control over numerical integration and outer loop convergence, leading to a speed-accuracy tradeoff in parameter estimation.
The runtime performance and speed-accuracy tradeoff of core frailtySurv functions are examined empirically in Appendix C. These simulations confirm the O (n) complexity of genfrail and O (n2) complexity of fitfrail using either log-likelihood maximization or normalized score equations. Frailty distributions without analytic Laplace transforms have the additional overhead of numerical integration inside the double-nested loop, although the growth in runtime is comparable to those without numerical integration. Covariance matrix estimation also has complexity O (n2), dominated by memory management and matrix operations. In order to obtain a tradeoff between speed and accuracy, the convergence criteria of the outer loop estimation procedure and convergence of numerical integration (for LN and IG frailty) can be specified through parameters to fitfrail. Accuracy of the regression coefficient estimates and frailty distribution parameter, as measured by the residuals, decreases as the absolute and relative reduction criteria in the outer loop are relaxed (Figure 18 in Appendix B). The simulations also indicate a clear reduction in runtime as numerical integration criteria are relaxed without a significant loss in accuracy (Figure 19 in Appendix B).
Choosing a proper frailty distribution is a challenging problem, although extensive simulation studies suggest that misspecification of the frailty distribution does not affect the bias and efficiency of the regression coefficient estimators substantially, despite the observation that a different frailty distribution could lead to appreciably different association structures (Glidden and Vittinghoff 2004; Gorfine, De-Picciotto, and Hsu 2012). There are several existing works on tests and graphical procedures for checking the dependence structures of clusters of size two (Glidden 1999; Shih and Louis 1995; Cui and Sun 2004; Glidden 2007). However, implementation of these procedures requires substantial extension to the current package, which will be considered in a separate work.
Supplementary Material
Acknowledgments
The authors would like to thank Google, which partially funded development of frailtySurv through the 2015 Google Summer of Code, and NIH grants (R01CA195789 and P01CA53996).
Footnotes
Kendall’s tau is denoted by κ to avoid confusion with τ, the end of the follow-up period.
Note that N and K are the parameters of genfrail that correspond to math notation n (number of clusters) and mi (cluster size), respectively.
The sandwich estimator currently only provides the covariance matrix of and not .
Contributor Information
John V. Monaco, Naval Postgraduate School
Malka Gorfine, Tel Aviv University.
Li Hsu, Fred Hutchinson, Cancer Research Center.
References
- Berntsen J, Espelid TO, Genz A (1991). “An Adaptive Algorithm for the Approximate Calculation of Multiple Integrals.” ACM Transactions on Mathematical Software, 17(4), 437–451. doi: 10.1145/210232.210233. [DOI] [Google Scholar]
- Brent RP (2013). Algorithms for Minimization without Derivatives. Courier Corporation. [Google Scholar]
- Breslow N (1974). “Covariance Analysis of Censored Survival Data.” Biometrics, 30(1),89–99. doi: 10.2307/2529620. [DOI] [PubMed] [Google Scholar]
- Brezger A, Kneib T, Lang S (2005). “BayesX: Analyzing Bayesian Structured Additive Regression Models.” Journal of Statistical Software, 14(11), 1–22. doi: 10.18637/jss.v014.i11. [DOI] [Google Scholar]
- Byrd RH, Lu P, Nocedal J, Zhu C (1995). “A Limited Memory Algorithm for Bound Constrained Optimization.” SIAM Journal on Scientific Computing, 16(5), 1190–1208. doi: 10.1137/0916069. [DOI] [Google Scholar]
- Calhoun P, Su X, Nunn M, Fan J (2018). “Constructing Multivariate Survival Trees: The MST Package for R.” Journal of Statistical Software, 83(12), 1–21. doi: 10.18637/jss. v083.i12. [DOI] [Google Scholar]
- Clauset A, Shalizi CR, Newman MEJ (2009). “Power-Law Distributions in Empirical Data.”SIAM Review, 51(4), 661–703. doi: 10.1137/070710111. [DOI] [Google Scholar]
- Clayton DG (1978). “A Model for Association in Bivariate Life Tables and Its Application in Epidemiological Studies of Familial Tendency in Chronic Disease Incidence.” Biometrika, 65(1), 141–151. doi: 10.1093/biomet/65.1.141. [DOI] [Google Scholar]
- Cox DR (1972). “Regression Models and Life-Tables.” Journal of the Royal Statistical SocietyB, 34(2), 187–220. [Google Scholar]
- Cox DR (1975). “Partial Likelihood.” Biometrika, 62(2), 269–276. doi: 10.1093/biomet/62.2.269. [DOI] [Google Scholar]
- Cui S, Sun Y (2004). “Checking for the Gamma Frailty Distribution under the MarginalProportional Hazards Frailty Model.” Statistica Sinica, 14(1), 249–267. [Google Scholar]
- Dardis C (2016). survMisc: Miscellaneous Functions for Survival Data. R package version0.5.4, URL https://CRAN.R-project.org/package=survMisc.
- Do Ha I, Lee Y, kee Song J (2001). “Hierarchical Likelihood Approach for Frailty Models.”Biometrika, 88(1), 233–233. doi: 10.1093/biomet/88.1.233. [DOI] [Google Scholar]
- Do Ha I, Noh M, Lee Y (2018). frailtyHL: Frailty Models via H-Likelihood. R package version2.1, URL https://CRAN.R-project.org/package=frailtyHL.
- Donohue MC, Xu R (2017). phmm: Proportional Hazards Mixed-Effects Models. R package version 0.7–10, URL https://CRAN.R-project.org/package=phmm.
- Duchateau L, Janssen P (2007). The Frailty Model. Springer-Verlag. [Google Scholar]
- Eddelbuettel D, François R (2011). “Rcpp: Seamless R and C++ Integration.” Journal of Statistical Software, 40(8), 1–18. doi: 10.18637/jss.v040.i08. [DOI] [Google Scholar]
- Genz AC, Malik A (1980). “Remarks on Algorithm 006: An Adaptive Algorithm for Numerical Integration over an N-Dimensional Rectangular Region.” Journal of Computational and Applied Mathematics, 6(4), 295–302. doi: 10.1016/0771-050x(80)90039-x. [DOI] [Google Scholar]
- Geyer CJ (2018). aster: Aster Models. R package version 0.9.1.1, URL https://CRAN.R-project.org/package=aster.
- Glidden DV (1999). “Checking the Adequacy of the Gamma Frailty Model for MultivariateFailure Times.” Biometrika, 86(2), 381–393. doi: 10.1093/biomet/86.2.381. [DOI] [Google Scholar]
- Glidden DV (2007). “Pairwise Dependence Diagnostics for Clustered Failure-Time Data.”Biometrika, 94(2), 371–385. doi: 10.1093/biomet/asm024. [DOI] [Google Scholar]
- Glidden DV, Vittinghoff E (2004). “Modelling Clustered Survival Data from MulticentreClinical Trials.” Statistics in Medicine, 23(3), 369–388. doi: 10.1002/sim.1599. [DOI] [PubMed] [Google Scholar]
- Goedman R, Grothendieck G, Højsgaard S, Pinkus A, Mazur G (2016). Ryacas: R Interface to the yacas Computer Algebra System. R package version 0.3–1, URL https://CRAN.R-project.org/package=Ryacas.
- Gorfine M, De-Picciotto R, Hsu L (2012). “Conditional and Marginal Estimates in Case-Control Family Data – Extensions and Sensitivity Analyses.” Journal of Statistical Computation and Simulation, 82(10), 1449–1470. doi: 10.1080/00949655.2011.581669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorfine M, Zucker DM, Hsu L (2006). “Prospective Survival Analysis with a General Semi-parametric Shared Frailty Model: A Pseudo Full Likelihood Approach.” Biometrika, 93(3), 735–741. doi: 10.1093/biomet/93.3.735. [DOI] [Google Scholar]
- Gu C (2014). “Smoothing Spline ANOVA Models: R Package gss.” Journal of StatisticalSoftware, 58(5), 1–25. doi: 10.18637/jss.v058.i05. [DOI] [Google Scholar]
- Hanagal DD (2009). “Modeling Heterogeneity for Bivariate Survival Data by Power VarianceFunction Distribution.” Journal of Reliability and Statistical Studies, 2(1), 14–27. [Google Scholar]
- Hasselman B (2017). nleqslv: Solve Systems of Nonlinear Equations. R package version 3.3.1,URL https://CRAN.R-project.org/package=nleqslv.
- Hirsch K, Wienke A (2012). “Software for Semiparametric Shared Gamma and Log-Normal Frailty Models: An Overview.” Computer Methods and Programs in Biomedicine, 107(3), 582–597. doi: 10.1016/j.cmpb.2011.05.004. [DOI] [PubMed] [Google Scholar]
- Johnson SG (2013). cubature. C library version 1.0.2, URL http://ab-initio.mit.edu/wiki/index.php/Cubature.
- Monaco JV, Gorfine M, Hsu L (2018). frailtySurv: General Semiparametric Shared Frailty Model. R package version 1.3.5, URL https://CRAN.R-project.org/package=frailtySurv. [DOI] [PMC free article] [PubMed]
- Moriña D, Navarro A (2014). “The R Package survsim for the Simulation of Simple and Complex Survival Data.” Journal of Statistical Software, 59(2), 1–20. doi: 10.18637/jss.v059.i02.26917999 [DOI] [Google Scholar]
- Munda M, Rotolo F, Legrand C (2012). “parfm: Parametric Frailty Models in R.” Journal of Statistical Software, 51(11), 1–20. doi: 10.18637/jss.v051.i11.23504300 [DOI] [Google Scholar]
- Pinheiro E, Weber WD, Barroso LA (2007). “Failure Trends in a Large Disk Drive Population.” In FAST, volume 7, pp. 17–23. [Google Scholar]
- R Core Team (2018). R : A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: URL https://www.R-project.org/. [Google Scholar]
- Ridout MS (2009). “Generating Random Numbers from a Distribution Specified by its Laplace Transform.” Statistics and Computing, 19(4), 439–450. doi: 10.1007/s11222-008-9103-x. [DOI] [Google Scholar]
- Rondeau V, Mazroui Y, Gonzalez JR (2012). “frailtypack: An R Package for the Analysis of Correlated Survival Data with Frailty Models Using Penalized Likelihood Estimation or Parametrical Estimation.” Journal of Statistical Software, 47(4), 1–28. doi: 10.18637/jss.v047.i04. [DOI] [Google Scholar]
- Shih JH, Louis TA (1995). “Inferences on the Association Parameter in Copula Models forBivariate Survival Data.” Biometrics, 51(4), 1384–1399. doi: 10.2307/2533269. [DOI] [PubMed] [Google Scholar]
- Smyth G, Hu Y, Dunn P, Phipson B, Chen Y (2017). statmod: Statistical Modeling. R package version 1.4.30, URL https://CRAN.R-project.org/package=statmod.
- The Diabetic Retinopathy Study Research Group (1976). “Preliminary Report on Effects of Photocoagulation Therapy.” American Journal of Ophthalmology, 81(4), 383–396. doi: 10.1016/0002-9394(76)90292-0. [DOI] [PubMed] [Google Scholar]
- Therneau TM (2018a). coxme: Mixed Effects Cox Models. R package version 2.2–7, URL https://CRAN.R-project.org/package=coxme.
- Therneau TM (2018b). survival: A Package for Survival Analysis in S. R package version2.42–3, URL https://CRAN.R-project.org/package=survival.
- Wienke A (2010). Frailty Models in Survival Analysis. CRC Press. doi: 10.1201/9781420073911. [DOI] [Google Scholar]
- Zucker DM, Gorfine M, Hsu L (2008). “Pseudo-Full Likelihood Estimation for Prospective Survival Analysis with a General Semiparametric Shared Frailty Model: Asymptotic Theory.” Journal of Statistical Planning and Inference, 138(7), 1998–2016. doi: 10.1016/j.jspi.2007.08.005. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.