Estimation of Relative Load From Bar Velocity in the Full Back Squat Exercise

Abstract

The use of bar velocity to estimate relative load in the back squat exercise was examined. 80 strength-trained men performed a progressive loading test to determine their one-repetition maximum (1RM) and load-velocity relationship. Mean (MV), mean propulsive (MPV) and peak (PV) velocity measures of the concentric phase were analyzed. Both MV and MPV showed a very close relationship to %1RM (R ² =0.96), whereas a weaker association (R ² =0.79) and larger SEE (0.14 vs. 0.06 m·s ⁻¹ ) were found for PV. Prediction equations to estimate load from velocity were obtained. When dividing the sample into 3 groups of different relative strength (1RM/body mass), no differences were found between groups for the MPV attained against each %1RM. MV attained with the 1RM was 0.32±0.03 m·s ⁻¹ . The propulsive phase accounted for ~82% of concentric duration at 40% 1RM, and progressively increased until reaching 100% at 1RM. Provided that repetitions are performed at maximal intended velocity, a good estimation of load (%1RM) can be obtained from mean velocity as soon as the first repetition is completed. This finding provides an alternative to the often demanding, time-consuming and interfering 1RM or nRM tests and allows implementing a velocity-based resistance training approach.

Introduction

The squat is one of the most widely used and effective resistance training exercises for strengthening the lower-limb, protecting against injuries and improving athletic performance ¹⁷ . The dynamic squat is a closed kinetic chain exercise ⁷ that involves the largest and strongest muscles of the body (quadriceps, hamstrings, gluteus maximus, triceps surae, erector spinae, etc.) and demands a coordinated multi-joint (spine, hip, knee and ankle) movement ^{15 31 37} . The squat is beneficial to many functional activities and sporting movements and it is considered a key training exercise in many strength and conditioning programs, as well as being commonly used in physical therapy and rehabilitation settings ^{6 37} . When performed with correct technique, proper loads and following an adequate learning progression, the squat has proved to be a safe exercise for the musculoskeletal system ^{3 17 27} .

Several technique variations of the squat exist ^{8 15 17 37 38} , the main one consisting in modifying the squatting depth ^{1 2 17 39} . Research has shown that increases in lower-body strength following squat training transfer positively to athletic performance in short-duration actions that demand maximal neuromuscular activation such as sprinting and vertical jumping, especially when parallel or deep squats are used ^{11 18 21 23 28 29 30 33} .

The kinematics and kinetics associated to resistance training are believed to be critical stimuli for neuromuscular adaptations to occur ^{5 37} . Research attention has recently been placed on monitoring movement velocity during resistance training ^{4 10 11 12 14 19 20 26 28 29 30 34 35} . Movement velocity is important because both the neuromuscular demands and the training effect itself largely depend on the velocity at which loads are lifted ^{12 28} . A very close relationship between relative load (percentage of one-repetition maximum, %1RM) and mean vertical bar velocity was found for exercises such as the bench press ^{14 35} , prone bench pull ³⁵ , half-squat ²⁰ , leg press ⁴ and squat ^{4 26} . This is a novel finding which has important practical applications for the prescription and monitoring of training load in resistance exercise ^{10 34} . Thus, a velocity-based resistance training (VBRT) approach has been successfully implemented in several studies to monitor training loads ^{9 11 12 28 29 30 32} or to provide a non-invasive and objective measure to quantify the neuromuscular fatigue induced by resistance exercise ^{13 24 25 29 30 34} . The load-velocity relationship of the deep or full squat has been reported in 2 studies ^{4 26} . The first was a reliability study ²⁶ that analyzed the effect of imposing a 2 s pause in the transition from eccentric to concentric action. In the second study ⁴ , a 3–4 s pause separated the eccentric and concentric phases of the squat. It is known that the introduction of a long pause between phases eliminates the contribution of the stretch-shortening cycle, thereby considerably reducing the obtained concentric velocities ²⁶ . However, to our knowledge, the load-velocity profile of the traditional full back squat (i. e., no pause between phases) exercise, as used in the above-mentioned studies ^{9 11 13 28 29 30 32 34} has not yet been analyzed.

It therefore seemed pertinent to provide a detailed analysis of the load-velocity relationship of the traditional full squat in a large sample of experienced strength-trained athletes from different sports in order to confirm the possibility of using bar velocity to estimate loading magnitude (%1RM), as well as to provide normative data for this population. An additional purpose of the present study was to identify the relative contribution of the propulsive and braking phases ³⁶ to total concentric duration among different percentages of 1RM in this fundamental resistance training exercise. Based on previous results from our research group ^{14 35} , the following hypotheses were formulated: 1) there exists an absolute mean bar velocity associated with each relative load (%1RM) in the full squat exercise; 2) the mean velocities corresponding to each %1RM would have an intermediate value between those reported for the bench press ¹⁴ and the prone bench pull ³⁵ , since the velocity attained with the 1RM load in the squat falls between that of these 2 exercises; and 3) no significant differences in the mean velocities associated with each %1RM would exist between subgroups of different levels of maximum relative strength (1RM/body mass) performance.

Materials & Methods

Subjects

80 men (age 23.6±4.7 years, body mass 74.6±10.2 kg, height 177.1±7.5 cm, body fat 11.3±4.2%) volunteered to take part in this study. Inclusion criteria were: i) being a competitive athlete capable of performing a technically correct squat exercise; and ii) having a 1RM strength/body mass ratio (relative strength ratio, RSR) higher than 1.00 in the deep squat. Subjects were senior national-level athletes in their sport: field hockey (n=18), track and field (n=20), volleyball (n=16) and Olympic wrestling (n=26) with a strength training background of 4–12 years. In the 12 months preceding this study, subjects had been performing 2–4 resistance training sessions per week and all incorporated the squat as part of their physical conditioning. After being informed of the purpose and testing procedures, subjects signed a written informed consent form prior to participation. The study met the ethical standards of this journal ¹⁶ and was conducted in agreement with the guidelines of the local institutional review board. Subjects were not taking any drugs, medications or dietary supplements known to influence physical performance.

Testing procedures

Subjects underwent 2 preliminary sessions during which they were familiarised with the testing equipment and exercise protocol. Squat depth was determined for each subject and several practice sets with light and medium loads (20–60% 1RM) were performed. A 14-inch 360° Nexgen Baseline goniometer (Nexgen Ergonomics, Point Claire, Quebec, Canada) was used to ensure that the knee angle (<45°) was consistent with that of a deep squat ¹⁷ . For each subject, testing was conducted over 2 sessions. The first session was used for body composition assessment, medical examination and personal data and health history questionnaire administration. On the second session, the individual load-velocity relationship and 1RM strength were determined by means of a progressive loading test as explained later. This session was conducted at the same time of day (17:00 h) for all subjects to control for circadian rhythm effects on neuromuscular performance ^{22 25} . Warm-up consisted of 5 min of stationary cycling at a self-selected easy pace, 5 min of lower-body joint mobilization exercises, three 30 m running accelerations, followed by 3 sets of 5 squat repetitions with fixed loads of 20, 30 and 40 kg.

A high-bar deep back squat ¹⁷ was used. It was performed starting from the upright position with the knees and hips fully extended, stance approximately shoulder-width apart with both feet positioned flat on the floor in parallel or externally rotated to a maximum of 15°. Each subject descended in a continuous motion until the top of the thighs reached below the horizontal plane, with knees flexed to a tibiofemoral angle of 35–45° in the sagittal plane, then immediately reversed motion and ascended back to the upright position. The bar was grasped with a closed pronated grip and placed on the upper part of the trapezius, while keeping a straight-ahead gaze and stable upright trunk posture ( Fig. 1 ). The eccentric phase was performed at a controlled mean bar velocity (~0.50–0.70 m·s ⁻¹ ) for standardization and security reasons. This had been practiced in the familiarization, and was accomplished with feedback from the linear velocity transducer (described later) so that participants could adjust their eccentric velocity to the required range. In addition, eccentric displacement was monitored to avoid an excessive reduction in the range of motion (ROM) as the lifted loads got heavier; thus, a limit of 10% loss in eccentric distance was established. If a repetition failed to meet these requirements, it was discarded and repeated after a 3 min rest. The concentric phase was performed at maximal intended velocity. Strong verbal encouragement and velocity feedback were provided to motivate subjects to give maximal effort. Jumping off the ground was not allowed, although subjects were permitted to raise their heels at the end of the concentric phase, which typically occurred when lifting the lighter loads. Initial load was set at 20 kg and was progressively increased until the attained mean propulsive velocity was lower than 0.70 m·s ⁻¹ . Thereafter, load was individually adjusted using smaller increments (5 down to 2.5 kg). The heaviest load that each subject could properly lift while completing full ROM and without any external help was considered to be his 1RM. 3 attempts were executed for light (mean propulsive velocity>1.15 m·s ⁻¹ ), 2 for medium (0.70–1.15 m·s ⁻¹ ), and only one for the heaviest (<0.70 m·s ⁻¹ ) loads. Inter-set rests were 3 min for the light and medium loads and 5 min for the heaviest loads. Only the best repetition at each load, according to the criterion of fastest mean propulsive velocity ³⁶ , was considered.

Fig. 1.

Starting a and transition from eccentric to concentric phase b positions of the full back squat performed in a Smith-type machine.

Measurement equipment and data acquisition

Height was measured to the nearest 0.5 cm during a maximal inhalation using a wall-mounted stadiometer (Seca 202, Seca Ltd., Hamburg, Germany). Body weight was determined and fat percentage estimated using an 8-contact electrode segmental body composition analyzer (Tanita BC - 418, Tanita Corp., Tokyo , Japan) with the subjects in a morning fasting state. The squat was performed using a Smith machine without any counterweight mechanism (Multipower Fitness Line, Peroga, Murcia, Spain). A linear velocity transducer (T-Force System Version 3.60, Ergotech, Murcia, Spain) automatically calculated the kinematics of every repetition and provided auditory and visual velocity feedback. Vertical bar velocity was sampled at 1 000 Hz and smoothed with a fourth-order low-pass Butterworth filter with no phase shift and 10 Hz cut-off frequency. Reliability of this system has been reported elsewhere ³⁴ .

Velocity variables analyzed

3 velocity outcome measures were used as performance variables in this study: 1) mean velocity (MV): average of the bar velocity values for the whole concentric phase of each repetition; 2) mean propulsive velocity (MPV): average of the bar velocity values of the propulsive phase, defined as that portion of the concentric action during which the measured acceleration ( a ) is greater than acceleration due to gravity, i. e., a ≥–9.81 m·s ^{−2 36} ; and 3) peak velocity (PP): the highest instantaneous bar velocity value registered at a particular instant (1 ms) during the concentric phase. Mean test velocity was defined as the mean of the MPV values, calculated each 5% from 40–95% 1RM, and derived from second-order polynomial fits to load-velocity data for each subject’s progressive loading test. Mean velocity attained with the 1RM load (V _1RM ) was also analyzed because it has been acknowledged as a characteristic variable of each resistance training exercise ^{14 35} .

Statistical analyses

Standard statistical methods were used for the calculation of means, standard deviation (SD), coefficient of variation (CV), coefficient of determination (R ² ), standard error of the estimate (SEE), 95% confidence intervals (CI) and Pearson correlation coefficients (r). Relationships between load (%1RM) and velocity were studied by fitting second-order polynomials to data because they provided slightly better fits than linear functions. Normality of the data was verified using the Shapiro-Wilk test. One-way ANOVA was used to detect differences between subgroups of subjects in the following variables: age, body fat percentage, RSR, mean test velocity, MPV attained against different percentages of 1RM and V _1RM . Scheffé post-hoc tests were used to identify the source of any significant differences. Eta-squared (η ² ) was calculated as between-groups sum of squares/total sum of squares and it was provided as a measure of the effect size (ES) in ANOVA. Analyses were performed using Prism 6.07 (GraphPad Software Inc., La Jolla, CA, USA). Significance was accepted at the P≤0.05 level.

Results

Squat performance

1RM strength for the squat was 107.0±21.5 kg (i. e., 1.44±0.22 normalized per kg of body mass). Subjects performed a total of 8.7±1.8 increasing loads up to the 1RM in the progressive loading test.

Relationship between relative load and velocity

The 3 velocity variables analyzed were plotted against %1RM, obtaining a total of 644 raw load-velocity data pairs. Loads <40% 1RM were then eliminated from further analyses. This was done because there exists an intrinsic limitation in the squat exercise to maximally apply force to the ground when using light loads (i. e., in order to obtain the maximum possible velocity, the subject has to jump off the ground, which was not permitted because the squat is not a jump). This results in considerable inter-subject variability in the velocities developed against loads <40% 1RM, together with the fact that such loads are seldom used in the actual practice of squat training. Second-order polynomials were fitted to the remaining 489 load-velocity data pairs ( Fig. 2 ).

Fig. 2.

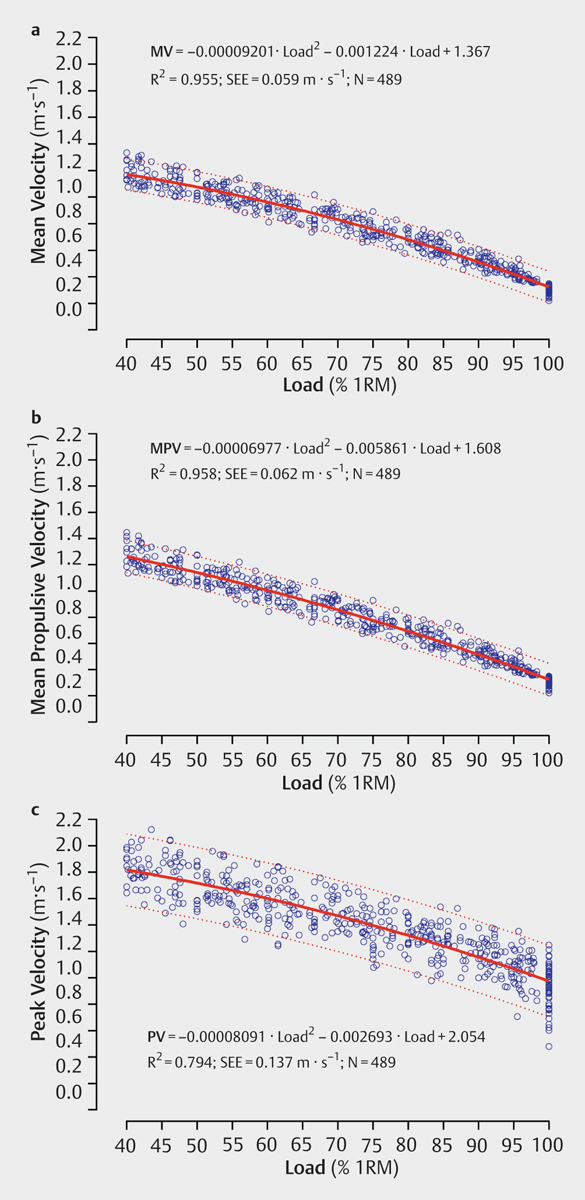
Relationships between relative load (%1RM) and bar velocity: a mean velocity (MV); b mean propulsive velocity (MPV); and c peak velocity (PV) for the full back squat exercise. Data obtained from raw load-velocity values derived from the progressive isoinertial squat loading tests performed on the sample of 80 athletes. Solid lines show the fitted curve to the data. Dotted lines indicate limits within which 95% of predictions will fall.

A very close relationship was found for MV (R ² =0.955) and MPV (R ² =0.958), whereas a lower association was observed for PV (R ² =0.794) ( Fig. 2 ). Individual curve fits for each test gave an R ² of 0.995±0.004 (range: 0.983–1.000; CV=0.35%) for MV, R ² of 0.995±0.003 (range: 0.986–1.000; CV=0.33%) for MPV and R ² of 0.981±0.016 (range: 0.917–0.999; CV=1.68%) for PV. The MV, MPV and PV values attained with each percentage of 1RM were obtained from these polynomial fits, from 40% 1RM onwards, in 5% increments ( Table 1 ). V _1RM was 0.32±0.03 m·s ⁻¹ (range: 0.24–0.37 m·s ⁻¹ ).

Table 1  Mean velocity (MV), mean propulsive velocity (MPV) and peak velocity (PV) attained with each %1RM, and relative contribution of the propulsive and braking phases to the total concentric duration in the full back squat exercise (n=80).

Load (%1RM)	MV (m·s −1 )	MV 95% Confidence Interval	MPV (m·s −1 )	MPV 95% Confidence Interval	PV (m·s −1 )	95% Confidence Interval	Propulsive Phase (%)	Braking Phase (%)
40	1.19±0.08	1.18–1.21	1.28±0.08	1.26–1.30	1.87±0.15	1.84–1.91	82	18
45	1.14±0.08	1.12–1.16	1.21±0.08	1.20–1.23	1.81±0.15	1.77–1.84	84	16
50	1.08±0.07	1.06–1.10	1.14±0.07	1.13–1.16	1.74±0.15	1.70–1.77	85	15
55	1.02±0.07	1.00–1.03	1.07±0.07	1.05–1.09	1.67±0.15	1.63–1.70	87	13
60	0.95±0.07	0.94–0.97	1.00±0.07	0.98–1.01	1.60±0.15	1.57–1.63	89	11
65	0.89±0.06	0.87–0.90	0.92±0.06	0.91–0.93	1.53±0.15	1.49–1.56	90	10
70	0.82±0.06	0.80–0.83	0.84±0.06	0.83–0.85	1.46±0.16	1.42–1.49	92	8
75	0.74±0.05	0.73–0.75	0.76±0.05	0.75–0.77	1.39±0.17	1.35–1.43	93	7
80	0.67±0.04	0.66–0.68	0.68±0.04	0.67–0.69	1.32±0.18	1.28–1.36	95	5
85	0.59±0.04	0.58–0.59	0.59±0.04	0.59–0.60	1.25±0.19	1.21–1.29	96	4
90	0.50±0.03	0.50–0.51	0.51±0.03	0.50–0.51	1.18±0.20	1.13–1.22	98	2
95	0.42±0.02	0.41–0.42	0.42±0.02	0.41–0.42	1.11±0.22	1.06–1.16	99	1
100	0.32±0.03	0.32–0.33	0.32±0.03	0.32–0.33	1.04±0.24	0.98–1.09	100	0

Values are mean±SD

Stability in the load-velocity relationship regardless of individual relative strength

In order to study whether the velocity attained with each %1RM was dependent upon individual strength levels, subjects were ranked according to their RSR and the total sample was divided into 3 subgroups: group 1 (G1), n=24, RSR≤1.30; group 2 (G2), n=29, 1.30<RSR≤1.50; and group 3 (G3), n=27, RSR>1.50. When separately analyzing the load-velocity relationship for each of these subgroups ( Fig. 3 ), no significant differences were found for the MPV attained against each % 1RM, mean test velocity or V _1RM between groups, with very small effect sizes (<0.02) observed for these variables ( Table 2 ). No correlation was found between V _1RM and RSR.

Fig. 3.

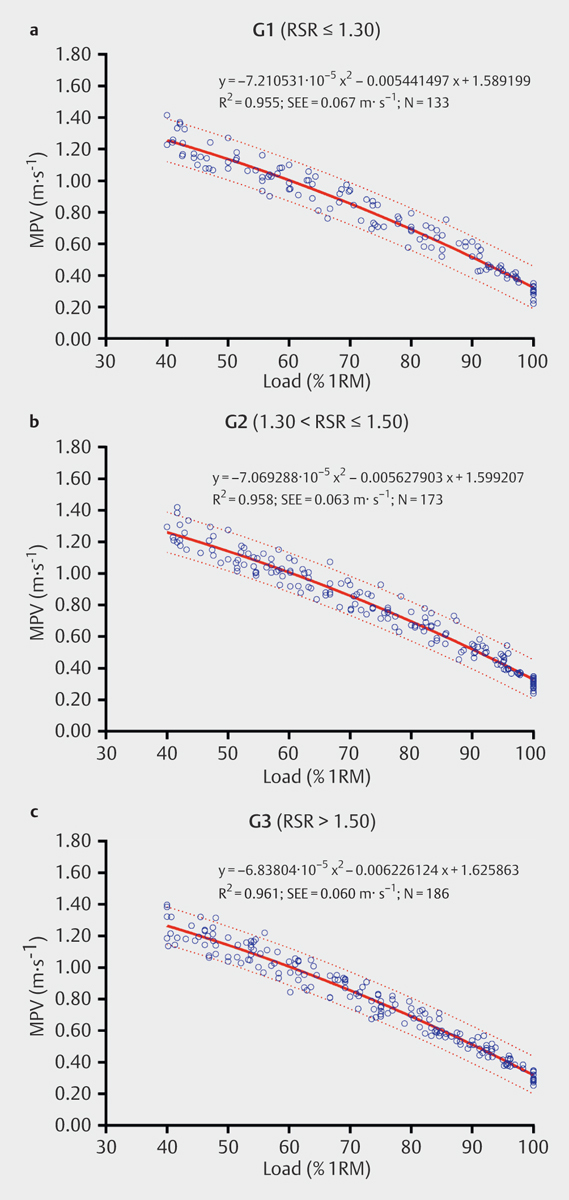
Relationships between relative load (%1RM) and mean propulsive velocity (MPV) in the squat exercise for the 3 subgroups of different relative strength ratio (RSR) that made up the sample: a G1 (n=24, RSR≤1.30); b G2 (n=29, 1.30<RSR≤1.50); and c G3 (n=27, RSR>1.50). Dotted lines indicate limits within which 95% of predictions will fall.

Table 2  Comparison of mean test velocity and mean propulsive velocity attained with different percentages of the 1RM between subgroups of different relative strength performance.

	G1 (n=24)	G2 (n=29)	G3 (n=27)	Effect Size (η 2 )
Age (years)	22.2±4.3	23.0±4.6	25.6±4.5 Ψ	0.093
Body fat (%)	12.8±4.0	11.0±4.2	10.2±4.1	0.067
1RM (kg)	93.4±10.9	100.1±12.1 ***	126.4±22.9 ΨΨΨ	0.438
RSR	1.20±0.09 † [1.02–1.30]	1.40±0.05 † [1.33–1.47]	1.68±0.16 † [1.51–2.17]	0.755
Mean test velocity (m·s −1 )	0.873±0.061	0.867±0.052	0.865±0.050	0.005
MPV with 40% 1RM (m·s −1 )	1.28±0.07	1.29±0.07	1.28±0.08	0.002
MPV with 50% 1RM (m·s −1 )	1.15±0.07	1.14±0.07	1.14±0.07	0.000
MPV with 60% 1RM (m·s −1 )	1.00±0.08	0.99±0.06	0.99±0.06	0.008
MPV with 70% 1RM (m·s −1 )	0.85±0.07	0.84±0.05	0.83±0.05	0.016
MPV with 80% 1RM (m·s −1 )	0.69±0.05	0.67±0.04	0.67±0.04	0.018
MPV with 90% 1RM (m·s −1 )	0.51±0.03	0.50±0.03	0.50±0.03	0.023
MPV with 1RM (m·s −1 )	0.31±0.04	0.32±0.03	0.32±0.03	0.003

RSR, relative strength ratio (1RM strength divided by body mass), with range indicated in brackets [minimum–maximum]; MPV, mean propulsive velocity; G1, G2 and G3 are 3 subgroups of the total (n=80) study sample. Eta-squared (η ² ) is reported as a measure of the effect size in the one-way ANOVA comparison between the subgroups

† All groups significantly different from each other (P<0.05)

Ψ Significantly different from G1 (P<0.05); ΨΨΨ Significantly different from G1 (P<0.001)

*** Significantly different from G3 (P<0.001)

Values are mean±SD

Predicting relative load from velocity data

Because in practice we are interested in estimating load (%1RM) from velocity measurements, if we take the velocity values as the independent variable, a prediction equation to estimate relative load (Load, %1RM) from velocity (MPV, in m·s ⁻¹ ) could be obtained:

Load (% 1RM) = –5.961 MPV2 – 50.71 MPV + 117.0 (R2 = 0.954; SEE = 4.02%) (1)

In cases where mean concentric velocity (MV) or peak velocity (PV) are used, the resulting equations were:

Load (% 1RM) = –12.87 MV2 – 46.31 MV + 116.3 (R2 = 0.948; SEE = 4.31%) (2)

Load (% 1RM) = –10.85 PV2 – 25.10 PV + 130.3 (R2 = 0.792; SEE = 8.57%) (3)

Contribution of the propulsive and braking phases to different loading conditions

Table 1 shows the contribution of the propulsive and braking phases ³⁶ to the total concentric duration from 40 to 100% 1RM, according to calculations made using the significant linear relationship that existed between %1RM (x) and relative contribution of the propulsive phase to concentric duration of the lift (y): y=0.30315 x+70.323 (r=0.95, P<0.001) from 579 individual data pairs obtained in the 80 progressive loading tests. As can be observed ( Table 1 ), propulsive phase accounted for ~82% of concentric duration at 40% 1RM, progressively increasing until reaching 100% at the 1RM load.

Discussion

The results of the present study confirm our first hypothesis that mean bar velocity attained against a given absolute load in the full squat can be used as a very good estimate of the load (%1RM) being lifted, provided that repetitions are performed at maximal intended velocity. A direct practical application of this finding is the possibility of monitoring, in real-time, the actual load being used by measuring velocity during training. This allows the prescription and monitoring of resistance training in terms of repetition velocities (instead of using percentages of 1RM), providing a more accurate adjustment and better individualization of the training load.

Of the 3 velocity variables analyzed in this study, both mean velocity measures (MV and MPV) provided a very close relationship to %1RM (R ² =0.96; Fig. 2a, b ), whereas peak velocity showed a weaker association (R ² =0.79; Fig. 2c ) and much larger SEE. Therefore, more accurate predictions of relative load can be obtained when using mean compared to peak velocity values. Prediction equations to estimate relative load from velocity data have been provided for this purpose (Equations 1-3). Previous research has shown that mean propulsive outcome measures should be preferred over mean concentric ones since they avoid underestimating an individual’s true neuromuscular potential when lifting light and medium loads ^{14 26 35 36} . Thus, if the measuring device allows the calculation of mean propulsive values, MPV should be the variable of choice to monitor during resistance training. However, if this is not feasible, MV can also be used to predict relative load from velocity (Equation 2).

As can be observed in Table 1 , differences in MPV between each 5% increment in relative load (from 40–100% 1RM) vary between 0.07 and 0.09 m·s ⁻¹ . From this it can be derived that when, following a training period, a subject increases the MPV attained against a given absolute load by ~7–9 hundredths of a meter per second, that weight would then represent a ~5% 1RM lower load. The same reasoning would be applicable had the subject decreased the velocity against the same load. It is important to note that loads lighter than 40% 1RM are not shown in Table 1 because such low loads are unsuitable for assessing the training effect in this particular exercise. As already mentioned, there exists an intrinsic limitation to maximally apply force to the ground when using light loads in the full squat. Thus, when trying to lift these loads at maximal intended velocity, athletes tend to jump off the ground. This was also the reason why variability in movement velocity decreased (lower SD and 95% CI values) as load (%1RM) increased ( Table 1 ; Fig. 2 ). Therefore, it is recommended that MPV values ≤~1.25 m·s ⁻¹ be used in the squat exercise in order to obtain reasonably accurate predictions of relative load from velocity(Equation 1). It is also interesting to note that the load that elicits a 1 m·s ⁻¹ velocity has been used in several studies to quantify the extent of neuromuscular fatigue following different resistance exercise protocols ^{11 12 13 28 29 34} . As can be observed in Table 1 , the load corresponding to a 1.00 m·s ⁻¹ MPV in the squat is 60% 1RM. This load is used because it allows a good expression of the effect of fatigue on velocity in addition to being relatively easy to move and quick to determine as part of the warm-up ³⁴ .

An issue worth mentioning is the importance of monitoring the eccentric displacement in the full squat in order to avoid an excessive reduction in ROM as the lifted loads get heavier (with the consequent change in the biomechanics of the exercise). Thus, based on our experience, and when direct measurement of the knee flexion angle is not available or is unpractical, a simple rule of thumb would be to aim for an eccentric squatting displacement of ~38–40% of each subject’s height and limit the loss of eccentric distance to a maximum of 10%.

The present results lend support to previous studies ^{14 35 36} which highlighted the importance of considering the contribution of the propulsive and braking phases as sub-phases of the concentric portion of a lift, when assessing strength in isoinertial conditions. The load-velocity relationship and the contribution of the propulsive and braking phases to concentric duration in the full squat ( Table 1 ) were different than those reported for the bench press or prone bench pull ^{14 35} . Thus, velocity for a given load (%1RM) in the squat was higher than that observed for the bench press ^{14 35} . Compared to the bench press, the longer ROM and stronger and larger muscle groups involved in the squat can explain the faster velocities of the latter exercise. Velocities reported for the prone bench pull ³⁵ , an upper-body exercise, were higher than those observed for the squat in the present study. The distinct skeletal muscle architecture and ROM, as well as the opposing muscle actions involved (pushing for the squat vs. pulling for the prone bench pull) are thought to be responsible for these differences in velocity between exercises. Hence, it is important to understand that the relationship between load (%1RM) and velocity is specific of each resistance training exercise and the exact outcome velocity measure used (mean, peak or mean propulsive values) ( Table 1 ; Fig. 2 ).

Interestingly, the velocity at which the 1RM is attained seems distinctive for each exercise and therefore can be used as a practical and objective criterion for a repetition to be considered a true maximum measure ^{14 35} . In the present study, V _1RM for the squat was 0.32±0.03 m·s ⁻¹ ; adding a standard deviation to the mean, the resulting velocity is 0.35 m·s ⁻¹ . Thus, a recommendation can be made to only consider as true 1RMs those repetitions with a mean concentric velocity not greater than 0.35 m·s ⁻¹ in the full back squat. The V _1RM value showed little variability between athletes, being independent of each subject’s relative strength ( Table 2 ). It is worth noting that as the V _1RM value of a given exercise increases (e. g., ~0.20 m·s ⁻¹ for the bench press ¹⁴ , ~0.35 m·s ⁻¹ for the back squat and ~0.50 m·s ⁻¹ for the prone bench pull ³⁵ ), the velocity attained with a given %1RM also increases, which supports the second hypothesis of this study.

In the present investigation we divided the total sample into 3 subgroups of different RSR in order to study whether the level of strength performance influenced the load- velocity relationship. It is remarkable that neither differences in MPV values for any %1RM nor in mean test velocity were observed between the G1, G2 and G3 subgroups ( Table 2 ). Indeed the effect sizes found for these variables were almost negligible (<0.02), whereas the ES for the grouping variable (RSR) was very large (0.76). In addition, when calculating the load-MPV relationship independently for these 3 groups ( Fig. 3 ) the obtained equations gave the same or almost identical (maximum difference of 0.01 m·s ⁻¹ ) velocity values for each %1RM than those obtained when using the general equation for the total sample ( Fig. 2b ). This indicates that the MPV values corresponding to each %1RM (in a range of 40–100% 1RM) in the full squat are very stable irrespective of the level of strength performance. This finding confirms our third hypothesis and allows us to generalize the obtained results to populations similar to that studied here (i. e., young strength-trained males with a 1.00≤RSR≤2.00 in the full squat). As a limitation of this study, we must however note that caution should be taken when using the equations provided here for calculating load (%1RM) from velocity, or vice versa, with other populations such as female athletes or athletes with significantly different RSR values, untrained persons, elderly people and persons suffering from some illness or disability.

Conclusions and practical applications

The findings of the present study complement and extend previous research by confirming an inextricable relationship between load and movement velocity in the full squat, which allows an adequate estimation of loading magnitude (%1RM) from velocity measurements, similar to that recently observed for other multi-joint resistance training exercises ^{4 14 20 35} . Hence, the load-velocity relationship appears specific to each exercise and can be used as a reference to implement a VBRT approach. By monitoring repetition velocity during the squat, it is possible to determine whether the proposed load (kg) for a given training session actually represents the effort (%1RM) that was intended. Using repetition velocity to prescribe and monitor the resistance training load offers several advantages worth noting over the traditional approach, based on 1RM or repetitions to failure (nRM) assessments:

1. A reasonably good estimate of loading magnitude (40–100% 1RM) can be obtained from mean velocity measurements (MPV or MV; Equations 1, 2), eliminating the need to perform the often demanding, time-consuming and interfering 1RM or nRM tests.

2. It is possible to determine the load (%1RM) being used “on the go”, as soon as the first repetition with any given absolute load is performed with maximal voluntary effort. This allows making adjustments to the training load at any time, resulting in better individualised training. In this regard, the warm-up period of the training session can serve to check whether or not the athlete is lifting the loads at the expected velocities, making the appropriate changes accordingly (increasing or decreasing the absolute loads to be used in that session).

3. Changes in the load-velocity relationship allow comparing different athletes’ profiles and/or track the neuromuscular profile of each athlete over time. In particular, monitoring the velocity attained against a given absolute load (or set of loads) allows controlling for the degree of fatigue and exertion during training.