GPU-accelerated molecular dynamics and free energy methods in Amber18: performance enhancements and new features

Abstract

We report progress in GPU-accelerated molecular dynamics and free energy methods in Amber18. Of particular interest is the development of alchemical free energy algorithms, including free energy perturbation and thermodynamic integration methods with support for non-linear softcore potential and parameter interpolation transformation pathways. These methods can be used in conjunction with enhanced sampling techniques such as replica exchange, constant pH molecular dynamics and new 12-6-4 potentials for metal ions. Additional performance enhancements have been made that enable appreciable speed-up on GPUs relative to the previous software release.

Graphical Abstract

Introduction

Molecular simulation provides an extremely powerful tool for the interpretation of experimental data, the understanding of biomolecular systems, and the prediction of properties important for molecular design. As the scope and scale of applications increase, so must the compute capability of molecular simulation software. The last decade has seen rapid advances motivated by the performance enhancements offered by the latest molecular dynamics software written for specialized hardware. Perhaps the most affordable and impactful of these are platforms using graphics processing units (GPUs).^1–7

The present application note reports on advances made in the latest release of the AMBER molecular simulation software suite (Amber18),⁸ and in particular, enhancements to the primary GPU-accelerated simulation engine (PMEMD). These advancements significantly improve the program’s execution of molecular simulations, and offer new, integrated features for calculating alchemical free energies^9,10 including Thermodynamic Integration (TI),^11–15 Free Energy Perturbation FEP)^15–19 and Bennett’s acceptance ratio and its variants (BAR/MBAR),^20–25 as well as enhanced sampling, constant pH simulation^26,27 and use of new 12-6-4 potentials.^28–30 Amber18 offers a broad solution for a wide range of free energy simulations, with expanded capability to compute forces in a hybrid environment of CPUs and GPUs, and establishes an add-on system for applying additional potential functions computed on the graphics processor without affecting optimizations of the main kernels. When run exclusively on GPU hardware, Amber18 shows consistent performance increases of 10% to 20% compared to Amber16 across Pascal (GTX-1080TI, Titan-XP, P100) and Volta architectures when running standard MD simulations, with more dependence on system size than architecture. Below we provide an overview of the software design, a description of new features, and performance benchmarks.

Software Design

Encapsulated free energy modules

The development of molecular simulation software designed for optimal performance on specialized hardware requires customization and careful redesign of the underlying algorithmic implementation. In the case of the current GPU consumer market, single precision floating point performance outstrips that of double precision performance by a significant amount. In order to address this issue in AMBER, new precision models^6,31 have been developed that leverage fixed point integer arithmetic to replace slow double precision arithmetic in certain key steps when higher precision is required, such as the accumulation of components of the force. Free energy simulations, due to the mixing/interpolation of hybrid Hamiltonians and the averaging of TI and FEP quantities, present new challenges with respect to precision compared with conventional MD simulation. The GPU enhanced features in Amber18 were designed to address these different precision requirements to ensure statistical and thermodynamically derived properties are indistinguishable from the CPU version of the code³² while maintaining or improving the level of performance of previous versions of AMBER for conventional MD simulations. To fulfill these goals, we utilized two architectural concepts of object-oriented programming: encapsulation and inheritance.³³ The original AMBER GPU data structures are encapsulated into base C++ classes, containing all coordinates, forces, energy terms, all simulation parameters and settings. New free energy classes are derived from the base classes that contain the original GPU functionality and data structures for MD simulations. New derived free energy classes inherit all the properties and methods of existing MD classes. Through encapsulation and inheritance, free energy capability can be implemented so that: 1. there is little or no need to modify the original MD GPU codes except they are wrapped into base classes now, since new add-ons can be implemented in the derived free energy classes; 2. the new speci c free energy algorithms and associated data structures are transparent to the base classes such that modifying or optimizing the base classes will have minimal effects on the derived classes; 3. derived free energy classes can utilize different algorithms, different precision models, and even different force fields.

Such encapsulation and inheritance approach, on the other hand, could introduce additional computational overhead, compared to direct modification of MD GPU kernels so that similar computational tasks are executed within the same kernels. Consequently the reported approach here will be ideal for new modules where only small portions of calculations needed to be altered, such as TI; while direct modification of MD GPU kernels will be suitable for situations where algorithms changes are global, e.g., incorporation of polarizable force fields.

Extensions of new modules

The present software design can be easily extended to accommodate implementation of new methods or algorithms. For example, the 12-6-4 potential modules have been implemented using this framework by treating the extra r⁻4 terms through add-on modules with minimal, if any, modification of MD CPU codes and GPU kernels.

For most developers, the CPU code remains the most accessible means for prototyping new methods. In select cases, where complex potentials are applied to only a small number of atoms, the CPU may afford performance advantages for development code that have to be fully optimized. To serve these needs, AMBER18 has a new “atom shuttling” system, which extracts information on a pre-defined list of selected atoms and transfers it between the host CPU memory and GPU device. In previous versions, all coordinates, forces, charges, and other data can be downloaded and uploaded between the host and device, at costs approaching 30% of the typical time step. When the majority of the system’s atoms will not influence the CPU computations, this is wasteful. The shuttle system accepts a pre-defined list of atoms and collects them into a buffer for a lighter communication requirement between the host and device. The cost of organizing the atoms into the list is minor, but the extra kernel calls to manage the list and the latency of initiating the transfer are considerations. In the limit of transferring very small numbers of atoms, the cost of the shuttle can be less than 1% of the total simulation time, but methods that require transferring the majority of atom data may be more efficient porting entire arrays with the methods in Amber16.

Features

The current Amber18 has a host of features available that work together to perform MD and free energy simulations (Table 1). A brief description of the most relevant features are provided below.

Table 1:

Comparison of free energy (FEP/TI) compatible features in Amber16 and Amber18 on CPUs and GPUs.

Free energy compatible feature		Amber16		Amber18
Category	Functionality	CPU	GPU	CPU	GPU
Ensemble	NVE	✓	✗	✓	✓
	NVT	✓	✗	✓	✓
	NPT	✓	✗	✓	✓
	semi-iso P	✗	✗	✗	✗
	CpHMD	✓	✗	✓	✓
Free Energy	TI	✓	✗	✓	✓
Analysis	MBAR	✓	✗	✓	✓
Enhanced	H-REMD	✓	✗	✓	✓
Sampling	AMD	✓	✗	✓	✓
	SGLD	✓	✗	✓	✗
	GAMD	✓	✗	✓	✓
Potentials	12-6-4	✓	✗	✓	✓

List of features that have compatibility with free energy (FEP/TI) methods in Amber16 and Amber18 on CPUs and GPUs. Red color indicates a feature not compatible with free energy methods (although it may be compatible with conventional MD). Green color indicates new free energy compatible feature in Amber18.

Direct implementation of alchemical free energy methods

Alchemical free energy simulations^9,10 provide accurate and robust estimates of relative free energies from molecular dynamics simulations,^{10,15,34–38} but are computationally intensive, and are often limited by the availability of computing resources and/or required turn-around time. The limitations can render these methods impractical, particularly for industrial applications.³⁹ GPU-accelerated alchemical free energy methods change this landscape, but have only recently emerged in a few simulation codes. The free energy methods implemented in the Amber18 GPU code build on the efficient AMBER GPU MD code base (pmemd.cuda), and include both thermodynamic integration and free energy perturbation classes.

Thermodynamic Integration (TI):^11–15 The free energy change from state 0 to state 1, ΔA_0→1, is approximately calculated by numerical integration of the derivative of the system potential energy U with respect to the target parameter λ:

$$\Delta A_{0\to 1}={\int }_0^1{\langle \frac{dU(\lambda ,\overrightarrow{q})}{d\lambda }\rangle }_{\lambda }d\lambda .$$ (1)

Free Energy Perturbation (FEP):^15–19 The free energy change between state 0 and 1, ΔA_0→1 is calculated by averaging the exponential of the potential energy differences sampled on the potential surface of state 0 (the Zwanzig equation¹⁶):

$$\Delta A_{0\to 1}={\beta }^{-1}\text{ln}{\langle e^{-\beta \left(U_1(\overrightarrow{q})-U_0(\overrightarrow{q})\right)}\rangle }_0={\beta }^{-1}\text{ln}{\langle e^{-\beta \Delta U(\overrightarrow{q})}\rangle }_0$$ (2)

The quantities calculated from FEP can be output for post-analysis through Bennett’s acceptance ratio and its variants (BAR/MBAR).^20–25

Both TI and FEP methods can be used for linear alchemical transformations, non-linear “parameter-interpolated” pathways⁴⁰ and so-called “softcore”^41–43 schemes for both van der Waals and electrostatic interactions. All above are available in the current Amber18 GPU release by utilizing the same input formats as the CPU version.

The GPU free energy implementation has been demonstrated to deliver speed-ups are generally significantly more than one order of magnitude when comparing a single GPU to a comparably priced single (multi-core) microprocessor (see Performance section for detailed benchmarks). The GPU free energy implementation code performs TI with linear alchemical transformations roughly at the speed of 70 % of running an MD simulation with the fast SPFP precision mode,³¹ similar to the ratios seen in the CPU counterpart.³² Overall, the free energy simulation speed-up relative to the CPU code is very similar to that for conventional MD simulation. As will be discussed in the next section, in certain instances the overhead (relative to conventional MD) for the linear alchemical free energy simulations can be greatly reduced by use of non-linear parameter-interpolated TI.⁴⁰

Parameter-interpolated thermodynamic integration

Amber18 is also able to exploit the properties of a parameter-interpolated thermodynamic integration (PI-TI) method,⁴⁰ which has recently been extended to support PME electro-statics, to connect states by their molecular mechanical parameter values. This method has the practical advantage that no modification to the MD code is required to propagate the dynamics, and unlike with linear alchemical mixing, only one electrostatic evaluation is needed (e.g., single call to particle-mesh Ewald). In the case of Amber18, this enables all the performance benefits of GPU-acceleration to be realized, in addition to unlocking the full spectrum of features available within the MD software. The TI evaluation can be accomplished in a post-processing step by reanalyzing the statistically independent trajectory frames in parallel for high throughput. Additional tools to streamline the computational pipeline for free energy post-processing and analysis are forthcoming.

Replica-Exchange Molecular Dynamics

During the past two decades, the replica exchange methods^44,45 have become popular in over-coming the multiple-minima problem by exchanging non-interacting replicas of the system at different conditions. The original replica exchange methods were applied on systems at several temperatures,⁴⁴ and have been extended to various conditions, such as Hamiltonian,⁴⁶ pH,⁴⁷ and redox potentials. Amber18 is capable of performing temperature, Hamiltonian, and pH replica exchange simulations using GPU. Hamiltonian replica exchange can be con-figured in a flexible way, as long as the “force field” (or equivalently the prmtop file) is properly defined for each replica. Hence, the newly implemented free energy methods in Amber18 can be performed as Hamiltonian replica exchange so that different λ windows can exchange their conformations. Other types of Hamiltonian replica exchange simulations, such as Hamiltonian tempering or umbrella sampling, can be easily setup as well.

Multiple dimension replica exchange simulations^48–53 where two or more conditions are simulated at the same time, are supported as well. By utilizing the multi-dimensional replica exchange capability, many practical combinations are possible to enhance sampling: such as TI simulation combined with temperature or pH replica exchange.

The con guration of GPU’s in Amber18 replica exchange simulations is very flexible in order to fit various types of computational resources. Ideally for load balancing, the number of replicas should be an integer multiple (typically 1–6) of the number of available GPU’s. One GPU can run one or multiple replicas given sufficient GPU memory is available, although one can expect some slow-down in the cases of multiple tasks running concurrently on a single GPU. Our experience shows that a 11GB GTX 1080TI GPU can handle six instances of typical kinase systems (around 30,000 to 50,000 atoms) without losing efficiency. One scenario is that to run free energy simulations with replica exchange on one multiple GPU node, e.g., executing 12 λ-windows on a 4-GPU or 6-GPU node with each GPU handling 3 or 2 λ-windows. Such scenarios take advantage of extremely fast intra-node communication and enable efficient performance optimization on modern large scale GPU clusters/supercomputers such Summit at Oak Ridge National Laboratory. In principle, a single replica can also be run in parallel on multiple GPUs but this is strongly discouraged as Amber18 is not optimized for this.

Constant pH Molecular Dynamics

Conventional, all-atom molecular simulations consider ensembles constrained to have predetermined fixed protonation states that are not necessarily consistent with any pH value. Constant pH molecular dynamics (CpHMD) is a technique that enables sampling of different accessible protonation states (including different relevant tautomers) consistent with a bulk pH value.^26,27 These methods have been applied to a wide array of biological problems, including prediction of pK_a shifts in proteins and nucleic acids, pH-dependent conformational changes, assembly and protein-ligand, protein-protein and protein-nucleic acid binding events.⁵⁴ These methods provide detailed information about the conditional probability of observing correlated protonation events that have biological implications. Very recently, a discrete protonation state constant pH molecular dynamics method has been implemented on GPUs, integrated with REMD methods (including along a pH dimension) and tested in AMBER.⁵⁵ The method has been applied for the first time to the interpretation of activity-pH pro les in a mechanistic computational enzymology study of the archetype enzyme RNase A.⁵⁶ The CpHMD method in Amber18 is compatible with enhanced sampling methods such as REMD, and is compatible with the new GPU-accelerated free energy framework.

The workflow of explicit Solvent CpHMD simulation has been described in detail elsewhere.⁵⁵ Briefly, the method follows the general approach of Baptista and co-workers^26,27 that involves sampling of discreet protonation states using a Monte Carlo sampling procedure. Simulations are performed in explicit solvent under periodic boundary conditions using PME to generate ensembles. The CpHMD method utilizes an extended force field that contains parameters (typically charge vectors) associated with changes in protonation state and reference chemical potentials for each titratable site calibrated for a selected GB model to obtain correct pK_a values in solution. In the Monte Carlo decision to accept or reject a trial protonation state, explicit solvent (including any nonstructural ions) is stripped and replaced using the selected GB model under non-periodic boundary conditions. Additional considerations are made for multi-site titration involving titratable residues that are considered “neighbors”.⁵⁵ If any protonation state change attempts are accepted, the explicit solvent is replaced, the solute is frozen, and MD is used to relax the solvent degrees of freedom for a short period of time. After relaxation is complete, the velocities of the solute atoms are restored to their prior values and standard dynamics resumes. Full details can be found in reference.⁵⁵

12-6-4 Potentials for Metal Ions

The GPU version of Amber18 (pmemd.cuda) is capable of utilizing 12-6-4 potentials, developed by Li et. al.²⁸ for metal ions in aqueous solution, and recently extended for Mg²⁺, Mn²⁺, Zn²⁺ and Cd²⁺ ions so as to have balanced interactions with nucleic acids.³⁰ The 12-6-4 potentials are derived from regular 12–6 potentials by adding r⁻⁴ terms, which has been proposed by Roux and Karplus.^57,58

The 12–6 potential⁵⁹ for non-bonded interactions is:

$$U_{ij}\left(r_{ij}\right)={ϵ}_{ij}\left[{\left(\frac{R_{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{ij}}{r_{ij}}\right)}^6\right]$$ (3)

where the parameters R_ij and ϵ_ij are the combined radius and well depth for the pairwise interaction and r_ij is the distance between the particles. Equation (3) can be expressed equivalently as:

$$U_{ij}\left(r_{ij}\right)=\frac{A_{ij}}{r_{ij}^{12}}-\frac{B_{ij}}{r_{ij}^6}$$ (4)

where $A_{ij}={ϵ}_{ij}{R}_{ij}^{12}$ and $B_{ij}=2{ϵ}_{ij}{R}_{ij}^6$.

The expanded 12-6-4 potential⁶⁰ is then:

$$\begin{gathered} U_{ij}\left(r_{ij}\right)={ϵ}_{ij}\left[{\left(\frac{R_{ij}}{r_{ij}}\right)}^{12}-2{\left(\frac{R_{ij}}{r_{ij}}\right)}^6-2\kappa R_{ij}^2{\left(\frac{R_{ij}}{r_{ij}}\right)}^4\right] \\ =\frac{A_{ij}}{r_{ij}^{12}}-\frac{B_{ij}}{r_{ij}^6}-\frac{C_{ij}}{r_{ij}^4} \end{gathered}$$ (5)

where C_ij is equivalent to B_ijκ, and κ is a scaling parameter with units of Å⁻². The additional attractive term, $\frac{C_{ij}}{r_{ij}^4}$, implicitly accounts for polarization effects by mimicking the charge-induced dipole interaction. The 12-6-4 potentials have showed a marked improvement over the 12–6 LJ nonbonded model.^28,30

Future Plan

The Amber18 development roadmap will extend sampling capabilites for free energy simulations to facilitate advancement of drug discovery,⁶¹ including: implementation of Gibbs sampling scheme⁶² to improve the exchange rates in replica exchange simulations, the self-adjusted mixture sampling (SAMS)⁶³ to optimize the simulation lengths for different lambda windows, and replica exchange with solute scaling (REST2),⁶⁴ a more efficient version of replica exchange with solute tempering⁶⁵ to stably and efficiently perform “effective” solute tempering replica exchange simulations.

Performance

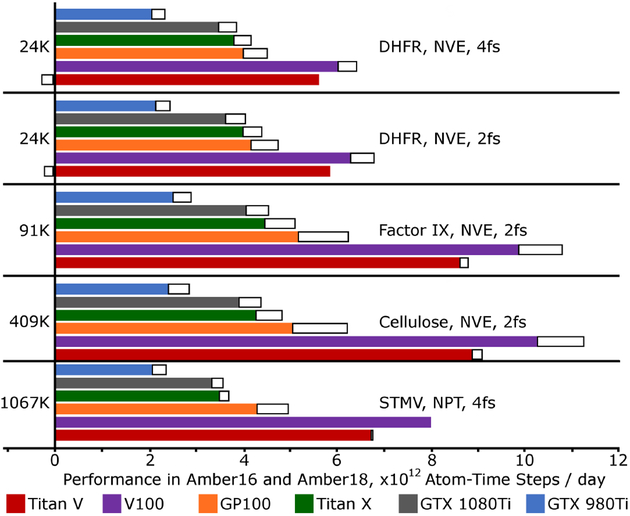
Amber18 runs efficiently on GPU platforms for both MD and free energy simulations. Performance benchmarks for equilibrium MD are shown in Figure 1 and listed for selected GPUs in Table 2, including comparisons with Amber16. The figure works in a particle-normalized metric, trillions of atom-time steps per day, which puts most systems on equal footing and shows performance improvements of up to 24%, without implying improper comparisons to other codes (the cutoffs used in these benchmarks are smaller than some other benchmarks, and other settings may not be comparable). Longer time steps, if safe, tend to improve overall throughput at a marginal increase in the cost of computing each step (requiring more frequent pair list updates). Small systems tend to perform less efficiently (small FFTs and pair list building kernels do not fully occupy the GPU). Virial computations are also costly, as seen for the Satellite Tobacco Mosaic Virus (STMV) system, the only one of this abbreviated list of benchmarks to include pressure regulation with a Berendsen barostat.

Figure 1:

Performance of Amber18 relative to Amber16 seen on multiple GPU architectures. Performance is given in a particle-normalized metric which emphasizes the number of inter actions that each card is able to compute in a given time. Performance in Amber16 is shown in solid color bars, and improvements with Amber18 in black outlined extensions. In a few cases, performance in Amber18 is lower than in Amber16, indicated by the extensions falling to the left of the y-axis. (Beta tests of an upcoming patch make Amber18 even faster, and consistently superior to Amber16.) System, ensemble, and time step are displayed on the right, while the system size (thousands of atoms) is given on the left. All systems were run with an 8 Å cutoff for real-space interactions and other default Amber parameters.

Table 2:

Comparison of MD simulation rates in Amber16 and Amber18 on CPUs and GPUs.

		Simulation Rate, ns/day
		GTX-980 Ti		GTX-1080 Ti		Titan-X
System	Atom Count	Amber16	Amber18	Amber16	Amber18	Amber16	Amber18
DHFR, NVE, 4fs	24K	347	382	588	657	643	710
DHFR, NVE, 2fs	24K	181	209	306	345	338	374
Factor IX, NVE, 2fs	91K	52	64	85	100	93	113
Cellulose, NVE, 2fs	409K	12	14	19	21	21	23
STMV, NVE, 4fs	1067K	8	9	12	13	13	14
		Simulation Rate, ns/day
		GP100		V100 (Volta)		Titan-V
System	Atom Count	Amber16	Amber18	Amber16	Amber18	Amber16	Amber18
DHFR, NVE, 4fs	24K	677	768	1020	1091	954	904
DHFR, NVE, 2fs	24K	353	404	532	577	497	477
Factor IX, NVE, 2fs	91K	114	137	217	238	189	194
Cellulose, NVE, 2fs	409K	25	29	50	49	43	41
STMV, NVE, 4fs	1067K	16	19	30	30	25	25

Timings for selected systems in Amber18 versus Amber16. The ensemble and time step are given in the left hand column. Other Amber default parameters included an 8 Å cutoff and ≤1 Å PME (3D-FFT) grid spacing.

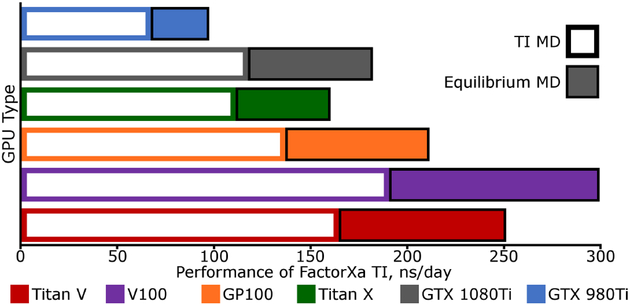
Using a GTX-1080Ti, still the most cost-effective GPU at the time of publication, the 23,558 atom Dihydrofolate Reductase (DHFR) benchmark (4 fs time step, constant energy) runs at 657 ns/day in Amber18 and 588 ns/day in Amber16. The same codes run the 90,906 atom blood clotting Factor IX system at 100 and 89 ns/day, respectively, with a 2 fs time step. Performance in thermodynamic integration free energy simulations for mutating ligands of the clotting Factor Xa system is shown in Figure 2. TI with linear alchemical mixing generally exacts a toll of 1/3 the speed that could be achieved in a conventional MD simulation. Additional pairwise computations between particles are present, but the secondary reciprocal space calculation is about 85% of the additional cost (this cost is eliminated in the PITI method⁴⁰). The main performance improvements derive from: 1. innovative spline tabulation look-up and particle mapping kernels for faster PME direct and reciprocal space calculations, and 2. more efficient memory access for bonded and non-bonded terms.

Figure 2:

Performance of Amber18 Thermodynamic Integration with linear alchemical mix ing on multiple GPU architectures relative to conventional MD. The color scheme for each GPU type is consistent with Figure 1, but the performance of TI is given by an open bar, while performance of the equivalent, “plain” MD system is given by a black-bordered solid extension. The test system is for the Factor Xa protein with the ligand mutation from L51a (62 atoms) to L51b (62 atoms). The system has total 41563 atoms and the whole ligand defined as the TI region.

Faster PME direct and reciprocal space calculations.

Most CPU codes use a quadratic or cubic spline for the derivative of the complementary error function used in the PME direct space energy term. Rather than costly conversion of floating point values into integer indexes for table look-ups, we take the IEEE-754 representation of the 32-bit floating point number for the squared distance and use its high fourteen bits, isolated by interpreting it as an unsigned integer and shifting right 18 bits, as an integer index into a logarithmically coarsening look-up table. This approach uses a minimum of the precious streaming multiprocessor (SMP) cache, collects a huge number of arithmetic operations into a single cubic spline evaluation, and typically leads to a 6–8% speed-up. The workflow of the non-bonded kernel was further improved by eliminating _shared_ memory storage and dealing with all particle comparisons within the same warp via _shfl instructions. This permitted us to engage not just 768 but 1280 threads on each SMP.

PME reciprocal space.

We have made improvements to the kernel that maps particles onto the 3DFFT mesh by parallel computation of B-spline coefficients for all three dimensions (utilizing 90 out of 96 threads in the block rather than less than 1/3 of them) and re-tuning the stencil for writing data onto the mesh to make better coalesced atomic transactions. This improves the throughput of the mapping kernel by more than 40%, and typically leads to a few percent speed-up overall.

More efficient memory access for bonded and non-bonded terms.

Rather than reach into global memory for the coordinates of each individual atom needed by any bonded term, we draw groups of topologically connected atoms at the start of the simulation and assign bond and angle terms to operate on the atoms of these groups. At each step of the simulation, the coordinates of each group are cached on the SMP and forces due to their bonded interactions are accumulated in _shared_ memory. Last, the results are dumped back to global via atomic transactions, reducing the global reads and writes due to bonded interactions more than ten-fold. The approach generalizes one described ten years ago for the Folding@Home client,⁶⁶ where bond and angle computations were computed by the threads that had already downloaded the atoms for a dihedral computation. Our approach makes much larger groups of atoms (up to 128) and does not compute redundant interactions. However, the block-wide synchronization after reading coordinates and prior to writing results may leave threads idle. The modular programming that creates our networks of interactions facilitates combining or partitioning the GPU kernels to optimize register usage and thread occupancy.

We have also gained a considerable amount of improvement by trimming the precision model where low significant bits are wasted. Rather than convert every non-bonded force to 64-bit integers immediately, we accumulate forces from 512 interactions (evaluated sequentially in sets of 16 by each of 32 threads in a warp) before converting the sums to integer and ultimately committing the result back to global memory. Because the tile scheme in our non-bonded kernel remains warp-synchronous, the sequence of floating-point operations that evaluates the force on each atom is identical regardless of the order the tile was called. In other words, each tile evaluation is immune from race conditions. Conversions to integer arithmetic always occur, as in Amber16, before combining the results of separate warps, as the coordination of different warps is not guaranteed. These optimizations therefore maintain the numerical determinism of the code: a given GPU will produce the identical answers for a given system and input parameters.

Minimal computational load on CPU and GPU/CPU intercommunication.

As it does for MD, Amber18 performs free energy computations almost entirely on the GPU and requires very little communication between the CPU and the GPU. This results in a tremendous practical advantage over other implementations in that independent or loosely coupled simulations (e.g., different lambda windows of a TI or FEP, possibly with REMD) can be run efficiently in parallel on cost-effective nodes that contain multiple GPUs with a single (possibly low-end) CPU managing them all without loss of performance. This is a critical design feature that distinguishes Amber18 free energy simulations from other packages that may require multiple high end CPU cores to support each GPU for standard dynamics and free energy calculations. The result is an implementation of TI/FEP that is not only one of the fastest available but also the most cost effective when hardware costs are factored in.

Conclusion

In this application note, we report new features and performance benchmarks for the Amber18 software official release. The code is able to perform GPU-accelerated alchemical free energy perturbation and thermodynamic integration highly efficiently on a wide range of GPU hardware. The free energy perturbation simulations output metadata that can be analyzed using conventional or multistate Bennett’s acceptance ratio methods. Additionally, thermodynamic integration capability is enabled for linear alchemical transformations, and non-linear transformations including softcore potentials and parameter-interpolated TI methods recently extended for efficient use with particle mesh Ewald electrostatics. These free energy methods can be used in conjunction with a wide range of enhanced sampling methods, constant pH molecular dynamics, and new 12-6-4 potentials for metal ions. The Amber18 software package provides a rich set of high-performance GPU-accelerated features that enable a wide range of molecular simulation applications from computational molecular biophysics to drug discovery.