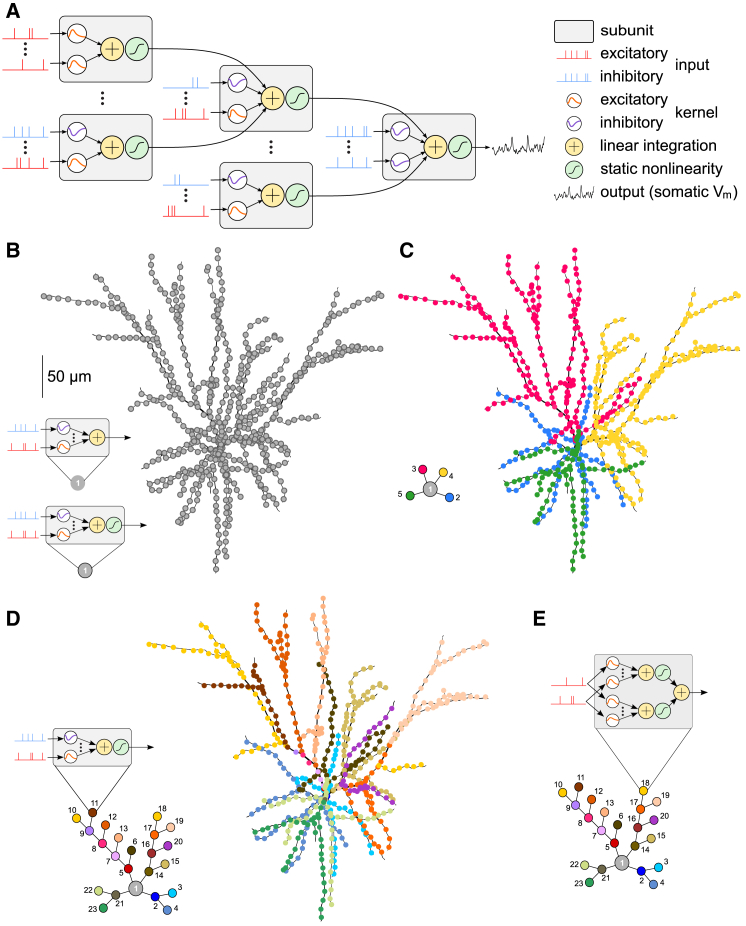
Figure 3.

A Hierarchical Linear-Nonlinear Model of Dendritic Integration

(A) Schematic of an hLN model with five subunits. Each subunit (gray boxes) receives input from a number of excitatory (red) and inhibitory spike trains (blue), filtered by positive (orange) or negative synaptic kernels (purple). The filtered inputs are summed linearly (yellow) and passed through a sigmoidal nonlinearity (green) before being integrated at the next stage of the hierarchy.

(B–E) hLN model architectures of increasing complexity (left) capturing synaptic integration in the biophysical model (right). Each colored circle of an hLN model corresponds to an individual subunit with input spike trains from a subset of synapses (correspondingly colored dots for excitatory synapses shown on the biophysical model morphology) and an output nonlinearity (except for the single subunit of the model in B, top, see also insets). Gray circles correspond to output subunits. Models from (B) to (D) expand the depth of the hierarchy from a 1-subunit (1-layer) “point neuron” model (B) to a 23-subunit (6-layer) model (D). The model in (E) expands the breadth of the hierarchy by multiplexing synaptic inputs such that each input spike train feeds into two parallel input channels with different synaptic kernels and nonlinearities (inset shows the schematic of a single, multiplexing subunit).