Highlights
-
•
Phylodynamic analysis gives insight into mycobacterium tuberculosis outbreaks.
-
•
Robust estimation of epidemiological parameters in Bern thanks to high sampling rate.
-
•
Infectious period for WTK cases significantly longer than in Bernese outbreak.
Keywords: Phylodynamic analysis, Tuberculosis outbreak, Epidemic dynamics, Transmission dynamics
Abstract
The fast evolution of pathogenic viruses has allowed for the development of phylodynamic approaches that extract information about the epidemiological characteristics of viral genomes. Thanks to advances in whole genome sequencing, they can be applied to slowly evolving bacterial pathogens like Mycobacterium tuberculosis. In this study, we investigate and compare the epidemiological dynamics underlying two M. tuberculosis outbreaks using phylodynamic methods. Specifically, we (i) test if the outbreak data sets contain enough genetic variation to estimate short-term evolutionary rates and (ii) reconstruct epidemiological parameters such as the effective reproduction number.
The first outbreak occurred in the Swiss city of Bern (1987–2012) and was caused by a drug-susceptible strain belonging to the phylogenetic M. tuberculosis Lineage 4. The second outbreak was caused by a multidrug-resistant (MDR) strain of Lineage 2, imported from the Wat Tham Krabok (WTK) refugee camp in Thailand into California.
There is little temporal signal in the Bern data set and moderate temporal signal in the WTK data set. Thanks to its high sampling proportion (90%) the Bern outbreak allows robust estimation of epidemiological parameters despite the poor temporal signal. Conversely, there is much uncertainty in the epidemiological estimates concerning the sparsely sampled (9%) WTK outbreak. Our results suggest that both outbreaks peaked around 1990, although they were only recognized as outbreaks in 1993 (Bern) and 2004 (WTK). Furthermore, individuals were infected for a significantly longer period (around 9 years) in the WTK outbreak than in the Bern outbreak (4–5 years).
Our work highlights both the limitations and opportunities of phylodynamic analysis of outbreaks involving slowly evolving pathogens: (i) estimation of the evolutionary rate is difficult on outbreak time scales and (ii) a high sampling proportion allows quantification of the age of the outbreak based on the sampling times, and thus allows for robust estimation of epidemiological parameters.
1. Introduction
Whole genome sequencing (WGS) of clinical M. tuberculosis isolates is performed retrospectively and allows to confirm/refute suspected epidemiological links to identify individuals contributing to transmission, and explore drug-resistance and/or compensatory mechanisms which emerged during anti-tuberculosis treatment (Walker et al., 2013; Gardy et al., 2011; Stucki et al., 2015; Coscolla et al., 2015a; Hatherell et al., 2016; Casali et al., 2016). Although WGS analysis has the potential to reveal more complex epidemiological dynamics such as how long the outbreak was not controlled, the time patients are infectious for, the proportion of sampled cases, and the transmission potential of different strains, these epidemiological parameters are rarely estimated for slowly evolving bacterial pathogens such as M. tuberculosis (Gardy et al., 2011; Hatherell et al., 2016; Tanaka et al., 2006). In the context of tuberculosis disease, answering those questions may help to evaluate and improve treatment strategies and control programs.
Phylodynamic analysis of real time WGS data can shed light on temporal dynamics of disease outbreaks, for example to determine if there is ongoing transmission (Hatherell et al., 2016). Here, we employ phylodynamic methods to shed further light on two M. tuberculosis outbreaks. The first outbreak was detected around 1991 in the city of Bern, Switzerland, where twenty-two related cases, mainly homeless individuals and substance abusers, were identified initially (Genewein et al., 1993). Using a novel combination of strain-specific SNP screening assay and targeted WGS, a tuberculosis cluster spanning 21 years and involving 68 patients was identified (Stucki et al., 2015; Tanaka et al., 2006). The genomic analysis revealed that this outbreak was caused by a Lineage 4 strain (Euro-American) of M. tuberculosis, and all but one showed no evidence of antibiotic resistant conferring mutations. The analysis revealed three sub-clusters within the outbreak, one of them associated to HIV coinfection (13 patients were coinfected with HIV).
The second data set consists of 30 MDR strains imported to California during resettlement of refugees from a refugee camp at Wat Tham Krabok (WTK) (Coscolla et al., 2015a). Whole genome analysis confirmed that the strains causing the outbreak were multidrug-resistant and belonged to the Lineage 2 (East-Asian, Beijing genotype) of M. tuberculosis. Genomic data supported a single case whose isolate occupied the central node of the transmission network indicating the presence of a super-spreader. Epidemiological data integrated with the transmission chain also demonstrated multiple independent importation events from Thailand with reactivation and transmission within California over a 22-year period.
In this study, we aim to understand the dynamics of tuberculosis outbreaks by inferring phylogenetic trees together with epidemiological parameters, particularly, transmission and recovery rates, from genome sequence data using phylodynamic methods.
2. Methods
2.1. Reconstruction of transmission dynamics
First, we explored the temporal signal in the sequence alignments using TempEst (Rambaut et al., 2016). The main analysis of both data sets was done within the Bayesian MCMC framework BEAST2 (Bouckaert et al., 2014). We assume that the phylogeny spanned by the genomic samples is a suitable approximation of the transmission tree, such that we can estimate epidemiological parameters simultaneously with the phylogenetic tree. Since we do not intend to estimate direction of transmission this assumption refers to the branching times of the phylogenetic tree approximating times at which transmissions occurred only. We employ two phylodynamic methods, the birth-death skyline plot (BDSKY) (Stadler et al., 2013) and the multi-type birth-death model (MTBD) (Kühnert et al., 2016). Both assume that an infection event can be considered as the “birth” of a newly infected individual, while a recovery event (successful treatment) is a “death”. While the BDSKY model assumes that an infected individual is immediately infectious upon infection, the MTBD model allows us to incorporate the fact that M. tuberculosis infections usually start with a latent period in which the infected individual is not yet infectious.
In both analyses, we employ a general time reversible substitution model with gamma distributed rate heterogeneity and a proportion of invariant sites (GTR+I+Γ). A relaxed lognormal clock is used to model the variation of evolutionary (substitution) rates across branches, such that we estimate a mean clock rate θ (per SNP per year), from which we compute the number of SNPs per genome per year, and standard deviation σ for the lognormal branch rate distribution. In addition to the SNP alignments we specify the proportions of A, C, G and T’s as constant site weights. All parameters are estimated jointly. The prior distributions used are summarized in Table 1.
Table 1.
Bayesian prior distributions used for phylodynamic analysis.
| Mean substitution rate θ | Standard deviation σ | Effective reproduction number Re | Recovery rate δ | Exposed rate σ | Sampling proportion s | Origin of sample | Removal (upon sampling) probability r | |
|---|---|---|---|---|---|---|---|---|
| Bern (BDSKY) | Unif(0,∞) | Exp(0.33) | LogN(0,1) | LogN (exp(0.5)*,1) |
– | Beta(45,5) | Unif(0,40) | Unif(0,1) |
| Bern (MTBD) | Unif(0,∞) | Exp(0.33) | LogN(0,1) | Fixed to 2, 4 or 6 | LogN(exp(m),1) m = 1/(2-1/δ)* |
Beta(45,5) | Unif(0,40) | Unif(0,1) |
|
Thailand/ California (BDSKY) |
Unif(0,∞) | Exp(0.33) | LogN(0,1) | LogN(exp(0.5)*,1) | – | Beta(10,90) | Unif(0,100) | Unif(0,1) |
Mean determined to correspond to an infected duration (i.e. the sum of the exposed and infectious periods) of 2 years.
2.1.1. Phylodynamic analysis with the birth-death skyline model
The birth-death skyline model (Stadler et al., 2013) describes a prior distribution for a transmission tree and is based on a stochastic birth-death process, with birth (λ), death (μ) and sampling (ψ) rates. Individuals become non-infectious upon sampling with probability r ∈ [0,1] (Gavryushkina et al., 2014). Typically, the probability r is close to 1 if sampling is accompanied by successful treatment. To investigate the change of epidemiological dynamics, the period covered by the phylogeny is divided into intervals, and parameters are constant within an interval but may change between intervals. We can estimate the effective reproduction number Re, through the alternative parametrization of the model using the effective reproduction number Re = λ /(μ + rψ), the rate at which individuals become non-infectious δ = μ + rψ and the sampling proportion s = ψ / (μ + ψ). We employ m = 5 intervals to estimate potential changes in Re, and assume that δ is constant through time. The sampling proportion s is set to zero before the first sample, and assumed to be a positive constant thereafter.
2.1.2. Phylodynamic analysis with the multi-type birth-death model – incorporating the latent period
The MTBD model allows us to incorporate and investigate the exposed phase. In the following we use the terms ‘latent’ and ‘exposed’ interchangeably, referring to the time during which individuals are infected but not yet infectious. The multi-type version of the birth-death skyline model (Kühnert et al., 2016) allows us to distinguish between two types of infected individuals: (i) those who are not yet infectious (typically assigned to a compartment E), and (ii) those who are infectious (compartment I). Previous work has indicated that phylogenetic tools can estimate the overall infected period (including the exposed and infectious phases), but that it is difficult to estimate the exposed and infectious periods separately (Stadler et al., 2014). Hence, we run three versions of this analysis, with the infectious period fixed to either 6 months (δ=2), 3 months (δ=4) or 2 months (δ=6) and report the results for each of those setups.
2.1.3. Model comparison
The goodness of fit of the chosen models was tested using path sampling (Baele et al., 2012). We tested the goodness of fit of (i) the clock model as well as (ii) the demographic model. As alternative models we used (i) a strict clock model and a relaxed clock model with exponentially distributed branch rates (Drummond et al., 2006), and (ii) the commonly used constant coalescent model (Kingman, 1982) and the Bayesian skyline model (Pybus et al., 2000). The path sampling analyses were run for 30 steps with a chain length of 1.000.000 each and a pre-burnin of 50%.
2.2. Data sets
Sampling procedures, strain isolation, sequencing, accession numbers for the sequences, and sequence analysis are described in detail in (Stucki et al., 2015). In brief, we used the Illumina platform to sequence 68 patients associated with the Bernese outbreak and 46 from the WTK outbreak spanning more than 10 and 36 years, respectively. Only one isolate per patient was included and the isolation dates of the strains were used as sampling times. The isolates obtained from the Bernese outbreak were sequenced using Illumina HiSeq 2000, with single-end reads of approximately 50 bp as described in (Stucki et al., 2015). The WTK outbreak was sequenced using an Illumina Genome Analyzer IIx, with single-end reads of also approximately 50 bp as described in Coscolla et al. (2015a). In both cases, reads were mapped against an inferred common ancestor sequence to all main lineages of the Mycobacterium Tuberculosis complex (Comas et al., 2010) using both Burrows-Wheeler Aligner v0.5.8c (BWA) (Li and Durbin, 2009) and SMALT (http://www.sanger.ac.uk/science/tools/smalt-0). Only positions consensual to both methods were considered. SNPs were determined with SAMtools (Li et al., 2009). Only SNPs with a coverage of at least 10 reads and a phred-scaled mapping quality value of 20 were considered. In addition, SNPs falling in genes annotated as PE/PPE/PGRS, “maturase”, “phage”, “insertion sequence” or “13E12 repeat family protein” were removed due to the uncertainty of mappings.
An alignment of 133 variable positions among 68 isolates from the Bern outbreak (Stucki et al., 2015) and an alignment of 150 variable positions among 30 Californian cases from the WTK outbreak were used (Coscolla et al., 2015a). Possible drug resistance conferring mutations as described in (Coscolla et al., 2015a) were excluded from the alignment.
3. Results
3.1. TB in Bern
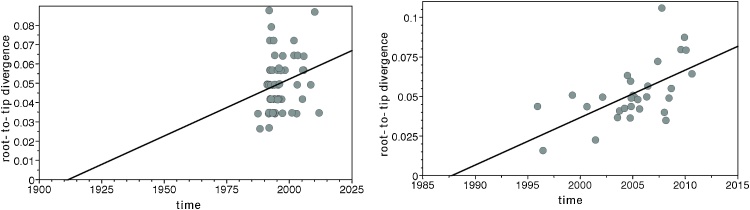
The Lineage 4 Bernese data set shows positive correlation between genetic divergence and sampling time, but there is little temporal signal (TempEst R2=0.05, see Fig. 1).
Fig. 1.
Plot of phylogenetic Root-to-tip distance relative to sampling time (TempEst). Each dot represents one sample per data set (left: Bern, right: WTK).
The epidemiological parameter estimates we obtain for the Bernese outbreak largely agree among the different model specifications. We estimate that the temporal origin of the Bernese data set was around 1986 with the 95% highest posterior density intervals (HPD) ranging from 1985 to 1988.
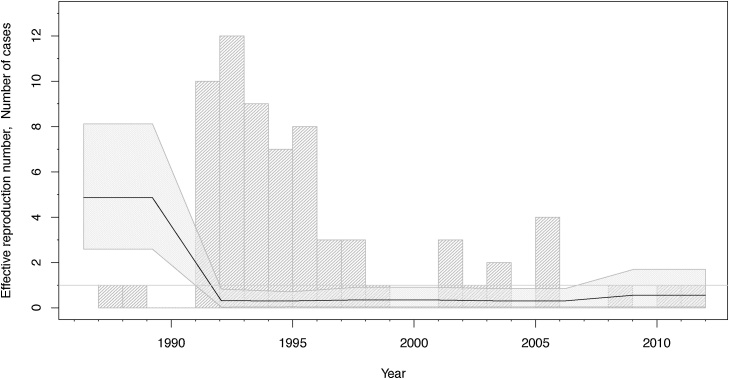
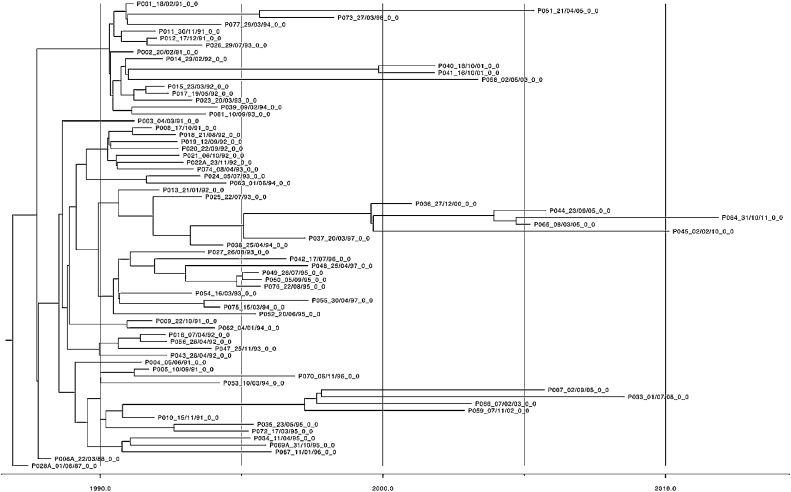
Assuming a model without an exposed phase (BDSKY) we estimate an initial high effective reproduction number Re of 4.9 (median, 95% HPD: 2.6–8.1). Around 1991, it declined drastically, staying below the epidemic threshold 1 for the rest of the sampling period (Fig. 2). The recovery rate δ is estimated to be 0.2 (median), suggesting an infected period of 5 years. The sampling proportion does not deviate from its prior distribution and is hence estimated at 90%. We estimate that the data set contains one sampled ancestor (95% HPD, 0–4), with infected individuals being removed upon sampling with 98% probability (95% HPD, 90–100%). The mean substitution rate is estimated to be 0.55 SNPs per genome per year (95% HPD, 0.32-0.86). Table 2 summarizes the median posterior estimates and their 95% HPD intervals. Fig. 3 shows the maximum clade credibility tree that was generated from the posterior distribution of trees using TreeAnnotator, which is part of BEAST version 2.4 (Bouckaert et al., 2014).
Fig. 2.
Bern reproduction number through time (BDSKY).
The median effective reproduction number (black line) with its 95% highest posterior density (HPD) interval (shaded area). The grey bars display a histogram of the number of cases diagnosed per year.
Table 2.
Bayesian Posterior results of phylodynamic analyses of both outbreaks.
| Mean number of SNPs per genome per year | Standard deviation σ | Effective reproduction number Re (before 1992) |
Effective reproduction number Re (after 1992) |
Recovery rate δ | Exposed rate σ | Sampling proportion s | Time of epidemic origin of sample | Removal (upon sampling) probability r | |
|---|---|---|---|---|---|---|---|---|---|
|
Bern (MTBD) δ = 2 |
0.72 (0.40-1.24) |
0.95 (0.60-1.34) |
2.28 (1.41-3.40) |
0.24 (0.06-0.50) |
2 (fixed) | 0.25 (0.16-0.38) |
0.87 (0.76-0.96) |
1986.75 (1985.03-1987.47) |
0.98 (0.93-1) |
|
Bern (MTBD) δ = 4 |
0.80 (0.41-1.50) |
1.00 (0.65-1.44) |
2.25 (1.39-3.33) |
0.22 (0.05-0.47) |
4 (fixed) | 0.24 (0.16-0.34) |
0.85 (0.73-0.95) |
1987.08 (1985.24-1987.47) |
0.98 (0.93-1) |
|
Bern (MTBD) δ = 6 |
0.83 (0.42-1.60) |
1.01 (0.65-1.43) |
2.23 (1.39-3.30) |
0.24 (0.06-0.48) |
6 (fixed) | 0.24 (0.16-0.34) |
0.83 (0.71-0.94) |
1987.2 (1985.07-1987.47) |
0.97 (0.92-1) |
| Bern (BDSKY) | 0.55 (0.32-0.86) |
0.90 (0.58-1.27) |
See Fig. 2. | 0.20 (0.12-0.29) |
NA | 0.90 (0.81-0.97) |
1986.39 (1985.4-1987.18) |
0.98 (0.90-1) |
|
|
Thailand/ California |
0.36 (0.11-0.57) |
0.27 (0.00055- 0.63) |
See Fig. 4. | 0.13 (0.037-0.27) |
NA | 0.08 (0.04-0.15) |
1975.58 (1935.85-1993.09) |
0.49 (0.10-1) |
|
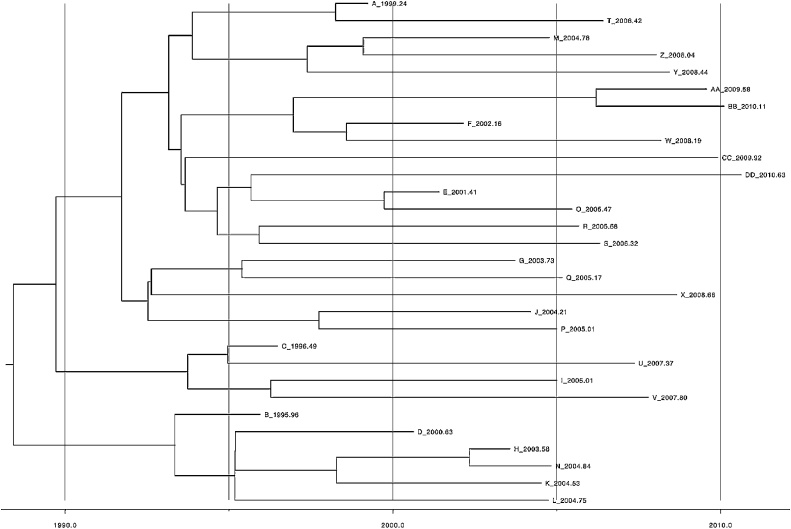
Fig. 3.
Bern maximum clade credibility tree.
Explicit incorporation of the exposed period in the MTBD model allows us to distinguish the average duration that infected individuals remain infectious. Due to the computational complexity of the model we only allowed one change in the effective reproduction number Re to have occurred in 1992. A more general setup (with more intervals for Re) leads to identifiability issues. Before 1992, we estimate median Re values around 2.25 and afterwards the median estimates are significantly below the epidemic threshold 1. Under the MTBD model we fixed the rate δ at which infected individuals become non-infectious to 2, 4 or 6 per year, suggesting an infected period of 6, 3 or 2 months. The median rate σ at which infected individuals become infectious is around 0.25, that is, on average infected individuals became infectious after 4 years in each of the three scenarios. Again, we estimate that the data set contains one sampled ancestor, with infected individuals being removed upon sampling with 98% probability. The mean number of SNPs per genome per year is estimated to be 0.72 (95% HPD, 0.40–1.24) when δ=2, 0.8 (95% HPD, 0.41-1.50) when δ=4 and 0.83 (95% HPD, 0.42-1.60) when δ=6 (Table 2).
3.2. TB in Hmong migrants from Thailand
The Lineage 2 WTK data set shows positive correlation between genetic divergence and sampling time, and a moderate level of temporal signal (TempEst R2=0.35).
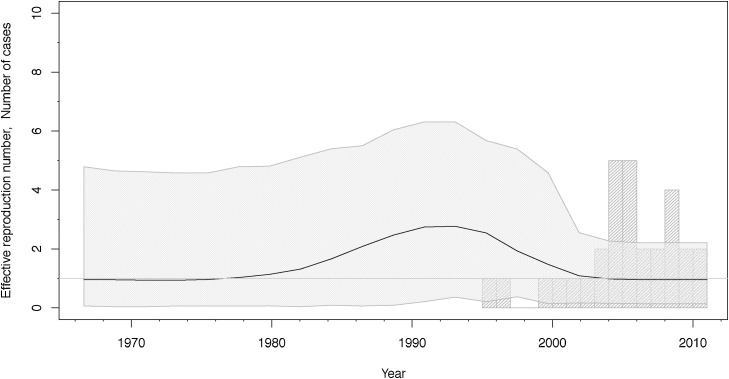
We analysed this data set under the BDSKY model, and allowed m = 4 intervals to estimate changes in the effective reproduction number Re. The temporal origin of this data set is estimated around 1976 with the 95% HPD interval ranging from 1935 to 1993. There is much uncertainty in the estimate of the effective reproduction number Re, its median and 95% HPD interval are shown in Fig. 4. The rate δ at which infected individuals become non-infectious is estimated to be 0.13 (median), suggesting an infected period of 8 years. The median sampling proportion estimate is 8% (95% HPD, 4–15%). We estimate that the data set contains no sampled ancestors (95% HPD, 0–2), with the probability to be removed upon sampling r = 64% (95% HPD, 10–100%). The mean number of SNPs per genome per year is estimated to be 0.36 (95% HPD, 0.11–0.57). Fig. 5 shows the maximum clade credibility tree that was generated from the posterior distribution of trees using TreeAnnotator (Bouckaert et al., 2014).
Fig. 4.
WTK reproduction number through time (BDSKY).
The median effective reproduction number (black line) with its 95% highest posterior density (HPD) interval (shaded area). The grey bars display a histogram of the number of cases diagnosed per year.
Fig. 5.
Hmong maximum clade credibility tree.
Due to the large uncertainty in the BDSKY estimates we did not attempt analysis of the WTK data set under the more complex MTBD model.
Table 3 summarizes the results of the path sampling analyses. Both data sets are best fit by the BDSKY demographic model combined with a relaxed clock model with lognormally distributed branch rates.
Table 3.
Overview of marginal likelihood estimates from Path Sampling analyses.
| Data | Demographic Model | Clock Model | Marginal Likelihood |
|---|---|---|---|
| WTK | BDSKY | UCLD | −5225011.591 |
| WTK | BSP | UCLD | −5411683.47 |
| WTK | ConstCoal | UCLD | −5411701.334 |
| WTK | BDSKY | SC | −5411679.402 |
| WTK | BDSKY | UCED | −5411681.248 |
| Bern | BDSKY | UCLD | −5236130.59 |
| Bern | MTBD | UCLD | −5236177.83 |
| Bern | BSP | UCLD | −5422820.42 |
| Bern | ConstCoal | UCLD | −5422845.13 |
| Bern | BDSKY | SC | −5422841.42 |
| Bern | BDSKY | UCED | −5422827.40 |
The highest marginal likelihood estimate for each data set is shown in bold.
4. Discussion
In this study, we used Bayesian phylodynamic methods to reconstruct the epidemiological dynamics of two M. tuberculosis WGS data sets corresponding to two unrelated outbreaks. We quantify the time of the start of the outbreaks, and the effective reproductive numbers through time.
The Bernese outbreak is characterized by (i) the outbreak being restricted to the medium size Swiss city Bern and (ii) a large sampling proportion. Indeed, many cases were sampled shortly after infection and subsequent cases have been recovered by a SNP screening assay and targeted WGS, such that an estimated 90% of secondary (i.e. infectious) cases linked to this outbreak are included in the data set. This high sampling proportion and the geographical containment of the Bernese outbreak are the likely cause of the higher confidence of the estimates obtained for this dataset, because the sampling times of sequences in a densely-sampled outbreak – combined with the genetic variation among them - are very informative for the age of an outbreak, and thus allow to time-calibrate the phylogeny and quantify transmission and recovery rates.
There is much uncertainty in the epidemiological parameters estimated from the WTK outbreak. The WTK data set has roughly half the number of samples and a much lower sampling proportion of 9% (median estimate). Furthermore, although the outbreak started in Thailand, our WTK data set consists entirely of cases imported into California. This sparse outbreak sample does not contain much information regarding the age of the outbreak, resulting in much uncertainty in the epidemiological estimates. Previous studies focussing on viral phylodynamics have shown that robust phylodynamic reconstruction is possible even when sampling proportions are low (Boskova et al., 2014). Hence, other factors must play a role, which we discuss below.
Our analyses were conducted using phylodynamic methods implemented in the Bayesian MCMC framework BEAST version 2.4 (Bouckaert et al., 2014), which means that we are estimating so-called time-trees using molecular clock models. Before using such models, one should explore the temporal signal in sequence alignments, which can be done using TempEst (Rambaut et al., 2016). While both data sets exhibit a positive correlation between genetic divergence and sampling time, there is a moderate level of temporal signal only in the WTK data set (R2 = 0.35). The WTK data set belongs to Lineage 2, for which Duchene et al. (Duchêne et al., 2016) were unable to reliably determine the evolutionary rate. As outbreak data sets are often not suitable for long-term mutation rate estimation this estimate should be taken with a grain of salt. For a robust long-term estimate, one would want to collect longitudinal data over a longer time period (Duchêne et al., 2016).
There is little temporal signal in the Lineage 4 Bernese data set (R2 = 0.05), which explains the uncertainty in our clock rate estimates of the Bernese outbreak. Our results show that the estimated time of the epidemic origin and the epidemiological parameters are robust to the differing clock rate estimates, see Table 2.
We hypothesize that the two data sets are an example of the time dependency of molecular rate estimates (Ho et al., 2005): the estimates of the evolutionary rate for the Bernese outbreak represent a high short-term rate of evolution, whereas due to the delayed sampling, the WTK estimate is a lower intermediate-term mutation rate of evolution. Hence, our evolutionary rate estimates are not suitable for comparison between the two M. tuberculosis lineages.
Our phylodynamic analyses allowed us to estimate the temporal dynamics of the Bernese outbreak. Despite the fact that the sampling dates range from 1987 to 2011, our results support the hypothesis that the epidemic peaked around 1990 (Stucki et al., 2015). This indicates that the peak of the outbreak occurred several years before it was detected. Indeed, most of the transmission events likely occurred between 1990 and 1991, although the majority of cases was only reported in 1993 (Stucki et al., 2015). This refutes the previous hypothesis that disease would have occurred shortly after infection, with short latent periods (W. H. Organization, 2015), due to the population characteristics in the affected population of the Bernese outbreak (homeless, substance abusers, etc.).
Both models employed for analysis of the Bernese outbreak (BDSKY and MTBD) suggest that the average infected period lasted about 4–5 years. While in BDSKY the infected period is equivalent to the infectious period, the infected period in the MTBD model is the sum of the infectious and exposed periods. In the latter we assume an infectious period of 2, 3 or 6 months (Sreeramareddy et al., 2009), and in each of those cases the exposed period is robustly estimated around 4 years. While this means that both models agree on the overall infected period to last around 4–5 years, we know that MTBD is the more realistic model. Hence, we conclude that – on average – an infected patient in the Bern outbreak was in the latent/exposed stage of the disease for about 4 years before becoming infectious and consequently being diagnosed and treated shortly after (Sreeramareddy et al., 2009).
For the WTK outbreak, we estimated an infectious period of eight years, which is significantly higher than the infectious period estimated for the Bernese outbreak (p-value <2.2 × 10−16). This may be due to a delay in sampling and treatment, due to the sampling having taken place in California after immigration from Thailand, such that patients were likely sick and infectious for longer. Furthermore, while the Bernese outbreak was caused by a sensitive strain, the WTK outbreak was caused by an MDR strain. Multidrug resistance is generally associated with poorer treatment success and prolonged infectiousness (Winston and Mitruka, 2012; Dye, 2009).
Hence, this difference in the estimated infectious period for the Bernese outbreak and the WTK outbreak is expected and supports our phylodynamic approach. More generally, a long infectious period is characteristic for a chronic disease like tuberculosis, particularly considering the difficulties in diagnosing the disease and the long delays in health seeking and treatment initiation (Yuen et al., 2015). Our estimates of the epidemiological parameters, particularly Re, are in line with previous estimates obtained from different M. tuberculosis data sets (Tanaka et al., 2006; Sanchez and Blower, 1997). However, due to the chronic nature of tuberculosis and the many factors influencing the transmission potential of individual patients (Brites and Gagneux, 2015; Coscolla et al., 2015b; Yruela et al., 2016), more work is needed to understand the complex dynamics influencing these parameters in different epidemiological settings.
We have employed the commonly used assumption that the infectious and exposed periods are exponentially distributed. Didelot et al. (Didelot et al. (2014)) have analysed a TB outbreak using a gamma distribution as prior distribution, but found that their posterior distribution had a mode of zero, suggesting that an exponential distribution is indeed suitable.
Our study shows that phylodynamic analysis of WGS data can shed light on the temporal dynamics of tuberculosis outbreaks. Analysis of the Bernese outbreak has revealed that even when there is little temporal signal, we can robustly estimate epidemiological parameters if the sampling proportion is large. Conversely, in the WTK outbreak there is much uncertainty in the epidemiological parameter estimates despite a moderate temporal signal. This may be due to a difference in transmission dynamics in Thailand versus California as well as the fact that the epidemic peak likely occurred before the first samples were taken.
Overall, we believe that real time outbreak WGS together with phylodynamic methods will improve future outbreak investigation as phylodynamic analysis can shed light on the timing of the epidemic origin and transmission dynamics through time.
Acknowledgements
DK gratefully acknowledges support from the ETH Zürich Postdoctoral Fellowship Program and the Marie Curie Actions for People COFUND, and the Swiss National Science Foundation (SNSF) for generously funding her research with a Marie Heim-Vögtlin fellowship. TS is supported in part by the European Research Council under the Seventh Framework Programme of the European Commission (PhyPD grant 335529). This work was further supported by the Swiss National Science Foundation (grants 310030_166687, IZRJZ3_164171, IZLSZ3_170834 and CRSII5_177163 to S.G.), the European Research Council (309540-EVODRTB to S.G.), and SystemsX.ch. The work on the tuberculosis outbreak investigations was supported by a grant from the Bernese Lung Association (LF). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- Baele G., Lemey P., Bedford T., Rambaut A., Suchard M.A., Alekseyenko A.V. Improving the accuracy of demographic and molecular clock model comparison while accommodating phylogenetic uncertainty. Mol. Biol Evol. 2012;29(September (9)):2157–2167. doi: 10.1093/molbev/mss084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boskova V., Bonhoeffer S., Stadler T. Inference of epidemiological dynamics based on simulated phylogenies using birth-death and coalescent models. PLoS Comput. Biol. 2014;10(11) doi: 10.1371/journal.pcbi.1003913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouckaert R. BEAST 2: a software platform for Bayesian evolutionary analysis. PLoS Comput Biol. 2014;10(4):e1003537. doi: 10.1371/journal.pcbi.1003537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brites D., Gagneux S. Co-evolution of Mycobacterium tuberculosis and Homo sapiens. Immunol. Rev. 2015;264(1):6–24. doi: 10.1111/imr.12264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casali N., Broda A., Harris S.R., Parkhill J., Brown T., Drobniewski F. Whole genome sequence analysis of a large isoniazid-resistant tuberculosis outbreak in London: a retrospective observational study. PLoS Med. 2016;13(October (10)):e1002137. doi: 10.1371/journal.pmed.1002137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comas I. Human T cell epitopes of Mycobacterium tuberculosis are evolutionarily hyperconserved. Nat. Genet. 2010;42(6):498–503. doi: 10.1038/ng.590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coscolla M. Genomic epidemiology of multidrug-resistant Mycobacterium tuberculosis during transcontinental spread. J. Infect. Dis. 2015;212(July (2)):302–310. doi: 10.1093/infdis/jiv025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coscolla M. M. tuberculosis T cell epitope analysis reveals paucity of antigenic variation and identifies rare variable TB antigens. Cell. Host Microbe. 2015;18(5):538–548. doi: 10.1016/j.chom.2015.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Didelot X., Gardy J., Colijn C. Bayesian inference of infectious disease transmission from whole-genome sequence data. Mol. Biol. Evol. 2014;31(7):1869–1879. doi: 10.1093/molbev/msu121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond A.J., Ho S., Phillips M., Rambaut A: relaxed phylogenetics and dating with confidence. PLoS Biology. 2006;4:e88. doi: 10.1371/journal.pbio.0040088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duchêne S. Genome-scale rates of evolutionary change in bacteria. Microb. Genom. 2016;2(November (11)):e000094. doi: 10.1099/mgen.0.000094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dye C. Doomsday postponed? Preventing and reversing epidemics of drug-resistant tuberculosis. Nat. Rev. Microbiol. 2009;7(1):81–87. doi: 10.1038/nrmicro2048. [DOI] [PubMed] [Google Scholar]
- Gardy J.L. Whole-genome sequencing and social-network analysis of a tuberculosis outbreak. N. Engl. J. Med. 2011;364(February (8)):730–739. doi: 10.1056/NEJMoa1003176. [DOI] [PubMed] [Google Scholar]
- Gavryushkina A., Welch D., Stadler T., Drummond A.J. Bayesian inference of sampled ancestor trees for epidemiology and fossil calibration. PLoS Comput. Biol. 2014;10(no. 12):e1003919. doi: 10.1371/journal.pcbi.1003919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Genewein A. Molecular approach to identifying route of transmission of tuberculosis in the community. Lancet. 1993;342(October (8875)):841–844. doi: 10.1016/0140-6736(93)92698-s. [DOI] [PubMed] [Google Scholar]
- Hatherell H.-A. Declaring a tuberculosis outbreak over with genomic epidemiology. Microb. Genom. 2016;2(May (5)):e000060. doi: 10.1099/mgen.0.000060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ho S.Y.W., Phillips M.J., Cooper A., Drummond A.J. Time dependency of molecular rate estimates and systematic overestimation of recent divergence times. Mol. Biol. Evol. 2005;22(7):1561–1568. doi: 10.1093/molbev/msi145. [DOI] [PubMed] [Google Scholar]
- Kingman J.F.C. The coalescent. Stochastic Process. Appl. 1982;13:235–248. [Google Scholar]
- Kühnert D., Stadler T., Vaughan T.G., Drummond A.J. Phylodynamics with migration: a computational framework to quantify population structure from genomic data. Mol. Biol. Evol. 2016;33(August (8)):2102–2116. doi: 10.1093/molbev/msw064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H., Durbin R. Fast and accurate short read alignment with Burrows-Wheeler transform. Bioinformatics. 2009;25(14):1754–1760. doi: 10.1093/bioinformatics/btp324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H. The sequence Alignment/Map format and SAMtools. Bioinformatics. 2009;25(16):2078–2079. doi: 10.1093/bioinformatics/btp352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pybus O.G., Rambaut A., Harvey P.H. An integrated framework for the inference of viral population history from reconstructed genealogies. Genetics. 2000;155(3):1429–1437. doi: 10.1093/genetics/155.3.1429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rambaut A., Lam T.T., Max Carvalho L., Pybus O.G. Exploring the temporal structure of heterochronous sequences using TempEst (formerly Path-O-Gen) Virus Evol. 2016;2(January (1)):vew007. doi: 10.1093/ve/vew007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez M.A., Blower S.M. Uncertainty and sensitivity analysis of the basic reproductive rate. Tuberculosis as an example. Am. J. Epidemiol. 1997;145(12):1127–1137. doi: 10.1093/oxfordjournals.aje.a009076. [DOI] [PubMed] [Google Scholar]
- Sreeramareddy C.T., Panduru K.V., Menten J., den Ende J. Time delays in diagnosis of pulmonary tuberculosis: a systematic review of literature. BMC Infect. Dis. 2009;9(June):91. doi: 10.1186/1471-2334-9-91. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler T., Kühnert D., Bonhoeffer S., Drummond A.J. Birth-death skyline plot reveals temporal changes of epidemic spread in HIV and hepatitis C virus (HCV) Proc. Natl. Acad. Sci. U. S. A. 2013;110(1):228–233. doi: 10.1073/pnas.1207965110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stadler T., Kühnert D., Rasmussen D.A., du Plessis L. Insights into the early epidemic spread of ebola in sierra leone provided by viral sequence data. PLoS Curr. 2014;6 doi: 10.1371/currents.outbreaks.02bc6d927ecee7bbd33532ec8ba6a25f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stucki D. Tracking a tuberculosis outbreak over 21 years: strain-specific single-nucleotide polymorphism typing combined with targeted whole-genome sequencing. J. Infect. Dis. 2015;211(April (8)):1306–1316. doi: 10.1093/infdis/jiu601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanaka M.M., Francis A.R., Luciani F., Sisson S.A. Using approximate Bayesian computation to estimate tuberculosis transmission parameters from genotype data. Genetics. 2006;173(July (3)):1511–1520. doi: 10.1534/genetics.106.055574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- W. H. Organization . 2015. Guidelines on the management of latent tuberculosis infection. [PubMed] [Google Scholar]
- Walker T.M. Whole-genome sequencing to delineate Mycobacterium tuberculosis outbreaks: a retrospective observational study. Lancet Infect. Dis. 2013;13(February (2)):137–146. doi: 10.1016/S1473-3099(12)70277-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winston C.A., Mitruka K. Treatment duration for patients with drug-resistant tuberculosis, United States. Emerg. Infect. Dis. 2012;18(July (7)):1201–1202. doi: 10.3201/eid1807.120261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yruela I., Contreras-Moreira B., Magalhã es C., Osó Rio N.S., Gonzalo-Asensio J. Mycobacterium tuberculosis complex exhibits lineage-specific variations affecting protein ductility and epitope recognition. Genome Biol. Evol. 2016;8(12):3751–3764. doi: 10.1093/gbe/evw279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuen C.M. Turning off the tap: stopping tuberculosis transmission through active case-finding and prompt effective treatment. Lancet. 2015;386(10010):2334–2343. doi: 10.1016/S0140-6736(15)00322-0. [DOI] [PMC free article] [PubMed] [Google Scholar]