Modelling the global spread of diseases: A review of current practice and capability

Highlights

• •Scoping review: mathematical models for global disease spread.
• •Extracted information: modelling method, input and validation data sources.
• •Model validation uncommon, perhaps a result of limited data availability.
• •Commercial data use has implications for review and reproducibility of results.

Abstract

Mathematical models can aid in the understanding of the risks associated with the global spread of infectious diseases. To assess the current state of mathematical models for the global spread of infectious diseases, we reviewed the literature highlighting common approaches and good practice, and identifying research gaps. We followed a scoping study method and extracted information from 78 records on: modelling approaches; input data (epidemiological, population, and travel) for model parameterization; model validation data.

We found that most epidemiological data come from published journal articles, population data come from a wide range of sources, and travel data mainly come from statistics or surveys, or commercial datasets. The use of commercial datasets may benefit the modeller, however makes critical appraisal of their model by other researchers more difficult. We found a minority of records (26) validated their model. We posit that this may be a result of pandemics, or far-reaching epidemics, being relatively rare events compared with other modelled physical phenomena (e.g. climate change). The sparsity of such events, and changes in outbreak recording, may make identifying suitable validation data difficult.

We appreciate the challenge of modelling emerging infections given the lack of data for both model parameterisation and validation, and inherent complexity of the approaches used. However, we believe that open access datasets should be used wherever possible to aid model reproducibility and transparency. Further, modellers should validate their models where possible, or explicitly state why validation was not possible.

1. Introduction

The complexity of containing person to person pandemic potential diseases has increased with the ease of global travel and closer connection of countries (Morens and Fauci, 2013). As humans found faster ways to travel (for example by horse, then ship) and engaged in wars and migrations, the opportunities for diseases to take hold, and result in pandemics, increased as pathogens were introduced into completely susceptible populations (Karlen, 1995). The greatest risk of transporting infections to naïve populations now comes from air travel (Karlen 1995). Understanding the way in which people move globally is therefore important for understanding the spread of diseases with pandemic potential, such as influenza, severe acute respiratory syndrome (SARS), and Ebola virus disease (World Health Organisation, n.d.).

Mathematical models can aid in the understanding of the risks associated with the spread of pandemic potential infectious diseases. For instance, models could predict: the chance that a disease will invade particular countries, the expected number of cases within a particular timeframe, or the expected effect of interventions. For this information to be of value, the model must be a sufficiently accurate representation of reality in order to provide useful outputs. All models have a trade-off between complexity and accuracy so it is important to assess which approach is most appropriate for each individual situation (Keeling and Rohani, 2008). Often multiple models may be developed to describe the same real-world event; this is a natural consequence of no model being completely accurate. Early in a disease outbreak response, real-world information is sparse. Confidence in model accuracy may be increased if multiple different, independent models, developed by independent research groups, converge on a qualitatively similar output (or they may provide clear insight to the reasons for different qualitative behaviour). For example, Mateus and Otete (2014) found that multiple models offer the same qualitative prediction that travel restrictions will not prevent the spread of influenza into susceptible populations.

According to Keeling and Rohani (2008), a good model should be both suited to its purpose (as simple as possible but no simpler) and parameterizable by available data. Deciding which mathematical methods to use is an important decision for modellers (Fowkes and Mahony, 1994) as evaluation of a model comes down to a subjective measure of usefulness (Keeling and Rohani, 2008). In some circumstances, for instance when modelling is conducted within the UK government, such decisions are made in discussion with the commissioner of the modelling rather than by the modeller alone. Directed by this view, we seek to identify what modelling techniques have been employed to predict the global spread of a pandemic potential disease and what data are available to parametrise these models. Confidence in model outputs is important as, in the case of disease spread models, health protection planning decisions may be directly influenced by these outputs. Confidence in model outputs can be increased through a process known as validation.

Validation is checking that a model, combined with its assumptions, provide a sufficiently accurate real-world representation to a sufficient level of accuracy (Carson, 2002; Sargent, 2011). What constitutes a sufficient level of accuracy must be a judgement made by the modeller (or, where relevant, the commissioner or stakeholders) as model validation always requires some subjective analysis (Barlas, 1996). Primarily, the validity of a particular model choice is not independent of the model purpose (Barlas, 1996). Validation can be considered as a multi-component process involving: conceptual validation, logical validation, experimental validation, operational validation and validation of the data used in the model (Landry, Malouin et al., 1983). The first two aspects are concerned with the conceptual model and its implementation, considering assumptions made about the real-world situation and verifying that a model implementation meets the criteria of the concept model. Operational validation is most relevant to the end-user of the model and focuses on cost-benefit analyses of proposed actions. In this review we are interested in what has been called experimental validation, pertaining to model efficiency and robustness. We consider validation to be done by comparing model predictions to a known outcome or, more weakly, by calibrating a model to a known outcome. Data validation of disease spread models has been discussed in Meslé et al. (2018).

In this review we assess the current state of mathematical models for global infectious disease spread in order to highlight common approaches and good practice, and identify any gaps for future research. We focus on identifying the model type, the input data that were used to parametrise the model, and the validation data used to assess model accuracy and judge quality. It is useful at this point to reflect that modelling infectious diseases, particularly emerging pandemics, is different to modelling environmental or physical phenomena (such as climate change or fluid dynamics). This is because the underpinning knowledge or empirical data are often rare or highly uncertain and the timescales for intervention relatively fast. We adopt a scoping study approach, as described by Arksey and O’Malley (2005) and Levac and O’Brien (2010), as this allows us to employ an iterative search approach and rapidly assess the literature. Scoping studies do not seek to provide a quality assessment of the literature but seek to provide an overview of the extent, range and nature of existing literature and highlight any research gaps (Arksey and O’Malley, 2005). Consequently, we do not seek to critically appraise each model as models have multiple trade-offs so a comparative framework for model design cannot be separate from a framework for assessing the quality of datasets.

2. Methods

2.1. Database searches

This scoping study was completed by a team of three individuals, as recommended by Levac and O’Brien (2010). The final agreed search terms are listed in Table 1 , chosen to capture literature addressing the global spread of pandemic potential diseases. Through following an iterative process whereby we refined search terms by examining the relevance of title hits, we decided to include certain specific model type terms: metapopulation, agent-based, and network. Similarly we included the disease-specific term influenza as this is the classical example of a pandemic disease and much literature exists around its spread. Remaining terms are more general to ensure that relevant literature was not missed.

Table 1.

Database search terms used for the literature review.

Search number	Search terms
Model terms
1	Mathematical
2	Metapopulation OR meta-population
3	Agent-based
4	Simulation
5	Network
6	#1 OR #2 OR #3 OR #4 OR #5
Disease terms
7	Disease spread
8	Influenza OR flu
9	#7 OR #8
Pandemic potential terms
10	Global
11	Pandemic
12	#10 OR #11
Movement terms
13	Travel*
14	Import*
15	Transport*
16	#13 OR #14 OR #15
Combining terms for final search
17	#6 AND #9 AND #12 AND #16

The searches, conducted on 1st July 2015, yielded 1453 records across three databases: 332 from Embase (1974-present), 439 from PubMed (1946-present), 682 from Scopus (1970-present). Record titles and abstracts from the three databases were imported into EndNote X7.3.1 (Thompson Reuters). Duplicates were identified and removed with the aid of the software’s ‘remove duplicate’ function, leaving 799 records to be reviewed.

Within these 799 records we identified two existing literature reviews of infectious disease model. Lee et al. (2009) focuses on articles where at least two intervention strategies for reducing the spread and morbidity from pandemic influenza are modelled; Mateus and Otete (2014) assesses the effectiveness of travel restrictions in the rapid containment of influenza strains with pandemic potential. Whilst both reviews are of interest, neither addresses the questions that we consider in this review.

2.2. Record screening

At all stages, screening was completed by two independent researchers, calling upon a third to resolve discrepancies. The researchers regularly discussed results to ensure the accurate assessment of records, with inclusion/exclusion criteria updated as necessary. The inclusion/exclusion criteria for both the initial sift and the full text screening are listed in Table 2 .

Table 2.

Scoping review inclusion and exclusion criteria.

Inclusion Criteria
Global spread of a human to human infectious disease
Specific models for far-reaching outbreaks of influenza like illnesses
Use of appropriate datasets

Exclusion Criteria
Abstract or full text not available in English or French
Articles not containing mathematical models: review papers, empirical studies, emergency response articles, microbiological studies, or disease surveillance.
Vector-borne diseases
Focus on treatment or vaccination
Not relevant models: in host, not disease-specific, not involving population-wide spread, computer viruses, social media/ internet/ phone modelling.

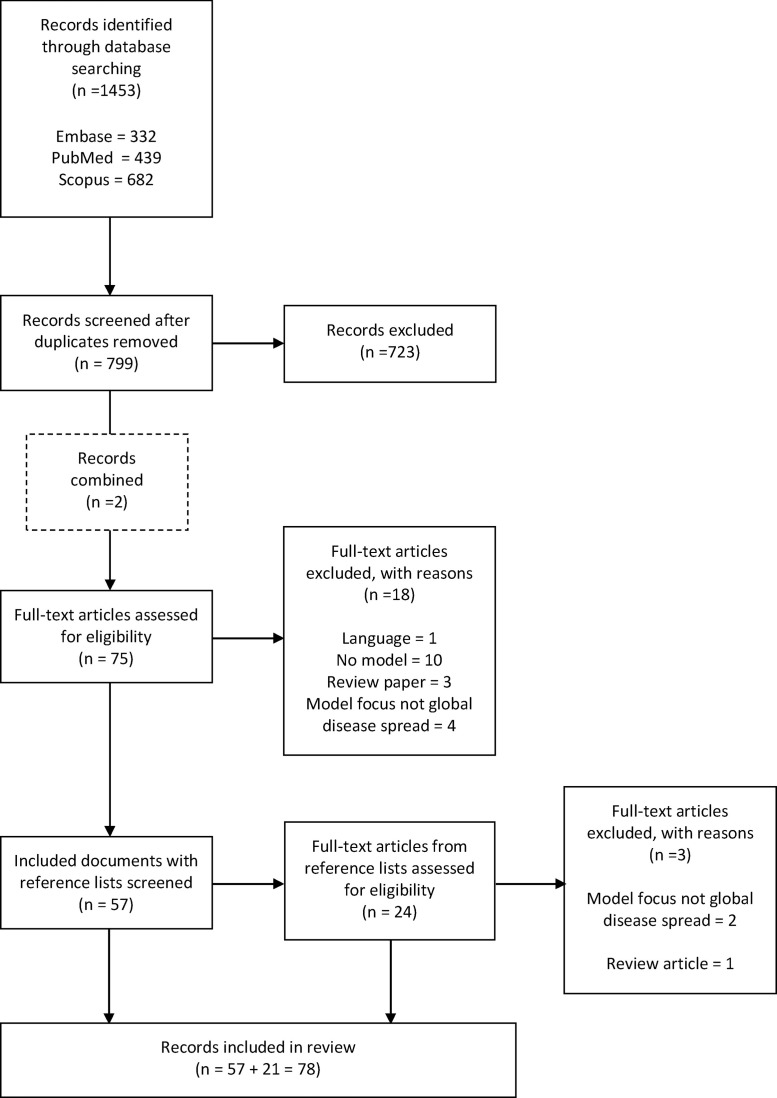
Title and abstract screening yielded 75 articles to be screened on full text, after which 57 records remained eligible for inclusion. The reference lists of all included records were screened on title and abstract, following an iterative process. This yielded a further 24 articles to be screened on full text, of which 21 records were eligible for inclusion. In total, 78 records have been included in this review. The screening process is represented in Fig. 1 .

Fig. 1.

Literature search process, including reasons for exclusion of articles screened on full text.

When completing the screening process, three records in particular were challenging.

• iRecord [71] considers influenza transmission between birds and humans and seeks to describe the seeding of a novel pandemic-potential strain where the virus jumps species. We retained this record, despite the cross-species transmission, as the developed model assumes virus evolution so that the strain becomes human to human transmissible.
• iiOne record identified during title and abstract screening was found to be a letter to the editor detailing a correction to another article in this review. We considered the correction to be an extension to the original article and thus analysed the two records as one: record [66].
• iiiWhen screening the references of [53] an unpublished manuscript3 was flagged to be reviewed on full text. It was not possible to find a copy of this manuscript so we were unable to continue the process with full text screening.

2.3. Information extraction

Two individuals extracted the information of interest: modelling approach; input data used, split into epidemiological, population, and travel data; validation data used. Epidemiological data concerns model parameters which describe the disease, such as the average length of infection. Population data relates to difference within the total modelled population, for example splitting the population into different age brackets or determining how many individuals live in a particular region. Travel data consists of information on travel patterns of individuals, either commuting or long-distance travel.

We consider the best validation method to use data sources independent of the input data. That is, the model parameters are estimated from datasets set apart from the dataset chosen for validation. This may be data from a different setting or a partition of the data used as input. An alternative form of validation is the fitting of the model to data (and so deriving at least one parameter from that data) to show qualitatively similar behaviour between model and validation data. Pragmatically, in a data poor setting, this is often used by necessity albeit as a weaker form.

3. Results

We are interested in identifying which modelling techniques and datasets are used in global disease spread models, including how many records have used particular methods. As we are not conducting a critical appraisal of each record we have not included a discussion of each individual record, however we refer to examples throughout our analysis.

For some records we had difficulty in extracting information. For example, a record may refer to a dataset within the main article text, however fail to provide a citation for the data source. We have labelled these records as ‘unclear’.

3.1. Identified modelling approaches

We wished to uniquely categorise our 78 records based on the modelling approaches adopted in each article, however this proved challenging. We attempted to provide the reader with a list of discrete model types, however this list became intractable as many records utilise a variety of mathematical and statistical techniques. We then attempted to split the records into statistical or mechanistic, but again had difficulty as, although some models are purely statistical, many of the mechanistic modelling papers also used statistical methods for some aspect of the model (for example record [36]). We have identified models that we consider to be purely statistical in nature so these form one model type. As our primary interest is finding models for the spread of disease through a large population, we have then split the remaining records on whether the models are agent-based or population-wide models. We consider population-wide models to be those where each individual is not tracked throughout the model (Table 3 ).

Table 3.

Summary of model classifications.

Model Classification
Model type	Records
Agent-based	10	[9, 15, 21, 24, 57, 58, 59, 62, 63, 69]
Population-wide	63	[1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 14, 16, 17, 18, 19, 20, 22, 23, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 48, 50, 51, 52, 53, 54, 55, 56, 61, 64, 65, 66, 67, 68, 70, 71, 72, 73, 74, 75, 76, 77, 78]
Statistical	5	[8, 13, 47, 49, 60]

One explicitly mentioned metapopulation model is GLEaM, appearing in records [4, 5, 6, 33, 70, 72]. This is a computational model which can be used to represent global infectious disease spread, which is based upon a metapopulation approach (Balcan et al 2010). Population mobility patterns (both local and global) are represented by distinct spatial regions which are connected by a network (Balcan et al 2010). This software tool is publicly available (http://www.gleamviz.org/), as presented in record [72]. Similarly, the model FluTE, described in [15] as an agent-based model for simulating influenza spread across major metropolitan areas, has open source code. The model considers travel within the US only rather than worldwide, however it may be possible to adapt the model to fit a global scale.

Record [78] is a cellular automaton model (CA). CA models involve a grid lattice made up of cells and, at each discrete time step, the state of an individual cell is affected by the states of its neighbours according to a predefined mathematical rule (Wolfram Math World). Infectious disease cellular automata models could involve each cell representing an individual who, at each time step, will be either susceptible, infected, or recovered; see, for instance, Keeling and Rohani (2008) for a more detailed description. Alternatively, in the case of [78], each cell represents one of a number of discrete spatial regions each with corresponding population. At each time step, the population for a discrete region is split into susceptible, infected, and recovered individuals and the sizes of these subpopulations vary dependent upon disease dynamics both within and between spatial regions.

Gravity models can be used to represent the flow of commodities, people, or information from one region to another, allowing them to be adapted to model infectious disease spread from a source location to a destination location (Rodrigue and Comtois, 2013). The measure of disease spread from one region to another is proportional to the sizes of the populations and the distance between them. Six records, [5, 11, 51, 57, 73, 77], made explicit reference to adopting this approach. Record [50] developed a gravity model for comparison with another approach, and [48] developed an anti-gravity model, where the speed of disease spread between regions is inversely proportional to the distance between regions.

3.2. Identified datasets

Sources of input data (epidemiological, population, and travel) and validation data have been identified from all 78 records, with some records reporting multiple sources contributing to the same data input type. We see from Table 4 that the majority of epidemiological data come from existing literature, by which we mean published journal articles as opposed to distinctly published datasets. Some records cite an international health organisation as their source of information, such as the Centers for Disease Control and Prevention, the European Centre for Disease Prevention and Control, or the World Health Organization.

Table 4.

Epidemiological data classification.

Epidemiological Data
Source	Records
Centers for Disease Control and Prevention (CDC)	4	[13, 41, 43, 51]
Census	1	[60]
European Centre for Disease Prevention and Control (ECDC)	1	[58]
Existing literature	51	[1, 2, 3, 4, 5, 6, 10, 12, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 32, 33, 34, 36, 37, 38, 39, 42, 43, 44, 45, 46, 49, 53, 55, 59, 61, 62, 63, 64, 66, 67, 69, 70, 72, 73, 76]
General Practitioner reports	1	[9]
National reports/ statistics	5	[13, 24, 26, 70, 77]
Personal communication	1	[60]
Surveillance data	3	[26, 48, 70]
World Health Organization (WHO) including the influenza surveillance system, FluNet	11	[8, 11, 36, 37, 41, 48, 49, 51, 71, 74, 78]
None	14	[7, 3 5, 40, 47, 50, 52, 54, 56, 57, 65]
Unclear		[30, 31, 68, 75]

Population data come from a wide range of sources, detailed in Table 5 . What sources are appropriate is model-dependent: the data aggregation and scale must match up with the model structure and parameters. Information is commonly taken from a census for the modelled region, or (inter-)national databases or statistics.

Table 5.

Population data classification.

Population Data
Source	Records
Census	22	[1, 3, 4, 7, 15, 16, 17, 18, 19, 20, 21, 23, 24, 32, 40, 42, 43, 51, 60, 69, 70, 73]
Center for International Earth Science Information	1	[33]
CIA World Factbook	2	[37, 46]
Eurostat	3	[1, 57, 58]
Existing literature	16	[10, 13, 15, 23, 24, 32, 45, 48, 49, 57, 59, 60, 69, 70, 73, 74]
International population Database	1	[46]
Landscan	1	[24]
National Geographic Information Services	1	[9]
National Statistics	4	[21, 57, 59, 70]
Organisation datasets	3	[21, 51, 59]
Polymod	1	[2]
Population database for specific country	5	[34, 36, 46, 49, 51]
Socioeconomic Data and Applications Center (SEDAC)	2	[6, 72]
Surveys	2	[21, 32]
United Nations database/ stats	3	[2, 42, 44]
World Bank population estimates	2	[8, 49]
World Gazetteer	1	[42]
None	36	[5, 11, 12, 14, 22, 25, 26, 27, 28, 29, 35, 38, 39, 41, 47, 50, 52, 53, 54, 55, 56, 61, 62, 63, 64, 65, 66, 71, 75, 76, 77, 78]
Unclear		[30, 31, 67, 68]

Table 6 shows that the main sources of travel data, aside from existing literature, are from national statistics or surveys, from IATA (International Air Transport Association) or from OAG. IATA is a trade association for the world’s airlines and has a variety of available datasets for purchase (IATA). These include passenger forecasts, air traffic statistics, and customisable datasets, which may provide more flexibility when designing a model to be parameterised by particular datasets. OAG is an air travel intelligence company which has a large network of air travel data, also available for purchase (OAG).

Table 6.

Travel data classification.

Travel Data
Source	Records
Airport/carrier-specific statistics/surveys	7	[1, 13, 26, 37, 39, 40, 67]
Census	5	[21, 32, 40, 70, 73]
Data In. Information out. (DIIO)	1	[42]
Eurostat	4	[1, 57, 58, 64]
Existing literature	17	[2, 10, 15, 27, 28, 29, 32, 33, 34, 38, 45, 53, 62, 67, 70, 73, 76]
IATA (International Air Transport Association)	16	[4, 5, 6, 8, 12, 16, 17, 18, 19, 20, 33, 34, 37, 41, 47, 72]
International Civil Aviation Organisation	2	[25, 67]
National Statistics/surveys	21	[5, 13, 14, 15, 21, 22, 24, 32, 34, 39, 43, 44, 48, 50, 62, 63, 64, 67, 70, 71, 77]
OAG	15	[6, 7, 11, 12, 23, 33, 34, 41, 44, 49, 54, 55, 56, 67, 72]
University of Manitoba Transport Information Group	1	[3]
World Tourism Organisation	2	[74, 75]
None	16	[9, 35, 36, 46, 51, 52, 59, 60, 61, 65, 66, 69, 78]
Unclear		[30, 31, 68]

3.3. Validation data

We find that 26 records that perform a type of model validation, shown in Table 7 . We identify 6 records where data independent of that used to parameterise a model is used to validate the model. This allows for an assessment of how flexible a model is i.e. how accurately it predicts outcomes for novel occurrences of disease outbreaks. Of these 6, the records [12], [19], [53], [67], [70] all produce plots of simulation results and of actual data so that the reader may visually compare the two. Record [13] is validated differently. The authors seek to explain the role of air travel on influenza epidemic fluctuations by performing time series analysis on pneumonia and influenza mortality data. Validation is achieved through comparing results against time series analysis from a separate viral surveillance dataset.

Table 7.

Validation data classification.

Validation Data
Validation Method	Data Sources and Records
Use of independent data source	6	H1N1pdm data = 1	[70]
		Other influenza data = 1	[13]
		WHO data = 5	[12, 13, 19, 53, 67]
Data fit	14	CDC data = 1	[43]
		H1N1pdm data = 4	[1, 4, 42, 57]
		Other influenza data = 7	[5, 21, 26, 36, 45, 69, 73]
		WHO data = 2	[20, 74]
Model-data comparison	3	Existing literature = 2	[23, 48]
		WHO data = 1	[51]
Model-model comparison	3	[10], [49], [58]
None	52	[2, 3, 7, 8, 9, 11, 15, 16, 17, 22, 25, 27, 28, 29, 30, 33, 35, 37, 38, 39, 40, 44, 46, 47, 50, 52, 54, 55, 56, 59, 60, 61, 62, 63, 64, 65, 66, 71, 72, 75, 78]
Future predictions		[6, 14, 24, 32, 34, 41]
Unclear		[18, 31, 68, 76, 77]

Twenty articles perform a pragmatic form of validation. Fourteen records have taken input values from a dataset and checked the model outputs against this dataset. This clarifies if a model is giving a sensible result, helping to understand the specific setting under consideration, however it has not been tested to see if it is applicable to other disease outbreaks. Three models are validated through comparison with data, however such comparison is either not with an independent dataset or is comparing only a single indicator, such as an R0 value, which gives a qualitative comparison. Whilst this provides some level of confidence in model accuracy, it is not as rigorous as validating against an alternative dataset. Three records report comparing model output with that of a different model. In this latter case, confidence in predictions may be increased if models qualitatively agree.

4. Discussion

We have identified records which contain models for the global spread of person to person infectious diseases. We have grouped the records based on the modelling method used and have extracted the types of data used both to parametrise and validate the models. Our aim was to gain an insight into the breadth of modelling techniques and what data is accessible. However, we have considered some key principles to be of importance when creating mathematical models: primarily that, when appropriate, data is available to parametrise and validate models; also that all data sources are clearly referenced to aid both transparency and reproducibility.

Some models are intentionally theoretical, looking to develop new ideas or present a new understanding of a fundamental mechanism of disease spread where the conclusions are, perhaps, more about appropriate mathematical approaches. This is certainly a valuable insight, but not what we are focussing on in this review as there is usually less focus on parameterisation and validation. For predictive models, we consider the ideal situation to be where the model may be parameterised by existing datasets, followed by being validated against an independent source of data. In some instances records are not clear about where data are from, for instance by not clearly giving references. This makes it difficult for anyone to reproduce or check the work or to subsequently use such data resources in their own work. So whilst models do use data for parameterisation and validation, this should be openly reported for model transparency.

We found 6 records, [12, 13, 19, 53, 67, 70], which were parameterized by existing data and validated by an independent dataset. Record [13] is a statistical model whereas the other five all under our population-wide model category, so validation is possible for different modelling approaches. Yet not all articles perform model validation. This may be because it can be difficult to find a suitable separate dataset for pandemics (or large epidemics) as they do not happen often. Also records and outbreak recording systems may have changed so much over time that those datasets which do exist may not be appropriate for comparison.

Most models in this review are for influenza. This may be a result of pandemic influenza being a relatively likely emerging infection, with a recent occurrence in 2009 and it is high on most countries’ national planning assessments (World Health Organization, 2011). It also has a well understood epidemiology and clear evidence of historical global spread. There have been 4 major outbreaks in recent history (1918, 1957, 1968 and 2009) (Monto and Sellwood, 2013), hence it is a disease where it is possible to get separate datasets for parameterisation and validation. However, as these outbreaks occur roughly once a generation, socio-cultural changes (such as changes in contact patterns), advances in medicine, and different surveillance mechanisms can make comparison difficult.

For parameterisation of models, the records, on the whole, use epidemiological and population datasets that are publicly available or at least verifiable. However, two often cited sources of travel data were IATA and OAG, both providing air travel data which can only be used under a commercial license. As access to such data is restricted, it can be difficult for researchers to critically appraise models which use data under commercial licenses, discussed further in Meslé et al. (2017). As travel patterns change over time, updated dataset access will be required to ensure models are parametrised to represent an up to date real-world situation. In the event of a disease outbreak this may delay the process of obtaining predictions. However, a benefit of using commercial data is that there are often different data format options available which customers can choose from. This may make the process of model development easier. As such data are updated over time then, provided the updated dataset is purchased, a model may remain informative for a longer period of time.

We appreciate the challenge of modelling emerging infections given the lack of data for both model parameterisation and validation and inherent complexity of the approaches used. However, researchers should attempt more robust validation, or justify explicitly why it was not possible. The articles reviewed indicate that appropriate models have been developed which can account for epidemiological complexity and population structures. However, the complexity of the models often leads to challenges in independent reproducibility of results by other modelling groups or thorough quality assessment prior to use to advise government. Simply sharing code/software or traditional peer review may not always be sufficient. For example, the UK civil service has adopted guidance on producing quality analysis to support quality assurance and governance of modelling advice: The Aqua Book (UK Government). This is a burden of effort on modelling groups, and we do not suggest this approach completely. That said, documenting assumptions on data and methods explicitly in tandem with the code and the input data will aid model transparency and aid future research. If data or models are not publicly available (or are proprietary) then results are not easily reproducible by other groups and so may not be taken seriously and achieve the impact the work deserves.

Author contributions

CEW: Database searches; inclusion/ rejection of records; primary contributor to manuscript write up.

MMIM: 2nd researcher for inclusion/ rejection of records; minor edits to text.

IMH: initial concept; some involvement in inclusion/rejection of records; contribution to manuscript write up.

All authors have approved the final draft of the manuscript.

Role of funding source

CEW and IMH have received funding from the PANDHUB project. This project has received funding from the European Union’s Seventh Framework Programme for research, technological development and demonstration under grant agreement no 607433. In addition to the listed authors CEW and IMH, the following persons constitute the PANDHUB consortium: Ilpo Kumala, Raija Koivisto and Satu Salo (VTT Technical Research Centre, Tampere, Finland); Pertti Pasanen, Petri Ruutu, Anniina Salmela and Anna-MariaVeijalainen (University of Eastern Finland, UEF, Kuopio, Finland); Nicolas Poirot and Nabila Laajail (Assistance Publique, Paris France); Emma Bennett (Public Health England, Porton Down, UK); Stéphane Bastier, and Audrey Berthier (MEDES, Toulouse, France); Jonathan Van-Tam and Joanne Enstone (University of Nottingham, Nottingham, UK).

http://pandhub-fp7-security.eu/.

MMIM is affiliated to the National Institute for Health Research Health Protection Research Unit (NIHR HPRU) in Emerging and Zoonotic Infections at University of Liverpool in partnership with Public Health England (PHE), in collaboration with Liverpool School of Tropical Medicine. Margaux MI Meslé is based at The University of Liverpool. The views expressed are those of the author(s) and not necessarily those of the NHS, the NIHR, the Department of Health or Public Health England.

Neither funding source had a role in the: study design; collection, analysis and interpretation of data; writing of the report; the decision to submit the article for publication.

No author has any conflict of interest.