Phylogenetic non-independence in rates of trait evolution

Abstract

Statistical non-independence of species’ biological traits is recognized in most traits under selection. Yet, whether or not the evolutionary rates of such biological traits are statistically non-independent remains to be tested. Here, we test the hypothesis that phenotypic evolutionary rates are non-independent, i.e. contain phylogenetic signal, using empirical rates of evolution in three separate traits: body mass in mammals, beak shape in birds and bite force in amniotes. Specifically, we test if evolutionary rates are phylogenetically interdependent. We find evidence for phylogenetic signal in evolutionary rates in all three case studies. While phylogenetic signal diminishes deeper in time, this is reflective of statistical power owing to small sample and effect sizes. When effect size is large, e.g. owing to the presence of fossil tips, we detect high phylogenetic signals even in deeper time slices. Thus, we recommend that rates be treated as being non-independent throughout the evolutionary history of the group of organisms under study, and any summaries or analyses of rates through time—including associations of rates with traits—need to account for the undesired effects of shared ancestry.

1. Introduction

Descent with modification [1] is of fundamental importance to evolutionary biology and is recognized in most traits under selection. Through evolutionary time, trait values will be more similar in closely related species than in distantly related species, because the variance of trait values will be proportional to the divergence in evolutionary time [2]. This equates to shared ancestry, i.e. phylogeny. The degree to which shared ancestry affects biological traits can thus be described by the proportion of variance in trait data across a comparative sample of species that can be explained by phylogenetic relations, or phylogenetic signal, e.g. K [3] or λ [4]. This has statistical implications, i.e. phylogenetic non-independence.

While acknowledgement of phylogenetic non-independence in phenotypic trait data has become common in comparative studies [5], it is not so for the rates of evolution (how fast organisms’ characteristics evolve). As rates are often used as proxies for adaptations [6,7], it is of immense importance that we understand their statistical properties, in particular, phylogenetic non-independence. However, we have not been able to identify any study in the literature that explicitly tests for phylogenetic signal in phenotypic evolutionary rates aside from rare instances in which this was implied [8].

Here, we test whether evolutionary rates contain phylogenetic signal using three empirical case studies: body mass in mammals [9], beak shape in birds [10] and bite force in terrestrial amniotes (electronic supplementary material). Our basic premise is that if the phylogenetic signal is detected in rates, then rates evolve along the branches of a phylogenetic tree in proportion to the passage of time and that closely related species are more similar in rates than distantly related species. Naturally, this necessitates a non-homogeneous distribution of rates across the branches of the tree, i.e. variable rates of phenotypic trait evolution [8,11–14].

2. Materials and methods

We obtained 100 sets of phenotypic evolutionary rates and the associated time-calibrated phylogenetic trees (time trees) from the authors of the three case studies (electronic supplementary material). As we would expect rates along all branches of a phylogenetic tree to be affected by shared ancestry, not just the tips, we tested for phylogenetic signal in rates along both terminal and internal branches, by time-slicing the phylogenetic tree. We time-sliced the three time trees at 1 Myr intervals for the mammals and birds (167 and 109 time slices, respectively), and at 5 Myr intervals for amniotes (65 time slices) (see electronic supplementary material for details). The latter interval was chosen for amniotes owing to their much longer evolutionary history (approx. 350 Myr) compared with mammals and birds. For each time-sliced tree, we matched the terminal branches to the corresponding branches in the complete time tree (electronic supplementary material, figure S1). We then assigned the corresponding rates to those terminal branches on the time-sliced tree as tip trait values. We fitted a maximum-likelihood (ML) phylogenetic generalized least-squares (GLS) model in BayesTraits V3 to estimate phylogenetic signal λ in rates at the tips for each time slice (GLS_λ). We tested GLS_λ against the null model in which λ is fixed to 0 (GLS_λ=0) as the likelihood ratio (LR_λ) between GLS_λ and GLS_λ=0 and determined significance using the χ² distribution (d.f. = 1). When λ was significant in greater than 95% of the sample in any given time slice, we determined that phylogenetic signal was present in that time slice. We also compared the significance of an alternative model in which λ is fixed to 1 (GLS_λ=1). The root estimate α of a GLS_λ=0 model is the equivalent of estimating the non-phylogenetic mean rate, while GLS_λ and GLS_λ=1 estimate the approximate phylogenetically corrected mean rates in our case.

3. Results

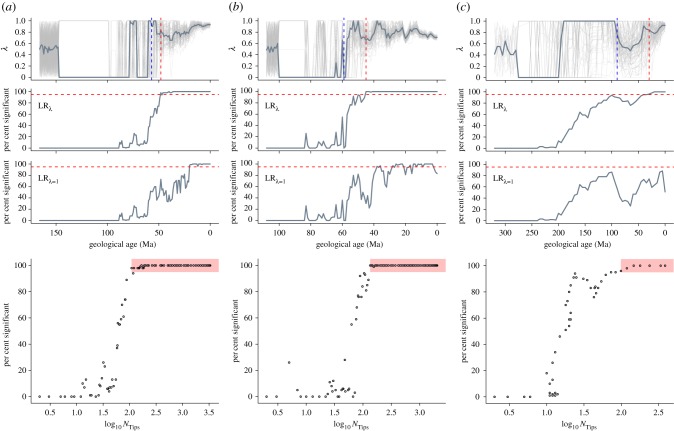
Overall, phylogenetic signal at the tips of the complete time trees are high (body mass in mammals, median λ = 0.926; beaks in birds, median λ = 0.729; and bite force in amniotes, λ = 1), providing evidence for strong effects of shared ancestry in rates of phenotypic trait evolution along the terminal branches. Phylogenetic signal in rates is generally high and significant in at least 95% of the sample in younger time slices—younger than: 48 Ma (mammals), 45 Ma (birds) and 30 Ma (amniotes) (figure 1; electronic supplementary material). Phylogenetic signal depreciates (drops in strength and significance) rapidly in deeper time slices (figure 1; electronic supplementary material). Fixing λ to 1 (GLS_λ=1) results in qualitatively similar patterns across time slices compared with when λ is estimated (GLS_λ) (figure 1), but the depreciation of λ starts at younger time slices compared with GLS_λ (figure 1).

Figure 1.

Phylogenetic signal in rates of trait evolution through time. Phylogenetic signal (λ) was estimated across time-sliced phylogenetic trees (top row) in three independent datasets: (a) mammalian body mass, (b) avian beak shape and (c) amniote bite force. Faint lines represent each of the 100 samples with the bold line representing the median λ. The percentage of the sample in which LR_λ (likelihood ratio between GLS_λ and GLS_λ=0) was significant is shown for each time slice (second row). Further, the fit of GLS_λ=1 is shown as the percentage of the sample in which LR_λ=1 (likelihood ratio between GLS_λ=1 and GLS_λ=0) was significant for each time slice (third row). Red dashed lines represent the 95% threshold. Blue dashed lines (top panels) represent the time slice for the 95% threshold as determined through simulations (electronic supplementary material figure S3). The relationship between the percentage of significant λ and N_Tips (bottom row) shows a clear drop off in the percentage from 95% of the sample (red shaded box).

4. Discussion

Through our time-sliced GLS models on three datasets, we demonstrate that evolutionary rates of phenotypic traits are indeed phylogenetically non-independent—λ is significant and high, along both the terminal and internal branches (figure 1). Crucially, although λ ceases to be significant in deeper time slices in all trees tested (figure 1), this reduction in phylogenetic signal most likely depends on two aspects of the rates in the focal time slice: (1) number of tips [15] and (2) rate heterogeneity (electronic supplementary material). Both reflect issues of statistical power, with the former concerning sample size (as determined through simulations; electronic supplementary material; figures S2 and S3) and the latter effect size (as evident from the effects of fossil tips; figure 1c; electronic supplementary material). Incidentally, unsampled tips of any sort (not just fossils) will likely increase rate heterogeneity should they be sampled. Additionally, information contained at the tips of an ultrametric tree (e.g. trait values) is expected to be lost progressively deeper in the tree (proportional to the phylogenetic variance–covariance structure) as subsequent evolution towards the tips overprints ancestral information; this is an issue plaguing phylogenetic comparative methods in general. Furthermore, because rates are estimated from the phylogeny using models with constant rate evolution as the underlying process of evolution, the resulting rates would inevitably contain phylogenetic signal. Whether this is true or not, it does not alter (rather it reinforces) our argument that inferred rates contain phylogenetic signal (regardless of the reason) and crucially that all downstream summaries and analyses of rates thus must account for phylogenetic non-independence. Thus, we argue that it is safest to assume that phylogenetic signal will be present and strong in deeper time slices [8].

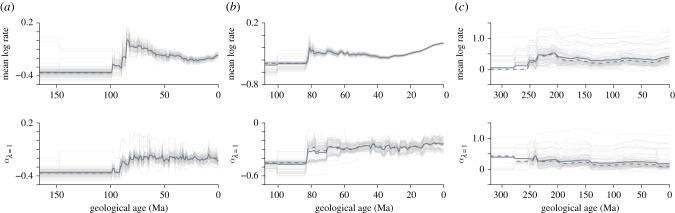
An important implication here is that as rates will be statistically non-independent at various time intervals throughout the history of the clade of interest, patterns gleaned from simple summaries (e.g. interval means) of rates through time (RTT) can potentially be misleading. Simple RTT plots are prevalent in recent literature (e.g. [10,16–21]), the profiles of which are routinely interpreted at face value, with peaks and troughs representing periods of bursts and declines in rates [16,17,19]. However, accounting for phylogenetic non-independence by assuming strong phylogenetic signal uniformly across all time slices [8]—i.e. phylogenetic mean α from our GLS_λ=1 models across time slices—results in phylogenetic RTT profiles that are often different from those of non-phylogenetic RTT (figure 2). Thus, non-phylogenetic RTT profiles cannot be taken at face value without knowledge of phylogenetic signal through time. More crucially, this implies that statistical analyses of rates need also account for phylogenetic non-independence. Testing hypotheses of external influences (ecological or environmental) on rates of evolution would require the application of appropriate phylogenetic statistical methods – e.g. phylogenetic regression models [14,22]. Not doing so would run the risk of misleading statistical results [2,5].

Figure 2.

Mean evolutionary RTT compared with phylogenetically corrected mean rates. Simple mean values of evolutionary rates at each time slice across the three datasets (a, mammalian body mass; b, avian beak shape; c, amniote bite force) show distinctive patterns of RTT. However, these patterns are far less prominent in phylogenetically corrected mean rates (α) through time. Values of α are the phylogenetic root estimates of the GLS_λ=1 model. Faint lines represent each Markov chain Monte Carlo run while the bold line shows the median value for each time slice.

As phenotypic evolutionary rates have been interpreted as reflecting the intensity of natural selection [6,14], that they contain phylogenetic signal implies that ancestors and descendants as well as closely related species either: (i) share intrinsic mechanisms for selection responsiveness (e.g. genetic predisposition), (ii) share similar levels of extrinsic selection pressures (e.g. similar ecological niches, environments, etc.) or (iii) both. Two (or more) species descended from a parent species would be expected to start their respective independent evolution with the same level of intrinsic responsiveness as well as extrinsic selection pressures as, and thus at the phenotypic evolutionary rate of, the parent species. The daughter species then would be subject to independent genetic mutations and selection pressures depending on their respective environments.

However, this is not to say that descendent rates are rigidly constrained by ancestry; exceptional rate shifts along individual branches are widely observed in many traits across various groups of organisms [8,9,11,14,23]. Such exceptional rate shifts can often be orders of magnitude greater than the background rate and occur instantaneously (with respect to geological time), such that the effects of ancestry may be marginal.

In conclusion, our analyses demonstrate that rates of phenotypic evolution estimated from phylogenetic trees using models of trait evolution are statistically non-independent (most likely owing to shared ancestry), across the tips and through time–we posit that our results are conservative, with phylogenetic signal actually being more prevalent. Thus, we recommend that phylogenetic non-independence be accounted for in summaries and analyses of evolutionary RTT, using appropriate phylogenetic comparative methods.

Data accessibility

Supporting data are made available through the Open Science Framework (https://osf.io/pn4ma/?view_only=2de49c7ad61944ed97c373783a7d1956) [24], and described in the electronic supplementary material.

Authors' contributions

All authors made substantial contributions to conception and design, acquisition of data, analysis and interpretation of data; drafted and revised the article critically for important intellectual content; gave final approval of the version to be published and agreed to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by the Leverhulme Trust (RPG-2013-185 and RPG-2017-071).