Simultaneous measurements of three-dimensional trajectories and wingbeat frequencies of birds in the field

Abstract

Tracking the movements of birds in three dimensions is integral to a wide range of problems in animal ecology, behaviour and cognition. Multi-camera stereo-imaging has been used to track the three-dimensional (3D) motion of birds in dense flocks, but precise localization of birds remains a challenge due to imaging resolution in the depth direction and optical occlusion. This paper introduces a portable stereo-imaging system with improved accuracy and a simple stereo-matching algorithm that can resolve optical occlusion. This system allows us to decouple body and wing motion, and thus measure not only velocities and accelerations but also wingbeat frequencies along the 3D trajectories of birds. We demonstrate these new methods by analysing six flocking events consisting of 50 to 360 jackdaws (Corvus monedula) and rooks (Corvus frugilegus) as well as 32 jackdaws and 6 rooks flying in isolated pairs or alone. Our method allows us to (i) measure flight speed and wingbeat frequency in different flying modes; (ii) characterize the U-shaped flight performance curve of birds in the wild, showing that wingbeat frequency reaches its minimum at moderate flight speeds; (iii) examine group effects on individual flight performance, showing that birds have a higher wingbeat frequency when flying in a group than when flying alone and when flying in dense regions than when flying in sparse regions; and (iv) provide a potential avenue for automated discrimination of bird species. We argue that the experimental method developed in this paper opens new opportunities for understanding flight kinematics and collective behaviour in natural environments.

1. Introduction

Measuring the three-dimensional (3D) flight of birds in nature has played an important role in understanding flight kinematics [1], collective motion [2], migration [3], animal ecology [4] and cognition [5]. Various 3D tracking techniques have been used in the field, including ‘ornithodolites’ (essentially a rangefinder mounted on a telescope) [6], radar [7], high precision GPS [8] and others. Among them, multi-camera stereo-imaging systems [9], which have been widely used by physicists and engineers to study fluid flows in the laboratory [10], are increasingly attracting the attention of biologists [11–15]. Due to their high temporal and spatial resolution, stereo-imaging systems allow the simultaneous 3D tracking of multiple individuals even in dense flocks [16]. They thus hold great promise for developing our understanding of avian flight, from the energetics of movement at an individual level [17] to the mechanisms underlying the rapid spread of information and maintenance of cohesion within flocks [18]. However, important methodological constraints still limit the accuracy of stereo-imaging systems and their potential for deployment to capture natural phenomena such as bird flocks under field conditions.

One major challenge in the application of stereo-imaging in the field is camera calibration. Stereo-imaging relies on matching the two-dimensional (2D) coordinates of an object as recorded on multiple different cameras to reconstruct its 3D world coordinates (x₁, x₂, x₃) through triangulation [9]. This stereo-matching procedure requires knowledge of various parameters for each camera such as their position and orientation (extrinsic parameters) and focal length and principal point (intrinsic parameters). The purpose of camera calibration is to determine these parameters. In early studies, calibration was done manually by measuring the relative position and orientation of each camera [19–21]. This method, however, places limitations on the arrangement of the cameras. More recently, however, the development of more advanced camera calibration techniques has relaxed these limitations. Camera parameters can be estimated based on a set of matched pixels between cameras, e.g. using the eight-point algorithm [9], and refined by bundle adjustment [22]. Here, we will adopt this calibration method and show that it allows us to focus on arranging the cameras so that the measurement accuracy is maximized rather than for ease of calibration.

This flexibility allows us to address the longstanding issue of the relatively low measurement accuracy in the out-of-plane direction compared to that in the in-plane directions. The distance between cameras, S, needs to be comparable to the distance to the object being imaged in order to achieve similar imaging resolution in all three directions. For example, S ≈ 50 m is desired when imaging birds that are 50 m away. However, requiring a large S raises many technical difficulties such as data transmission and synchronization between cameras. Evangelista et al. [23] and Cavagna et al. [21] used S ≈ 9 m and S ≈ 25 m, respectively, to record flocks at distances greater than 80 m. Pomeroy & Heppner [20] used S ≈ 60 m, but their system was only able to record a limited number of images. To the best of our knowledge, no high-speed imaging system with S > 50 m or with S comparable to the distance to the birds being imaged has been developed.

Even with improved accuracy, there can be difficulties in reconstructing the world coordinates of all objects in the field of view when optical occlusion occurs and the images of two objects overlap on the image plane of a single camera. Typical stereo-matching is based on one-to-one matching: each detected bird in any single view is associated with at most one bird in the other views. Thus, this method will only reconstruct one object from bird images that overlap, and some bird positions will be lost. When tracking flocks over long times, failures in reconstructing the positions of all birds can compound and result in broken trajectories. By tracking before stereo-matching, several researchers [24–26] relaxed the one-to-one matching constraint and allowed a single measurement on each 2D image to be assigned to multiple objects. Zou et al. [27] and Attanasi et al. [28] solved this problem by introducing a global optimization framework that allows all possible matches and then optimizes the coherence between cameras across multiple temporal measurements. However, optimizing across multiple views and multiple times incurs significant additional computational processing time, especially when the number of birds is large. A method based on information only from a single current time step that solves the optical occlusion problem robustly is not currently available.

Additionally, when the number density of birds in the images increases and the number of cameras is limited, so-called ‘ghost’ particles may arise due to false matches across views. In this case, the typical procedure of doing temporal tracking after stereo-matching [29] may fail to reconstruct all trajectories. One can try to solve this problem by relying on temporal information in addition to purely spatial information to predict the 2D locations of each bird on each image, for example, and tracking before stereo-matching [24,30]. A simpler solution is to increase the number of cameras. Stereo-imaging systems with four or more cameras have been used in laboratory studies [29] and in a field study to track a single bird [11,17]. However, to our knowledge, no system with four or more cameras has been used for measuring a large number of animals in the field [16,19–21,23].

Finally, existing stereo-imaging measurements of birds in natural settings have access only to bird position and associated kinematics; due to resolution limitations in both space and time, empirical data on wing motion in natural environments are very limited [11]. Wing motion is typically only documented for trained birds flying in laboratory wind tunnels [31] where high-resolution bird images can be more easily recorded. When birds are flying at distances far away (approx. 50 m) and each bird covers only a few pixels on images, accurately calculating wing motion becomes very challenging. Thus, most analyses of collective behaviour only rely on positions [32], velocities [33] and accelerations [18] of birds. The wing motion is not available along 3D trajectories, even though it is what is directly controlled by birds in response to changing environmental and social stimuli. Wing motion can be measured by fitting tags containing inertial sensors (accelerometers and gyroscopes) on individual birds [1,34], but such systems are often costly, have limited battery life, and may not be practical for smaller species or large flocks [35].

Here, we describe an improved field-deployable stereo-imaging system for bird flight measurements in the field that addresses all these difficulties. We test our system on flocks of wild corvids (jackdaws, Corvus monedula; and rooks, Corvus frugilegus). To improve the image resolution, we developed a portable system using laptop-controlled USB cameras with S ≈ 50 m to record birds at distances of 20–80 m. To handle optical occlusion in a faster way, we introduce a new, simple stereo-matching procedure based on associating every detected bird on each camera with a 3D position. Thanks to the portability of USB cameras, we use four cameras so that the stereo-imaging system can resolve individual birds even in flocks with high densities. With these improvements in measurement accuracy, we are able to measure wing motions and wingbeat frequency along individual 3D trajectories of birds in the field. We argue that information on wingbeat frequency in addition to velocity and acceleration allows us to better understand the flight kinematics and collective behaviour of birds in their natural environment.

2. Material and methods

2.1. Camera arrangement and calibration

When developing a high-speed stereo-imaging system for field applications, it is important to maintain portability. To fulfil this requirement, we used four monochrome USB3-Vision CMOS cameras (Basler ace acA2040-90um). Each has physical dimensions of 4 × 3 × 3 cm³, a sensor resolution of 2048 × 2048 pixels, a pixel size of 5.5 µm, and is connected to a laptop (Thinkpad P51 Mobile Workstation) through a USB 3.0 port. The laptop serves as both power supply and data storage device for the camera, making the system very portable. Given that the bandwidth of a USB 3.0 port is ≈400 MB/s, the maximal frame rate is 90 frames per second (fps). The laptop has a 512 GB Solid-State Drive (PCIe NVWe) supporting a writing speed of greater than 1000 Mb/s. We use one laptop for each pair of two cameras, which allows us to continuously record at 80 fps for greater than 20 s. Higher frame rates can also be reached by reducing the image size; e.g. when using 1024 × 1024 pixels, 300 fps could be achieved. The four cameras are hardware-synchronized by connecting with a function generator (Agilent 33210A) using BNC cables. We fit each camera with a lens with a focal length of 8 mm and an angle of view of 71° (Tamron, M111FM08). In field tests, we found that the performance of the laptops was reduced when running on their own internal batteries. We thus used external batteries to power the laptops as well as the function generator. In deployments with less stringent performance requirements, however, external batteries may not be necessary.

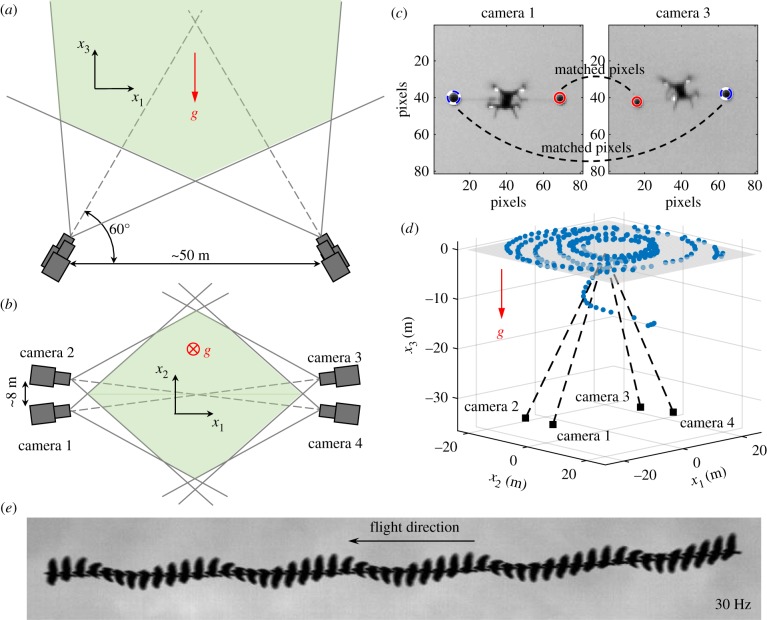
A typical arrangement of the four cameras is shown in figure 1a,b. Two pairs of cameras are separated by S ≈ 50 m, which can easily be extended to 100 m by increasing the BNC cable length (given that BNC cables support long-distance signal transmission). This distance is similar to the distance from the cameras to the birds being imaged in this study. The distance between cameras in each pair is ≈8 m, since the high data rates supported by the USB 3.0 protocol limit cable length. However, it would be possible to extend this distance as well by using an active data transfer cable. All cameras point to the sky with an angle to the horizontal plane of ≈60°. Cameras 1 and 3 are located in the same vertical plane, and cameras 2 and 4 are located in another vertical plane. At a height of 50 m, the fields of view of the four cameras have an overlap area of 60 × 60 m², with a spatial resolution of 4.0 cm per pixel at the centre of images. The coordinate system is also shown in figure 1, where −x₃ is aligned with the gravity direction. Note that the actual arrangement varies slightly for every deployment. On different days, we moved the camera system to different locations to ensure we captured images of different individuals. Note too that since the cameras are free-standing, they can easily be placed on irregular or steep terrain.

Figure 1.

(a,b) Camera arrangement in the vertical and horizontal planes, respectively. (c) Sample images of balls on camera 1 and 3 showing the matched pixels across cameras. (d) Reconstructed camera positions and points used for calibration in 3D space. (e) A sample time series of jackdaw images captured by one camera recording at 30 Hz. (Online version in colour.)

To calibrate the cameras, we followed a procedure based on that described in [36]. We attached two balls of different sizes (10 and 12 cm) to either end of a stick mounted on an unmanned aerial vehicle, which was flown through the 3D tracking volume. Figure 1c shows sample images of the two balls. The distance between the balls is fixed at 1.0 m, which provides a physical scale for the camera calibration. The locations of the balls in the images are automatically extracted to generate matched pixels between cameras. About 200 to 300 sets of matched points are detected in a typical calibration run and are used to estimate the fundamental matrix of each camera as well as the 3D locations of the matched points. Sparse bundle adjustment is then used to refine the camera parameters. The x₃ direction is found by fitting a 2D plane to the 3D points that are located at a constant height. Figure 1d shows the reconstructed camera and ball locations in 3D space. The re-projection error, defined as the root-mean-square distance between the original 2D points and those generated by re-projecting the 3D points on the 2D images, is less than 0.5 pixels. This entire calibration process takes 10–20 min: 5–10 min for recording the calibration points, 4–8 min for extracting the matched points from the images, and 2 min for calculation of the camera parameters.

2.2. Capturing images of flocking birds in the field

We recorded flocks of corvids flying towards winter roosts in Mabe and Stithians, Cornwall, UK from December 2017 to February 2018. We focused predominantly on jackdaws flying in flocks, but also recorded cases where either jackdaws or rooks flew in isolated pairs, allowing us to extract comparable measures of wingbeat frequency in the two species. Both jackdaws and rooks are highly social members of the corvid family and form large winter flocks, often including birds of both species. Whereas research on collective movement typically assumes individuals are identical and interchangeable, 2D photographic studies suggest that birds within corvid flocks typically fly especially close to a single single-species neighbour, likely reflecting the lifelong, monogamous pair bonds that form the core of corvid societies [37]. How individuals respond to the movements of others within these dyads and across the flock as a whole is not yet understood.

The birds typically leave their foraging grounds in the late afternoon. Different flocks often merge as they fly towards pre-roosting assembly points (often at established sites such as rookeries) before flying to their final roosting location where they spend the night. As flight trajectories towards roosts or pre-roosts are fairly consistent each evening, we were able to position the camera system so that flocks flew overhead. Nevertheless flocks did not always fly perfectly through the measurement volume; for example, they may fly out of the field of view of cameras 1 and 2, and thus only be captured by cameras 3 and 4. We only use data where the birds were seen on all four cameras. In our measurements, the distance from the birds to the image plane is about 20–60 m, given that the cameras are placed on tripods on the ground. Jackdaws have body lengths in the range 34–39 cm, translating to a size of 5–20 pixels on the camera sensors. Though higher frame rates can be reached, the data presented in this paper are recorded at 40 or 60 fps, which is still much larger than the jackdaw wingbeat frequency (which is typically in the 3–6 Hz range [38]). The time-varying bird shape is therefore resolved (figure 1e) and can be used for the calculation of wingbeat frequency.

2.3. Stereo-matching and three-dimensional tracking

To construct 3D trajectories from images, we perform stereo-matching frame by frame and then tracking in time. First, we locate the birds on each 2D image. For each image, we first subtract a background image calculated by averaging 50 temporally consecutive images where the background exhibits only minor changes. A global intensity threshold is then applied to segment the image into distinct blobs of pixels corresponding to one or more birds. The threshold is manually set and is low enough so that all the birds are detected. There are only a few false detections, which we reject later during the stereo-matching phase if no matched blobs in other views are found. In our datasets, the images typically have low sensor noise levels (that is, nearly uniform backgrounds) and the number of false detections is less than 2% of the total number of birds. For each segmented blob, we calculate the intensity-weighted centroid and treat it as the bird centre. This location does not necessarily yet represent the bird body centre due to time-varying wing morphologies (figure 1e), but will be revised later to obtain both body and wing motions.

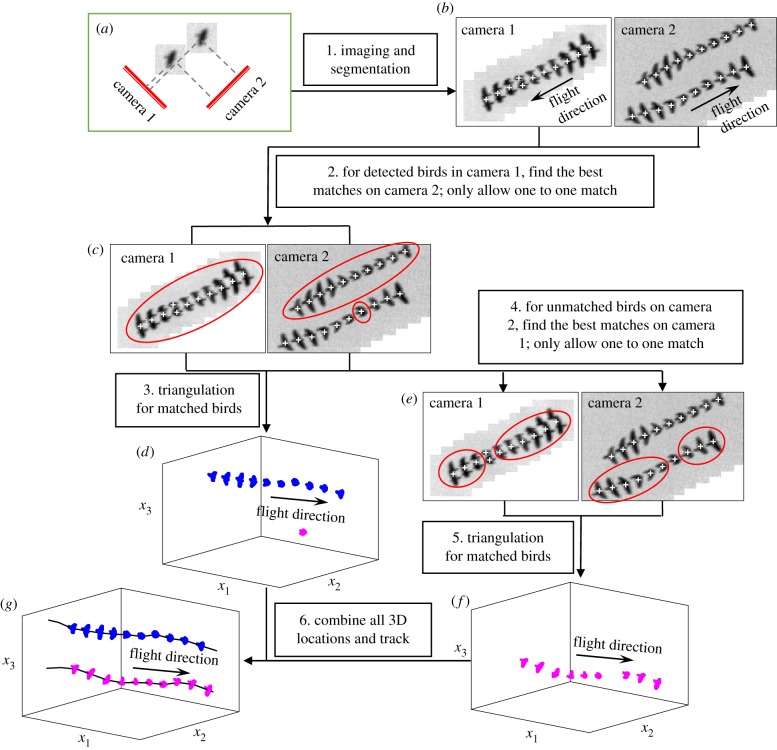
Then, stereo-correspondences are established between all the 2D measurements. To solve the optical occlusion problem, we introduce a new stereo-matching method based on associating every detected bird on each camera with a 3D position. For convenience, we illustrate our proposed method with a set-up of two cameras, though in our actual field system we use four cameras. As shown in figure 2a,b, the images of two birds may overlap on camera 1, but appear to be separated on camera 2. If we follow a typical one-to-one matching procedure, not all birds in camera 2 will be used to calculate 3D locations. However, by including the additional step of searching the un-used birds in view 2 and calculating their corresponding 3D positions we can recover the missing birds. The detailed procedure is as follows: for every detected bird on camera 1 (figure 2c), we search for candidate matches on other views that are located within a tolerance ε of the epipolar lines [25,39]. All the candidates are combined into a list and used to compute multiple 3D locations using a least-squares solution of the line of sight equations [40]. Each of these potential 3D locations is scored by a ray intersection distance (that is, the residual from the least-squares solution). The smaller the score is, the more likely this potential location is a true 3D location. Thus, only the potential location with the smallest score is selected as a candidate. Ideally, a true 3D location would have a score of 0 given perfect camera calibration and no error in the 2D centroid detection. In reality, however, the score is never 0. Thus, we set a threshold (with a typical value of 0.3 m, roughly the size of one bird) below which this 3D location is treated as a real bird location. Otherwise, if the score is larger than the threshold, we treat the 2D location as a false detection at the initial segmentation process. As shown in figure 2d, the 3D locations corresponding to all detected birds in camera 1 are reconstructed via this procedure. During this step, we mark the birds on view 2 that have been used for the calculation of the true 3D locations. Then, we consider the remaining unmarked birds on camera 2 (figure 2e), and reconstruct their corresponding 3D positions using the same method as was used for camera 1. The 3D locations of the missing birds are calculated as shown in figure 2f. Finally, the reconstructed results in figure 2d,f are combined to generate the 3D locations of all birds. For reference, we provide corresponding Matlab codes to perform these 3D reconstructions (see Data accessibility).

Figure 2.

Schematic of the stereo-matching and tracking procedures to solve the optical occlusion. (a) The camera set-up for imaging two birds, where the images of two birds overlap on camera 1 and separate on camera 2. (b) Time series of bird images on the two cameras, with the detected bird 2D locations marked as crosses. (c) Stereo-matching for all detected birds on camera 1, with the matched birds shown in the circles. (d) Reconstructed 3D positions for the matched birds in (c). (e) Stereo-matching for all unmatched birds on camera 2, with the matched birds shown in the circles. (f) Reconstructed 3D positions for the matched birds in (e). (g) The 3D trajectories of the two birds. (Online version in colour.)

Once the 3D positions have been determined at every time step, they are linked in time to generate trajectories (figure 2g). We use a three-frame predictive particle tracking algorithm that uses estimates of both velocity and acceleration. This method has been shown to perform well in the biological context for tracking individuals in swarms of midges [41]. It is also able to handle the appearance and transient disappearance of particles from the field of view by extrapolation using a predictive motion model. Details of this procedure are described in [10]. Finally, the velocities and accelerations are calculated by convolving the trajectories with a Gaussian smoothing and differentiating kernel [42]. In the following sections, we will use v_i and a_i to denote the velocity and acceleration in one of the three Cartesian directions (x₁, x₂, x₃) denoted by index i. The same bold symbols are used to denote vectors, e.g. x, v, a. The flight speed U is calculated as .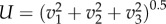

2.4. Body and wing motions

As mentioned above, the 2D locations of the birds are determined based on intensity-weighted centroids of segmented pixel blobs, and may not accurately capture the true body centre. As a result, the reconstructed 3D trajectory couples both the body and wing motions. However, since the wing motion has much higher frequency than the body motion, one can decouple the two effects in the frequency domain. To do so, we first calculate the body acceleration 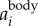by filtering the measured acceleration 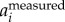in the frequency domain:

2.1

where F and F⁻¹ denote the Fourier and inverse Fourier transform, f is the frequency, and f_cut is the filter cut-off frequency. Typically, there is a peak in the power spectrum of F(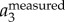) that corresponds to the time-averaged f_wb of each trajectory. In our dataset, the time-averaged f_wb for different birds varied from 2.5 to 7 Hz, and we used f_cut = 1 Hz for all birds. The body velocity 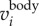and position 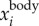are then obtained by integrating the body acceleration. Then, the wing motion 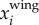is obtained by subtracting the body motion from the measured motion:

2.2

Following a procedure similar to [43], the time variation of f_wb is calculated by applying a continuous wavelet transform (CWT) to 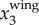. Here, the CWT is applied to 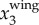since the wing motion is usually dominant in x₃ direction given the primarily horizontal flight of the birds. Two factors may affect the accuracy of this estimate of f_wb. First, as the distance from bird to the image plane increases, the imaging resolution, and thus the accuracy of 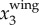, decreases. Given that the wing motion has an amplitude of the order of a wing length (≈0.3 m for jackdaws), we are able to measure the wing motion for birds flying up to 80 m away given our current imaging system. For more distant birds, one would need a lens with a longer focal length to capture the wing motion. Second, when birds make turns, the wing motion has components in the x₁ or x₂ directions. The magnitude of 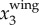reduces, and a higher image resolution is required to resolve 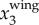. We calculated f_wb for birds whose maximal 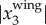is larger than 0.04 m, the image resolution at a height of 50 m. For the data presented here, fewer than 3% of the birds have a maximal 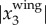smaller than 0.04 m.

We also attempted to separate body and wing motions by setting a cut-off frequency in F(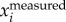) or F(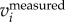). We tested the three methods on a numerically generated trajectory x^measured = t + 1 + sin(2π × 5t), where first two terms represent the body motion and the last term the wing motion with f_wb = 5 Hz. We found that x^body obtained by setting a cut-off frequency for F(a^measured) or F(v^measured) had a mean error of less than 0.1%, while for F(x^measured) had a mean error of 2%. We also compared the three methods on a real trajectory and found a similar trend: x^body obtained by setting a cut-off frequency for F(a^measured) and F(v^measured) is more accurate than that obtained by setting a cut-off frequency for F(x^measured). Since velocity and acceleration are time derivatives of position, F(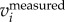) and F(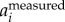) have stronger peaks at f_wb compared to that of F(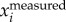). Thus, setting a cut-off frequency in F(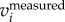) or F(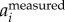) removes the wingbeat motion more reliably. Here, we opt to calculate body motion by setting a cut-off frequency in F(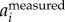). One can obtain similar results by setting a cut-off frequency in F(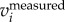). Attanasi et al. [18] used a low-pass filter on the 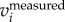(similar to setting a cut-off frequency in F(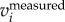)) and then differentiated it to obtain 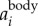. We compared 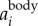calculated from both methods and the results are very similar.

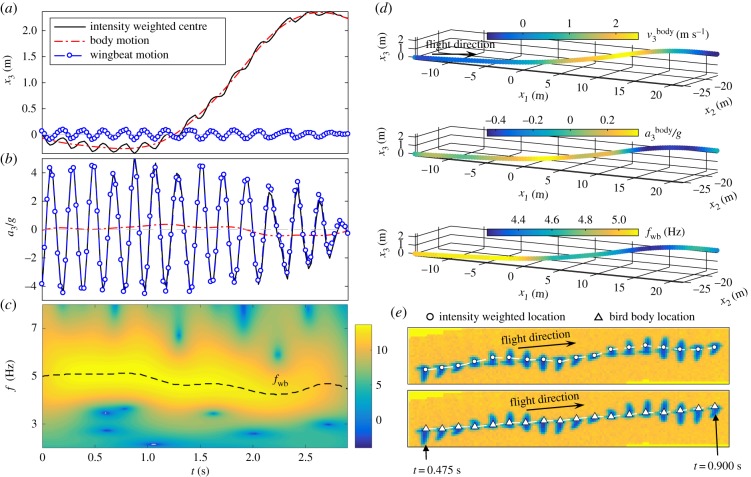
To illustrate our method, figure 3a shows a sample time trace of 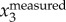, 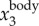and 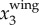. It clearly shows that 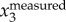contains both a low-frequency body motion and a high-frequency wing motion. The value of 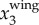varies from 0.15 to −0.15 m, which is comparable to the wing length of a jackdaw. Figure 3b shows 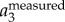, 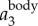and 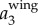corresponding to the position traces shown in figure 3a. All the values are normalized by the gravitational acceleration g (g = 9.78 m s⁻²). 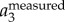is clearly dominated by 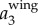, and has a magnitude up to 4g. The magnitude of 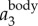is much smaller. Figure 3c shows the power spectrum obtained by applying a CWT to 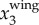. The time variation of f_wb, the frequency at which the power spectrum peaks at each time step, is shown by the dashed line. Figure 3d plots the same 3D trajectory coloured by 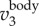, , 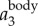and f_wb, showing that we can measure not only velocity and acceleration but also wingbeat frequency along the 3D trajectory of each bird. Clearly, f_wb is not always constant, but rather depends on speed and flight behaviour. Indeed, as we argue below, the variation of f_wb can provide additional information to characterize bird behaviour.

Figure 3.

(a) Time evolutions of 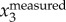, , 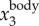and 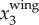. (b) Time evolutions of 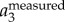, , 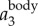and 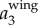. (c) Power spectrum (on a log scale) obtained from a continuous wavelet transform of 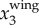and time evolution of f_wb (dashed line). (d) The same 3D trajectory coloured by 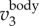, 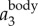and f_wb. (e) Time series of bird images on one camera, along with their intensity weighted centres (top row) and 2D locations obtained by re-projecting 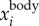onto images (bottom row). (Online version in colour.)

To demonstrate that the proposed method indeed captures the bird body centre, we can re-project 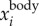onto one of the 2D images, as shown in figure 3e. The top image shows the 2D positions based on the intensity weighted centroid, while the bottom image shows the 2D positions obtained from re-projecting 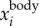onto the camera. Even with the uncertainties in the camera calibration, the re-projected 2D positions still detect the body centres very accurately. The average value of 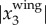over all the trajectories is 0.03 m and the maximal value of 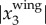is 0.17 m. Therefore, the improvement of the estimate of the body centre location after removing the wing motion can be as high as 0.17 m, and has a mean value of 0.03 m. In the following sections, we report only these body positions, and omit the ‘body’ indication for simplicity.

2.5. Statistical analyses

Analyses were conducted in R version 3.1.2. Comparisons of wingbeat frequency of birds flying alone or in groups were conducted using linear mixed models (lme package) with a random term to account for group membership. Wingbeat frequency was fitted as the response term, with flight speed and grouping (in a flock or in isolation) as explanatory terms.

3. Results

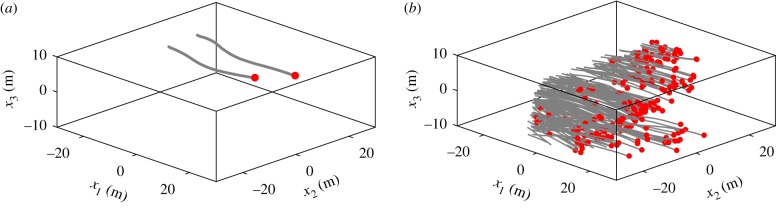
We recorded six flocking events (flocks #1–6) consisting of 50 to 360 individuals. Flock #1 includes jackdaws only, and flocks #2–6 include both jackdaws and rooks. It was known beforehand via visual and vocal cues obtained during the data recording process whether the flocks contained single or mixed species. We also recorded 32 jackdaws and 6 rooks flying in isolated pairs or alone, which we defined as birds flying at least 10 m away from a large group. The species of these non-flocking birds were also identified and known beforehand through visual and vocal cues. Sample trajectories are provided in figure 4a,b. Details of all the trajectories are provided in table 1.

Figure 4.

Sample trajectories of jackdaws flying in an isolated pair (a) and in flock #1 (b). (Online version in colour.)

Table 1.

Summary of the datasets included in this paper. The reported numbers in the last four columns are the mean values and standard errors. D₂ is the distance to the second nearest neighbour.

date	flock #	total number of birds	bird species	trajectory length (s)	U (m s−1)	fwb in flapping modes (Hz)	D2 (m)
flying in a group
2018-01-29	1	354	jackdaw	2.7 ± 0.1	13.7 ± 0.1	4.70 ± 0.04	2.5 ± 0.1
2018-02-04	2	224	jackdaw, rook	2.8 ± 0.0	14.3 ± 0.1	4.37 ± 0.05	2.9 ± 0.1
2018-02-04	3	186	jackdaw, rook	2.3 ± 0.1	15.4 ± 0.1	4.58 ± 0.06	3.2 ± 0.1
2018-02-04	4	75	jackdaw, rook	3.1 ± 0.1	14.1 ± 0.1	4.01 ± 0.12	5.4 ± 0.5
2018-02-09	5	110	jackdaw, rook	1.7 ± 0.1	17.6 ± 0.1	4.69 ± 0.10	4.6 ± 0.3
2018-02-09	6	67	jackdaw, rook	1.8 ± 0.1	17.6 ± 0.2	4.68 ± 0.13	3.5 ± 0.3
flying in isolated pairs or alone
—	—	32	jackdaw	2.5 ± 0.2	12.2 ± 0.4	4.00 ± 0.13	>10
—	—	6	rook	2.8 ± 0.6	12.8 ± 1.9	2.91 ± 0.11	>10

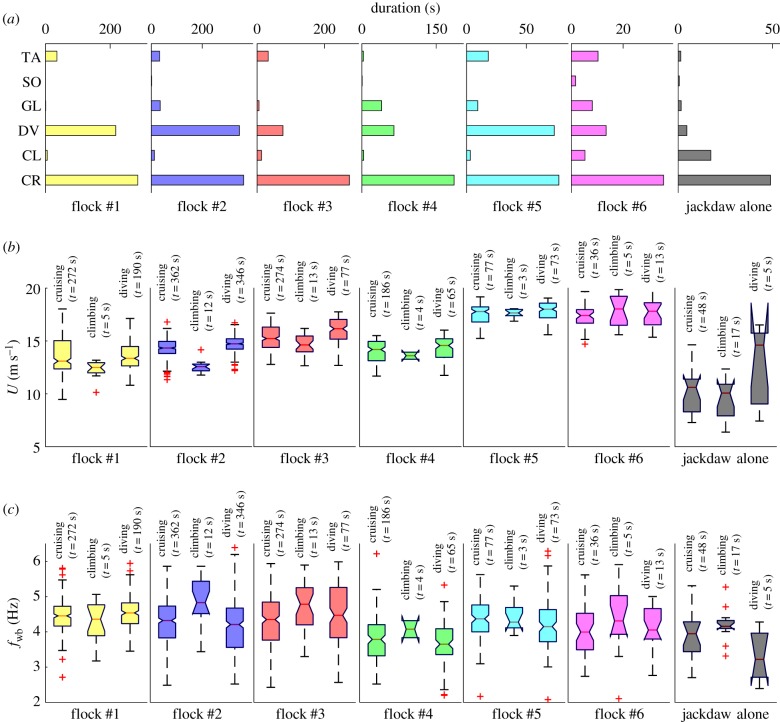
We classified the trajectories into six flight modes based on the magnitudes of f_wb, v₃ and |a|: three flapping modes where f_wb > 2 Hz and |a| < 8 m s⁻², cruising (|v₃| < 1 m s⁻¹), climbing (v₃ > 1 m s⁻¹), and diving (v₃ < −1 m s⁻¹); two non-flapping modes where f_wb < 1 Hz and |a| < 8 m s⁻², gliding (v₃ < −1 m s⁻¹) and soaring (v₃ > 1 m s⁻¹); and one mode where |a| > 8 m s⁻² indicating turning or accelerating. The sample times for the non-flapping modes and the turning or accelerating mode were relatively short compared to the flapping modes (figure 5a). We therefore only report the statistics of U and f_wb in the three flapping modes (figure 5b,c). For most cases, f_wb is highest in climbing mode and lowest in diving mode, and U is lowest in climbing mode and highest in diving mode. We note that we varied the threshold of v₃ from 0.5 to 2 m s⁻¹ in separating the different flapping modes and found that the general trends observed in figure 5b,c do not change.

Figure 5.

(a) Time durations, (b) flight speed, and (c) wingbeat frequency of different flight modes for flocks #1–6 and for jackdaws flying in isolated pairs or alone. For (a), TA, turning or accelerating; SO, soaring; GL, gliding; DV, diving; CL, climbing; CR, cruising. (Online version in colour.)

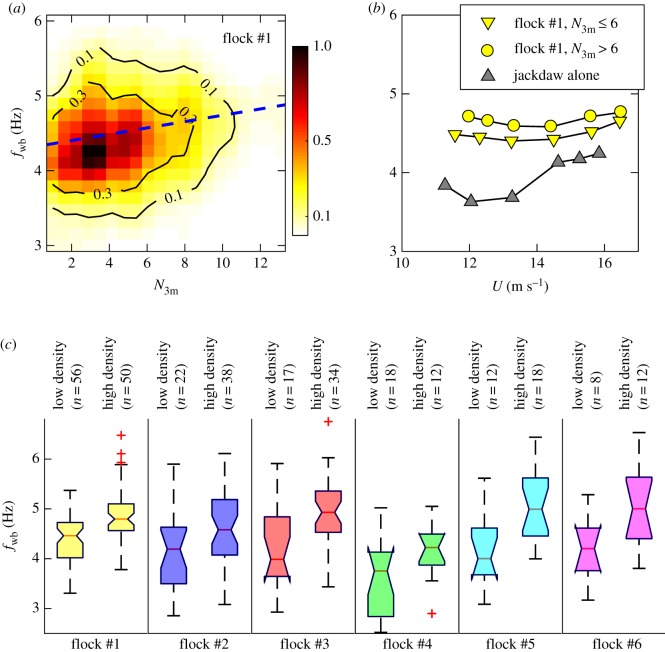
Table 1 shows that jackdaws flying as isolated pairs or as single birds have a lower wingbeat frequency than jackdaws flying in the single-species flock #1. Linear mixed model analysis confirms this result: controlling for the effect of flight speed (Est (s.e.) = 0.045 (0.019), t = 2.33, p = 0.02), birds flying in isolation have a lower wing beat frequency than those in a flock (Est (s.e.) −0.663 (0.129), t = −5.14, p < 0.001). This means that flocking jackdaws flapped their wings, on average, 42 (±10) times more per minute than when flying in isolation (282 ± 2 wingbeats/minute versus 240 ± 8 wingbeats/minute). We thus investigated the effect of local density on the flight performance of individuals. To estimate the local density, we counted the number of birds N_{3 m} within a sphere of fixed radius of 3 m. As shown in figure 6a, f_wb increases with N_{3 m} (Pearson correlation coefficient = 0.20, p < 0.01). We also plotted the flight performance curves, i.e. the relation between f_wb and U, for jackdaws in flock #1 and for jackdaws flying alone (figure 6b). All curves had their minimum wingbeat frequency at moderate flight speed. Moreover, for birds flying in a group, increasing N_{3 m} moves the curves upward. In all other five mixed-species flocks, birds in the denser region had higher wingbeat frequencies (figure 6c). One may argue that this trend may be due to a preference for bird species with lower f_wb (here, rooks) to fly in less dense regions. Given that rooks have f_wb = 2.9 ± 0.1 Hz (table 1), we can exclude most rooks from our analysis by ignoring birds whose mean f_wb is smaller than 4 Hz; when doing so, we found that the same trend exists (electronic supplementary material, figure S1).

Figure 6.

(a) Joint PDFs of f_wb and N_{3 m} (number of neighbours within 3 m of the focal bird) for jackdaws in cruising flight in flock #1. The dashed line is a linear fit to the data. (b) Flight performance curves for jackdaws in the cruising flight mode. Each point is calculated by averaging more than 800 measurements, and error bars are smaller than symbol size. (c) Box plots of wingbeat frequency averaged over flapping modes. For each flock, we selected birds that are flying in low density regions defined by N_{3 m} < mean(N_{3 m}) − std(N_{3 m}), and that are flying in high density regions defined as N_{3 m} > mean(N_{3 m}) + std(N_{3 m}). (Online version in colour.)

We also compared the flight performance curves for jackdaws and rooks flying alone or in isolated pairs (figure 7). Clearly, the two species have different flight performance curves, with the larger rooks having lower wingbeat frequencies than jackdaws at the same flight speed. Due to our limited sample size for rooks, we were not able to compare f_wb at higher speeds. To determine whether species differences in wingbeat frequency persist when the two species flock together, we manually identified 8 rooks and 12 jackdaws in mixed-species flocks on the basis of visible morphological characteristics. Extracted f_wb values for these individuals show that rooks still have lower wingbeat frequency than jackdaws (rook = 3.4 ± 0.4 Hz, jackdaw = 4.2 ± 0.3 Hz) (electronic supplementary material, table S1).

Figure 7.

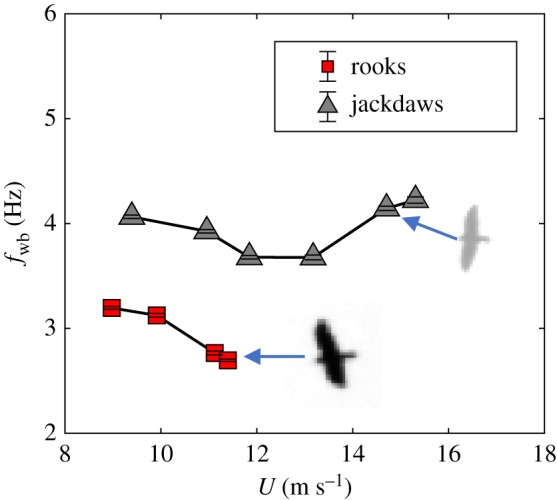
Flight performance curves of jackdaws and rooks flying alone or in isolated pairs. All data are calculated in the cruising flight mode. Error bars show the standard error of f_wb and are smaller than the symbol size. Inset bird images are taken from one of the cameras (jackdaw wing is broader closer to the body than the outer parts, while the rook wing is more even size along its length). (Online version in colour.)

4. Discussion

In this paper, we have described a new stereo-imaging system for tracking the 3D motion of birds in the field. The new system overcomes the technical difficulty of extending the distance between cameras and improves the accuracy of 3D stereo-reconstruction. It allows the measurement of not only velocity and acceleration but also wingbeat motion and frequency along the 3D trajectory. In addition, we have developed a new stereo-matching algorithm to solve the optical occlusion problem. This is based solely on information in instantaneous frames, and thus is much faster than global optimization [27,28] when solving for data associations across multiple views and time steps. We have demonstrated the new reconstruction algorithm on dense flocks ranging in size to over 300 birds. A detailed comparison of the reconstruction accuracy between our method and global optimization is, however, beyond the scope of this paper.

When applying our method to birds flying alone, we showed that measurements of wingbeat frequency along 3D trajectories allow us to better understand the flight kinematics of birds. First, the system allows us to characterize the flight performance of birds in the wild without the need to fit bio-logging tags. Our results confirm the typically reported U-shaped flight performance curve (with wingbeat frequency reaching a minimum at moderate flight speed) measured in wind tunnel experiments [44]. Moreover, the system allows us to compare flight speeds and wingbeat frequencies in different flight modes. The reason that birds vary flight modes may be due to a balance between flight speed and energy expenditure [45,46]. We observed that the birds' total energy (that is, the sum of the kinetic and gravitational potential energy) increases with the flight height. We thus suggest that birds may increase their total energy by increasing wingbeat frequency during climbing, and lower their total energy by decreasing wingbeat frequency during diving. Finally, the birds have a mean diving angle of −6° to the horizontal plane, and a mean climbing angle of 6°. These values may provide valuable guidance for designing wind tunnel experiments that are as faithful as possible to real flying conditions [47].

When applying the system to study group flight, we argue that measurements of wingbeat frequency within flocks provide new opportunities to understand collective motion. Using wingbeat frequency as a proxy for energy consumption [1] allows us to study whether birds flying in groups save energy. Although flying in a group offers many benefits, such as reduced risk from predation [48,49], our data suggest that flying in a group also comes at a cost, as f_wb was higher for birds flying in a group than flying in isolated pairs or alone (an average difference of 42 wingbeats per minute), and increased with local density. The same trend was reported for observations of groups of pigeons by Usherwood et al. [1]. The explanation proposed by those authors was that flying in a dense group requires more manoeuvres and coordinated motion to avoid collisions. Our data support this explanation since birds flying in groups make more turning and accelerating manoeuvres than birds flying alone (figure 5a).

Finally, the fact that many birds form mixed species flocks offers important opportunities to examine the impacts of individual heterogeneity on collective motion [50]. However, addressing this issue requires techniques to accurately classify birds within mixed-species flocks. Here, we show that our system allows us to quantify the different wingbeat frequencies of two closely related species—jackdaws and rooks—when they fly alone or in mixed-species groups. An appropriate generic thresholding of wingbeat frequency to separate jackdaws and rooks in mixed-species flocks, however, remains to be determined.

The proposed method can be applied to other birds or even other flying animals (e.g. insects) if the following requirements are met: (i) their flight routes, feeding grounds, or roosts are known; (ii) the imaging spatial resolution is high enough that the body and wings are distinguishable; and (iii) the recording temporal resolution is high enough to sample the wing movements. For example, to study birds of different sizes, one could bring the cameras closer to or further from the objects being imaged and select lenses with suitable focal lengths. To study insects with higher wingbeat frequency (e.g. greater than 50 Hz), one could use cameras that record data at higher frame rates. In addition, our method is very easy to reproduce under other experimental conditions. We provide Matlab codes (see Data accessibility) so others can compute 3D motion and wingbeat frequency from raw images. Therefore, our method provides important opportunities for studies of both the flight kinematics of individuals and the collective behaviour of groups under natural conditions.

Ethics

All field protocols were approved by the Biosciences Ethics Panel of the University of Exeter (ref. 2017/2080) and adhered to the Association for the Study of Animal Behaviour Guidelines for the Treatment of Animals in Behavioural Research and Teaching.

Data accessibility

We provide data including images recorded by four cameras, camera parameters, videos showing the time variation of the bird 3D positions, and plain text files that include bird id number, positions, times, velocities, accelerations, and wingbeat frequencies at every time step. We also provide the Matlab codes that were used to: (i) detect birds on images; (ii) reconstruct birds' 3D locations using the new stereo-matching algorithm; (iii) track individual's 3D motions; and (iv) calculate wing motion and wingbeat frequency from tracking results. The code and data are available at: https://github.com/linghj/3DTracking.git and https://figshare.com/s/3c572f91b07b06ed30aa.

Authors' contributions

H.L., N.T.O. and A.T. conceived the ideas; H.L. and N.T.O. designed the methodology; G.E.M. and A.T. collected the data; H.L. and N.T.O analysed the data; G.E.M. and A.T. performed the statistical analysis; all led the writing of the manuscript. All authors contributed critically to the drafts and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported by a Human Frontier Science Program grant to A.T., N.T.O. and R.T.V., Award Number RG0049/2017.