Segment-specific associations between local haemodynamic and imaging markers of early atherosclerosis at the carotid artery: an in vivo human study

Abstract

Low and oscillatory wall shear stress (WSS) has long been hypothesized as a risk factor for atherosclerosis; however, evidence has been inferred primarily from model and post-mortem studies, or clinical studies of patients with already-developed plaques. This study aimed to identify associations between local haemodynamic and imaging markers of early atherosclerosis. Comprehensive magnetic resonance imaging allowed quantification of contrast enhancement (CE) (a marker of endothelial dysfunction) and vessel wall thickness at two distinct segments: the internal carotid artery bulb and the common carotid artery (CCA). Strict criteria were applied to a large dataset to exclude inward remodelling, resulting in 41 cases for which personalized computational fluid dynamic simulations were performed. After controlling for cardiovascular risk factors, bulb wall thickening was found to be weakly, but not significantly, associated with oscillatory WSS. CE at the bulb was significantly associated with low WSS (p < 0.001) and low flow helicity (p < 0.05). No significant associations were found for the CCA segment. Local haemodynamics at the bulb were significantly correlated with blood flow rates and heart rates, but not carotid bifurcation geometry (flare and curvature). Therefore low, but not oscillatory, WSS is an early independent marker of atherosclerotic changes preceding intimal thickening at the carotid bulb.

1. Introduction

There is ample evidence suggesting that disturbed blood flow plays a central role in the focal development of plaques at major arterial branches, supporting the so-called haemodynamic hypothesis of atherosclerosis [1]. In particular, wall shear stress (WSS) having low average magnitude and large oscillatory (directional) changes during the cardiac cycle is recognized as an atheroprone haemodynamic phenotype [2]. The first direct evidence was provided by Ku & co-workers [3], who observed a positive correlation between locations of oscillatory shear in an in vitro model of a carotid artery and intimal thickening in post-mortem human carotid arteries.

Biological mechanism studies have since detailed how low and oscillatory WSS creates a pro-atherogenic environment through the activation of multiple signalling pathways and transcription factors promoting endothelial cell (EC) inflammatory activation, altered gene expression and function, conditions which we refer to as endothelial dysfunction. To further elucidate the precise haemodynamic cues leading to endothelial dysfunction, some studies noted differences in low versus oscillatory WSS on the impairment of endothelial nitric oxide production [4] and EC proliferation [5]. In a murine model of atherosclerosis obtained by placement of a perivascular cast around the carotid artery to induce disturbed haemodynamics, atherogenesis was observed both in the low WSS region upstream of the device and in the low and oscillatory WSS region downstream of it, but with differences between the regions in terms of expression of pro-atherogenic factors [6]. However, several caveats have been raised about the use of devices or surgical modifications to induce haemodynamic disturbances, because they may trigger mechanisms unrelated to atherogenesis [7].

Large clinical imaging studies using high-resolution magnetic resonance imaging (MRI) have provided indirect evidence in vivo of a haemodynamic influence on early wall thickening at the carotid bifurcation, a preferred site of plaque development. The CARDIA study showed weaker associations with cardiovascular (CV) risk factors for the internal carotid artery (ICA) and bulb compared to the common carotid artery (CCA) segment, and speculated that the difference was ‘likely linked to bifurcation geometry and differences in haemodynamics’ [8]. The ARIC study showed that inward remodelling at the ICA occurs at a lower wall thickness (WT) threshold than the CCA [9], and that carotid bifurcation geometry (a surrogate marker of local haemodynamics) is an independent predictor of early wall thickening at the carotid bulb [10]. The latter study also highlighted the confounding effect of inward remodelling on identifying relationships between local haemodynamics and wall thickening. Most recently, the BioImage study confirmed distinct patterns of inward versus outward remodelling at ICA, bifurcation and CCA segments [11]. A pooled analysis of ultrasound carotid intima-media thickness (IMT) from four large clinical trials found a consistent pattern in the circumferential distribution of early wall thickening from the CCA to the ICA [12], suggestive of helical flow and WSS distribution along the carotid bifurcation.

More direct investigations of haemodynamics and atherosclerosis in humans have typically focused on patients with already-developed coronary or carotid plaques [13–15], and so are difficult to extrapolate to early atherosclerosis. Even studies of early atherosclerosis must take special care to avoid secondary effects of wall thickening on the lumen geometry and its induced haemodynamics (i.e. due to the lumen reduction and consequent WSS increase) [10]. Moreover, the earliest preclinical manifestations of atherosclerosis, namely EC dysfunction and inflammation, appear prior to wall thickening and apparent structural changes of the vessel wall [16,17].

Such limitations can be overcome by using contrast-enhanced MRI, since the uptake of the gadolinium contrast agent into the wall is mediated mainly by the increased EC permeability associated with EC dysfunction [18,19]. Moreover, as already noted, MRI can be used to measure WT in vivo [20], and it provides the anatomical and functional information required for subject-specific computational modelling and classification of local haemodynamic conditions [21]. In the present study, we deploy these non-invasive techniques, for the first time together, in order to test the hypothesis that, for the carotid bifurcation, markers of disturbed WSS and intravascular haemodynamics (or their geometric surrogates) are associated with early atherosclerotic changes (i.e. WT and/or contrast enhancement (CE)) at the carotid bulb versus the CCA.

2. Methods

2.1. Study participants

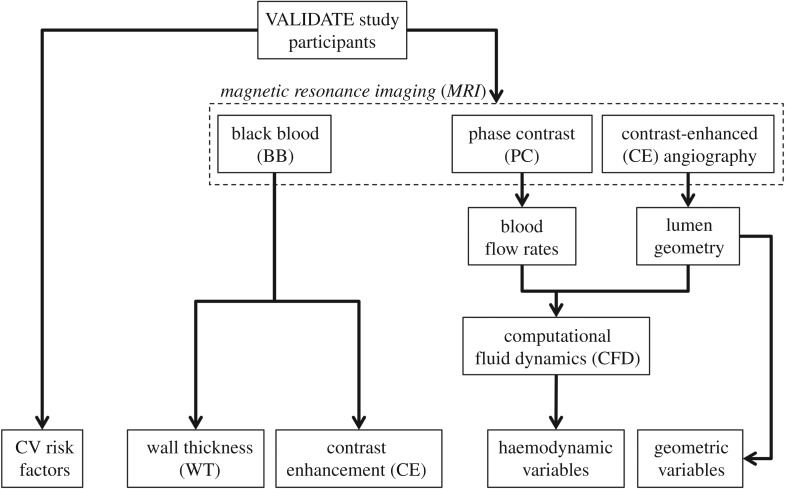
Data for this study were acquired as part of the broader VALIDATE (Vascular Aging – The Link that Bridges Age to Atherosclerosis) study, which included coronary and carotid imaging, as well as other CV risk factor measurements. Institutional review board approval was obtained and participants provided informed consent. Approval for the present sub-study and use of anonymized data was given by the VALIDATE study centre. An overview of the methods is provided in figure 1. Risk factors and imaging data were acquired contemporaneously, and so the present analysis is cross-sectional in nature.

Figure 1.

Schematic diagram of the study design, showing how imaging data contribute to define vessel wall, haemodynamic and geometric variables.

2.2. Magnetic resonance imaging

MRI scans were performed on a 3 T scanner (Achieva, Philips Healthcare; Best, The Netherlands) using a bilateral four-channel phased-array carotid coil (Pathway MRI; Seattle, WA, USA). All scans were performed on the right carotid artery. The protocol included 3D time-of-flight, 3D contrast-enhanced magnetic resonance angiography (CE-MRA), phase contrast MRI (PC-MRI) and black blood MRI (BB-MRI).

CE-MRA was acquired following intravenous injection of the contrast agent, using an elliptic-centric 3D coronal protocol with 1.2 × 0.8 × 0.8 mm³ resolution zero-padded to 0.6 mm isotropic. A representative CE-MRA image is shown in figure 2. Retrospectively-gated, 2D cine PC-MRI images were acquired prior to contrast medium injection at the CCA, ICA and external carotid artery (ECA) with 5 mm slice thickness and 0.5 × 1.0 mm² resolution zero-padded to 0.5 mm isotropic. Further details of the CE-MRA and PC-MRI protocols are provided elsewhere [22].

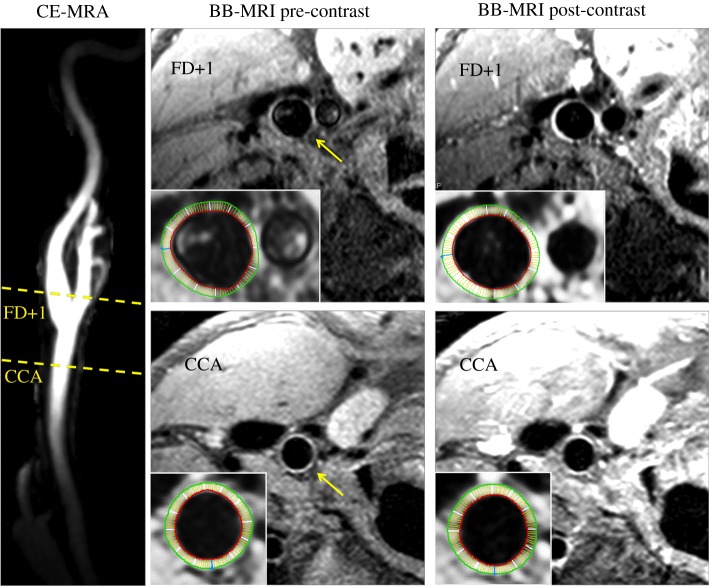
Figure 2.

Representative MRI images, showing locations of the CCA and FD + 1 slices on a maximum intensity projection of the 3D CE-MRA of the carotid bifurcation; and BB-MRI slices from those locations both pre- and post-contrast, with vessel-of-interest identified by yellow arrow. Insets show inner and outer boundaries of the segmented vessel walls, with white radial lines delineating the 12 sectors over which CE and WT were computed.

T1-weighted BB-MRI images were acquired both before and after the CE-MRA using an ECG-triggered, 2D double inversion-recovery protocol with repetition time of 1 RR interval, echo time of 8 ms, and echo train length of 10. A single 2 mm slice was placed at the CCA at a distance 1.5 cm proximal to the flow divider, with 0.51 × 0.6 mm² in-plane resolution zero-padded to 0.27 mm isotropic. A separate series of 2-mm slices was acquired at the same resolution, centred at the carotid bifurcation and placed transverse to the nominal CCA–ICA tract. Representative BB-MRI images are shown in figure 2, and further details are provided elsewhere [20].

2.3. Vessel wall measurements

WT was measured as previously described [20], and shown in figure 2. Briefly, the inner and outer wall boundaries were segmented semi-automatically from edge-enhanced pre- and post-contrast BB-MRI images. This was done for the CCA slice, and for the ICA at the first slice distal to the flow divider, a standard location hereafter referred to as FD + 1 where atherosclerotic lesions are usually observed [1,3]. The contours were used to compute WT at 12 equally spaced sectors. CE was computed as the relative change in sector intensities from the pre- to post-contrast BB-MRI images. Signal intensities were standardized using spinal cord signal intensity if included in the image, or noise contour mean. For each participant, CCA-WT and CCA-CE were defined as the respective maximum values from the 12 sectors. For ICA-WT and ICA-CE, the maxima from the FD + 1 slice data were determined, excluding the four sectors adjacent to the flow divider to avoid possible artefactual thickening, or focal enhancement due to the carotid body.

Exclusion criteria were applied, as summarized in table 1. In detail, of the initial cohort of 129 VALIDATE cases, 22 were excluded because either WT or CE could not be measured reliably, or because the FD + 1 slice was greater than 25° oblique to the vessel axis, which could artificially inflate ICA-WT values [23]. Additionally, as we have previously demonstrated [10], it was critical to identify cases with inward remodelling, since this would result in a WSS increase through the narrowing of the lumen, potentially obscuring the relationship between haemodynamics and WT. A further 36 cases were therefore excluded for having WT exceeding outward remodelling criteria defined previously from the ARIC study [9].

Table 1.

Summary of exclusion criteria.

no. of cases	description
129	initial cohort of VALIDATE cases
−13	low quality BB-MRI and/or could not reliably measure WT or CE at FD + 1 slice
−9	oblique FD + 1 slice (greater than 25°)
−36	inward remodelling (ICA-WT > 1.38 mm or CCA-WT > 2.06 mm)
71	potential cases for CFD
−19	low quality CE-MRA and/or could not reliably segment lumen
−4	low quality PC-MRI and/or could not reliably segment flow rates
−7	lumen indentation evident after segmentation
41	cases for CFD versus wall variables

2.4. Computational fluid dynamics

As shown for a representative case in figure 3a, lumens were segmented from CE-MRA volume using a level set method [10], including the proximal CCA to at least five diameters upstream of the bifurcation to minimize the impact of inlet truncation on computed bifurcation flow patterns [25]. As detailed in table 1, 19 cases were excluded to avoid unreliable or insufficiently long CFD models. Of the segmented cases, a further seven were excluded owing to evident lumen indentation near the bifurcation, suggesting inward remodelling.

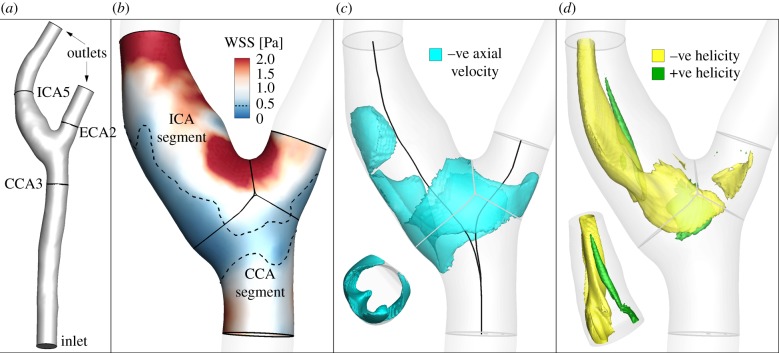
Figure 3.

Summary of haemodynamic analysis for a representative case, showing: (a) segmented lumen surface, including flow extensions for CFD; (b) the computed WSS magnitude, automatically clipped and then divided into CCA and ICA segments, with dotted line shows region of low WSS; (c) negative axial velocity, used to calculate VolRec (inset: axial view of ICA segment, showing protrusion of negative axial velocity into the lumen; –ve: negative); and (d) helical flow patterns visualized using local normalized helicity (LNH, the normalized dot product of velocity and vorticity vectors [24]; −ve: negative, +ve: positive), with signed LNH values identifying counter-rotating flow patterns (inset: rotated view of ICA segment, showing asymmetric LNH).

Subject-specific flow rate waveforms were extracted from the cine PC-MRI series. Inlet flow rate waveforms were measured from the PC-MRI slice at the proximal CCA, placed transverse to the nominal long axis of the CCA at a distance 1.5 cm proximal to the flow divider. For the outlets, ICA and ECA flow rates were obtained from a PC-MRI slice acquired 5 mm distal to the flow divider in a separate acquisition. Individual heart rates were prescribed (64 ± 11 bpm, range 46–85). To ensure instantaneous mass conservation in the CFD model, ICA and ECA flow rates were rescaled to add up to the CCA flow rate at each point in time along the cardiac cycle. Pulsatile flow rates were prescribed as fully developed (Womersley) velocity profiles at the CCA inlet and ICA outlet; the ECA outlet was traction free, as detailed in previous studies [25]. Owing to poor-quality PC-MRI, four cases were excluded.

Computational haemodynamics simulations were carried out using a validated in-house finite-element solver [21]. Finite-element meshes comprised approximately 250 000 quadratic tetrahedral elements on average, with 0.5 mm side length, roughly equivalent to 2 million linear tetrahedra and 0.25 mm node spacing, previously shown to sufficiently converge WSS [21]. Temporal resolution was 4800 time-steps per cardiac cycle, and at least three cardiac cycles were used to ensure convergence of the pulsatile flow fields. Further details on CFD settings are reported elsewhere [21,25].

2.5. Haemodynamic and geometric variables

Following Gallo et al. [26], we computed three established WSS-based descriptors, i.e. the time-averaged WSS magnitude (TAWSS), oscillatory shear index (OSI) and relative residence time (RRT, a combination of TAWSS and OSI quantifying low and/or oscillatory shear). Additionally, we computed an emerging descriptor of multidirectional shear, transverse WSS (transWSS) [27]. All models were clipped at CCA, ICA and ECA planes corresponding to 3, 5 and 2 radii along their respective lengths, denoted CCA3, ICA5 and ECA2 (figure 3a). To determine objective thresholds for ‘disturbed’ flow, data from all cases were pooled to identify the lower 20th percentile value of TAWSS (being that low WSS was of interest), and upper 20th percentile values of OSI, RRT and transWSS. The resulting thresholds were TAWSS = 0.455 Pa, OSI = 0.145, RRT = 3.10 Pa⁻¹, transWSS = 0.345 Pa. Branches were split into CCA and ICA segments (figure 3b) using an automated approach [28]. For each segment, the surface area exposed to OSI, RRT and transWSS above, or TAWSS below, its respective threshold value was calculated, and normalized by the respective segment's surface area. These normalized variables are denoted as LSA (low shear area), OSA (oscillatory shear area), RTA (residence time area) and TSA (transverse shear area).

In addition, the volume of recirculating flow, an intravascular marker of disturbed flow shown to correlate with atherosclerotic biomarkers [29], was computed by projecting the CFD-computed vector velocity field along the local vessel centre lines (i.e. axial direction), and then integrating all finite-elements containing a mean negative axial velocity component (figure 3c). This volume of recirculating flow was then normalized by the respective segment volume, and denoted VolRec [29]. Intravascular flow structures were also characterized in terms of helical flow (figure 3d), a spiraling motion recognized as an important factor in suppressing flow disturbances, and hence potentially atheroprotective [24]. For each carotid segment, the time and volume average of the norm of the internal product of velocity and vorticity vectors was computed and denoted as AvgHel [24]. Local normalized helicity (LNH), the normalized internal product between local velocity and vorticity vectors [30], was used to visualize helical blood flow patterns inside the bifurcation. The formulation of the investigated haemodynamic descriptors is reported in table 2. Finally, bifurcation flare and CCA curvature, previously shown to be significantly associated with ICA-WT [10], were calculated as described previously [31], in order to test the so-called geometric risk hypothesis of atherosclerosis [1,32].

Table 2.

Investigated haemodynamic descriptors. WSS is the (time-varying) WSS vector; T is the period of the cardiac cycle; n is the unit vector normal to the arterial surface at each element; V is the volume; 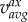is the axial component of the cycle-averaged velocity vector; v is the (time-varying) velocity vector; and ω is the (time-varying) vorticity vector.

WSS-based haemodynamic parameters
time-averaged WSS (TAWSS)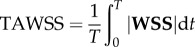
oscillatory shear index (OSI)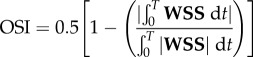
relative residence time (RRT)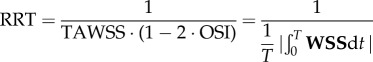
transverse wall shear stress (transWSS)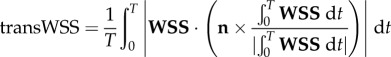

bulk-flow-based haemodynamic parameters
volume of recirculation (VolRec)	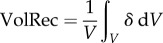where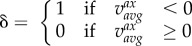
average helicity intensity (AvgHel)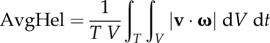

2.6. Statistical analysis

Bivariate correlations among CV risk factors, wall variables, haemodynamic variables and geometric variables were determined using Pearson product-moments when both variables were continuous, otherwise Spearman rank ordering was used. Linear regressions were used to identify relationships between each haemodynamic variable and either WT or CE as the dependent variable. Multiple regressions were used to control for CV risk factors that were independently correlated with WT or CE variables (as given by a stepwise multiple regression analysis), or for evaluating associations between the combination of bifurcation flare and CCA curvature versus WT or CE. Regressions are reported as the individual standardized correlation coefficient (β). For all analyses, significance was assumed for p < 0.05.

3. Results

Descriptive statistics for CV risk factors are summarized in table 3. Stepwise multiple regressions revealed that ICA-WT was significantly associated with sex (β = 0.518, p = 0.0021) and inversely with HDL (β = −0.378, p = 0.019), and so both were used to adjust ICA-WT in subsequent (multiple) linear regressions with geometric or haemodynamic variables. CCA-WT was significantly associated with BMI (β = 0.428, p = 0.033) and was similarly adjusted. Neither ICA-CE nor CCA-CE was found to be significantly associated with any CV risk factors, so no adjustment was performed. CE and WT were not correlated with each other for either segment, and so independent linear regressions could be carried out.

Table 3.

Descriptive statistics for cardiovascular (CV) risk factors.

CV risk factor	mean ± s.d. or %
age, years	58.5 ± 11.7
sex, male	41%
race, white	63%
BMI, kg m−2	27.0 ± 5.9
ever smoker	25%
hypertension	58%
diabetes mellitus	22%
triglycerides, mg dl−1	99.4 ± 74.6
HDL, mg dl−1	61.2 ± 21.5
LDL, mg dl−1	105.4 ± 29.4
glucose, mg dl−1	88.5 ± 14.4

Linear regressions (table 4) revealed significant associations between haemodynamic and wall variables for the ICA segment. Notably, CE was strongly and positively associated with LSA (β = 0.534, p = 0.0003) and RTA (β = 0.493, p = 0.001), whereas a negative regression coefficient (β = −0.337, p = 0.031) indicates that elevated AvgHel served to suppress CE. WT was weakly associated with OSA (β = 0.338, p = 0.031) and AvgHel (β = −0.310, p = 0.049), but not after adjusting for sex and HDL (although OSA was near-significant, at p = 0.057). For the CCA segment, no haemodynamic associations were found for CE, or for WT either before or after adjustment for BMI.

Table 4.

Standardized coefficients (β) from linear regressions of segment-specific haemodynamic variables versus contrast enhancement (CE) or wall thickness (WT), adjusted for CV risk factors. Bolded entries are statistically significant.

haemodynamic or	contrast enhancement		wall thickness
geometric variable	ICA-CE	CCA-CE	ICA-WT	CCA-WT
LSA	0.534‡	−0.061	0.238	0.211
OSA	0.216	−0.084	0.292	0.265
RTA	0.493†	−0.097	0.280	0.256
TSA	−0.209	−0.123	−0.008	−0.123
VolRec	−0.055	−0.176	0.122	−0.237
AvgHel	−0.337*	−0.018	−0.200	−0.188
flare	−0.039	−0.109	−0.055	−0.269
curvature	0.229	−0.298	−0.135	−0.059

*p < 0.05; ^†p < 0.01; ^‡p < 0.001.

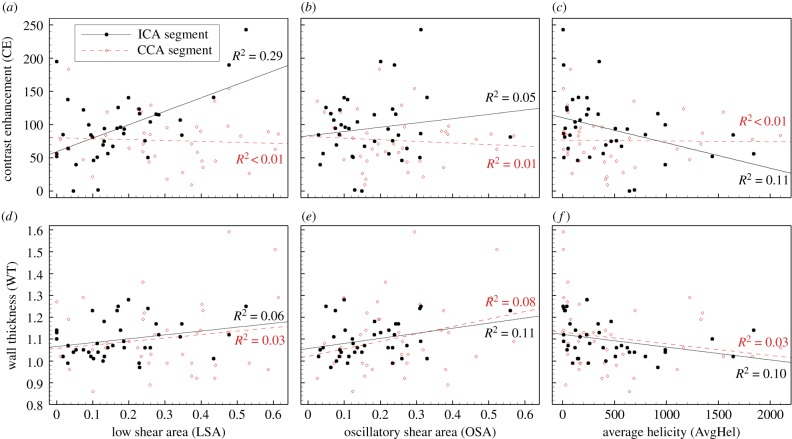
The segment-specific nature of these haemodynamic associations is further illustrated in figure 4, focusing on LSA, OSA and AvgHel (RTA was found to be highly correlated with LSA (r = 0.91, p < 1 × 10⁻¹⁶) and so was considered redundant). Associations between the segment-specific haemodynamic variables and their respective segmental CE were consistently (albeit not necessarily significantly) stronger for the ICA versus CCA segments, whereas, for (unadjusted) WT, associations appeared similar for the ICA versus CCA segments.

Figure 4.

Linear regressions illustrating segment-specific differences in haemodynamic associations with CE, but not wall thickness (unadjusted). CE versus LSA at the ICA was the only significant correlation among those shown, with p < 0.001.

Regarding purported geometric risk factors for atherosclerosis, table 4 also shows that neither CE nor WT was associated with bifurcation flare and CCA curvature. Per table 5, neither of these geometric variables was correlated with low or oscillatory shear, although flare was correlated with helicity (r = 0.489, p = 0.001). On the other hand, peak systolic flow rate was correlated with OSA (r = 0.575, p = 6 × 10⁻⁵), whereas inflow and heart rates were more weakly (and negatively) correlated with higher LSA (p < 0.05).

Table 5.

Bivariate correlation coefficients (r) for selected haemodynamic variables at the ICA segment versus geometric and flow variables. Bolded entries are statistically significant.

haemodynamic variable	flare	curvature	cycle average inflow rate	peak systolic inflow rate	heart rate
LSA	−0.162	0.176	−0.390*	−0.336*	−0.380*
OSA	−0.260	0.018	0.265	0.575‡	0.163
AvgHel	0.489†	0.008	0.011	−0.071	0.078

*p < 0.05; ^†p < 0.01; ^‡p < 0.001.

4. Discussion

Our study aimed to fill the gap between clinical imaging studies that have shown segment-specific associations between CV risk factors and early wall thickening, providing circumstantial evidence for a haemodynamic influence at the carotid bulb, and those that have shown direct haemodynamic associations with the presence of or changes in already-developed plaques. For the carotid bifurcation, the segment-specific approach takes advantage of the known propensity for carotid plaques to form at the ICA bulb, while the CCA, typically spared of plaques, serves as an intraindividual control.

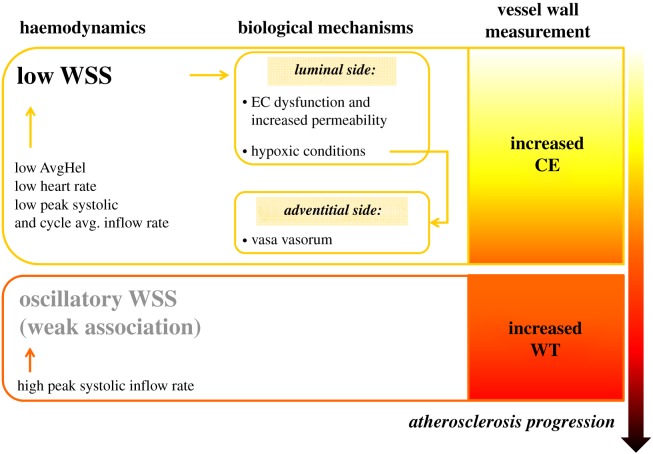
Thus, despite our relatively small sample size (owing to the complexity of the data acquisition and analysis, and need to avoid the confounding effects of inward remodelling), the segment-specific study design allowed us to reveal a strong and significant association between low WSS (i.e. LSA) and CE at the carotid bulb. On the other hand, our sample size may have been too small to confirm a possible association between oscillatory shear and bulb WT. Since endothelial dysfunction and the related processes leading to an increased contrast medium uptake precede wall thickening and frank atheroma formation [16,17], and we found no significant correlation between CE and WT, our findings suggest that low WSS is an earlier driver of atherosclerotic changes than oscillatory WSS. Below, in separate sections, we discuss how the present findings (i) impact the popular ‘low and oscillatory shear theory’ of atherogenesis; (ii) might explain (or, at least, be consistent with) the current understanding of mechanobiological mechanisms underlying atherogenesis; (iii) may square with the many haemodynamic variables that have been proposed over the years. Moreover, we discuss whether lumen geometry alone may still be considered a local risk marker for atherogenesis. A visual summary of the main findings is given in figure 5.

Figure 5.

Schematic of the main findings. The relative exposure to low WSS and oscillatory WSS appears to be associated with different facets of early atherosclerosis at the carotid artery. Low WSS is associated with increased contrast uptake at the carotid bulb, whereas oscillatory shear is (weakly) associated with increased bulb thickness. Low shear links and explains both mechanisms of increased CE (i.e. CE coming from luminal or adventitial side). Associations between low or oscillatory WSS with other haemodynamic and flow rate-related variables are also shown.

4.1. Low versus oscillatory wall shear stress in early atherosclerosis

As highlighted by Peiffer et al. [7], the current consensus on atheroprone WSS as ‘low and oscillatory’ derives from the early work by Ku et al. [3], which showed a correlation between oscillatory shear index (a then-novel marker of WSS directional changes) derived from an anthropomorphic carotid bifurcation flow model and measurements of focal intimal thickening from post-mortem human carotid arteries. As Peiffer et al. pointout, however, haemodynamic variables quantifying low and oscillatory WSS have since been applied at different stages in the disease process, and then extrapolated to studies of early atherosclerosis [7]. This extrapolation is crucial in light of the high sensitivity of WSS to variations of lumen geometry due to inward remodelling, potentially obscuring the relationship between low WSS and early atherosclerosis. For example, in a large community cohort, Bijari et al. [10] showed that carotid bifurcation flare (a proven surrogate marker of disturbed WSS) appeared, counterintuitively, to be predictive of bulb wall thinning, and only after excluding cases with inward remodelling (N.B., using the same WT criteria as the present study) was the expected association with wall thickening uncovered. We are therefore confident that our findings reflect, as much as possible in a clinical cohort study, the impact of haemodynamic factors on early atherosclerosis.

As also highlighted by Peiffer et al. [7], confusion arises also from the common conflation of the terms ‘low’ and ‘oscillatory’ shear, especially because the formula for OSI includes TAWSS in its denominator. Fluid mechanically, TAWSS implies a region of stagnant or sluggish flow, irrespective of its direction, whereas OSI indicates a dynamic recirculation region where the flow direction reverses during the cardiac cycle, resulting in oscillatory (but not necessarily low) TAWSS. We reasonably expected some correlation between TAWSS and OSI, as previously shown by Lee et al. [33] and more recently Gallo et al. [26], although those studies were based on the whole bifurcation versus the present segment-specific approach. In fact, for this study we found that LSA and OSA at the ICA segment were not correlated (r = 0.243, p = 0.126), which reinforces that low and oscillatory shear are distinct haemodynamic stimuli. This is consistent with animal studies suggesting distinct vascular responses to low versus low and oscillatory WSS [6,17], leading to different atherosclerotic lesion phenotypes and vulnerability [6], and a clinical study demonstrating a modulating effect of oscillatory WSS in atherosclerotic lesion progression in coronary arteries [15].

4.2. Biological mechanisms linking low wall shear stress to endothelial dysfunction

The presented association between LSA and CE at the carotid bulb is consistent with the idea of CE being an early marker of endothelial dysfunction caused by flow stagnation [18]. In fact, low WSS has been reported to increase EC permeability by increasing the presence of leaky junctions and EC apoptosis [34]. Moreover, Feng et al. [5] recently reported on the ability of low WSS to upregulate ECs hypoxia-inducible factor 1α, leading to enhanced glycolysis, excessive rates of EC proliferation and associated vascular leakiness and inflammation. Such WSS-mediated processes on ECs would tend to increase contrast agent uptake from the luminal side into the vessel wall.

The presence of adventitial vasa vasorum may also be postulated as a reason for increased CE. Such presence is expected in regions characterized by relative hypoxia and associated local oxidative stress and inflammation [35], conditions known to occur in correspondence with regions of flow stagnation and low WSS like the carotid bulb [36]. Computational and animal studies on carotid bifurcations have reported a decreased oxygen tension at the carotid bulb compared to CCA as a consequence of low WSS [36,37], proving that oxygen transport to the wall is regulated by the blood phase. Thus, the slowly recirculating flow at the LSA provides a fluid mechanical barrier to oxygen transport.

Although our study design does not allow us to separate the luminal versus adventitial source of augmented CE uptake, the present relation between LSA and increased CE ultimately suggests a connection between both mechanisms. In fact, high LSA implies a slow or stagnant flow, providing, concurrently: (i) the cue for inflammatory changes underlying EC permeability increase; and (ii) a fluid mechanical barrier to oxygen transport, exposing ECs and in general the vessel wall to hypoxic conditions, substantiating the presence of adventitial vasa vasorum [35]. This is corroborated by the above-noted experiments showing low shear-induced EC glycolysis [5], which plays an essential role in promoting vasa vasorum formation [38].

4.3. Making sense of the alphabet soup of haemodynamic parameters

Evidence underlining how ECs are exposed to a complex haemodynamic milieu that can be only partially described by ‘low and oscillatory’ WSS has stimulated a proliferation of haemodynamic parameters to incorporate the description of WSS ‘multidirectionality’ [27] and intravascular flow features [24]. By testing directly associations with early atherosclerosis for a number of these recently proposed parameters, our study represents the most comprehensive to date of haemodynamic associations with early atherosclerotic changes in humans.

Unlike previous observations in rabbit aortic branch ostia [27] or murine carotid artery [39], here transWSS was not associated with any of our measured wall variables. This can be presumably ascribed to the peculiar local haemodynamics at the human carotid bulb, where, as previously observed [26], highest transWSS concentrates at uncommon locations for atherosclerosis, i.e. the bifurcation apex. Similarly, while Martorell et al. [29] previously showed that atherosclerotic and thrombotic biological markers like oxidized LDL uptake and monocyte adhesion were positively correlated with various haemodynamic parameters quantifying the volume of recirculating flow, VolRec among them, in the present study VolRec was not associated with either WT or CE. This may be due to its inclusion of intravascular slow flow (see inset of figure 3c), whereas LSA is specific to the wall. Indeed, at the ICA segment, VolRec was not significantly correlated with LSA, although it was with OSA (r = 0.402, p = 0.009). This gives a mixed message about the specificity of intravascular volume of recirculation as an easier-to-measure surrogate of disturbed WSS.

Conversely, intravascular helicity intensity (i.e. AvgHel) was found to be inversely associated with CE at the carotid bulb, recapitulating the known beneficial influence of helical flow in suppressing flow disturbances [25], and supporting its use as an in vivo imaging marker [40]. Indeed, a significant negative correlation was found between AvgHel and LSA at the ICA (r = −0.429, p = 0.005), explaining the significant association of both LSA and AvgHel with CE at the ICA segment. Since helical flow at the bifurcation is promoted by curvature of the CCA [25], the present results also reinforce the need for computational and physical model studies to reconstruct a sufficient length of CCA in order to accurately determine bifurcation haemodynamics.

4.4. Whither geometric risk of atherosclerosis

The notion that an individual's artery geometry might connote some risk of developing atherosclerosis dates back at least to the early 1980s [32]. Such ‘geometric risk’ markers have been proposed considering specific geometric attributes of the carotid bifurcation, by virtue of their influence on local flow patterns [31]. However, because lumen geometry is, ultimately, just a surrogate for the local haemodynamics, Bijari et al. [10] found only a weak association between geometry and WT despite a sample of nearly 300 cases, and conceded that it might mask a stronger relationship between haemodynamics versus WT. This is consistent with the present study, which found stronger, albeit not significant, associations between WT and haemodynamic variables, but not between WT and geometric variables. An obvious explanation is our smaller sample size, nearly an order of magnitude lower than Bijari et al.'s.

We also did not find any significant correlation between WSS and geometric variables as Bijari et al. had reported [31]; however, their study was based on models with truncated CCA inlets, and all with the same flow waveform, whereas other studies have shown an influence of both inlet length and subject-specific flow rates on carotid bifurcation haemodynamics [25,41]. As further evidence of the latter, we found a strong positive correlation between OSA and peak systolic inflow rates. Physically, this reflects that higher peak systolic flows are inevitably followed by steeper post-systolic deceleration, which precipitates flow separation, enhanced recirculation and WSS oscillations. In addition, LSA negatively correlated with both heart rate and cycle-averaged flow rate, the former because slower heart rate implies elongation of the late diastolic phase, when flow velocities are low and sluggish flow is typically observed, and the latter because lower average inflow rate implies lower inflow TAWSS to begin with. A significant positive correlation found between flare and ICA helicity intensity seems contradictory given their nominal roles in suppressing and promoting flow disturbances, respectively; however, it is consistent with the fluid mechanics of flow separation at an expansion (i.e. flare), which is known to promote flow helicity [30].

Taken together, these findings emphasize the need to include subject-specific flow data in computational and experimental studies of carotid bifurcation haemodynamics, and serve as a reminder that the relationship between geometry and haemodynamics is difficult to encapsulate in simple geometric variables alone. Under conditions where local haemodynamics are difficult to measure and surrogate markers are sought, our findings would suggest equal attention be given to geometry and flow variables.

4.5. Limitations

Several potential limitations may have affected the present study. The strict exclusion criteria limited the sample size available, which, as we noted, may have impacted the significance of haemodynamic associations with WT. This was not unexpected: in their study of segment-specific CV risk factors for more than 3000 individuals, Polak et al. [8] reported associations of IMT with conventional CV risk factors with total model R² values of 0.27 for the CCA and 0.11 for the carotid bulb, a difference that was attributed to local haemodynamic factors and presumably provides a bound to the influence of haemodynamic versus conventional CV risk factors. Moreover, regarding the strongly significant association between CE versus LSA at the ICA, leverage analysis [42], suggested by visual inspection of figure 4a, revealed that the three rightmost points had high leverage, and that removing the two highest-leverage points resulted in a loss of significance. Such leverage dependence may also point to a relationship between LSA and CE that is not a simple linear one, but rather one in which CE is only triggered above a certain LSA threshold (e.g. LSA ≈ 0.3 per figure 4a). In either case, further adequately powered investigations are warranted to elucidate the nature of the relationship between LSA and CE. On the other hand, significance of the (weaker) association between AvgHel and CE at the ICA was preserved even after removal of points identified as high-leverage (three rightmost points, figure 4c).

At current resolutions, MRI is unable to discriminate the three vessel layers [43], and so our WT wall variable was only a surrogate for intimal thickening. Similarly, our CE wall variable was a surrogate for endothelial dysfunction, albeit a biologically plausible one, as previously outlined. This is also supported by recent reports in coronary artery segments that showed CFD-derived low WSS was independently associated with epicardial and microvascular endothelial dysfunction after acetylcholine infusion [44].

Slow blood flow near the wall could in principle cause artefactual WT or CE in regions of lowest WSS, i.e. at the ICA. We, therefore, took extreme care to minimize this by adjusting inner wall contours using information from both pre- and post-contrast BB-MRI, and from multi-planar reconstructions of the CE-MRA source images. Such artefacts would have had the effect of overestimating WT, thus reducing bulb diameter and hence bifurcation flare, which in turn would lead to higher WSS (i.e. lower LSA values). Thus, if these artefacts were present we would have expected to find negative correlations between WT and LSA, which was not the case here.

As a result of this intensive analysis, our measurements of WT and CE were based on individual axial slices through the CCA and the ICA, and thus no information about the longitudinal extent of the region subject to early wall thickening or its maximum thickness was available. In their segment-specific study of carotid WT, Watase et al. [11] measured WT over five slices at each segment, and reported maximum WT at the CCA and ICA of 1.1 ± 0.2 mm (mean ± s.d. in 557 arteries) and 1.1 ± 0.4 mm (899 arteries), respectively. These values and their relative standard deviations compare favourably with our measurements of maximum WT (CCA: 1.10 ± 0.16 mm, ICA: 1.10 ± 0.08 mm), thus we consider them representative of the respective segments. Also like that study, we did not perform any p-value adjustments (e.g. Bonferroni correction) for multiple tests, thus associations with p-values close to 0.05 should be considered exploratory and hypothesis generating, and need to be confirmed in subsequent studies.

We used an objective, automated approach to split the bifurcation into ICA and CCA segments [28]; however, as figure 3 shows, there could be overlap in the extension of disturbed WSS from ICA to CCA. Indeed, between these segments there were significant correlations for LSA (r = 0.516, p = 0.001), OSA (r = 0.367, p = 0.018) and AvgHel (r = 0.779, p = 2 × 10⁻⁹). Similarly, WTs at the ICA and CCA segments were strongly correlated (r = 0.535, p = 5 × 10⁻⁴), as was CE, albeit more weakly (r = 0.360, p = 0.027). Such ‘cross-talk’ may have impaired the segment-specific associations for WT; however, as figure 4 showed, segmental associations for CE were clearly evident.

In order to quantify the haemodynamics of each carotid bifurcation, we ultimately had to reduce a complex, 3D, time-varying WSS field to single numbers, albeit as objectively as possible. Encouragingly, the objective threshold for low WSS ended up being 0.455 Pa, which is remarkably close to the commonly accepted low WSS threshold of 0.4 Pa [2]. More generally, image-based CFD suffers from uncertainties and assumptions (e.g. Newtonian viscosity, rigid walls, as discussed elsewhere [45]), which might influence the relationships described in the present study. Nonetheless, the only alternative, i.e. direct measurement of the velocity field and WSS from in vivo imaging (e.g. PC-MRI) is similarly affected by several limitations and inaccuracies [46].

Finally, like most human studies of haemodynamics and early atherosclerosis, our conclusions are drawn from cross-sectional data. Prospective validations are therefore warranted and encouraged.

5. Conclusion

Different facets of early atherosclerosis at the carotid bifurcation appear to be associated with low versus oscillatory WSS. From the present results, low WSS is strongly associated with CE, a marker of endothelial dysfunction, while oscillatory WSS is more weakly associated with wall thickening. Owing to its causative role in determining WSS, helical flow intensity may serve as a convenient and pragmatic surrogate intravascular flow marker of contrast medium uptake and low WSS.

Our study thus confirms what large carotid MRI studies have only been able to infer: that haemodynamic variables, or their geometric and flow rate surrogates, represent independent risk factors to potentially augment systemic CV risk factors for identifying individuals at greater susceptibility for atherosclerosis at the carotid bulb. Nevertheless, their incremental value, clinical utility and cost-effectiveness as risk markers for atherosclerosis remain to be determined [47].

Data accessibility

Haemodynamic, geometric, imaging markers and cardiovascular risk factor data for each subject of the study are provided as the electronic supplementary material in the form of file ‘data.xlsx'

Authors' contributions

D.G., P.B.B., U.M., E.G.L., B.A.W. and D.A.S., conception and design of the study; Y.Q., Y.J.X., M.E. and B.A.W., acquisition and analysis of in vivo data; D.G., P.B.B., U.M., D.H., B.A.W. and D.A.S., simulation analysis and interpretation of data; D.G., P.B.B., U.M., B.A.W. and D.A.S., drafting of the manuscript. All authors revised the manuscript critically for important intellectual content, and provided final approval for publication.

Competing interests

The authors have no competing interests.

Funding

The VALIDATE study is supported by contract no. NO1-AG-3-1003 from the National Institute on Aging, NIA and, in part, by the Intramural Research Program of the NIA. D.A.S. was supported by a Mid-Career Investigator Award from the Heart and Stroke Foundation. D.G. was supported by the Joint Project for the Internationalization of Research 2014 from Compagnia di San Paolo and Politecnico di Torino.