A topographic mechanism for arcing of dryland vegetation bands

Abstract

Banded patterns consisting of alternating bare soil and dense vegetation have been observed in water-limited ecosystems across the globe, often appearing along gently sloped terrain with the stripes aligned transverse to the elevation gradient. In many cases, these vegetation bands are arced, with field observations suggesting a link between the orientation of arcing relative to the grade and the curvature of the underlying terrain. We modify the water transport in the Klausmeier model of water–biomass interactions, originally posed on a uniform hillslope, to qualitatively capture the influence of terrain curvature on the vegetation patterns. Numerical simulations of this modified model indicate that the vegetation bands arc convex-downslope when growing on top of a ridge, and convex-upslope when growing in a valley. This behaviour is consistent with observations from remote sensing data that we present here. Model simulations show further that whether bands grow on ridges, valleys or both depends on the precipitation level. A survey of three banded vegetation sites, each with a different aridity level, indicates qualitatively similar behaviour.

1. Introduction

Self-organization of vegetation into community-scale spatial patterns has been observed in the drylands of five continents [1,2]. These distinctive patterns occur on a large spatial scale and may be monitored via satellite, so there has been growing interest in determining whether they hold information on the health of these ecosystems, or even provide an early warning sign of ecosystem collapse in response to desertification [3,4]. Given that only a handful of pattern characteristics can be reliably measured remotely, a more detailed understanding of the mechanisms that control these characteristics may help assess the potential for such ecosystem health predictions. Our modelling efforts, aimed at capturing the observed arcing-direction of vegetation bands relative to the direction of the mean elevation gradient, suggest the placement of vegetation patterns on the terrain as a potential indicator for aridity stress. Higher levels of precipitation are required to support vegetation bands on the ridgelines than in the valleylines in the model, suggesting that vegetation bands confined to lower elevation channels may be the most vulnerable to collapse under increased aridity stress.

Measured along the direction of the prevailing elevation gradient, a typical band pattern consists of patches of vegetation on the scale of tens of metres (i.e. band width), alternating with stretches of barren ground on the scale of tens to hundreds of metres, with this motif often repeating over a region of more than 10 km in length (note scale bars in figure 1). Banded patterns undergo ecological dynamics, notably colonizing areas upslope to the bands during periods of plentiful rainfall, and retreating from downslope areas during periods of scarcity, resulting in a slow uphill migration of the bands over time [7]. Measurements indicate that it would take almost a century for a vegetation band to travel its approximate 30 m width [7,8], while the earliest observations, from aerial photography, provide less than an 80-year window for tracking the pattern dynamics predicted by models. Consequently, any proposal for using remote sensing data to validate and improve upon model predictions of dynamics is fraught with challenges.

Figure 1.

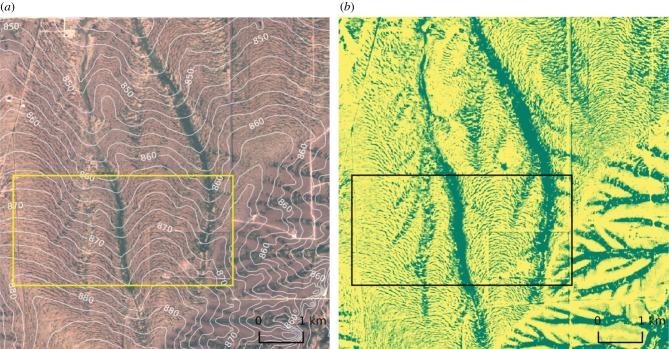
Aerial photographs of vegetation patterns found in the Horn of Africa alongside (a) a schematic adapted from [5] showing typical orientation relative the topography. The vegetation bands are aligned transverse to the slope and arc convex-upslope. The banded patterns in image (b), adapted from [5], appear within topographic depressions and the darker unpatterned regions of image (c), adapted from [6], are reported to be slightly elevated relative to the vegetation arcs. Arrows in (a) and (b) indicate downhill direction.

In the absence of temporal data over an appropriate timescale, there has been a focus in some modelling efforts on predicting the dependence of spacing between vegetation bands as a function of climate characteristics such as mean annual precipitation or aridity, or trends with the elevation grades. This, however, has proven a difficult test for validating models due to the predicted multistability of patterned states, and a lack of marked trends in observational data [9,10].

One potentially fruitful direction for modelling efforts is to broaden predictions to underused measurable spatial features of the patterns, such as the width and length of the bands (rather than only their spacing), and the curvature of the bands. Such pattern characteristics may vary across a given site in response to locally varying exogenous factors such as topography, soil type, and grazing or human pressure. Studying the response of the vegetation patterns to local changes in environmental conditions at a given site with uniform climate characteristics provides additional information about the system. The observed spatial variation may then be exploited to test and constrain models, rather than being treated as noise to be averaged over. Critical to such an effort is to have spatial information about the exogenous factor(s). The work in this manuscript is based on spatial variability associated with large-scale topographic heterogeneity, which we study via digital elevation data sampled globally at a scale appropriate for pattern variation, e.g. approximately 30 m [11].

The leading-order effect of topographic heterogeneity on vegetation pattern formation is associated with the prevailing elevation gradient. This plays an essential role in the formation and morphology of dryland vegetation patterns. A grade as small as approximately 0.2% introduces anisotropy in the overland waterflow, thus favouring ordered banded patterns over isotropic ‘flat terrain patterns’ [12,13]. Vegetation bands, such as those of figure 1, alternate rhythmically with stripes of bare soil, and are oriented perpendicular to the prevailing elevation grade. The earliest reported observations of vegetation bands, taken in the Horn of Africa, note the importance of even slight variation of the elevation grade in shaping banded vegetation patterns. The first such report, by MacFadyen in 1950 [5], points out that vegetation bands appear within modest topographic depressions or ‘valleys’ aligned along the grade and are arced convex-upslope (figure 1a). The subsequent 1957 observations reported by Greenwood [6], provide additional examples, including one where the bands exhibit a general convex-downslope pattern on a ‘ridge’ between valley lines. The bands were even conjectured by Boaler and Hodge in 1964 to approximate elevation contours [14].

The arcuation of vegetation bands has remained largely unexplored in the modelling literature beyond the original efforts of Lefever & Lejeune [15,16]. Simulations of their model, posed for a uniformly sloped terrain, show an ordered rectangular array of convex-upslope arced band segments. In this case, the arcing is associated with spontaneous break-up of a stripe pattern into a regular configuration of segments of the stripes that form the arcs, a possible deformation of the flat terrain gap or spot patterns. A similar phenomenon of spontaneous break-up and arcing of the vegetation stripes was also reported for the generalized Klausmeier model on a uniform slope [17], in this case due to secondary modulational instabilities of stripes that occur as the precipitation parameter of the model decreases. None of these modelling studies report observations of vegetation segments that are arced convex-downslope, nor do they investigate the type of topographic confinement of the patterns illustrated in figure 1b.

In this manuscript, we present a mechanism for arcing motivated by early observations of topographic influence on the shape of banded vegetation patterns and recent work highlighting the potential connection to surface water flow (S Iams, C Topaz 2017, personal communication). We employ a modelling framework within the class of reaction–advection–diffusion models that describes nonlinear interactions between continuous biomass and water fields, as well as advective water transport and diffusive biomass dispersal [18]. Our investigations are based on the simplest and earliest model of this type, one proposed by Klausemeier [19] for striped patterns on a uniform hillslope. We generalize the water transport term in the model, denoted T(W) below, to take into account possible positive and negative terrain curvature associated with valleys and ridges. We investigate the non-dimensional form of the model, given by

1.1

and

1.2

where W(x, y, t) is the water field and B(x, y, t) is the biomass field. Here the parameter a represents water input to the system in terms of the mean annual precipitation, and m parametrizes the plant mortality rate. Water loss due to evaporation, in the dimensionless form of the equations, is captured by the −W term and transpiration by the nonlinear −WB² term, which accounts for the biomass growth term +WB². The nonlinear dependence of transpiration on biomass heuristically captures a positive infiltration feedback between the biomass and the water. In Klausmeier's formulation, the water transport is uniformly advected downhill

1.3

This term is essential for the existence of a family of stable travelling stripe patterns that migrate uphill [20,21].

We consider a topographic extension of the Klausmeier water transport term, which is based on an assumption that water flow is proportional to the local elevation gradient. In dimensionless form, it is given by

1.4

where z = ζ(x, y) is the elevation function. See table 1 for comparison of this topographic extension to other water transport models. We use a terrain with simple channel-like geometry

1.5

to explore the influence that the resulting modified water transport has on the predicted vegetation patterns. This idealized terrain consists of alternating ridge lines (k₀y = 2πn) and valley lines (k₀y = π + 2πn) aligned along a hillslope. This idealized elevation profile allows us to investigate how cross-slope terrain curvature, controlled by the parameter σ, influences the vegetation patterns that form on ridges and in valleys.

Table 1.

A summary of water transport models with references and equation numbers where appropriate. Here W represents the water field in the Klausmeier modelling framework (equation (1.1)), v characterizes the downhill waterflow rate on a uniform slope, γ ≥ 1 allows for possibly nonlinear diffusion with rate d [22], H represents surface water height of the Gilad model [23] and ζ represents the elevation. See electronic supplementary material for a detailed discussion of the advection-only extension.

water transport model	expression	equation	reference
original Klausmeier	TKvx(W) = vWx	(1.3)	[19]
(diffusion) generalized	TDvx(W) = d∇2(Wγ) + vWx	—	[22]
advection-only extension	TAζ(W) = ∇ζ · ∇W	—	—
topographic extension	Tζ(W) = ∇ · (W∇ζ)	(1.4)	—
	= ∇ζ · ∇W + W∇2ζ	(3.1)	—
Gilad	TGζ(H) = ∇ · (H∇(ζ + H))	—	[23]
	= ∇ · (H∇ζ) + ∇2(H2/2)	—

More mechanistically detailed models than Klausmeier's, such as the Rietkerk model [24] and Gilad model [23], differentiate water into soil and surface components. This allows an infiltration feedback, a mechanism relevant for vegetation pattern formation in many environments, to be modelled explicitly. The Gilad model [23,25] has also been formulated with a general topography for the surface water advection. It assumes an advective velocity in the transport term that is proportional to ∇(ζ + H), where H is the surface water height above the terrain. Other model studies have additionally sought to capture the influence of vegetation patterns in the formation of terracing of the underlying terrain along the hillslope through a coupling with erosion and soil transport dynamics [26]. The influence of topographic variation at the scale of individual plants has also been investigated in connection to the transition from banded vegetation patterns to vegetation following irregular drainage patterns [27].

Our investigation, based on our topographically extended version of the Klausmeier model, provides insight into the possible impact of pattern-scale (approx. 100 m–1 km) spatial heterogeneity in topography on the shape of bands, and their occurrence relative to the landscape. In particular, the model lends a simple interpretation to the impact of terrain curvature as increasing (for ridgelines) or decreasing (for valleylines) water loss rate. The following prediction then emerges: as aridity increases, the vegetation bands switch from occurring on ridgelines, convex-downslope, to being confined to valleylines, convex-upslope.

This manuscript is structured as follows. In §2, we report the empirical relationship between arcing-direction of vegetation bands and the sign of the underlying terrain curvature for five sites in Western Australia, finding that convex-upslope arcs tend to occur within valleys, and convex-downslope arcs occur atop ridges. In §3, we investigate the influence of the proposed modification of the transport T(W), equation (1.4), in the Klausmeier model for the idealized terrain given by equation (1.5). We find that the topographically extended Klausmeier model qualitatively captures key topography-dependent features such as the curvature of the arced patterns, in a manner consistent with our reported observations. Moreover, it provides a way to characterize how terrain curvature impacts the location of vegetation patterns relative to both aridity and topographic features such as high versus low ground in a gently rolling landscape. Finally in §4, we discuss how these predictions are borne out for sites on three different continents where patterns are observed. Additional details about simulations for the topographically extended Klausmeier model along with results based on a simplified version of the Gilad model with idealized terrain (1.5) appear in the electronic supplementary material.

2. Topographic influence on vegetation arcing in Australia

We investigate the relationship between vegetation band arcing and terrain curvature in the Western Creek basin (figure 2) southwest of Newman, WA, Australia (−23.5° N, 119.5° E), where vegetation bands have been previously reported [27]. A visual inspection of the area yielded 21 spatially distinct sites featuring vegetation banding. Of these we selected the five with the most well-defined vegetation bands (figure 2), ranging in area from 5 to 16 km².

Figure 2.

Five sites displaying banded vegetation patterns in the Western Creek Basin southwest of Newman, Australia (−23.5° N, 119.5° E), alongside a map indicating the relative location of each site. The Sentinel-2A images [28] were taken near the end of the Australian wet season, see scale bars for relative sizes. Map derived from image available via Wikimedia Commons. (Online version in colour.)

We use two sets of remote sensing data in our analysis: Sentinel-2A multi-band satellite imagery [28] with 10 m resolution, and a smoothed digital elevation model (DEM) provided by Geoscience Australia [29] with one arc-second (approx. 30 m) resolution. Selected Sentinel images were taken on 5 March 2017, near the end of the Australian wet season and the topographic data were derived from the Shuttle Radar Topography Mission elevation dataset [11].

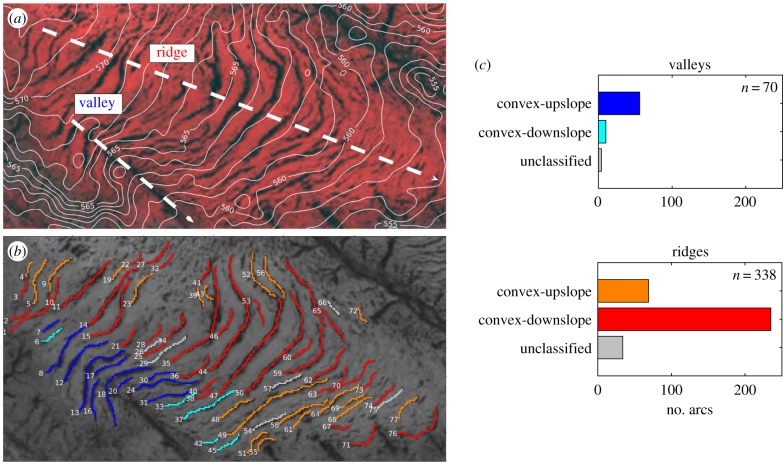
At each site, we identify topographic ridge and valley lines by visual inspection of the elevation contour map (figure 3a). We then manually mark each identifiable vegetation band in a satellite image of the given site and record whether the band occurs in a valley or on a ridge (figure 3b). In instances where bands cross multiple ridge or valley regions, we divide the band into sections that are each restricted to a single valley or ridge. We find that 82% of the 408 bands identified across the five sites appear on ridges. For vegetation bands with a visually identifiable direction of curvature (91% of bands), we further classify them as arcing in the convex-upslope or convex-downslope directions (figure 3b,c). We identify 80% of the bands within valleys as convex-upslope and 70% of the bands on ridges as convex-downslope.

Figure 3.

(a) An example site with elevation contours (solid white) and manually identified ridge/valley lines (dashed white, with arrows indicating the downhill direction). (b) The manually identified arcs are coloured by the classification: convex-upslope in valley (blue), convex-downslope in valley (cyan), convex-upslope on ridge (orange) and convex-downslope on ridge (red). (c) Bar chart of the 408 vegetation arcs from the five sites of figure 2 that have been manually identified and classified as appearing in either a valley or on a ridge and as convex-upslope or convex-downslope. (Online version in colour.)

This evidence supports the observational claim that the direction of arcing of the vegetation bands correlates with the sign of curvature of the underlying terrain [5,6,14]. We note that our analysis does not discern a curvature direction for 9% of the bands, and topographic features that appear on length scales of a few hundred metres or less (e.g. the small scale ridges and valleys at the bottom of figure 3a,b) were neglected. This may account for some of the inconsistencies between the data and observational claims.

3. Modelling the influence of topography

The majority of vegetation bands at the Australian sites (figure 2) appear on ridges and the bands in the Horn of Africa (figure 1) tend to appear in valleys. Observations across both sites suggest a consistent trend that vegetation bands arc convex-upslope in valleys and convex-downslope on ridges. In this section, we show, using the modelling framework proposed by Klausmeier as a template, that this topographic influence can be captured via water transport. In particular, we motivate and explore a topographically extended Klausmeier model consisting of equations (1.1) and (1.2) with water transport T_ζ(W) given by equation (1.4) on the idealized terrain with elevation ζ given by equation (1.5). We also extract predictions from this model about how the location of patterns for a given terrain, e.g. whether patterns are predominantly on ridges or valleys, may depend on the level of aridity.

The topographically extended model reduces to the original Klausmeier model on uniformly sloped terrain or the original Klausmeier model with a modified linear water loss rate on uniformly curved terrain. We can express equation (1.4) as

3.1

and note that the first term on the right-hand side represents advection downhill with rate proportional to the local slope and the second term represents accumulation of water if the terrain curvature is positive and diversion of water if the curvature is negative. In the case that ∇²ζ is constant, this uniform curvature term adds a term proportional to W into equation (1.1). In §3.3, we exploit this observation in our analysis to predict when patterns might be expected to form on ridges versus valleys within the model.

3.1. A model topography

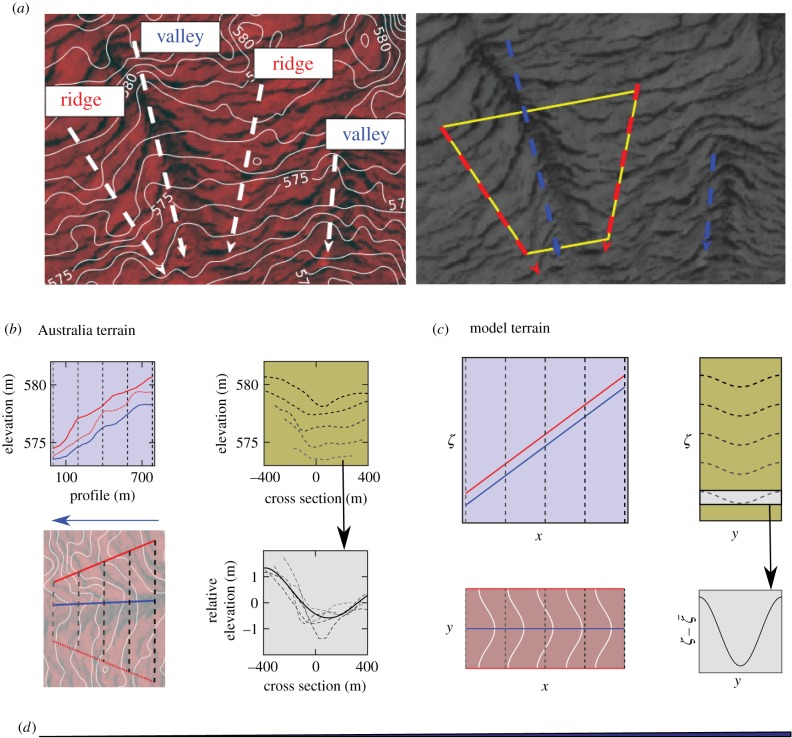
Figure 4a shows an example of banded vegetation patterns organized around modestly curved topographic ‘valleys’ and ‘ridges’ aligned along the slope at the Australian site in figure 2b. Figure 4b provides detailed topographic information about the trapezoid region marked in figure 4a. The valley line follows an approximate 0.6% average grade downhill, and a fourth-order polynomial fit of elevation relative to the mean for five equally spaced cross sections show the typical cross sectional ridge-valley elevation difference is on the order of 1 m, while the distance between the ridge lines is more than 300 m.

Figure 4.

(a) The left image shows elevation contours (solid white) on a section of the patterned site in figure 2d. A few approximate ridge and valley lines (white dashed) are shown with arrows pointing downhill. The yellow trapezoid in the right greyscale image indicates a typical topographic structure consisting of a valley aligned along the grade surrounded by two ridges. (b) Elevation contours for the trapezoid region in (a) are shown together with their profiles along the grade (above) and along cross sections transverse to the grade (right). A fourth-order polynomial fit (solid black) is shown for the elevation relative to the mean of the cross sections (dotted grey). Note that the profile distance is taken to be distance along the valley line and the associated ridge elevations are found by orthogonal projection. (c) Model topography given by equation (1.5) with v = 10, σ = 5, L_x = 100 and L_y = 50. Elevation contours along with cross sections show the height of ridge (red) and valley (blue) relative to the change in elevation that results from uniform slope along x. Note that the scale for elevation in (a) and (b) is greatly exaggerated relative to the x- and y-dimensions. (d) For reference, the triangle at the bottom is drawn to scale with a 0.6% grade corresponding to the mean of the example shown in (b). (Online version in colour.)

As a simple approximation of this characteristic topographic variation, we consider the idealized topography given by equation (1.5) and depicted in figure 4c, consisting of a periodic array of valleys and ridges aligned along the x-axis with uphill in the positive x-direction. In our model simulations, we fix the dimensionless slope parameter to v = 10, similar to the value in [8]. Based on mesh size considerations, we choose k₀ = 2π/L_y with L_y = 50. The parameter σ, which we refer to as the channel ‘aspect’, controls the cross-slope elevation difference between the ridge and valley lines. We consider channel aspect 0 ≤ σ ≤ 6; the average slope transverse to a channel from a valley to a ridge is smaller, but of the same order of magnitude, as the slope along the x-direction, consistent with figure 4b. The upper bound on the channel aspect parameter σ is restricted by our choice of water transport, equation (1.4), and terrain parameters. For σ > 1/vk²₀ ≈ 6.33, the effective water loss rate in equation (1.1) along the valley line y = L_y/2 will be negative, causing a global and potentially unphysical change in the solution structure of the model.

3.2. Simulation results

We use the idealized terrain given by equation (1.5), fix the plant mortality to m = 0.45 [19], and explore the influence of precipitation a and channel aspect σ on patterns within the topographically extended Klausmeier model. Time simulations were carried out using a fourth-order exponential time differencing scheme [30,31]. More details and additional numerical results appear in an electronic supplementary material.

For uniformly sloped terrain, the water transport is the same as Klausmeier's (i.e. T_ζ(W) = T^K_vx(W)), and there exists a uniformly vegetated state, with 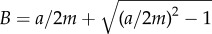, which is stable provided the precipitation level a is sufficiently high. If precipitation drops below a threshold a = a_T, the uniform state loses stability due to a bifurcation that produces a periodic travelling wave pattern consisting of straight vegetation bands transverse to the slope that are migrating slowly uphill [20]. A lower threshold a = a_O marks the smallest precipitation level that can support just a single isolated band of vegetation on the domain, the so-called ‘oasis state’ [22]. Within the range a_O < a < a_T, there exists a multiplicity of stable travelling patterns consisting of periodically spaced bands, each with different periods, and possibly different orientations relative to the grade [17]. When there is too little precipitation, i.e. a < a_O, only the bare soil or ‘desert state’ exists.

For small channel aspect, e.g. σ = 0.5 as in figure 5, numerical simulation indicates that travelling band patterns persist and develop a transverse modulation such that the arcing-direction of the vegetation bands matches the direction of curvature of elevation contours. We note that, while their signs of curvature match, the vegetation bands do not closely follow the elevation contours. Moreover, numerical experiments described in the electronic supplementary material show that turning off the accumulation term (∇²ζ)W of T_ζ(W) in equation (3.1) causes the arced bands to straighten out into the banded patterns of the original Klausmeier model. Hence the advective term alone does not account for the curvature of the bands in our simulations.

Figure 5.

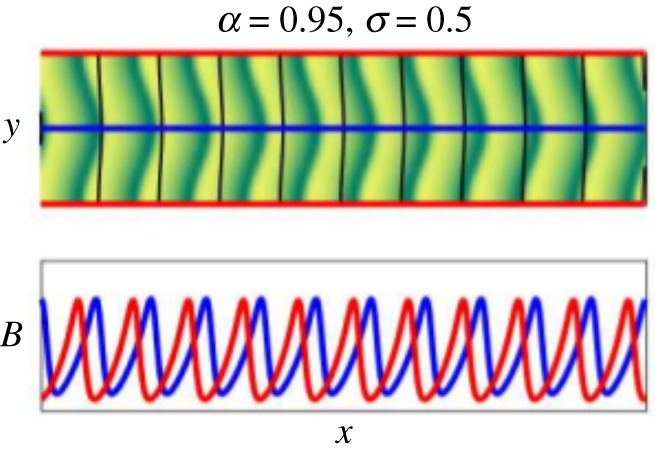
Upper frame shows biomass field on the full two-dimensional domain at t = 1000 with the modestly curved elevation contours (black) superimposed. Green (yellow) on the colour scale represents high (low) biomass values. While the vegetation bands are more significantly arced than the elevation contours, the direction of curvature consistently matches across the domain for both. The lower frame shows one-dimensional profiles of the biomass along ridge (red) and valley (blue) lines. Periodic domain: L_x = 200, L_y = 50. Parameters: a = 0.95, m = 0.45, v = 10, k₀ = 2π/L_y. (Online version in colour.)

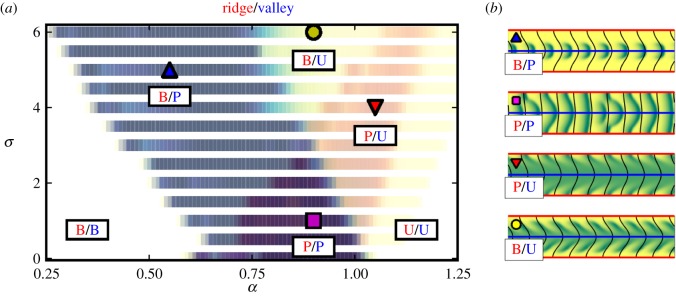
The bottom panel of figure 5 shows little difference between the pattern characteristics on the ridgeline and those along the valleyline. However, for deeper channels (associated with larger channel aspect σ) we find that the pattern characteristics may differ significantly between ridges and valleys, with the further possibility that patterns may end up confined to some part of the terrain. Figure 6 summarizes the various types of patterns in the (a, σ) parameter plane, classified by their ridge/valley states, as either bare soil (B), patterned (P) or uniform vegetation (U).

Figure 6.

(a) Maximum amplitude of patterns on ridges and valleys in (a, σ)-plane when precipitation a is decreased and then increased for fixed channel aspect σ. Yellow indicates small amplitude while red (blue) indicates large amplitude on ridge (valley) and purple indicates large amplitude on ridge and in valley. Each region is labelled by ridge/valley state as bare soil (B), patterned (P) or uniformly vegetated (U). (b) Biomass from simulations initialized with uniform vegetation and parameters associated with the labelled points the (a, σ)-plane are shown for t = 1000. Parameters: m = 0.45, v = 10, k₀ = 2π/50. (Online version in colour.)

Figure 6a shows the maximum ridge (valley) pattern amplitudes obtained from simulations by red (blue) intensity at each point in the (a, σ)-plane. Purple indicates where patterns appear on both ridges and valleys, while yellow indicates where no significant pattern amplitudes appear on either ridges or valleys. The visualization of the simulation data in figure 6a does not distinguish between uniform vegetation cover and bare soil, so we additionally label each region of the parameter space based on the ridge/valley states (e.g. B/P indicates bare ridge and patterned valley). Figure 6b provides example biomass profiles with ridge (valley) lines along which pattern amplitudes are computed marked in red (blue). Additional details about the simulations used to generate figure 6 are provided in the electronic supplementary material.

Considering the effects of water redistribution in directions transverse to the slope can provide some insight into the emergence of the various types of patterns shown in figure 6. We highlight the following observations:

• —For low water availability (e.g. blue up triangle) arced vegetation segments are confined to valleys (B/P). The topography diverts water away from the ridges which remain bare, even though the precipitation level would be sufficient to sustain stripe patterns on a uniformly sloped domain. Simulations also show that these confined patterns persist to lower precipitation levels than would be possible on uniformly sloped terrain.
• —For larger precipitation values (e.g. purple square), some of the arcs may connect across the ridges to form continuous bands (P/P). This occurs for precipitation values where patterns would appear on uniformly sloped terrain. It also requires shallow topographic variation transverse to the grade, so that the water redistribution is insufficient to cause bare soil on ridges or uniform vegetation cover in valleys.
• —At higher precipitation levels (e.g. red down triangle), patterns consist of uniform vegetation cover in valleys and arced gaps on ridges (P/U). In this case, water is diverted away from the ridges, allowing the pattern to persist even when the precipitation is high enough to sustain a uniform vegetation on uniformly sloped terrain.
• —If the aspect σ is large enough (e.g. yellow circle), water diversion and accumulation will result in uniform vegetation in valleys and bare soil on ridges. We find in this case that the chevron-like patterns are confined to the intermediate topographic zone between the uniformly vegetated valleys and the bare ridges.

3.3. Terrain curvature as an effective change in water loss rate

In the topographically extended Klausmeier model, the terrain acts to divert water from ridges to valleys, effectively altering local rates of water loss and accumulation. Focusing analysis on ridge and valley lines allows us to use this interpretation to make predictions about the transitions between the various vegetation states of the two-dimensional, spatially inhomogeneous model based on two spatially homogeneous one-dimensional models with different water loss rates (figure 6). Specifically, we consider a one-dimensional model applicable to ridge and valley lines of the form

3.2

and

3.3

where the parameter r characterizes an effective water loss rate and it differs between the ridges and the valleys. Using the idealized topography given by equation (1.5), the water equation, equation (1.1), along a ridge or valley line reduces to equation (3.2) with effective water loss rate given by

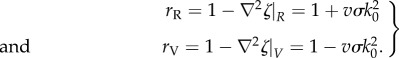3.4

On ridges the effective water loss rate r_R is increased by the fact that water is diverted away, and in valleys the effective water loss rate r_V is decreased by the accumulation of water. Neglecting the B_yy term in the biomass equation, equation (1.2), the patterns along ridge and valley lines can each be described by the system of one-dimensional PDEs (3.2) and (3.3) that correspond to Klausmeier's original model with an effective water loss rate r. As with the two-dimensional version of the model, we restrict our parameters to ensure that the effective water loss rate always remains positive: σ ≤ 1/vk²₀.

In the context of this one-dimensional approximation, the uniform state loses stability in a so-called Turing–Hopf (TH) bifurcation at a_T, leading to the onset of pattern formation. Weakly nonlinear analysis shows that the periodic travelling wave solution branch emanating from TH will be supercritical for all values of σ in valleys and for σ ≲ 0.85 on ridges. In the cases where it is subcritical, numerical continuation shows that the interval Δa of coexistence of patterned states and the uniform state for fixed σ is typically ≲3% of the interval of existence for patterned states. We can therefore reasonably approximate the upper bound for the existence of patterns by a_T. The disappearance of the oasis state, consisting of a single pulse of vegetation, occurs through a saddle–node bifurcation (SN_O) at a_O. Numerical continuation of the one-dimensional model shows that, for fixed σ, no other patterned state that bifurcates from the uniform state exists at lower values of a. We therefore take a_O as the lower bound of the range of existence of patterns. The interval for existence of patterns in the one-dimensional models is therefore given by a_O < a < a_T [22,32].

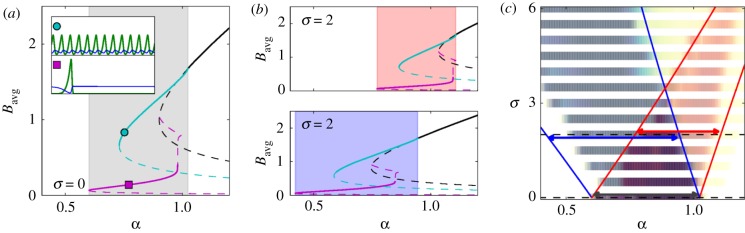
Figure 7a shows the bifurcation diagram computed via numerical continuation [33] for the uniform vegetation branch, TH branch and oasis branch for σ = 0 along with examples of biomass profiles for these two patterned states. We omit other branches with intermediate numbers of vegetation stripes between these two extremes. Since both the ridge and valley models reduce to the original Klausmeier model in one dimension for the σ = 0 case, the grey-shaded region indicates the interval of existence for patterns for both. As σ increases, illustrated by σ = 2 in figure 7b, the bifurcation structure of these states remains qualitatively the same but the interval of existence is shifted to higher precipitation values on ridges and lower precipitation values in valleys. The difference in behaviour here reflects the intuition that more water is available to the vegetation in the valleys than on the ridges. We also note that the ridge patterns exist over a narrower precipitation interval than the valley patterns for fixed channel aspect σ > 0.

Figure 7.

(a) Bifurcation diagram of one-dimensional Klausmeier model given by equations (3.2) and (3.3) showing uniform vegetation state (black) and two of the family of travelling wave solutions that bifurcate from the upper branch of this state: the Turing–Hopf branch (cyan) and the branch corresponding to a single pulse of biomass on the domain (magenta). Stable (unstable) solutions are indicated by thick solid (thin dashed) lines and at least one solution from this family is stable within the interval of a shaded in grey. (b) Bifurcation diagrams for the model with effective water loss rate corresponding to the ridge and valley for σ = 2 are compared to the model with σ = 0. The region shaded red (blue) indicates the existence of stable travelling wave solutions for the model associated with the ridge (valley). (c) Boundaries of predicted regions of existence for ridge (red) and valley (blue) patterns based on one-dimensional models. The results are superimposed on the two-dimensional simulations shown in figure 6a for comparison. These numerical continuation results were computed with AUTO [33], see §3.3 for more details. Parameters: v = 10, m = 0.45, k₀ = 2π/50, L_x = 200. (Online version in colour.)

Figure 7c shows the interval of existence for the one-dimensional ridge (red) and valley (blue) patterns in the (a, σ)-plane, superimposed on the results of our two-dimensional simulations from figure 6a. The lines, indicating birth and death of one-dimensional patterns on ridges and valleys, slightly overestimate the range of patterns in the (a, σ)-plane compared to the full two-dimensional model. This may be due to early transitions between states when noise is added to the numerical simulations or because of interactions between the ridge and valley neglected by the one-dimensional models. We note that for sufficiently small channel aspect σ the existence intervals overlap, and the model predicts states with patterns both on ridges and in valleys. Near σ ≈ 3.5, there is a transition point above which the existence regions for ridge and valley patterns no longer overlap. In this parameter range, the prediction is that patterns may exist in the valleys, with bare ridges, for low precipitation a, or, for higher a, patterns may be confined to the ridges, with uniform vegetation in the valleys.

4. Ridge and valley patterns in Australia, Ethiopia and USA

Our analysis of the topographically extended Klausmeier model suggests that water transport resulting from terrain curvature plays an important role in generating arced vegetation bands. The model predicts that regions with relatively high water availability (represented by the precipitation parameter a in the model) will exhibit vegetation patterns on ridges where water is diverted away, and regions with relatively low water availability will exhibit patterns in valleys where water can accumulate. While we do not expect to be able to make quantitative predictions within Klausmeier's simple modelling framework, we can assess qualitative predictions through observations of vegetation on ridges and in valleys from remote-sensing data. We assume that a given site samples different ridge and valley curvatures with approximately no change in average water availability. We note that, in contrast to the idealized terrain underlying the predictions summarized in figure 6, the height and width associated with adjacent ridges and valleys are rarely equal for real topographies.

Banded vegetation patterns are observed in dryland environments with mean annual precipitation (MAP) ranging from 150 to 800 mm [2]. Factors such as temperature and soil characteristics can strongly influence the amount of water effectively available to plants for growth, so it is useful to characterize water availability by the aridity index (AI), which captures the degree of imbalance between the influx of rainfall and the potential outflux of water due to evaporation and plant transpiration [34]. The sites in Australia considered in §2 (figure 2) have an aridity index of 0.15, falling near the middle of the range where patterns are typically observed (AI = 0.05–0.3) [2]. We discuss the predictions of the topographically extended Klausmeier model in the context of these Australian sites along with two additional sites: the less arid Ft Stockton, USA (AI = 0.19) and the more arid Haud region of Ethiopia (AI = 0.08). Table 2 details locations and water availability characteristics for all three sites.

Table 2.

Banded vegetation sites considered in this study, along with aridity index (AI), potential evapotranspiration (PET) and mean annual precipitation (MAP) values for each site. Values for AI and PET are given by the Global Aridity and PET Database [35] and MAP is computed from the product of these values.

site	continent	coordinates	AI	PET (mm)	MAP (mm)	references
Haud	Africa	(8.00, 47.58)	0.08	1889	144	[5,6,14]
Newman	Australia	(−23.50,119.60)	0.15	1881	278	[27]
Ft Stockton	North America	(31.60,−103.08)	0.19	1676	320	[36,37]

As noted in §2, the majority of vegetation bands at the Australian sites appear on ridges which tend to be oriented convex-downslope. The valleys are largely populated by uniform vegetation cover, and the vegetation bands that do appear within valleys tend to be oriented convex-upslope. In the context of the topographically extended model, the Australian sites therefore appear to fall above the transition point (e.g. a ≈ 0.9 in figure 6) where a wider range of curvatures support ridge patterns than valley patterns but below the upper bound (e.g. a ≈ 1 in figure 6) for the existence of valley patterns at any curvature value.

The region near Ft Stockton, TX, USA [36,37] shown in figure 8 exhibits vegetation bands on the upper left of the image, while the lower right is populated by vegetation organized within what appears to be a network of drainage channels. The bands appear mostly on ridges (oriented convex-downslope) but also in shallow valleys (oriented convex-upslope), as expected by the relatively high aridity index at this site. The series of ridges and valleys within the box displays uniform vegetation cover in the two deeper valleys and patterns in the shallower valleys, with the valley patterns more densely vegetated than the ridge patterns.

Figure 8.

Satellite image (a) and maximum NDVI (b) of a 7 km by 7 km region northwest of Ft Stockton, TX, USA that exhibits vegetation bands on the northwest face (upper left) of a hill. The boxed region shows a 5 km by 2.5 km area with a series of ridges and valleys aligned along the slope. The broad ridge on the right of the box is about 2 km across, measured between the two uniform vegetation valleys, and has a valley-to-ridge elevation gain of about 5 m. Four smaller valleys can also be observed with characteristic transverse width of 300–400 m and transverse elevation changes less than a metre. The mean slope along this northwest face is about 0.6% (approx. 40 m over 6.6 km). The southeast face (lower right) is steeper, with an average grade of about 0.75%, and the vegetation is organized into a network of channels with ridge-to-ridge spacing ranging from 300 m to 800 m and valley-to-ridge depth ranging from 1 m for the narrower channels to 6 m for the larger central channels that the narrower channels feed into. The satellite imagery comes from Sentinel 2 [28] while the elevation comes from the US National Elevation Dataset [38]. The RGB image was chosen from the least cloudy day between October 2016 and May 2017. High (low) values for maximum NDVI at each pixel over the 2 year period May 2015 to May 2017 are shown with green (yellow). (Online version in colour.)

The region in Ethiopia shown in figure 9 is located just east of the site shown in figure 1b. As expected by the relatively low aridity index, vegetation bands are confined to valleys, with sparse vegetation cover on ridges. The elevation contours indicate that the ridges are more sharply curved than the valleys, and the vegetation tends to appear where the grade is relatively low (approx. 0.2–0.3%). The boxed area on the left exhibits banded vegetation, clearly oriented convex-uplsope, within a relatively narrow valley. The boxed area on the right is situated within a broad, relatively flat region. Here, there is neither a consistent trend in the direction of vegetation band arcing, with bands often appearing nearly straight, nor is there a consistent trend in the curvature of the topography. Elevation data with higher spatial resolution may help address whether the processes that set the observed lengths and curvatures of the vegetation arcs in broad flat regions of this type are driven by variation in topography or by other effects.

Figure 9.

Satellite image (a) and maximum NDVI (b) of a 21 km by 10 km region of Ethiopia located just east of the site shown in figure 1b. Two areas within the image are highlighted by boxes. The left is a channel aligned along a overall slope of about 0.2% grade with an approximate ridge-to-ridge distance of 3 km. The vegetation pattern, with bands arcing convex-upslope, appears within a 2 km region surrounding the valley line where the transverse elevation has a 2 m variation from minimum to maximum. The region highlighted on the right is within a broad, relatively flat valley with an overall 0.3% grade and transverse variations of less than 1 m across the 4 km width of the box. The satellite imagery comes from Sentinel 2 [28] while the elevation data are ALOS [39] with spectral smoothing [40]. The RGB image is of the least cloudy day between October 2016 and May 2017 and the NVDI shows maximum value at each pixel over the same time period. (Online version in colour.)

In addition to vegetation patterns, the region shown in figure 9 exhibits two large basins with uniform vegetation cover. While the curvature transverse to the grade is not significantly greater in the basins than in the patterned valleys nearby, these basins are formed from curvature along directions both transverse and parallel to the slope. As the topographically extended model predicts that both curvatures will contribute to the effective decrease in water loss rate, uniform vegetation cover within basins of this type is qualitatively consistent with the model predictions.

5. Conclusion

We have developed an extension to the Klausmeier model for banded vegetation patterns that captures the influence of terrain curvature on water transport. The model simulations indicate a correlation between the arcing-direction of vegetation bands and the sign of curvature of the underlying terrain, consistent with observational evidence from sites in Australia presented in §2, and also early observational studies of patterns in the Horn of Africa [5,6,14]. While the simulated vegetation bands arc in the same direction as the underlying elevation contours in the topographically extended model, they do not always closely match the contours. The model therefore predicts that the bands do not sit transverse to the local gradient everywhere, which has seen some support in observations relating to small-scale (approx. 10 m) disruptions of water flow [37]. Future work to develop a more detailed understanding of the underlying mechanism that sets the magnitude of vegetation band curvature in the topographically extended Klausmeier model as well as in more hydrologically accurate modelling frameworks may provide additional insight into how terrain shapes vegetation patterns via water transport. Reduction to a phase description for the travelling waves [41] may prove to be a useful path towards this goal. The results may also be of interest to band formation in other contexts such as mussel bed patterns, where experiments that test driving forces and explore ecological impacts have been possible [42].

Comparison between the predictions based on the topographically extended model and our observations from Australia, the USA and Ethiopia in §4 shows qualitative agreement with respect to where patterns occur relative to topographic features such as ridges and valleys. Limited simulations of a simplified version of the Gilad model (see electronic supplementary material) indicate that these predictions obtained within the Klausmeier modelling framework (e.g. figure 6) remain qualitatively unchanged by subdividing the water field into surface flow and soil moisture. A more complete understanding of the extent to which results obtained with the highly conceptual Klausmeier model generalize to more hydrologically accurate models is required. Of particular interest are modelling frameworks that can resolve the fast timescales of rainfall events and surface waterflow dynamics, as well as relatively slower vegetation and soil moisture dynamics [43,44]. For instance, similar results regarding the influence of terrain curvature on pattern shape, location and migration speed have been reported by a more mechanistically detailed modelling study [45]. While this detailed model captures the intermittent nature of water input and the possible influence of vegetation patterns on the underlying terrain, its complexity makes it challenging to extract the dominant process by which the topography influences the vegetation patterns.

In this study, we have focused on the role of topography in shaping vegetation bands, but many other mechanisms and environmental heterogeneities are likely to be involved as well. For example, biomass feedback on water transport, boundary effects imposed at the edges of the patterns, spontaneous band break-up and interactions between different species of vegetation may all play an important role in the pattern formation process. Studies in the context of peatland pattern [46,47] provide a template for constructing and probing simple modelling frameworks that can capture other possible mechanisms in order to identify differences in predictions. This could suggest ways to leverage spatial heterogeneity in observational data to help determine dominant mechanisms at play. Exploring currently available data for aspects of the phenomenon that have the potential to exhibit observable differences in response to inhomogeneity can, in turn, inform such future model investigations.

By investigating the arcing direction of vegetation bands within a simple modelling framework and with an appropriately idealized terrain, we have identified a possible link between band curvature and ecosystem fragility. Specifically, our model study suggests that convex upslope vegetation bands, confined to the lower ground of a landscape, may be closer to a collapse under increased aridity stress than convex downslope bands on the higher ground of a gently rolling terrain.

Data accessibility

All data are publicly available [11,28,29,35,38,39].

Authors' contributions

P.G. conceived the modelling approach, carried out the numerical simulations and took the lead in drafting the manuscript. All authors participated in the data analysis and interpretation, contributed to the writing of the manuscript and gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

This work was supported in part by the National Science Foundation grant no. DMS-1440386 to the Mathematical Biosciences Institute (P.G.), National Science Foundation grants DMS-1517416 (M.S.) and DMS-1547394 (K.G.) and the James S. McDonnell Foundation (K.G.).